Trading Experiments using Financial Agents in

a Simulated Cloud Computing Commodity Market

John Cartlidge

Department of Computer Science, University of Bristol

Merchant Venturers Building, Woodland Road, Bristol BS8 1UB, U.K.

Keywords:

Software Agents, Multi-agent Simulation, Auctions, Financial Markets, Cloud Computing, CReST.

Abstract:

In September 2012, Amazon, the leading Infrastructure as a Service (IaaS) provider, launched a secondary

marketplace venue for users to buy and sell cloud resources between themselves—the Amazon EC2 Reserved

Instance Marketplace (ARIM). ARIM is designed to encourage users to purchase more long-term reserved

instances, thus generating more stable demand for the provider and additional revenue through commission on

sales. In this paper, we model ARIM using a multi-agent simulation model populated with zero-intelligence

plus (ZIP) ﬁnancial trading agents. We demonstrate that ARIM offers a new opportunity for market makers

(MMs) to proﬁt from buying and selling resources, but suggest that this opportunity may be ﬂeeting. We also

demonstrate that altering the market mechanism from a retail market (where only sellers post offers; similar

to ARIM) to a continuous double auction (where both buyers and sellers post offers) can result in higher sale

prices and therefore higher commissions. Since IaaS is a multi-billion dollar industry and currently the fastest

growing segment of the cloud computing market, we therefore suggest that Amazon may proﬁt from altering

the mechanism of ARIM to enable buyers to post bids.

1 INTRODUCTION

In recent years, cloud computing has enjoyed a me-

teoric rise that continues to trend. The worldwide

public cloud services market for 2013 has been esti-

mated at $131 billion, with Infrastructure as a Service

(IaaS; estimated at $9 billion) expected to continue

as the fastest growing segment of the market (Gart-

ner, 2013). The largest (and oldest) IaaS provider is

Amazon Web Services (AWS). AWS deliver scalable,

pay-as-you-go compute capacity through their Elas-

tic Cloud Compute (EC2) service. EC2 has three vir-

tual machine (VM) instance tariffs: (1) On-Demand,

pay per hour with no long-term commitment; (2) Re-

served, pay a one-time payment for each instance re-

served and then receive a signiﬁcant discount on the

hourly charge for that instance; and (3) Spot, bid on

unused capacity and run those instances for as long as

the bid exceeds the current spot price, which ﬂuctu-

ates with supply and demand. The reserved instance

(RI) model offers users the cheapest predictable ac-

cess to compute resources, and beneﬁts the provider

by offering more predictable revenue and resource de-

mand. However, since RIs are sold with terms of ei-

ther 12-months or 36-months, to efﬁciently utilise this

option users must be able to accurately forecast their

personal demand over the (relatively long) lifetime of

the instance. As a result, many users opt for the less

risky on-demand model, which makes resource and

revenue planning more difﬁcult for the provider.

To overcome this, in September 2012, AWS

launched a secondary marketplace venue for cloud

users to re-sell unwanted time (in whole months) re-

maining on RIs; thereby making RI purchases more

ﬂexible and hence less risky for users. For instance, a

user predicting high sustained demand over the next

two months may purchase a 12-month reserved in-

stance from the provider, and then re-sell the remain-

ing 10 months on ARIM once the RI is no longer

needed. Alternatively, if a RI with 2-months remain-

ing is available on ARIM, then the user can purchase

the exact time required. Therefore, as long as ARIM

is a liquid market—such that it is easy for a seller

to ﬁnd a buyer and vice versa—then much of the

risk involved in purchasing RIs is removed. As a

result, more users gain access to the cheaper RI tar-

iff, while the provider beneﬁts from more predictable

demand (i.e., the ratio of RI to on-demand sales in-

creases). Further, the provider also generates addi-

tional revenue by charging sellers a commission (cur-

311

Cartlidge J..

Trading Experiments using Financial Agents in a Simulated Cloud Computing Commodity Market.

DOI: 10.5220/0004925303110317

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 311-317

ISBN: 978-989-758-016-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

rently 12%) on all ARIM transactions.

ARIM is likely to have signiﬁcantly impacted

the dynamics of the market for cloud computing re-

sources. To investigate this potential impact, we

present a multi-agent simulation model of ARIM us-

ing CReST, the Cloud Research Simulation Toolkit

(Cartlidge & Cliff, 2013). Agents have intrinsic de-

mand for cloud resources, which is satisﬁed either

by purchasing directly from the provider (on-demand

or reserved) or via the secondary market (reserved).

To model ﬁnancial trading behaviour, agents use the

zero-intelligence plus (ZIP) pricing algorithm (Cliff

& Bruten, 1997) to trade on the secondary market.

We demonstrate that ARIM offers an opportunity

for market makers (MMs)—speculators with no in-

trinsic desire for a commodity—to buy and sell re-

sources for proﬁt. However, we estimate that this

opportunity will be ﬂeeting—as the market becomes

more liquid, the average price of a resource will fall

too low for a MM to proﬁt. We also demonstrate that

if the market mechanism of ARIM is changed from a

retail market, where sellers post offers to sell and buy-

ers stay silent, to a continuous double auction, where

buyers can also post offers to buy, then the market

dynamics are signiﬁcantly altered. In particular, we

demonstrate that a continuous double auction is likely

to generate more commission for the provider. Given

that ARIM is operated by the largest provider in a

multi-billion dollar industry, this result could have

signiﬁcant commercial impact.

This paper is organised as follows. In Section 2 we

review the literature on ﬁnancial markets and trading

agents, before describing our experimental method in

Section 3. In Section 4 we present results from a se-

ries of experiments investigating the impact of market

mechanism and MMs on market dynamics. Conclu-

sions are drawn in Section 5.

2 BACKGROUND

2.1 Cloud Computing

Cloud computing is the latest step-change in the de-

livery of computing services, offering on-demand net-

work access to a shared pool of conﬁgurable com-

puting resources. By accessing shared resources,

cloud users reduce costs associated with managing

hardware and software, while beneﬁtting from the

economies of scale enjoyed by ultra-large scale cloud

providers (Hayes, 2008; Mell & Grance, 2011).

The term “cloud computing” encapsulates both

the applications delivered “as a Service” and the un-

derlying hardware and software infrastructure located

in ultra-large scale data centres that make the con-

cept viable (Armbrust, Fox, Grifﬁth, Joseph, Katz,

Konwinski, Lee, Patterson, Rabkin, Stoica, & Za-

haria, 2009). This infrastructure is commonly known

as a cloud and can be public (available to all, at a

cost), private (owned by an organisation and accessi-

ble only to members), or a hybrid of the two; while a

cloud service application delivered to end users is of-

ten referred to as Software as a Service (SaaS), Plat-

form as a Service (PaaS), or Infrastructure as a Ser-

vice (IaaS), depending on which level of the software

stack is provided. SaaS describes high-level end user

applications that are accessed remotely over the in-

ternet and includes ubiquitous software applications

such as GoogleMail, Facebook, and Twitter. IaaS de-

scribes lower-level applications that offer users access

to the underlying cloud hardware via a virtualisation

layer. Typically, for IaaS, users purchase Virtual Ma-

chine (VM) instances that are installed with a user se-

lected operating system (OS) and offer access to vir-

tual CPU, RAM, and hard disk storage. These VMs

can then be conﬁgured by the user to provide the spe-

ciﬁc functionality required. From the user’s perspec-

tive, accessing a VM instance in the cloud is equiva-

lent to remote accessing their own physical hardware.

Finally, at the intermediate level, PaaS offers a suite of

software libraries and interfaces—a platform—upon

which users can build and integrate their own soft-

ware applications. However, for clarity, in this paper,

when we consider cloud resources, we refer to IaaS

VM instances and not the higher-level software appli-

cations (Facebook, Twitter, etc.) that are built on top.

The on-demand delivery model for cloud com-

puting resources offers a variety of beneﬁts for busi-

ness consumers: the ability to start and stop VM in-

stances when required affords ﬂexibility and scale-out

opportunities; no up-front capital expenditure on (of-

ten under-utilised) compute infrastructure needed to

cover peak business demand increases efﬁciency; and

outsourcing maintenance and support reduces costs

(Armbrust et al., 2009). However, the on-demand

model is not necessarily ideal for cloud providers, as

they attempt to adhere to strict Service Level Agree-

ments in the face of ﬂuctuating demand. If providers

could accurately forecast future resource demand,

then they would have the opportunity to reduce costs

by optimising electricity purchases, engineering staff,

and hardware utilisation, etc. (Rogers & Cliff, 2013).

Unlike on-demand VM instances that can be started

and stopped by users with no warning, long-term RIs

offer providers an opportunity for capacity planning.

For this reason, AWS have introduced ARIM—a sec-

ondary marketplace for users to buy and sell RIs be-

tween themselves. This introduction increases the

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

312

ﬂexibility of RIs and is designed to increase their rel-

ative popularity.

2.2 Continuous Double Auction

An auction is a mechanism whereby sellers and buy-

ers come together and agree on a transaction price.

Many different auction mechanisms exist, each gov-

erned by a different set of rules. In this paper, we

focus on the Continuous Double Auction (CDA), the

most widely used auction mechanism and the one

used to control all the world’s major ﬁnancial ex-

changes. The CDA enables buyers and sellers to

freely and independently exchange quotes at any time.

Transactions occur when a seller accepts a buyer’s

“bid”, or when a buyer accepts a seller’s “ask”. Al-

though it is possible for any seller to accept any

buyer’s bid, and vice versa, it is in both of their inter-

ests to get the best deal possible at any point in time.

Thus, transactions execute with a counter party that

offers the most competitive quote.

Many CDAs utilise an “orderbook” to match

counterparties for execution. The orderbook is an or-

dered list of all bids (in price descending order) and

an ordered list of asks (in ascending order). The best

bid and ask at any given time are the current high-

est bid and the lowest ask. If a new bid (ask) enters

the orderbook at a price higher (lower) than the best

ask (bid), it will immediately execute against it at the

price of the ask (bid). If the bid (ask) has a value lower

(higher) than the best ask (bid), then it will enter the

orderbook and remain in the list of bids (asks). If the

orderbook is visible, then traders are able to see the

price and volume available at any given time.

The auction design of ARIM allows sellers to post

asks at any time. These asks are ordered by price (as-

cending) and visible to all market participants. Thus,

ARIM can be considered as equivalent to the ask-side

of a standard orderbook. However, ARIM contains no

equivalent of an orderbook’s bid-side. That is, there is

no stored list of bids. At any time, a buyer can choose

to accept (execute against) an ask that is displayed,

but a buyer cannot post a bid offer that is lower than

the best ask price. Therefore, buyers cannot advertise

their willingness to trade. We describe this kind of

auction as a “retail” market.

Vernon Smith (1962) explored the dynamics of

CDA markets in a series of Nobel Prize winning

experiments using small groups of human partici-

pants. Smith showed that markets quickly tended to-

wards the theoretical equilibrium price (the price at

which the quantity demanded equals the quantity sup-

plied). However, when Smith explored a variation

on the CDA where only sellers could post asks (a

retail market), he showed that the experimental mar-

ket tended to a price lower than the theoretical equi-

librium. Smith suggested that this may have been a

result of irrational human behaviour. However, in a

series of experiments designed to replicate Smith’s

work, but using artiﬁcial trading agents (the ZIP trad-

ing algorithm; see below) rather than humans, Dave

Cliff was able to repeat Smith’s result. Once again,

retail markets tended to a price lower than the market

equilibrium (Cliff & Bruten, 1997, pp. 49-55). How-

ever, since there were no humans in the market (only

software trading agents), this time the result could not

be attributed to human behaviour.

In this paper, we model ARIM using a popula-

tion of ZIP trading agents and investigate the effect

of altering the market structure of ARIM from a retail

market (where the orderbook contains only asks) to

a CDA (where the orderbook contains both bids and

asks). Given the results independently achieved by

Smith using a population of humans, and Cliff using a

population of trading agents, we may expect the price

of cloud resources to be lower in a retail market than

a CDA market. We test this in Section 4. However,

ﬁrst, we introduce the ZIP algorithm.

2.3 Zero-Intelligence Plus (ZIP)

ZIP agents are proﬁt-driven traders that adapt using

a simple learning mechanism: adjust proﬁt margins

based on the price of other bids and offers in the mar-

ket, and decide whether to make a transaction or not.

When a decision to raise or lower a ZIP trader’s proﬁt

margin is taken, ZIP modiﬁes the value using market

data and an adaptation rule based on the Widrow and

Hoff (1960) “delta” rule (for full details of the ZIP

algorithm, refer to Cliff & Bruten, 1997, pp. 41-45).

The ZIP strategy has become a popular bench-

mark for CDA experiments. In their IBM study, Das,

Hanson, Kephart, and Tesauro (2001) concluded that

ZIP was a dominant strategy, beating humans in ex-

perimental trials and matching the performance of

their own modiﬁed GD (Gjerstad & Dickhaut, 1998)

algorithmic trader. ZIP has since been used in many

experimental economics papers (for a detailed litera-

ture review, see De Luca, Szostek, Cartlidge, & Cliff,

2011), and has been modiﬁed in many studies to ac-

commodate different market designs (for a review, see

Stotter, Cartlidge, & Cliff, 2013).

However, in the majority of studies, ZIP traders

are designated as either “buyers” or “sellers” and are

presented with a series of assignments to trade; for

example “buy one unit of stock at price no more than

$200”. This process inherits directly from Smith’s

original behavioural economics experiments (Smith,

TradingExperimentsusingFinancialAgentsinaSimulatedCloudComputingCommodityMarket

313

1962) and is equivalent to ZIP acting as a “Sales

Trader”—that is, executing orders on behalf of some-

body else. One notable exception to this is a Master’s

thesis study that enabled ZIP traders to act as elec-

tronic arbitrageurs (i.e., to buy and sell on their own

behalf for proﬁt) to investigate the role of arbitrage in

equilibrating trade prices across segmented markets

(van Montfort, Bruten, & Rothkrantz, 1997).

In this study, we also allow ZIP traders to buy

and sell on their own behalf. Each trader contains a

ZIP pricer for pricing bids and a separate ZIP pricer

for pricing asks. Within the population, traders have

intrinsic demand for cloud resources (i.e., they are

cloud users). Each month, traders can either buy re-

sources (RIs, or on-demand instances) directly from

the provider, or trade RIs on ARIM. While most

traders are only concerned with buying and selling re-

sources to fulﬁl their intrinsic demand, we open the

possibility for traders to buy and sell RIs even when

they don’t have demand. Such traders can be consid-

ered as “market makers” (MMs)—that is, they aim to

buy low and sell high to gain a proﬁt and have no in-

trinsic demand for the underlying commodity. We use

this model to investigate the impact that MMs have

on the dynamics of ARIM, and under what conditions

market making offers a proﬁtable opportunity.

3 EXPERIMENTAL METHOD

The Cloud Research Simulation Toolkit (CReST) was

developed at the University of Bristol to address the

need for a robust simulation modeling tool for re-

search and teaching of data center management and

cloud provision. CReST is a stand-alone application,

written in Java, and is freely available open source

under a GNU General Public License v3.0 (CReST,

2013). For details on the architecture of CReST, re-

fer to Cartlidge and Cliff (2013). All code used to

run experiments reported in this paper is available to

download in CReST version 0.5.0 (CReST, 2013).

For the experimental model, we have a population

of trading agents (size P), a cloud provider, a market-

place for trading RIs, and two types of cloud resource:

RIs (with m-month term) and on-demand. The mar-

ketplace has two design settings: CDA, which con-

tains a full orderbook; and retail, in which the or-

derbook contains only sellers’ asks. Each month, a

proportion of traders, D, is given a unit of demand

for a cloud resource. To satisfy their demand, traders

can either purchase resources in the marketplace, or

purchase directly from the provider. A trader that

purchases an on-demand instance from the provider

is forced to use that instance immediately (to satisfy

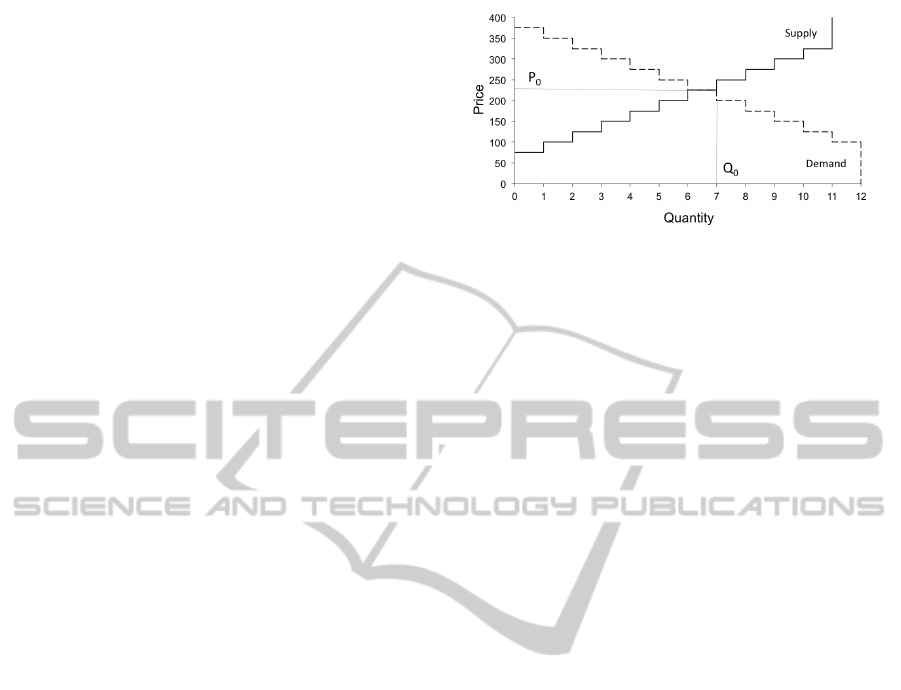
Figure 1: Supply and Demand.

their demand). However, a trader that purchases a RI

can either: use the ﬁrst month to satisfy demand and

then resell the remaining m − 1 months in the market-

place; use the ﬁrst month to satisfy demand and then

continue to use the RI in subsequent months to satisfy

further demand; or sell the entire m-months term of

the RI in the marketplace without ever using it. We

consider traders that only ever buy RIs to resell in the

marketplace (i.e., traders that never have intrinsic de-

mand) as market makers. To trade in the marketplace,

each trader has an internal ZIP engine for pricing bids

and a separate internal ZIP engine for pricing asks

(using the same parameters as Cliff & Bruten, 1997,

p. 45). We run the model for a ﬁxed number of months

and collect statistics each month on the traders’ prof-

its and loss, the provider’s balance sheet and inventory

of sales, and the sequence of trades that execute in the

marketplace.

In the following section, we present results from

a series of experiments. In particular, we investigate:

(1) the effect of the marketplace design, i.e., CDA or

retail; and (2) the impact of market makers. Each ex-

perimental condition is repeated 30 times, with mean

values recorded for each run. Following the Central

Limit Theorem, with 30 observations the mean ap-

proximately follows a Normal distribution. There-

fore, 95% conﬁdence intervals can be calculated and

plotted. Where conﬁdence intervals do not overlap,

then results are signiﬁcant at the 0.05 level.

4 RESULTS

4.1 Retail versus CDA

To observe the effect of changing the market design

from CDA to retail, here we perform a strict repli-

cation of Cliff’s retail market ZIP trader experiments

(Cliff & Bruten, 1997, pp. 49-55), which were them-

selves a replication of Smith’s retail market human

trader experiments (Smith, 1962). We model a set

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

314

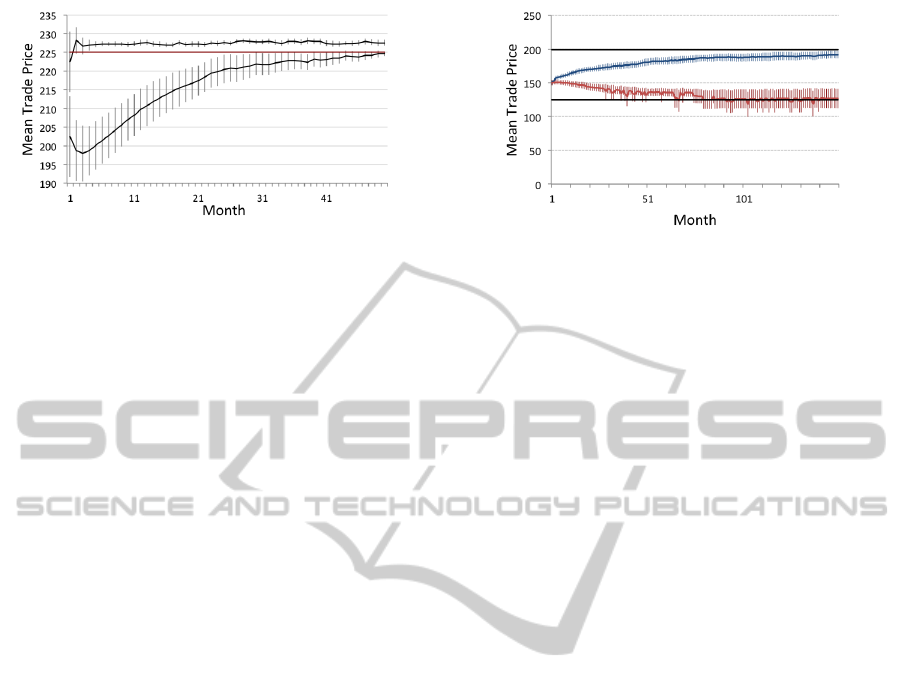
Figure 2: Mean monthly trade prices (30 runs; ±95% con-

ﬁdence interval). The red line plots P

= 225. In the CDA

market (top line), prices quickly stabilise within 1% of P

In the retail market (bottom line), prices are initially 10%

below P

before asymptotic convergence to P

of 12 buyers and 11 sellers, each with a unique limit

price (the maximum bid price, or minimum ask price)

to trade. Here, we do not allow traders to trade on

their own behalf, i.e., there are no MMs. Each month,

buyers are issued with one unit of demand and sellers

are issued with one RI to sell, with each trader always

having the same limit price. Figure 1 presents the

supply and demand curves for the market (identical

to Smith, 1962, p. 21). These curves plot the quantity

demanded and quantity supplied at every price point

(the limit prices of traders). The theoretical market

equilibrium is the point where the two curves inter-

sect, that is: (Q

) = (7,225). Therefore, if the

market equilibrates, we expect 7 RIs to trade each

month at a value of $225.

Figure 2 plots mean monthly trade price for both

markets. In the CDA market (top-line), we see

that prices approach equilibrium (P

= 225; red line)

within the ﬁrst few months and then stabilise approx-

imately 1% above equilibrium (this elevation may be

caused by a bias in the conversion of real-valued proﬁt

margins to integer-valued order prices, but this re-

quires further investigation). In contrast, for the retail

market (bottom-line), we see prices are initially 10%

below equilibrium, before steadily converging on P

around month 50. Interestingly, this behaviour has

qualitative similarity with the early human trader ex-

periments, where Smith concluded: “that markets in

which only sellers competitively publicize their offers

tend to operate to the beneﬁt of buyers at the expense

of sellers” (Smith, 1962, p.22). Results are also quali-

tatively similar to those of Cliff’s 10 period retail mar-

ket experiments, where mean price was consistently

below $200, but steadily rising each month (Cliff &

Bruten, 1997, p. 52). Had Cliff run his experiment

for longer, it is likely that he would have achieved the

same result.

It is clear from these results that the retail mar-

Figure 3: Mean monthly trade prices (30 runs; ±95% conﬁ-

dence interval) in a market where only MMs sell on ARIM.

The CDA market (blue) converges to D

buy

= 199, while the

retail market (red) converges to M

sell

= 125.

ket design is less efﬁcient than the CDA design—

although the retail market eventually converges to

equilibrium, during the time that the market is trad-

ing away from equilibrium, there are inefﬁciencies in

the market that can be exploited. For this reason, in

the following experiments, we investigate the impact

of MMs that attempt to proﬁt from inefﬁciencies in

the market.

4.2 Market Makers

Here, we create a simpliﬁed model of ARIM. We

assume that on-demand instances cost P

= $200

per month and RI instances have a term of 2 months

and cost P

= $250 per unit (and therefore cost

/month = $125 when fully utilised). Each month,

traders have unit demand with probability 0.5. There-

fore, on average, half the population of traders are is-

sued with one unit of demand; we call these traders

“demand traders”. Demand traders are prepared to

buy a one-month RI on ARIM for a maximum limit

price of D

buy

= $199 (i.e., one dollar less than P

). If

a demand trader does not purchase on ARIM, the unit

demand for the month can be satisﬁed by purchas-

ing either an on-demand resource (with probability

p(od), or a 2-month RI (with probability 1 − p(od)).

If the demand trader purchases a 2-month RI, then

the following month the RI can be used to satisfy

next months demand (occurring with probability 0.5).

If the demand trader has no demand the following

month, the trader can sell the remaining month on

ARIM. On such occasions, the demand trader sets a

sell limit price of D

sell

= $50, i.e., the marginal dif-

ference between P

and P

. The model also con-

tains MM traders that each purchase RIs at the start

of each month and then immediately attempt to re-

sell them on ARIM over the following two months.

MMs set a sell limit price of M

sell

= $125, i.e., equal

to P

/month.

TradingExperimentsusingFinancialAgentsinaSimulatedCloudComputingCommodityMarket

315

Figure 3 shows mean monthly trade price for

a market in which only MMs sell on ARIM—i.e.,

p(od) = 1.0, so no demand traders select to purchase

RIs from the provider. The population contains 50

agents and therefore mean demand each month is 25.

There is one MM in the population. The MM ini-

tially purchases i

t=0

= 10 RIs each month (and there-

fore, from the second month onwards can sell 20 re-

sources on ARIM). Each month, the MM updates i

following a simple rule—if all units were sold this

month, then next month i

t+1

= i

+ 0.2, else i

t+1

− 0.2. In this way, the MM attempts to balance

supply of RIs on ARIM to fulﬁl population demand.

Since the demand each month ﬂuctuates (with con-

stant mean=25), the MM sometimes has over-supply

and sometimes has under-supply. Therefore, the equi-

librium price in the market ﬂuctuates rapidly between

= D

buy

= 199 (when MM supply is less than de-

mand) and P

= M

sell

= 125 (when MM supply is

greater than demand). When demand exactly equals

supply, P

= 162. Figure 3 shows the mean monthly

trade price in a retail market (red) and a CDA mar-

ket (blue). In retail markets, mean trade price con-

verges to P

= M

sell

= 125. At this price, the MM

no longer makes a proﬁt on each unit traded. How-

ever, in the CDA market, mean trade price converges

to P

= D

buy

= 199. At this price, the MM makes a

proﬁt of $74 per unit sold. This is a striking result.

We can explain this by considering the sensitivity of

retail markets to oversupply. As shown in Figure 2,

and concluded by Smith (1962), retail markets “oper-

ate to the beneﬁt of buyers”. As such, each month

the MM oversupplies the market, the market has a

stronger downwards movement than the correspond-

ing upwards movement when the MM undersupplies

the market. Therefore, despite the MM continually

trying to balance supply and demand, prices continue

to fall until there is no marginal proﬁt on each unit

of trade. In contrast, the CDA market does not react

more strongly to oversupply than undersupply. There-

fore, using the same update rule on supply, the MM

does not force down prices and by marginally under-

supplying the market is able to continue to proﬁt from

each trade. This demonstrates that a change in market

mechanism can lead to a radical divergence in mean

market price.

In the previous experiment, ARIM sellers were all

MMs. In reality, however, we expect demand traders

to make use of ARIM. To model this behaviour, we

repeat the previous experiment but this time allow

demand traders to purchase RIs. At the start of the

run, p(od) = 1.0, but is then reduced each month

by 0.025 (purposely chosen to be an order of mag-

nitude smaller than the responsiveness, δi = 0.2, of

Figure 4: Mean monthly trade prices (30 runs; ±95% con-

ﬁdence interval) in a retail (red) and CDA (blue) ecology.

the MM). Initially, therefore, no demand traders are

re-selling on ARIM. However, more demand traders

are attracted to ARIM each month. By month 100,

a quarter of demand traders are re-selling on ARIM,

and by month 200 half of all demand traders are re-

selling on ARIM. There is only one MM, set to ini-

tially purchase i

t=0

= 5 RIs per month (each month

t+1

= i

+ 0.2 if all RIs sold, else i

t+1

= i

− 0.2).

Thus, the market initially has excess demand.

Figure 4 plots mean trade prices in a retail ecol-

ogy (red) and a CDA ecology (blue). We see that

there are three distinct phases. Initially, the excess de-

mand for RIs on ARIM leads to a price increase. This

encourages the MM to supply more RIs on ARIM,

which drives the price lower, eventually converging

on M

sell

= 125. At this point, the MM no longer

makes a proﬁt on each unit traded. During the second

phase, the market price remains stable at M

sell

= 125.

During this period, the MM gradually reduces supply

and at the same time there is an increase in demand

traders re-selling RIs on ARIM. For demand traders,

selling under utilised RI capacity for $125/month is

attractive, since this is greater than D

sell

= $50, the

marginal monthly unit cost of an RI to a demand

trader. Eventually, there are so many demand traders

re-selling on ARIM that the market enters the third

stage around month 200. At this point supply on

ARIM exceeds demand and the price falls once again,

eventually converging on D

sell

= $50. During this

phase the price is too low for the MM to proﬁt and

the MM leaves the market entirely. Note, however,

that although the phases are qualitatively similar in

both ecologies, during phase 1 and phase 3, the CDA

market (blue) trades at consistently higher prices than

the retail market (red). This demonstrates that when

the market is not at equilibrium saturation (i.e., when

there is not a prolonged over-supply) then the CDA

market will trade at higher prices than the retail mar-

ket. We present this as evidence that it may be beneﬁ-

cial (in terms of commission revenue) for Amazon to

alter the design of ARIM from a retail to a CDA.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

316

5 CONCLUSIONS

We have presented a simple multi-agent based simul-

tation model of the Amazon EC2 Reserved Instance

Marketplace (ARIM); a secondary market venue for

trading cloud computing resources. Within the sim-

ulation model, a population of zero-intelligence plus

(ZIP) ﬁnancial trading agents buy and sell resources

in the market. Some traders act as market makers

(MMs), such that they buy resources for the sole pur-

pose of re-selling for proﬁt. Other traders are “de-

mand traders” that have intrinsic demand for cloud

resources and utilise the secondary market only to

buy resources at a cheaper price than offered by the

provider, or to ofﬂoad underutilised resources that

have previously been bought. ARIM is a “retail” mar-

ketplace, where only sellers can advertise prices; un-

like a continuous double auction (CDA), where both

buyers and sellers can advertise their desire to trade

at any time. We have demonstrated that retail mar-

kets can produce lower trade prices than a CDA and

conclude that Amazon may increase commission on

sales if they alter the mechanism of ARIM from a re-

tail market to a CDA. Given that the market for cloud

resources is a multi-billion dollar industry, even small

increases in commission could equate to signiﬁcant

proﬁt. On the evidence presented here, we suggest

that this is what Amazon should do. Finally, we have

demonstrated that ARIM has opened an opportunity

for MMs to proﬁtably enter the market. However, as

ARIM becomes more popular, this opportunity will

disappear.

ACKNOWLEDGEMENTS

This work was supported by EPSRC grant number

EP/H042644/1.

REFERENCES

Armbrust, M., Fox, A., Grifﬁth, R., Joseph, A. D., Katz,

R., Konwinski, A., Lee, G., Patterson, D., Rabkin,

A., Stoica, I., & Zaharia, M. (2009). Above the

clouds: A berkeley view of cloud computing. Tech.

rep. EECS-2009-28, University of California, Berke-

ley.

Cartlidge, J., & Cliff, D. (2013). Comparison of cloud mid-

dleware protocols and subscription network topolo-

gies using CReST, the cloud research simulation

toolkit. In Desprez, F., Ferguson, D., Hadar, E.,

Leymann, F., Jarke, M., & Helfert, M. (Eds.),

3rd Int. Conf. Cloud Computing & Services Sci-

ence (CLOSER-2013), pp. 58–68 Aachen, Germany.

SciTePress.

Cliff, D., & Bruten, J. (1997). Minimal-intelligence agents

for bargaining behaviours in market-based environ-

ments. Tech. rep. HPL-97-91, Hewlett-Packard

Labs.

CReST (2013). CReST - the Cloud Research Simulation

Toolkit. [Online] https://sourceforge.net/projects/

cloudresearch/ [retrieved: Oct, 2013].

Das, R., Hanson, J., Kephart, J., & Tesauro, G. (2001).

Agent-human interactions in the continuous double

auction. In Nebel, B. (Ed.), 17th Int. Joint Conf. Art.

Intell. (IJCAI-01), pp. 1169–1176. Morgan Kauf-

mann.

De Luca, M., Szostek, C., Cartlidge, J., & Cliff, D. (2011).

Studies of interactions between human traders and

algorithmic trading systems. The Future of Com-

puter Trading in Financial Markets–Foresight Driver

Review–DR13. Crown Copyright.

Gartner (2013). Gartner says worldwide public cloud

services market to total $131 billion: Iaas con-

tinues as fastest-growing market segment. http://

www.gartner.com/newsroom/id/2352816.

Gjerstad, S., & Dickhaut, J. (1998). Price formation in dou-

ble auctions. Games and Economic Behavior, 22(1),

1–29.

Hayes, B. (2008). Cloud computing. Communications of

the ACM - Web Science, 51(7), 9–11.

Mell, P., & Grance, T. (2011). The NIST deﬁnition of

cloud computing. Tech. rep. NIST Special Publi-

cation 800-145, National Institute of Standards and

Technology, U.S. Department of Commerce.

Rogers, O., & Cliff, D. (2013). Contributory provision

point contracts—a risk-free mechanism for hedging

cloud energy costs. Journal of Cloud Computing:

Advances, Systems and Applications, 2(10).

Smith, V. (1962). An experimental study of comparative

market behavior. J. Political Economy, 70, 111–137.

Stotter, S., Cartlidge, J., & Cliff, D. (2013). Exploring

assignment-adaptive (ASAD) trading agents in ﬁ-

nancial market experiments. In Filipe, J., & Fred,

A. L. N. (Eds.), 5th Int. Conf. on Agents & Artiﬁ-

cial Intelligence, Vol. 1 - Agents (ICAART-2013), pp.

77–88 Barcelona, Portugal. SciTePress.

van Montfort, G. P. R., Bruten, J., & Rothkrantz, L. (1997).

Arbitrageurs in segmented markets. Tech. rep. HPL-

97-120, Hewlett-Packard Labs.

Widrow, B., & Hoff, Jr., M. E. (1960). Adaptive switching

circuits. Inst. Radio Engineers, Western Electron.

Show and Conv. (IRE WESCON), Conv. Rec., 4, 96–

104.

TradingExperimentsusingFinancialAgentsinaSimulatedCloudComputingCommodityMarket

317