Combining Simulated Annealing and Monte Carlo Tree Search for

Expression Simpliﬁcation

Ben Ruijl

1,2

, Jos Vermaseren

, Aske Plaat

and Jaap van den Herik

Tilburg University, Tilburg center for Cognition and Communication, Warandelaan 2, 5037 AB Tilburg, The Netherlands

Nikhef Theory Group, Science Park 105, 1098 XG Amsterdam, The Netherlands

Keywords:

MCTS, Simulated Annealing, UCT, SA-UCT, Horner Schemes, Common Subexpression Elimination.

Abstract:

In many applications of computer algebra large expressions must be simpliﬁed to make repeated numerical

evaluations tractable. Previous works presented heuristically guided improvements, e.g., for Horner schemes.

The remaining expression is then further reduced by common subexpression elimination. A recent approach

successfully applied a relatively new algorithm, Monte Carlo Tree Search (MCTS) with UCT as the selection

criterion, to ﬁnd better variable orderings. Yet, this approach is ﬁt for further improvements since it is sensi-

tive to the so-called “exploration-exploitation” constant C

and the number of tree updates N. In this paper we

propose a new selection criterion called Simulated Annealing UCT (SA-UCT) that has a dynamic exploration-

exploitation parameter, which decreases with the iteration number i and thus reduces the importance of explo-

ration over time. First, we provide an intuitive explanation in terms of the exploration-exploitation behavior

of the algorithm. Then, we test our algorithm on three large expressions of different origins. We observe that

SA-UCT widens the interval of good initial values C

where best results are achieved. The improvement is

large (more than a tenfold) and facilitates the selection of an appropriate C

1 INTRODUCTION

In High Energy Physics (HEP) expressions with mil-

lions of terms arise from the calculation of processes

described by Feynman diagrams. Typically, these ex-

pressions have to be numerically integrated to predict

cross sections and particle decays in collision pro-

cesses. For example, in the Large Hadron Collider

in CERN such calculations were essential to conﬁrm

the likely existence of the Higgs boson.

In order to predict the effects of currently undis-

covered particles and to improve the accuracy of cur-

rent HEP models, higher-order loop corrections are

needed, causing the size of the expressions to grow

exponentially. The intermediate forms of these ex-

pressions may often take terabytes of disk space.

Novel approaches are required to simplify these ex-

pressions to make evaluation feasible.

To simplify expressions Horner schemes and com-

mon subexpression elimination (CSEE) may be used.

Horner’s rule for simplifying expressions goes back

to 1819 (Horner, 1819). CSEE is commonly used in

compiler construction (Aho et al., 1988). In (Kuipers

et al., 2013a) the ﬁrst application of MCTS for ﬁnd-

ing a better variable ordering was presented, using

UCT (Kocsis and Szepesv

ari, 2006a) as the selection

criterion (see section 3). The MCTS performance is

sensitive to the choice of three parameters: C

, N, and

R. C

is the constant that governs the exploration-

exploitation choices of the algorithm, N is the num-

ber of tree updates, and R is the number of times the

MCTS is repeated. At the previous ICAART con-

ference the sensitivity to C

and N was presented

(van den Herik et al., 2013b). At CCIS/BNAIC the

sensitivity to R was recognized (van den Herik et al.,

2013a; Kuipers et al., 2013b). We believe that the

practical applicability of the algorithm will improve

as the sensitivity to these parameters is harmonized.

This paper focuses on C

. We modify the UCT

formula by introducing an exploration-exploitation

parameter T (i), which decreases with the current it-

eration number i, effectively making the constant C

a variable T (i). As a result, the ﬁrst iterations will be

explorative and throughout the search, the child se-

lection will gradually become more exploitative, fa-

voring optimizing a local minimum over exploration.

The parameter T is similar to the role of the temper-

ature in simulated annealing (hence the name T ). We

refer to the new formula as Simulated Annealing UCT

(SA-UCT).

We have tested our algorithms on three large ex-

pressions of different origins and we observed that

SA-UCT widens the interval of good initial temper-

atures T (0), where the number of operations is near

724

Ruijl B., Vermaseren J., Plaat A. and van den Herik J..

Combining Simulated Annealing and Monte Carlo Tree Search for Expression Simpliﬁcation.

DOI: 10.5220/0004925707240731

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 724-731

ISBN: 978-989-758-015-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

the global minimum, by more than a tenfold for all

three test expressions.

The paper is structured as follows. Section 2 pro-

vides a background and related work on expression

simpliﬁcation and MCTS. Section 3 presents our new

selection criterion called SA-UCT. Section 4 shows

our measurement results. Section 5 presents the con-

clusion and section 6 gives an outlook on future work.

2 BACKGROUND

Numerous methods for simplifying expressions have

been proposed. Here we mention Horner schemes

(Knuth, 1997), common subexpression elimination

(Aho et al., 1988), Breuer’s growth algorithm for sys-

tems of expressions (Breuer, 1969), and partial syn-

tactic factorization (Leiserson et al., 2010). In this

paper we focus on two of these: Horner schemes and

common subexpression elimination.

2.1 Horner Schemes

One elementary method of reducing the number of

multiplications in an expression is based on Horner’s

rule (Horner, 1819; Knuth, 1997; Ceberio and

Kreinovich, 2004). Horner’s rule is straightforwardly

lifting a variable outside brackets. For multivari-

ate expressions Horner’s rule can be applied multi-

ple times, once for each variable. The order of the

extracted variables is called a Horner scheme. For ex-

ample:

+ x

y + x

z ⇒ x

(y + x(y

+ z)) (1)

By twice extracting the variable x (i.e., x

and x), the

number of multiplications is reduced from 9 to 4. The

number of additions remains the same, which is a gen-

eral property of Horner schemes.

In multivariate expressions with n variables, there

are n! ways of extracting variables. For example, the

above expression could also be transformed to

z + y(x

(1 + xy)) (2)

by ﬁrst extracting y and then x. Using this scheme, we

have 7 multiplications left. Thus, this Horner scheme

is inferior to the ﬁrst one.

The problem of selecting an optimal ordering is

NP-hard (Ceberio and Kreinovich, 2004). A heuristic

that works reasonably well is to select the variables

according to their frequency of occurrence (“occur-

rence order”), see e.g., (Kuipers et al., 2013a). How-

ever, this does not always yield good results, also not

when combined with common subexpression elimi-

nation (see below).

b +

a e

Figure 1: A common subexpression (shaded) in a commu-

tative and associative tree.

2.2 Common Subexpression

Elimination

A way to reduce the number of operations even fur-

ther is to perform a common subexpression elimina-

tion (CSEE). This strategy is well known in the ﬁeld

of compiler construction (Aho et al., 1988). CSEE

creates new symbols for each subexpression that ap-

pears twice or more. Consequently, the subexpression

has to be computed only once. Figure 1 shows an ex-

ample of a subexpression in a tree representation.

We note that there is an interplay between Horner

and CSEE in the following example:

sin(x) + cos(x) + sin(x)x + cos(x)x =

sin(x) + cos(x) + x(sin(x) + cos(x)) =

T + xT

Most practical methods of detecting common subex-

pressions will not ﬁnd sin(x) + cos(x) as a subexpres-

sion in the ﬁrst line, whereas in the second line it is

detected. Hence, we observe that Horner schemes can

expose common subexpressions.

2.3 Monte Carlo Tree Search

Because there is an interplay between Horner

schemes and CSEE, a trade-off exists between (1) se-

lecting the optimal Horner scheme that most reduces

the number of multiplications and (2) selecting the

Horner scheme that exposes the maximum number of

CSEs. The contrast is between (1) a Horner scheme

that reduces many multiplications, but has few CSEs,

and (2) an average Horner scheme that exposes many

CSEs. Category (2) would probably reduce the num-

ber of operations more than category (1). To ﬁnd the

best option, an optimization method is needed.

Our goal is to minimize the total number of op-

erations after both the Horner scheme and the CSEE

have been applied to the expression. Motivated by the

successes in (Kuipers et al., 2013a), we apply Monte

Carlo Tree Search (MCTS) to our set of large expres-

sions. A rich literature exists on MCTS, which is suc-

CombiningSimulatedAnnealingandMonteCarloTreeSearchforExpressionSimplification

725

cessfully applied in the game of Go (Coulom, 2007).

For an overview, see, e.g., (Browne et al., 2012).

An outline of the MCTS algorithm is displayed

in ﬁgure 2. A tree is built in which each node is a

variable that will be extracted. The tree will be built

iteratively. At each iteration, a leaf (or a not fully ex-

panded node) is chosen according to a selection crite-

rion (see 2(a)) and section 3). This node is (further)

expanded by randomly picking one of the unvisited

children (see 2(b)). Starting from this new leaf, we

continue the path by randomly selecting children (i.e.,

variables) that have not been selected so far (see 2(c)).

The complete path is our Horner scheme

. For this

scheme, we compute a score ∆, which is the number

of operations after the Horner scheme and CSEE have

been applied (see 2(c) again). Finally, the result is

propagated backwards through the tree (see 2(d)). For

a more detailed explanation of MCTS, see (Browne

et al., 2012).

Thus, MCTS is able to capture the trade-off of the

Horner scheme and CSEE by using a score ∆ which is

the number of operations of the ﬁnal expression after

Horner and CSEE have been applied.

Since we are interested in the best Horner scheme,

we keep track of the best path that we come across

during the tree updates. This path may not be com-

pleted in the tree if the tree did not reach the bottom

or if there was another random playout that is better

than the (partial) path through the tree.

The essence of MCTS is to ﬁnd a proper trade-

off between exploiting nodes that have been char-

acterized as good and exploring other (new) nodes

that may contain a promising path. The challenge

of a good algorithm is in balancing the exploration-

exploitation issue.

In the next section we modify the exploration part

of the UCT selection criterion to scale with the it-

eration number. In related work a different strat-

egy has been applied to make the importance of ex-

ploration versus exploitation iteration-number depen-

dent. For example, Discounted UCB (Kocsis and

Szepesv

ari, 2006b) and Accelerated UCT (Hashimoto

et al., 2012) both modify the average score of a

node (see below) to discount old wins over new ones.

In contrast, this work focuses on the exploration-

exploitation constant C

3 OUR ALGORITHM: SA-UCT

In many MCTS implementations UCT (eq. (3)) is

chosen as the selection criterion (Browne et al., 2012;

Note the difference with games such as Go, where only

the ﬁrst move is needed.

Kocsis and Szepesv

ari, 2006a):

argmax

children c of s

¯x(c) + 2C

2lnn(s)

n(c)

(3)

where c is a child node of node s, ¯x(c) the average

score of node c, n(c) the number of times the node c

has been visited, and C

the exploration-exploitation

constant. This constant determines the importance of

visiting a child that has not been visited often (explo-

ration), relative to visting a child with a high average

score (exploitation).

If this constant is high, more

iterations will be spent on exploration and if this con-

stant is low, the iterations will be spent on exploita-

tion. Generally, a higher C

results in broader trees,

whereas a smaller C

yields deeper trees.

For our application, it matters that the tree is ex-

panded as deeply as possible, since we want to op-

timize the entire Horner scheme, instead of just se-

lecting the optimal ﬁrst node, as is the case in games

such as Go (please note, this is an important differ-

ence). Therefore, it is more important that the last

iterations are used to deepen the tree and improve the

current local minimum than performing additional ex-

plorations. To achieve this, we introduce a dynamic

exploration-exploitation parameter T (for Tempera-

ture) that linearly decreases with the number of itera-

tions:

T (i) = C

N − i

(4)

where i is the current iteration number, N the pre-

set maximum number of iterations, and C

the initial

exploration-exploitation constant at i = 0.

Our new best child criterion becomes:

argmax

children c of s

¯x(c) + 2T

2lnn(s)

n(c)

(5)

where c is a child of node s, ¯x(c) is the average score

of child c, n(c) the number of visits at node c, and

T the dynamic exploration-exploitation parameter of

eq. (4).

Thus, the ﬁrst iterations are used for exploration

and gradually the focus shifts to exploitation and opti-

mization of the currently found local minimum. This

process can be thought of as a variant of simulated

annealing (Kirkpatrick et al., 1983), where a temper-

ature determines the probability of exploring energet-

ically unfavorable states. Starting at high tempera-

tures, there is a great deal of exploration and when

In our application, the average score is the number

of operations without optimizations divided by the average

number of operations for visited paths through this node,

see (Kuipers et al., 2013a).

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

726

Random scheme

∆

Figure 2: An overview of the four phases of MCTS: selection (a), expansion (b), simulation (c), and backpropagation (d).

The selection of a not fully expanded node is done using the best child criterion. ∆ is the number of operations left in the ﬁnal

expression, after the Horner scheme and CSEE have been applied. See also (Browne et al., 2012).

the temperature gradually decreases, the system con-

verges to a local minimum. In our case, the decreasing

exploration-exploitation parameter T takes the role of

the temperature. Because of the similarity between

these approaches, we call eq. (5) “Simulated Anneal-

ing UCT (SA-UCT)”.

4 RESULTS

In (Kuipers et al., 2013a), a sensitivity analysis of dif-

ferent parameters of MCTS is presented, which shows

that there is a small interval of C

for which the num-

ber of operations is close to the global best. We call

this the region of interest. Below we investigate how

this region changes if we use SA-UCT as selection

criterion. Our experimental setup is as follows: we

compare the number of operations after the Horner

scheme and CSEE have been applied for ﬁxed N and

different C

for SA-UCT (eq. (5)) with those for the

original UCT (eq. (3)). In SA-UCT, C

is the starting

value (initial temperature) T (0). We randomly sam-

ple 4000 dots for each graph (not to be confused with

the number of operations on the y-axis that also starts

with 4000).

We shall perform a sensitivity analysis of C

the number of operations for three expressions from

mathematics and physics, namely HEP(σ), res(7,5),

and F13, see (Kuipers et al., 2013a). HEP(σ) and F13

arise from parts of different Feynman diagrams and

res(7,5) is a resultant (an object commonly used in

number theory).

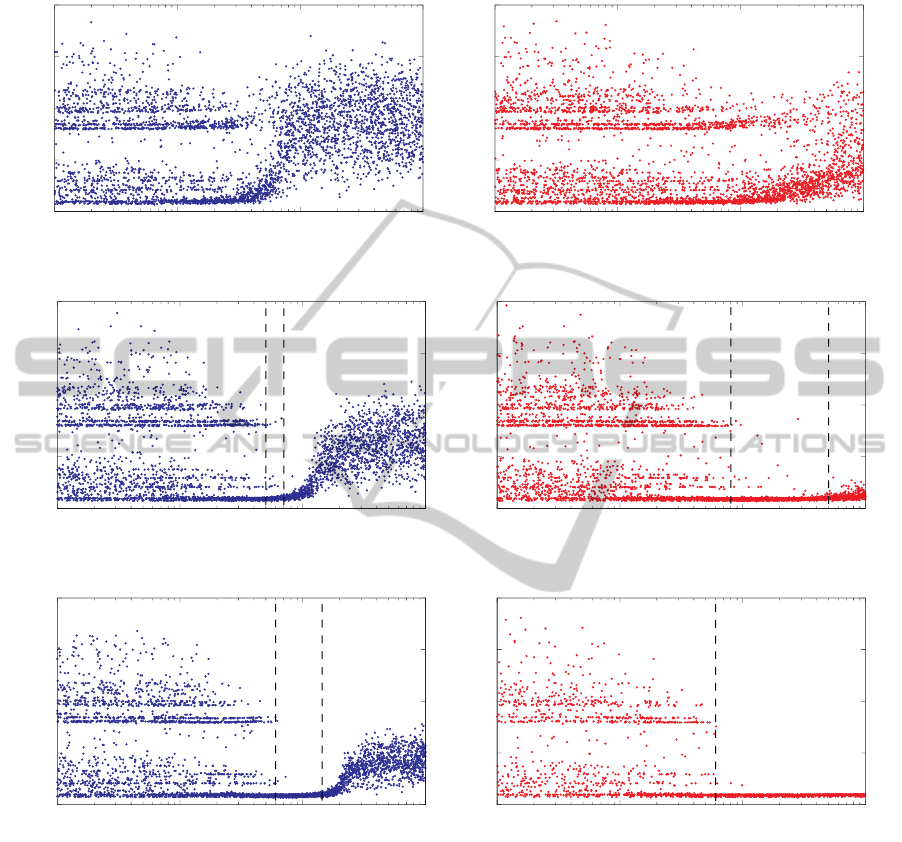
In ﬁgure 3 we show the results for HEP(σ) with 15

variables. The ﬁgures on the left are generated using

UCT. The ﬁgures on the right use SA-UCT (where C

is the initial temperature). Figure 3(a) and 3(b) are

measured with N = 300 tree updates, 3(c) and 3(d)

with N = 1000, and 3(e) and 3(f) with N = 3000 up-

dates. We see that for both algorithms there are dif-

ferent regions: one region in 3(a) and 3(b), two re-

gions in 3(f) and three regions in 3(c), 3(d), and 3(e).

The regions are separated by dashed lines. The re-

gions are called low, intermediate and high. In ﬁg-

ure 3(e) these regions are most prominent. At low

we observe that there are multiple local minima,

indicated by high-density band structures (three are

prominently visible). At intermediate values of C

we have the region of interest where only the near

global minimum is present. At high values there is a

diffuse region with no distinguishable local minima.

This happens when there is too much exploration.

Comparing the graphs on the left and on the right,

we see that the linearly decreasing C

causes a hori-

zontal stretching, which makes the region of interest

larger. If we look at the middle graphs, 3(c) and 3(d),

where the number of updates N = 1000, the region of

interest is approximately [0.8, 5.0] for a linearly de-

creasing C

, whereas it is roughly [0.5, 0.7] for a con-

stant C

. Thus, SA-UCT makes the region of interest

about 20 times larger for HEP(σ), relative to the unin-

teresting low C

region with local minima which did

not grow signiﬁcantly. For N = 3000, the difference

in size of the region of interest is even larger.

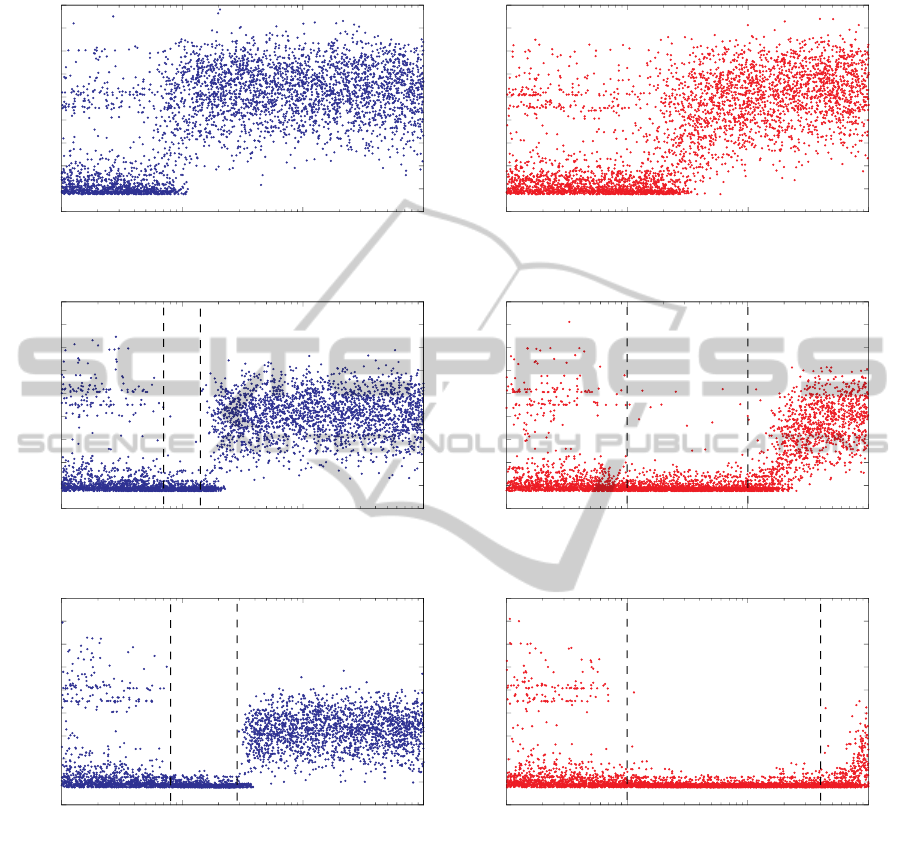
In ﬁgure 4 we have tested our method on

an expression from the ﬁeld of mathematics,

namely a resultant res(7,5), where res(m, n) =

res

(

∑

i=0

∑

i=0

), as described in (Leiserson

et al., 2010). While from a different ﬁeld, we still ob-

serve the band structures at low C

and the widening

of the region of interest occurs here as well. For ﬁgure

4(c) with N = 1000 tree updates using UCT the region

of interest is approximately [0.07, 0.15] and for 4(c)

CombiningSimulatedAnnealingandMonteCarloTreeSearchforExpressionSimplification

727

HEP(σ) with 15 variables

(a) N = 300

4000

4500

5000

5500

6000

0.01 0.1 1 10

Number of operations

(b) N = 300

4000

4500

5000

5500

6000

0.01 0.1 1 10

Number of operations

4000

4500

5000

5500

6000

0.01 0.1 1 10

Number of operations

(d) N = 1000

4000

4500

5000

5500

6000

0.01 0.1 1 10

Number of operations

(e) N = 3000

4000

4500

5000

5500

6000

0.01 0.1 1 10

Number of operations

(f) N = 3000

4000

4500

5000

5500

6000

0.01 0.1 1 10

Number of operations

Figure 3: HEP(σ) with 15 variables: the number of operations is on the y-axis and C

on the x-axis. A lower number of

operations is better. On the left, we show UCT with constant C

and on the right we show SA-UCT where C

is the starting

value of T . Each graph contains 4000 runs (dots) of MCTS. Figure 3(a) and 3(b) are measured with N = 300 tree updates,

3(c) and 3(d) with N = 1000, and 3(e) and 3(f) with N = 3000 updates. As indicated by the dashed lines, an area with an

operation count close to the global minimum appears, as soon as there are sufﬁcient tree updates N. This area is wider for

SA-UCT than for UCT.

using SA-UCT it is approximately [0.1, 1.0]. This

means that the region of interest has become about

10 times wider. In section 6 we continue our ﬁndings

on this polynomial in a discussion.

In the full version of this work (Ruijl et al., 2013)

we show the results for our third expression, called

F13, which again stems from the ﬁeld of high en-

ergy physics and has 22 variables. Since the depth

of a complete tree is equal to the number of vari-

ables, more tree updates are required to reach the ﬁ-

nal node for F13, compared to the other two expres-

sions. From the graphs we see that structure emerges

around N = 1000. For UCT, there are two clouds:

one near the global minimum and one near a higher

local minimum. Contrary to the previous two expres-

sions, F13 does not have a band structure at low C

but exhibits a diffuse cloud near the global minimum.

However, we see that this cloud is wider (roughly 50

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

728

res(7,5) with 14 variables

(a) N = 300

13000

14000

15000

16000

17000

18000

19000

20000

21000

22000

0.01 0.1 1 10

Number of operations

(b) N = 300

13000

14000

15000

16000

17000

18000

19000

20000

21000

22000

0.01 0.1 1 10

Number of operations

13000

14000

15000

16000

17000

18000

19000

20000

21000

22000

0.01 0.1 1 10

Number of operations

(d) N = 1000

13000

14000

15000

16000

17000

18000

19000

20000

21000

22000

0.01 0.1 1 10

Number of operations

(e) N = 3000

13000

14000

15000

16000

17000

18000

19000

20000

21000

22000

0.01 0.1 1 10

Number of operations

(f) N = 3000

13000

14000

15000

16000

17000

18000

19000

20000

21000

22000

0.01 0.1 1 10

Number of operations

Figure 4: res(7,5) polynomial with 14 variables: the number of operations is on the y-axis and C

on the x-axis. A lower

number of operations is better. On the left, we show UCT with constant C

and on the right we show SA-UCT where C

the starting value of T . Each graph contains 4000 runs (dots) of MCTS. Figure 4(a) and 4(b) are measured with N = 300 tree

updates, 4(c) and 4(d) with N = 1000, and 4(e) and 4(f) with N = 3000 updates. As indicated by the dashed lines, an area

with an operation count close to the global minimum appears, as soon as there are sufﬁcient tree updates N. This area is wider

for SA-UCT than for UCT.

times at N = 1000) for SA-UCT than for UCT, as was

the case for HEP(σ) and res(7,5). Since the band is

still broad, multiple samples are required to approach

the global minimum, regardless of C

. This is gov-

erned by the R parameter (van den Herik et al., 2013a;

Kuipers et al., 2013b), and is consequently a topic for

future research.

5 CONCLUSIONS

In this work we proposed a new UCT formula,

called SA-UCT, that has a decreasing exploration-

exploitation parameter T , similar to the temperature

in simulated annealing. We have compared the perfor-

mance of SA-UCT to the performance of UCT using

three large expressions from physics and mathemat-

ics. From our experimental results we may provision-

CombiningSimulatedAnnealingandMonteCarloTreeSearchforExpressionSimplification

729

(a) Forward scheme

13000

14000

15000

16000

17000

18000

19000

20000

21000

22000

0.01 0.1 1 10

Number of operations

(b) Backward scheme

13000

14000

15000

16000

17000

18000

19000

20000

21000

22000

0.01 0.1 1 10

Number of operations

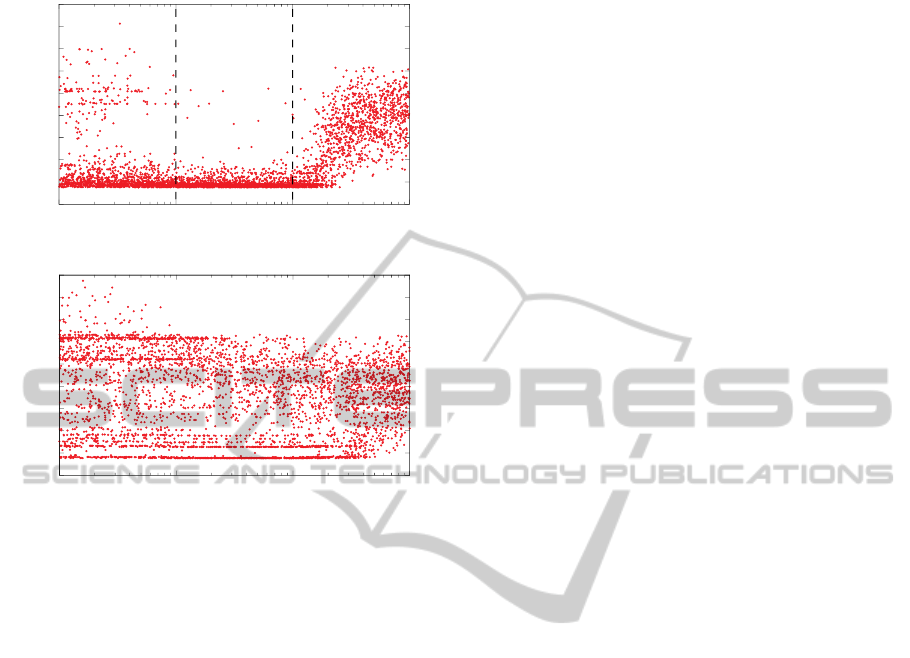
Figure 5: res(7,5): differences between forward (top) and

backward (bottom) Horner schemes, at N = 1000 tree up-

dates with SA-UCT. Forward Horner schemes generate a

region of C

where the number of operations is near the

global minimum, whereas backward schemes have multiple

high-density local minima and a diffuse region.

ally conclude that SA-UCT signiﬁcantly increases the

range of initial temperatures C

for which good re-

sults are obtained. This facilitates the selection of an

appropriate C

During our research, we uncovered multiple areas

for future research.

6 DISCUSSION / FUTURE WORK

We start the discussion by distinguishing normal

Horner scheme constructions from reversed construc-

tions, also called forward and backward respectively.

In the backward scheme, we create the Horner scheme

from the inside out, reversing the extraction order. For

example, in eq. (2) the forward scheme is y, x and the

backward scheme is x, y. The distinction between the

two constructions is important for MCTS, because by

its nature the tree of MCTS is asymmetric: the chil-

dren of the root are all explored, but most nodes at

the bottom will not. Since we are interested in the en-

tire path, this means that the end of the path will be

underexplored compared to the beginning of the path.

If large improvements can be made by carefully se-

lecting variables at the end of the scheme, these opti-

mizations will likely not be found. Figure 5 illustrates

the effect that a forward and a backward scheme have

on the res(7,5) expression, where N = 1000 and SA-

UCT is used. A forward scheme yields the three re-

gions mentioned in section 4, whereas the backward

scheme yields multiple local minima and a diffuse

area for every C

. The difference between forward

and backward schemes is present for both SA-UCT

and UCT, although it is more prominent in the lat-

ter. For UCT with C

> 0.1, the tree often does not

reach the end if the number of variables is larger than

15. The path is then completed using the random de-

fault policy, which selects a single path and conse-

quently does no exploration. For SA-UCT, the tree

often does reach the end and some exploration occurs,

because a low and exploitative C

effectively explores

deeper in the tree. However, this effect is not sufﬁ-

cient to smooth out the differences between forward

and backward schemes, as can be seen in ﬁgure 5. We

found that choosing a backward scheme for HEP(σ)

and F13 leads to signiﬁcant improvements. Whether

we can predict beforehand (by looking at the expres-

sion) if forward or backward search has to be used is

a topic of current research. Additionally, other ways

than forward or backward construction of the Horner

schemes could be used. For example, one could put

more emphasis on the middle part of the scheme, by

making the ﬁrst variables map to the middle of the

Horner scheme and working outwards from the cen-

ter. Here again additional work is needed to predict

which Horner scheme construction works best.

Also, more research is needed to ﬁnd quickly a

value of C

in the region of interest. If the number of

tree updates N is sufﬁciently high, the region of in-

terest becomes so large that even a binary search may

be sufﬁcient to ﬁnd a good C

. In order to understand

what N is required to obtain such a large region of

interest, the relation between an adequate N and the

number of variables has to be further investigated.

Furthermore, the performance of SA-UCT has to

be measured for different applications. Examples are

the travelling salesman problem and Go. Many Go

implementations currently set C

= 0, effectively dis-

abling UCT, but perhaps a small value for C

is fruit-

ful if SA-UCT is applied (Lee et al., 2009).

Moreover, additional work is needed to examine

different schemes for decreasing C

. For example,

the current depth in the tree may be a good candi-

date. One other possibility is detecting if the best

child selection gets stuck in a local minimum and

‘over-explores’ a branch. If this is the case, the T

could be increased to ﬁnd further minima in unex-

plored branches. Different cooling functions could

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

730

also be tried, such as exponentially decreasing T.

Finally, we believe that the use of domain speciﬁc

knowledge can be fruitfully explored if the expression

has sufﬁcient structure. To conﬁrm this belief more

research is needed.

This work is supported in part by the ERC Ad-

vanced Grant no. 320651, “HEPGAME”.

REFERENCES

Aho, A. V., Sethi, R., and Ullman, J. D. (1988). Compilers:

Principles, Techniques and Tools. Addison-Wesley.

Breuer, M. A. (1969). Generation of Optimal Code

for Expressions via Factorization. Commun. ACM,

12(6):333–340.

Browne, C., Powley, E., Whitehouse, D., Lucas, S., Cowl-

ing, P., Rohlfshagen, P., Tavener, S., Perez, D.,

Samothrakis, S., and Colton, S. (2012). A Survey of

Monte Carlo Tree Search Methods. Comp. Int. and AI

in Games, IEEE Trans. on, 4(1):1–43.

Ceberio, M. and Kreinovich, V. (2004). Greedy Algo-

rithms for Optimizing Multivariate Horner Schemes.

SIGSAM Bull., 38(1):8–15.

Coulom, R. (2007). Efﬁcient Selectivity and Backup Op-

erators in Monte-Carlo Tree Search. In Proceedings

of the 5th International Conference on Computers and

Games, CG’06, pages 72–83, Berlin. Springer-Verlag.

Hashimoto, J., Kishimoto, A., Yoshizoe, K., and Ikeda, K.

(2012). Accelerated UCT and Its Application to Two-

Player Games. Lecture Notes in C.S., 7168:1 – 12.

Horner, W. (1819). A New Method of Solving Numerical

Equations of All Orders by Continuous Approxima-

tion. W. Bulmer & Co. Dover reprint, 2 vols 1959.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Op-

timization by simulated annealing. Science, 220:671–

680.

Knuth, D. E. (1997). The Art of Computer Program-

ming, Volume 2 (3rd Ed.): Seminumerical Algorithms.

Addison-Wesley Longman Pub. Co., Inc., Boston.

Kocsis, L. and Szepesv

ari, C. (2006a). Bandit based Monte-

Carlo Planning. In In: ECML-06. LNCS 4212, pages

282–293. Springer.

Kocsis, L. and Szepesv

ari, C. (2006b). Discounted UCB.

Video Lecture. In the lectures of PASCAL Second

Challenges Workshop 2006.

Kuipers, J., Plaat, A., Vermaseren, J., and van den Herik, J.

(2013a). Improving multivariate Horner schemes with

Monte Carlo Tree Search. Computer Physics Commu-

nications.

Kuipers, J., Ueda, T., and Vermaseren, J. (2013b). Code Op-

timization in FORM. http://arxiv.org/abs/1310.7007.

Lee, C.-S., Wang, M.-H., Chaslot, G., Hoock, J.-B., Rim-

mel, A., Teytaud, O., Tsai, S.-R., Hsu, S.-C., and

Hong, T.-P. (2009). The Computational Intelligence

of MoGo Revealed in Taiwan’s Computer Go Tour-

naments. IEEE Trans. Comput. Intellig. and AI in

Games, 1(1):73–89.

Leiserson, C. E., Li, L., Maza, M. M., and Xie, Y. (2010).

Efﬁcient Evaluation of Large Polynomials. In In Proc.

International Congress of Mathematical Software -

ICMS 2010. Springer.

Ruijl, B., Plaat, A., van den Herik, J., and Vermaseren,

J. (2013). Combining Simulated Annealing and

Monte Carlo Tree Search for Expression Simpliﬁca-

tion. http://arxiv.org/abs/1312.0841.

van den Herik, J., Kuipers, J., Vermaseren, J., and Plaat, A.

(2013a). Investigations with Monte Carlo Tree Search

for ﬁnding better multivariate Horner schemes. Com-

mun. in Computer and Information Science 2013. In

press.

van den Herik, J., Plaat, A., Kuipers, J., and Vermaseren,

J. (2013b). Connecting Sciences. In ICAART 2013

- Proceedings of the 5th International Conference on

Agents and Artiﬁcial Intelligence, pages IS–7 – IS–16.

CombiningSimulatedAnnealingandMonteCarloTreeSearchforExpressionSimplification

731