
Energy-efficient Multicast Routing by using Genetic Local Search
Valeri Katerinchuk
1
, Andreas Albrecht
2
and Kathleen Steinh¨ofel
1
1
Department of Informatics, King’s College London, Strand Campus, London, U.K.
2
School of Science and Technology, Middlesex University London, The Burroughs, London, U.K.
Keywords:
Energy Efficiency, Wired Networks, Multiple Multicast Requests, Multicast Routing, Simulated Annealing,
Genetic Algorithm, Hybrid Algorithm, Partially Mixed Crossover.
Abstract:
Energy-efficient multicast routing algorithms have predominantly focused on wireless or ad-hoc mobile net-
works. However, since the turn of the century the need for energy efficient approaches to routing in wired
networks has been steadily rising. In this paper, we introduce an objective function for multicast routing in
wired networks taking energy consumption into consideration. A number of hybrid Genetic and Simulated An-
nealing based algorithms have been shown to be able to find better solutions to the multicast routing problem
compared to solely Genetic or Simulated Annealing based algorithms. Our approach adapts a population-
based hybrid algorithm for routing multiple simultaneous multicast requests. We examine the performance
in terms of energy efficiency against solutions found by Logarithmic Simulated Annealing and Genetic based
algorithms. We find that the hybrid approach, in 87% of instances, was able to find superior solutions, and
in 96% of instances, solutions superior or equal to the best solution given by either Simulated Annealing or
Genetic approaches. The extent of the improvement however varied greatly from a few hundred to within ten
Joules, with the improvement on the best solution ranging from 5.6 to 531.5 Joules.
1 INTRODUCTION
Multicasting is the transmission of data simultane-
ously from one source to multiple destinations within
a telecommunications network. Unlike the more in-
efficient point-to-point methodology of Unicasting,
Multicasting takes advantage of parallelism in the net-
work. The Multicast Routing Problem (MRP) is the
problem of routing one or many such multicast re-
quests through a network, often by means of con-
structing a spanning tree, while minimising the usage
of one or more limited network resources.
Since the MRP had been shown to be NP-
complete in (Karp, 1972), numerous heuristics have
been proposed to find near-optimal solutions. In
(Wang et al., 2003) a Simulated Annealing (SA)
based algorithm for the MRP is presented which was
shown by tests against the benchmark National Sci-
ence Foundation network to find solutions within 5%
of the optimum. Genetic algorithms (GA) have been
shown to obtain comparable solutions (Zhang and Le-
ung, 1999), while demonstrating a greater variance in
solution quality, obtained results closer than 2% to the
optimal in an average of 91% of runs. Work by (Wang
et al., 2006) on three implemented algorithms has also
shown GA and a SA based approaches to be com-
parable, with the GA able to obtain slightly superior
solutions while the SA based algorithm obtained so-
lutions faster and performed better on inputs the GA
struggled to obtain near-optimal solutions on. Recent
work examining hybrid GA and SA based algorithms
has shown them to generally be able to locate supe-
rior solutions to purely GA or SA approaches when
applied to routing both a single (Xu et al., 2013) and
multiple multicast requests (Zahrani et al., 2008).
Predominantly, papers considering algorithms for
multicast routing define the MRP as a single request
routing problem, where a message must be routed
to all members of a single multicast group. How-
ever, realistically networks utilising protocols capable
of true multicast routing are commonly faced with a
number of simultaneous requests over multiple mul-
ticast groups. Unfortunately, the number of algo-
rithms dealing with optimisation for multiple simulta-
neously routed multicast requests is few and primar-
ily focused on Quality of Service (QoS) (Galiasso and
Wainwright, 2001; Zahrani et al., 2008).
Moreover, the majority of algorithms for the MRP
have featured either a QoS based cost function or a
generic cost metric across each edge of a multicast
routing (Pinto and Barn, 2006; Xu, 2011). A growing
number of papers are considering the importance of
740
Katerinchuk V., Albrecht A. and Steinhöfel K..
Energy-efficient Multicast Routing by using Genetic Local Search.
DOI: 10.5220/0004926907400746
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 740-746
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

energy conservation in wireless and ad-hoc networks
(Banerjee et al., 2003; Olagbegi and Meghanathan,
2010; Xi and Yeh, 2010). For wired networks the
need for energy-efficient algorithms is steadily grow-
ing. The last decade has seen the number of inter-
net users rising rapidly with only 8% of the worlds
population in 2001 to 38.8% in 2013 according to
the Global ICT developments statistics provided by
the Internet Telecommunications Union. By contrast,
routing and wired connectivity equipment are con-
strained by technology limitations. As the data traffic
increases, so does the energy required for the trans-
mission of data and the need for energy-efficientrout-
ing. Another facet of this increase in energy consump-
tion is the contribution network routing makes to ris-
ing CO
2
levels. The SMART 2020 study suggests the
internet could account for 12% of global CO
2
levels
by 2020. Existing papers considering energy efficient
multicast routing rarely maintain an energy function
considering energy loss factors unique to wired net-
works. In his paper (Ajibesin et al., 2013) introduces
an energy function focusing primarily on the amount
of data per unit of time as the measure of energy us-
age. A number of other papers(Lun et al., 2006; Xu
and Qu, 2009) a general cost function over the links
of the routing. However, there exist multiple factors
influencing energy expenditure over wired networks.
In our paper we present an adaptation of the al-
gorithm presented in (Zahrani et al., 2008) toward
energy-efficient routing for the MRP. We propose
a new energy function for the capacity constrained
MRP representing the energy cost of multicast rout-
ing in wired telecommunications networks.
We test the implemented algorithm over a num-
ber of network instances taken from the Beasley JE.
OR library, calculating the energy cost of the edges
using the proposed energy function, against a Loga-
rithmic Simulated Annealing and Genetic algorithms.
We find that in the majority of cases the hybrid ap-
proach is able to find solutions closer to or as near the
optimum as the best solutions found by the other two
algorithms.
2 FORMALISATION
Communication networks consist of nodes connected
through links. The nodes transmit and receive
information, while the links transport information
between the nodes. Links have a limited capacity for
carrying information at any one time.
A communication network is represented by graph
G = (V, E) where node set V = {m
1
,m
2
..m
i
} nodes
and a set of links E = {l
1
,l
2
..l
i
} where each link l
j
connects two nodes in V. A link l = (v
i
,v
j
,c) where
v
i
,v
j
∈V, c is a capacity limit on the information that
can traverse at one time over l minus the capacity
requirement of the current traffic over l. We also
define an energy cost function Co over E such that
each link l
i
in E has an associated cost of transmitting
data over that link Co(l
i
). A multicast routing request
is defined as
m = [s ⇒ D,C],
where s ∈ V is the source node of m,
D = {v
1
,v
2
,..v
i
} ⊆ V is the set of destination
nodes and C is the capacity required by each trans-
mission s ⇒ v
i
and represents bandwidth lost due to
the amount of data to be transmitted and the routing
protocol used by the message.
The MRP for multiple simultaneous multicast
routing requests is defined as
[P = G;Co;M],
where M = {m
1
,m
2
,..m
i
}. We adopt a Steiner
tree representation of the routing of a single multicast
routing request over G. All data is routed over G
simultaneously.
2.1 Energy Cost Function
A successful routing of request m
i
∈ M is a subgraph
G
r
= (V
r
,E
r
) representing a Steiner tree over G,
where for every link l ∈ E
r
, c(l) ≥ 0. There are
numerous factors which influence the amount of
energy necessary for a routing separated broadly
into energy loss in the nodes, energy loss in the
links and initial cost of transmission, dependent on
data volume. The energy required E
t
for a multicast
routing is therefore defined as
E
t
= E
in
+
∑
V
r
(E
v
) +
∑
E
r
(E
l
),
where E
in
is the initial energy required to trans-
mit the message, E
v
i
is the energy loss at vertex i and
E
l
i
is the energy lost during transmission over link i.
The initial energy required to transmit a message
is taken as a function of the amount of data being
transmitted. It is defined as E
bit
∗n
bit
, where E
bit
is
the energy per bit, taken as 0.09/8=0.01125 joules -
the maximum estimated energy cost of sending a bit
of data over the internet (Gupta and Singh, 2003). By
n
bit
we denote the number of bits of data to be mul-
ticast over the network, which is set to 1000 bits per
request rendering E
in
= 11.25 joules.
Energy-efficientMulticastRoutingbyusingGeneticLocalSearch
741

The energy loss, E
v
i
= k, associated with trans-
mitting a request over a router i, in active mode, is a
constant for each node given by
k = L
d
+ L
m
+ 2log
2
N(L
s
), (1)
where L
d
and L
m
are multiplexer and demultiplexer
losses respectively, L
s
is the switch element inser-
tion loss and N is the number of input/output ports of
the switch with the relation 2log
2
N(L
s
) representing
the total energy lost in the cable-independent matrix
switch (Ramamurthy et al., 1999).
The energy lost routing the request over l
i
∈ E
r
,
E
l
i
= E
in
(l
i
) −E
out
(l
i
) with E
in
(l
i
) being the energy
of the transmission entering the link and E
out
(l
i
) the
energy of the transmission exiting the link. As the
signal is amplified to compensate for any energy lost
when exiting a node we may assume E
in
(l
i
) = E
in
.
The energy loss in l
i
is dependant on the attenuation
α of the wire over its length. The attenuation of the
wire is given in (Rajagopal, 2007; Kuphaldt, 2013) as
α = 10log
10
E
in
(l
i
)
E
out
(l
i
)
, (2)
in decibels per unit length, and varies depending on
the type of wire. For the purpose of this paper we as-
sume all links are facilitated by the popular category
5e (cat5e) wires. The TIA-EIA-568 standards docu-
ment gives the formula for calculating the attenuation
wire based on frequency and wire type used f as
α = k
1
p
f + k
2
∗ f +
k
3
√
f
db/100m, (3)
where k
1
= 1.967, k
2
= 0.023 and k
3
= 0.05 are con-
stants specific to the wire type. Frequency f is taken
as 100Mhz - the highest allowable frequency for the
cat5e wire given by the TIA-EIA sandards. There-
fore the attenuation per 100m of cat5e wire is α =
21.975db (Joules per 100m per second). The output
power of a link E
out
(l
i
) can then be found by
E
out
(l
i
) = E
in
(l
i
)/10
α∗(ln/100)
10
, (4)
where ln is the length of the wire in meters.
However, as the output power drops rapidly with
distance it must be amplified regularly to prevent the
signal becoming too weak to identify. The TIA-EIA
standards recommend a maximum length of cable of
100m in order for the signal to remain recognisable,
and we will assume that every link will have an am-
plifier at 100m intervals which boosts the signal to
starting levels. The total energy loss over link l
i
then
becomes
E
l
= (E
in
(l
i
) −E
out
(l
i
)) ∗a
n
+ E
l
c
, (5)
where a
n
is the number of amplifiers, E
out
(l
i
) now
represents energy after 100m of wire and E
l
c
=
E
in
(l
i
) −E
in
(l
i
)/10
α∗(l
c
/100)
10
, is the energy lost due to
attenuation over the length of wire l
c
≤100, not com-
pensated for by amplifiers.
Assuming as before that E
in
(l
i
) = E
in
= 0.01125∗
n
bit
, and that n
bit
is constant for all transmissions
(1000 for the purpose of this study), the energy lost
after 100m can now be represented as a constant
E
in
(l
i
) −E
in
(l
i
)/10
α∗(100/100)
10
= 11.25, (6)
measured in Joules per second. The energy lost trans-
mitting along edge l
i
can be summarised as
E
l
= 11.25∗a
n
+ E
l
c
, (7)
As every link l in a Steiner tree representing a suc-
cessful routing G
r
of m
i
is connected to exactly one
originator v
i
and destination node v
j
, k may be safely
added to the total energy loss of transmitting over link
l
i
E
t
= E
in
+
∑
E
r
(11.25∗a
n
+ E
l
c
+ k), (8)
rendering it irrelevant for the purpose of minimising
the energy function. Similarly, E
in
= 11.25 in the
above equation represents a constant for every mul-
ticast routing request and can be ignored for the pur-
pose of finding the minimum cost routing resulting in
the final equation representing energy cost of a rout-
ing over G as
E
t
=
∑
E
r
((E
in
(l
i
) −E
in
(l
i
)/10
α∗(100/100)
10
) ∗a
n
+ E
l
c
),
(9)
which may further be reduced, given (6), to
E
t
=
∑
E
r
(11.25∗a
n
+ E
l
c
). (10)
with
Co(l
i
) = 11.25∗a
n
+ E
l
c
(11)
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
742

3 HYBRID MULTICAST
ROUTING ALGORITHM
In this paper we adopt the genetic local search with
pre-processing by logarithmic simulated annealing al-
gorithm presented in (Zahrani et al., 2008). The prob-
lem of minimising
∑
E
Co(l
i
) over G, subject to s,
D and C has been shown to be NP-complete (Karp,
1972). As each request may need to be rerouted re-
peatedly in order to satisfy capacity constraints and as
part of the SA and elitist Partially Mixed Crossover
(PMX) approaches it employs the KMB(Kou et al.,
1981) heuristic algorithm to estimate the Steiner tree
for each network routing. The KMB has been shown,
on average, to produce Steiner trees 5% over the cost
of a minimum Steiner tree(Doar and Leslie, 1993) and
has been known to find minimum values for numerous
benchmark problems (Koch and Martin, 1998).
The neighbourhood operator used by both the SA
and GA stages of the algorithm takes a pair of ran-
dom numbers between 1 and r, where r is the total
number of multicast requests. The order of all re-
quests between these two numbers is reversed. This is
done in order to preserve any desirable dependencies
of requests resulting in low cost solutions. The algo-
rithm utilises a two stage process to estimate an opti-
mal routing of multiple multicast routing requests:
3.1 LSA Pre-processing
The primary purpose of the LSA pre-processing step
is to perform an energy landscape analysis refining
an estimate of Γ, representing the maximum escape
height from local minima in the solution space. That
is to say, an estimate of the difference in cost of a
worse accepted solution when compared to a solution
representing a local minima that must be met in order
to guarantee exiting any local minima. Initial solu-
tions for the algorithm are generated by the KMB and
an initial estimate of Γ is obtained by
Γ =
G
est
10
, (12)
with G
est
representing the difference between the best
and worst solutions found, initially set to the differ-
ence between two initial solutions. The algorithm de-
rives initial temperature from the estimate of Γ and
maintains a logarithmic cooling schedule. Through-
out its execution the Simulated Annealing algorithm
constantly updates G
est
with the difference between
the current best and worst solution. Upon the termi-
nation of the LSA gamma is re-estimated using (12)
updated with the new value for G
est
. The best solution
found by the LSA is added to the initial population
of the Genetic PMX algorithm. As the Genetic algo-
rithm is elitist, always conserving the current best so-
lution between runs, this ensures that good solutions
found by the LSA are conserved.
Begin
Generate initial solution;
Generate initial value for
G
est
;
Generate initial value for Gamma;
Calculate initial temperature;
for (int i=0; i<constant; i++)
{
Generate neighbouring solution N;
if (cost(N)>currentworst)
{
currentworst+= cost(N);
}
if (cost(N)<cost(Bestsolution)
{
Bestsolution = N;
G
est
=currentworst-cost(Bestsolution)
}
if (cost(current)>cost(N))
{
accept neighbour solution;
}
else
{
accept neighbour solution
with probability determined
by current temperature;
}
}
End.
3.2 Genetic Local Search
Upon initialisation, a population of initial solutions
is generated using the KMB. The bulk of the Ge-
netic Local search algorithms consists of three iter-
ated steps. For each solution in the population, ini-
tially the algorithm performs only downward steps,
accepting only solutions which improve upon the
cost. Once a local minima is reached the algorithm
switches modes performing upward steps until the es-
cape height h = Γ
est
+ C
o
(E
r
(m
i
)) is reached where
Γ
est
is the estimate of gamma provided by the pre-
processing step. The above procedure is repeated for
every solution in the population. The algorithm then
performs a PMX operation, adding, in the first run the
best solution generated by the Simulated Annealing
step. The three steps are repeated until a set number
of PMX operations have occurred. The best current
solution is conserved between PMX operations.
Begin
Generate initial solutions;
Obtain
Gamma
est
from LSA;
for (N steps)
{
for (each solution in population)
{
for (M steps)
{
While (true)
{
Begin downward steps;
if (local minima is reached)
{
Energy-efficientMulticastRoutingbyusingGeneticLocalSearch
743
break;
}
}
While (true)
{
Begin upward steps;
if (
Gamma
est
+cost(minima)
is reached)
{
break;
}
}
}
Begin PMX;
save current best solution;
}
}
End.
4 COMPUTATIONAL
EXPERIMENTS
We have implemented the algorithm described in
section (3). For the computational experiments the
benchmark problem instances of steinb6 (50 nodes,
100 edges), steinb7 (75 nodes, 94 edges), steinb8 (75
nodes, 94 edges), steinb10 (75 nodes, 150 edges),
steinb11 (75 nodes, 150 edges) and steinb18 (100
nodes, 200 edges) were taken from the Beasley JE.
OR library to represent the input graphs G. Edge costs
were extrapolated from the problem instances by ap-
plying the energy function to the edge costs given in
the steinb instances where the steinb edge costs were
taken to represent distance of the links in hundreds
of meters. As detailed in (2.1), we have taken the en-
ergy/bit from (Gupta and Singh, 2003) to be 0.001125
joules and have set the number of bits per transmis-
sion to 1000. The capacity limit c of each edge is
initially set to 12.
For the energy function, we assume no loss due to
deformation or imperfections in the wire. Amplifiers
are assumed to be positioned along the links at 100m
intervals as specified by the TIA-EIA standards doc-
ument. The energy lost transmitting 1000 bits of data
over 100m is rounded down to 11.2 Joules/second.
Once a routing of all multicast requests is established,
all transmissions are considered instantaneous (taken
as 1 second for the purposes of the experiment). We
assume all nodes in the graphs to be identical T640
routers in active mode.
The steinb 6, 7 and 8 instances were tested against
a single request set of 9 multicast requests given in
Table 1. The algorithm was run five times for each
input instance.
For the steinb10,11 and 18 instances twenty mul-
ticast routing requests were obtained from (Zahrani
et al., 2008) shown in Table 2.
Table 1: Set of multicast requests for steinb 6, 7 and 8.
m
i
s D C
1 36 7,23,25,40 3
2 17 15,30,31,40,41,46 2
3 48 36,50 5
4 2 6,14,18,23,27,33,47,49 4
5 41 13,22,27,35,50 2
6 30 5,12,28,31,44,45 2
7 23 13,14,28,41 ,35,45 1
8 10 5,20,31,40 3
9 16 18,20,22,23 2
Table 2: Set of multicast requests for steinb11,10 and 18.
m
i
s D C
1 24 20.29.30 3
2 55 4,21,41 5
3 10 5,20,31,40 3
4 41 13,22,27,35,50 2
5 17 15,30,31,40,41,46 2
6 14 6,16,36,4 4
7 67 23,29 6
8 69 10,40,54 2
9 13 28 7
10 53 13,14,28,41,52,55 1
11 50 5,12,28,31,44,45 2
12 36 7,23,25,40 3
13 52 9,13,22,55 2
14 2 6,14,18,23,27,33,47,49 4
15 48 36,58 8
16 61 15,20,33,38 6
17 14 9,16,31,43,44 3
18 9 4,6,7,30,31,35 2
19 66 18,20,22,23 2
20 75 33,57 7
These were formed into three sets of multicast re-
quests M
1
, M
2
and M
3
containing 9, 15 and 20 mul-
ticast requests respectively. For M
1
and M
2
the al-
gorithm was run five times on two of the three input
instances and five times on all three input instances
for M
3
.
In the experiments we compared the quality of so-
lutions found by the joint PMX and LSA algorithms
to those obtained by running the LSA and PMX with
random walk alone. Tables 3-5 show the total energy
values for solutions obtained when routing multicast
requests across steinb 6,7 and 8 respectively, when
routed by LSA only, PMX only and PMX with LSA
pre-processing algorithms. Tables 6-8 show the to-
tal energy values for solutions obtained when rout-
ing multicast requests sets M
1
, M
2
and M
3
across
steinb10,11 and 18 respectively, when routed by LSA
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
744
only, PMX only and PMX with LSA pre-processing
algorithms.
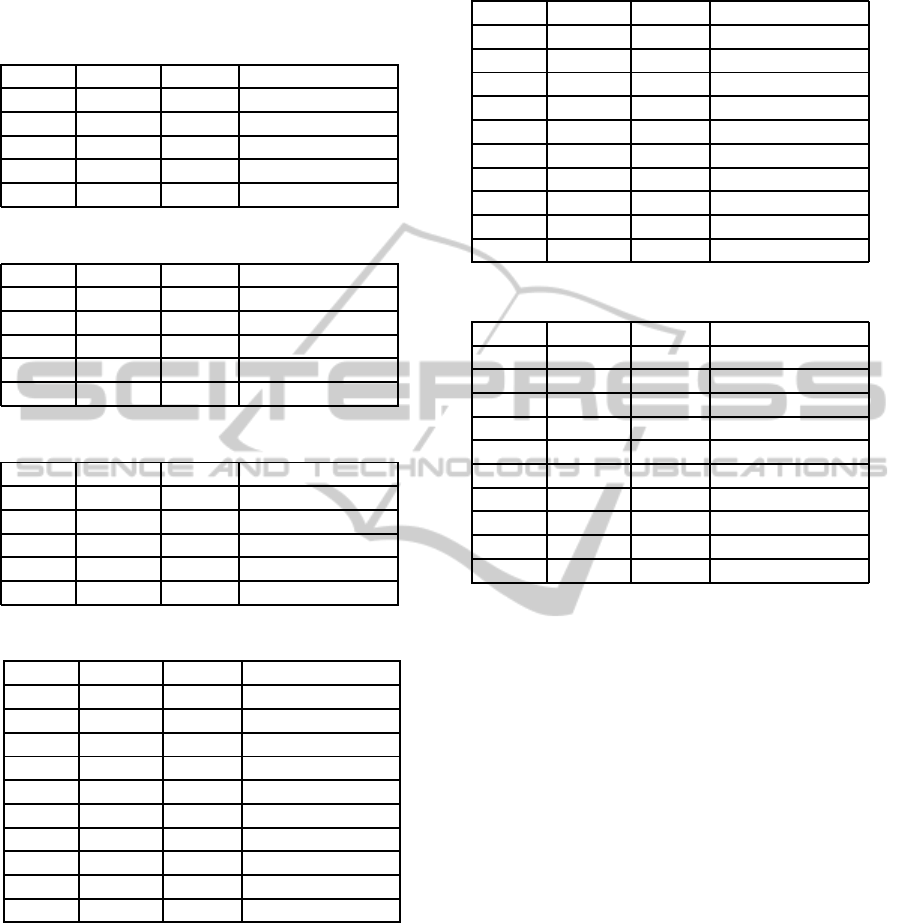
Table 3: Total energy cost of steinb6 solutions.
P
i
size E
t
LSA E
t
GA E
t
GA with LSA
9 3855.6 3785.1 3785.1
9 3691.4 3844.3 3622.3
9 3785.1 3817.9 3757.6
9 3743.8 3759.8 3690.1
9 3706.5 3747.2 3697.5
Table 4: Total energy cost of steinb7 solutions.
P
i
size E
t
LSA E
t
GA E
t
GA with LSA
9 7613.1 7682.1 7447.8
9 7672.0 7541.2 7380.8
9 7593.6 7832.3 7511.1
9 7672.0 7671.2 7394.8
9 7627.8 7911.0 7434.6
Table 5: Total energy cost of steinb8 solutions.
P
i
size E
t
LSA E
t
GA E
t
GA with LSA
9 5635.7 5789.1 5600.4
9 5644.2 5698.5 5571.3
9 5670.8 5666.3 5571.3
9 5611.2 5691.5 5667.2
9 5743.9 7604.3 5639.0
Table 6: Total energy cost of steinb10 solutions.
P
i
size E
t
LSA E
t
GA E
t
GA with LSA
9 3940.9 4126.3 3789.5
9 3957.0 3899.1 3832.7
9 3835.7 4011.2 3701.5
9 3921.2 4046.6 3835.0
9 3947.0 4021.6 3947.0
20 9497.6 9532.9 9094.4
20 9534.2 9965.1 9295.3
20 9508.8 9678.3 9150.9
20 9464.0 9772.9 9229.1
20 9564.8 9893.3 9216.6
We found that in 96% of instances the solution
found by the hybrid algorithm was superior or equal
to the best solution found by either the LSA or the
PMX algorithms alone. Interestingly, in a large num-
ber of instances the LSA outperformed the PMX with
random walk and was able to find a superior solution.
5 CONCLUSIONS
In this paper we presented a new energy function
for the energy-efficient Multicast Routing Problem
Table 7: Total energy cost of steinb11 solutions.
P
i
size E
t
LSA E
t
GA E
t
GA with LSA
15 4233.6 4413.2 4233.6
15 4222.4 4402.2 4135.9
15 6619.2 4423.5 4217.0
15 4222.4 4472.9 4188.0
15 4233.6 4426.1 4153.4
20 5495.2 5331.9 5226.8
20 5693.6 6413.3 5471.8
20 5555.9 5934.1 5336.4
20 5667.2 6117.5 5451.5
20 5492.4 5423.3 5417.7
Table 8: Total energy cost of steinb18 solutions.
P
i
size E
t
LSA E
t
GA E
t
GA with LSA
9 3483.2 3532.5 3389.3
9 3640.0 3789.3 3570.4
9 3572.8 3711.4 3492.0
9 3495.5 3752.4 3411.6
9 3547.1 3669.5 3455.6
20 8681.1 8712.8 8681.1
20 8642.0 9030.6 8598.8
20 8615.1 8761.7 8083.6
20 8742.8 9136.2 8766.8
20 8791.3 8881.9 8778.0
in wired networks. We extended the algorithm pre-
sented in (Zahrani et al., 2008) to calculate energy
efficient solutions to the MRP over multiple simul-
taneously routed multicast requests. We have shown
that an energy-efficient PMX with random walk al-
gorithm employing LSA pre-processing was able to
find, 87% of the time, superior solutions than either
LSA or PMX alone, 96% of the time, solutions su-
perior or equal to the best solution given by LSA or
PMX. The extent of the improvement however varied
greatly from a few hundred Joules to within twenty.
The range of improvement on the best solution for
steinb 6, 7 and 8 instances was from 9 to 276.4 Joules.
The range of improvement on the best solution for
steinb 10, 11 and 18 instances was between 5.6 and
531.5 Joules. Future work may include considering
the impact of routing requests with varying amount of
data on the routing of multiple multicast request sets
and incorporating into the energy function energy loss
due to the protocol used.
REFERENCES
Ajibesin, A. A., Wajiga, G. M., Odekunle, M. R., and
Egunsola., O. K. (2013). Energy-efficient multi-
cast in wired and wireless networks: Analysis and
Energy-efficientMulticastRoutingbyusingGeneticLocalSearch
745

performance measures. In Computational Intelli-
gence, Communication Systems and Networks (CIC-
SyN), 2013 Fifth International Conference on, pages
131–136.
Banerjee, S., Misra, A., Yeo, J., and Agrawala, A. (2003).
Energy-Efficient Broadcast and Multicast Trees for
Reliable Wireless Communication.
Doar, M. and Leslie, I. M. (1993). How bad is naive mul-
ticast routing. In IEEE INFOCOM., volume 1, pages
82–89.
Galiasso, P. and Wainwright, R. L. (2001). A hybrid genetic
algorithm for the point to multipoint routing problem
with single split paths. In Proceedings of the 2001
ACM Symposium on Applied Computing, SAC ’01,
pages 327–332. ACM.
Gupta, M. and Singh, S. (2003). Greening of the internet.
In Proceedings of the 2003 Conference on Applica-
tions, Technologies, Architectures, and Protocols for
Computer Communications, SIGCOMM ’03, pages
19–26. ACM.
Karp, R. M. (1972). Reducibility among combinatorial
problems. In Miller, R. E., Thatcher, J. W., and
Bohlinger, J. D., editors, Complexity of Computer
Computations, The IBM Research Symposia Series,
pages 85–103. Springer US.
Koch, T. and Martin, A. (1998). Solving steiner tree prob-
lems in graphs to optimality. Networks, 32:207–232.
Kou, L., Markowsky, G., and Berman, L. (1981). A fast
algorithm for steiner trees. Acta Informatica, 15:141–
145.
Kuphaldt, T. R. (2000-2013). Lessons In Electric Circuits –
Volume 3.
Lun, D. S., Ratnakar, N., Mdard, M., Koetter, R., Karger,
D. R., Ho, T., Ahmed, E., and Zhao, F. (2006).
Minimum-cost multicast over coded packet networks.
IEEE TRANS. INF. ON THE, pages 2608–2623.
Olagbegi, B. S. and Meghanathan, N. (2010). A review
of the energy efficient and secure multicast routing
protocols for mobile ad hoc networks. International
Journal on Applications of Graph Theory In wire-
less Ad Hoc Networks And sensor Networks, 2:1–15.
arXiv:1006.3366 [cs].
Pinto, D. and Barn, B. (2006). Multiobjective multicast
routing with ant colony optimization. In Network
Control and Engineering for Qos, Security and Mo-
bility, V, pages 101–115.
Rajagopal, K. (2007). Engineering Physics. PHI Learning
Pvt. Ltd.
Ramamurthy, B., Datta, D., Feng, H., Heritage, J. P., and
Mukherjee, B. (1999). Impact of transmission impair-
ments on the teletraffic performance of wavelength-
routed optical networks. Journal of Lightwave Tech-
nology, 17:1713–1723.
Wang, X., Cao, J., Cheng, H., and Huang, M. (2006). QoS
multicast routing for multimedia group communica-
tions using intelligent computational methods. Com-
put. Commun., 29:2217–2229.
Wang, X., Cheng, H., Cao, J., Zheng, L., and Huang,
M. (2003). A simulated-annealing-based QoS mul-
ticasting algorithm. In International Conference on
Communication Technology Proceedings, 2003. ICCT
2003, volume 1, pages 469–473 vol.1.
Xi, Y. and Yeh, E. (2010). Distributed algorithms for mini-
mum cost multicast with network coding. IEEE/ACM
Transactions on Networking, 18:379–392.
Xu, Y. (2011). Metaheuristic Approaches for QoS Multicast
Routing Problems. PhD thesis.
Xu, Y. and Qu, R. (2009). A grasp approach for the delay-
constrained multicast routing problem. In Proceed-
ings of the 4th Multidisciplinary International Confer-
ence on Scheduling: Theory and Applications, pages
99–104.
Xu, Y., Qu, R., and Li, R. (2013). A simulated anneal-
ing based genetic local search algorithm for multi-
objective multicast routing problems. Annals of Oper-
ations Research, 206:527–555.
Zahrani, M. S., Loomes, M. J., Malcolm, J. A., Ullah, A.
Z. M. D., Steinhoefel, K., and Albrecht, A. A. (2008).
Genetic local search for multicast routing with pre-
processing by logarithmic simulated annealing. Com-
puters & Operations Research, 35:2049–2070.
Zhang, Q. and Leung, Y.-W. (1999). An orthogonal genetic
algorithm for multimedia multicast routing. Transac-
tions on Evolutionary Computation, 3:53–62.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
746
