
Research on Techniques for Building Energy Model
Dimitrios-Stavros Kapetanakis
1
, Eleni Mangina
2
and Donal Finn
1
1
School of Mechanical and Material Engineering, University College of Dublin, Dublin, Ireland
2
School of Computer Science and Informatics, University College of Dublin, Dublin, Ireland
1 STAGE OF THE RESEARCH
Forecasting of building thermal and cooling loads,
without the use of simulation software, can be
achieved using data from Building Energy
Management Systems (BEMS). Experience in
building modelling has shown that data analysis is a
key factor in order to produce accurate results.
Commercial buildings incorporate BEMS to control
the Heating Ventilation and Air-Conditioning
(HVAC) system and to monitor the indoor
environment conditions. Measurements of
temperature, humidity and energy consumption are
typically stored within BEMS. These measurements
include underlying information regarding buildings’
thermal response. Data Mining is utilised to explore
the data, to search for consistent patterns and/or
systematic relationships between variables, and then
to validate the findings by applying the detected
patterns to new subsets of data. The process of data
mining within the current research project consists
of three stages: (1) the initial exploration, (2) model
building or pattern identification with
validation/verification, and (3) deployment (i.e., the
application of the model to new data in order to
generate predictions). The data used for the purposes
of this research project has been gathered from two
commercial buildings, located in Dublin and Cork,
Ireland.
The research described in this paper is at its
initial stage, where an extensive literature review of
building energy modelling has been conducted, the
research plan is defined, the research skills are being
developed and original research work is initiated. In
February 2014, the first year of the three-year
programme will be completed.
2 OUTLINE OF OBJECTIVES
This project focuses on a novel approach for cost-
effective modelling of actual data from commercial
buildings, with models that can be assembled rapidly
and deployed easily. This approach will constitute a
practical research testbed to optimise multiple
objectives related to the buildings’ energy modelling
research area: i) development of a novel approach
for predicting thermal and cooling loads of
commercial buildings; ii) highly accurate predictions
in terms of thermal and cooling loads; iii) scalability
of the new approach to any commercial building and
iv) minimum commissioning and maintenance effort
requirements.
3 RESEARCH PROBLEM
Predictions of building thermal and cooling load can
be obtained using appropriate simulation software.
Building simulation software require detailed
building geometry as well as physical data, such as
construction elements, U-values, etc. in order to
simulate the operation of a building. These
parameters are often unknown, especially for older
buildings, thus introducing rough estimations and
significant commissioning effort in real-world
applications.
An alternative way to forecast these loads is to
take advantage of the data recorder within BEMS.
As already mentioned measurements of temperature,
humidity and energy consumption are the ones
stored within BEMS. Useful information regarding
the thermal response of buildings are contained in
these measurements.
Utilization of measured data can produce
predictions of buildings energy consumption. These
predictions can be used to improve the efficiency of
the HVAC system and hence reduce the amount of
energy consumed. The accuracy of the prediction is
a crucial factor regarding the maximization of
energy savings. This project will attempt to answer
the following research questions:
Can historical measured data of buildings be
used to predict thermal and cooling load?
Which is the best methodology to adopt for
model development?
22
Kapetanakis D., Mangina E. and Finn D..
Research on Techniques for Building Energy Model.
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

What is the innovation and novelty of the new
model?
How accurate and scalable is the new model?
Which are the commissioning requirements of
the new model?
4 STATE OF THE ART
American Society of Heating, Refrigerating and Air-
Conditioning Engineers (ASHRAE) classify
building analytical methods into dynamic and steady
state approaches, as summarised in Figure 1
(ASHRAE, 2009). The difference between steady-
state and dynamic methods is the consideration of
effects such as thermal mass and/or capacitance.
Steady-state methods do not take into account
effects that cause temperature transients.
Conversely, building transient behaviour, which
includes effects such as building warm-up or cool-
down periods, is captured using the dynamic
methods.
Figure 2 illustrates another way to classify the
methods outlined in Figure 1. The key difference is
that the analytical methods are classified based on
the underlying computational methodology rather
than a transient/steady-state demarcation. Three
categories can be observed using this classification,
namely, “White”, “Grey” and “Black” box models.
“White-box” models use physical principles to
calculate the thermodynamics and energy behaviour
of the whole building level or of sub-level
components (Zhao and Magoulès, 2012). The
second category “black-box” models, includes the
data-mining methods, which utilises extensive
measurement of input and output variables in order
to determine correlated relationships between
different variable combinations. The third category
includes models that use both physical and data-
mining methods and are called hybrid or “Grey-box”
models. One can observe that the two different
approaches for classifying the existing
methodologies are two different aspects of the same
issue.
All methods use physical principles or data-
mining techniques and at the same time are either
dynamic or steady-state. This point becomes clearer
while using a colour coding as shown in Figure 1
and Figure 2. White, grey and black colours are used
in Figure 1 to discriminate the white, grey and black
box models. Steady-state methods are coloured with
blue and dynamic methods with orange in Figure 2.
White-box methods do not meet the basic
requirement of this project, which is the use of
historical data and avoidance of detailed building
geometry and construction data.
Figure 1: Categorization of methods used to estimate
building energy performance based on ASHRAE
Handbook (ASHRAE, 2009).
Figure 2: Categorization of analytical methods to estimate
building energy performance based on the underlying
methodology.
Hence, they are not included in a detailed
manner in this research. Furthermore, grey-box
methods combine the use of white- and black-box
methods thus it is reasonable to eliminate them as
well, due to the presence of white-box methods.
Based on the literature review for black-box
methods regression, support vector machine (SVM)
and artificial neural network (ANN) models seem
suitable for generating predictions. Their
Building Energy
Performance
Dynamic Methods
Computer Simulation
(EnergyPlus, DOE-2, etc)
Computer Emulation
(TRNSYS, HVACSIM+)
Artificial Neural Networks
Thermal Networks
Steady State
Methods
Simple linear regression
Multiple regression
Modified degree-day method
Variable-base degree day
method
ASHRAE bin method and
data-driven bin method
Building Energy
Performance
White-box
Models
Variable-base
degree-day
Bin method
Computer
Simulation
Computer
emulation
Grey-box
Models
Thermal
networks
Hybrid models
Black-box
Models
Simple linear
regression
Multiple
regression
Artificial neural
networks
Support Vector
Machine
Genetic
algorithms
ResearchonTechniquesforBuildingEnergyModel
23

performance and accuracy will be explored further
to determine which one is the most appropriate for
this specific application. Genetic algorithms are
mainly used for optimization rather than forecasting
and for that reason are excluded from deeper
investigation.
An overview of regression, SVM and ANN
methods including their advantages and
disadvantages alongside interesting case-studies
follows.
4.1 Regression Models
The correlation of energy consumption with all
influencing variables can be achieved with the use of
regression models. Development of these empirical
models is based on historical performance data,
which need to be collected prior to the training of
the models. The main objectives of these models are
the prediction of energy usage, prediction of energy
indices and estimation of important parameters of
energy usage. Examples of these parameters are the
total heat capacity, total heat loss coefficient and
gain factors (Zhao and Magoulès, 2012).
In general, regression models can be divided into
simple and multiple regression. Simple regression
models were frequently used in the late ’90s to
correlate energy consumption with climatic
parameters, to obtain building energy behaviour
(Bauer and Scrartezzini, 1998); (Westergren et al.,
1999). Multiple regression analysis is used to predict
a single dependent variable, such as heating demand,
by a set of independent variables, such as shape
factor, building time constant, etc. Multiple
regression shares assumes: linearity of relationships,
same level of relationship throughout the range of
the independent variable, interval or near-interval
data, absence of outliers and data whose range is not
truncated (Catalina et al., 2008). Multiple regression
models can be separated in two major categories,
multiple linear regression models and multiple non-
linear regression models.
4.1.1 Multiple Linear Regression
Multiple linear regression models are also known as
conditional demand analysis (CDA) models and are
usually applied to the building energy forecasting
area (Foucquier et al., 2013). The idea of using the
linear regression for the prediction of energy
consumption in buildings was first proposed by Parti
(1980). The deduction of the energy demand from
the sum of several end-use consumptions added to a
noise term which was the innovation regarding this
method.
The underlying principle of multivariate linear
regression is the prediction of an output variable Y as
a linear combination of input variables (X
1
,X
2
,…,X
p
)
plus an error term ε
i
(Foucquier et al., 2013).
01122
... , [1, ]
ii pipi
Y
x
xxin
(1)
In Equation (1), n is the number of sample data, p is
the number of variables and α
0
a bias. For instance,
when the output variable is internal temperature the
external temperature, humidity, solar radiation and
lighting equipment can be considered as input
variables (Foucquier, et al., 2013).
Essentially, multiple linear regression models
can be applied both for predicting or forecasting
energy consumption and for data-mining. The main
advantage of these methods is the simplicity of
implementation by non-expert users, since no
parameter needs to be tuned. Nevertheless, multiple
linear regression models imply a major drawback
due to their inability to solve nonlinear problems.
This causes limitations to the flexibility of the
prediction and at the same time presents difficulties
to manage the correlation between several variables.
4.1.2 Multiple Non-linear Regression
Non-linear regression models are of the same basic
form as linear regression models:
(),
iii
fXaY
(2)
The error terms are usually assumed to have a value
of zero, constant variance and to be uncorrelated,
just as for linear regression models. Often, a normal
error model is utilized which assumes that the error
terms are independent normal random variables with
constant variance. The correlation between the input
and output variables can take different forms in
order to fit the available data series. Two examples
of non-linear regression models widely applied in
practice are exponential and polynomial regression
models.
4.1.3 Case Studies
In this section interesting case-studies of regression
models are given. At first, two case-studies which
applied multiple linear regression models are stated
followed by multiple non-linear regression case-
studies.
Lam et al., (2010) developed multiple linear
regression models for office buildings for the five
major climates in China. These models can be used
to estimate the potential energy savings during the
initial design stage when different building schemes
and concepts are being examined. A total of 12 key
ICAART2014-DoctoralConsortium
24

building variables were identified through
parametric and sensitivity analysis and considered as
inputs in the regression models. More recently,
Aranda et al., (2012) used multiple linear regression
models to predict the annual energy consumption in
the Spanish banking sector. The energy consumption
of a bank branch was predicted as a function of its
construction characteristics, climatic area and energy
performance. Three models were finally obtained.
The first one was used to make predictions for the
whole banking sector, while the rest estimated the
energy consumption for branches with low winter
climate severity (Model 2) and high winter climate
severity (Model 3).
Catalina et al., (2008) worked on the
development and validation of multiple regression
models to predict monthly heating demand for
single-family residential buildings in temperate
climates. The inputs for the regression models were
the building shape factor, building envelope U-
value, window to floor area ratio, building time
constant and climate, which was defined as a
function of temperature and heating set-point. It was
found that quadratic (second-order) polynomial
models were the most appropriate solution for the
problem. In order to validate the models, 270
different scenarios were analysed. The average error
was 2% between the predicted and simulated values.
An update to the aforementioned work was
published by Catalina et al., (2013). A new model to
predict the heating energy demand, based on the
main factors that influence the building heat
consumption, was introduced. Influencing factors
were: the building global heat loss coefficient, south
equivalent surface and difference between indoor set
point temperature and “sol-air temperature”. Once
again, polynomial multiple regression models were
used and a three input model was found to be the
most appropriate for this problem. The model was
tested and demonstrated relativly good accuracy
considering its simplicity and generality. Human
behaviour was also taken into account in the creation
of this model, improving the accuracy of the
predictions.
4.2 Support Vector Machine
The SVM is an artificial intelligence technique that
is usually used to solve classification and regression
problems. It was introduced by Vapnik and Cortes
(1995). As already described, the regression method
is used to characterise a set of data with a specific
equation. The type of the regression equation is
determined by the user. The technique which allows
the demarcation of a set of data in several categories
is called classification. Once again, the
characteristics of each category are given by the
user.
SVM is mainly used with a regression method to
predict the energy consumption of buildings. The
determination of the optimal generalisation of the
model to promote sparsity is the basic principle of
the SVM for regression. A given training dataset
from a nonlinear problem is [(x
1
,y
1
),..,(x
n
,y
n
)], where
x
i
and y
i
is the input and output space respectively.
The approach to solve this problem is to overcome
the nonlinearity by transforming the nonlinear
relation between x and y in a linear map. To achieve
that, the nonlinear problem must be sent to a high-
dimensional space called the feature space. The aim
is to determine the function f(x) that best fits the
behaviour of the problem as with all the known
regression techniques. A special feature of the SVM
is that it authorises an error or an uncertainty ε
around the regression function (Foucquier et al.,
2013). The form of the f(x) function is the following:
,(() )x
x
bf
(3)
where, Φ represents a variable in the high-
dimensional feature space and <,> is a scalar
product, ω and b are estimated by the following
optimisation problem.
*
*
,, ,
1
*
*
1
min 2
2
,()
,()
,0
i
n
ii
b
i
ii i
iii
ii
C
subject to
yxb
xby
(4)
where, C is a regularisation parameter, which
introduces a trade-off between the flatness of f(x)
and the maximal tolerated deviation larger than ε,
given by users, ξ
i
and ξ
i
*
are two slack variables,
which allow the constraints to be flexible. In
addition, a kernel function defined as a dot product
in the feature space k(x,x’)= <Φ(x),Φ(x’)> is created
to allow the substitution of the complex nonlinear
map with a linear problem without having to
evaluate Φ(x). Examples of kernel function used in
regression by SVM are the linear [k(x
i
,x) = x
i
·x],
polynomial [k(x
i
,x)= (x
i
·x+c)
d
] and radial basis
function (RBF) kernel (Foucquier et al., 2013).
One of the main advantages of the SVM model is
the fact that the optimisation problem is based on the
structural risk minimisation principle. The
minimisation of an upper bound of the
generalization error consisting of the sum of the
ResearchonTechniquesforBuildingEnergyModel
25

training error is the objective of this method. This
principle is usually encountered at the empirical risk
minimisation which only minimises the training
error. An additional advantage is that with this
method there are fewer free parameters of
optimisation. Application of the SVM technique
requires the adjustment of the regularisation constant
C and the margin ε. At the same time, this
adjustment is one of the hardest steps of this method.
The main drawback of the SVM method is the
selection of the best kernel function corresponding
to a dot product in the feature space and the
parameters of this kernel (Foucquier et al., 2013).
4.2.1 Case Studies
Support vector machine models have been used for
predicting energy consumption in buildings quite
recently. Dong et al., (2005) were the first to
introduce the use of SVM for prediction of the
building energy consumption. The objective of their
work was to examine the feasibility and applicability
of SVM in building load forecasting area. In order to
test the developed SVM model, four commercial
buildings in Singapore were selected randomly as
case studies. The input variables were the mean
outdoor dry-bulb temperature, the relative humidity
and the global solar radiation. The kernel function
used was the radial basis function kernel. The
obtained results were found to have coefficients of
variance less than 3% and percentage of error within
4%.
Li et al., (2009) used the SVM model in
regression to predict hourly building cooling load for
an office building in Guangzhou, China. The
outdoor dry-bulb temperature and the solar radiation
intensity were the input parameters for this model.
Results indicated that the SVM method can achieve
accurate predictions and that it is effective for
building cooling load prediction. A comparison of
the newly developed SVM model against different
artificial neural networks was published by the same
research group later the same year (Li et al., 2009).
The SVM model was compared with the traditional
back propagation neural network, the radial basis
function neural network and the general regression
neural network. All prediction models were applied
at the same office building in Guangzhou, China.
The models were evaluated based on the root mean
square error and mean relative error. Simulation
results showed that these models were effective for
building cooling load prediction. The SVM and
general regression neural network methods achieved
better accuracy and generalisation than the back
propagation neural network and radial basis function
neural network methods.
Hou and Lian (2009) also used a SVM model for
predicting cooling load of a HVAC system in a
building in Nanzhou, China. The performance of the
SVM with respect to two parameters, C and ε, was
explored using stepwise searching method based on
radial-basis function kernel. Actual prediction
results showed that the SVM forecasting model,
whose relative error was about 4%, may perform
better than autoregressive integrated moving average
ones.
4.3 Artificial Neural Networks
Artificial neural network (ANN) is a generic
denomination for several simple mathematical
models that try to simulate the way a biological
neural network (for instance human brain) works.
The main characteristic of such models is the
capability of learning the ‘‘rule’’ that controls a
physical phenomenon under consideration from
previously known situations and extrapolate results
for new situations. This learning process is called
network training. The development of artificial
neural networks is based on the observation of the
biological neural network behaviour (Neto and
Fiorelli, 2008).
Several possible arrangements for artificial
network have been suggested, generating different
and distinct network models, since it is not well
known how a biological neuron is arranged (Fausett,
1994). The feed-forward model is the most known
and simple network arrangement, illustrated in
Figure 3. In this model, the neurons are placed in
several layers. The first one is the input layer, which
receives inputs from outside. The last layer, called
output layer, supplies the result evaluated by the
network. Between these two layers, a network can
have none, one or more intermediate layers called
the hidden layers. The input layer is usually
considered a distributor for incoming signal, hidden
layers are signal classifiers, and output layer is the
organizer of obtained responses (Neto and Fiorelli,
2008).
An important detail about the feed-forward
model is that the neurons of a given layer are only
connected with the previous layer and the next one.
Other possible more sophisticated network
arrangements are possible as well, for instance the
Self-Organising Maps creates models in which the
network itself changes its arrangement during the
training phase.
ICAART2014-DoctoralConsortium
26

Figure 3: Typical structure of an artificial neural network.
One of the advantages of this method is that it
does not need to detect the potential co-linearity
included in the problem. Another advantage of the
artificial neural networks is its ability to deduce
from data the relationship between different
variables without any assumptions or any postulate
of a model. Moreover, it overcomes the
discretisation problem and is able to manage data
unreliability. This method suggests a large
variability of the predicted variable form (binary 0
or 1, yes/no, continuous value, etc.) and an efficient
simulation time.
Conversely, artificial neural networks are
significantly limited by the fact that a relevant
database should be available in order to be applied.
In fact, it is of vital importance to train the network
with an exhaustive learning basis, which consists of
representative and complete samples. For instance,
samples in different seasons or in different moments
of the day or during weekend or holidays etc. as well
as samples, which contain the same amount of
information. An additional disadvantage of the
artificial neural network is its large number of
undetermined parameters, for which there are no
rules to determine (Foucquier et al., 2013).
4.3.1 Case Studies
Artificial neural networks have been applied by
researchers to analyse various types of building
energy consumption, such as heating and cooling
load, under different conditions.
Kalogirou et al., (1997) implemented back
propagation neural networks at an early design stage
in order to predict the required heating load of
buildings. The network was trained based on 250
known cases of heating load, varying from large
spaces of 100 m
2
floor area to very small rooms.
Input data included the areas of windows, walls,
partitions and floors, the type of windows and walls,
classification on whether the space has a roof or
ceiling, and the design room temperature. Another
artificial neural network for the estimation of daily
heating and cooling loads was developed by the
same group of researchers (Kalogirou et al., 2001).
A multi-slab feed-forward architecture having 3
hidden slabs was used and each slab comprised of 36
neurons. The accuracy of this network was within
the acceptable level (relative error 3.5%).
The predictions of an artificial neural network
can be made on an hourly basis as well. Gonzalez
and Zamarreno (2005) were based on a special kind
of artificial neural network, which feeds back part of
its outputs, to predict the hourly energy consumption
in buildings. The network was trained by means of a
hybrid algorithm. The inputs of the network were
current and forecasted values of temperature, the
current load and the hour and the day. The achieved
results demonstrated high precision.
The performance of adaptive ANN models that
are capable of adapting themselves to unexpected
pattern changes in the incoming data was evaluated
by Yang et al., (2005). Two adaptive models were
proposed and evaluated, accumulative training and
sliding window training. These models can be used
for real-time on-line building energy prediction.
Moreover, they used both simulated (synthetic) and
measured datasets. When synthetic data was used
the two models appeared to have equal performance
in terms of coefficient of variation (CV). On the
other hand, when real measurements were used the
sliding window training performed better than
accumulative training, CV of 0.26 compared to 2.53
respectively.
More recently, Ekici and Aksoy (2009) used an
ANN to predict building energy needs benefitting
from orientation, insulation thickness and
transparency ratio. A back propagation network was
preferred and available data were normalised before
being presented to the network. The calculated
values compared to the outputs of the network gave
satisfactory results with a deviation of 3.4%.
Dombayci (2010) developed an artificial neural
network model in order to forecast hourly heating
energy consumption of a model house. The hourly
heating energy consumption of the model house was
calculated with degree-hour method. The model was
trained with heating energy consumption values of
years 2004–2007 and tested with heating energy
consumption values for the year 2008. Best estimate
was found with 29 neurons and a good coherence
was observed between calculated and predicted
values.
A comparison between detailed model
simulation and artificial neural network for
ResearchonTechniquesforBuildingEnergyModel
27
forecasting building energy consumption was
published by Neto and Fiorelli in 2008. EnergyPlus
was used as the model based on physical principles.
Results of this study indicate that EnergyPlus
consumption forecasts present an error range of
±13% for 80% of the tested database. Major source
of uncertainties in the detailed model predictions are
the improper evaluation of lighting, equipment and
occupancy schedules. The artificial neural network
model results had an average error of about 10%
when different networks for working days and
weekends were implemented. The outcome of this
study was that both models are suitable for energy
consumption forecast.
In the same year Aydinalp-Koksal and Ugursal
(2008) compared the use of neural network against
conditional demand analysis (CDA) and engineering
approaches for modelling the end-use consumption
in the residential sector in Canada. The prediction
performance and the ability to characterise the
consumption of the aforementioned methods were
compared in this study. The results indicated that
neural networks and CDA are capable of accurately
predicting the energy consumption in the residential
sector as well as energy simulation programs.
Moreover, the effects of socio-economic factors
were estimated using the neural network and the
CDA model, where possible. Neural network model
was proved to have higher capability of evaluating
these effects compared to the CDA model.
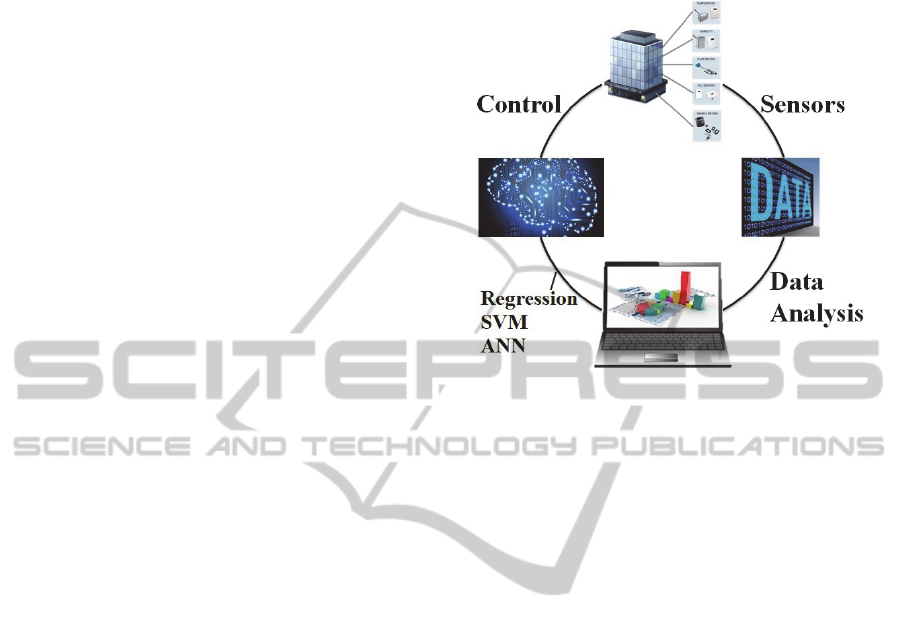
5 METHODOLOGY
Based on the methodologies described earlier new
models will be developed taking account of the key
principles outlined in the objectives. In order to
achieve this, the sequence presented below will be
followed:
Acquisition of real measured data of a
commercial building (testbed 1) from installed
sensors;
Data analysis;
Development of the new models;
Improvement of models accuracy;
Evaluation of new models based on accuracy and
on-line training capability;
Selection of the most suitable model;
Examination of model scalability with the use of
another commercial building (testbed 2);
Determination of commissioning and
maintenance effort for the implementation of the
model.
The methodology that is described in this
sequence is also illustrated in Figure 4.
Figure 4: Development of methodology.
The first step of this methodology is to acquire as
much data as possible from BEMS already installed
in a commercial building. Afterwards, data analysis
is employed to replace missing data and correlate
variables to obtain a complete and comprehensive
dataset. The ultimate goal of this data mining
process is to assist with building load prediction,
where incomplete data is available.
Data Mining is utilised to explore the data, to
search for consistent patterns and/or systematic
relationships between variables, and then to validate
the findings by applying the detected patterns to new
subsets of data.
In order to determine the new model the
selection of the optimum model between regression,
SVM and ANN models is required. Different
multiple regression models will be developed
alongside numerous SVM models and several
architectures of ANN and tested in order to reach the
optimum one. The chosen model amongst the
aforementioned will be selected based on its
accuracy and tested for its ability to train on-line.
The scalability of the model will be the next
thing under examination. Data from a second
commercial building will be introduced to the model
and its ability for accurate predictions will be tested
once again.
Finally, commissioning and maintenance effort
for the implementation of the new model will be
determined. Hence, the model will be evaluated
based on its ability to meet the necessary
requirements.
ICAART2014-DoctoralConsortium
28

6 EXPECTED OUTCOME
The expected outcome of this project is the
development of a novel whole-building energy
model. The model will take advantage of historical
measured data of commercial buildings in order to
generate accurate prediction of heating and cooling
load. Data analysis will be one of the milestones of
this project, since usually measurements include
missing values due to equipment malfunction,
maintenance, etc. An efficient method of dealing
with missing values related with acquired datasets
will be the first outcome of the project.
Once a comprehensive dataset is obtained, the
most suitable methodology for this application is
going to be selected between regression, SVM and
ANN models. An evaluation of the developed
models will take place based on the accuracy of each
model and its ability to train on-line or not. The
selection of the most appropriate model will be the
second outcome.
After the selection process, the chosen model
will be evaluated based on its scalability. The ability
of forecasting heating and cooling loads of two
different given building within the same level of
accuracy will be the criterion. If the chosen model
does not have the desired scalability, then another
model will be selected from the previous procedure
and examined based on its scalability. Finally, the
effort required for commissioning and maintenance
of the model should be as little as possible. The final
outcome should be a scalable model with minimum
commissioning and maintenance requirements.
Ideally, this novel approach of estimating the
thermal and cooling load of commercial buildings
could be implemented to the control of the BEMS.
In this way, the efficiency of the HVAC systems of
the building could be improved reducing the energy
consumption at the same time. This will also lead to
a reduction of the energy cost of commercial
buildings.
REFERENCES
Aranda, A. et al., 2012. Multiple regression models to
predict the annual energy consumption in the Spanish
banking sector. Energy and Buildings, Volume 49, pp.
380-387.
ASHRAE, 2009. Energy Estimating and Modeling
Methods. In: ASHRAE Handbook-Fundamentals.
Atlanta: American Society of Heating, Refrigerating
and Air-Conditioning Engineers, Inc., pp. 32.1-32.33.
Aydinalp-Koksal, M. & Ugursal, V. I., 2008. Comparison
of neural network, conditional demand analysis, and
engineering approaches for modeling end-use energy
consumption in the residential sector. Applied Energy,
85(4), pp. 271-296.
Bauer, M. & Scrartezzini, J., 1998. A simplified
correlation method accounting for heating and cooling
loads in energy-efficient buildings. Energy and
Buildings, 27(2), pp. 147-154.
Catalina, T., Iordache, V. & Caracaleanu, B., 2013.
Multiple regression model for fast prediction of the
heating energy demand. Energy and Buildings,
Volume 57, pp. 302-312.
Catalina, T., Virgone, J. & Blanco, E., 2008. Development
and validation of regression models to predict monthly
heating demand for residential buildings. Energy and
Buildings, Volume 40, pp. 1825-1832.
Dombayci, A., 2010. The prediction of heating energy
consumption in a model house by using artificial
neural networks in Denizli–Turkey. Advances in
Engineering Software, 41(2), pp. 356-362.
Dong, B., Cao, C. & Lee, S. E., 2005. Applying support
vector machines to predict building energy
consumption in tropical region. Energy and Buildings,
37(5), pp. 545-553.
Ekici, B. B. & Aksoy, U. T., 2009. Prediction of building
energy consumption by using artificial neural
networks. Advances in Engineering Software, 40(5),
pp. 356-362.
Fausett, L., 1994. Fundamentals of neural networks:
architectures, algorithms, and applications. Upper
Saddle River, NJ, USA: Prentice-Hall, Inc.
Foucquier, A. et al., 2013. State of the art in building
modelling and energy performances prediction: A
review. Renewable and Sustainable Energy Reviews,
Volume 23, pp. 272-288.
González, P. A. & Zamarreño, J. M., 2005. Prediction of
hourly energy consumption in buildings based on a
feedback artificial neural network. Energy and
Buildings, 37(6), pp. 595-601.
Hou, Z. & Lian, Z., 2009. An Application of Support
Vector Machines in Cooling Load Prediction. Wuhan,
s.n., pp. 1-4.
Kalogirou, S. A., Neocleous, C. C. & Schizas, C. N., 1997.
Building heating load estimation using artificial neural
networks. s.l., s.n., pp. 1-8.
Kalogirou, S., Florides, G., Neocleous, C. & Schizas, C.,
2001. Estimation of Daily Heating and Cooling Loads
Using Artificial Neural Networks. Napoli, Clima
2000.
Lam, J. C., Wan, K. K. W., Liu, D. & Tsang, C. L., 2010.
Multiple regression models for energy use in air-
conditioned office buildings in different climates.
Energy Conversion and Management, 51(12), pp.
2692-2697.
Li, Q. et al., 2009. Applying support vector machine to
predict hourly cooling load in the building. Applied
Energy, 86(10), pp. 2249-2256.
Li, Q. et al., 2009. Predicting hourly cooling load in the
building: A comparison of support vector machine and
ResearchonTechniquesforBuildingEnergyModel
29

different artificial neural networks. Energy Conversion
and Management, 50(1), pp. 90-96.
Neto, A. H. & Fiorelli, F. A. S., 2008. Comparison
between detailed model simulation and artificial neural
network for forecasting building energy consumption.
Energy and Buildings, 40(12), pp. 2169-2176.
Parti, M. & Parti, C., 1980. The total and appliance-
specific conditional demand for electricity in the
household sector. Bell Journal of Economics, Volume
11, pp. 309-321.
Vapnik, V. & Cortes, C., 1995. Support-Vector Networks.
Machine Learning, Volume 20, pp. 273-297.
Westergren, K.-E., Högberg, H. & Norlén, U., 1999.
Monitoring energy consumption in single-family
houses. Energy and Buildings, 29(3), pp. 247-257.
Yang, J., Rivard, H. & Zmeureanu, R., 2005. On-line
building energy prediction using adaptive artificial
neural networks. Energy and Buildings, 37(12), pp.
1250-1259.
Zhao, H.-X. & Magoulès, F., 2012. A review on the
prediction of building energy consumption. Renewable
and Sustainable Energy Reviews, 16(6), pp. 3586-
3592.
ICAART2014-DoctoralConsortium
30
