Forests of Latent Tree Models for Genome-Wide Association Studies

Phan Duc Thanh

LINA, UMR CNRS 6241, Ecole Polytechnique de l’Universit de Nantes, Nantes, France

1 CONTEXT

With the ﬁnalization of the Human Genome Project in

2003, it was conﬁrmed that any two individuals share,

on average, 99.9% of their genome with each other.

It is the sole 0.1% genetic variations that explain why

individuals are physically different or inherit a greater

risk of contracting disorders, such as heart disease or

cancer. Therefore, identifying the genetic factors un-

derlying disease can potentially play a crucial role in

developing new treatments and has been one of the

main focus of human genetics research during the last

thirty years (Hechter, 2011). Among different ap-

proaches that have been proposed, association study

stands out as one of the most successful path, even

though its potential is yet to be fully tapped.

During the past decades, a great deal of effort has

been put into the investigation of heritable suscep-

tibility to complex diseases which, contrary to rare

monogenic disorders, are thought to be affected by,

not a single one, but multiple genetic variants. In ef-

fect, according to a hypothesis known as common dis-

eases - common variants (CDCV), it is conjectured

that most of the risk of common disorders, such as

cancers, could be explained by common variations in

several genes. Since these variants are common, they

are susceptible to detection using association studies.

Traditionally, the strategies for association study

involve performing analysis with only a small num-

ber of loci (DNA locations) pre-chosen with the help

of prior knowledge. For example, ﬁne-mapping stud-

ies are conducted only in a pre-selected candidate

region of 1-10Mb (one Mb equals 10

nucleotides).

Thanks to new advances in techniques for genotyping

and sequencing genomes, researchers started to work

on seeking genetic variations potentially associated

to common diseases throughout the entire genome

(GWAS). In the following years, the HapMap Project

and its successor, the 1000 Genomes Project, were

launched with the hope to establish a catalogue of

human genome regions in which people of different

populations have differences.

In a nutshell, GWASs seek to identify combi-

nations of markers (DNA sequence with a known

location) whose frequency vary systematically be-

tween individuals with different disease states (Bald-

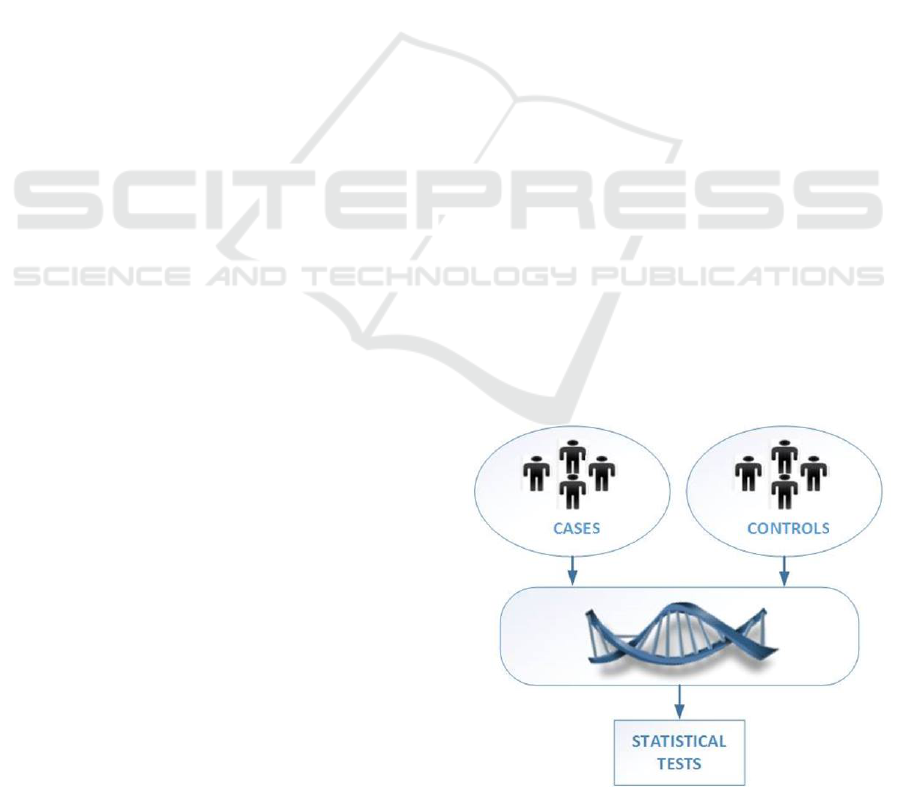
ing, 2006). Its most basic form consists in comparing

allele frequencies in cases and controls, as depicted

in Figure 1, on data of generally large size (hundreds

of millions genetic variants from thousands of peo-

ple). The goal is to identify the loci on the genome

for which the distributions of observations are signif-

icantly different, using statistical tests (e.g. the Chi

test). In that case, we have reasons to believe that

the gene affecting the trait might be located some-

where in the neighborhood of the pinpointed region.

The unit variants, called single-nucleotide polymor-

phisms (SNPs) (single base-pair changes in the DNA

sequence), are very often used as markers in GWASs.

SNPs are by far the most abundant type of variant in

human.

Figure 1: GWAS procedure.

Apart from identifying disease-related factors, an-

other motivation for GWASs is the increasing deep

societal mutation observed in Western countries. In

France, about 12% of the gross domestic product are

currently dedicated to the public health expenditure,

whereas this percentage was only 3% 30 years ago.

For a main part, this ever increasing share of pub-

lic health expenditure is to be related to the gain in

Duc Thanh P..

Forests of Latent Tree Models for Genome-Wide Association Studies.

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

longevity, which favours the emergence of chronic

diseases by elderly subjects. Therefore, a better un-

derstanding of gene susceptibility to pathologies is

expected to better control public health expenditure.

Other applications of GWASs can be found in

pharmacology where scientists seek to correlate pat-

terns of variations associated with phenotypes such as

adverse drug responses and drug metabolism or par-

ticularly in personalized medicine where healthcare

decisions can be guided by individuals’ genetic pro-

ﬁle.

Many evidences obtained have led to believe that

the CD-CV hypothesis holds. It is then essential to

obtain the most common patterns of human genetic

variation, hence the motivation for the Human Hap-

lotype Map (HapMap) project and its successor, the

1000 Genomes Project (a haplotype can be informally

described as a cluster of nearby SNPs). The main goal

of these international efforts is to identify and cata-

logue variations and their relations across the entire

human genome from various populations. From these

databases, we are able to study a known phenomenon

called linkage disequilibrium (LD), referring to the

dependence between SNPs at two or more sites.

LD plays a role of huge importance in GWASs for

various reasons. A well-designed study will have a

good chance of including one or more SNPs that are in

strong LD with a common causal variant. LD reﬂects

the blurring of the ancestral genome, mainly but not

only due to combinations and mutations. Standard

statistical approaches that do not take into account this

type of correlation between variables will not work

well on genome-wide data.

The explosion of complex GWAS data has re-

quired the development of new analysis methods for

dealing with challenges regarding, among others, sta-

tistical power increase and false discovery rate con-

trol. Within bioinformatics in particular, probabilistic

graphical models (PGMs) are considered as powerful

machine learning approaches thanks to their capacity

for capturing complex relationships and dealing with

high-dimensionality. In this regard, the main purpose

of this thesis is to design PGM-based GWAS strate-

gies that are capable of effectively ﬁnding suscepti-

bility to complex diseases.

The rest of this paper is organized as follows. We

will ﬁrst provide a brief overview of various LD mod-

elling approaches relying on machine learning tech-

niques, and among them on PGM-based methods; we

will then discuss different challenges that may arise;

the outline of desired objectives we aim to achieve, as

well as the research methodology, will also be given,

followed by a presentation of the current research

stage.

2 STATE OF THE ART

The complex structure of LD in the human genome

was revealed by the HapMap project. More specif-

ically, it is claimed that LD is highly structured

into the so-called “haplotype block structure” regions

(Patil et al., 2001) where statistical dependences be-

tween contiguous markers (called blocks) alternate

with shorter regions characterized by low statistical

dependences. In addition to complexity, a systemic

whole-genome analysis with high-density data typ-

ically involves a large number of variables, which

poses a tremendous challenge in terms of scalability.

Interestingly, LD may offer a solution to dimen-

sionality reduction. Relying on the “haplotype block

structure”, various approaches have been proposed to

perform multi-SNP association test with haplotypes,

i.e. inferred data underlying genotypic data such as

in (Schaid, 2004), or partitioning the genome accord-

ing to spatial correlation (Pattaro et al., 2008). By

contrast, the method proposed in (Han et al., 2008)

chooses to select SNPs informative about their con-

text - or SNP tags. The HaploBuild software pro-

gram (Laramie et al., 2007) allows the construction

of more biologically relevant haplotypes that are not

constrained by arbitrary length, thus making it able to

learn ”haplotype cluster structure”.

In general, LD exhibited among physically close

loci is stronger than LD between SNPs that are farther

apart. In other words, LD decays with distance. Lim-

itations of previous stated methods include not taking

into account long-range dependences. Besides, these

methods do not consider the fuzzy nature of LD which

refers to the fact that LD block boundaries are not ac-

curately deﬁned over the genome.

Probabilistic graphical models (PGMs), due to

their appealing characteristics, represent an appropri-

ate framework and have gained indeed signiﬁcant at-

tention from researchers to analyse LD .

2.1 Probabilistic Graphical Models in

Linkage Disequilibrium Modelling

Graphical models provide rich families of graph-

based probabilistic models of joint multivariate prob-

ability distributions that capture properties of con-

ditional independence between variables (Friedman

et al., 2000). In a graph, nodes represent the variables

and edges denote direct dependences between these

variables. There are two main classes of probabilistic

graphical models, namely Bayesian Networks (BNs)

and Markov Random Fields (MRFs).

As pointed out, PGMs allow to capture complex

dependences between SNPs (due to LD). In addition,

ForestsofLatentTreeModelsforGenome-WideAssociationStudies

we can also integrate useful prior domain knowledge

to enhance the model quality as well as to improve

the performance of its construction. For example, as

PGMs can describe very well local dependences, by

limiting the network of dependences for each node

within a certain physical range, we can dramatically

reduce the model’s complexity (Verzilli et al., 2006).

However, although PGMs had long been widely rec-

ognized as a powerful formalism in the bioinformatics

domain in gene expression studies and linkage analy-

sis, they received much less attention in genetic asso-

ciation studies up to recently.

2.1.1 Markov Random Fields

MRFs are a class of PGMs where undirected graphs

are used to represent dependences. The study of ap-

plying MRFs in modelling LD has been rather active

since ﬁrst paper by Alun Thomas et al. (Thomas and

Camp, 2004) in which they restricted the computa-

tion of the joint distribution to a tractable subclass

of MRFs called decomposable (or equivalently trian-

gulated). The idea is to use a simulated annealing

search strategy which, given a decomposable graph,

computes efﬁciently the score of one of its neighbour

graphs.

Also relying on Decomposable MRFs (DMRF),

Verzilli et al. in (Verzilli et al., 2006) proposed to

model haplotype blocks explicitly as cliques. More-

over, each clique is labelled with a boolean value

(1/0) indicating the existence of at least one edge be-

tween some vertex in the clique and the phenotype

(i.e. disease) vertex. Since checking the decompos-

ability property is computationally demanding, the

authors opted to select appropriate moves to preserve

this property while browsing the search space of DM-

RFs.

2.1.2 Bayesian Networks

Bayesian Networks, on the other hand, employ

acyclic directed graphs to specify joint distribution

over the variables. The models within this class can

be further categorized into two different paradigms:

with and without latent variables (LV). An LV repre-

sents factors that exist but are unobservable and may

induce correlations between observed variables that

do not correspond to direct causal relations (Kollar

and Friedman, 2009).

Belonging to the former category, BNTagger is

a method proposed by Lee and Shatkay in (Lee and

Shatkay, 2006) for SNP tag selection. To efﬁciently

learn the structure, the authors opted for a greedy

search strategy with random restarts. The ﬁnal aim

of this modelling is to determine a subset of indepen-

dent and highly predictive SNPs.

BN models with LVs have also been studied to

model and exploit LD. The general principle com-

prises using the structural expectation maximization

(SEM) algorithm (Friedman et al., 2000) to infer the

structure as well as the model parameters. Neﬁan, for

instance, proposed a method (Neﬁan, 2006) based on

the concept of Embedded Bayesian Networks (EBN).

EBNs are hierarchical BNs where a subset of ob-

served nodes have as parent only one latent node, to

form a latent class model (LCM).

The two-layer model employed by Neﬁan can

possibly be enriched with SNP dependences. Ne-

ﬁan’s block-based approach involves ﬁrst splitting the

genome into contiguous windows (i.e. blocks), then

learning an LCM for each window. Afterwards, SEM

is applied to learn dependences between SNPs and be-

tween LVs. However, this model imposes that vari-

ables in the same LCM must be spatially contiguous

on the genome. Further, the window size is ﬁxed to a

small value. A consequence is a severe lack of ﬂexi-

bility. To address this shortcoming, another two-layer

BN was proposed by Zhang and Ji (Zhang and Ji,

2009) which can be described as a mere set of non-

connected LCMs. This model relaxes several condi-

tions of the previous one, including that the SNPs in

the same cluster are not required to be spatially con-

tiguous and that the cluster sizes can vary. However,

the number of clusters is a parameter which has to be

speciﬁed.

2.2 Scalable Methods

None of these aforementioned methods scales well

with the number of SNPs and number of individu-

als in the observed population. Several methods have

been proposed to address this problem in the GWAS

context. Among those, Hidden Markov models

(HMMs) were used by Scheet and Stephens (Scheet

and Stephens, 2006) to infer haplotypes. Therein,

the latent states correspond to ancestral haplotypes.

This model can deal with either block-like LD struc-

ture or gradual decline of LD with distance. It is

implemented in the well-known accurate and scal-

able fastPHASE program (one thousand individuals

and hundreds of thousands of genetic markers). Be-

sides, in contrast with block-based models, this model

provides ﬂexibility since it allows ancestral haplotype

membership to change at any SNP site.

In contrast with Scheet and Stephen, Browning

and Browning proposed the variable-length Markov

chain (VLMC) where no pre-speciﬁcation of the

structure, such as the number of ancestral haplotypes,

BIOSTEC2014-DoctoralConsortium

is required (Browning and Browning, 2009). VLMCs

allow the memory length to vary along the chain. This

work resulted in the widely used BEAGLE tool which

scales particularly well with datasets of hundreds of

thousands of markers describing thousands of individ-

uals.

Another possibility to obtain scalability is through

interval graphs in which each vertex may be associ-

ated with an interval of the genome and edges connect

any two strictly overlapping intervals. These graphs

can be proved to be decomposable, thus resolving

the non-decomposability issue (Thomas, 2009). On

the other hand, local computation of the likelihood is

implemented during the Markov chain Monte Carlo

(MCMC) sampling devoted to interval updating. In-

tervals are particularly appealing to account for LD

extent around a locus. Finally, more recent works ex-

ploiting graph theory properties were shown to actu-

ally help achieve notable performance gain in DMRF

structure learning (Abel and Thomas, 2011; Thomas

and Green, 2009).

Unfortunately, none of the aforementioned ap-

proaches lends itself to incorporate data to reinforce

evidence for genotype-disease association identiﬁca-

tion, in a GWAS context. In addition, the model

choice for VLMC in BEAGLE cannot take into con-

sideration long-range or hierarchical dependences in

genotype data.

In conclusion, even though PGMs have been used

and have shown promises as an alternative to tradi-

tional GWAS analysis methods, they still have various

limitations to address. In addition, only a few number

of model based strategies have been proposed up to

now to perform GWASs.

3 RESEARCH PROBLEMS

Despite the early successes of GWASs, various chal-

lenges remain to be addressed. First of all, the

task of analyzing SNP combinations across the en-

tire genome is very challenging computationally, due

to the large number of SNPs in high-density GWAS

data. Further, the complexity increases exponentially

with the number of SNPs to consider (this issue is

known as “the curse of dimensionality”), which has

necessitated the development of innovative methods.

Besides, as the number of SNPs is usually signiﬁ-

cantly bigger than the number of individuals, we often

face the so-called small n-large p problem, for which

traditional statistical methods cannot be applied. In

addition to the enormous quantity of variables, the re-

lationships among variables (i.e. SNPs) as well as be-

tween disease susceptibility genotypes and diseases

are very complex and far from being fully understood.

Failing to take into consideration these types of high-

order, non-linear correlations, a GWAS strategy will

likely be unable to efﬁciently identify the causal vari-

ants.

On the other hand, a good study design should

take account of additional prior knowledge, for var-

ious reasons. In effect, even if the computational

methods can identify correctly disease-related SNPs,

it can be translated into improving health care deci-

sion know-how only if the context of biology is taken

into account (Moore et al., 2010). These kinds of do-

main knowledge can come from various forms such

as prior biological ﬁndings or supplementary data

sources. For instance, gene ontology, gene-gene in-

teractions and transcription factors’ targets data can

potentially provide useful information.

Furthermore, the evaluation of the innovative

GWAS strategies will require the fast generation of

realistic genome-wide simulated data. For this pur-

pose, a gold standard is HapGen (Su et al., 2011)

which consists in simulating genotypes given the phe-

notypes. However, because it generates both geno-

typic and phenotypic data for each simulation, it is

considered not fast enough for our needs.

Last but not least, conducting effectively exper-

iments on massive genome-wide datasets demands

high performance software codes. This is a com-

mon issue for many ﬁelds which require dealing with

large-scale computation. The implementation should

be resource-optimized while able to maintain a certain

degree of user-friendliness to facilitate the communi-

cation of results. Moreover, it should be noted that it

is not always easy to provide output that is simulta-

neously visual and easy to navigate. This last point

is relevant due to the needs for communicating results

with other collaborators of different backgrounds (e.g.

geneticists, physicians).

4 OUTLINE OF OBJECTIVES

Since the ﬁrst successful GWAS in 2005 (Klein et al.,

2005), the amount of yearly published studies has

constantly increased, reaching more than 2300 stud-

ies in 2011. Nowadays, GWAS has evolved to be a

major method to identify genetic risk factors for dis-

eases. As pointed out, PGMs have proven to be very

promising for the statistical analysis of GWAS data

but their potential is yet to be fully achieved. In this

thesis work, we wish to explore this path, develop-

ing novel computational PGM-based GWAS strate-

gies for unravelling the underlying genetic structure

of common disorders.

ForestsofLatentTreeModelsforGenome-WideAssociationStudies

Carried out at the KOD team of the LINA labora-

tory and in the framework of the ANR project named

SAMOGWAS, the objectives of this thesis are numer-

ous and varied, which include but are not limited to:

• model the genetic data at the genome scale and de-

sign the corresponding method to construct such

models

• develop, evaluate and compare several PGM-

based GWAS strategies,

• apply the best strategy on real biological data.

The ﬁrst goal is to establish a framework for

modelling genotype data, based on a class of PGMs

called forests of Latent Tree Models. Within this

framework, we will then design and compare several

GWAS strategies. Central to our design is the incor-

poration of domain knowledge to enhance the GWAS

strategies. Besides, we aim to address the lack of

methods for GWAS strategy evaluation and valida-

tion. Finally, in the context of GWASs, the computa-

tion involved typically takes a long time, ranging from

days to weeks and even months (Fabregat-Traver and

Bientinesi, 2012). As a consequence, we also plan to

deliver highly-optimized applications to realize effec-

tively the work.

5 METHODOLOGY

This multidisciplinary and interdisciplinary work will

be carried out in an incremental manner, in close col-

laboration with multiple partners (geneticists, genetic

epidemiologists, computer scientists and mathemati-

cians). The main idea is to establish a modelling

framework based on the Forests of Latent Tree Mod-

els (F models).

First introduced by Zhang and initially called hi-

erarchical latent class models (Zhang, 2004), F mod-

els are tree-structured Bayesian networks where leaf

nodes are observed while internal nodes are not. In

latent tree models (LTMs), multiple latent variables

organized in a hierarchical way allow to depict a large

variety of relations encompassing local to higher-

order dependences, as depicted in ﬁgure 2. The sur-

vey in (Mourad et al., 2013) provides an exhaustive

review of the different classes of methods used for

learning the structure of LTMs. Among these meth-

ods, there is one simple procedure which relies on ag-

glomerative hierarchical clustering and consists in it-

erating two main steps: (i) discovering cliques of de-

pendent variables; (ii) synthesizing cliques’ informa-

tion by latent variables (Mourad et al., 2010).

A ﬁrst version of this speciﬁc learning algo-

rithm has been shown to be tractable on bench-

marks describing 100000 variables for 2000 individu-

als (Mourad et al., 2011). The theoretical complexity

was proved to scale linearly with the number of SNPs

and quadratically with the number of individuals. The

versatile LTMs offer an adapted framework to encode

the fuzzy nature of linkage disequilibrium blocks. Be-

sides, as previously shown, by introducing latent vari-

ables, LTMs can enable data dimensionality reduc-

tion. The scalability comes from the reduction of the

data dimension, due to the subsumption of variables

through latent variables. The ﬂexibility comes from

the generality of the forest (i.e. it is not constrained to

be a binary topology; moreover, the (discrete) latent

variables may have different cardinalities).

Figure 2: Latent tree model. The light shade indicates the

observed variables whereas the dark shade points out the

latent variables.

In addition to PGMs, Random Forest (RF) is an-

other Machine Learning technique which is often em-

ployed in GWASs, thanks to its advantage in analyz-

ing high dimensional data. A speciﬁc adaptation of

the Random Forest method has been investigated by

the GIGA-R partner of the SAMOGWAS project, to

perform GWASs, leading to the T-tree model (Botta

et al., 2008). In contrast with the standard applica-

tion to GWASs of a Random Forest-based method, the

idea is to exploit the haplotype block structure by re-

placing SNP-based splits with haplotype block-based

splits in this decision tree-based method. In addition

to genotyped cases and controls, this algorithm thus

needs as input a decomposition of the set of SNPs into

haplotype blocks.

We also observed that in the F model, each la-

tent variable represents a haplotype block while a de-

composition of the set of SNPs into haplotype blocks

is requested to run the T-tree-based approach. Con-

versely, the haplotype block importance computed by

the T-tree-based method could be exploited by the F

model to target a potentially causal block for the stud-

ied disease. Thus, a combination of these two models,

where the clusters identiﬁed by F models will serve as

prior knowledge for T-tree models, looks like a very

promising perspective.

BIOSTEC2014-DoctoralConsortium

On top of this, various GWAS strategies will be

designed based on the aforementioned models. For

example, a GWAS strategy based on F-models should

involve traversing the forest for ﬁnding the most sig-

niﬁcantly associate nodes. A solution for this consists

in running a best-ﬁrst search traversal for any sub-

tree rooted in a latent variable signiﬁcantly associated

with the disease.

In parallel, various sets of real-life data will be

collected. These datasets will be used for the ﬁnal

validation of the results which will then be interpreted

together with biologists. We will also incorporate

to our GWAS strategies supplementary transcriptome

data and additional knowledge from gene ontologies

and from gene annotation databases, with the help of

our collaborators. This incorporation will likely al-

low the enrichment of the models as well as the cross-

conﬁrmation of putative associations between genetic

factors and disease.

Regarding the evaluation of model-based strate-

gies, we need a method that can quickly and re-

liably generate consistent genotypic, transcriptomic

and phenotypic data. First, the current standard meth-

ods for GWAS data simulation are not very efﬁcient

because they generate both genotypic and phenotypic

data for each simulation. In contrast, when a GWAS

relies on the time-consuming construction of a com-

plex model of the LD (i.e. the F model), we wish

to generate only simulated phenotypes while keeping

the same genotypic data for all simulations. For this

purpose, the key is to sequentially sample the phe-

notypes according to a probability distribution that

accounts for the total number of cases to be gener-

ated and the current number of cases already gener-

ated. Second, generating both GWAS data and sim-

ulated transcriptomic data in a consistent way repre-

sents a real challenge. For this purpose, we will inves-

tigate several adaptations of the previously described

method.

Last but not least, as previously stated, our

work’s realization needs to be robust and efﬁcient

for handling computation-intensive tasks. The idea

to achieve performance-optimized implementation re-

lies mainly on CPU-based parallelization of code.

The applications will be able to be deployed on multi-

core as well as grid computing systems. Finally, since

F Models are based on graphs, several approaches

for effectively visualizing and manipulating F mod-

els will be explored. One of them relies on the Tulip

visualization tool designed to display and annotate

large graphs (Auber, 2004). Such visual representa-

tions may enable better analysis of results by the end

users.

6 STAGE OF THE RESEARCH

Started in October 2013, this thesis will be carried on

for the next 3 years within the KOD team at the Ecole

Polytechnique de l’Universit

e de Nantes, under the

supervision of Christine Sinoquet and Philippe Leray.

Currently at the early stage, we are working within the

methodology previously stated on several aspects in-

cluding the implementation of the framework. We are

now designing and implementing a framework opti-

mized for high-performance computing, a crucial ne-

cessity for deep GWAS analysis. The idea consists

mainly in using parallel C++ coding for CPU-based

systems, facilated by OpenMP (Dagum and Menon,

1998) and Open MPI (Gabriel et al., 2004). OpenMP

is an application programming interface (API) that

supports multi-platform shared memory multipro-

cessing whereas Open MPI is a popular implemen-

tation of the standardized Message Passing Interface

(MPI) allowing to run applications across computer

clusters. We also rely on a Bayesian Network library

called ProBT, provided by the ProbaYes partner in the

SAMOGWAS project (www.probayes.com). Once

ﬁnished, we will use this application as back-end for

carrying out experiments to evaluate F-Model-based

GWAS on simulated data (spring 2014). Front-end

applications for visualizing and manipulating analysis

results are also going to be provided. For the former

task, the genome-wide visualization of the F models

can be implemented in C++ with the help of the Tulip

library (http://tulip.labri.fr/TulipDrupal/). In parallel

with these implementation and test tasks, in the ﬁrst

half of 2014, a thorough methodological work focus-

ing on additional data integration will be conducted

in collaboration with the INSERM partner (i.e. biolo-

gists).

7 EXPECTED OUTCOME

Already considered as an important bio-medical re-

search interest, GWASs are still a relatively young

area which have generated numerous and varied dif-

ﬁcult challenges. After this thesis work, we hope

to obtain a proven GWAS model-based integrative

strategy and a novel simulation strategy satisfying

the conditions previously mentioned. We also antici-

pate to have a reliable high-performance software im-

plementation of both the model learning algorithms

and the model-based GWAS strategies. The back-

end applications will be deployed on the GIGA-R and

INSERM grid computing platforms to provide high

quality analysis services. Above all, this multidisci-

plinary work is expected to help expand our knowl-

ForestsofLatentTreeModelsforGenome-WideAssociationStudies

edge about genetic variants that inﬂuence the suscep-

tibility to complex diseases. In the process, it may

help gain progress across multiple-domains, includ-

ing:

• machine learning and data mining: statistical

models and techniques for dealing with GWAS

data that take account high-dimensionality and

variable correlation will be designed; methods for

the improvement of models through integrating

additional knowledge will be proposed;

• medicine: the methods designed intend to bring

new evidence of genetic disease susceptibility

as well as individual genetic susceptibility to

drugs, thus offering perspectives for personalized

medicine;

• public health: our work will contribute to account-

ing for the societal evolution trend toward early

gene susceptibility detection to improve preven-

tion or surveillance;

• economy: The animal and plant biology domains

are also concerned with respect to the selection of

phenotypes of interest in agronomy as well;

• high-performance computing for GWASs: cutting

edge techniques for implementing GWAS strate-

gies and large-scale machine learning approaches

will be implemented.

REFERENCES

Abel, H. J. and Thomas, A. (2011). Accuracy and computa-

tional efﬁciency of a graphical modeling approach to

linkage disequilibrium estimation. Statistical applica-

tions in genetics and molecular biology, 10(1).

Auber, D. (2004). Tulip: A huge graph visualization frame-

work. In Graph Drawing Software, pages 105–126.

Springer.

Balding, D. J. (2006). A tutorial on statistical methods for

population association studies. Nature Reviews Ge-

netics, 7(10):781–791.

Botta, V., Hansoul, S., Geurts, P., and Wehenkel, L. (2008).

Raw genotypes vs haplotype blocks for genome wide

association studies by random forests. In Proc. of

MLSB 2008, second workshop on Machine Learning

in Systems Biology.

Browning, B. L. and Browning, S. R. (2009). A uniﬁed ap-

proach to genotype imputation and haplotype-phase

inference for large data sets of trios and unrelated in-

dividuals. The American Journal of Human Genetics,

84(2):210–223.

Dagum, L. and Menon, R. (1998). Openmp: an industry

standard api for shared-memory programming. Com-

putational Science & Engineering, IEEE, 5(1):46–55.

Fabregat-Traver, D. and Bientinesi, P. (2012). Comput-

ing petaﬂops over terabytes of data: The case of

genome-wide association studies. arXiv preprint

arXiv:1210.7683.

Friedman, N., Linial, M., Nachman, I., and Pe’er, D. (2000).

Using bayesian networks to analyze expression data.

Journal of computational biology, 7(3-4):601–620.

Gabriel, E., Fagg, G. E., Bosilca, G., Angskun, T., Don-

garra, J. J., Squyres, J. M., Sahay, V., Kambadur, P.,

Barrett, B., Lumsdaine, A., et al. (2004). Open mpi:

Goals, concept, and design of a next generation mpi

implementation. In Recent Advances in Parallel Vir-

tual Machine and Message Passing Interface, pages

97–104. Springer.

Han, B., Kang, H., Seo, M. S., Zaitlen, N., and Eskin, E.

(2008). Efﬁcient association study design via power-

optimized tag snp selection. Annals of human genet-

ics, 72(6):834–847.

Hechter, E. (2011). On genetic variants underlying common

disease. PhD thesis, Oxford University.

Klein, R. J., Zeiss, C., Chew, E. Y., Tsai, J.-Y., Sackler,

R. S., Haynes, C., Henning, A. K., SanGiovanni, J. P.,

Mane, S. M., Mayne, S. T., et al. (2005). Complement

factor h polymorphism in age-related macular degen-

eration. Science, 308(5720):385–389.

Kollar, D. and Friedman, N. (2009). Probabilistic graphical

models: principles and techniques. The MIT Press.

Laramie, J. M., Wilk, J. B., DeStefano, A. L., and Myers,

R. H. (2007). Haplobuild: an algorithm to construct

non-contiguous associated haplotypes in family based

genetic studies. Bioinformatics, 23(16):2190–2192.

Lee, P. H. and Shatkay, H. (2006). Bntagger: improved tag-

ging snp selection using bayesian networks. In ISMB

(Supplement of Bioinformatics), pages 211–219.

Moore, J. H., Asselbergs, F. W., and Williams, S. M. (2010).

Bioinformatics challenges for genome-wide associa-

tion studies. Bioinformatics, 26(4):445–455.

Mourad, R., Sinoquet, C., and Leray, P. (2010). Learning

hierarchical bayesian networks for genome-wide asso-

ciation studies. In Proceedings of COMPSTAT’2010,

pages 549–556. Springer.

Mourad, R., Sinoquet, C., and Leray, P. (2011). A hier-

archical bayesian network approach for linkage dis-

equilibrium modeling and data-dimensionality reduc-

tion prior to genome-wide association studies. BMC

bioinformatics, 12(1):16.

Mourad, R., Sinoquet, C., Zhang, N. L., Liu, T., Leray, P.,

et al. (2013). A survey on latent tree models and ap-

plications. J. Artif. Intell. Res.(JAIR), 47:157–203.

Neﬁan, A. V. (2006). Learning snp dependencies using em-

bedded bayesian networks. In IEEE Computational

Systems, Bioinformatics Conference, pages 1–6.

Patil, N., Berno, A. J., Hinds, D. A., Barrett, W. A.,

Doshi, J. M., Hacker, C. R., Kautzer, C. R., Lee,

D. H., Marjoribanks, C., McDonough, D. P., et al.

(2001). Blocks of limited haplotype diversity revealed

by high-resolution scanning of human chromosome

21. Science, 294(5547):1719–1723.

Pattaro, C., Ruczinski, I., Fallin, D., and Parmigiani, G.

(2008). Haplotype block partitioning as a tool for

dimensionality reduction in snp association studies.

BMC genomics, 9(1):405.

BIOSTEC2014-DoctoralConsortium

Schaid, D. J. (2004). Evaluating associations of haplotypes

with traits. Genetic epidemiology, 27(4):348–364.

Scheet, P. and Stephens, M. (2006). A fast and ﬂexible

statistical model for large-scale population genotype

data: applications to inferring missing genotypes and

haplotypic phase. The American Journal of Human

Genetics, 78(4):629–644.

Su, Z., Marchini, J., and Donnelly, P. (2011). Hapgen2:

simulation of multiple disease snps. Bioinformatics,

27(16):2304–2305.

Thomas, A. (2009). Estimation of graphical models whose

conditional independence graphs are interval graphs

and its application to modelling linkage disequilib-

rium. Computational statistics & data analysis,

53(5):1818–1828.

Thomas, A. and Camp, N. J. (2004). Graphical modeling of

the joint distribution of alleles at associated loci. The

American Journal of Human Genetics, 74(6):1088–

1101.

Thomas, A. and Green, P. J. (2009). Enumerating the junc-

tion trees of a decomposable graph. Journal of Com-

putational and Graphical Statistics, 18(4):930–940.

Verzilli, C. J., Stallard, N., and Whittaker, J. C. (2006).

Bayesian graphical models for genomewide associa-

tion studies. The american journal of human genetics,

79(1):100–112.

Zhang, N. L. (2004). Hierarchical latent class models for

cluster analysis. The Journal of Machine Learning

Research, 5:697–723.

Zhang, Y. and Ji, L. (2009). Clustering of snps by a

structural em algorithm. In Bioinformatics, Systems

Biology and Intelligent Computing, 2009. IJCBS’09,

pages 147–150. IEEE.

ForestsofLatentTreeModelsforGenome-WideAssociationStudies