
Networks and Imitations in an Agent based Asset Market
Souhir Masmoudi
CERGAM, Aix-Marseille University, France & URECA, University of Sfax, Sfax, Tunisia
1 STAGE OF THE RESEARCH
Revising and proofreading the draft.
2 OUTLINE OF OBJECTIVES
The basic argument for mimetic behavior is that
economic agents can be heavily influenced by the
behavior of their neighbors where neighbours are
defined as those with whom they have sufficient
contact to be informed about the forecasting strategy
that they follow and their success. Their
anticipations of the evolution of prices are the result
of their evaluation of the forecasting strategies’
success rather than on their own personal
anticipations. So agents can switch from one
forecasting strategy to another as the success of
strategies changes. We study how the imitation of
the rules of others as well as the structure of their
interaction can influence the market share of agents
and the prices of the asset traded on this market.
3 RESEARCH PROBLEM
How do the structures of information exchange
regarding the success of investment strategies
among investors influence the price volatility in
financial markets? How do the different ways in
which investors change their investment strategies
based on the acquired information from their
“friends” and “colleagues” affect the answer to this
question? These are the questions we try to answer
in this paper by conducting computational
experiments in an artificial asset market in which
investors who exhibit mimetic behavior operate and
switch from one forecasting strategy to another.
4 STATE OF THE ART
Understanding the relationship between the structure
of interactions among investors who imitate each
other and the dynamics of prices in financial markets
are of interest to us for, at least the following three
reasons (1) There is a growing awareness among
economists and policy markers alike that we need to
deal better with heterogeneity across agents and the
interaction among those (boundedly rational)
heterogeneous agents. (2) Among various
dimensions of bounded rationality, there has been
increasing interests among economists and
researchers in understanding the consequences of
mimetic behavior not only in financial markets
(Föllmer et al., 2005; Kirman, 1993; Lux, 1995; Lux
and Marchesi, 1999; Topol, 1991) but also in other
fields in management such as Marketing (Choi et al.,
2010; Zhou, 2006) and Strategy (Giarratana and
Mariani, 2013; Posen et al., 2013). Imitation impact
is also finding applications in various contexts such
as anthropology (Goodwin and Heritage, 1990),
social psychology (Levine et al., 1993), political
environment (McKinley, 1901). Furthermore, (3)
rapidly cumulating evidence shows the importance
of better understanding the ways local interaction
structures influence aggregate outcomes (Panchenko
et al., 2013; Jackson, 2008; Shiller, 1995; Shiller and
Pound, 1989).
5 METHODOLOGY
In this paper, we embed the model of Föllmer et al
(2005) into a family of network structures that can
be generated simply by a model of Watts and
Strogatz (1998) namely regular one dimentional
lattice networks, small world networks, and random
networks. In the model of Föllmer et al (2005), asset
market prices are determined as temporary equilibria
and agents’ excess demand is a function of the prices
they expect in the next period. For simplicity, agents
(who are investors) in our model use, at any point in
56
Masmoudi S..
Networks and Imitations in an Agent based Asset Market.
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
time, one of the following two forecasting strategies:
“chartists” and “fundamentalists.” Agents switch
between these two strategies by mimicking the
“successful” strategies employed by their local
neighbors. We consider two mimicking rules, the
most profitable rule and the average rule, by varying
the definition of “successful” strategies.
Under the most profitable rule, an agent copies
the forecasting strategy used by the most successful
neighbour. Under the average rule, an agent adopt
the forecasting strategy that resulted in the higher
average profit among their neighbors who were
using it. These two appear particularly adapted to a
model with boundedly rational agents (Ellison and
Fudenberg, 1995; Schlag, 1998; Selten and
Ostmann, 2001). In addition, we introduce a small
noise in the mimicking rule so that with a small
probability agents fail to employ the forecasting
strategy that these mimicking rules specify, and use
the other rule.
We employ computational experiments because,
as noted by the pioneering research in this field
(Arthur, 1994; Palmer et al., 1994), traditional
analytical approaches have difficulty in taking into
account changes individual behaviors and in
considering realistic market microstructures except
in a very few special cases. Computational models
are very often used in analyzing behavioral models
with heterogenous agents (Brock and Hommes,
1998; Hommes, 2006; LeBaron, 2006; Tedeschi et
al., 2010).
5.1 Anticipations and Price Formation
Process
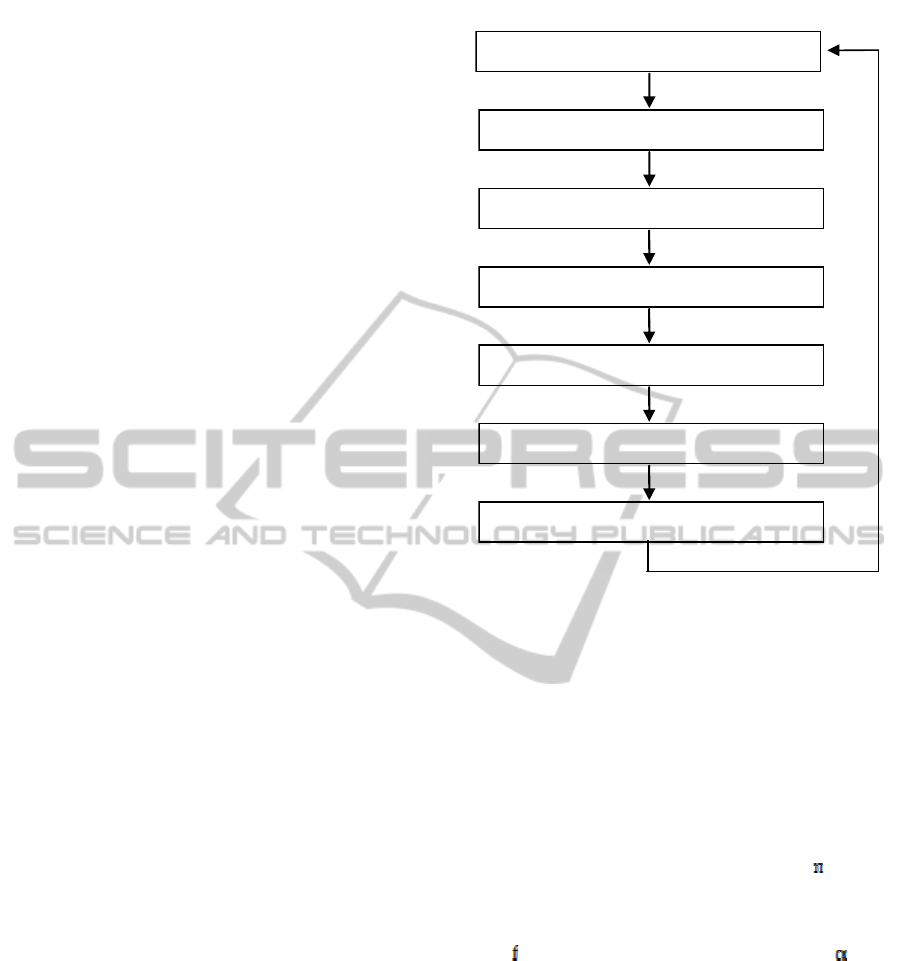
Our model progresses in the following way. We
initialize the model by creating interaction network
among agents, and assign investment strategies
among agents so that a half of investors are using
chartist investment strategy and remaining half are
using fundamentalist investment strategy. The
agents using each investment strategies are spread
randomly throughout the network. In each period,
each investor forms price expectation based on the
forecasting strategy s/he uses. The price expectation
of each investor determines his or her demand
schedule in that period, which in turn determines the
market price. The realized market price determines
the profit of each investor. Agents update their
forecasting strategies based on the mimicking rule
and the model enters the next period. This process is
summarized in Figure 1.
This process is summarized in.
Figure 1: Model progress.
In this section, we first describe the forecasting
strategies, and price determination process. The
creation of network structure is described in the next
section.
We consider a model that involves two different
types of forecasting strategies: “chartists” and
“fundamentalists.”
Fundamentalists are investors who follow the
fundamental rule, which predicts that market prices
will (gradually) return to their “fundamental” level.
Thus, the expected price for fundamentalist
for the
period t1 is given by
s
P
α
f
P
(1)
where
is the fundamental value of the asset. is a
constant that represents the fundamentalist’s
estimate of the speed of price adjustments. We
suppose that it is the same for everybody (in our
simulations we set α0.1). As is clear from
equation (1), if P
is below what traders believe to be
the fundamental value, they anticipate a price
increase. On the other hand, if P
exceeds the
fundamental value, they anticipate a price decrease.
Chartist’s strategy relies only on the history of
previous prices observed in financial markets and we
shall refer to investors following this strategy as
chartists. The latter attempt to extrapolate the past
movements of the stock price to predict its future
NetworkStructureConstructed
Initialization
Ex
p
ectations Formed
ExcessDemandCom
p
uted
MarketPriceDetermined
ProfitsCom
p
uted
Forecastin
g
Strate
gy
U
p
dated
NetworksandImitationsinanAgentbasedAssetMarket
57

price and form their expectations on the basis of the
history of the asset’s prices. To simplify matters we
have supposed that agents use only one observation
from the past. However they could be sophisticated
time series econometricians and this would not
change the analysis. Thus, the expected price for
chartist
for the period t1 is given by
s
P
αP
P
(2)
where αis the investor’s current estimates of the
speed of the trend-cycle. Equation (2) shows that if
P
is above P
, a chartist anticipates a price
increase. On the other hand, if P
is below P
, she
anticipates a price decrease.
Given the price forecast and an investor’s
idiosyncratic liquidity demand in each period, the
net demand schedule for the investor is determined.
Following the specification used by Föllmer et al
(2005), we define net demand schedule for agent
,
e
p in period as
e
p
logs
log
η
(3)
where s
is the expected price for agent in period
, P
is the asset price andη
is the exogenous
random liquidity demand. We assume thatη
⋲
1;1.
In other words, the net demand of agent
involves an exogenous liquidity demand and an
endogenous amount reflecting the deviation of the
price from the expected price. A positive net demand
at price
of the investor reflects his intention to buy
the stock at the price. If her net demand is negative,
she sells the stock at the price.
The equilibrium asset price in period
, P
is
defined as
e
P
0
⋲
(4)
Applying Equation (3) to Equation (4) gives the
asset price P
P
e
∗
∑
⋲
(5)
where η
∗
∑
η
⋲
. All agents obtain profits in
period
based on the order they have placed in
period t1, e
P
at the market price as
follows
П
P
P
e
P
(6)
Agents then forecast next period’s price at each step
and form their excess demand, which in turn
determines the next period’s price. In the next period
given the realised price, and profits, a new
forecasting rule is chosen, forecasts are made and
excess demand is determined.
Let us first show the outcomes of the model when
agents do not change their forecasting strategies.
These outcomes will serve as benchmarks when we
introduce mimicking and local interaction structures.
shows the time series of prices for three different
scenarios: (1) 0% chartists, (2) 50% chartists and (3)
100% chartists. In each case, we assume that there
are 100 investors in the market.
We can see from that figure that prices become
more volatile when there are more chartists in the
market.
We quantify price volatility by computing the
coefficient of variation of prices c
: a neutral
measure often used to gauge dispersion’s degree.
c
σ
μ
(7)
Figure 2: Difference in price evolution between a chartist
regime, a fundamentalist regime and a fifty-fifty regime.
The coefficient of variation of prices is defined
as the ratio of the standard deviation of prices σ for a
given period to the mean of prices μ for the same
period. This coefficient of price variation is between
14.5% and 25.6% when 50% of investors in the
market are chartists. This is relatively high because
it does not exceed 17.6% in case of complete
absence of chartists. When there are 100% chartists,
the coefficient of price variation can reach 127%.
The presence of chartists makes the price less stable
and sometimes drives it far away from the
fundamental value.
Our artificial asset market, even when there is no
switching between strategies, is thus able to
reproduce the stylized facts observed in real
financial market and illustrates in particular that
excess volatility of stock prices occurs when the
market is dominated by chartists (Kirman 2010
Chapter 4, Kirman and Teyssiere 2002, Föllmer et
al., 2005, Lux and Marchesi, 1999). However, while
these models allowed for switching of agents’
strategies, they did not consider the structure of local
0
20
40
60
80
100
1 101 201 301 401 501 601 701 801 901
Prices
Time
100Chartists 0Chartists
ICAART2014-DoctoralConsortium
58

interactions between agents. This is what this paper
introduces as we describe in the next section.
5.2 Network Topologies
As soon as we recognize that local interaction
between agents conditions their behavior, we have to
specify the network which governs that interaction.
The fact that networks play a significant role in
agents’ behavior and interaction in financial markets
and thus, in replicating the stylized facts of financial
time series has been recognized in the literature (See
e.g. Cont and Bouchaud 2000, Alfarano and
Milaković 2008.)
We want to investigate to what extent network
structure matters when, as in our model agents
mimic their neighbors. We employ the model of
Watts and Strogatz (1998) to generate a family of
network structures that spans regular network (one
dimensional lattice) and random network. The
method they used to generate various is as follows:
They consider a random rewiring method. They start
from a one-dimensional regular network with k
degree. That is each node is connected to k/2 closest
nodes on each side by undirected edges. And each
link is randomly rewired with probability
.
For p0, the graph network remains to be a
regular lattice. The degree of disorder increases with
increasing
. When p1 all edges are rewired
randomly. The graph is referred to as a “small-
world” network for intermediate values of p0
1.
We want to show how the differences in the network
structure determined by the various values of
influences the market share of agents and the asset
price volatility. To generate the different graphs, we
choose the method of Watts and Strogatz and the
formal notion of clustering coefficient that they
introduced. We study three different network
topologies (at both extreme values of p and for
intermediate values of p).
The Figure 3 below shows examples of networks
generated according to this model for three different
values of rewiring probability
. A regular network
(when the rewiring probability is equal to 0 p 0)
which is highly clustered and has a large
characteristic path lengths, a random network (when
the rewiring probability equals 1
p1
) which is
poorly clustered but has a short characteristic path
length and a small world network p 0.1 which
exhibits two properties, small average shortest path
length and large clustering coefficient. Watts and
Strogatz (1998) vary the basic parameter and show
that it is only in a small range of values that a small
world network is observed.
In our model, unlike Watts and Strogatz (1998),
we consider directed links to allow for the
possibilities that while agent
is observing carefully
about forecasting strategies used by agent
and its
performance, agent
does not pay attention to what
agent
does.
Regular Lattice Small World Network Random Graph
p=0 p=0.1 p=1
Figure 3: Network structure with N=100 nodes and k=4
neighbors.
5.3 Network Structure, Mimicking
Strategies and Prices Volatility
The basic argument for mimetic behavior is that
economic agents can be heavily influenced by the
behavior of their neighbors where neighbours are
defined as those with whom they have sufficient
contact to be informed about the forecasting strategy
that they follow and their success. Their
anticipations of the evolution of prices are the result
of their evaluation of the forecasting strategies’
success rather than on their own personal
anticipations. So agents can switch from one
forecasting strategy to another as the success of
strategies changes. We assume that all agents update
their forecasting rule at the same time and in every
period of timet. This is not entirely a passive
behavior in that the agents can choose whom to
imitate. We study how the imitation of the rules of
others can influence the prices of the asset traded on
this market.
As we have mentioned we examine the
consequences of two mimicking rules: the most
profitable rule and the average rule. When the most
profitable rule is adopted, traders follow the strategy
used by the most successful neighbor; each of them
compares the profit recorded in the previous period
of all his neighbors and copies the strategy of the
most profitable one. The average rule is designed to
copy the forecasting strategy, which resulted in the
highest average profit for those using it; they
compare the profit of neighbours who have used
NetworksandImitationsinanAgentbasedAssetMarket
59

each strategy in the previous period and then copy
the one, which resulted in higher average profit.
There are of course other rules which we would
have been justified in adopting such as the least
profitable rule (agents never copy the strategy used
by the least profitable neighbor), but for simplicity
we have chosen the two basic rules discussed above.
Indeed, these two appear particularly adapted to
a model with boundedly rational agents and they
have been studied in the literature. See for example,
Selten and Ostmann (2001), for the max rule and
Ellison and Fudenberg (1995) and Schlag (1998) for
the average rule.
We restrict our attention to mimicking rules with
limited memory. In particular, in this paper we have
decided to focus on the memory length of one that is
the profit realized in the previous period and not on
the cumulative profits or on the weighted average of
past-recorded profits. Choosing the cumulative
profits in the performance measure does not allow
for the fact that the most profitable agent may not
have always used her current strategy. This make it
difficult to determine which specific strategy worked
most effectively. We avoid this difficulty therefore
by only considering only one lag to measure agents’
performances.
We conduct simulations for the two mimicking
rules in three different network structures: a regular
network (rewiring probability
=0), a random
network (rewiring probability
=1) and a small
world graph (rewiring probability
=0.1) to
investigate if and how the network structure
influences agents’ market share. We follow
Panchenko et al (2013) in choosing p0.1 to
generate a small world network.
We start with a market in which half of the
investors are chartists and the other half are
fundamentalists. It should be noted that the
simulations assume that the fundamental value is at
all times constant.
We analyze the evolution of the distribution of
forecasting strategies for N 100agents. We study
two cases: K=4 (Each agent is connected to a small
fraction of the entire network: each one has 4
neighbors) and K=10 (Each agent has 10 neighbors).
Since there are only two strategies: a chartist
strategy and a fundamentalist strategy, we look at
one strategy: the chartist strategy.
In each case, a total of 100 of simulations were
conducted, each with 1000 periods of trading. We
ignore the first 250 periods and compute the fraction
of chartists and the market price for the last 750
periods of simulations. The network is regenerated
for each simulation and we check whether each time
the graph is connected.
We also study an additionally stochastic version
of our model. We assume that agents, with a small
probability, fail to employ the forecasting strategy
that these mimicking rules specify, and use the
opposite. The interaction between chartists and
fundamentalists leads to the evolution in their
market share; the proportion of each group in the
market is based on the choice of each investor of
how to update her forecasting strategy.
5.3.1 The Deterministic Model
5.3.11 Each Agent Has 4 Neighbors (K=4)
We now discuss the relationships between the
network structure, the mimicking rules and the
distribution of the forecasting strategies. The aim is
to show the impact of the mimicking rule and the
network topology on the distribution of the two
groups in the market and to demonstrate the effect of
the latter on price volatility.
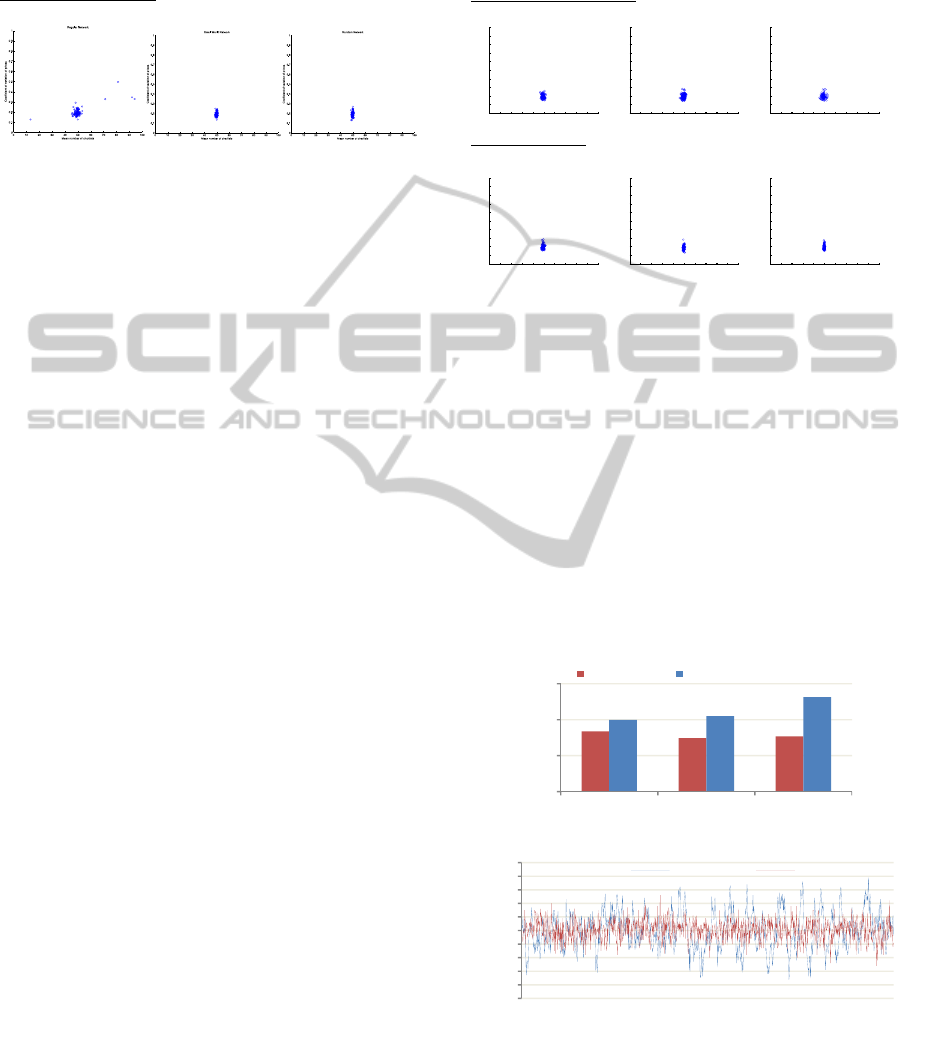
Figure 4 shows some simulated times series of
the evolution of chartists’ fraction for all networks
when the most profitable rule is adopted. We
observe that the network topology influences the
speed with which the system gets absorbed in one
extreme or the other. The regular graph is highly
clustered large world. Because of this, the
information transmission between agents who are
not neighbors is very slow. A small world network
represents both a low diameter and a high clustering
coefficient.
When the rewiring probability increases, both the
clustering coefficient and the diameter of the
network decrease thereby speeding up the spreading
of information. We notice that the stabilization is
more rapid than in the regular network.
The chance that both types of investors co-exist
in the market for a long time decreases significantly
in the small world network and disappears
completely in the random network. This
demonstrates that information transmission is much
faster in the random network.
However, few of these observed results are
representative cases. To better understand the
properties of the distribution of the forecasting
strategies generated by the three considered
networks, we show scatter graphs summarizing the
joint evolution between the coefficient of variation
of prices and the mean number of chartists computed
for the last 750 periods for each simulation (See
Figure 5.)
ICAART2014-DoctoralConsortium
60

Figure 4: Some simulated times series of the evolution of
chartists’ fraction for various network topologies when the
most profitable rule is adopted.
Histograms show the distribution of the chartist’s
fraction over simulations. For the regular network
model, the histogram of the fraction of chartists
shows that in half of the simulations the fraction of
chartists or fundamentalists reaches an extremity
within a relatively short period of time (less than 250
periods). The other half of the simulations indicates
that stability comes later as shown in
Figure 5. A
smaller persistence of the concurrent presence of
both investing types is demonstrated in less than
10% of the simulations in the case of the small
world network. In the case of the random graph, the
system clings on to situation of only one forecasting
strategy in a very short timeframe.
Fundamentalists are more likely to dominate the
market (61%) than chartists (39%) for the regular
network. A Similar finding is observed for the other
two network topologies. Prices volatility increases
along with the proportion of chartists. The
coefficient of price variation in some cases can rise
to 135%. When the proportion of chartists is high in
the market, the price of the asset may become
unstable and deviate continuously from its
fundamental value.
In the case of the average rule, the network
structure does not affect the distribution of
forecasting strategies. Neither chartists nor
fundamentalists dominate. A simultaneous existence
of these two groups is demonstrated for all network
topologies. The share of each type of agents
fluctuates around the half the number of agents (See
Figure 6.)
These results show a sharp difference between
the two mimicking rules when agents are connected
to a small fraction of the network. For the most
profitable rule, everyone is looking for the most
successful neighbor and copying exactly his
strategy. On the contrary, when the average rule is
followed, even if in a neighborhood one of the two
strategies is most profitable, on average investors
following these strategies may make the same
amount of profits and this does not give the same
results.
Contrary to the case of the most profitable rule,
the observed time series are representative outcomes
Most profitable Rule
Figure 5: The price dispersion and the share of agents for
different network topologies when all agents adopt the
most profitable Rule. Left: Cloud of points representing
the joint evolution between the coefficient of variation of
prices and the mean number of chartists for all simulations
(each point represents a simulation). Right: Histograms
show the distribution of chartists’ fraction over
simulations. Above: Regular network. Middle: Small
world network. Below: Random network.
0
20
40
60
80
100
1 251 501 751
Chartists'fraction
Regularnetwork
0 100 22 77 51
Meannumberofchartists:
0
20
40
60
80
100
1 251 501 751
Chartists'fraction
Smallworldnetwork
0 100 10 88
Meannumberofchartists:
0
20
40
60
80
100
1 251 501 751
Chartists''fraction
Randomnetwork
0 100 100 0
Meannumber ofchartists:
0 10 20 30 40 50 60 70 80 90 10 0
0
10
20
30
40
50
60
70
80
90
100
Histogram K4UP2Reg
Chartists Frac tion
Simulations frequencies
0 10 20 30 40 50 60 70 80 90 10 0
0
10
20
30
40
50
60
70
80
90
100
Histogram K4UP2S W N
Chartists Frac tion
Simulations frequencies
0 10 20 30 40 50 60 70 80 90 10 0
0
10
20
30
40
50
60
70
80
90
100
Histogram K4UP2Rand
Chartists Frac tion
Simulations frequencies
NetworksandImitationsinanAgentbasedAssetMarket
61

Figure 6: Representative time series simulations of
fluctuations in fraction of chartists for the three network
structures when the average rule is adopted.
of the evolution of the fractions of the two types of
agents (See Figure 7.) The coefficient of price
variation is between 14.23% and 31.19%. The
interval of the volatility’s degree is close to that in
the case of absence of imitation due to the fact that
both types of investors exist in similar proportions.
Average Rule
Figure 7: The price dispersion and the share of agents for
different network topologies when all agents adopt the
average Rule. Cloud of points representing the joint
evolution between the coefficient of variation of prices
and the mean number of chartists for all simulations. Left:
Regular network. Middle: Small world network. Right:
Random network.
5.3.12 Each Agent Has 10 Neighbors (K=10)
This section also illustrates the impact of mimicking
rules and network structures on chartists’
distribution for the two different updating rules and
for three different network structures with the
difference that agents are connected to a greater
fraction of the network. Each agent has 10
neighbors.
Figure 8 shows that increasing the number of
neighbors has an impact on the speed with which all
individuals end up taking the same strategy. Similar
results were found for the small world and the
random networks. The system gets absorbed in one
of the two extremes fairly quickly. This can be
explained by the structural properties of the small
world network and the random network and more
precisely by their small characteristic path length.
On the other hand, for the regular network, the
stabilization is slower but still much rapid than in the
case of k=4.
Most profitable Rule k=10
Figure 8: The price dispersion and the share of agents for
different network topologies when all agents adopt the
most profitable Rule. Left: Cloud of points representing
the joint evolution between the coefficient of variation of
prices and the mean number of chartists for all simulations
(each point represents a simulation). Right: Histograms
show the distribution of chartists’ fraction over
simulations. Above: Regular network. Middle: Small
world network. Below: Random network.
Fundamentalists appear to dominate the market
in over 60% of simulations whatever the network
topology. The coefficient of price variation, as
expected, is high when chartists predominate.
When the average rule is followed, the distributions
of agents produced when each investor has 4
neighbors are very similar to those produced when
each agent has 10 neighbors. Both types of investors
exist in similar proportions for all network
topologies. This can clearly be attributed to the fact
that profits made by chartists’ group are much the
same as those realized by fundamentalists’ group.
5.3.2 The Stochastic Model
So far, we have seen that a sharp difference exists
between the most profitable rule and the average
rule. Indeed, without the noise and when the most
0
20
40
60
80
100
1 101 201 301 401 501 601 701 801 901
Chartists'fraction
Time
Regular SmallWorld Random
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of variation of prices
Regular Network
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of variation of prices
Smal l World Network
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of variation of prices
Random Network
ICAART2014-DoctoralConsortium
62
profitable rule is adopted the chance that both types
of investors exist simultaneously in the market for a
Average Rule k=10
Figure 9: The price dispersion and the share of agents for
different network topologies when all agents adopt the
average Rule. Cloud of points representing the joint
evolution between the coefficient of variation of prices
and the mean number of chartists for all simulations. Left:
Regular network. Middle: Small world network. Right:
Random network.
long time decreases significantly in the small world
network and disappears completely in the random
network. However, the network structure does not
affect the distribution of the two groups of agents
when the average rule is adopted. A simultaneous
existence of these two types is shown for all network
topologies.
This subsection presents a doubly stochastic
version of our model. We assume that agents, with a
small probability (0.1), (a “trembling hand”), fail to
employ the forecasting strategy that these mimicking
rules specify, and use the alternative strategy.
5.3.21 Each Agent Has 4 Neighbors (K=4)
In the presence of noise in the mimicking rule, the
average rule and the most profitable rule lead to the
similar average fraction of two groups in the market
for all network structures. When the noise is small
and when agents are mimicking their local
neighbors, this provided periods of simultaneous
existence of both trading strategies whatever the
mimicking rule and whatever the network topology
introduces the price dispersion and the share of
agents over simulations for the two different
updating rules adopted and for three networks
topologies: the regular network, the small world
network, and the random network. The mean
number of chartists for all networks structures and
for the two updating rules is near the average. The
price volatility for the three different network
structures does not exceed 28.2%. The values are
also close across the different topologies of the
network.
There is, however, difference in the volatility of
the fraction of agents between the two rules even in
the presence of noise in the mimicking behavior.
Figure 11 graphs the coefficient of variation of
chartists ‘ proportion averaged over all simulations
Most profitable Rule
Average Rule:
Figure 10: The price dispersion and the share of agents for
different network topologies for the two mimicking rules.
Cloud of points representing the joint evolution between
the coefficient of variation of prices and the mean number
of chartists for all simulations. Left: Regular network.
Middle: Small world network. Right: Random network.
relative to the volatility of chartist’s proportion.
Indeed, when the most profitable rule is used there is
greater volatility. This is because each individual
plays the action of the best neighbor. We also show
that this volatility increases when there are more
random links, as the spread of the influence of the
lucky chartist in the network is higher. But if we are
looking in terms of average payoffs this is no longer
observed.
Figure 11: Difference in the volatility of the fraction of
chartists between the most profitable and the average rule.
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of v ariation of prices
Regular Network
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of v ariation of prices
Smal l World Network
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of v ariation of prices
Random Network
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of variation of prices
Regular Network
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of variation of prices
Smal l World Network
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean number of chartists
Coefficient of variation of prices
Random Network
0
0,1
0,2
0,3
Reg SWN Rand
Volatilityofchartists'
fraction
AverageRule MostprofitableRule
0
10
20
30
40
50
60
70
80
90
100
1 101 201 301 401 501 601 701 801 901
Chartists'fraction
Time
Mostprofitable Average
NetworksandImitationsinanAgentbasedAssetMarket
63
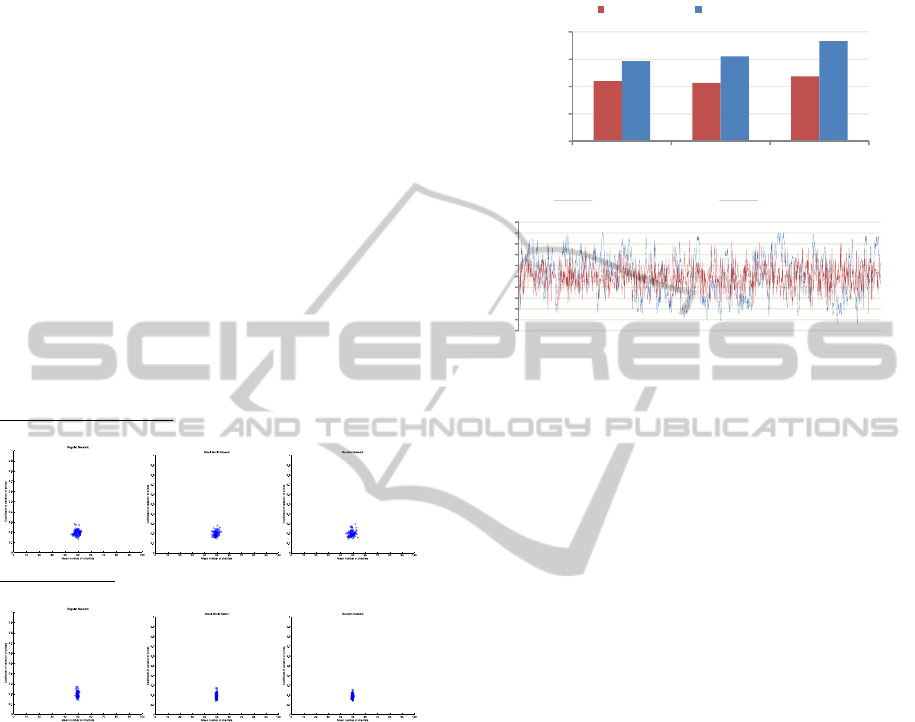
5.3.22 Each Agent Has 10 Neighbors (K=10)
In this subsection we extend the analysis to the
neighborhood of size ten. Let us consider
Figure 12,
which shows considerable similarity between the
two neighborhood cases. We thus note that the
distributions of agents produced by the two updating
rules when each investor has 4 neighbors are the
same as those produced when each agent has 10
neighbors. The average rule and the most successful
rule lead to the same distribution of the two groups
in the market. We demonstrate a concurrent
existence of both trading strategies with sometimes a
more pronounced presence of one of the two groups.
Profits generated by chartists and fundamentalists
groups sometimes rise and sometimes fall
accordingly. Moreover, an increasing relationship
between the number of neighbors and volatility of
fraction of chartists has been illustrated as shown in
Figures 11 and 13.
Most profitable Rule:
Average Rule:
Figure 12: The price dispersion and the share of agents for
different network topologies for the two mimicking rules.
Cloud of points representing the joint evolution between
the coefficient of variation of prices and the mean number
of chartists for all simulations. Left: Regular network.
Middle: Small world network. Right: Random network.
6 EXPECTED OUTCOME
Our results show a sharp difference between the
outcomes of two mimicking rules, the most
profitable and the average rules, when agents are
connected to a small fraction of the network (k=4
and k=10). When the most profitable rule is adopted,
the network topology influences the speed with
which all agents end up taking the same strategy.
When the rewiring probability increases, both the
clustering coefficient and the diameter of the
network decrease thereby speeding up the spreading
of information. Information transmission also
increases, as the number of neighbors is higher.
Figure 13: Difference in the volatility of the fraction of
chartists between the most profitable and the average rule.
Fundamentalists are more likely to dominate the
market than chartists. There is a greater chance that
the profit of the best performing fundamentalist is
higher than the profit of the best performing chartist
and that the average profit of fundamentalists
exceeds the average profit of chartists. When the
proportion of chartists is high in the market, the
price of the asset may become unstable and deviate
systematically from its fundamental value. On the
other hand, In the case of the average rule, neither
chartists nor fundamentalists dominate. A
simultaneous existence of these two groups is
demonstrated.
The difference in the outcome between two
mimicking rules, however, disappears when the
noise in the mimetic behavior is larger. In the
presence of noise in mimicking rule, the average rule
and the most successful rule lead to the similar
average fraction of two groups in the market
whatever the network structure. There is, however,
difference in the volatility of the fraction of agents
between the two rules even in the presence of noise
in the mimicking behavior. The most profitable rule
experiences greater volatility, and this volatility
increases when there are more random links, as well
as the number of neighbors each agent has.
In addition, we notice that price volatility
increases monotonically with an increase in the
proportion of chartists. Interaction between these
two types of investors involving endogenous
modification of strategies according to their
performance leads to unstable prices. Asset prices
0
0,1
0,2
0,3
0,4
Reg SWN Rand
Volatilityofchartists'
fraction
AverageRule MostprofitableRule
0
10
20
30
40
50
60
70
80
90
100
1 101 201 301 401 501 601 701 801 901
Chartists'fraction
Time
MostprofitableRule AverageRule
ICAART2014-DoctoralConsortium
64

may move away for considerable periods from
fundamentals and then return abruptly. This is due to
the link between the profitability and the fraction of
the different strategies, which engenders a self-
reinforcing contagion process.
REFERENCES
Alfarano, S., and Milaković, M. (2008). Should Network
Structure Matter in agent-Based Finance? Econ. Work.
Pap. Christ.-Albrechts-Univ. Kiel Departement Econ.
Arthur, W. B. (1994). Inductive reasoning and bounded
rationality. Am. Econ. Rev. 84, 406–411.
Brock, W. A., and Hommes, C. H. (1998). Heterogeneous
beliefs and routes to chaos in a simple asset pricing
model. J. Econ. Dyn. Control 22, 1235–1274.
Choi, Hui, and Bell (2010). Spatiotemporal Analysis of
Imitation Behavior Across New Buyers at an Online
Grocery Retailer. J. Mark. Res. 47, 75–89.
Cont, R., and Bouchaud, J.P. (2000). Herd behavior and
aggregate fluctuations in financial markets.
Macroecon. Dyn. 4, 170–196.
Ellison, G., and Fudenberg, D. (1995). Word-of-mouth
communication and social learning. Q. J. Econ. 110,
93–125.
Föllmer, H., Horst, U., and Kirman, A. (2005). Equilibria
in financial markets with heterogeneous agents: a
probabilistic perspective. J. Math. Econ. 41, 123–155.
Giarratana, M. S., and Mariani, M. (2013). The
relationship between knowledge sourcing and fear of
imitation. Strat. Manag. J.
Goodwin, C., and Heritage, J. (1990). Conversation
Analysis. Annu. Rev. Anthr. 19, 283–307.
Hommes, C. H. (2006). Chapter 23 Heterogeneous Agent
Models in Economics and Finance. In Handbook of
Computational Economics, (Elsevier), pp. 1109–1186.
Kirman, A. (1993). Ants, rationality, and recruitment. Q.
J. Econ. 108, 137–156.
Kirman, A. (2010). Complex Economics: Individual and
Collective Rationality (London).
Kirman, A., and Teyssiere, G. (2002). Microeconomic
models for long memory in the volatility of financial
time series. Stud. Nonlinear Dyn. Econ. 5, 281–302.
LeBaron, B. (2006). Chapter 24 Agent-based
Computational Finance. In Handbook of
Computational Economics, (Elsevier), pp. 1187–1233.
Levine, J. M., Resnick, L. B., and Higgins, E. tor. (1993).
Social Foundations of Cognition. Annu. Rev. Psychol.
44, 585–612.
Lux, T. (1995). Herd Behaviour, Bubbles and Crashes.
Econ. J. 105, 881–896.
Lux, T., and Marchesi, M. (1999). Scaling and criticality
in a stochastic multi-agent model of a financial
market. Nature 397, 498–500.
McKinley, A. E. (1901). The transition from Dutch to
English Rule in New York: A study in political
imitation. Am. Hist. Rev. 6, 693–724.
Palmer, R. G., Brian Arthur, W., Holland, J.H., LeBaron,
B., and Tayler, P. (1994). Artificial economic life: a
simple model of a stockmarket. Phys. Nonlinear
Phenom. 75, 264–274.
Panchenko, V., Gerasymchuk, S., and Pavlov, O.V.
(2013). Asset price dynamics with heterogenous
beliefs and local network interactions. J. Econ. Dyn.
Control http://dx.doi.org/10.1016/j.jedc.2013.06.015.
Posen, H. E., Lee, J., and Yi, S. (2013). The power of
imperfect imitation. Strat. Manag. J. 34, 149–164.
Schlag, K. H. (1998). Why imitate, and if so, How? A
boundedly rational approach to multi-armed bandits. J.
Econ. Theory 78, 130–156.
Selten, R., and Ostmann, A. (2001). Imitation equilibrium.
Homo Oeconomicus 43, 111–149.
Shiller, R. J. (1995). Conversation, information, and herd
behavior. Am. Econ. Rev. 85, 181–185.
Shiller, R. J., and Pound, J. (1989). Survey evidence on
diffusion of interest and information among investors.
J. Econ. Behav. Organ. 12, 47–66.
Tedeschi, G., Iori, G., and Gallegati, M. (2010). Herding
effects in order driven markets: The rise and fall of
gurus (Department of Economics, City University,
London).
Topol, R. (1991). Bubbles and volatility of stock prices:
effect of mimetic contagion. Econ. J. 101, 786–800.
Trichet, J.-C. (2010). Reflections on the nature of
monetary policy non-standard measures and finance
theory. Open. Address ECB Cent. Bank. Conf. Frankf.
18 Novemb. 2010 http://www.ecb.europa.eu/
press/key/date/2010/html/sp101118.en.html.
Watts, D. J., and Strogatz, S. H. (1998). Collective
dynamics of “small-world” networks. Nature 393,
440–442.
Zhou (2006). Innovation, Imitation, and new product
performance: The case of China. Ind. Mark. Manag.
35.
NetworksandImitationsinanAgentbasedAssetMarket
65
