Low Complexity Spatial Similarity Measure of GPS Trajectories

Radu Mariescu-Istodor, Andrei Tabarcea, Rahim Saeidi and Pasi Fr

anti

Speech and Image Processing Unit, School of Computing, University of Eastern Finland, Joensuu, Finland

Keywords:

GPS Trajectory, Spatial Similarity, MGRS, Cell Approximation, Sampling Frequency, Interpolation, Dilation.

Abstract:

We attack the problem of trajectory similarity by approximating the trajectories using a geographical grid

based on the MGRS 2D coordinate system. We propose a spatial similarity measure which is computationally

feasible for big data collections. The proposed measure is based on cell matching with a similarity metric

drawn from Jaccard index. We equip the proposed method with interpolation and dilation to overcome the

problems missing data and different sampling frequencies when comparing two trajectories. The proposed

measure is implemented online in the framework of Mopsi

cs.uef.ﬁ/mopsi

1 INTRODUCTION

In recent years, GPS technology has been widely

available in consumer devices, especially in smart-

phones

, which count as more than a half on total

mobile phone sales

. Furthermore, most of the users

utilize their phone to ﬁnd their location, amongst

other services

. The wide availability of GPS-enabled

smartphones that are also connected to the Internet

has made the collection of large amount of location-

based data possible. Such data includes geo-tagged

photos, videos and geographical trajectories. Col-

lecting geographical trajectories has practical appli-

cations in ﬂeet management, sports tracking, rec-

ommending tourist trajectories, improving navigation

and determining mobility patterns.

Having a large-scale collection of GPS trajecto-

ries raises the challenge of how to organize the data,

how to present it in a meaningful way and how to

ﬁlter out irrelevant data. Computing trajectory sim-

ilarity is a tool that can be used in addressing those

challenges (Agrawal et al., 1993). A problem in com-

puting similarity of GPS trajectories is that the large

amount of data does not permit processing raw trajec-

tories in real time.

Time series analysis of one-dimensional data

abiresearch.com/research/product/1005746-mobile-

device-user-interfaces

gartner.com/newsroom/id/2623415

pewinternet.org/Reports/2012/Location-based-servi

ces.aspx

across the time has been used for analyzing stock

changes, weather data and biomedical measurements

(Hamilton, 1994; Chan and Fu, 1999; Worsley and

Friston, 1995; Lange and Naumann, 2011). Despite

the signiﬁcant research output on time series analy-

sis, the concept of computing similarity for traces of

moving objects in the framework of spatio-temporal

databases has been studied much less. Finding k-

nearest trajectories, indexing and clustering of spatio-

temporal data are among the recent directions of re-

search with many applications to make queries in

moving object databases (Frentzos et al., 2007a; Ni

and Ravishankar, 2007; Frentzos et al., 2007b; G

uting

et al., 2010; Pelekis et al., 2011). These algorithms

can be applied also for measuring the trajectory simi-

larity (Hu and Steenkiste, 2006).

Using Euclidean distance is not practical for the

case that the length of two trajectories are not equal

(Yanagisawa et al., 2003). Dynamic time warping

handles matching two sequences of different length

but it is very sensitive to noisy data (Berndt and Clif-

ford, 1994). Algorithms like longest common subse-

quence (LCS) (Vlachos et al., 2002b; Vlachos et al.,

2002a) or edit distance on real sequence (EDR) (Chen

et al., 2005) are designed to account for noisy and

missing data but they are not perturbation free. Con-

sidering M trajectories of N points on average, the

computational complexity of these algorithms is at

minimum O(M

· N

). Hence, these algorithms can-

not provide real-time results when dealing with a

large collection of data.

These algorithms do not utilize time stamps. By

Mariescu-Istodor R., Tabarcea A., Saeidi R. and Fränti P..

Low Complexity Spatial Similarity Measure of GPS Trajectories.

DOI: 10.5220/0004940500620069

In Proceedings of the 10th International Conference on Web Information Systems and Technologies (WEBIST-2014), pages 62-69

ISBN: 978-989-758-023-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

using the timing information a complete movement

proﬁle can be provided and the similarity of two tra-

jectories can be used in trajectory clustering applica-

tions. The similarity measurement in LCS and EDR

are based on point-to-point distance calculations. In

the event of having two trajectories with different

sampling frequency, LCS and EDR cannot provide

correct similarity measure (Frentzos et al., 2007b).

Although it is always possible to use a trajectory re-

duction or approximation algorithm to represent a tra-

jectory with far less representatives for similarity cal-

culation, the quality of such an approximation algo-

rithm and overhead computational complexity is de-

batable (Ni and Ravishankar, 2007).

In this paper, we propose a fast method of comput-

ing trajectory similarity by approximating the trajec-

tories using a geographical grid based on a 2D coor-

dinate system. This process reduces a trajectory from

points to cells with order of magnitude less details in

representation and subsequently in distance calcula-

tions. We employ an asymmetric similarity metric in-

spired by Jaccard index. Dealing with GPS data col-

lection, it is common to have bunch of data points lost

or compare trajectories traveled by car with walking

speed trajectories. We propose interpolation and di-

lation of trajectories represented as cells to overcome

these difﬁculties. In the results section we simulate

missing data and trajectory sampling frequency mis-

match with two example trajectories and demonstrate

the efﬁciency of the proposed approach. Conclusions

are drawn after the discussion of results.

2 MOPSI

Mopsi is a research project location-based service

developed at the University of Eastern Finland by

Speech and Image Processing Group from the School

of Computing. (Fr

anti et al., 2011) Mopsi offers

multiple applications of location-aware systems, be-

ing a test-bed for various research topics that involve

location-aware data. It contains tools for collecting,

processing and displaying location-based data, such

as photos or trajectories, along with social media in-

tegration. The main topics addressed in Mopsi are

collecting location-based data, mining location data

from web pages, processing, storing and compress-

ing of GPS trajectories, detecting transportation mode

from GPS trajectories, recommending points of in-

terest, using location information in social networks,

detecting users actions by using their location and

building location-based games with the help of user-

generated collections.

Location-based data is very common among web-

Figure 1: Mopsi application on web showing an example of

two trajectories which display a common region.

pages, especially when their content describe com-

mercial services, landmarks or public institutions.

However, the location data is more commonly pre-

sented in a human-readable way and not as geograph-

ical coordinates, which are more accurate and easier

to be automatically identiﬁed. We propose a method

to automatically identify location information from

web-pages by detecting postal addresses (Fr

anti et al.,

2010).

Mopsi provides tools to collect GPS trajectories

and it includes more than 9000 trajectories composed

of over 7 million points by the end of 2013. Mopsi

uses fast retrieval and displaying of the data (Waga

et al., 2013) based on GPS trajectory polygonal ap-

proximation (Chen et al., 2012a). GPS trajectories are

also compressed for optimizing storage space (Chen

et al., 2012b). Transport mode information can be

also retrieved by automatically analyzing GPS trajec-

tories (Waga et al., 2012). The algorithm uses a sec-

ond order Markov model to segment the trajectories

and to detect car, bicycle, running or walking trans-

portation modes.

The relevance of location-based media can be as-

sessed by considering several aspects such as time, lo-

cation, content or social network (Fr

anti et al., 2011),

which are used to create a context for each user. A

personalized recommender system can recommend

relevant data based on user location and user context

(Waga et al., 2011). Such data can be geotagged pho-

tos, services conﬁrmed by administrators or GPS tra-

jectories. Users can share their location in real-time

by using mobile phone location-aware applications.

This allows for the detection of various location-

based actions such as meetings, visiting or passing-

by points of interest (Mariescu-Istodor, 2013). Mopsi

also includes location-based games, such as O-Mopsi

(Tabarcea et al., 2013), which is an orienteering game

using the data from a user-generated photo collection.

Mopsi provides tools for collecting location-based

LowComplexitySpatialSimilarityMeasureofGPSTrajectories

Figure 2: MGRS grid zones (source

data with mobile devices. It is available on most

mobile operating systems (Android, iOS, Windows

Phone, Symbian). The server-side processes the data

collected by the user and displays the data collec-

tion. It also provides social features and integration

which social media, with functionalities such as chat-

ting, friends tracking and sharing data to Facebook.

The Mopsi routes module provides tools for trajectory

recording and displaying the large amount of data in

reasonable time. Trajectory similarity is the newest

addition to the Mopsi routes module.

3 TRAJECTORIES

In Mopsi we record a user’s location at a certain time

as a point p

= (x

), where x

is the latitude,

is the longitude and t

is the timestamp of point k.

An ordered sequence of these points, deﬁnes a spatial

trajectory R = (p

,...,p

). We calculate the similar-

ity between a reference trajectory R

and all the other

M − 1 trajectories in the database, R

, m = 1, . . . , M.

The similarity of two trajectories can be calculated

as the Jaccard index:

J(R

) =

∩ R

∪ R

, (1)

Instead of this symmetric measure we want to ﬁnd

out if the reference trajectory is completely covered

by another trajectory. Thus, we consider the follow-

ing asymmetric similarity metric:

Sim(R

) =

∩ R

, (2)

Sim(R

) =

∩ R

. (3)

earth-info.nga.mil/GandG/coordsys/grids/universal grid syst

em.html

The ﬁrst one shows what percentage of R

is shared

with R

and the second shows what percentage of R

is shared by R

. The way that we perform intersection

operator is described in the following sections after

we quantize the trajectories into cells.

3.1 Cell Approximation

In a preprocessing step, we generate a cell repre-

sentation for a trajectory after it has been recorded.

The Military Grid Reference Systems (MGRS) is an

alpha-numeric system for expressing UTM/UPS co-

ordinates. MGRS is used by NATO to locate points on

earth. A single alpha-numeric value references a po-

sition that is unique for the entire earth (see Figure 2).

MGRS is a projected coordinate system which uses a

2-dimensional Cartesian horizontal position orienta-

tion, so that locations are identiﬁed independently of

vertical position. MGRS shares several characteris-

tics with UTM such as the division of earth into pro-

jection zones and using easting and northing in meters

within a designated zone. The main differences are

that a MGRS zone is a 100km square within a UTM

zone, whilst a UTM zone is usually 6 degrees in east-

west and 8 degrees in north-south area and also that

the notation of the areas is different. Based on the

coordinate resolution, MGRS can deﬁne a grid with

square cells with the length starting from 100km up

to 10m or even 1m.

We approximate a trajectory R = {(x

)}

k=1

a sparse binary matrix representation C where,

(C)

i j

(

1 0 < x

− iL < L, 0 < y

− jL < L

0 Otherwise

, (4)

where L stands for the cell length (25 meters in this

paper) and indexes i and j span over in horizontal and

vertical cells that trajectory R is residing inside. Fig-

ure 3 shows how the reference trajectory is approxi-

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

Figure 3: Example of a trajectory of 420 points being rep-

resented by 35 cells using the approximation in Equation 4.

The cell representation is not continuous. The gaps appear

because of the ﬁxed cell size, variations in movement speed

(or different sampling frequencies) and missing GPS loca-

tions. It is likely for such gaps to appear especially when

users are moving by car, train or plane.

mated by cells. Generating the cell representation for

a trajectory of average length of N points is done in

O(N) time.

3.2 Measuring Similarity

The similarity between two trajectories R

can

now be calculated as:

Sim(R

) =

 C

, (5)

where C

and C

are the cell representations of R

and R

, respectively, C

C

is a Hadamard product

of two matrices C

and C

deﬁned as (C

 C

)

i j

)

i j

·(C

)

i j

and kCk

represents the `

-quasinorm.

In implementation, C

and C

are multiplied element

by element and then we measure the number of non-

zero elements. Figure 4 shows two sample trajectories

being matched.

Assuming we have the cell representation C of a

reference trajectory R we calculate the similarity for

all trajectories in database in two steps. First, we ﬁnd

all the trajectories which share at least one cell with

the reference trajectory. This has a time complexity of

O(N

· (q + M

)) where q represents the steps needed

by the database system to perform the search (N

 N

and M

 M). In contrast to the average length N of

a trajectory R, we deﬁne N

= kCk

as the number

of non-zero elements in cell-approximated version of

R. In a similar way, M

indicates the number of other

trajectories that share at least one cell with trajectory

R. Secondly, we calculate the trajectory similarity

according to Equation (5) with a time complexity of

O(M

· N

). The overall complexity of the similarity

Figure 4: Matching two trajectories using the cell repre-

sentation. The green cells denote the reference trajectory

and the gray cells represent the other trajectory. The ’x’

symbol is used to mark the cells shared by two trajectories;

Sim(C

) = 40% and Sim(C

) = 31%

scoring is O(M

· N

) (assuming q constant by adding

a proper indexing structure in the database).

In Figure 4 the straighforward application of the

similarity scores yield similarity scores of 40% and

31% even though the trajectories seem to have more

than 50% similarity by visual inspection. In the next

subsections we analyze why this happens.

3.3 Interpolation

When the user is traveling fast or when recording fre-

quency is low we notice gaps in the trajectory repre-

sentation by cells. Gaps can also appear due to lack of

GPS signal. Figure 5 shows three examples when dif-

ferent sized gaps appear in the cell representation of a

trajectory. In cell approximation stage in Equation 4,

we process the trajectory data points in the sequence

they are recorded. In this way, the sequence of cells

being detected as “1s” are used to determine if the

next cell is connected to the current cell and ﬁnd a

potential gap in cell-approximation.

In order to ﬁll the gap, the line equation between

two cells is obtained from the start and end points as

j = f (i) =

− j

− i

(i − i

) + j

(6)

where i

and j

are the coordinates of one cell and

, j

are the coordinates of the other cell. The line

in Equation 6 is then sampled by the cells that it is

passing through and then set respective cell values as

i j

) = 1.

By performing interpolation, the trajectory simi-

larity presented in Figure 4 is now updated as plotted

in Figure 6. The similarity values are still below the

visual expectations. The reason is that two cell repre-

sentations may not overlap even though the trajecto-

ries are close to each other.

LowComplexitySpatialSimilarityMeasureofGPSTrajectories

Figure 5: Interpolation between two cells in order to ﬁll a

gap; three example situations are depicted.

Figure 6: The trajectory having gaps is interpolated and the

matching of the two trajectories becomes: Sim(C

) =

41% and Sim(C

) = 33%.

3.4 Dilation

A frequent situation is that two nearby trajectory seg-

ments are evolving along each other in cell represen-

tation instead of overlapping. An example is provided

in Figure 7 We solve this issue by applying morpho-

logical dilation on the trajectories and taking into ac-

count the neighbouring cells of a trajectory. We deﬁne

as a result of binary dilation of sparse binary rep-

resentation C by binary structure S with

= C ⊕ S = T (C ∗ S), (7)

where ⊕ deﬁnes the binary dilation and ∗ indicates the

convolution operator. In the Equation 7, T (·) stands

for binarization transform as

T ((C ∗ S)

i j

) =

(

0 0 ≤ (C ∗ S)

i j

< 1

1 Otherwise

(8)

Figure 7: We see that two trajectories which are close

enough to be considered similar can be represented by dif-

ferent cells. Only a single cell is shared by the cell repre-

sentation of the two trajectories.

Figure 8: The reference trajectory is dilated and the match-

ing of the two trajectories becomes: Sim(C

) = 64%

and Sim(C

) = 53%.

Figure 8 shows how a trajectory is dilated with the

following structure

S =





1 1 1





. (9)

Then the two trajectories are matched when one of

the trajectories is dilated. The similarity score is now

calculated with C

and C

as in Equation 5. Typi-

cally the number of cells used in the trajectory repre-

sentations increases by a factor of 3 when dilation is

applied.

4 RESULTS

We implement our method in a real-world application,

as a prototype using the Mopsi project route analy-

sis module

. We investigate issues that may appear

cs.uef.ﬁ/mopsi/?tab=routes&userId=13&routeId=137882401

9381&similarity=true

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

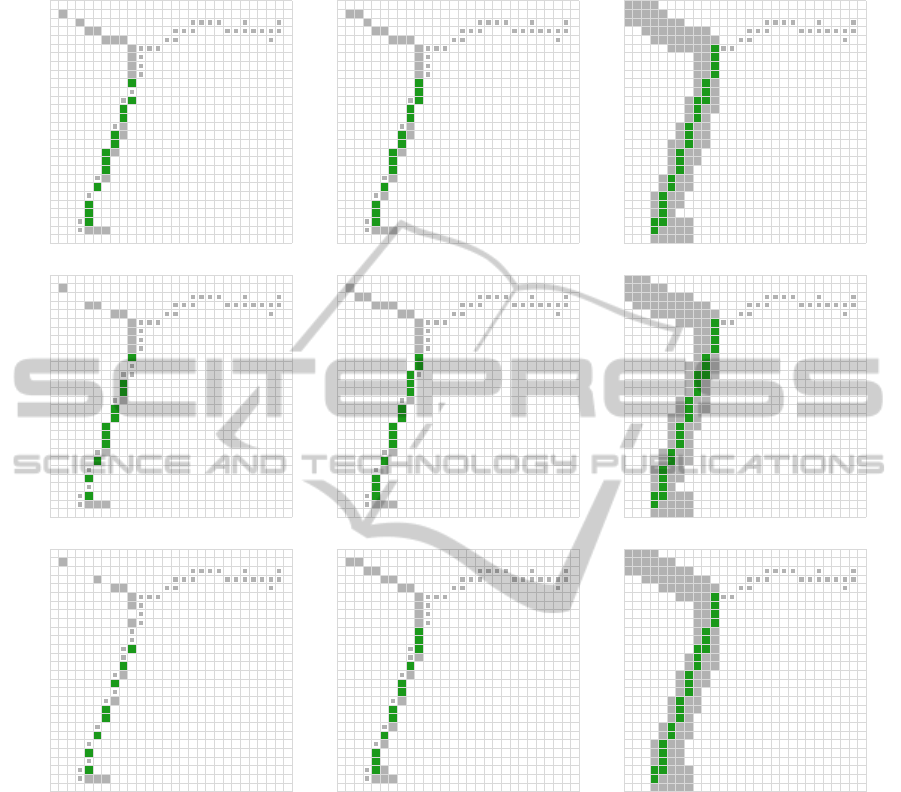
No post-processing Interpolated Interpolated and Dialated

29%

31%

53%

10x

24%

31%

53%

15x

18%

27%

53%

Figure 9: Simulating different sampling frequencies by subsampling the reference trajectory with a factor of 5x, 10x and 15x.

when collecting GPS trajectories in a practical appli-

cation such as different sample rates, interpolation of

collected points or breaks in the GPS signal caused by

technical or environmental problems.

Firstly, as shown in Figure 9, we investigate how

a different sampling frequency impacts the similarity

score calculation. The reference trajectory is subsam-

pled with factor f by only keeping every f

element

from the original trajectory. We notice that the in-

terpolation step doesn’t increase the similarity scores

signiﬁcantly. However, when followed by dilation,

the similarity score indicates robustness against vari-

ations in sampling frequency which is a desired prop-

erty for a trajectory matching procedure.

The other common issue while recording a trajec-

tory is loss of location information for a brief period

of time. This can happen, for example, if the user

goes through a building, a tunnel or simply due to de-

vice software error. We simulate this behavior and

see how the similarity scoring is affected in Figure 10.

When removing 90 points we notice that the similar-

ity score has dropped even when using interpolation

and dilation. This happened because we removed a

signiﬁcant amount of subsequent points (20% of the

trajectory). Interpolation does not have enough infor-

mation to reconstruct the trajectory appropriately and

consequently, loss of many data points in a trajectory

is detrimental for similarity calculations.

The proposed method is implemented in two steps

for real-world application: the preprocessing step,

LowComplexitySpatialSimilarityMeasureofGPSTrajectories

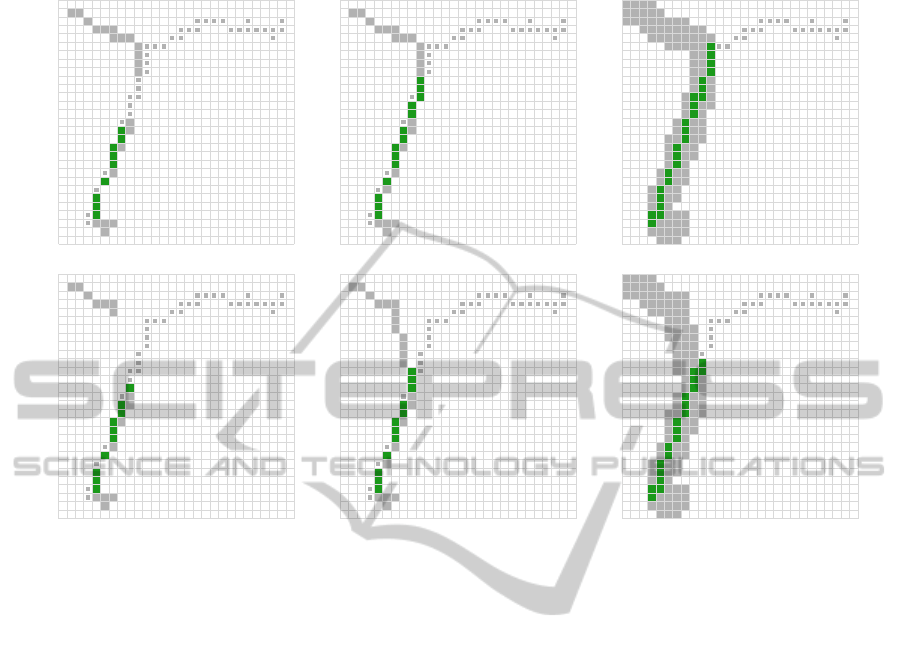
No post-processing Interpolated Interpolated and Dialated

(-50)

20%

31%

53%

(-90)

22%

27%

42%

Figure 10: Simulating loss of GPS signal by removing 50 and 90 sequential points from the reference trajectory.

done when a new trajectory is added into the sys-

tem and the similarity score calculation step, per-

formed when searching all the similar trajectories of a

given trajectory. When not using interpolation or di-

lation the time complexity for the preprocessing step

is O(M · N) for M trajectories of average length N

points. The similarity score calculation has a time

complexity of O(M

· N

). After interpolation is ap-

plied there will be an increase on the N

and M

pa-

rameters which increase, however, stay at the same

order of magnitude. N

increases by the number of

cells added trough interpolation and M

increases by

the number of trajectories that share at least one cell

with interpolated trajectory. The dilation stage in-

creases the N

and M

parameters once more. N

typ-

ically increases by a factor of 3 and M

grows by

the number of trajectories that share the cells that

are added to the representation as a result of dila-

tion. The overall complexity for M trajectories in the

database is governed by O(M · N) for cell approxi-

mation and O(α · M · M

· N

) for similarity score cal-

culation including interpolation and dilation (α ≈ 6,

 M, N

 N). The similarity cell approxima-

tion complexity of O(M · N) is negligible compared

to O(α · M · M

· N

) for score calculation. Hence, the

overall computational complexity of the proposed ap-

proach is dominated by O(α · M · M

· N

) which is

comparably much less than O(M

· N

) for other sim-

ilarity metrics presented in section 1.

5 CONCLUSIONS

We presented a method for computing similarity be-

tween trajectories in a large data collection. Because

trajectories are likely to have different speed proﬁle

and missing points, interpolation and dilation tech-

niques are employed before the scoring. We have

demonstrated that the method is robust except when

many points are removed and dramatically affect the

structure of a trajectory. In that situation there is sim-

ply not enough information to rebuild the path and

provide correct similarity values. The method was

implemented in Mopsi, where for a given trajectory

we display a list of similar paths in reverse order of

the similarity scores.

REFERENCES

Agrawal, R., Faloutsos, C., and Swami, A. (1993). Efﬁcient

similarity search in sequence databases. Springer.

Berndt, D. J. and Clifford, J. (1994). Using dynamic time

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

warping to ﬁnd patterns in time series. In KDD work-

shop, volume 10, pages 359–370. Seattle, WA.

Chan, K.-P. and Fu, A. W.-C. (1999). Efﬁcient time se-

ries matching by wavelets. In Data Engineering,

1999. Proceedings., 15th International Conference

on, pages 126–133. IEEE.

Chen, L.,

Ozsu, M. T., and Oria, V. (2005). Robust and

fast similarity search for moving object trajectories. In

Proceedings of the 2005 ACM SIGMOD international

conference on Management of data, pages 491–502.

ACM.

Chen, M., Xu, M., and Fr

anti, P. (2012a). Compression

of gps trajectories. In Data Compression Conference

(DCC), 2012, pages 62–71. IEEE.

Chen, M., Xu, M., and Fr

anti, P. (2012b). A fast O(N) mul-

tiresolution polygonal approximation algorithm for

GPS trajectory simpliﬁcation. IEEE Transactions on

Image Processing, pages 2770–2785.

anti, P., Chen, J., and Tabarcea, A. (2011). Four aspects of

relevance in location-based media: content, time, lo-

cation and network. In Web Information Systems and

Technologies (WEBIST’11), International Conference

on, pages 413–417.

anti, P., Tabarcea, A., Kuittinen, J., and Hautam

aki, V.

(2010). Location-based search engine for multimedia

phones. In Multimedia and Expo (ICME), 2010 IEEE

International Conference on, pages 558–563. IEEE.

Frentzos, E., Gratsias, K., Pelekis, N., and Theodor-

idis, Y. (2007a). Algorithms for nearest neighbor

search on moving object trajectories. Geoinformatica,

11(2):159–193.

Frentzos, E., Gratsias, K., and Theodoridis, Y. (2007b).

Index-based most similar trajectory search. In Data

Engineering, 2007. ICDE 2007. IEEE 23rd Interna-

tional Conference on, pages 816–825. IEEE.

uting, R. H., Behr, T., and Xu, J. (2010). Efﬁcient k-

nearest neighbor search on moving object trajectories.

The VLDB Journal, 19(5):687–714.

Hamilton, J. D. (1994). Time series analysis, volume 2.

Cambridge Univ Press.

Hu, N. and Steenkiste, P. (2006). Quantifying internet end-

to-end route similarity. In Passive and Active Mea-

surement Conference, volume 2006, pages 101–110.

Lange, D. and Naumann, F. (2011). Efﬁcient similarity

search: arbitrary similarity measures, arbitrary com-

position. In Proceedings of the 20th ACM interna-

tional conference on Information and knowledge man-

agement, pages 1679–1688. ACM.

Mariescu-Istodor, R. (2013). Detecting user actions in

MOPSI. Master’s thesis, University of Eastern Fin-

land.

Ni, J. and Ravishankar, C. V. (2007). Indexing spatio-

temporal trajectories with efﬁcient polynomial ap-

proximations. Knowledge and Data Engineering,

IEEE Transactions on, 19(5):663–678.

Pelekis, N., Kopanakis, I., Kotsifakos, E. E., Frentzos,

E., and Theodoridis, Y. (2011). Clustering uncer-

tain trajectories. Knowledge and Information Systems,

28(1):117–147.

Tabarcea, A., Wan, Z., Waga, K., and Fr

anti, P. (2013).

O-mopsi: Mobile orienteering game using geotagged

photos. pages 300–303.

Vlachos, M., Gunopulos, D., and Kollios, G. (2002a). Ro-

bust similarity measures for mobile object trajectories.

In Database and Expert Systems Applications, 2002.

Proceedings. 13th International Workshop on, pages

721–726. IEEE.

Vlachos, M., Kollios, G., and Gunopulos, D. (2002b). Dis-

covering similar multidimensional trajectories. In

Data Engineering, 2002. Proceedings. 18th Interna-

tional Conference on, pages 673–684. IEEE.

Waga, K., Tabarcea, A., Chen, M., and Fr

anti, P. (2012).

Detecting movement type by route segmentation and

classiﬁcation. In Collaborative Computing: Net-

working, Applications and Worksharing (Collaborate-

Com), 2012 8th International Conference on, pages

508–513. IEEE.

Waga, K., Tabarcea, A., and Fr

anti, P. (2011). Context

aware recommendation of location-based data. In Sys-

tem Theory, Control, and Computing (ICSTCC), 2011

15th International Conference on, pages 1–6. IEEE.

Waga, K., Tabarcea, A., Mariescu-Istodor, R., and Fr

anti,

P. (2013). Real time access to multiple GPS tracks.

pages 293–299.

Worsley, K. J. and Friston, K. J. (1995). Analysis of fMRI

time-series revisitedagain. Neuroimage, 2(3):173–

181.

Yanagisawa, Y., Akahani, J.-i., and Satoh, T. (2003). Shape-

based similarity query for trajectory of mobile objects.

In Mobile data management, pages 63–77. Springer.

LowComplexitySpatialSimilarityMeasureofGPSTrajectories