Automated Generation of High School Geometric Questions Involving

Implicit Construction

Rahul Singhal

, Martin Henz

and Kevin McGee

School of computing, National University of Singapore, Singapore, Singapore

Department of Commmunications and New Media, National University of Singapore, Singapore, Singapore

Keywords:

Automated Deduction, Constructive Geometry, Graph-based Knowledge Representation.

Abstract:

We describe a framework that combines a combinatorial approach and automated deduction to generate geom-

etry problems which require implicit constructions for their solution. This is an extension of our framework

developed for generating geometric questions without construction. Such a system would help teachers to

quickly generate large numbers of questions involving implicit construction on a geometry topic. Students can

explore, revise and master speciﬁc topics covered in classes and textbooks based on construction-based gener-

ated questions. This system may also help standardize tests such as GMAT and SAT. Our novel methodology

uses (i) a combinatorial approach for generating geometric ﬁgures and objects for construction (ii) automated

deduction to generate new questions and solutions. By combining these methods, we are able to generate

questions involving ﬁnding or proving relationships between geometric objects based on a speciﬁcation of the

geometry objects, concepts, theorems and construction object to be covered by the questions. Experimental

results show that a large number of questions can be generated in a short time.

1 INTRODUCTION

Construction-based Euclidean geometry questions

refers to geometric questions which require construc-

tions, namely, to ﬁnd proofs with additional lines,

points, or arcs constructed by a compass and a ruler.

Finding a construction is a hard task even for hu-

man problem solvers. Since one can draw many seg-

ments and arcs at any point of a proof, the search

space is enormous. Hence generating construction-

based questions on a user-selected geometric topics is

a more challenging task.

It is important to understand construction-based

geometry when studying a course because it does not

follow any set pattern. In Euclidean geometry, one

can only learn the axioms and results proven from

these axioms. The student must apply these axioms

with no set pattern or list of steps for solving such

questions. Therefore, a question may have (possibly

inﬁnitely) many solutions. To practice the required

problem solving skills, students require a large num-

ber of different types of geometry questions on vari-

ous concepts which requires implicit construction of

various geometric objects. Generally, textbooks and

online sites provide a limited predeﬁned number of

such type of questions for each topic. Once practiced,

these questions lose their purpose of enhancing stu-

dent thinking. The tedious and error-prone task of

generating high-quality questions challenges the re-

sources of teachers. Hence, there is a need for soft-

ware which assists both teachers and students to gen-

erate geometry questions and solutions.

Apart from helping users, the framework of gen-

erating questions has scientiﬁc contributions to other

research areas, such as Intelligent tutor systems (ITS)

and Massive Online Open Courses (MOOC).

Various research has been performed in automated

deduction of theorems at high school level in the ge-

ometry domain, although none with the goal of au-

tomatic construction-based question generation. In-

stead, they mainly demand users to generate the ques-

tion with the help of tools. In addition, they mainly

focus on solving and assessment of the questions.

Our survey shows that the currently available geom-

etry systems, such as JGEX, Geogebra, Cinderella

and Sketchpad, are not able to automatically generate

questions of user speciﬁed geometry topics. The clos-

est software is GRAMY tool which can solve ques-

tions involving implicit constructions. However it is

unable to generate such questions.

The aim of this paper is to develop a framework

that can be used to generate construction-based geom-

467

Singhal R., Henz M. and McGee K..

Automated Generation of High School Geometric Questions Involving Implicit Construction.

DOI: 10.5220/0004947904670472

In Proceedings of the 6th International Conference on Computer Supported Education (CSEDU-2014), pages 467-472

ISBN: 978-989-758-020-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

etry questions based on speciﬁc inputs, such as geom-

etry objects, theorems and construction objects to be

involved in their solution. For a given set of geome-

try objects, the algorithm can generate a large set of

questions along with their solutions. The solutions

will involve user desired theorems directly or indi-

rectly. Hence the framework can generate questions

to test the theorem on various geometry objects and

concepts.

Generated questions from our framework having

implicit construction may involve algebraic computa-

tions for a solution. Currently, we restrict the rela-

tionships between quantitative entities to linear ones.

Our framework has a predeﬁned database of theo-

rems, concepts and construction objects which can be

used for generating questions. Given a set of user-

selected construction objects, our system can gener-

ate all possible questions using an existing database

of concepts and theorems.

The main contributions of this paper are as fol-

lows:

1. Our geometry question generator combines the

complementary strengths of a combinatorial ap-

proach, pattern matching and deductive reason-

ing. Construction-based geometry questions can

be generated which were not possible previously.

2. A substantial evaluation is provided that demon-

strates the effectiveness of our generator. The

question generator was able to generate most

of the questions, involving implicit construc-

tion, covered in the textbooks based on targeted

queries.

2 RELATED WORK

There are several automated theorem proving system

in the geometric domain such as JGEX (Gao and Lin,

2004), Cinderella and Geometry Explorer (Wilson

and Fleuriot, 2006) that allows users to build proofs

based on geometric constructions. Angle method

(Gao and Lin, 2004), Wu’s method and Grobner basis

method (Chou et al., 1994) are some of the methods

used by the existing geometry systems for automat-

ically proving geometric theorems. However, these

methods are either not suitable for question genera-

tion or the approach used is not suitable for the high

school geometric domain. Hence, the geometric sys-

tems are unable to automatically generate geometric

questions.

GRAMY (Matsuda and Vanlehn, 2004) is a ge-

ometric system that can solve geometric questions

which require implicit construction. It uses a for-

ward chaining search followed by a backward step to

suggest a construction. GRAMY can only discover

proofs that do not involve arithmetic operations. For

example, it cannot ﬁnd proofs that involve inequali-

ties and ratios.

An algorithm developed by Rohit (R. Singh and

Rajamani, 2012) used a numerical approach for solv-

ing geometric questions involving construction. The

algorithm uses the concept of randomness instead of

performing symbolic reasoning. Hence, the solutions

generated by this algorithm are based on numerical

reasoning and out of the scope of high school mathe-

matics.

Our original framework can generate geometric

questions based on concepts, theorems and user-

selected geometric objects. However, it cannot gen-

erate construction based questions. Current work is

an extension of the framework developed in (annony-

mous, 2013).

3 GEOMETRY QUESTION

GENERATION TASK

Mathematically a geometry question Q generated by

our system can be represented by a sextuple (Ob-

ject O, Concept C, Theorem T, Construction objects

CObj, Relationship R, Query type Qt) where:

• O ∈ (lines, triangles, square, circle, ... )

• C ∈ (perpendicular, parallel, midpoint, angle-

bisector, circumcircle...)

• T ∈ (Pythagorean theorem, similarity theorem,

various triangle-theorems, ...)

• CObj ∈ (perpendicular, parallel, midpoint, angle-

bisector...)

• R ∈ (syntactic, quantitative)

• Qt ∈ (syntactic, quantitative)

In order to generate geometry questions, the user has

to provide a set of geometry objects O such as tri-

angles, squares, etc., a set of concepts C and a set

of construction objects CObj such as perpendicular,

parallel, midpoint, etc., which the user would like to

cover in the generated question. Optionally the user

may select a set of theorems T to be tested by the

question. The relationship R can be either syntac-

tic such as perpendicular, parallel, etc., or quantita-

tive such as the giving the length of an object, the ra-

tio of two quantities etc. The query type Qt is the

type of generated question that can be asked to ﬁnd

the hidden relationship which can be calculated from

the given information. The solution of the generated

question would require construction of user-selected

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

468

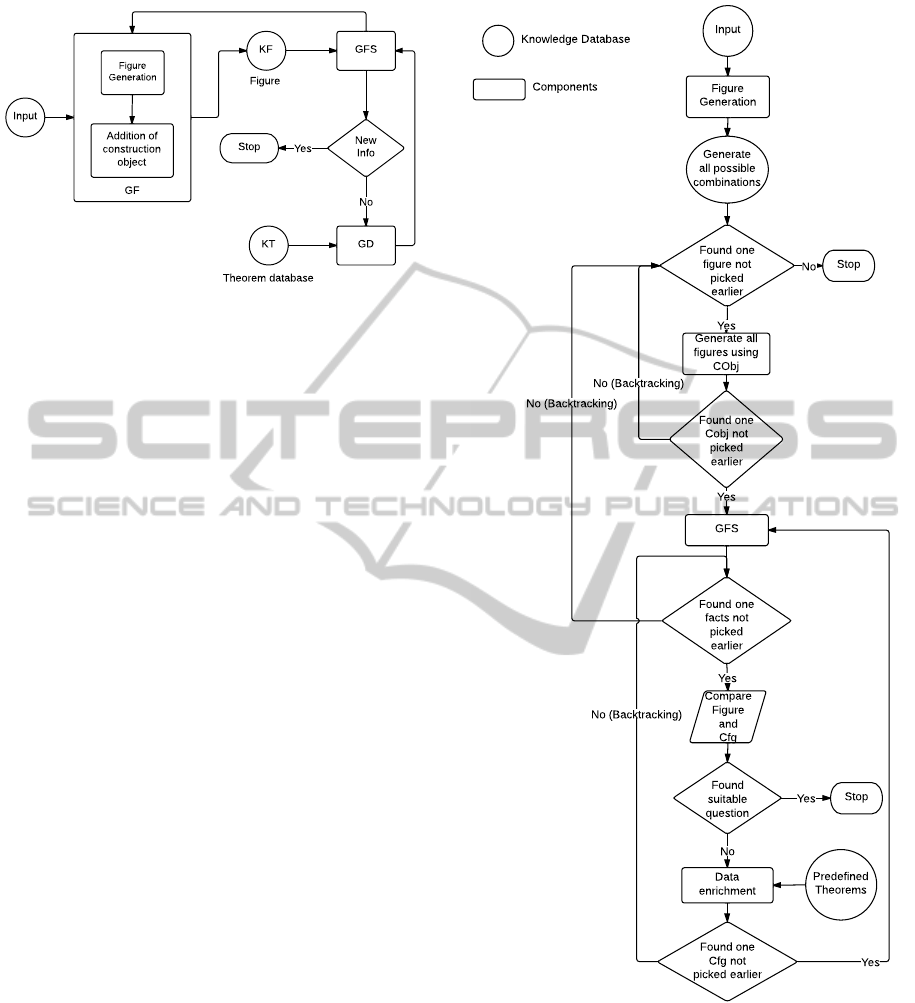
Figure 1: Connection of framework components and knowl-

edge representations.

CObj. Next section describes the framework for gen-

erating such questions.

4 QUESTION GENERATION

FRAMEWORK

Our framework comprises three major components

along with the knowledge databases used for stor-

ing geometry ﬁgures and a set of predeﬁned theo-

rems. Figure 1 shows the connection of these com-

ponents. The input consists of geometric objects,

concepts, theorems and construction objects selected

by the user. The input is fed into the ﬁrst com-

ponent, Generating Figure (GF). This component is

used for generation of geometric ﬁgures from the in-

put. Each ﬁgure constitutes a diagrammatic schema

(DS) (Greeno et al., 1979) and a set of unknown vari-

ables representing the relationship between geometric

objects. User-selected construction objects are added

to the ﬁgure generated by GF according to the algo-

rithm described in the section 4.3. The geometric ﬁg-

ure is passed to the second component, Generating

Facts and Solutions (GFS). This component is used

to ﬁnd values for the unknown variables representing

possible relationships to be covered by the generated

question. GFS makes use of the predeﬁned knowl-

edge database of axioms. It results in the formation

of a conﬁguration (Cfg) containing known values for

some relationships between its objects. New infor-

mation is derived from the conﬁguration Cfg. New

information refers to the generation of suitable ques-

tions. A question is considered suitable if it covers the

essential information such as a new fact and a proper

reasoning for the generated fact. A new fact would not

be related to the construction object CObj. However,

the reasoning of the fact generation would involve the

use of CObj.

Figure 2: Flow diagram of the algorithm for generating

questions.

If the suitability conditions for the generated con-

ﬁguration (Cfg) are not met then the conﬁguration is

fed into the last component, Generating data for the

ﬁgure (GD). GD assigns values to unknown variables

of relationships. Repeated processing by GD makes

the questions generated from Cfg easier and easier,

because the values assigned by GD appear as given

facts in the generated questions. GD makes use of

AutomatedGenerationofHighSchoolGeometricQuestionsInvolvingImplicitConstruction

469

a predeﬁned set of theorems and makes sure that the

assignment results in successful generation of geom-

etry questions. The conﬁguration generated from this

component is again passed to the GFS component and

this loop continues until a question is found which

meets suitability conditions.

4.1 Algorithm

Figure 2 represents the ﬂowchart describing the al-

gorithm for generating geometric questions involv-

ing implicit construction. Algorithm 1 describes the

ﬂowchart in further detail.

In this section, Algorithm 1 is explained with the

help of a running example. Figure 3 shows the step

by step execution of the algorithm. We select the fol-

lowing input in our example.

• Object: triangle and line segment

• Concept: perpendicular

• Construction object: Parallel lines

• Theorem: Pythagorean Theorem

• Number of questions: 1

Area Triangle ABE is 18

length(B,C,10)

Apollonius Theorem

length (A, B, 8) (Given)

length (A, C, 6) (Given)

length (A, F, 5) (Calculated)

Pythagoras Theorem

length (A, E, 4) (Given)

length (F, E, 3) (Given)

(a)

(b)

(c)

(d)

Figure 3: (a) The ﬁgure generated by using triangle and

perpendicular as the geometry objects using the GF func-

tion. (b) A parallel line is drawn parallel to ”CB” from E

meeting ”AB” at ”F”. (c) The data is generated for (b) us-

ing the GD component. (d) The new fact not involving EF

and its derivation involving EF using the GFS component

generated from the ﬁgure shown in (c).

In the next subsections, we will describe each

framework component and its interaction with the

knowledge databases.

Data: User selects object(s), concept(s),

construction-object(s), theorem(s)

and the number of questions to be

generated.

Result: Question with single or multiple

solutions.

1. Generate all possible ﬁgures consisting

of geometry objects using GF function

from the given input.

2. Find one ﬁgure which has not been

picked earlier. If found, go to next step

else terminate.

3. Add Cobj using the algorithm

mentioned in the section 4.3.

4. If new ﬁgure is generated, go to next

step else do backtracking.

5. Save this ﬁgure using KF knowledge

database.

6. Assign values to variables of ﬁgure

obtained in second step from the

predeﬁned knowledge database of

axioms through GFS function.

Conﬁgurations (Cfg) are generated

from this step.

7. Find one Cfg not picked earlier. If

found, goto next step. If not found,

backtracking to step 2.

8. Compare Cfg with the previously

stored ﬁgure.

9. If the comparison gives the desired

suitability then the Cfg is declared as a

generated question and the algorithm

stops. If the conditions are not met or

more number of questions are required,

go to the next step.

10. Conﬁguration Cfg obtained from GFS

is fed into the third component, GD, to

assign more unknown variables. It

makes use of KT, a predeﬁned database

of theorems.

11. From the conﬁgurations obtained from

GD, ﬁnd a new conﬁguration Cfg

which has not been chosen earlier. If

found, goto step 3. If all conﬁgurations

have been chosen earlier, goto step 5.

Algorithm 1: Algorithm for generating geometry

questions.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

470

4.2 Generating Figure Conﬁguration

from the User Input (GF)

This is the ﬁrst step executed by Algorithm 1 de-

scribed in Section 4.1. This component is further

divided into two sub-components, Figure Genera-

tion and Addition of construction object. First sub-

component generates a ﬁgure through the combina-

tion of a predeﬁned number of ways to combine ge-

ometric objects. Currently, we are focusing on trian-

gles and line segments. Hence our algorithm includes

combinations in which various triangles and lines can

intersect. Furthermore, we are currently limiting our

algorithm to the intersection of two triangles. Adding

more objects may make the ﬁgure more complex, pos-

sibly leading to unusual questions that are not com-

monly found in textbooks. However there is no limi-

tation on the intersection of lines and triangles.

Adding Construction Object from the Figure

Generated by GF

This component is used for adding geometric objects

which will not be shown in the generated question.

However, the construction of the object would be re-

quired by the user to prove/solve the questions. Gen-

erally, more than one construction object can be added

for generating questions. However, we have limited

our algorithm to addition of single object. Addition

of two or more objects may lead to the generation of

questions very hard to solve and may not solve the

purpose of testing the concepts.

Figure 4 describes the algorithm for adding a con-

struction object in a ﬁgure (input) generated by the

ﬁrst sub-component. The algorithm ﬁrst checks for

the user-selected construction objects. If the user has

selected an object, the algorithm looks for the pre-

existence of the selected construction object. In case

the object is not present, algorithm adds it in the ﬁg-

ure and terminates. The algorithm does nothing if the

user-selected object is already present in the ﬁgure.

Currently, our algorithm is limited to the construc-

tion of a line between two existing points, parallel,

Figure 4: Explains the algorithm for adding construction

objects in a given ﬁgure.

perpendicular line and median in a given ﬁgure.

4.3 Generating Facts and Solutions

(GFS)

This component is responsible for ﬁnding the values

of unknown variables of the generated conﬁguration

from the other components. This component acts as

question generator and solver. The unknown variables

whose values have been found represent the generated

questions. The steps that leads to ﬁnding the unknown

variables represent the solution. The algorithm will

consider only those facts which do not include CObj

but make use of CObj for reasoning. Figure 3d shows

an example of such a fact. The new fact is related

to the length of side CB of a triangle. However, it

requires the construction of a perpendicular line from

E to AB.

There may be several ways for ﬁnding the val-

ues of the unknown variables. In such cases, this

component shows all solutions. For generating the

new facts, it uses a predeﬁned database of theorems.

The theorems are represented in the form of axioms.

We have used The School Mathematics Study Group

(SMSG) axiomatic system, which is a combination of

Birkhoffs and Hilberts axiom (Francis,2002) systems.

More details can be found in an algorithm (annony-

mous, 2013).

4.4 Generating New Conﬁgurations

(GD)

This component starts with a search for user-selected

theorems. If the user has not chosen any theorem,

a theorem is non-deterministically selected from the

predeﬁned knowledge database of theorems. Our al-

gorithm terminates when all theorems have been se-

lected once for a given ﬁgure conﬁguration. After

theorem selection, pattern matching on the theorem

ﬁgure is performed. If a matching pattern is found, a

set of input and/or output values are assigned to the

chosen pattern. This assignment is done with the help

of a predeﬁned set of theorems. In case no pattern is

found, a new theorem is chosen from predeﬁned the-

orem database, KT, and the whole process is repeated

until we get the desired conﬁguration. More details

can be found here (annonymous, 2013).

5 IMPLEMENTATION

Each component of our tool is implemented indepen-

dently, using state-of-the-art libraries and systems.

AutomatedGenerationofHighSchoolGeometricQuestionsInvolvingImplicitConstruction

471

DE || BC, Area of

Triangle ADE is 10,

4DE = BC,

Find Area of Triangle

CED ?

BD = CD, EA = AD, AC = 30

BD = CD, 4EA = ED, AC = 30,

Area of Triangle ABE = 18

BD = CA, AB = CD, BC = 6,

Find Area Triangle OBC

Figure 5: Figure (a) can be solved by drawing a perpendic-

ular from E to AB (b) A perpendicular is drawn from D to

CB (c) A parallel line is drawn from D to AC (d) A parallel

line is drawn from E to BD (e) Three lines are drawn joining

existing points, AR, BP, CQ.

C++ is used for performing calculations and Python

is used for implementation of the algorithm and pre-

deﬁned knowledge databases. Constraint Handling

Rules (CHR) (Fr

uhwirth and Raiser, 2011) are used

for generating new facts from the axioms and the

given facts. For implementing knowledge representa-

tion, the graph database Neo4j (Vicknair and Macias,

2010) is used. Both questions and a set of predeﬁned

theorems are represented using Neo4j.

Results

Our system can generate geometry questions using

the framework described in Section 4. Currently, our

knowledge database of objects contains line segments

and triangles. In addition, we have a predeﬁned set

of more than 100 theorems. The generated questions

cover four construction objects, e.g. perpendicular

line. Figure 5 shows various questions generated by

our system on selecting ”triangle” as object and vari-

ous CObj such as parallel line, perpendicular line and

median. The dashed lines in the Figure 5 represent

construction of the CObj required to solve the ques-

tion.

GRAMY (Matsuda and Vanlehn, 2004) is a ge-

ometric system that can solve geometric questions

which require implicit construction. However, due to

inavailability of GRAMY’s source code, we cannot

validate the questions generated by our framework.

6 CONCLUSION

In this paper, we provide a framework for the au-

tomatic generation and solving of geometric ques-

tions which require implicit construction of geomet-

ric objects for their solution. Our system is able to

quickly generate large numbers of questions on spe-

ciﬁc topics based on construction objects. Such a

system will help teachers reduce the time and effort

spent on the tedious and error-prone task of generat-

ing construction-based questions.

Future work involves conducting experiments in

which the teachers would be asked to differentiate be-

tween the textbook questions and the framework gen-

erated questions. Another major improvement would

be to generate questions according to the required dif-

ﬁculty level in addition to the implicit construction of

objects.

REFERENCES

annonymous (2013). Automated generation of geometry

questions for high school mathematics. In Sixth Inter-

national Conference on Computer Supported Educa-

tion.

Chou, S. C., Gao, X. S., and Zhang, J. Z. (1994). Machine

proofs in geometry: Automated production of read-

able proofs for geometry theorems.

uhwirth, T. and Raiser, F., editors (March 2011). Con-

straint Handling Rules: Compilation, Execution, and

Analysis.

Gao, X.-S. and Lin, Q. (2004). Mmp/geometer a software

package for automated geometric reasoning. In Win-

kler, F., editor, Automated Deduction in Geometry,

volume 2930 of Lecture Notes in Computer Science,

pages 44–66. Springer Berlin Heidelberg.

Greeno, G., J., Magone, and Maria E. Chaiklin, S. (1979).

Theory of constructions and set in problem solving.

Technical report, Pittsburg Univ Pa Learning Research

and Development Center.

Matsuda, N. and Vanlehn, K. (2004). Gramy: A geome-

try theorem prover capable of construction. J. Autom.

Reason., 32(1):3–33.

R. Singh, S. G. and Rajamani, S. (2012). Automatically

generating algebra problems. In AAAI.

Schrijvers, T. and Demoen, B. (2004). The k.u.leuven chr

system: Implementation and application.

Vicknair, C. and Macias, M. (2010). A Comparison of a

Graph Database and a Relational Database.

Wilson, S. and Fleuriot, J. D. (2006). Geometry explorer:

A tool for generating diagrammatic full-angle method

proofs. Technical report, University of Edinburgh.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

472