
Integrated STEM in Elementary Grades Using Distributed
Agent-based Computation
Pratim Sengupta, Gokul Krishnan and Mason Wright
Mind, Matter & Media Lab, Vanderbilt University, Peabody College, Nashville, TN, U.S.A.
Keywords: Computational Thinking, Tangible Interfaces, Agent-based Programming, Visual Programming,
K-12 Science Education, User-centered Design, Integrated STEM, Engineering Education.
Abstract: We investigate how the integration of visual agent-based programming and computationally augmented
physical structures can support curricular integration across STEM domains for elementary grade students.
We introduce ViMAP-Tangible, a socio-technically distributed computational learning environment, which
integrates ultrasonic sensors with the ViMAP visual programming language using a distributed computation
infrastructure. In this paper, we report a study in which 3
rd
and 4
th
grade students used ViMAP-Tangible to
engage in collaborative design-based activities in order to invent “drawing machines” for generating
geometric shapes. The curricular activities integrate engineering practices such as user-centered design,
mathematical reasoning about multiplication, rates and fractions, and physical science concepts central to
learning Newtonian mechanics. We identify the key affordances of the learning environment and our
pedagogical approach in terms of the relationship between the structural elements of students’ physical
constructions and computational models, and their learning outcomes, both in terms of computational
thinking, and the domain-specific, mathematical and scientific knowledge that they began developing.
1 INTRODUCTION
Integration of the individual domains of science,
technology, engineering, and mathematics (STEM)
is now recognized as a central pedagogical aim of
engineering and science education reform at the K-
12 level (Nathan, Srisurichan, Walkington,
Wolfgram, Williams, & Alibali, 2013; Berland,
2013). STEM integration is considered in the US
education policy statements to be necessary for
several objectives: a) supporting STEM education,
including the preparation of future STEM
researchers; b) for developing informed citizens;
and, c) for supporting workforce development in an
increasingly complex economy (Katehi et al., 2009;
NRC, 2007, 2010; Nathan et al., 2013).
Integrated STEM necessitates integrating diverse
domains by highlighting big ideas that transcend
these different domains (Nathan et al., 2013;
Schunn, 2009; Roehrig, Moore, Wang, & Park,
2012). However, the generation of these ideas
involves material agency, conceptual agency and
participation in a community of practice. For
example, engineering educators have argued that
some of the most essential “skills” in engineering
“arise out of engagements not only with formal
representations, but also with tools, materials, and
other people” (Johri & Olds, 2011, p. 163).
Similarly, historians, philosophers and sociologists
of science have shown that the development of
scientific knowledge (e.g., big ideas such as laws of
physics) is deeply intertwined with the invention of
representational systems and tools, as well as the
development of communicative representational
practices (e.g., modeling) (Giere, 1999; Pickering,
1993). The representational systems and tools
include both semiotic systems (e.g., calculus and
computational modeling languages) and mechanical
devices (e.g., bubble chambers and particle
accelerators). This is known as the Science as
Practice perspective, and has been adopted as a key
pedagogical framework for K-12 science education
in the US (NRC, 2008).
Given this background, we believe that the focus
on Integrated STEM is synergistic with the recent
focus on computational thinking (Wing, 2006, 2010;
NRC, 2010). Wing (2006) described computational
thinking as a general, analytic approach to problem
solving, designing systems, and understanding
human behaviors. Sengupta, Kinnebrew, Basu,
67
Sengupta P., Krishnan G. and Wright M..
Integrated STEM in Elementary Grades Using Distributed Agent-based Computation.
DOI: 10.5220/0004949500670078
In Proceedings of the 6th International Conference on Computer Supported Education (CSEDU-2014), pages 67-78
ISBN: 978-989-758-021-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Biswas & Clark (2013) argued that computational
thinking is evident in the form of epistemic and
representational practices such as problem solving,
design, programming, and modeling.
Pedagogy that supports the development of
representational practices associated with
computational thinking can bring together different
domains in science, such as biology and physics, in
middle school classrooms through the use of agent-
based, visual programming languages designed
specifically for modeling scientific phenomena
(Sengupta et al., 2013). In agent-based
programming, a user creates a computer program by
using simple rules to command the movement and
behavior of computational agents, e.g., the Logo
turtle (Papert, 1980; diSessa, Abelson & Polger,
1991; Repenning, 1993; Kelleher & Pausch, 2005;
Resnick et al., 2009; Sengupta & Farris, 2012;
Sengupta et al., 2013). In this paper, we extend this
argument and propose that a particular form of
agent-based programming and modeling, in which
control of a computational agent is socio-technically
distributed, can be leveraged to integrate diverse
STEM domains for children in elementary grades.
The learning environment we present here can be
best understood as a socio-technically distributed
activity system. This is because ViMAP-Tangible
distributes the control of a single computational
agent socially between two collaborating users, and
technologically, between two physical machines and
a virtual algorithm. The goal of each student dyad in
this study was to design, build, test and refine a
hybrid (computational and physical) computational
machine for generating geometric shapes. Our
pedagogical approach emphasized User-Centered
Design (UCD), i.e., students were asked to design
their machines with usability (Norman, 1998) as a
key focus, which has been shown to be a crucial
element of product engineering but challenging to
implement pedagogically.
Our paper makes three contributions. First, we
present a pedagogical framework for integrating key
engineering practices – UCD, collaboration and
computational thinking - with math and science
education. To this end, we present a theoretical
framework that integrates relevant literature from
multiple domains: computational thinking,
Integrated STEM, Agent-based and Tangible
Computation in education, User Centered Design,
Design-based Learning and Collaboration in
engineering practice and education. Second, we
present a technological innovation in the form of
ViMAP-Tangible, and a set of curricular activities,
which were designed to bring about such integration.
Third, while recent efforts have focused on
designing and implementing Integrated STEM
curricula at the college level (Sanders, 2009), middle
school (Berland, 2013) and high schools (Nathan et
al., 2013), we demonstrate that younger children (3
rd
and 4
th
graders) can be brought into the fold of
Integrated STEM education that also includes a
focus on developing computational thinking.
2 THEORETICAL FRAMEWORK
2.1 Computational Thinking in K-12
Computational thinking is an increasingly ubiquitous
epistemic and representational practice in all fields
of science and engineering (Wing, 2006; NRC,
2010). As Sengupta et al. (2013) pointed out,
computational thinking draws on concepts that are
fundamental to computing and computer science, but
also includes practices (e.g., modeling, abstraction,
reformulation, simulation, verification) that are
central to a large number of scientific, engineering,
and mathematical disciplines. This sentiment is also
reflected in the model ACM K-12 computer science
curricula for middle schools (Tucker et al., 2003),
and the recently concluded National Academy of
Education panel on computational thinking (NRC,
2010), which argued for integrating computational
thinking with existing K-12 curricula in other
domains such as mathematics and science.
Wing (2006) argued that a key characteristic of
computational thinking is design-based thinking.
Design is a form of problem solving in which
thinking, tool manipulation, and materials are
reflected in the iterative construction of an artifact
(Bucciarelli, 1994; Simon, 1969; Perkins, 1986).
From a pedagogical perspective, design challenges
provide learners opportunities for testing and
revising their developing conceptions and
understanding, and interweave action and
development with reflection and refinement to
facilitate deep learning (Kolodner et al., 2003).
Researchers have shown that students’ construction
failures, when scaffolded appropriately, provide
additional opportunities for learning (Kolodner et
al., 2003; Papert, 1980; Harel, 1990; Penner, Lehrer
& Schauble, 1998).
2.2 Integrated STEM as Pedagogy
Integrated STEM has been defined as technological
and engineering design-based learning approaches
that intentionally integrate concepts and practices of
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
68

science and/or mathematics education with content
and process of technology and/or engineering
education (Sanders, 2009; McCulloch & Ernst,
2013).
As Nathan et al. (2013) pointed out, integration
necessitates a pedagogical approach in which fields
are integrated, rather than merely combined (cf.
Dyer, Reed, & Berry, 2006; Satchwell & Loepp,
2002). The emphasis on “integration” implies that
diverse fields of knowledge and practice should be
merged in a manner that reveals big ideas that
transcend specific disciplines (Nathan et al., 2013;
Schunn, 2009; Roehrig, Moore, Wang, & Park,
2012).
Nathan et al. (2013) argued that big ideas that are
regarded as invariants in math and science are
represented using different inscriptions, both
material and semiotic, as well as in different social
interactions, such as in lectures or group work. As
such, Nathan et al. (2013) argued that STEM
integration in a high school level project-based
engineering classroom can be viewed as the
production and maintenance of cohesion of invariant
relations across the broad range of representations
that exist in the engineering classroom.
Similarly, Berland also argued that STEM
integration can be brought about by a particular class
of activities that she termed STEM-design
challenges (Berland, 2013). In such activities,
students are posed an engineering design challenge
that can only be completed when relevant math and
science concepts are applied (e.g., Coyle, Jamieson
& Sommers, 1997; Fortus et al., 2004; Kanter, 2010;
Kolodner et al., 2003). In such activities,
pedagogically, these concepts represent domain-
specific learning goals in science and math.
One of our central goals in this paper is to
demonstrate that computational representational
practices that are supported by agent-based
programming and the design and development of
usable physical control mechanisms for controlling
agent-behaviors, can integrate representational
practices and conceptual development across
multiple STEM domains.
2.3 Agent-based Visual Programming
& Tangible Computation for
Children
The literature on designing agent-based
programming languages and environments for
novice programmers highlights the following
affordances. First, agent-based programming has
been shown to be intuitive for novice programmers,
as it leverages learners’ embodied intuitions about
movement in space (Papert, 1980). Second, agent-
based programming can also help children learn
scientific concepts in physics and biology (diSessa,
Abelson & Ploger, 1993; Repenning, 1993;
Sengupta & Farris, 2012; Sengupta et al., 2013).
Third, agent-based programming can help develop
computational literacy through the design of self-
expressive digital narratives and games using visual
agent-based environments such as Scratch (Maloney
et al., 2004) and Alice (Conway, 1997).
Our choice of visual programming as the mode
of programming is grounded in the literature on
computer science education. Children find it difficult
to understand the syntax and semantics of
programming (Spohrer & Soloway, 1986; Perkins,
1988). They also find it challenging to effectively
control the flow of a program using loops and
conditionals (du Boulay, 1989). Researchers have
also found that alleviating syntax problems helps
students focus on the semantic ones (Hohmann,
1992; Soloway, 1993; Anderson, 1989; Mannila,
Peltomaki & Salakoski, 2006). Visual programming
– in which students construct programs using
graphical objects in a drag-and-drop interface– has
been shown to be effective in alleviating these
difficulties (Kelleher & Pausch, 2005). Examples of
agent-based visual programming environments are
AgentSheets (Repenning, 1993), StarLogo TNG
(Klopfer, Yoon, & Um, 2005), Scratch (Maloney et
al., 2004), ViMAP (Sengupta, Farris & Wright,
2012) and Alice (Conway, 1997).
Researchers have also started focusing in on the
integration of tangible computation with agent-based
modeling and programming for novice learners
(Suzuki & Kato, 1995; Blackwell, 2003; Horn &
Jacob, 2007; Blikstein & Wilensky, 2009). Blikstein
and Wilensky (2009) showed that linking multi-
agent computer models with real-world phenomena
by using sensors could enable undergraduate
students to learn authentic scientific and engineering
concepts and practices. Tangible programming
languages such as AlgoBlock (Suzuki & Kato, 1995)
and Tern (Horn & Jacob, 2007; Horn et al., 2011)
have also been used to teach young children
programming.
In AlgoBlock, lexical elements of the Logo
language are assigned to sealed metal boxes, about
20 cm on each side. These blocks can be assembled
by plugging each block, via connectors on the sides,
into neighboring blocks. These blocks are connected
to the computer using a wired interface. A complete
Logo algorithm could be constructed by assembling
a sufficient number of blocks on a tabletop, and the
IntegratedSTEMinElementaryGradesUsingDistributedAgent-basedComputation
69

results of running the program are visible in the form
of an animated submarine on screen (Suzuki & Kato,
1995). Horn and colleagues developed Tern, in
which users construct programs by arranging and
organizing wooden blocks with computer-vision
fiducials (black and white symbols), which are then
scanned by a program to generate a Logo algorithm.
Tern has been used effectively to teach young
learners programming and robotics, both in informal
and formal settings (Horn, Crouser & Bers, 2011;
Horn & Jacob, 2007).
While tangible and visual programming offer
two different interactional modes of programming
for the learner, Horn, Crouser & Bers (2011) have
argued for introducing a hybrid approach in which
learners (users) can elect to work either using
tangible blocks, or by using a visual (graphical)
programming interface, to generate the same
algorithm. They found that such a hybrid approach
was more advantageous than using either approach
individually.
2.4 User Centered Design: Practice and
Pedagogy
User Centered Design (Norman, 1998; Norman &
Draper, 1986) emphasizes the importance of
understanding the needs of the users in order to
design usable systems. Norman (1998) argued that
central principles of designing for people to support
understandability and usability are: a) providing a
good conceptual model to the user, which will allow
them to predict the effects of their actions on the
designed system; and b) making things visible, i.e.,
by carefully considering the relationship between the
design of “controls” of a system and its “placement”
(location) so that it makes the function of the control
intuitively available for the user.
However, there is variability in how design
researchers have defined and operationalized UCD:
while there is a general agreement that UCD
requires paying attention to the needs of the user,
and involving the user in the system design process,
there is relatively less agreement on how user
involvement can be accomplished (Vredenburg,
Mao, Smith, & Carey, 2002; Gulliksen, Göransson,
Boivie, Blomkvist, Persson, & Cajander, 2003;
Karat, 1996). Vredenburg et al. (2002) defined UCD
as the practice of the following principles: the active
involvement of users for a clear understanding of
user and task requirements, iterative design and
evaluation, and a multi-disciplinary approach.
Gulliksen et al. (2003) further elaborated on the
principles and argued that in addition to involving
the user throughout the design process, the following
principles are necessary to be enacted in practice in
order to support UCD: 1) rapid prototyping during
the early phases of the design process; 2) a cyclic
iterative process of designing solutions interwoven
with evaluation; 3) multi-disciplinary design teams
that bring together distributed expertise for the
various design components; and 4) an integrated
design process, in which
the system, the work
practices, on-line help, training, organization, etc.
should be developed in parallel.
In this paper, we adopt Gulliksen et al.’s (2003)
definition of UCD as a key element of our
pedagogical approach. There is some evidence that
designing for instructional use can act as a
productive pedagogical model for K-12 science
education (Carver et al., 1992; Harel, 1990; Brown
and Campione, 1993). Brown and Campione (1993)
noted that fifth and sixth graders developed a deeper
understanding of science concepts while they sought
causal explanations to incorporate into HyperCard
documents they developed to teach their classmates.
A few studies have also focused on children
designing agent-based instructional software for
mathematics (e.g., Harel, 1990) and instructional
games in science and mathematics (e.g., Kafai et al.,
1998). In all of these studies, students not only
developed a deeper understanding of the target
science or math concepts, but also developed
substantial expertise in programming.
An interesting finding across these studies is that
children find the consequentiality of their design
projects in terms of designing for use to be quite
motivating, but at the same time, they do not regard
the involvement of users as a useful component of
their design process (Carver et al., 1992; Kafai et al.,
1998). Carver et al. found that "getting someone to
try out the presentation" was regarded by middle
school students as one of the least important tasks to
accomplish during their design process; instead, they
believed that the designers themselves could act as
users during the design process. Similarly, in Kafai
et al.’s work, children who designed educational
software did so largely without involving real users
in their design process. This in turn resulted in the
design of user interfaces that were confusing for the
real users (Kafai et al., 1998). This is in striking
contrast to Norman’s (1998) famous dictum that
because the interface guides the interactions between
the user and the product, it should therefore guide
the design of the rest of the product.
These studies suggest that the involvement of
users during the design process therefore requires
explicit instructional scaffolding by the teacher. In
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
70

fact, once “real” users tested the children’s designs,
Carver et al. (1992) found that the design documents
designed by the children to scaffold user interaction
with their designs increased greatly in terms of
making explicit the connections between the
different aspects of their design, as well as
explaining how to use the designed artifact. In
Norman’s terms (Norman, 1998), one can therefore
conclude that involvement of user feedback during
the design cycle enhances the usability of the
product, as it makes clear to the designers the need
to make things visible to the user.
2.5 Collaboration in Engineering
Practice & STEM Education
Collaboration and teamwork hold a significant place
in engineering practice (Bucciarelli, 1994). As Johri
(2012) pointed out, engineers increasingly work
collaboratively around the globe; technology is a
primary driver of such arrangements. Anderson,
Courter, McGlamery, Nathans-Kelly and Nicometo
(2010) studied engineering work across six
engineering firms that examined engineers’ self-
valuation of important work characteristics. They
found remarkable similarities across settings in
which most engineers saw their work as
collaborative problem solving, and greatly valued
communication skills and working in a team.
In the field of education research, collaboration
and cooperation have been defined as conceptually
distinct processes. Roschelle & Teasley (1995)
defined collaboration as “a coordinated,
synchronous activity that is the result of a continued
attempt to construct and maintain a shared
conception of a problem” (Roschelle & Teasley,
1995; p. 70). Dillenbourg (1999) defined the
distinction between collaboration and cooperation as
follows: “In cooperation, partners split the work,
solve sub-tasks individually and then assemble the
partial results into the final output. In collaboration,
partners do the work ‘together.’” (p. 8).
Productive collaborative tasks create positive
interdependence among learners, which can be
understood as the coordinated activity of multiple
people for accomplishing a specific learning
objective (Kreijns, Kirschner & Jochems, 2003;
Antle & Wise, 2013). White & Pea (2011) argued
that collaborative tasks are likely to be most
effective when they are sufficiently open-ended and
complex to necessitate contributions from each
member of a group (e.g., see Cohen, 1994), and
when participants engage the task and one another in
ways that sustain their diverse contributions (e.g.,
see Barron, 2003). In the literature in computer
supported collaborative learning, collaboration is
often fostered through variations on the “jigsaw”
script in which each student only has access to part
of the information (i.e. one piece of the puzzle)
needed to solve a collaborative task (Miyake,
Masukawa & Shirouzou, 2001).
Research suggests that collaboration can indeed
enhance science and math learning through the
creation of productive opportunities for shared
inquiry and discourse. Pathak, Kim, Jacobson &
Zhang (2010) showed that dyadic discourse in an ill-
structured inquiry activity when exploring a
scientific phenomenon using agent-based
simulations, creates opportunities for reflective
reasoning. Specifically in the context of learning
kinematics using agent-based programming,
researchers have showed that collaborative design of
graphical, mathematical and computational
representations of motion creates productive
opportunities for within-group “conversations for
conceptual change” (diSessa et al., 1991; Sherin et
al., 1993). Similarly, in math education, researchers
have focused on how learning in collaborative
settings leads students to develop mathematical
discourse by productively appropriating their group
members’ ways of talking or acting (Carlsen, 2010;
Moschkovich, 2004; Radford, 2006; Lai & White,
2011).
Of particular relevance to our paper is the
argument that meditational tools – that include both
tangible and computational artifacts – can support
collaborative learning by creating opportunities for
each group member to attend to what the other is
doing, by making actions visible and gaze
observable in supporting collaborative meaning-
making (Antle & Wise, 2013; Fernaeus &
Tholander, 2006; Hornecker, 2005; Suzuki & Kato,
1995; Baker et al., 1999; Suthers et al., 2008). These
studies showed that the presence of tangible artefacts
in a shared transaction space (Hornecker, 2005)
grounds the interaction between group members by
providing a referential anchor for conversation,
which can be referred to by using both verbal and
gestural communication channels. Of direct
relevance to our study, Fernaeus & Tholander
(2006) found that when students worked
collaboratively using a tangible programming
language for learning agent-based programming,
they formed subgroups dynamically, and
furthermore, and these subgroups further
collaborated with one another on the different
activities to accomplish their goals.
IntegratedSTEMinElementaryGradesUsingDistributedAgent-basedComputation
71
3 THE VIMAP-TANGIBLE
LEARNING ENVIRONMENT
3.1 The Representational
Infrastructure
Three key elements of ViMAP-Tangible are:
(1) Agent-based visual programming: ViMAP
(Sengupta, Farris & Wright, 2012) serves as the
agent-based, visual programming language for our
learning environment. ViMAP consists of library of
graphical programming primitives designed
specifically to support learning of mathematics,
kinematics and biology, a construction zone where
learners can generate an algorithm by using a drag-
and-drop interface that is easy to understand for
children, and a NetLogo environment (Wilensky,
1999) to allow learners to visualize the results of
their algorithm. Similar to Alice and Scratch,
ViMAP provides a drag-and-drop interface for
constructing programs that is easy to use and
understand for children. Commands in ViMAP
include both domain-general abstractions (e.g.,
loops, conditionals), as well as domain-specific
commands (e.g., for controlling speed, distance and
acceleration of the turtles).
(2) Tangible and gestural representation of digital
information: In ViMAP-Tangible, students can use
gestures and/or mechanical devices in order to
control different variables by linking them to sensors
through their ViMAP programs. The ultrasonic
distance sensors we used in this study measure the
distance from the sensor itself to the nearest object
in its field of operation. Some of the ViMAP
programming primitives were designed specifically
to allow users to set the values of different agent-
variables (e.g., color, speed, acceleration, pen-width,
horizontal and vertical displacements) based on the
sensor-readings. For example, the “set <step-size>
equal-to <sensor-reading>” command sets the
distance the agent on the screen travels equal to the
reading of the ultrasonic sensor. That is, when a
learner uses this command in her/his algorithm,
moving a hand towards the sensor (i.e., closer) will
cause the turtle to travel a shorter distance.
(3) Distributed control of virtual agent: In ViMAP-
Tangible, multiple students can simultaneously
control the behavior of a single agent. In the version
of ViMAP-Tangible we report here, control of the
behavior and attributes of a single computational
agent is distributed across two ultrasonic sensors,
which are connected to ViMAP via an Arduino
TM
microcontroller (Figure 2). We believe that such a
setting can foster positive interdependence (Antle &
Wise, 2013), since it requires the coordinated action
of both the group members in order to
computationally implement and physically enact a
successful and non-redundant control mechanism.
3.2 Curricular Activities
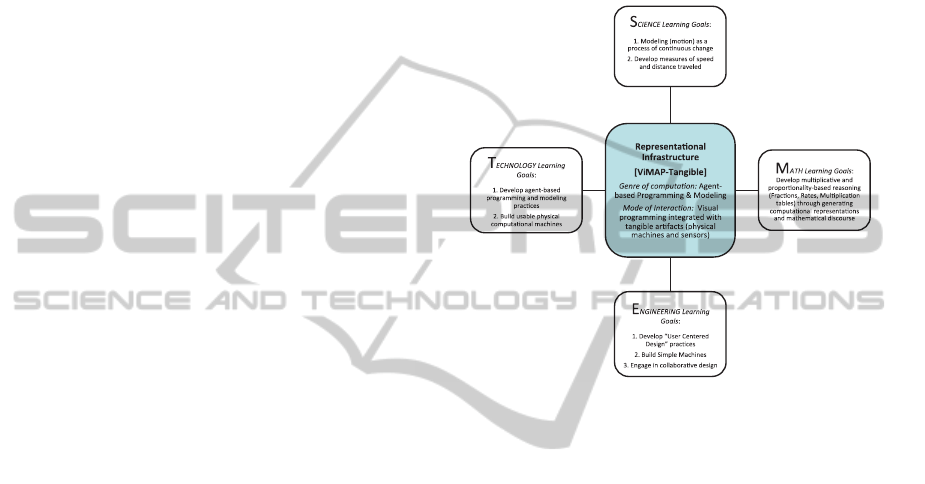
Figure 1: Domain-Specific Learning Goals for STEM
Integration Using ViMAP-Tangible.
The curricular activities consisted of three phases,
and were designed to integrate multiple domain-
specific learning goals. These learning goals are
shown in Figure 1.
During the first phase of our curriculum, students
were introduced to agent-based programming using
ViMAP. Students learned to generate “open” and
“closed” geometric shapes (e.g. squares, circles,
spirals) using ViMAP. In the second phase, students
used these shapes to represent models of phenomena
involving continuous change over time. We watched
segments of the movie The Lorax in class, after
which students identified various events depicted in
the movie (such as Lorax running and accelerating,
objects in free fall, etc.) that could be modeled using
ViMAP shapes. This phase was designed to
establish shape drawing as a consequential (Gresalfi
& Ingram-Noble, 2008) activity that is not only
valuable for its visual aesthetics, but that can also be
used as a computational model of change over time.
In both these phases, each student worked
individually. Our previous work has shown that
these two phases can effectively introduce students
to the basics of agent-based programming, and
students also learn to use their programs (i.e.,
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
72

geometric shapes) as models of motion in Phase 2
(Sengupta & Farris, 2012).
Figure 2: The ViMAP-Tangible Distributed Computation
Infrastructure.
The third phase used a STEM design challenge
(Berland, 2013), in which students worked in dyads
to design and develop a tool for shape drawing using
ViMAP. The nature of the tool that the dyads were
asked to build was a hybrid computational machine
consisting of a physical control structure (i.e., a
simple machine), and a ViMAP program, which
would together control the movement of the virtual
agent (ViMAP turtle) on screen. Each student was
asked to design a mechanical control for one sensor,
but the dyad was responsible for jointly designing
the ViMAP program. Emphasis on User Centered
Design was maintained throughout this phase as
follows: First, students themselves acted as the
users; thereafter, students from other groups acted as
users (this is the main user-testing phase for the
purposes of our analysis); and during the final day of
the class, students’ parents were invited to visit the
class to test their children’s designs.
Our pedagogical approach emphasized several of
Gulliksen et al.’s (2003) core principles of UCD.
These included the following: an emphasis on rapid
prototyping during the early phases of the design
process; a cyclic iterative process of designing
solutions interwoven with evaluation; and within
group distributed expertise for different design
components.
4 RESEARCH QUESTIONS
We investigate the following research questions:
1. How are students’ computational and
mechanical representations shaped by the
following curricular foci:
1.1. User-Centered Design?
1.2. Collaboration between learners?
2. What is the relationship between the structural
characteristics of students’ physical and
computational inventions and the development
of their scientific and mathematical knowledge?
5 SETTING & METHOD
The study took place in a metropolitan city in the
form of an enrichment program for elementary
school children, conducted in a classroom on the
campus of a large private university in the mid-
southern USA. Classes met once a week (9:00 a.m.
to 11:30 a.m.) on six consecutive Saturday
mornings. Students were recruited through an online
solicitation sent to the local elementary schools.
None of the students in this course had any prior
programming experience, and we particularly
encouraged female students to apply. Students were
admitted on a first-come, first-served basis. There
were 16 participants, out of which eight students
were in 3rd grade, and eight were in 4th grade. Five
of the students were female, and three of them were
in 3rd grade. The ethnic composition of the students
whose work we analyzed for this paper is as follows:
White (7), Asian American (4), and African
American (3). Two students were absent for multiple
days, and their work has not been analyzed.
The first author acted as the lead instructor for
the study. Both the authors also collected data in the
form of videotaped in-depth interviews with the
participants, the software and hardware artifacts
(i.e., ViMAP programs and physical machines)
designed by the students, and field notes. The
interviews were conducted while the learners were
engaged in the modeling and programming
activities. In some cases, the interviews ensued when
the learner called upon the researcher in order to
help him or her with a difficulty. In other cases,
researchers conducted interviews in order to ask
learners to explain their programs or models.
Similar to Carver et al. (1992), we believe that
the role of the teacher in such a design-based
classroom can be best described as using the
cognitive apprenticeship framework (Collins, Brown
& Newman, 1987). That is, the teacher(s) supported
students' development of representational practices
in some cases by explicitly modeling certain
elements of the design practices (e.g., by acting out
the ViMAP commands physically in class), and in
other cases, prompting students to reflect on the
changes they are making to their designs in terms of
their affordances.
Our data consisted of student-generated artifacts,
field notes, and video-recorded interviews of
IntegratedSTEMinElementaryGradesUsingDistributedAgent-basedComputation
73

students with the researchers. We analyzed this data
by identifying themes and sub-themes using the
double coding method (Miles & Huberman, 1994).
To present our analysis, we used a case study-based
approach. Our selection of cases was guided by the
following criteria: representativeness and typicality.
Representativeness implies that the selected cases
should aptly represent key aspects of the
instructional and learning processes. These key
aspects, in turn, are defined based on the putative
research question(s). Typicality implies that the
selected case(s) should potentially represent aspects
of the process of learning experienced by the
majority of the student population.
We answered the research questions (RQs) as
follows. In order to investigate the role of UCD and
collaboration (RQ1), we compared the intermediate
and final products of the students' design activities
before and after user testing (during Phase 3) to
check for improvements. In order to investigate the
affordances of the students’ designs in terms of the
scientific and mathematical concepts and discourse
that the students engaged in their designs (RQ2), we
analyze the structure of each group’s physical
machines, their ViMAP program (i.e., programming
commands), and their instructions for users in terms
of the type(s) of mathematical measures generated
by each group. The children generated these
measures in order to provide explicit instructions to
users for operating and understanding their
machines. These measures in turn were categorized
either as a) mathematical i.e., involving either
multiplicative or proportionality-based reasoning, or
reasoning involved in understanding geometric
coordinate systems; or b) physics-based, i.e.,
indicative of reasoning about the measurement of
speed and distance. 20% of the data reported here
was blind-coded by an additional coder not involved
with our study (Cohen’s Kappa = 0.95).
6 FINDINGS
6.1 Pedagogical Affordances of UCD &
Collaboration
Across all the groups, we found that (1) the
distributed computing infrastructure resulted in
positive interdependence (Kreijns et al., 2003)
among students, where members of each group
made coordinated, non-redundant contributions
towards a common goal; and (2) a focus on User-
Centered Design resulted in students refining both
the software and hardware components of their
programs by engaging in iterative design cycles.
Figure 3A (Top Left): Jerry’s pulley mechanism for
controlling turn of the turtle via Sensor 1; Figure 3B (Top
Right): Chuck’s machine for controlling the speed of the
turtle via Sensor 2. Figure 3C (Bottom) is a screenshot of
their ViMAP program for generating a square, and shows
how it responds to the sensors.
An illustrative case is the work of Chuck and
Jerry (Figure 3A, 3B & 3C). During Phase 3, they
built two separate machines to represent specific
hand movements over the sensors. Jerry’s machine
consisted of a flat LEGO plate that could be lowered
or raised above an ultrasonic distance sensor (Sensor
1 in Figure 3), using a pulley mechanism, to control
the turn angle of the computational agent. Chuck’s
machine also comprised of a horizontal LEGO
surface that could be lowered or raised above a
distance sensor (Sensor 2 in Figure 3), using a
manually operated crank lift, to control the step-size
of the turtle.
In order to facilitate better collaboration between
group members, during Phase 3, students’ ViMAP
programs became iteratively more refined with
fewer bugs and redundancies. For example, in their
initial versions, Chuck and Jerry had linked multiple
turtle variables to each of the sensors, and after a
few attempts, realized that their coordinated actions
would make such a design redundant. Instead, they
decided to divide their responsibilities: one person
would control the turn, while the other would control
the speed of the turtle, thereby, creating positive
interdependence. Another effect of collaboration
was the shared development of mathematical
measures within each group, which in turn fostered
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
74

mathematical and physics-related discourse and
representational practices. This is discussed in
Section 6.2.
We also found that students’ ViMAP programs
and instructions for users, post user-testing, were
more generative, and communicative. We found that
the final designs of six out of seven groups allowed
users to draw multiple shapes, whereas their initial
designs during Phase 3 were more constrained and
could only generate a specific shape (typically, a
circle). This improvement was a direct result of user
testing, as nearly every user demanded to be able to
draw more than one shape using the same tool. In
some cases we also noticed that the reliability of the
output of their ViMAP program also improved as a
result of improvement of their physical structures.
For example, both Chuck and Jerry realized that they
had to improve the flatness of the surfaces that were
generating the sensor-readings, because their users
were unable to generate reliable outputs. This
resulted in Chuck introducing a flat paper strip to
cover the bottom of the LEGO plates, while Jerry
created a wider plate to control sensor readings more
reliably.
6.2 Relationship between Children’s
Inventions & Learning Math and
Physics
6.2.1 Designs That Primarily Supported
Learning Rate and Kinematics
Figure 4 shows an example of student work in which
two students, Seana and Curly, built two separate,
manually operated, wheeled cars, with flat surfaces
in front (stacked LEGO bricks) to represent the palm
of a hand. The operating mechanism involves
pushing the car towards or away from the sensor,
where distance of the flat surface (representing the
“palm of a hand”) from the sensor generates the
reading of the ultrasonic sensor. The distance of one
of the cars from the sensor controls the speed of the
ViMAP turtle, while distance of the other car from
the second sensor controls the rotation of the turtle.
A total of two groups of students developed two cars
as their drawing machines.
After user-testing, Seana and Curly realized that
they had to provide instructions to the user on how
fast they would have to move each car in order to
generate the desired shape(s). This is because, in
their design, moving the two cars at different rates
resulted in different shapes. Neither student had any
experience in calculating rates or speed prior to this
study, nor were they formally instructed during this
class to calculate the rates. However, they used the
computer clock and cell phones as timers, and
figured out by trial and error how fast they had to
move each car in terms of the time taken by their
cars to travel specific distance(s) in order to generate
the desired shape(s). This also resulted in making
their designs more communicative by annotating the
track at specific positions, along with some written
and verbal instructions for users regarding how fast
they needed to move the cars between these
annotated positions. Although this was a rough
measure of rate, we believe that this is a productive
entry point into learning kinematics through the
development of consequential physics talk, as well
as mathematical discourse on rates – i.e., through
engaging in “conversations for conceptual change”
(diSessa et al., 1991).
Figure 4A: Seana and Curly’s ViMAP program for shape
drawing.
Figure 4B (Left) and 4C (Right): Seana (dressed in black)
and Curly (dressed in blue and white) take turns in moving
their “cars” towards the ultrasonic sensors. Seana controls
the rotation, and Curly controls the step-size of the Turtle.
6.2.2 Designs That Primarily Supported
Multiplicative and
Proportionality-based Reasoning
An example of this type of design is Chuck and
Jerry’s work described in Section 6.1. Jerry’s
machine controlled the angular turn, and the user
could generate readings from 1 – 10 (inches) by
using the pulley mechanism. However, the user
could also alter the numerical parameter of the
“Repeat” command in the ViMAP program, which
in turn would effectively multiply the sensor reading
by that parameter. Chuck used a similar strategy to
let users control the step-size of the turtle; he had
created several visible marks on his towers at
increments of a third of the maximum height, so that
IntegratedSTEMinElementaryGradesUsingDistributedAgent-basedComputation
75

the user can generate shapes of three levels of
magnification.
Chuck and Jerry, who were both beginning to
learn multiplication tables in their regular math
class, thus got an opportunity to use and further
develop their multiplicative and proportionality-
based reasoning in order to make their designs work.
We found that a total of three groups of students also
invented this type of design.
6.2.3
Designs That Primarily Supported
Learning the Cartesian Coordinate
System
Two groups of students developed machines similar
to Chuck and Jerry, but using a Cartesian coordinate
system in their ViMAP program. One of their
machines controlled the translational displacement
of the turtle, while the other controlled the vertical
displacement of the turtle. To do so, they used
ViMAP commands such as “jump-X-by <Sensor-
reading>” and “jump-Y-by <Sensor-reading>”,
respectively. An illustrative example is the case of
Ken & Yang. As they iteratively refined the various
combinations of translational and vertical
displacements that would generate the different
shapes, they became familiarized with the NetLogo
XY-coordinate space. They realized during user-
testing that it is much easier for users to control their
machines if they are provided with coordinates for
the vertices of target shapes such as equilateral
triangles and rectangles. This was evident in their
instructions for users on the final day.
7 CONCLUSION & DISCUSSION
In this paper, we have presented a socio-technically
distributed pedagogy for Integrated STEM in
elementary grades. Integrated STEM is a necessarily
interdisciplinary enterprise, and given the nature of
elementary classrooms (K-4), where the same
teacher is responsible of teaching all disciplines, we
believe that K-4 is a great setting for such curricula.
The cases we presented show that 3
rd
and 4
th
grade
students were indeed able to successfully participate
productively in an engineering design process that
highlights User Centered Design and collaboration –
key elements of the practice of engineering.
Furthermore, we also showed that in the process,
students were able to iteratively develop expertise in
agent-based programming, as well as mathematical
and scientific discourse and representational
practices such as measurement and modeling.
Our paper also represents the first attempt to
integrate agent-based computational thinking with
engineering, curricular science and math within a
single curriculum in elementary grades. To this end,
we presented a pedagogical innovation in the form
of new socio-technically distributed computational
environment - ViMAP-Tangible - and a set of
curricular activities in the genre of STEM Design
Challenges (Berland, 2013). The computational
abstractions in the form of ViMAP programming
language, as well as the associated epistemic and
representational practices such as measurement and
modeling - act as invariants that facilitate cohesion
across the STEM domains (Nathan et al., 2013).
Our curricular design proposes a mechanism for
bringing about such cohesion using a socio-
technically distributed computational infrastructure.
Following Berland (2013), we maintained focus on
engineering practices from the beginning (Phases 1
& 2) by engaging students in design, in the form of
iterative development and refinement of their
computational models. Furthermore, we leveraged
the synergy between tangibility and collaborative
learning in a manner that introduced students to
another key engineering practice (i.e., collaborative
design). This in turn supported the development of
scientific and mathematical knowledge by creating
opportunities for reflection and positive
interdependence.
ACKNOWLEDGEMENTS
Financial support was provided by the National
Science Foundation (NSF Early CAREER #
1150230).
REFERENCES
Antle, A. N. and Wise, A.F. 2013. Getting down to details:
Using learning theory to inform tangibles research and
design for children. Interacting with Computers, 25, 1.
Baker, M., Hansen, T., Joiner, R., & Traum, D. 1999. The
role of grounding in collaborative learning tasks.
Collaborative learning: Cognitive and Computational
Approaches, 31-63.
Barron, B. (2003). When smart groups fail. The Journal of
the Learning Sciences, 12(3), 307-359.
Berland, L. K. 2013. Designing for STEM Integration.
Journal of Pre-College Engineering Education
Research (J-PEER), 3(1), 3.
Bordogna, J., Fromm, E., Ernst, E. W. 1993. Engineering
education: Innovation through integration. Journal of
Engineering Education, 82(1), 3-8.
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
76

Boulay, B. D., O'Shea, T., & Monk, J. 1981. The black
box inside the glass box: Presenting computing
concepts to novices. International Journal of Man-
Machine Studies, 14(3), 237-249.
Bucciarelli, L. L. 1994. Designing engineers. MIT.
Carlsen, M. 2010. Appropriating geometric series as a
cultural tool: a study of student collaborative learning.
Educational Studies in Mathematics, 74, 95–116.
Carver, S. M., Lehrer, R., Connell, T., & Erickson, J.
(1992). Learning by hypermedia design: Issues of
assessment and implementation. Educational
Psychologist, 27(3), 385-404.
Collins, A., Brown, J. S., & Newman, S. E. 1989.
Teaching the crafts of reading, writing, and
mathematics. Cognition and instruction: Issues and
agendas, 453-494.
Conway, M. 1997. Alice: Easy to Learn 3D Scripting for
Novices. Technical Report, School of Engineering and
Applied Sciences, University of Virginia,
Charlottesville, VA.
Coyle, E. J., Jamieson, L. H. & Sommers, L. S. 1997.
EPICS: A model for integrating service-learning into
the engineering curriculum. Michigan Journal of
Community Service Learning, 4, 81–89.
du Boulay, B. 1989. Some difficulties of learning to
program. In E. Soloway & J.C. Spohrer (Eds.),
Studying the novice programmer (pp. 283-299).
diSessa, A. A., Abelson, H., and Ploger, D. 1991. An
Overview of Boxer. Journal of Mathematical
Behavior, 10(1), 3-15.
diSessa, A., Hammer, D., Sherin, B., & Kolpakowski, T.
1991. Inventing graphing: Children's meta-
representational expertise. Journal of Mathematical
Behavior, 10(2), 117-160.
Dyer, R. R., Reed, P. A., & Berry, R. 2006. Investigating
the relationship between high school technology
education & test scores for algebra I & geometry.
Journal of Technology Education, 17(2), 7–17.
Fernaeus, Y., Tholander, J. 2006. Finding design qualities
in a tangible programming space, in: Proceedings of
Conference on Human Factors in Computing Systems,
Montreal, Quebec, Canada. ACM Press, pp. 447-456.
Fortus, D., Dershimer, R. C., Krajcik, J., Marx, R. W. &
Mamlok-Naaman, R. 2004. Design-based science and
student learning. Journal of Research in Science
Teaching, 41(10), 1081–1110.
Giere, R. N. 1999. Using models to represent reality.
In Model-based reasoning in scientific discovery (pp.
41-57). Springer US.
Gresalfi, M., & Ingram-Goble, A. 2008. Designing for
dispositions. In: Proceedings of the 8th International
conference for the learning sciences-Volume 1 (pp.
297-304). ISLS.
Gulliksen, J., Göransson, B., Boivie, I., Blomkvist, S.,
Persson, J., Cajander, Å. 2003. Key principles for
user-centred systems design. Behaviour and
Information Technology,
22(6), 397-409.
Guzdial M. 1995 Software-realized scaffolding to
facilitate programming for science learning.
Interactive Learning Environments, 4(1). 1-44.
Harel, I. 1990. Children as software designers: a
constructionist approach for learning mathematics. The
Journal of Mathematical Behavior, 9 (1): 4.
Hohmann, L., Guzdial, M., & Soloway, E. 1992. SODA:
A computer-aided design environment for the doing
and learning of software design. In Computer Assisted
Learning (pp. 307-319). Springer Berlin Heidelberg.
Horn, M.S., Crouser, R.J., Bers, M.U. 2011. Tangible
interaction and learning: The case for a hybrid
approach. Personal and Ubiquitous Computing, 16(4),
379-389.
Horn, M.S. and Jacob, R.J.K. 2007. Designing Tangible
Programming Languages for Classroom Use. In Proc.
Tangible and Embedded Interaction TEI’07, 159-162,
ACM.
Hornecker, E. 2005. A design theme for tangible
interaction: Embodied facilitation, in: Proceedings of
CSCW, Paris, France. Springer, pp. 23-44.
Johri, A., & Olds, B. M. 2011. Situated engineering
learning: Bridging engineering education research and
the learning sciences. Journal of Engineering
Education, 100(1), 151-185.
Kafai, Y. B., Franke, M., Ching, C., & Shih, J. (1998).
Game design as an interactive learning environment
fostering students’ and teachers’ mathematical
inquiry. International Journal of Computers for
Mathematical Learning, 3(2), 149–184.
Kreijns, K., Kirschner, P.A., Jochems, W. 2003.
Identifying the pitfalls for social interaction in
computer-supported collaborative learning
environments: A review of the research. Computers in
Human Behavior, 19, pp. 335-353.
Katehi, L., Pearson, G., Feder, M. A. 2009. Engineering in
K-12 education: Understanding the status and
improving the prospects. Washington, DC: National
Academies Press, 2009.
Kelleher, C. & Pausch, R. 2005. Lowering the barriers to
programming: a taxonomy of programming
environments and languages for novice programmers,
ACM Computing Surveys, Vol. (37) 83–137.
Klopfer, E., Yoon, S. and Um, T. 2005. Teaching
Complex Dynamic Systems to Young Students with
StarLogo. The Journal of Computers in Mathematics
and Science Teaching; 24(2): 157-178.
Kolodner, J. L., Camp, P. J., Crismond, D., Fasse, B.,
Gray, J., Holbrook, J., & Ryan, M. (2003). Problem-
based learning meets case-based reasoning in the
middle-school science classroom: Putting Learning By
Design
TM
into practice. The Journal of the Learning
Sciences, 12(4), 495-547.
Lai, K., & White, T. 2012. Exploring quadrilaterals in a
small group computing environment. Computers &
Education, 59(3), 963-973.
Maloney, J., Burd, L., Kafai, Y., Rusk, N., Silverman, B.,
and Resnick, M. (2004) Scratch: A Sneak Preview. In
Proc. of Creating, Connecting, and Collaborating
through Computing, 104-109.
McCulloch, A. W., Ernst, J. V. 2012. Estuarine
Ecosystems: Using T & E Signature Approaches to
Support STEM Integration. Technology and
IntegratedSTEMinElementaryGradesUsingDistributedAgent-basedComputation
77

Engineering Teacher, 72(3), 13-17.
Moschkovich, J. N. 2004. Appropriating mathematical
practices: a case study of learning to use and explore
functions through interaction with a tutor. Educational
Studies in Mathematics, 55, 49–80.
Miles, M. B. & Huberman, A. M. 1994. Qualitative Data
Analysis: An Expanded Sourcebook.
Miyake, N., Masukawa, H., Shirouzou, H. 2001. The
complex jigsaw as an enhancer of collaborative
knowledge building in undergraduate introductory
science courses. In Proc. of European CSCL, 454-461.
NAE and NRC. 2009. Engineering in K–12 Education:
Understanding the Status and Improving the
Prospects. The National Academies Press.
Nathan, M. J., Srisurichan, R., Walkington, C., Wolfgram,
M., Williams, C., & Alibali, M. W. 2013. Building
Cohesion Across Representations: A Mechanism for
STEM Integration. Journal of Engineering
Education, 102(1), 77-116.
National Research Council (NRC). 2008. Taking science
to school: Learning and teaching science in grades K–
8. National Academy Press.
National Research Council (NRC). 2010. Report of a
Workshop on The Scope and Nature of Computational
Thinking. The National Academies Press.
Norman, D. A. 1998. The design of everyday things. New
York.
Norman, D. A., & Draper, S. W. 1986. User centered
system design; new perspectives on human-computer
interaction. L. Erlbaum Associates Inc.
Papert, S. 1980. Mindstorms: children, computers, and
powerful ideas. Basic Books, Inc. New York, NY.
Penner, D. E., Giles, N. D., Lehrer, R., & Schauble, L.
(1997). Building functional models: Designing an
elbow. Journal of Research in Science
Teaching, 34(2), 125-143.
Perkins, D. N. 1986. Knowledge as design. Hillsdale, NJ:
L. Erlbaum Associates.
Perkins, D. N., & Simmons, R. 1988. Patterns of
misunderstanding: An integrative model for science,
math, and programming. Review of Educational
Research, 58(3), 303-326.
Pickering, A. 1993. The mangle of practice: Agency and
emergence in the sociology of science. American
Journal of Sociology, 559-589.
Redish, E. F. and Wilson, J. M. 1993. Student
programming in the introductory physics course:
M.U.P.P.E.T. Am. J. Phys. 61: 222–232.
Repenning, A. 1993. Agentsheets: A tool for building
domain-oriented visual programming, Conference on
Human Factors in Computing Systems, 142-143.
Roschelle, J., & Teasley, S. D. 1995. The construction of
shared knowledge in collaborative problem solving.
In
Computer supported collaborative learning (pp. 69-
97). Springer.
Roehrig, G. H., Moore, T. J., Wang, H. H., & Park, M. S.
2012. Is Adding the E Enough? Investigating the
Impact of K-12 Engineering Standards on the
Implementation of STEM Integration. School Science
and Mathematics, 112(1), 31-44.
Sanders, M. 2009. Integrative STEM education: Primer.
The Technology Teacher, 68(4), 20–27.
Satchwell, R. E., & Loepp, F. L. 2002. Designing and
implementing an integrated mathematics, science, and
technology curriculum for the middle school. Journal
of Industrial Teacher Education, 39(3), 41–66.
Sengupta, P., & Farris, A. V. 2012. Learning kinematics in
elementary grades using agent-based computational
modeling: a visual programming-based approach.
In Proceedings of 11
th
International Conference of
Interaction Design & Children (pp. 78-87). ACM.
Sengupta, P., Farris, A.V, & Wright, M. 2012. From
Agents to Aggregation via Aesthetics: Learning
Mechanics with Visual Agent-based Computational
Modelling. Technology, Knowledge & Learning. 17
(1-2), pp 23 - 42.
Sengupta, P., Kinnebrew, J.S., Basu, S., Biswas, G., &
Clark, D. 2013. Integrating Computational Thinking
with K-12 Science Education Using Agent-based
Computation: A Theoretical Framework. Education
and Information Technologies, 18 (2), 351-380.
Sherin, B., diSessa, A. A., & Hammer, D. M. 1993.
Dynaturtle revisited: Learning physics through
collaborative design of a computer model. Interactive
Learning Environments, 3(2), 91-118.
Simon, H. A. (1969). The sciences of the artificial.
Cambridge, MA.
Spohrer, J. C., & Soloway, E. 1986. Novice mistakes: Are
the folk wisdoms correct? Communications of the
ACM, 29(7), 624-632.
Suzuki, H., Kato, H. 1995. Interaction-level support for
collaborative learning: AlgoBlock - an open
programming language, in: Proceedings of CSCL,
Erlbaum Associates, Hillsdale, NJ, pp. 349- 355.
Tucker, A., Deek, F., Jones, J., McCowan, D., Stephenson,
C., & Verno, A. 2003. A model curriculum for K-12
computer science: Final report of the ACM K-12 task
force curriculum committee. New York, NY: ACM.
Wilensky, U. 1999. NetLogo [Computer Software].
Northwestern University, Evanston, IL.
Wing, J. M. 2006. Computational Thinking.
Communications of the ACM, vol. 49(3), pp. 33-35.
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
78
