
A New Method for the Creation of MOOC-ready Database of Test
Questions
Azam Beg
College of Information Technology, United Arab Emirates (UAE) University, Building E1, Al-Ain, U.A.E.
Keywords: Formative Assessment, Massive Open Online Course (MOOC), Engineering Education, Distance Learning,
e-Learning, Training, Digital Circuit Design, Combinational Logic.
Abstract: Recently, there has been a wide interest in the massive open online courses (MOOCs) that are freely
available to the students from all over the world. Due to the large scale of MOOCs, the instructors (even
with their teams of graders) cannot assess all the examinations and quizzes themselves. Peer grading eases
the assessment burden but has its shortcomings. Ideally, the assessments should be fully automated and
should also allow partial grading. Additionally, a sizeable database of questions is needed so that an
individual student or a group of students are not able to see all the questions by repeatedly attempting the
quizzes. In this paper, we present a Matlab-based method for automatically generating a large number of
questions and their (intermediate and final) answers for a MOOC or a traditional classroom-based course on
digital circuit design. The method that enables formative assessment is also applicable to other courses in
engineering and sciences.
1 INTRODUCTION
Different methods of distance learning have existed
for many years. Short video tutorials were
popularized by Khan Academy (Anon, 2014f) that
was founded in 2006, while fully online courses
have been offered by some universities since 2008
(Koller, 2013). One of the first massive open online
courses (MOOCs) offered by the University of
Illinois, Springfield, was attended by more than
2500 students, in 2011 (Anon 2011). TED and
iTunesU (Anon ,2014e) also came about in the same
timeframe.
MOOCs became very well-known after more
than 100,000 students signed up for a Stanford
University course. A large number of full-length
courses are now available through different sources
for millions of students enrolled from all over the
globe (Frank, 2012; Mitros et al., 2013).
The popularity of MOOCs is driven by the no-
cost availability of the course content. Unlike
traditional courses, there are no enrolment limits for
the students and there are relatively low
requirements on faculty facilitation after a course
has been developed (Briggs, 2013).
Currently, Coursera (Anon, 2014c), Udacity
(Anon, 2014h), and EdX (Anon, 2014d) are three
major sources of MOOCs albeit with different
missions, strategies, and tactics. Coursera’s offerings
mainly come from a few select universities inside
and outside the US. Their upper-level courses are
somewhat specialized. Udacity has used rather
elaborate production methods in the course
preparation and delivery; the courses are for lower-
level maths and science, and are relatively few in
numbers. EdX’s offerings fall somewhere in
between Coursera’s and Udacity’s.
The popular learning management systems such
as Blackboard (Anon, 2014a) and Canvas (Anon,
2014b) have also jumped the MOOC bandwagon.
While MOOCs democratize the learning, they
tend to deviate from traditional in-class courses in
many respects. Due to the sheer number of course
enrolees, they present a set of challenges never
encountered before. The challenges lie in the areas
of course design, delivery and assessment
(Daradoumis et al., 2013).
One of main challenges for MOOCs has been the
impracticability of human review of individual
student learning progress and the assessments
(Fournier, 2013). So the student work, including
quizzes, have been either computer-graded or
assessed by the peers. Automatic grading,
understandably, has so far been limited and
492
Beg A..
A New Method for the Creation of MOOC-ready Database of Test Questions .
DOI: 10.5220/0004950604920496
In Proceedings of the 6th International Conference on Computer Supported Education (CSEDU-2014), pages 492-496
ISBN: 978-989-758-020-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Combinational logic topics and the mechanisms for assessing them.
insufficient in nature. For student assignments that
involve mathematical proofs, detailed designs, and
essays, evaluation and proper feedback still remain
the stumbling blocks. These lacunas in the
assessment process are some of the hurdles in
MOOCs being accepted as for-credit courses
(Briggs, 2013; Miranda et al., 2013).
Many MOOCs have, to some degree, relied on
peer-grading as an assessment tool. However, such
grading is fraught with issues, such as the grader’s
bias due to his/her own performance, and possibly
large differences in the graders’ and the gradees’
cultural and lingual backgrounds. How much time a
grader spends on grading also comes into play
(Piech, 2013). Providing rubrics to the graders helps
achieve some degree of uniformity (Sandeen, 2013).
In this paper, we provide a mechanism for
making the online assessment more effective while
retaining automation. This is done by creation of a
large number of test questions that are suitable for
formative assessment. This set of questions can be
utilized for a very large number of cohorts. The
questions also allow checking of intermediate as
well as final answers. Although our method is
applicable to many courses in science and
engineering, we will cover examples mainly from a
course in electrical/computer engineering.
2 TACKLING THE ASSESSMENT
CHALLENGE
Having an effective assessment is crucial for the
ultimate acceptance of MOOC as a replacement of a
traditional in-class course. Georgia Institute of
Technology’s recently proposed MOOC-based
Master of Science (MOOMS) faces “a potential
threat” from their evaluation system that would not
fully assess, and would therefore “lead to an
ineffective program” (Briggs, 2013).
Although having the students take proctored
examinations is an option, it would incur some cost
(vs. the completely free option) to the student.
Traditional test-banks accompanying the
textbooks are mostly limited in size. Someone
signing in with multiple accounts could repeat a quiz
until he is able to get a perfect score. Therefore, the
test-banks are not suitable for MOOCs’ class-sizes.
Our proposed approach involves the use of
Matlab (Anon, 2014g) for generating a very large
number of questions and answers so that repeated
attempts by a single person or by a group has little
chances of seeing the same questions. We employ
Perl CGI scripts to generate the webpages that
display the problems and grade them automatically.
2.1 Assessment of a Course on Digital
Circuit Design
In this section, we present the topics from a course
that we have taught for several years, “Digital
Design and Computer Organization.”
One of the course outcomes is that the students
are able to “analyze and design combinational
circuits.” The course topics related to the outcome
are: logic gates, combinational building blocks, the
analysis of combinational circuits, and the design of
combinational circuits (see Figure 1). The last topic
is the most complex of all, and entails a longer
multi-step process. Obviously, for such as question,
the grading based on a single, final answer is
insufficient to provide effective feedback to a
student. So partial grading should be done.
Assessing the design problem conventionally
requires step-by-step checking by a human grader.
ANewMethodfortheCreationofMOOC-readyDatabaseofTestQuestions
493

2.1.1 Assessing Topic 1: Logic Gates and
Combinational Building Blocks
The students are expected to learn about the symbols
of different logic gates and combinational building
blocks.
Examples of logic gates are INV, AND, NAND,
OR, NOR, and XOR, mostly with 2 or more inputs.
Assessing the knowledge of the gates involves
matching the symbols with their names (not too
complex of a task but essential in nature). The
second type of questions require filling in of truth
tables of gates with multiple inputs.
The combinational building blocks include
decoders, encoders, multiplexers, etc. Besides many
inputs, some of these blocks have multiple outputs.
The assessment questions include building of the
blocks with individual gates using a schematic entry
module. The other type of questions includes
completion of the truth tables for different blocks.
See an example in Figure 2.
As one can see, by using the truth table entries
and the schematic module, it is possible to both
perform the partial grading and the checking of the
detailed answers.
Figure 2: A sample problem for Topic 1: Filling in the
truth table for a combinational block (3-to-8 decoder).
2.1.2 Assessing Topic 2: Analysis of
Combinational Circuits
The learning expectations are met if the students are
able to: (1) draw a simple schematic for a given
Boolean function; (2) write the Boolean equation for
a given circuit; (3) create a properly-sized truth table
(i.e., dependent upon the number of inputs and
output/s), and fill in the binary values; and (4)
transform a circuit into the one that uses only the
NAND or the NOR gates. A sample question
generated with Matlab and presented (in online
format) with a Perl script is shown in Figure 3.
Figure 3: A sample problem for Topic 2: Combinational
circuit analysis by writing the Boolean equation and
completing the truth table.
2.1.3 Assessing Topic 3: Design of
Combinational Circuits
The students taking this course should be able to
design combinational circuits by: (1) creating a truth
table that lists all combinations of inputs and
output(s), (2) creating minimized Boolean functions
using Karnaugh maps (K-maps), and (3) drawing the
final circuit-schematic. The problems can also be
descriptive in nature, but such questions would be
limited in number, and hence not suitable for
MOOCs. One of the solutions is to present problems
that require minimization of a sum-of-products (SOP
or sum-of-minterms) or product-of-sums (POS or
product-of-maxterms). Using Matlab, we have
created a very large number of problems (see the
code in Appendix A), i.e., several thousand for three
inputs, and a few million for four inputs.
A design example based on the sum-of-minterms
and the sum-of-don’t cares is shown in Figure 4. The
students exhibit their knowledge of design by filling
in the two tables and by typing in the final equation.
2.2 Evaluation of Question Database
We have seen signs of success with some initial use
of the automatically generated tests. In the coming
academic year, we are planning to fully utilize the
question database in the Digital Design and
Computer Organization in our university. The
questions will be loaded in (the currently-used)
BlackBoard learning management system.
Traditionally, during a given semester, we give
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
494
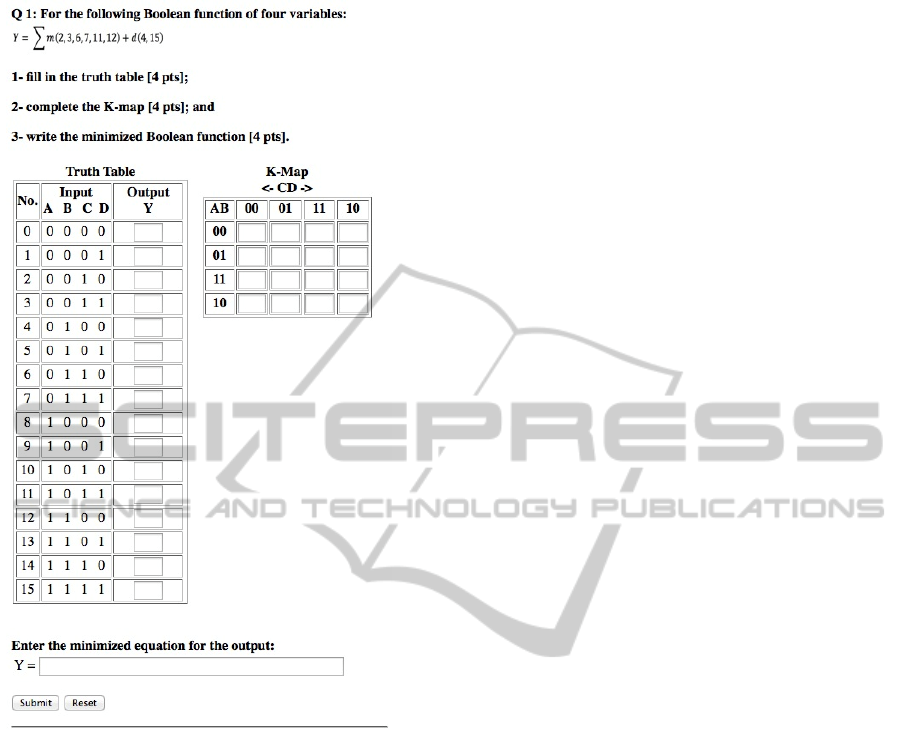
Figure 4: A sample problem for Topic 3: Design of a
combinational circuit by (a) filling in the truth table, (b)
using the K-map, and (c) writing the final minimized
equation.
one quiz to the students on every topic of digital
design. Due to the limited number of questions in
our current test-bank, we have limited the test-
attempts to one. With the availability of a much
larger number of quiz questions, we will be able to
offer the students some questions only for practice;
no grades will be assigned for these questions. The
number of quizzes would also increase; for each
topic, the students may be allowed two attempts
without exposing them to all the questions.
We will evaluate the effectiveness of our new
database of questions by (1) comparing the
upcoming semester’s test-scores with the scores of
the last four semesters’, and (2) by conducting a
student survey about the usefulness of the practice-
quizzes in improving their understanding of different
topics.
3 CONCLUSIONS
A new and powerful mechanism for creating
assessment questions for a digital design course’s
combinational logic problems. Future applications of
the method include question-generation for other
topics in other courses taught at other institutions, in
the traditional and the MOOC formats.
Microelectronics, analog circuit design, and
computer architecture are some of the courses in
which the presented technique can be utilized.
REFERENCES
Anon, 2014a. BlackBoard. Available at: http://
www.blackboard.com [Accessed January 1, 2014].
Anon, 2014b. Canvas. Available at: http://
www.instructure.com/ [Accessed January 1, 2014].
Anon, 2014c. Coursera. Available at: https://
www.coursera.org/ [Accessed January 1, 2014].
Anon, 2011. eduMOOC: Online Learning Today... and
Tomorrow. Available at: https://
sites.google.com/site/edumooc/ [Accessed January 1,
2014].
Anon, 2014d. EdX. Available at: http://www.edx.org
[Accessed January 1, 2014].
Anon, 2014e. iTunes U. Available at: http://
www.apple.com/apps/itunes-u/ [Accessed January 1,
2014].
Anon, 2014f. Khan Academy. Available at: http://
www.khanacademy.org [Accessed January 1, 2014].
Anon, 2014g. Mathworks - Matlab and Simulink for
Technical Computing. Available at:
http://www.mathworks.com [Accessed January 1,
2014].
Anon, 2014h. Udacity. Available at: https://
www.udacity.com/ [Accessed January 1, 2014].
Briggs, L. L., 2013. Assessment Tools for MOOCs.
Available at: http://campustechnology.com/
articles/2013/09/05/assessment-tools-for-moocs.aspx
[Accessed January 1, 2014].
Daradoumis, T. et al., 2013. A Review on Massive E-
Learning (MOOC) Design, Delivery and Assessment.
2013 Eighth International Conference on P2P,
Parallel, Grid, Cloud and Internet Computing,
pp.208–213.
Fournier, J., 2013. Coursera at the UW: The challenges,
benefits, and surprises of teaching a MOOC,
Frank, S. J., 2012. Review: MITx’s online circuit and
analysis course. IEEE Spectrum, pp.27–28.
Koller, C. D. et al., 2013. Tuned Models of Peer
Assessment in MOOCs. In The 6th International
Conference on Educational Data Mining (EDM 2013).
Memphis, TN, USA, pp. 153–160.
Miranda, S. et al., 2013. Automatic generation of
assessment objects and Remedial Works for MOOCs.
2013 12th International Conference on Information
ANewMethodfortheCreationofMOOC-readyDatabaseofTestQuestions
495

Technology Based Higher Education and Training
(ITHET), pp.1–8.
Mitros, P. F. et al., 2013. Teaching Electronic Circuits
Online: Lessons from MITx’s 6.002x on edX. , pp.2–5.
Sandeen, C., 2013. Assessment’s place in the new MOOC
world. RPA Journal, 8, pp.5–12. Available at:
http://www.rpajournal.com/dev/wp-content/uploads/
2013/05/SF1.pdf.
APPENDIX
The Matlab code for generating an exhaustive list of
sum-of-minterms and sum-of-don’t-cares for a given
number of input variables is given in Figure 5a.
For three variables/inputs, a total of 3,248
different questions are generated, some of which are
shown in Figure 5b.
nVar = 3; % number of input-variables
N = -1+2^nVar % maximum possible minterms
arrN = 0:N; % array containing all minterms
% arbitrarily, between 50% and 80% of the values are “trues”
for sel = ceil(0.5*N):ceil(0.8*N)
% select 'sel' terms from the arrN array
minterms = combnk(arrN, sel);
[rwMT tmp] = size(minterms);
% for each set of minterms, vary “don’t cares”
for i = 1:rwMT
% arbitrarily, up to 50% of 1’s can become “don't cares”
for doNotCareCount = 0:ceil(0.5*sel)
mintermRow = sum_m(i,:);
% use all combinations of “don’t cares”
arrDoNotCares = combnk(mintermRow, doNotCareCount);
[rwDNC tmp] = size(arrDoNotCares);
for j = 1:rwDNC
% array of don't-care terms
dontCareRow = arrDoNotCares(j,:);
% final array of minterms
finalMinTermRow = setdiff(mintermRow, dontCareRow);
end
end
end
end
(a)
…
3202: y = sum_m (1, 3, 6) + sum_d (0, 2, 4)
3203: y = sum_m (1, 4, 6) + sum_d (0, 2, 3)
3204: y = sum_m (2, 3, 4) + sum_d (0, 1, 6)
3205: y = sum_m (2, 3, 6) + sum_d (0, 1, 4)
3206: y = sum_m (2, 4, 6) + sum_d (0, 1, 3)
3207: y = sum_m (3, 4, 6) + sum_d (0, 1, 2)
3208: y = sum_m (1, 2, 3, 4, 5) + sum_d (0)
3209: y = sum_m (0, 2, 3, 4, 5) + sum_d (1)
3210: y = sum_m (0, 1, 3, 4, 5) + sum_d (2)
…
(b)
Figure 5: (a) The Matlab script for generating an exhaustive set of sum-of-product equations, and (b) a sample set of 3-
variable sum-of-product equations created by the script.
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
496
