
Graph Mining for Automatic Classification of Logical Proofs
Karel Vacul
´
ık and Lubo
ˇ
s Popel
´
ınsk
´
y
Knowledge Discovery Lab, Faculty of Informatics, Masaryk University, Botanick
´
a 68a,
CZ-602 00 Brno, Czech Republic
Keywords:
Graph Mining, Frequent Subgraphs, Logic Proofs, Resolution, Classification, Educational Data Mining.
Abstract:
We introduce graph mining for evaluation of logical proofs constructed by undergraduate students in the intro-
ductory course of logic. We start with description of the source data and their transformation into GraphML.
As particular tasks may differ—students solve different tasks—we introduce a method for unification of res-
olution steps that enables to generate generalized frequent subgraphs. We then introduce a new system for
graph mining that uses generalized frequent patterns as new attributes. We show that both overall accuracy
and precision for incorrect resolution proofs overcome 97%. We also discuss a use of emergent patterns and
three-class classification (correct/incorrect/unrecognised).
1 INTRODUCTION
Resolution in propositional logic is a simple method
for building efficient provers and is frequently taught
in university courses of logic. Although the struc-
ture of such proofs is quite simple, there is, up to
our knowledge, no tool for automatic evaluation of
student solutions. Main reason may lie in the fact
that building a proof is in essence a constructive task.
It means that not only the result—whether the set
of clauses is contradictory or not—but rather the se-
quence of resolution steps is important for evaluation
of correctness of a student solution.
If we aimed at error detection in a proof only, it
would be sufficient to use some search method to find
the erroneous resolution step. By this way we even
would be capable to detect an error of particular kind,
like resolution on two propositional letters. However,
there are several drawbacks of this approach. First,
detection of an error not necessary means that the so-
lution was completely incorrect. Second, and more
important, by search we can hardly discover patterns,
or sequence of patterns, that are typical for wrong
solutions. And third, for each kind of task – reso-
lution proofs, tableaux proofs etc. – we would need
to construct particular search queries. In opposite, the
method described in this paper is usable, and hope-
fully useful, without a principal modification for any
logical proof method for which a proof can be ex-
pressed by a tree.
In this paper we propose a method that employs
graph mining (Cook and Holder, 2006) for classifi-
cation of the proof as correct or incorrect. As the
tasks—resolution proofs—differs, there is a need for
unified description of this kind of proofs. For that
reason we introduce generalized resolution schemata,
so called generalized frequent subgraphs. Each sub-
graph of a resolution proof is then an instance of one
generalized frequent subgraph. In Section 2 we in-
troduce the source data and their transformation into
GraphML (GraphML team, 2007). Section 3 dis-
cusses preliminary experiments with various graph
mining algorithms. Based on these results, in Sec-
tion 4 we first introduce a method for construction
of generalized resolution graphs. Then we describe
a system for graph mining that uses different kinds
of generalized subgraphs as new attributes. We show
that both overall accuracy and precision for incor-
rect resolution proofs overcome 97%. Discussion and
conclusion are in Sections 5 and 6, respectively.
2 DATA AND DATA
PRE-PROCESSING
The data set contained 393 different resolution proofs
for propositional calculus, 71 incorrect solutions and
322 correct ones. Each student solved and handwrote
one task. Two examples of solutions are shown in
Fig. 1.
To transform the students proofs into an electronic
version we used GraphML (GraphML team, 2007),
which uses an XML-based syntax and supports wide
range of graphs including directed, undirected, mixed
563
Vaculík K. and Popelínský L..
Graph Mining for Automatic Classification of Logical Proofs.
DOI: 10.5220/0004963405630568
In Proceedings of the 6th International Conference on Computer Supported Education (CSEDU-2014), pages 563-568
ISBN: 978-989-758-020-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
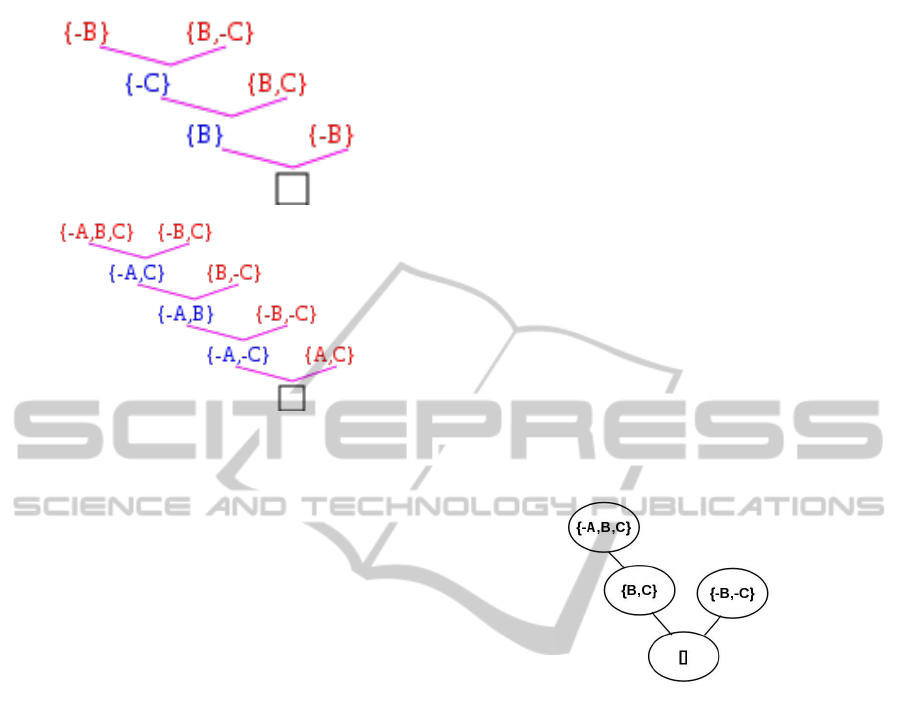
Figure 1: An example of a correct and an incorrect resolu-
tion proof.
graphs, hypergraphs, etc.
Common errors in proofs are the following: rep-
etition of the same literal in the clause, resolving on
two literals at the same time, incorrect resolution—
the literal is missing in the resolved clause, resolv-
ing on the same literals (not on one positive and one
negative), resolving within one clause, resolved lit-
eral is not removed, the clause is incorrectly copied,
switching the order of literals in the clause, proof is
not finished, resolving the clause and the negation of
the second one (instead of the positive clause).
3 FINDING CHARACTERISTIC
SUBGRAPH FOR RESOLUTION
PROOFS
The first, preliminary, experiment—finding charac-
teristic subgraphs for incorrect and correct resolution
proofs—aimed at evaluating the capabilities of partic-
ular algorithms. They were performed on the whole
set of data and then separately on the sets representing
correct and incorrect proofs. The applications pro-
vided frequent subgraphs as their output for each set
of data which help in identifying and distinguishing
between subgraphs that are characteristic for correct
and incorrect proofs, respectively. One such subgraph
is depicted in Fig. 2.
Specifically, we performed several experiments
with four algorithms (Brauner, 2013)—gSpan (Yan
and Han, 2002), FFSM (Huan et al., 2003), Sub-
due (Ketkar et al., 2005), and SLEUTH (Zaki, 2005).
With gSpan we performed experiments for different
minimal relative frequencies ranging from 5 to 35 per
cent. The overall running time varied from a few mil-
liseconds to tens of milliseconds and the number of
resulting subgraphs for all three data sets varied from
hundreds to tens according to the frequency. Size
of the output varied from hundreds to tens of kilo-
bytes. With FFSM we tuned the parameters of our
experiments so that the results were comparable to
gSpan. Comparable numbers of resulting subgraphs
were obtained in less time with FFSM. Despite the
two-file output representation, the size of the output
was slightly smaller in comparison to gSpan. With
Subdue we performed several experiments for differ-
ent parameter settings. The results were promising:
we obtained from 60 to 80 interesting subgraphs in
less than tenths of a second. The maximal size of out-
put was 20 kilobytes. Unlike Subdue, SLEUTH finds
all frequent patterns for a given minimum support.
Figure 2: Characteristic subgraph for incorrect resolution
proofs.
To sum up the examined methods for mining in
general graphs, although all of them are acceptable
for our purpose, Subdue and SLEUTH seemed to be
the best. Subdue offers a suitable input format that is
convenient for data classification. Readability of the
output and, most of all, the relatively small number
of relevant output graphs, makes Subdue preferable
for finding frequent subgraphs in that type of data. A
wide choice of settings is another advantage. In the
case of SLEUTH, input trees, either ordered or un-
ordered, can be considered. It is possible to search
induced or embedded subtrees. The main advantage,
when compared to Subdue, is that SLEUTH com-
putes for a given minimum support a complete set of
frequent subgraphs. For that reason we have chosen
SLEUTH for the main experiment, i.e., for extracting
frequent subgraphs and use those subgraphs as new
boolean attributes for two tasks, classification of a res-
olution proof as correct or incorrect and classification
of the main error in the solution, if it has been classi-
fied as wrong.
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
564

4 FREQUENT SUBGRAPHS FOR
CLASSIFICATION
4.1 Description of the Method
The system consists of five agents (Zhang and Zhang,
2004; Kerber, 1995). For the purpose of building
other systems for evaluation of graph tasks (like reso-
lution proofs in different calculi, tableaux proofs etc.),
all the agents have been designed to be as independent
as possible.
The system is driven by parameters. The main
ones are minimum accuracy and minimum precision
for each class, minimum and maximum support, a
specific kind of pattern to learn (all frequent or emerg-
ing (Dong and Li, 1999)) and minimum growth rate
for emerging patterns.
Agent A1 serves for extraction of a specified
knowledge from the XML description of the student
solution. It sends that information to agent A2 for
detection of frequent subgraphs and for building gen-
eralized subgraphs. A2 starts with the maximum sup-
port and learns a set of frequent subgraphs which sub-
sequently sends as a result to two kinds of agents, A3
and A4i. Agent A3 serves for building a classifier that
classifies the solution into two classes—CORRECT
and INCORRECT. Agents A4i, one for each kind of
error, are intended for learning the rules for detection
of the particular error.
In the step of evaluation of a student result there
are two possible situations. In the case that a par-
ticular classifier has reached accuracy (or precision)
higher than its threshold, agents A3 and A4i send the
result to agent A5 that collects and outputs the report
on the student solution. In the case that a threshold
has not been reached, messages are sent back to A2
demanding for completion of the set of frequent sub-
graphs, actually in decreasing minimum support and
subsequently, learning new subgraphs. If the mini-
mum support reaches the limit (see parameters), the
system stops.
We partially followed the solution introduced in
(Zhang, 2004). The main advantage of this solution
is its flexibility. The most important feature of the
solution that is based on agents is interaction among
agents in run-time. As each agent has a strictly de-
fined interface it can be replaced by some other agent.
New agents can be easily incorporated into the sys-
tem. Likewise, introduction of a planner that would
plan experiments will not cause any difficulties. Now
we focus on two main agents—the agent that learns
frequent patterns and on the agent that learns from
data where each attribute corresponds to a particu-
lar frequent subgraph and the attribute value is equal
to 1 if the subgraph is present in the resolution tree
and equal to 0 if it is not. The system starts with a
maximum support and learns a kind of frequent pat-
terns, based on the parameter settings. In the case that
the accuracy is lower than the minimum accuracy de-
manded, a message is sent back to frequent pattern
generator. After decreasing the minimum support the
generator is generating an extended set of patterns, or
is selecting only emerging patterns. The system has
been implemented mostly in Java and employs learn-
ing algorithms from Weka (Hall et al., 2009) and an
implementation of SLEUTH.
4.2 Generalized Resolution Subgraphs
4.2.1 Unification on Subgraphs
To unify different tasks that may appear in student
tests, we defined a unification operator on subgraphs
that allows finding of so called generalized sub-
graphs. Briefly saying, a generalized subgraph de-
scribes a set of particular subgraphs, e.g., a subgraph
with parents {A, −B} and {A, B} and with the child
{A} (the result of a correct use of a resolution rule),
where A, B, C are propositional letters, is an instance
of generalized graph {Z, −Y }, {Z,Y } → {Z} where
Y, Z are variables (of type proposition). The ex-
ample of incorrect use of resolution rule {A, −B},
{A, B} → {A, A} matches with the generalized graph
{Z, −Y }, {Z,Y } → {Z, Z}. In other words, each sub-
graph is an instance of one generalized subgraph. We
can see that the common set unification rules (Dovier
et al., 2001) cannot be used here. In this work we fo-
cused on generalized subgraphs that consist of three
nodes, two parents and their child. Then each gener-
alized subgraph corresponds to one way—correct or
incorrect—of resolution rule application.
4.2.2 Ordering on Nodes
As a resolution proof is, in principal, an unordered
tree, there is no order on parents in those three-node
graphs. To unify two resolution steps that differ only
in order of parents we need to define ordering on
parent nodes
1
. We take a node and for each propo-
sitional letter we first count the number of negative
and the number of positive occurrences of the let-
ter, e.g., for {−C, −B, A,C} we have these counts:
(0,1) for A, (1,0) for B, and (1,1) for C. Following
the ordering Ω defined as follows: (X,Y ) ≤ (U,V ) iff
(X < U ∨ (X = U ∧Y ≤ V )), we have a result for the
1
Ordering on nodes, not on clauses, as a student may
write a text that does not correspond to any clause, e.g.,
{A, A}.
GraphMiningforAutomaticClassificationofLogicalProofs
565

node {C, −B, A, −C}: {A,−B,C, −C} with descrip-
tion ∆ = ((0,1), (1,0), (1,1)). We will compute this
transformation for both parent nodes. Then we say
that a node is smaller if the description ∆ is smaller
with respect to the Ω ordering applied lexicographi-
cally per components. Continuing with our example
above, let the second node be {B,C, A, −A} with ∆ =
((0,1), (0,1), (1,1)). Then this second node is smaller
than the first node {A, −B,C, −C}, since the first com-
ponents are equal and (1,0) is greater than (0,1) in case
of second components.
4.2.3 Generalization of Subgraphs
Now we can describe how the generalized graphs are
built. After the reordering introduced in the previous
paragraph, we assign variables Z,Y,X,W,V,U,. . . to
propositional letters. Initially, we merge literals
from all nodes into one list and order it using the
Ω ordering. After that, we assign variable Z to the
letter with the smallest value, variable Y to the letter
with the second smallest value, etc. If two values
are equal, we compare the corresponding letters only
within the first parent, alternatively within the second
parent or child, e.g., for the student’s (incorrect)
resolution step {C, −B, A, −C}, {B,C, A, −A} →
{A,C}, we order the parents getting the re-
sult {B,C, A, −A}, {C, −B, A, −C} → {A,C}.
Next we merge all literals into one list
{B,C, A, −A,C, −B, A, −C, A,C}. After reordering,
we get {B,-B,C,C,C,-C,A,A,A,-A} with ∆ = ((1,1),
(1,3), (1,3)). This leads to the following renaming of
letters: B → Z, C → Y , and A → X . Final generalized
subgraph is {Z,Y, X, −X}, {Y, −Z, X , −Y } → {X,Y }.
In the case that one node contains more propositional
letters and the nodes are equal (with respect to the
ordering) on the intersection of propositional letters,
the longer node is defined as greater. At the end, the
variables in each node are lexicographically ordered
to prevent from duplicities such as {Z, −Y } and
{−Y, Z}.
4.3 Classification of Correct and
Incorrect Solution
For testing of algorithm performance we employed
10-fold cross validation. At the beginning, all student
solutions have been divided into 10 groups randomly.
Then for each run, all frequent three-node subgraphs
in the learning set have been generated and all gener-
alization of those subgraphs have been computed and
used as attributes both for learning set and for the test
fold. The results below are averages for those 10 runs.
We used four algorithms from Weka package, J48
decision tree learner, SMO Support Vector Machines,
IB1 lazy learner and Naive Bayes classifier. We ob-
served that the best results have been obtained for
minimum support below 5% and that there were no
significant differences between those low values of
minimum support.
The best results have been reached for general-
ized resolutions subgraphs that have been generated
from all frequent patterns, i.e. with minimum sup-
port equal to 0% found by Sleuth (Zaki, 2005). The
highest accuracy 97.2% was obtained with J48 and
SMO. However, J48 outperformed SMO in precision
for the class of incorrect solutions—98.8% with re-
call 85.7%. For the class of correct solutions and J48,
precision reached 97.1% and recall 99.7%. The aver-
age number of attributes (generalized subgraphs) was
83. The resulting tree is in Fig. 3. The worst perfor-
mance displayed Naive Bayes, especially in recall on
incorrect solutions that was below 78%. Summary of
results can be found in Table 1.
If we look at the most frequent patterns which
were found, we will see the coincidence with patterns
in the decision tree as the most frequent pattern is
{Z}, {−Z} → {#} with support 89%. This pattern is
also the most frequent for the class of correct proofs
with support 99.7%, next is {Y, Z}, {−Y, Z} → {Z}
with support 70%. Frequent patterns for incorrect
proofs are not necesarilly interesting in all cases. For
example, patterns with high support in both incorrect
and correct proofs are mostly unimportant, but if we
look only at patterns specific for the class of incorrect
proofs, we can find common mistakes that students
made. One such pattern is {Y, Z}, {−Y, −Z} → {#}
with support 32% for the incorrect proofs. Other sim-
ilar pattern is {−X ,Y, Z}, {−Y, X } → {Z} with sup-
port 28%.
4.4 Complexity
Complexity of pattern generalization depends on the
number of patterns and the number of literals within
each pattern. Let r be the maximum number of literals
within a 3-node pattern. In the first step, ordering of
parents must be done which takes O
r
for counting
the number of negative and positive literals, O
r log r
for sorting and O
r
for comparison of two sorted
lists. Letter substitution in the second step consists
of counting literals on merged list in O
r
, sorting the
counts in O
r log r
and renaming of letters in O
r
.
Lexicographical reordering is performed in last step
and takes O
r log r
. Thus, the time complexity for
whole generalization process on m patterns with du-
plicity removal is O
m
2
+ m(4r + 3r log r)
.
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
566

Table 1: Results for frequent subgraphs.
Algorithm Accuracy [%] Precision for incorrect proofs [%]
J48 97.2 98.8
SVM (SMO) 97.2 98.6
IB1 94.9 98.3
Naive Bayes 95.9 98.6
= TRUE
= TRUE
= FALSE
= TRUE
= FALSE
= FALSE
pattern1
{#}
{Z} {-Z}
pattern12
{Z}
{-X,Y,Z} {-Y,X}
negative (15.0)
pattern30
{-X}
{-X,Y,Z} {-Y,-Z}
negative (4.0) positive (330.0/9.0)
negative (44.0/1.0)
Figure 3: Decision tree with subgraphs as nodes.
Now let the total number of tree nodes be v, num-
ber of input trees n, the number of patterns found by
Sleuth m, the maximum number of patterns within a
single tree p, time complexity of Sleuth O
X
, time
complexity of sleuth results parsing O
Y
, time com-
plexity of classifier (building and testing) O
C
. Fur-
thermore, we can assume that m p, m n and
m r. Then the total time complexity of 10-fold
cross validation is O
m
2
+ nmp + v + X +Y +C
.
5 DISCUSSION
5.1 Emerging Patterns
We also checked whether emerging patterns would
help to improve performance. All the frequent pat-
terns were ranked with GrowthRate metric (Dong and
Li, 1999) separately for each of the classes of cor-
rect and incorrect solutions. Because we aimed, most
of all, to recognize wrong resolution proofs, we built
two sets of emerging frequent patterns where the pat-
terns emerging for incorrect resolution proofs have
been added to the set of attributes with probability
between 0.5 and 0.8, and the emerging patterns for
the second class with probability 0.5 and 0.2, respec-
tively. Probability 0.5 stands for equilibrium between
both classes.
It was sufficient to use only 10–100 top patterns
according to GrowthRate. The best result has been
reached for 50 patterns (generalized subgraphs) when
probability of choosing an emerging pattern for incor-
rect solution has been increased to 0.8. Overall accu-
racy overcome 97.5% and precision on the class of in-
correct solutions reached 98.8% with recall 87.3%. It
is necessary to stress that the number of attributes was
lower, only 50 to compare with 83 for experiments in
Table 1. We again used 10-fold cross validation.
5.2 Classification into Three Classes
To increase precision on the class of incorrect proofs,
we decided to change the classification paradigm and
allow the classifier to leave some portion of exam-
ples unclassified. The main goal was to classify only
those examples for which the classifier returned high
certainty (or probability) of assigning a class.
We used validation set (1/3 of learning examples)
for finding a threshold for minimal probability of clas-
sification that we accept. If the probability was lower,
we assigned class UNKNOWN to such an example.
Using 50 emerging patterns and threshold 0.6, we
reached precision on the class of incorrect solutions
99.1% with recall 81.6% which corresponds to 73 ex-
amples out of 90. It means that 17 examples were
not classified to any of those two classes, CORRECT
and INCORRECT solution. Overall accuracy, preci-
sion and recall for the correct solutions were 96.7%,
96.2% and 99.4%, respectively.
GraphMiningforAutomaticClassificationofLogicalProofs
567

5.3 Inductive Logic Programming
We also checked whether inductive logic program-
ming (ILP) can help to improve the performance un-
der the same conditions. To ensure it, we did not use
any domain knowledge predicates that would bring
extra knowledge. For that reason, the domain knowl-
edge contained only predicates common for the do-
main of graphs, like node/3, edge/3, resolutionStep/3
and path/2. We used Aleph system (Srinivasan, 2001).
The results were comparable with the method de-
scribed above.
6 CONCLUSION AND FUTURE
WORK
Our principal goal was to build a robust tool for
an automatic evaluation of resolution proofs that
would help teacher to classify student solutions.
We showed that with the use of machine learning
algorithms—namely decision trees and Support Vec-
tor Machines—we can reach both accuracy and pre-
cision higher than 97%. We showed that precision
can be even increased when small portion of exam-
ples was left unclassified.
The solution proposed is independent of a partic-
ular resolution proof. We observed that only about
30% of incorrect solutions can be recognize with a
simple full-text search. For the rest we need a solu-
tion that employs more sophisticated analytical tool.
We show that machine learning algorithms that use
frequent subgraphs as boolean features are sufficient
for that task.
As future work we plan to use the results of this
system for printing report about a particular student
solution. It was observed, during the work on this
project, that even knowledge that is uncertain can be
useful for a teacher, and that such knowledge can be
extracted from output of the learning algorithms.
ACKNOWLEDGEMENTS
This work has been supported by Faculty of
Informatics, Masaryk University and the grant
CZ.1.07/2.2.00/28.0209 Computer-aided-teaching for
computational and constructional exercises. We
would like to thank Juraj Jur
ˇ
co for his help with data
preparation.
REFERENCES
Brauner, B. (2013). Data mining in graphs. http://is.
muni.cz/th/255742/fi_b/.
Cook, D. J. and Holder, L. B. (2006). Mining Graph Data.
John Wiley & Sons.
Dong, G. and Li, J. (1999). Efficient mining of emerging
patterns: Discovering trends and differences. pages
43–52.
Dovier, A., Pontelli, E., and Rossi, G. (2001). Set unifica-
tion. CoRR, cs.LO/0110023.
GraphML team (2007). The graphml file format. http:
//graphml.graphdrawing.org/ [Accessed: 2014-
01-09].
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. H. (2009). The weka data min-
ing software: An update. SIGKDD Explor. Newsl.,
11(1):10–18.
Huan, J., Wang, W., and Prins, J. (2003). Efficient mining of
frequent subgraphs in the presence of isomorphism. In
Proceedings of the Third IEEE International Confer-
ence on Data Mining, ICDM ’03, pages 549–, Wash-
ington, DC, USA. IEEE Computer Society.
Kerber, R., L. B. S. E. (1995). A hybrid system for data
mining. In Goonatilake, S., K. S., editor, Intelligent
Hybrid Systems, chapter 7, pages 121–142. Willey &
Sons.
Ketkar, N. S., Holder, L. B., and Cook, D. J. (2005). Sub-
due: Compression-based frequent pattern discovery in
graph data. In Proceedings of the 1st International
Workshop on Open Source Data Mining: Frequent
Pattern Mining Implementations, OSDM ’05, pages
71–76, New York, NY, USA. ACM.
Srinivasan, A. (2001). The Aleph Manual.
http://web.comlab.ox.ac.uk/oucl/research/
areas/machlearn/Aleph/ [Accessed: 2014-01-09].
Yan, X. and Han, J. (2002). gspan: Graph-based substruc-
ture pattern mining. In Proceedings of the 2002 IEEE
International Conference on Data Mining, ICDM ’02,
pages 721–, Washington, DC, USA. IEEE Computer
Society.
Zaki, M. J. (2005). Efficiently mining frequent embedded
unordered trees. Fundam. Inf., 66(1-2):33–52.
Zhang, Z. and Zhang, C. (2004). Agent-Based Hybrid Intel-
ligent Systems. SpringerVerlag.
Zhang, Z., Z. C. (2004). Agent-Based Hybrid Intelligent
Systems, chapter Agent-Based Hybrid Intelligent Sys-
tem for Data mining. In (Zhang and Zhang, 2004).
CSEDU2014-6thInternationalConferenceonComputerSupportedEducation
568
