
Reduction in Mutation Testing of Java Classes
Ilona Bluemke and Karol Kulesza
Institute of Computer Science, Warsaw University of Technology, Nowowiejska 15/19, Warsaw, Poland
Keywords: Mutation Testing, Cost Reduction, Java Testing.
Abstract: In mutation analysis many simple modification of the original program called “mutants” are created. Test
cases which are supposed to identify the introduced program changes are designed. Each mutant must be
“killed” by a test case, i.e. the test case should detect the purposely introduced modification. Mutation
testing is known to be effective but computationally demanding and time consuming because a large
number of mutants has to be tested. Mutation score, which is the fraction of mutants that are killed by a test
set, is often used to evaluate the effectiveness of mutation testing. An interesting research question is if the
number of mutants can be reduced without significantly decreasing the effectiveness of the test. We were
exploring selective reductions of mutants generated for Java programs. The results of several experiments
conducted in the Eclipse environment are presented in this paper. These results show that selective
reduction in mutants can significantly reduce the cost of testing with acceptable mutation score and code
coverage.
1 INTRODUCTION
The general idea of mutation testing is that faults
used in mutation testing represent mistakes made by
a programmer so they are deliberately introduced
into the program to create a set of faulty programs
called mutants. Each mutant program is obtained by
applying a mutant operator to a location in the
original program. Mutation operators are defined
based on programming language characteristics and
common mistakes programmers make. Typical
mutation operators include replacing one operator e.
g. ‘+’ by another e.g. ‘-‘ or replacing one variable by
another. Mutation operators have been defined for
many languages e.g. Fortran (e.g. Offut et al. 1996),
C (e.g. Agrawal H. et al., 1989), C# (Derezińska,
2012, 2013) and Java (e.g. Kim et al. , 2001).
The tester designs tests that make these mutant
programs behave differently from the original
program. If the test is able to detect the change (i.e.
one of tests fails), then the mutant is said to be
killed.
Mutation testing is very effective at measuring
the adequacy of a test suite, but it can be
computationally expensive and time consuming. It is
expensive because mutation operators generate a
large number of mutants and all these mutants must
be run against the test set thus causing high
computational cost. Testers have to analyse mutants
and design tests to kill them. Some mutants cannot
be killed because they behave the same as the
program under test for all tests. Such mutants are
called equivalent. The identification of equivalent
mutants is usually done “by hand” and needs a lot of
time.
Mutation score is a kind of quantitative test
quality measurement that examines a test suite's
effectiveness. It is defined as the ratio of the number
of killed mutants to the total number of non-
equivalent mutants.
The reduction of the number of mutants will
decrease the computational and “human” costs.
Several reduction methods proposed are listed in
section 2.
The objective of this paper is to examine what is
the impact of selecting some subsets of mutants
generated for each mutation operator and for the
method for Java programs, on the mutation score
and the code coverage. This kind of experiments is
not quite new, some of them are also mentioned in
section 2. Due to the effort needed to conduct such
experiments all of them were made on very limited
number of classes, programs (4-10) so repeating
them on other programs, with the usage of other
tools, other operators and in different environment,
seems to us worthy and important. In (Bluemke,
2013) we described completely different, than in this
paper, reduction of mutants by randomly sampling.
297
Bluemke I. and Kulesza K..
Reduction in Mutation Testing of Java Classes.
DOI: 10.5220/0004992102970304
In Proceedings of the 9th International Conference on Software Engineering and Applications (ICSOFT-EA-2014), pages 297-304
ISBN: 978-989-758-036-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

The main ideas of reducing the number of
mutants and related work are briefly described in
section 2. The results of experiments are presented
in section 3 and some conclusions are given in
section 4.
2 REDUCTIONS OF MUTANTS
AND RELATED WORK
Interesting survey of mutation techniques was
published in 2011 by Jia and Harman, they also
created a repository (Mutation, 2011) containing
many papers on mutation. Recently Bashir and
Nadeem (2012) published a survey on object
mutation and Offut (2011) presented fascinatingly
the past, the present and the future of mutation.
One of the greatest challenges to the validity of
mutation testing is the number of mutants that are
semantically equivalent to the original program.
Equivalent mutants produce the same output as the
original program for every possible input.
Determining which mutants are equivalent is a
tedious activity, usually not implemented in tools.
The impact of equivalent mutants is studied in (Grun
et al, 2009). Techniques have been devised to
identify equivalent mutants using program slicing
(Hierons et al., 1999), compiler optimization (Offut
and Craft, 1994), constraint solving (Offut and Pan,
1997) and, more recently, impact assessment (Grun
et al, 2009). Equivalent mutants are still difficult to
remove completely (Schuler and Zeller, 2010).
Recently, in 2014, a
systematic literature review
regarding the equivalent mutant problem was published
by Madeyski et.al .
It is not feasible to use every possible mutant of
the program under test, even after all the equivalent
mutants have been removed. It is therefore necessary
to select a subset of mutants that allow the test suite
to be evaluated within a reasonable period of time.
Some research has been conducted to reduce the
number of mutants by selecting certain operators,
sampling mutants at random, or combining them to
form new higher-order mutants. Mutant sampling
was proposed by Acree (1980) and Budd (1980).
The problem of reducing the cost of mutation testing
was studied in several papers. Mathur and Wong
(1995) proposed two techniques limiting the number
of mutants: randomly selected x% mutants, and
constrained mutation (only a few specific types of
mutants are used and others are ignored).
Slightly different approach to mutants’ sampling
was proposed by Scholive, Beroulle and Robach
(2005). They proposed to choose a subset (10%) of
mutants generated for each mutation operator. The
selection was not performed randomly, they choose
different percentages of mutants in the mutant
subsets generated from different operators. This idea
we used as a basis for our experiments with selective
reductions described in section 3. The proportion of
mutants selected from each operator was the
function of its stuck-at fault coverage efficiency.
They conducted experiment on a benchmark
comparing the random and the proposed sampling
technique. With the classical random sampling
technique, the mutation score obtained was 85.62%
while with sampling strategy mutation score
increased to 88.18%.
Offutt, Rothermel and Zapf (1996) were
examining constrained mutation (some mutation
operators were ignored). Using the results of the
above mentioned experiments and performing others
experiments Mresa and Bottaci (1999) proposed the
set of efficient operators – eff. Researchers have
found that statement deletion operator has relatively
few mutants, but yields tests that are almost as
effective as using all mutants. Delamaro et.al. (2014)
extend this idea. Theirs paper presents results from
mutation operators that delete variables, operators,
and constants. Bluemke and Kulesza (2013)
examined randomly sampling mutants in Java
programs. The experiment shows that randomly
sampling 60% or 50% of mutants in Java programs
can significantly reduce the cost of testing with
acceptable mutation score and code coverage. These
subsets of mutants were also effective in detecting
hand seeded errors. Another approach to the mutant
reduction problem was proposed by Patrick, Oriol
and Clark (2012). They propose to use static analysis
to reduce mutants.
The above listed approaches to reduce the costs
of mutation were aimed at reduction the number of
mutants. The literature lacks a theoretical result that
articulates how many mutants are needed in any
given situation. Recently Amman Delamaro and
Offut, 2014, presented a way to identify precisely
how many mutants are needed in the context of a
given test set. According to them the size of this set
appears to be much smaller than the set delivered by
current approaches to mutation.
3 EXPERIMENT
The goal of our experiment was to explore the
selective reduction of mutants generated by the
mutation operator. We based our reductions on rules
proposed by Scholive, Beroulle and Robach (2005)
ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications
298

briefly described in section 2 but we decided to
examine the selective reductions more thoroughly.
We were reducing 40% to 90% of generated mutants
using step of 10% as a reduction value. In this paper
the experimental results of selecting subsets of
mutants generated for each mutation operator
(named as OP) and for mutation operators dedicated
to method (named as METHOD) are presented while
in (Bluemke and Kulesza, 2013) we showed the
results of randomly reducing the sets of mutants for
the same classes.
Our experiments were conducted in the Eclipse
environment. MuClipse and CodePro plugins were
used for the mutation testing. Two special tools:
Mutants Remover and Console Output Analyzer
(Kulesza, 2012) were implemented especially for
these experiments. Eight Java classes (listed in Table
1), were tested. For these classes 53 to 556 mutants
were generated.
Table 1: Tested classes.
class Project methods code
mutants/e
quivalent
mutants
Recipe CoffeeMaker
14 84 138/15
CoffeeMaker CoffeeMaker
8 102 285/17
Money CodePro JUnit
Demo
14 59 53/4
MoneyBag CodePro JUnit
Demo
17 114 54/6
Element MapMaker
10 80 380/20
Board NetworkShipBattl
e
12 123 270/3
Wall jet-tetris
7 79 290/19
Stack javasol
26 176 556/30
3.1 Plan of Experiment
For each class, being the subject of our experiment,
firstly all mutants were generated by MuClipse using
traditional operators operating only at the method
level i.e., changing lines of code that fit a certain
pattern (i.e., switching operands, replacing + with -,
etc.) and at the class-level: changing keywords that
indicate the type of class or the methods involved
(i.e. overloading a given method, changing a class to
static, etc.).
Secondly, the test cases killing these mutants
were generated using JUnit, part of CodePro plugin.
Console Output Analyzer was identifying test cases
not killing mutants. The identification of equivalent
mutants, based on the analysis of source code of the
original program and its mutants was time
consuming. Equivalent mutants were indicated and
removed “manually”. The tester had to construct
several test cases especially for non-equivalent
mutants to obtain an adequate test suite. The number
of test cases generated automatically by CodePro
was only 28.78% so quite a lot of time was spend on
constructing test cases “manually”. The number of
mutants killed by automatically generated tests was
47.15%. Such low values of mutants killed by
automatically generated tests were also reported in
other papers e.g. (Segura et al., 2011). Based on the
results of Mresa and Bottaci research (1999)
effective test sequence were built. Informally, each
test in an effective sequence is non-redundant with
respect to the tests that precede it.
The initial set of all generated mutants was
reduced by sampling and selective mutations. Due to
time limitations and the effort needed to construct
test cases, identify equivalent mutants and remove
them, for each class being the subject of this
experiment, only 18 sets of mutants were
constructed which is not sufficient to obtain
statistically correct results.
In the next step test cases “killing” all mutants in
the set were produced. Firstly the CodePro generator
was generating test cases and Console Output
Analyzer was identifying test cases not killing
mutants. For the not “killed” mutants the test cases
prepared for the whole set of mutants were used.
In Table 2 the code coverage (instruction
coverage) for each class being the subject of our
experiments is given for all generated mutants.
Table 2: Code coverage and method coverage for all
generated mutants.
class coverage
for all
mutants
methods covered
methods
Recipe 95.90% 14 14
CoffeeMaker 98.20% 8 7
Money 84% 14 10
MoneyBag 74.20% 17 13
Element 99% 10 10
Board 99% 12 12
Wall 100% 7 7
Stack 94.50% 26 23
As far as we know, there are no commonly
agreed limits defining satisfying killing factor so we
arbitrary assumed that test cases killing 95% of all
mutants are adequate. Also arbitrary, we assumed
that 2% decrease of the code coverage (instruction
coverage) is acceptable. With these values we
evaluated the sets of mutants and theirs test cases.
We also assumed arbitrary that subset of
mutants satisfying both criteria (95% killed
mutants factor and 2% decrease in code
coverage) is adequate for testing. For the majority
ReductioninMutationTestingofJavaClasses
299

of classes the coverage is greater than 90%, only for
classes Money and MoneyBag (Codepro) is less. In
these classes mutants were not generated for four of
its methods (last column of Table 2) and this caused
the low value of code coverage.
In following sections the results of reducing the
number of mutants generated for mutation operators
and methods reductions are presented.
3.2 Results for OP Reduction
In the OP reduction only part of generated mutants
by a mutation operator (class level and method
level) is used in testing. From 40% to 90% of
generated mutants were removed using step of 10%
as a reduction value. If the number of mutants
disable the removal of multiplicity of 10%, formula
(1) was used:
(1)
Where:
• U – number of mutants which should be removed,
• LM – number of mutants for mutation operator,
• prc – percentage of mutants to be removed,
• int – integer part of a number.
Mutants Remover tool (Kulesza, 2012) was used
to remove mutants. To minimize the “random
element” in our experiment the process of removing
mutants was tripled for different prc values and the
modified sets of mutants were stored in files
class_name_OP_(100% - prc)_i.
The results of testing using constraint subset are
given in Table 3. The mean values greater than 95%
of killed mutants for all tested classes were obtained
for subset produced for prc values 40%, 50% and
60%.
In Table 4 the degradation in the code coverage
for OP reduction is shown. The degradation not
greater than 2 % (to the code coverage for all
mutants) was obtained for two reduced sets of
mutants OP_60 and OP_50. These sets are satisfying
both our criteria described in section 3.1.
3.3 Results for METHOD Reduction
We treated each method as a “whole” and the
number of mutants generated for this method was
reduced by 40% to 90% for each mutation operator.
In METHOD reductions for each method and for
each mutation operator (method level) part of its
mutants were removed. Next, independently, parts of
mutants generated for each operator (at the method
level) were removed and at last, mutants for each
operator at the class level were reduced.
Table 3: Percentage of killed mutants in OP subsets.
class/subset OP_60 % OP_50 % OP_40 % OP_30 % OP_20 % OP_10 %
Recipe
94.31
94.85 90.24 87.53 82.93 62.60
CoffeeMaker
99.13 98.88 98.51 98.38 97.01
94.78
Money
97.28
91.84 92.52 91.16 85.71 68.03
MoneyBag
97.22 95.83 95.14
91.67 88.19 87.50
Element
98.70 98.33 96.94 95.09
91.85 86.11
Board
98.75 98.75 97.50 96.63
94.13 91.89
Wall
99.63 99.51 99.14 98.77 97.91
93.36
Stack
98.10 98.23 96.64
93.92 87.77 75.41
average
97.89 97.03 95.83
94.14 90.69 82.46
Table 4: The degradation of code coverage for OP reduction.
class/subset OP_60 OP_50 OP_40 OP_30 OP_20 OP_10
Recipe
2%
2.37% 5.10% 7.10% 8.65% 30.60%
CoffeeMaker
0% 0% 0% 0% 0.27%
2.73%
Money 2.07%
0.47%
3% 2.07% 6.47% 16.63%
MoneyBag
0% 0%
2.67%
1.43%
4.27% 2.43%
Element
0.23% 0.47% 1.17%
2.10% 3.37% 4.77%
Board 2.07% 2.17% 4.07% 5.17% 9.23% 6.10%
Wall
0% 0% 0.27% 0.27% 0.27% 1.70%
Stack
1.87% 1.20%
2.63% 5.87% 5.43% 8.27%
average 1.03% 0.83% 2.36% 3% 4.74% 9.15%
ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications
300
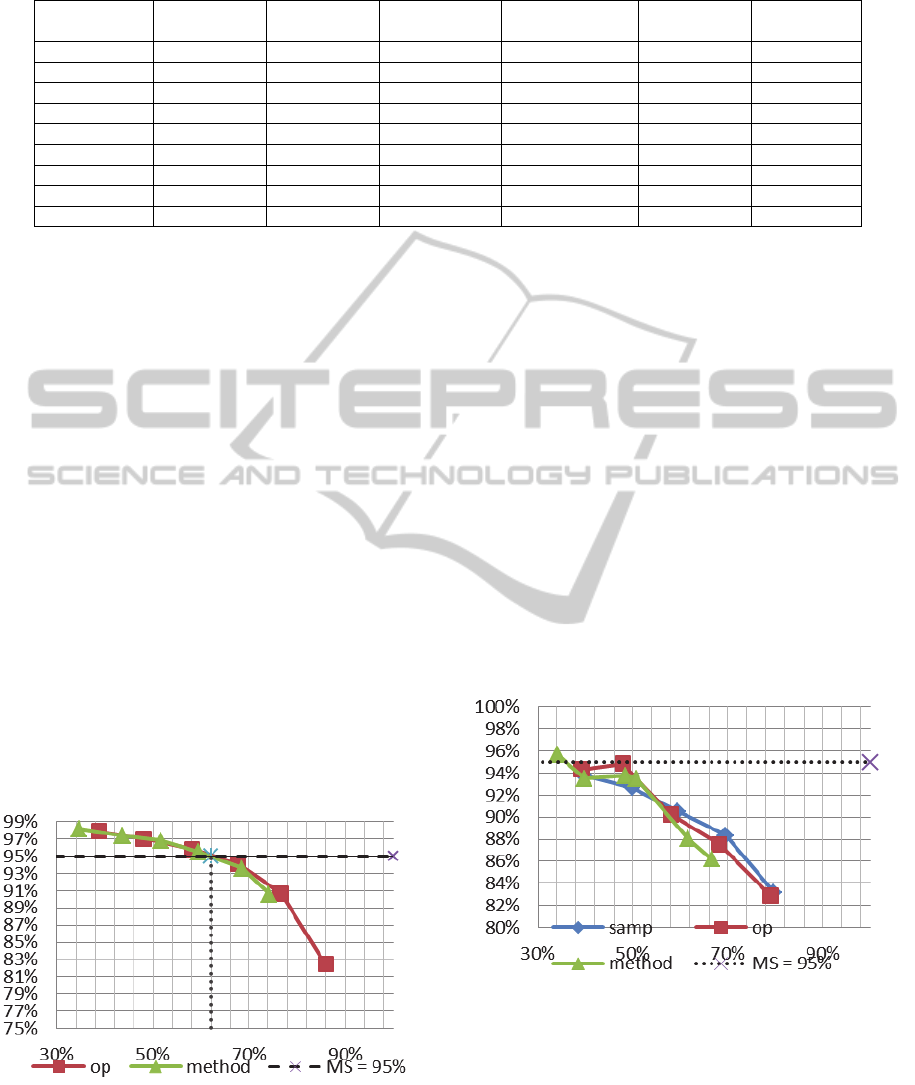
Table 5: Percentage of killed mutants in METHOD subsets.
Class/subset M-D_60 % M-D _50 % M-D _40 % M-D _30 % M-D _20 % M-D _10 %
Recipe
95.66
93.50 93.77 93.50 88.08 86.18
CoffeeMaker
99.25 99.13 98.63 98.38 97.14 96.52
Money
96.60 95.92
94.56 89.80 89.80 87.76
MoneyBag
97.92 95.83 95.14 95.14 95.14
93.06
Element
98.15 98.24 97.78 96.57
94.35 88.33
Board
99.00 98.63 98.50 96.25
94.63 91.01
Wall
99.75 99.51 99.02 99.26 98.52 97.54
Stack
99.05 98.48 97.02
94.74 90.87 84.09
average
98.17 97.40 96.80 95.46
93.57 90.56
The reductions were performed for each method
of a class independently. The exact number of
mutants eliminated was also calculated using the
formula (1) and Mutants Remover tool was used in
the elimination process.
In Table 5 the results for reducing METHOD
subsets of mutants are presented. The average value
95% of killed mutants was obtained for subset
produced for prc values 30%, 40%, 50% and 60%.
For 48 subset of mutants the 95% of killed mutants
was obtained in 31 subsets. The level 95% of killed
mutants was even available for class Recipe, for
60% of mutants, such good results were not
available for this class in the OP reduction (section
3.2).
In Fig. 1 mean values of killed mutants factor in
OP and METHOD reduction are presented as a
function of eliminated mutants for OP and
METHOD reductions. It can be seen that these
values are similar till the 95% level. These
reductions decreased the number of mutants
significantly (about 62%) with only small (5%)
decrease in killed mutants factor.
Figure 1: Mean values of killed mutants” factor in OP and
METHOD reduction.
Similar measures were also obtained for
randomly sampled reductions, described in
(Bluemke and Kulesza, 2013), but the killed mutants
factor was worse than for OP and METHOD
reductions.
We also observed during experiments that if the
number of mutants significantly decreased, till a
specified level (e.g. 55% for class Recipe Fig. 2.) the
OP and METHOD reductions were less efficient
than random elimination of mutants described in
(Bluemke and Kulesza, 2013). Decreasing the
number of mutants lowers the killed mutants factor
which can be seen in Fig. 1 and Fig. 2. It may
happen, that for a file with less number of mutants
the killed mutants factor will be greater, this can be
observed in Fig. 2. For class Recipe for file OP_60
killed mutants factor was 94.31%, while for file
OP_50, containing less elements than OP_60, the
value of killed mutants factor was slightly greater
and equal to 94.85%. This phenomenon is caused by
random factor in the elimination of mutants.
Figure 2: Killed mutants factor for class Recipe in OP,
METHOD and random sampling – SAMP.
In Fig. 1, Fig. 2 and in Fig. 3 it can be observed
that the ‘METHOD’ curve stops before the others.
This is caused by formula 1 used for the calculation
of the number of mutants reduced in prc% step of
reduction. This formula is used, if the number of
mutants for the operator is too low to use directly
prc%. Example: LM=7, and we want to reduce 90%.
ReductioninMutationTestingofJavaClasses
301
From formula 1 we obtain U=6 mutants to be
removed which is 6/7= 85.71% . For subsets SAMP
(random reduction ) and OP (Fig. 3) the numbers of
mutants were significantly greater, than for
METHOD, so it was easier to reduce it close to e.g.
90%.
In Table 6 the decrease of code coverage for
METHOD reduction comparing to the coverage of
full set of mutants is presented. The mean decrease
of 2% was for subsets obtained for reductions 40% to
70% of mutants (METHOD_60 - METHOD_30.
Each of these subsets enabled also the mean values of
killed mutants to be greater than 95% thus satisfying
ours both criteria (section 3.1). Even for the subset
METHOD_10 the mean decrease in code coverage is
only 3% and is significantly lower than for subsets
SAMP_10 - random elimination (Bluemke and
Kulesza, 2013) and OP_10 (accordingly 17.90% and
9.15%). In METHOD reduction mutants are
eliminated independently for each method so it is not
possible to eliminate all mutants for a method thus
making its code not covered. In OP and randomly
reduction such situation may happen.
Table 6: Decrease code coverage for METHOD reduction
comparing to the coverage of full sets of mutants.
class/
subset
M-
D_60
%
M-D
_50 %
M-D
_40 %
M-D
_30 %
M-D _20
%
M-D _10
%
Recipe 3.03 3.73 4.07 3.73 11.20 13.27
CoffeeMa
ker
0 0 0 0 0.27 0.53
Money
0 0 0 0 0 0.47
MoneyBa
g
0 0.87 1 0.43 0.87 0.87
Element
0.70 0.70 0.93 0.93 1.87
4.20
Board
1.57
2.10
1.57 1.73
4.13 3.20
Wall
0 0 0 0.27 0 0.27
Stack
0.43 0.87 0.87 1.30 1.83 1.30
average 0.72 1.03 1.05 1.05 2.52 3.01
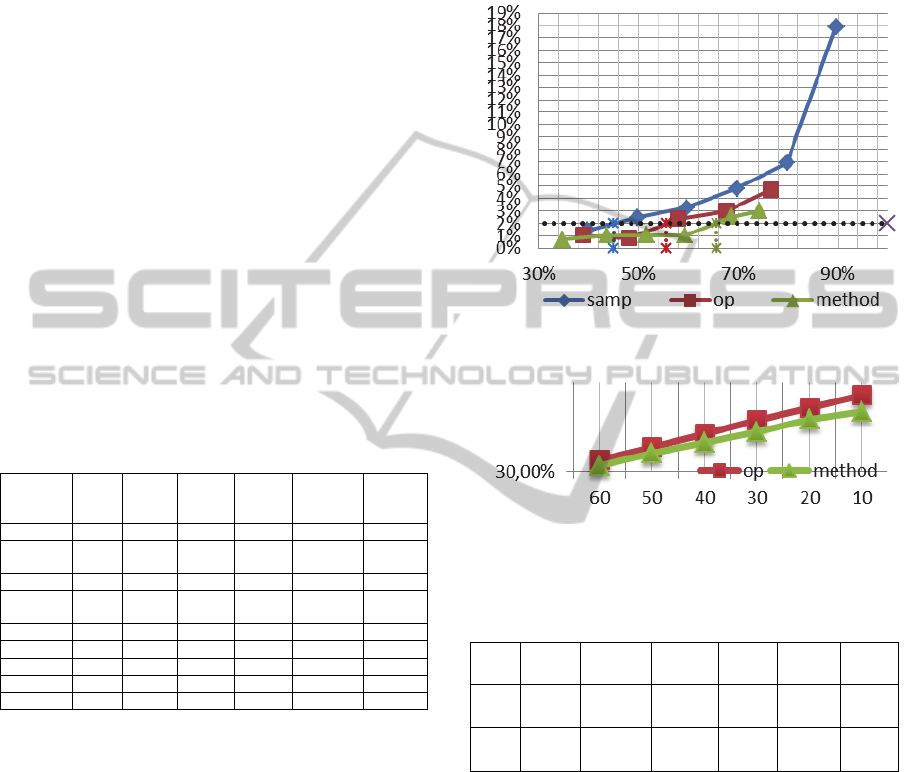
In Fig. 3. the mean decrease of code coverage for
OP, METOD and random reduction, denoted as
samp, (Bluemke and Kulesza, 2013) of mutation is
shown.
3.4 Reduction of Computation Cost
We evaluated each subset obtained after mutants
reduction in terms of computational costs. We
observed the decrease of the number of: mutants, test
cases necessary for maximal killed mutant factor and
total runs in testing.
3.4.1 Reduction of Mutants
In Table 7 the mean values of mutants for different
prc values (section 3.1 formula 1) are given. These
numbers may differ, as can be seen in Fig. 4. In
Table 7 bold fonts are used for subsets satisfying
both criteria (section 3.1). From these subsets the
greatest reduction level was almost 60%, for subset
METHOD_30 (prc=70%).
Figure 3: Mean decrease of code coverage for OP,
METOD and random reduction – samp of mutants
Figure 4: Decrease of the number of mutants as function
of 100%-prc (section 3.1, formula1).
Table 7: Reduction of mutants for different prc values
(formula 1, section 3.1).
subset/
prc
40 % 50 % 60 % 70 % 80 % 90 %
OP
38.84 48.05
58.05 67.61 76.58 85.91
MET
HOD
34.67 43.63 51.63 59.41
68.55 74.16
3.4.2 Reduction of Test Cases
Each generated mutant has to be executed for at least
one test case. The less test cases there are, the fewer
executions are needed. The reduced number of
mutants and reduced number of test cases
significantly decrease the total number of test
executed in the testing process. The decrease in the
total number of executed test is presented in Table 8
for METHOD reduction. Bold font is used for subset
satisfying both our criteria (section 3.1). The last
row shows the mean percentage of reduced tests for
all classes. It can be noticed that the reduction in
total number of executed tests is significant: 68.41%.
ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications
302

Table 8: Number of executed tests for METHOD reductions.
Class/subset full M-D_60 M-D _50 M-D _40 M-D _30 M-D _20 M-D _10
Recipe 1631 963.67 855.67 660.33 648 406.67 343
CoffeeMaker 4130
2286.33 1848 1507.67 1111 684.33 451.33
Money 412
247 184.33
169 117 96 94.67
MoneyBag 330
180.33 160.67 146.67 137.33 96.33
99.33
Element 6126
3406.67 2871 2275 1787.67
1165.33 644.33
Board 2399
1408
1242.33
986 763
601.67 386.33
Wall 2145
1301 962.67 793.67 539.33 398.67 198.33
Stack 21785
13060.33 10560.67 8604
6521 4136 2496.67
Average
reduction
42.01% 52.17% 60.35% 68.41%
78.04% 83.45%
4 CONCLUSIONS
Experimental research has shown mutation testing to
be very effective in detecting faults e.g.: (Bluemke
and Kulesza, 2011), (Frankl et al., 1997), (Andrews
et al., 2005), unfortunately it is computationally
expensive so some researchers propose parallel
execution of tests (Mateo and Usaola, 2013), others
constraining the sets of mutants. The contribution of
our research is the detailed examination of selective
reduction of mutants generated for mutation
operators including class operators in Java programs.
The mean values, greater than 95% of killed
mutants for almost all tested classes, were obtained
after reductions 40%-60% of generated mutants for
OP subsets. Even better results were obtained for
sampling METHOD subsets. For these subset only
30% of mutants were able to kill 60% of mutants in
average and the degradation in the code coverage
was less than 1%.
However our experiment was made in different
environment and on different language, we
confirmed the observation of Scholive et. al. (2005)
that selective reductions of mutants are better than
the random ones.
Our experiment shows that reduction in mutants
generated for mutation operator (regular and class
level) in Java programs can significantly reduce the
cost of testing. The reductions in numbers of
mutants and executed test are easily visible (Tables
7-8). Even better reductions can be achieved by
logic mutations (Kaminski et al., 2011) but they
require special test cases.
The experiments reported in this paper were time
consuming so only 8 Java classes were tested. The
number of programs used in other experiments on
mutation’ subset were similar. It is difficult to know
if 8 classes is sufficiently large sample from which
to generalize and so similar studies on larger sets of
classes will be useful. Due to the effort needed in
performing the experiment we were not able to use
statistically significant number of mutants for
random selection. However the results of our
experiments support the results presented in
literature, some of which were made on other
programming languages, e.g. (Mathur and Wong,
1995), (Scholive et al., 2005), (Offut et al., 1996),
(Polo et al., 2009) it seems to us that confirming
experiments is important in science.
All the results of this study have been obtained
using the set of mutation operators available in
MuClipse. Clearly, these results cannot be applied
directly to mutation systems that use different
operators. Efficiency relationships will, nonetheless,
be present between any set of operators. In future it
would be interesting to compare the results of our
experiment with minimal set of mutants quite
recently proposed by Amman, Delamaro and Offutt
(March 2014) .
ACKNOWLEDGEMENTS
We are very grateful to the reviewers for many
valuable remarks.
REFERENCES
Acree A.T., 1980. On mutation, Ph.D. thesis, Georgia
Institute of Technology, Atlanta.
Agrawal H. et al., 1989. Design of mutant operators for
the C programming language. Software Engineering
Research Center, Purdue University, West Lafayette in
Technical Report SERC-TR-41-P, March 1989.
Ammann P., Delamaro M.E., Offutt J., 2014. Establishing
Theoretical Minimal Sets of Mutants. In Proc. of the
IEEE Int. Conf on Software Testing, Verification, and
Validation. 21-30.
Andrews J. H., Briand L. C., Labiche Y., 2005. Is
mutation an appropriate tool for testing experiments?
ReductioninMutationTestingofJavaClasses
303

In: Proc. ICSE, pp. 402-411.
Bashir B. M., Nadeem A, 2012. Object Oriented Mutation
Testing: A Survey. IEEE: 978-1-4673-4451-7/12.
Bluemke I., Kulesza K., 2011. A Comparison of Dataflow
and Mutation Testing of Java Methods. In:. Advances
in Intelligent and Soft Computing, vol. 97, pp. 17-30,
Springer.
Bluemke I., Kulesza K., 2013. Reduction of computational
cost in mutation testing by sampling mutants. In
Advances in Intelligent and Soft Computing, vol. 224,
Springer, pp. 41-51. DOI:10.1007/978-3-319-00945-
2_4
Budd T.A. , 1980. Mutation analysis of program test data.
Ph.D. thesis, Yale Univesity, New Haven,
Connecticut.
CodePro JUnit Demo - https://developers.google.com/java
-dev-tools/codepro/doc/features/junit/CodeProJUnit
Demo.zip.
CoffeeMaker, accessed 2012 - http://agile.csc.ncsu.edu/
SEMaterials/tutorials/coffee_maker
Delamaro M.E., Offutt J., Ammann P., 2014. Designing
Deletion Mutation Operators. In Proc. of the IEEE Int.
Conf on Software Testing, Verification, and
Validation. 11-20.
Derezińska A., Rudnik M., 2012. Quality Evaluation of
Object-Oriented and Standard Mutation Operators
Applied to C# Programs, TOOLS Europe 2012, LNCS
7304, pp. 42–57, Springer.
Derezińska A., 2013. A Quality Estimation of Mutation
Clustering in C# Programs. In: New Results in
Dependability and Computer Systems, AISC 224, pp.
183-194, Springer.
Frankl P. G., Weiss S. N., Hu C. , 1997. All-uses versus
mutation testing: an experimental comparison of
effectiveness. J. Syst. Softw., vol. 38, no. 3: 235-253.
Grun B., Schuler D., Zeller A., 2009. The impact of
equivalent mutants. In Proceedings of the 4th
International Workshop on Mutation Testing.
Hierons R., Harman M., Danicic S., 1999. Using program
slicing to assist in the detection of equivalent mutants.
Softw. Test. Verif. Rel., vol. 9, no. 4: 233-262.
javasol - http://sourceforge.net/projects/javasol accessed
2012.
jet-tetris - http://sourceforge.net/projects/jet-tetris .
Jia Y, Harman M., 2011. An Analysis and Survey of the
Development of Mutation Testing. IEEE Transactions
on Software Engineering, vol. 37 no. 5, 649 – 678.
Jumble - http://jumble.sourceforge.net/index.ht, 2010.
Kaminski G. et al. , 2011. A logic mutation approach to
selective mutation for programs and queries.
Information and Software Technology, vol. 53, pp.
1137–1152.
Kim S., Clark J. A., McDermi J. A., 2001. Investigating
the effectiveness of object-oriented testing strategies
using the mutation method. In Proceedings of the 1st
Workshop on Mutation Analysis (MUTATION’00),
published ii Mutation Testing for the New Century.
San Jose, California, 6-7 October 2001, pp. 207–225.
Kulesza K, 2012. Mutation testing computational cost
reduction using mutants sampling and selective
mutation, M.Sc. thesis, Institute of Computer Science,
Warsaw University of Technology.
Madeyski L., et al., 2014. Overcoming the Equivalent
Mutant Problem: A Systematic Literature Review and
a Comparative Experiment of Second Order Mutation.
IEEE Trans. on Soft. Eng.,vol. 40: no 1. 23 – 42.
MapMaker - Godlewski Ł., 2008. , Institute of Computer
Science, Warsaw University of Technology,
unpublished.
Mateo P. R., Usaola M. P.., 2013. Parallel mutation
testing. Softw. Test. Verif. Reliab. vol.23: 315–350.
Mathur A. P., Wong W.E, 1995. Reducing the cost of
mutation testing: an empirical study. J. Syst. Softw.,
vol. 31, no. 3 185-196.
Mresa E.S., Bottaci L., 1999. Efficiency of mutation
operators and selective mutation strategies: An
empirical study. Soft. Testing, Ver. and Rel. , vol. 9
(4): 205-232.
Mutation repository (modified VII 2011) http://crestweb
.cs.ucl.ac.uk/resources/mutation_testing_repository/,
MuClipse, accessed 2012 http://muclipse.sourceforge.net/
index.php .
NetworkShipsBattle , 2010. Network game, Suchowski J
Institute of Computer Science, Warsaw University of
Technology, unpublished.
Offutt A. J., Craft W. M., 1994. Using compiler
optimization techniques to detect equivalent mutants.
Softw. Test. Verif. Rel., vol. 4, no. 3: 131-154.
Offutt J., Rothermel G., Zapf C., 1996. An experimental
determination of suffcient mutation operators. ACM
Trans. on Soft. Eng. and Methodology, vol. 5 (2): 99-
118.
Offutt A. J., Pan J., 1997. Automatically detecting
equivalent mutants and infeasible paths. Softw. Test.
Verif. Rel., vol. 7, no. 3: 165-192, Sep. 1997
Offutt J., 2011. A mutation carol: Past, present and future,
Information and Software Technology vol. 53, pp.
1098–1107.
Patrick M., Oriol M., Clark J.A., 2012. MESSI: Mutant
Evaluation by Static Semantic Interpretation. In: Proc.
IEEE Fifth Int. Conf. on Software Testing, Verification
and Validation. pp. 711- 719.
Segura S., et al.,2011. Mutation testing on an object-
oriented framework: An experience report. Inf. and
Soft. Technology vol. 53, pp. 1124–1136
Schuler D., Zeller A., 2010. (Un-)covering equivalent
mutants. In: Proc. ICST, pp. 45-54.
Scholive M., Beroulle V., Robach C., 2005. Mutation
Sampling Technique for the Generation of Structural
Test Data. In: Proc. of the Conf. on Design,
Automation and Test in Europe, vol. 2: 1022 – 1023.
ICSOFT-EA2014-9thInternationalConferenceonSoftwareEngineeringandApplications
304
