Optimization of Gas Turbine Compressor Blade Parameters for

Gas-dynamic Efficiency under Strength Constraints

Leonid Shabliy and Aleksandr Cherniaev

Samara State Aerospace University, Moskovskoe r., Samara, Russia

JSC "CADFEM-CIS", Avrora st., Samara, Russia

Keywords: Multiobjective Optimization, Compressor Blade, Fluid-Structure Interaction, Genetic Algorithm.

Abstract: This article describes an approach for optimization of gas turbine compressor blade based on one-way fluid-

structure interaction (FSI) analysis coupled with evolutionary optimization algorithm. Commercial CFD and

FE code ANSYS was used for the simulations. Paper gives detailed description of developed geometric

model, CFD and FE models, as well as description of employed optimization technique. Obtained results

indicate that adiabatic efficiency and pressure rate of compressor can be increased up to 23% and 7%

correspondingly by rational selection of relative positions of compressor blade cross-sections.

1 PROBLEM

Gas turbine power plants (gas turbines) are

increasingly used as power sources in a variety of

military and civilian applications. This includes

propulsion for air, land, overwater and even

underwater applications, as well as electric power

plants, pumping stations, etc. Gas turbine power

plants, in comparison with the piston engines, have

greater body-weight capacity, more favorable

traction performance and longer service life. They

do not need any cooling system and thus have no

problems associated with it. In addition, they are

unpretentious in operation, being easy to run at

lower temperatures, not requiring fine air

purification and having high environmental

performance, as well as relatively low emissions and

low consumption of oil.

Major disadvantage of gas turbine engines is

complexity of their design. This results in the high

cost of their life cycle (Kuzmenko et al., 2007). In

turn, complexity of design results from the mutual

influence of different physical processes

simultaneously occurring in gas turbine. Reduction

of life-cycle costs of a gas turbine requires its

optimization with regard to different efficiency

parameters (e.g., adiabatic efficiency and pressure

rate of compressor, weight) and taking into account

multiple constraints (e.g., strength, stiffness, natural

frequencies etc.)

A number of examples of such analyses have

been described in the literature. In (Lian and Liou,

2005) multi-objective optimization was performed to

maximize stage pressure ratio and minimize weight

of NASA rotor67 compressor blade. It was

conducted over 32 design variables controlling

geometry of 4 cross-sections along the blade span.

Optimization resulted in 1.8% and 5.4%

improvement of baseline design for pressure ratio

and weight, correspondingly. Simulations used

TRAF3D CFD code combined with response surface

generator and genetic algorithm. In (Lee and Kim,

2000) and, more recently in (Samad and Kim, 2008),

optimization was carried out for two conflicting

objectives, such as total pressure ratio and adiabatic

efficiency, using only 3 design variables controlling

geometry of stacking line of compressor blade. As in

the previous case, genetic algorithm was used in

(Samad and Kim, 2008) as optimization technique.

In (Chen et al, 2007) blade parameterization

technique was developed to reduce number of design

variables in optimization. Optimization was

performed using combination of gradient-based

algorithm with response surface approximations.

1.73% of increase in adiabatic efficiency for NASA

rotor37 was reported. Another example of

parameterization of compressor blades for multi-

objective optimization is given in (Sommer and

Bestle, 2011). The parameterization technique is

based on the use of B-splines. Presented simulations

were two-dimensional.

This short review allows determining two main

523

Shabliy L. and Cherniaev A..

Optimization of Gas Turbine Compressor Blade Parameters for Gas-dynamic Efﬁciency under Strength Constraints.

DOI: 10.5220/0004994905230528

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),

pages 523-528

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

distinctive features of existing approaches to

optimization of compressor blades. First, they

consider the problem as multi-objective. Second,

rational techniques for decreasing of a number of

design variables are continuously been sought.

In this paper we present an approach for optimal

design of compressor blades aiming to maximize

such conflicting parameters as adiabatic efficiency

and pressure rate of compressor. All simulations in

our study are full scale and three-dimensional. As

compared to results presented in the literature, our

approach is different in taking into account strength

constraints due to coupled CFD-FE simulations and

in use of formalized procedure for choosing design

variables based on parameters correlation study.

Described optimal design procedure, instead of

being based on an in-house code, utilizes

commercial widely used software ANSYS, which

makes it reproducible and ready-to-use by

engineering practitioners.

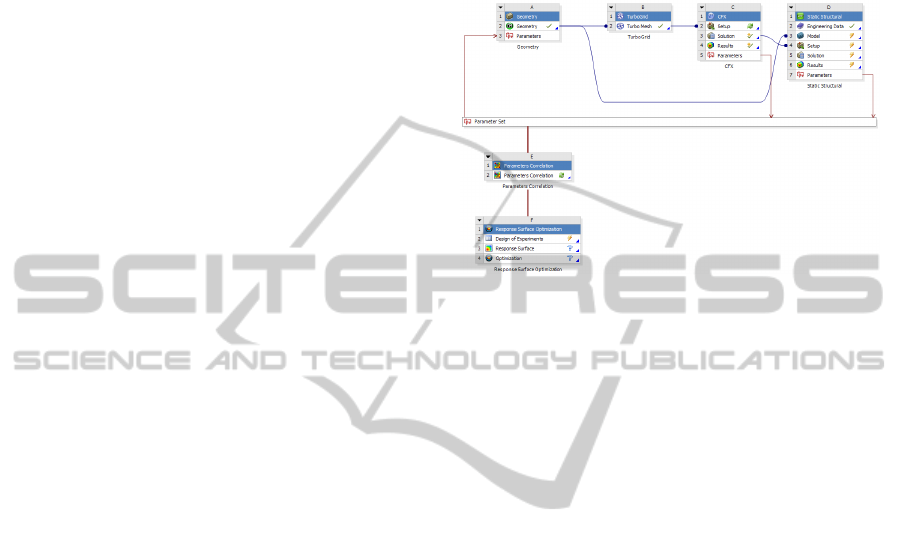
2 NUMERICAL SIMULATIONS

All simulations were done in the ANSYS

Workbench environment using the following set of

modeling applications (Figure 1):

 ANSYS Design Modeler for geometric modeling

(DesignModeler User Guide, 2011);

 ANSYS TurboGrid for high-quality hexagonal

meshing of inter-blade channel (ANSYS

TurboSystem User Guide, 2011);

 ANSYS CFX for gas dynamics simulations

(ANSYS CFX-Solver Modeling Guide, 2011);

 ANSYS Static Structural for strength analysis

(ANSYS Mechanical Application User's Guide,

2011);

 Parameters Correlation and Response Surface

Optimization toolboxes for identification of most

influencing design variables, calculation of

response surfaces and optimization (Design

Exploration User Guide, 2011).

In general, a single simulation loop can be

described as follows. First, for a given set of design

variables created by response surface generator, a

geometric model of compressor blade is constructed.

This procedure was automated by establishing

parametric relationships between blade geometric

elements (see section 2.1). Next, this model is

discretized in Turbogrid and transferred to ANSYS

CFX to perform gas-dynamics analysis. This

analysis has two goals. First, it evaluates adiabatic

efficiency and pressure rate of the compressor, and

second, it calculates pressure field on the blade,

which is then transferred to ANSYS Static Structural

and used there as loading condition for strength

analysis. This scheme implements so called one-way

fluid-structure interaction (FSI) procedure. In Static

Structural, strength is assessed by means of von

Mises criterion.

Figure 1: ANSYS Workbench project configured for

optimization of compressor blade.

Such direct analyses are repeated few times to

construct response surfaces for design objectives

(pressure rate and adiabatic efficiency) and

constraint (maximum von Mises stress in the

model). Once this part is accomplished, genetic

algorithm implemented in ANSYS DesignXplorer is

used to solve multiobjective optimization problem.

In the next subsections, each step of this

procedure is described in more details.

2.1 Geometric Model

The parametric geometry model was built in

ANSYS Design Modeler and consisted of a blade

and a shank. Blade was built using three cross-

sections (blade profile on the hub, the middle and

peripheral diameter) by Skin/Loft operator

(Figure 2). Each profile was constructed according

to the method of circular arcs and line segments

(Figure 3) and had the following variable

parameters:

 blade angles at the input (β

) and outlet (β

);

 chord (b);

 radius of the input (R

) and output (R

out

) edges.

Parameterization of the profile was carried out by

specifying geometric and dimensional constraints.

Dimensional constraints were defined by a set of

equations which establish relationships between

parameters of cross-sections (Figure 4). For

example, the angles between blade sides and its

horizontal axis (A12 and A13) can be found as inlet

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

524

Figure 2: Blade geometry model with highlighted profiling

cross-sections.

Figure 3: Blade profile sketch with imposed dimensional

constraints.

vane angle plus/minus the half of inlet sharpening

angle w

Plane4.A12=@beta1 - @w1/2

Plane4.A13=@beta1 + @w1/2

Due to the fact that sketches of blade cross-

sections were built in separate planes, each profile

had two more degrees of freedom in the global

coordinate system, namely the flat shift in the

tangential plane. This allowed utilizing in parametric

framework well-known technique of shifting blade

cross-sections, which is typically used for

discharging a blade from the aerodynamic forces.

Therefore blade geometry, being the most

complex part of the vane, depends on a large number

of parameters. Even though we used in this work

relatively simple profiling technique, it resulted in

more than 20 independent variables. To reduce the

number of parameters in optimization, it was

decided to vary only the following ones:

 inlet angles at each section (β

1_0

, β

1_1

, β

1_2

);

 shift of middle and peripheral sections (ΔX

ΔX

);

 fillet radius at the junction of the fir-tree root and

blade (R).

Figure 4: Design Modeler Parameter Manager Window.

ExportPoints tool from BladeEditor module of

ANSYS Design Modeler was used to transfer the

geometric model of inter-blade channel to

TurboGrid. FlowPath operation was used to indicate

the meridional sections (Figure 5). For adequate

representation of fillet geometry in gas-dynamic

analysis, density of sections was higher in the hub

region. Position (Span) of each section was

parameterized using algebraic expressions as a

function of the radius of the fillet R (Figure 5).

Figure 5: Parameterization of Span element using

FlowPath operation: blade with large fillet radius has

less layers (left) than blade with small fillet radius (right).

2.2 Gas-Dynamic Model

As it was mentioned before, TurboGrid was used to

create a mesh of inter-blade channel (Figure 1).

Typically, finer mesh provides higher precision of

numerical simulations. However, optimal design

problems require multiple analyses with different

sets of design variables. Thus a compromise

between simulation accuracy and computational cost

should always be sought. Based on this, in the

OptimizationofGasTurbineCompressorBladeParametersforGas-dynamicEfficiencyunderStrengthConstraints

525

present work meshing of inter-blade channel

resulted in 60 elements. This allowed maintaining

sufficient accuracy in representation of physical

phenomena of interest and solving the optimization

problem in about 60 hours.

The gas-dynamic model was created in the CFX-

Pre preprocessor using Turbo-mode tool. The air

was set as working body and option of domain

motion was set to the constant speed rotation.

Boundary conditions were also given constant,

which included absolute incident velocity of the air

at the inlet and static pressure at the outlet

(Figure 6).

Figure 6: Model prepared for gas-dynamic simulation

(left) and obtained results: streamlines and pressure

contours (right).

Figure 7: Dependence of efficiency on the angle of the

blade inlet in the middle section.

For further reduction of computational expenses,

rough convergence criteria were set, including the

residual (RMS) of 0,001 and the maximum number

of iterations of 150. The accuracy of the results was

found to be enough for adequate representation of

the physical phenomenon of interest and conducting

parametric studies.

Results obtained in a trial calculation allowed

estimating the dependence of flow parameters on the

shape of the blades (Fig. 7).

2.3 Finite Element Model

Pressure field exported from CFX to Static structural

and results of FE analysis for equivalent stresses are

exemplified in Figure 8. As expected, applied

loading creates a stress concentration region at the

filleted area near junction of the fir-tree root and the

blade.

Figure 8: Blade finite element model: imposition of

aerodynamic loads (upper) and equivalent stresses (lower).

The main loads acting on the blade are the

aerodynamic and centrifugal forces. The

aerodynamic load is transmitted to the blade as the

pressure of gas flow field calculation. In such

loading conditions, stress-strain state is determined

by the following parameters:

 fillet radius (R), which determines the size of the

stress concentration zone;

 relative position of the central and peripheral

sections, which influence distance between

center of gravity of the blade and its center of

rotation. In turn, it influences value of the

centrifugal force.

3 OPTIMIZATION PROCEDURE

3.1 Choice of Design Variables

It is obvious that the problem under consideration, in

terms of optimization, refers to the class of NP-

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

526

complete problems. It means that dimension of

design space exponentially depends on the number

of variables. Thus, it is important to identify the

most important input parameters and exclude from

consideration those which have low influence on the

design criteria and constraints. This can help

significantly reduce complexity of the optimization

problem in terms of computational time.

Global sensitivity analysis was carried out to

assess dependence of adiabatic efficiency, pressure

rate and maximum equivalent stress on inlet angles,

shift of middle and peripheral cross-sections and

fillet radius. For these calculations, Parameter

Correlation tool from ANSYS DesignXplorer was

used.

Results of the calculations presented in Figure 9.

They allowed drawing the following conclusions:

 the value of adiabatic efficiency and pressure

ratio mainly depends on blade angles at inlet,

middle and far-sections, as well as (to a lesser

extent) fillet radius;

 maximum equivalent stress is mainly affected by

the shifts of middle and peripheral cross-

sections, as well as by a fillet radius and a blade

angle at the inlet.

Based on this, it was decided to use all of the

above parameters as variables in optimization

problem.

Figure 9: Dependence of the upcoming criteria

optimization of variable parameters.

3.2 Optimization Formulation

As a result, the optimization problem can be

formulated as follows:

Maximize efficiency=f(α

1_0

,α

1_1

,α

1_2

,Δx

,R), and

Maximize π

= f (α

1_0

, α

1_1

, α

1_2

, Δx

, R)

under the constraint of σ

max

≤ [σ],

where α

1_0

, α

1_1

, α

1_2

– blade inlet angles to the cross

sections 0…2; Δx

, Δx

– shift of cross

sections at tangential plane; R – fillet radius at the

junction of the blade in fir-tree root.

The first step in solving any optimization

problem using ANSYS DesignXplorer is

construction of response surfaces for design

objectives and constraints. In the current work,

response surfaces were represented using second

order polynomials. Some of them are shown in

Figure 10. “Central composite design” method was

used to select sample points.

Figure 10: The constructed response surface parameters to

be optimized (in the axes α1_1, α1_2): maximum

equivalent stress (on the top), adiabatic efficiency (in the

middle), pressure ratio (on the bottom).

The ranges of the design parameters were as

follows: ±5 mm for the displacement of middle and

peripheral sections; 30...70º for the angles; 2...5 mm

for the fillet radius. The maximum allowable

equivalent stress for the titanium blade was assumed

to be 800 MPa. Equal weighting factors were used

for both design criteria.

OptimizationofGasTurbineCompressorBladeParametersforGas-dynamicEfficiencyunderStrengthConstraints

527

In the next stage, optimization strategy was chosen.

The only method available in DesignXplorer for

multiobjective optimization is so called Genetic

Algorithm. This method implements mathematical

model of evolutionary process.

3.3 Optimization Results

When importances of design criteria are not equal,

all possible optimal solutions belong to so-called

Pareto front. Calculated Pareto front for the current

problem is shown in Figure 11.

Figure 11: Pareto front.

Results obtained for the case of equal importance

are presented in Table 1. Their comparison with the

corresponding values for baseline design is shown in

Figure 12. Increase of adiabatic efficiency and

pressure ratio obtained as a result of optimization is

equal to 23 and 7%, respectively.

Table 1: The values of the design parameters of the blade,

obtained during optimization.

Parameter Optimal value

, degrees 42.52

, degrees 32.11

, degrees 47.53

Δx

, mm 4.92

Δx

, mm -0.83

R, mm 2.75

Figure 12: Comparison of the original and the optimized

shape of the blade.

4 CONCLUSIONS

Multiobjective optimization of gas turbine

compressor blade parameters has been performed

using ANSYS software. Significant increase of gas-

dynamic efficiency in terms of adiabatic efficiency

and pressure ratio was achieved with strength

constraints remained satisfied. Obtained results

indicate that presented approach can be successfully

used for the optimal design of compressor blades.

REFERENCES

Kuzmenko M. L., Shmotin Yu. N., Egorov I. N.,

Fedechkin K. S., 2007. Optimization of the gas turbine

engine parts using methods of numerical simulation.

In Proceedings of the ASME Turbo Expo, 2007,

Vol. 6, pt. A, pp. 425-431.

Lian Y., Liou M. S., 2005. Multi-Objective Optimization

of Transonic Compressor Blade Using Evolutionary

Algorithm. Journal of Propulsion and Power, 21 (6).

Lee S-Y, Kim K-Y., 2000. Design optimization of axial

flow compressor blades with three dimensional

Navier-Stokes solver. KSME International Journal,

14(9), 2000, pp. 1005 - 1012.

Samad A., Kim K-Y., 2008. Multi-objective optimization

of an axial compressor blade. Journal of Mechanical

Science and Technology, 22, 2008, pp. 999-1007.

Chen N., Zhang H., Xu Y., Huang W., 2007. Blade

Parameterization and Aerodynamic Design

Optimization For a 3D Transonic Compressor Rotor.

Proceedings of the 8th International Symposium On

Experimental and Computational

Aerothermodynamics of Internal Flows. Lyon, July

2007. Paper reference: ISAIF8-0021.

Sommer L., Bestle D., 2011. Curvature driven two-

dimensional multi-objective optimization of

compressor blade sections. Aerospace Science and

Technology, 15(4), 2011, pp. 334 - 342.

ANSYS User's Guides (DesignModeler, TurboSystem,

CFX-Solver Modeling Guide, Design Exploration,

Mechanical Application), 2011. ANSYS, Inc.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

528