Decision Trees and Data Preprocessing to Help Clustering Interpretation

Olivier Parisot, Mohammad Ghoniem and Beno

ıt Otjacques

Public Research Centre Gabriel Lippmann, Belvaux, Luxembourg

Keywords:

Clustering Interpretation, Decision Trees, Data Preprocessing, Evolutionary Algorithms.

Abstract:

Clustering is a popular technique for data mining, knowledge discovery and visual analytics. Unfortunately,

cluster assignments can be difﬁcult to interpret by a human analyst. This difﬁculty has often been overcome

by using decision trees to explain cluster assignments. The success of this approach is however subject to

the legibility of the obtained decision trees. In this work, we propose an evolutionary algorithm to cleverly

preprocess the data before clustering in order to obtain clusters that are simpler to interpret with decision trees.

A prototype has been implemented and tested to show the beneﬁts of the approach.

1 INTRODUCTION

Clustering is a data mining technique designed to

split data into homogeneous groups, so that simi-

lar elements are assigned to the same cluster while

dissimilar elements are assigned to separate clus-

ters. There are various families of clustering algo-

rithms (hierarchical/partitional, fuzzy/hard, distance-

based/density-based, etc.). In this paper, the term

clustering refers also to the cluster assignment result-

ing from applying a clustering algorithm on a dataset.

Many approaches have been proposed to evalu-

ate clustering quality (Gan et al., 2007). Nonetheless,

once a clustering is computed from data, its interpre-

tation is a critical and non-trivial task for the end-

user (Aggarwal and Reddy, 2013). To explain how

the objects are assigned to each cluster, several ap-

proaches can be used (Gan et al., 2007; Jain, 2010).

Firstly, visual exploration is often applied by using

various techniques like scatterplots, projections, and

dendrograms for hierarchical clustering. Secondly, a

statistical study of each cluster can be achieved (by

computing minimum/maximum/mean values for each

attribute), and cluster centroids can be used to de-

ﬁne representative items for the clusters. Thirdly, a

comparison to a ground truth can be carried out when

available. Finally, machine learning can be used to

gain insight about clusters: a convenient approach

consists in building a decision tree with a cluster as

its target variable in order to explain why an element

is assigned to it (Qyu et al., 2004).

In fact, decision trees are powerful tools for de-

cision support, data mining and visualization (Bar-

Figure 1: A decision tree representing a ﬁctive cluster as-

signment that is explained by using the age feature.

low and Neville, 2001; van den Elzen and van Wijk,

2011), as they use a formalism that is intuitive and

easy to understand (Murthy, 1998). More precisely,

given a dataset containing n features A

,...,A

, a de-

cision tree can explain the value of the feature A

(of-

ten called class) according to the values of the other

features (A

, with j different to i). Graphically, de-

cision trees are frequently represented by node-link

diagrams (Figure 1). In addition, decision trees can

be automatically built from data by using numerous

techniques (Kotsiantis, 2013) e.g., the well-known

C4.5 (Quinlan, 1993) and CART (Breiman et al.,

1984) algorithms. Once built, a decision tree can

be characterized by two important properties: its size

(the number of nodes) and its accuracy regarding the

data (estimated using the error rate, i.e. the ratio of

elements which are not correctly explained using the

tree) (Breslow and Aha, 1997).

However, in some cases, they can be large and dif-

ﬁcult to visualize (Herman et al., 1998). This makes

the use of complex decision trees for cluster inter-

pretation a daunting endeavor for a human analyst.

Parisot O., Ghoniem M. and Otjacques B..

Decision Trees and Data Preprocessing to Help Clustering Interpretation.

DOI: 10.5220/0005001300480055

In Proceedings of 3rd International Conference on Data Management Technologies and Applications (DATA-2014), pages 48-55

ISBN: 978-989-758-035-2

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Therefore, we propose an original preprocessing ap-

proach to transform the data, so that the clusters ob-

tained from the transformed data can be more easily

interpreted as they yield a simpler decision tree.

The rest of this article is organized as follows.

Firstly, related work is discussed. Then, the presented

method is described. Finally, a prototype is presented,

and the results of experiments are discussed.

2 RELATED WORK

As a clustering can be interpreted using decision trees,

simpliﬁcation techniques can be valuable. Yet, sev-

eral methods have been proposed to reduce the size

of decision trees with a minimal impact on their accu-

racy.

Firstly, pruning is a well-known simpliﬁcation

procedure (Breslow and Aha, 1997). It removes the

parts of the decision tree having a low explicative

power (i.e. by removing the branches that explain too

few cases and the branches with a high error rate). In

a recent work, the pruning algorithm is driven by the

dimensions of the decision tree (Stiglic et al., 2012).

Nevertheless, applying pruning on a decision tree is

likely to reduce its accuracy (Breslow and Aha, 1997).

Secondly, a simpliﬁed decision tree can be

obtained by working directly on the data. Com-

monly used as a preliminary step in machine

learning (Famili et al., 1997), data preprocessing

transforms a dataset to facilitate its use in a given

task (visualization, knowledge extraction, support

for modeling etc.) (Kandel et al., 2011). More

precisely, data preprocessing is a generic term

which regroups several kinds of data manipulation

tasks (Engels and Theusinger, 1998): ”cleaning”

(treatment of noise/extreme/redundant/unknown

values, etc.), ”dimensionality altering” (construc-

tion/transformation/selection of features, etc.) and

”quantity altering” (selection/sampling of data

records). As these transformations aim at simplifying

the data (in terms of dimensionality, number of

possible values, etc.), they can also help reduce the

size of the associated decision tree (at the expense of

accuracy). However, preprocessing has to be care-

fully used because it generally causes information

loss e.g., feature or records deletion.

Thirdly, it is possible to combine visualization,

user interaction and simpliﬁcation techniques in or-

der to produce decision trees that are easier to in-

spect (van den Elzen and van Wijk, 2011). Typically,

simplifying a huge decision tree can be achieved by

collapsing large parts of it and allowing the analyst

expand them interactively.

In this paper, we aim at providing a clustering that

can be explained with a simple and accurate decision

tree. To this end, our approach consists in preprocess-

ing the data prior to clustering in order to obtain sim-

pler trees that are more suitable for cluster interpreta-

tion, while keeping both the intensity of data transfor-

mation and clustering alteration under control.

3 CONTRIBUTION

3.1 Overview of the Method

By cleverly transforming the dataset before clustering

(Algorithm 1), our method aims to obtain a slightly

different clustering that will yield a simpler decision

tree compared to the initial dataset. In other words,

simpler data lead to simpler clusterings that are easier

to interpret.

Algorithm 1: Method.

Require:

1: a dataset DS

Ensure:

2: preprocess the dataset DS to obtain a transformed

dataset DS

3: compute the clusters from the dataset DS

4: compute a decision tree that explains the cluster

assignment

However, to correctly appreciate the obtained

cluster interpretation, it is critical to check the mod-

iﬁed dataset and the related clustering. To do that,

the method should control the data transformation,

in order to retain the most signiﬁcant parts of the

dataset. Moreover, the clustering alteration should be

measured by comparing the modiﬁed clustering to the

original one.

3.2 Data Transformation Control

There are several metrics to gauge the intensity of data

transformation (Wang and Wang, 2007). In this work,

we use the data completeness ratio (DCR) (Parisot

et al., 2013) to reﬂect the loss of information due

to data preprocessing methods (e.g., record deletion,

loss of precision after discretization). More precisely,

the DCR of a modiﬁed dataset is obtained by comput-

ing the ratio of values that are kept unchanged during

the preprocessing steps. Hence, a DCR close to 100%

represents a slight transformation (and conversely, a

DCR close to 0% represents a considerable transfor-

mation).

DecisionTreesandDataPreprocessingtoHelpClusteringInterpretation

3.3 Clustering Alteration Control

In addition, the clustering should keep the same

global meaning as in the initial data. Following our

method (Algorithm 1), the data are preprocessed and

the clusters are identiﬁed on the basis of transformed

values, not on the original information: so it leads to

different results. As a consequence, the cluster in-

terpretation based on the original variables becomes

questionable (Dolnicar and Gr

un, 2008). The com-

parison of the modiﬁed clustering to the initial clus-

tering requires appropriate metrics as discussed in the

literature (Wagner and Wagner, 2007). In this work,

the Jaccard index (JI) is used (Deﬁnition 1) (Jaccard,

1908) to measure clustering overlap. Other candidate

indicators include the Rand index.

Deﬁnition 1. Given two clusterings C and C

, we

deﬁne the following values:

= pairs in the same cluster in C and C

= pairs in the same cluster in C, not in the same

cluster in C

= pairs in the same cluster in C

, not in the same

cluster in C

Using them, the Jaccard index is computed as

follows: JI = N

/(N

+ N

)

In practice, the closer the Jaccard index is to 1, the

more overlapping the clusterings (and vice versa).

3.4 An Evolutionary Algorithm

In this work, a dataset transformation is deﬁned as

an ordered sequence of data preprocessing operations

(like discretization, normalization, feature selection,

etc.). Given a list of possible data preprocessing op-

erations, we have to ﬁnd a sequence of operations

that ﬁnally leads to a simpler decision tree for clus-

ter assignment. In fact, this problem leads to a classic

search one: there is a large count of possible solu-

tions and it is not reasonable to evaluate all of them.

Search heuristics may be used to solve this kind of

problems. In this category, evolutionary algorithms

are well-known (BDack et al., 1991) and often consid-

ered as efﬁcient (Rudolph, 1996). Recently, an evolu-

tionary algorithm was proposed to automatically ﬁlter

data (Derrac et al., 2012).

Likewise, we propose an evolutionary algorithm

for this problem (Algorithm 2). The input is a dataset

and the output is a transformed dataset leading to a

clustering that is interpretable using a simpler deci-

sion tree. The data transformation and the clustering

alteration are controlled with two threshold parame-

ters: the minimum data completeness ratio and the

minimum Jaccard index.

Algorithm 2: Evolutionary algorithm.

Require:

1: a dataset DS, a minimum DCR, a minimum JI

Ensure:

2: Generate and evaluate a list of sequences of pre-

processing operations L (initial population)

3: while (no stagnation of best sequence) and (not

only similar sequences) do

4: Select two parent sequences S

and S

from L

5: Cross-over of S

and S

: build a new child se-

quence of preprocessing operations S

new

6: Mutation of the child sequence S

new

7: Evaluate the sequence S

new

and add it into L

8: Identify and remove the worst sequence S

worst

from L

9: Identify the best sequence S

best

in L and test if

stagnation

10: end while

11: Apply the best sequence S

best

on the dataset DS

to produce a dataset DS

12: return the dataset DS

The most important aspect of evolutionary algo-

rithms is the evaluation of the possible solutions (of-

ten called ﬁtness). Here, the following metrics are

used to evaluate the sequence: the decision tree size,

the decision tree error rate, the data completeness ra-

tio, the amount of overlap between the initial and

resulting clusterings measured by the Jaccard index.

Based on this evaluation method, the algorithm aims

at ﬁnding a sequence of preprocessing operations

leading to:

• A modiﬁed dataset whose data completeness ratio

is higher than a threshold.

• An altered clustering that is interpretable with a

small decision tree, while the Jaccard index com-

puted between this clustering and the initial one is

higher than a threshold.

To achieve this goal, the algorithm is conﬁgured

with two parameters: P (the population size, i.e. the

count of possible solutions) and M (the maximum

count of loops with best sequence stagnation). The

algorithm follows different steps. First of all, an ini-

tial list of P sequences is built, and each sequence

is deﬁned with a randomly chosen data preprocess-

ing operation (line 2). Then, while the current best

solution does not stagnate (regarding M) and the list

of possible solutions contains different sequences (i.e.

leading to a cluster assignment decision tree with the

same size) (line 3), the following steps are repeated:

• The tournament strategy (BDack et al., 1991) is

used to select two parent sequences from the cur-

DATA2014-3rdInternationalConferenceonDataManagementTechnologiesandApplications

rent list of sequences (line 4). The selected se-

quences are randomly cut and merged into a new

child sequence (line 5).

• A data preprocessing operation is randomly se-

lected and added into the child sequence (line 6);

after that, the child sequence is evaluated and

added into the current list of sequences (line 7).

• In order to keep a constant count of sequences (P),

the algorithm removes the sequence that leads to

the largest decision tree (line 8).

• The current best solution is identiﬁed and a stag-

nation test checks if the best solution remains un-

changed over several loops (regarding M) (line 9).

At the end (line 11), the obtained solution is a

transformed dataset leading to a clustering that is eas-

ier to interpret.

3.5 Usage of the Algorithm

The evolutionary algorithm proposed in this paper

aims at transforming data to help cluster interpreta-

tion. This transformation is controlled by two pa-

rameters, the minimal Jaccard index and the mini-

mal data completeness ratio, in order to obtain both

a dataset and a clustering that are close to the origi-

nal ones. Letting the user tweak these parameters can

be useful to analyze data following the visual analyt-

ics paradigm (Keim et al., 2008). Hence, results can

be produced and reﬁned iteratively in order to support

cluster interpretation through visual inspection by the

end-user, trading accuracy for interpretability.

4 EXPERIMENTS

4.1 Prototype & Evaluation Protocol

A prototype has been developed in JAVA as a stan-

dalone tool. It is based on WEKA, a widely-used data

mining library (Witten et al., 2011) that provides al-

gorithms for decision tree induction, clustering and

preprocessing. The graphical representation of the de-

cision trees relies on the JUNG library (O’Madadhain

et al., 2003). The prototype provides a user interface

for results exploration (including statistics and data

visualizations) and user interaction e.g., to stop the

algorithm when a satisfactory solution is found.

We evaluated our approach on a selection of

datasets with various characteristics (record & feature

count, etc.) (Bache and Lichman, 2013; Torgo, 1998).

The datasets have been chosen with cluster interpreta-

tion in mind. For instance, several datasets have been

discarded because they lead to trivial clusterings such

as the spambase and magic04 datasets.

In order to check the impact of our method, we

have transformed these datasets with different values

for the minimal Jaccard index and the minimal data

completeness ratio. Then, we have compared the de-

cision trees explaining the clusterings of the origi-

nal vs. transformed datasets. In this work, we used

the popular k-means clustering algorithm (Gan et al.,

2007; Aggarwal and Reddy, 2013; Jain, 2010). Deci-

sion trees have been generated with J48 (Witten et al.,

2011), a widely used implementation of the C4.5 al-

gorithm (Quinlan, 1993). The pruning phase has been

enabled during the execution of the C4.5 algorithm, in

order to initially obtain small trees and check the ben-

eﬁts of our approach.

During the tests, the following data preprocessing

operations have been considered:

• supervised and unsupervised feature selection,

• constant features deletion,

• missing values imputation/marking/deletion,

• outliers marking/deletion,

• attribute transformation (numerics to nominals,

nominals to binaries, nominals to numerics, etc.).

Lastly, the evolutionary algorithm has been empir-

ically conﬁgured as follows: the population count (P)

has been set to 50, and the stagnation count (M) has

been set to 200.

4.2 Results

The results (Tables 1 & 2 & 3) show the decision

trees obtained in the following cases with k-means

(k=2, 3, 4). For the sake of clarity, the tables do not re-

port the sequences of preprocessing operations which

have been found:

• CASE 1: Clustering of the original dataset and

computation of the cluster assignment decision

tree.

• CASE 2: Execution of the evolutionary algorithm

(Algorithm 2) to obtain a modiﬁed dataset, clus-

tering of the modiﬁed dataset and computation of

the cluster assignment decision tree.

The results show that the evolutionary algorithm

(Algorithm 2) is able to ﬁnd data transformation se-

quences that meet our expectations: the modiﬁed data

(’CASE 2’) lead to clusters that are interpretable with

simpler decision trees than those obtained from the

original data (’CASE 1’).

In fact, the decision trees in ’CASE 2’ are smaller

because they represent altered and simpler clusterings

DecisionTreesandDataPreprocessingtoHelpClusteringInterpretation

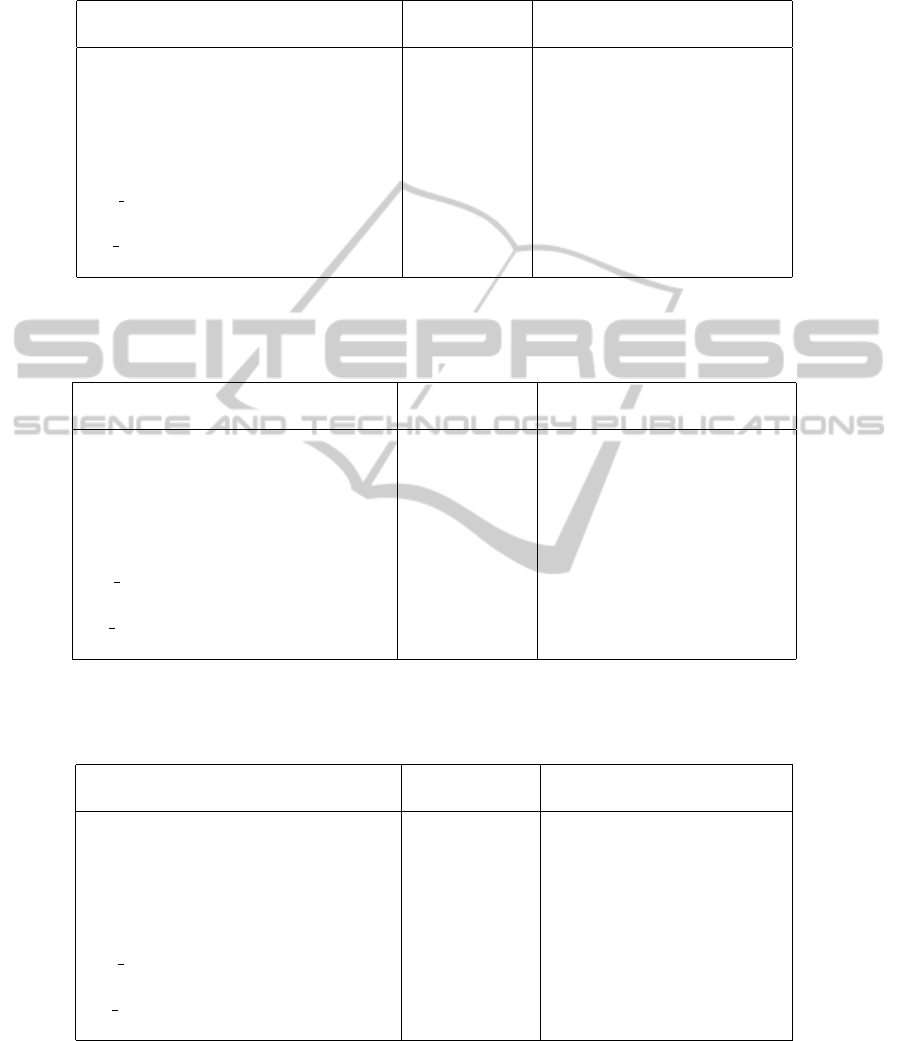
Table 1: Clustering interpretation after the computation of 2 clusters: for CASE 1 & 2, the decision tree sizes and the error

rates are reported. For CASE 2, the Jaccard index (JI) and the data completeness ratio (DCR) are reported to show the

clustering alteration and the intensity of the data transformation.

Dataset CASE 1 CASE 2

name #rows #features size error size error JI DCR

autos 205 26 27 5.36% 8 2.92% 0.50 42%

vehicle 846 18 19 0.71% 6 0.23% 0.81 40%

cmc 1,473 10 77 1.90% 3 0% 0.40 100%

winequality-red 1,599 12 47 0.69% 3 0% 0.48 100%

SkillCraft1 3,395 20 201 1.88% 3 0% 0.41 95%

sick 3,772 30 67 0.80% 3 0% 0.58 96%

cpu act 8,192 22 223 0.69% 3 0% 0.61 82%

pol 15,000 49 17 0% 3 0% 0.47 100%

cal housing 20,460 9 279 0.40% 3 0% 0.58 89%

adult 32,561 15 609 0.95% 3 0% 0.55 47%

Table 2: Clustering interpretation after the computation of 3 clusters: for CASE 1 & 2, the decision tree sizes and the error

rates are reported. For CASE 2, the Jaccard index (JI) and the data completeness ratio (DCR) are reported to show the

clustering alteration and the intensity of the data transformation.

Dataset CASE 1 CASE 2

name #rows #features size error size error JI DCR

autos 205 26 18 4.88% 9 5.36% 0.51 96%

vehicle 846 18 35 0.82% 5 0% 0.41 89%

cmc 1,473 10 23 0.34% 4 0% 0.52 60%

winequality-red 1,599 12 99 1.94% 7 0.12% 0.41 92%

SkillCraft1 3,395 20 233 2.44% 25 0.09% 0.50 90%

sick 3,772 30 51 0.40% 5 0.05% 0.52 97%

cpu act 8,192 22 49 0.16% 4 0% 0.40 91%

pol 15,000 49 143 0.40% 5 0% 0.45 100%

cal housing 20,460 9 241 0.30% 5 0.01% 0.54 89%

adult 32,561 15 1267 1.50% 25 0% 0.40 47%

Table 3: Clustering interpretation after the computation of 4 clusters: for CASE 1 & 2, the decision tree sizes and the error

rates are reported. For CASE 2, the Jaccard index (JI) and the data completeness ratio (DCR) are reported to show the

clustering alteration and the intensity of the data transformation.

Dataset CASE 1 CASE 2

name #rows #features size error size error JI DCR

autos 205 26 51 6.34% 17 6.82% 0.46 92%

vehicle 846 18 15 0.59% 5 0% 0.67 63%

cmc 1,473 10 44 1.08% 12 0.40% 0.41 90%

winequality-red 1,599 12 145 3.25% 33 0.43% 0.37 83%

SkillCraft1 3,395 20 339 2.95% 55 0.73% 0.36 90%

sick 3,772 30 47 0.45% 11 0% 0.80 70%

cpu act 8,192 22 179 0.44% 14 0% 0.38 91%

pol 15,000 49 293 0.60% 47 0.10% 0.47 53%

cal housing 20,460 9 391 0.53% 66 0.10% 0.40 66%

adult 32,561 15 1301 2.25% 104 0.02% 0.40 53%

built on data which have been modiﬁed by the evolu-

tionary algorithm.

Moreover, the produced decision trees often have

a good accuracy. This means that the cluster assign-

ment logic is well captured by the trees. For example,

the clustering of the unmodiﬁed adult dataset (k=2)

leads to a tree of size 609: as is, the tree is not in-

telligible. In comparison, the clustering of the trans-

DATA2014-3rdInternationalConferenceonDataManagementTechnologiesandApplications

formed dataset leads to a tree of size 3 (Table 1). By

computing (k=3) clusters for the same dataset, a sim-

pler tree is obtained (25 nodes instead of 1267). While

the interpretation of a tree of size 25 may not be triv-

ial, a tree with 1267 nodes is unreadable (Table 2).

Additionally, in most cases a light data transfor-

mation is needed to get simpler clustering interpre-

tation trees, as expressed by high data completeness

ratio ﬁgures. For example, if we examine the cmc

dataset, the discretization of the ﬁrst numeric attribute

sufﬁces to obtain a much smaller clustering decision

tree. In contrast, the adult dataset needs a more inten-

sive transformation to simplify the tree (numerizing

all nominal attributes).

Finally, a Jaccard index mostly close to 0.5 indi-

cates that signiﬁcant differences were found between

the initial and the resulting clusterings. Even if we

have observed that correct results can be obtained

while keeping a high Jaccard index, a powerful sim-

pliﬁcation implies a substantial clustering alteration.

The following sections show the transformation

sequences found by our algorithm for two use-cases.

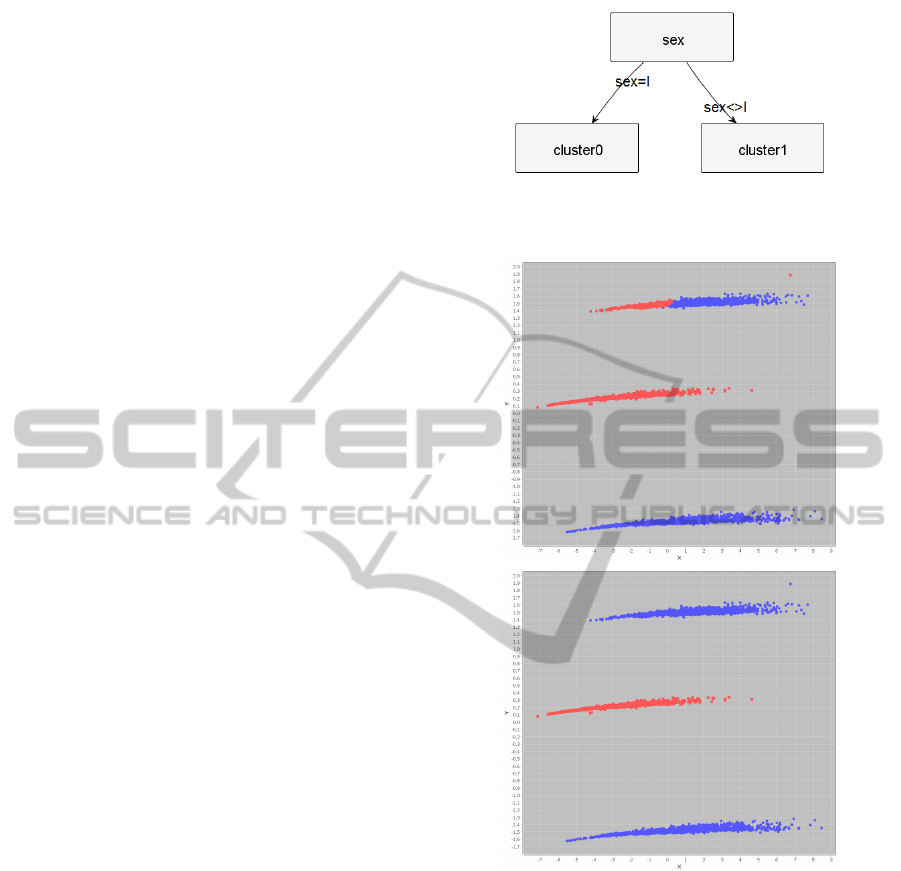
4.3 Example 1: the abalone Dataset

We have considered abalone, a widely-used

dataset (Bache and Lichman, 2013). It contains

the description of 4177 abalones having 8 attributes

including sex and length.

By simply using the k-means algorithm (k=2), we

obtain clusters that can be interpreted with a decision

tree of size 26. The error rate of the decision tree is

equal to 14.4% which is substantial.

Using our approach, we obtain a dataset for which

the clustering can be interpreted with a decision tree

of size 3 with an error rate close to 0% (Figure 2).

In fact, the evolutionary algorithm found that replac-

ing the nominal sex attribute by several binary at-

tributes allowed to obtain a more interpretable clus-

tering. Thus, the obtained tree is simple and shows

that the sex attribute allows to explain the cluster as-

signment (infants in the ﬁrst cluster, non-infants in the

other one). Lastly, the data completeness ratio is high

(88.9%) and the measured Jaccard index (0.78) shows

a strong agreement on cluster assignments.

To inspect the impact on the clusterings, well-

known projection methods can be used (Gan et al.,

2007). In Figure 3, PCA projections (i.e. Principal

Component Analysis) are used to show the clusters

before and after the preprocessing. According to these

projections, the clusters are different. But if we take a

look at the decision tree for cluster assignment (Fig-

ure 2), we can see that the interpretation is simpler.

Figure 2: Cluster assignment (k-means, k=2) for ’abalone’

after transformation by the evolutionary algorithm.

Figure 3: PCA projections for the abalone dataset for 2

clusters: the axes represent the two main principal compo-

nent. The ﬁrst one is colored with the original clusters (top),

the second one with the transformed clusters (bottom).

4.4 Example 2: the vehicle Dataset

As another example, we have considered the vehicle

dataset (Bache and Lichman, 2013). It contains the

description of 846 vehicles with 18 attributes.

By computing the k-means clustering (k=3), we

obtain a result that can be interpreted with a deci-

sion tree of size 35. With our approach, we obtain

a transformed dataset whose clustering can be inter-

preted with a decision tree of size 5 (Figure 4).

To obtain this transformed dataset, the following

DecisionTreesandDataPreprocessingtoHelpClusteringInterpretation

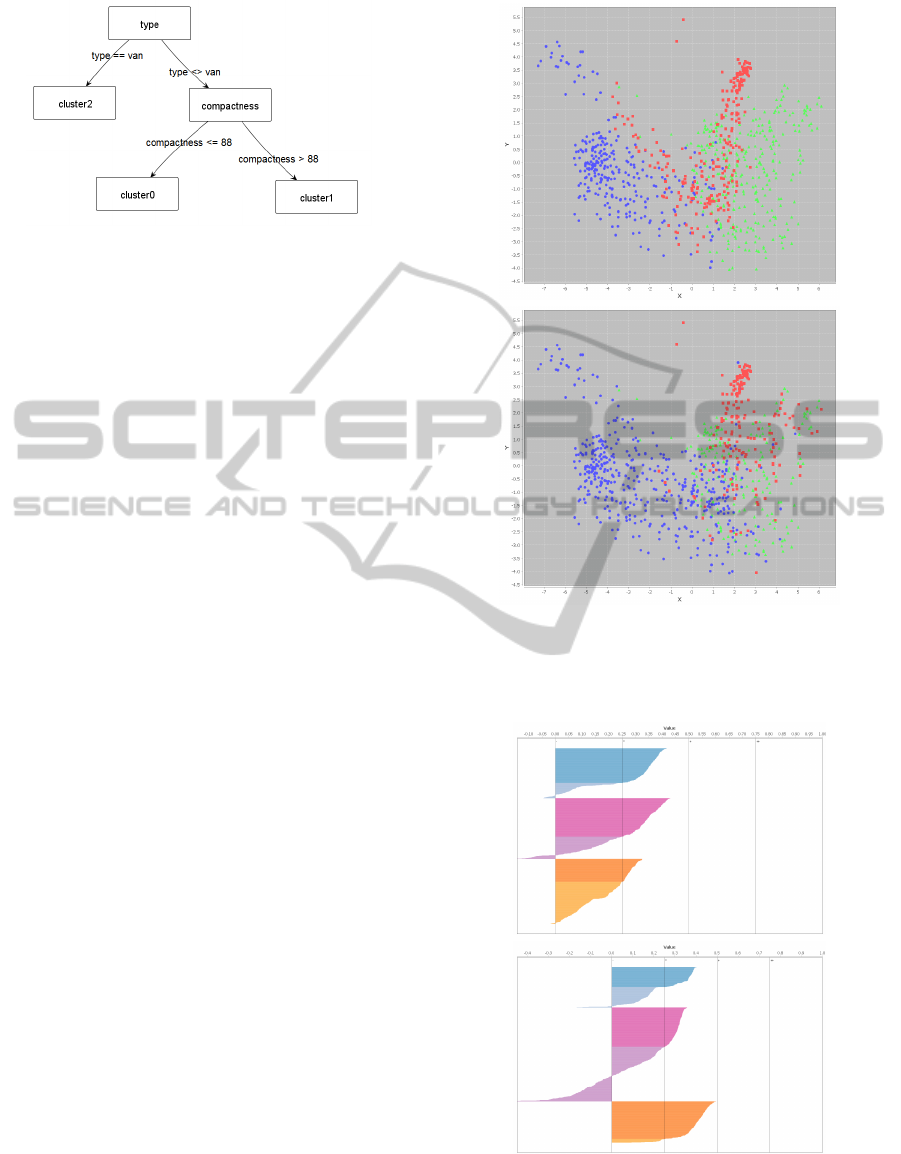
Figure 4: Cluster assignment (k-means, k=3) for ’vehicle’

after transformation with the evolutionary algorithm.

sequence of preprocessing operations has been dis-

covered by our evolutionary algorithm:

1. transformation of the ﬁrst nominal attribute to sev-

eral binaries attributes,

2. discretization of the ﬁrst numeric attribute,

3. marking of extreme values and outliers,

4. and ﬁnally transformation of the second nominal

attribute to several binaries attributes.

This sequence of operations causes some informa-

tion loss because the resulting data completeness ratio

is equal to 63%.

It causes clustering perturbation too: the Jaccard

Index is equal to 0.67 after the transformation. To

observe it, PCA projections have been computed be-

fore and after the preprocessing (Figure 5). In addi-

tion, Silhouette plots help to observe the quality of the

clustering (Rousseeuw, 1987): the results show that

the clusters are less correct (Figure 6).

As a result, the clustering is simpler to interpret,

but different than the one computed on the initial data.

Hence, our method allows the user to tune the trade-

off between simplicity of cluster interpretation and

agreement with the initial clustering. In other words,

it provides a way to build a simple clustering decision

tree that can be considered as an approximation of the

initial clustering decision tree. In addition, it provides

a modiﬁed dataset for which the cluster assignment is

correct, which may be subjected to a visual inspection

by the domain experts.

5 CONCLUSION

In this paper, we presented a method to help clustering

interpretation. It relies on an evolutionary algorithm

that transforms data so that the clustering of these

modiﬁed data can be explained with a simple cluster

assignment decision tree. The method has been de-

veloped in a Java prototype, and its effectiveness was

demonstrated and discussed on several datasets.

Figure 5: PCA projections for the vehicle dataset for 3 clus-

ters: the axes represent the two main principal components.

The ﬁrst one is colored with the original clusters (top), the

second one with the transformed clusters (bottom).

Figure 6: Silhouette plots for the vehicle dataset for 3 clus-

ters (with and without data transformation). The x axis rep-

resents the Silhouette value, the y axis represents the ele-

ments. Larger Silhouette values indicate a better clustering.

DATA2014-3rdInternationalConferenceonDataManagementTechnologiesandApplications

Typically, the method can be used to discover pat-

terns from raw business data and support result expla-

nation. In future work, we will conduct user exper-

iments to evaluate the usefulness of our method for

interpreting the insights found from data. In addition,

we will apply the method on large real-world environ-

mental datasets. To this end, we will improve our ap-

proach to support large datasets by using incremental

techniques for clustering and decision tree induction.

REFERENCES

Aggarwal, C. and Reddy, C. (2013). Data Clustering: Algo-

rithms and Applications. Chapman & Hall/CRC D.M.

and K.D. Series. Taylor & Francis.

Bache, K. and Lichman, M. (2013). UCI machine learning

repository.

Barlow, T. and Neville, P. (2001). Case study: Visualiza-

tion for decision tree analysis in data mining. In Pro-

ceedings of INFOVIS’01, INFOVIS ’01, pages 149–,

Washington, DC, USA. IEEE Computer Society.

BDack, T., Hoffmeister, F., and Schwefel, H. (1991). A

survey of evolution strategies.

Breiman, L., Friedman, J. H., Olshen, R. A., and Stone, C. J.

(1984). Classiﬁcation And Regression Trees. Chap-

man and Hall, New York.

Breslow, L. A. and Aha, D. W. (1997). Simplifying decision

trees: A survey. Knowl. Eng. Rev., 12(1):1–40.

Derrac, J., Cornelis, C., Garca, S., and Herrera, F. (2012).

Enhancing evolutionary instance selection algorithms

by means of fuzzy rough set based feature selection.

Information Sciences, 186(1):73 – 92.

Dolnicar, S. and Gr

un, B. (2008). Challenging factor–

cluster segmentation. Journal of Travel Research,

47(1):63–71.

Engels, R. and Theusinger, C. (1998). Using a data metric

for preprocessing advice for data mining applications.

In ECAI, pages 430–434.

Famili, A., Shen, W.-M., Weber, R., and Simoudis, E.

(1997). Data preprocessing and intelligent data anal-

ysis. Intelligent Data Analysis, 1(1–4):3 – 23.

Gan, G., Ma, C., and Wu, J. (2007). Data clustering - The-

ory, Algorithms and Applications. ASA-SIAM series

on statistics and applied probability. SIAM.

Herman, I., Delest, M., and Melancon, G. (1998). Tree vi-

sualisation and navigation clues for information visu-

alisation. Technical report, Amsterdam, Netherlands.

Jaccard, P. (1908). Nouvelles recherches sur la distribution

ﬂorale. Bulletin de la Soci

e vaudoise des sciences

naturelles. Impr. R

eunies.

Jain, A. K. (2010). Data clustering: 50 years beyond k-

means. Pattern Recognition Letters, 31(8):651–666.

Kandel, S., Heer, J., Plaisant, C., Kennedy, J., van Ham,

F., Riche, N. H., Weaver, C., Lee, B., Brodbeck, D.,

and Buono, P. (2011). Research directions in data

wrangling: Visualizations and transformations for us-

able and credible data. Information Visualization,

10(4):271–288.

Keim, D., Andrienko, G., Fekete, J.-D., G

org, C., Kohlham-

mer, J., and Melanc¸on, G. (2008). Information vi-

sualization. chapter Visual Analytics: Deﬁnition,

Process, and Challenges, pages 154–175. Springer-

Verlag, Berlin, Heidelberg.

Kotsiantis, S. (2013). Decision trees: a recent overview.

Artiﬁcial Intelligence Review, 39(4):261–283.

Murthy, S. K. (1998). Automatic construction of decision

trees from data: A multi-disciplinary survey. Data

Min. Knowl. Discov., 2(4):345–389.

O’Madadhain, J., Fisher, D., White, S., and Boey, Y. (2003).

The JUNG (Java Universal Network/Graph) frame-

work. Technical report, UCI-ICS.

Parisot, O., Bruneau, P., Didry, Y., and Tamisier, T. (2013).

User-driven data preprocessing for decision support.

In Luo, Y., editor, CDVE, volume 8091 of LNCS,

pages 81–84. Springer Berlin Heidelberg.

Quinlan, J. R. (1993). C4.5: Programs for Machine Learn-

ing. Morgan Kaufmann.

Qyu, M., Davis, S., and Ikem, F. (2004). Evaluation of

clustering techniques in data mining tools.

Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to

the interpretation and validation of cluster analysis.

Journal of computational and applied mathematics,

20:53–65.

Rudolph, G. (1996). Convergence of evolutionary algo-

rithms in general search spaces. In Proceedings of

IEEE Int. Conf. on Evolutionary Computation, pages

50–54.

Stiglic, G., Kocbek, S., Pernek, I., and Kokol, P. (2012).

Comprehensive decision tree models in bioinformat-

ics. PLoS ONE, 7(3):e33812.

Torgo, L. (1998). Regression datasets.

www.dcc.fc.up.pt/∼ltorgo/Regression/DataSets.html.

van den Elzen, S. and van Wijk, J. (2011). Baobabview:

Interactive construction and analysis of decision trees.

In Visual Analytics Science and Technology (VAST),

2011 IEEE Conference on, pages 151–160.

Wagner, S. and Wagner, D. (2007). Comparing clusterings:

an overview. Universit

at Karlsruhe.

Wang, S. and Wang, H. (2007). Mining data quality in com-

pleteness. In ICIQ, pages 295–300.

Witten, I. H., Frank, E., and Hall, M. A. (2011). Data

Mining: Practical Machine Learning Tools and Tech-

niques. Elsevier.

DecisionTreesandDataPreprocessingtoHelpClusteringInterpretation