
Quantification of Information Uncertainty
for the Purpose of Condition Monitoring
Pavel Ettler
1
and Kamil Dedecius
2
1
COMPUREG Plzeˇn, s.r.o., N´adraˇzn´ı 18, 306 34 Plzeˇn, Czech Republic
2
Institute of Information Theory and Automation, Academy of Sciences of the Czech Republic,
Pod Vod´arenskou vˇeˇz´ı 4, 182 08 Prague, Czech Republic
Keywords:
Condition Monitoring, Fault Detection and Diagnosis, Probabilistic Logic, Subjective Logic, Mathematical
Modelling.
Abstract:
Pervasive uncertainty of information which affects to some extent functionality of every control and infor-
mation system concerns naturally the condition monitoring systems as well. Uncertainty can practically be
disregarded when monitoring a single component, but it should be taken into account when compounding
extensive amount of information within a hierarchical diagnostic system. When using uncertain informa-
tion for expression of inner system’s relations, probabilistic and namely subjective logic may do a good turn.
However, the key problem remains how to quantify the uncertainty on the lowermost level of the monitoring
system. The paper introduces several solutions based on inspection of either a single measured signal or a
couple of correlated signals.
1 INTRODUCTION
Condition monitoring has become a rapidly devel-
oping area utilizing various approaches and meth-
ods. While at least some elements of diagnostics are
involved in almost every nowadays control system,
methodologies for systematic contexture of informa-
tion about condition of particular system components
into a comprehensive form are still evolving.
This paper aims to contribute to hierarchical as-
sessment of system conditions (in terms of reliabil-
ity), focusing on information uncertainty which may
propagate among different system parts. For exam-
ple, uncertainty included in a single spurious mea-
surement may eventually lead to inappropriate deci-
sions of the control system, yet the signal is not nec-
essarily completely wrong.
Most state of the art solutions taking the hierar-
chical character of the monitored system into account
are based on deterministic methods, often with heuris-
tic decision rules. Classical field of hierarchical sys-
tem monitoring are computer and telecommunication
networks. Here, the existing approaches allow scal-
able monitoring of the network and its devices, from
physical state variables (e.g. CPU temperature, fan
speeds, network load) up to the state of provided ser-
vices. Examples of such monitoring (and manage-
ment) systems are the celebrated open-source project
Nagios (Kocjan, 2008) or commercial products like
IBM Tivoli Network Manager or Nexus’ NexusME-
TER. Although their adoption to industrial systems
is nontrivial if possible, they are indeed a valuable
source of inspiration.
The initial results of the international consortium
focusing on the design of a hierarchical monitoring
system are presented. The underlying philosophy is to
avoid as much heuristics from the system as possible.
In this respect, the application of probabilistic and
particularly subjective logic (Jøsang, 2013) for prop-
agation of information about components condition is
a promising alternative to existing methods. One of
the key problems connected with this approach con-
sists in generating inputs for the condition monitoring
system based on subjective logic principles.
The paper introduces several ideas for its solution
and is organized as follows: The next section sketches
the system to be built, defines basic entities, formu-
lates the problem and introduces the calculus of sub-
jective logic. Subsequent section offers several means
how to quantify the uncertainty and is followed by a
section of examples and conclusions.
127
Ettler P. and Dedecius K..
Quantification of Information Uncertainty for the Purpose of Condition Monitoring.
DOI: 10.5220/0005006901270132
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 127-132
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
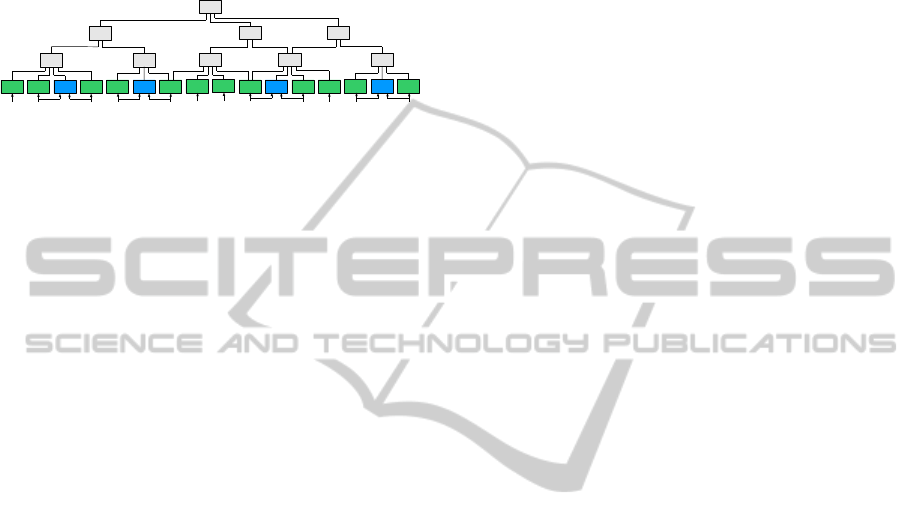
2 CONDITION MONITORING OF
A HIERARCHICAL SYSTEM
Ideas of the paper concern a hierarchical condition
monitoring system the example of which is depicted
in Figure 1.
Figure 1: Example of a hierarchical condition monitoring
system.
The green lowermost blocks monitor single com-
ponents of the control system such as measured sig-
nals, sensors, actuators which provide feedback about
their status and other hardware and possibly also soft-
ware units. The blue blocks guard proper relations be-
tween pairs of correlated signals. Information about
health of system components is then propagated up-
wards the pyramidal structure allowing to evaluate
condition or health of logical subsystems and – on the
uppermost level – of the entire system. The natural
question, answered below, is how to combine the in-
formation about the condition of these units together.
2.1 Compounding of Information
A particular lowermost block of the system in Fig-
ure 1 provides information about the condition of the
ith monitored element; say a measured signal, which
can be called signal health h
i
. In the simplest case, h
i
can be assumed a binary variable, which can take just
two values true|false or 0|1 where h
i
= 1 represents
perfect condition of the signal and h
i
= 0 means its
failure. Then, the health h
h
1
∧h
2
of a subsystem which
relies on simultaneous operation of two signals with
healths h
1
and h
2
can be expressed using the logical
conjunction (AND) operator as
h
h
1
∧h
2
= h
1
∧ h
2
,
where h
h
1
∧h
2
is evaluated according to respectivetruth
table. Existing binary logic operators allow to respect
various relations within the system. For instance, the
disjunction (OR) operator can reflect redundancy of
sensors; the modus ponendo ponens rule (MP opera-
tor) can reflect inner relations of a smart sensor, etc.
However, considering health as the binary variable
makes the system rather coarse from two points of
view:
– It may not be obvious how to rate health of a com-
ponent just 0 or 1;
– Malfunction of one component may result in eval-
uation of status of the whole system as ”in failure”
regardless the component’s importance and relia-
bility of basal information.
Employment of the probabilistic logic brings the
possibility to represent health as a probability, i.e. a
number p(h) ∈ [0, 1]. Then, the above mentioned ex-
ample of health of two simultaneously working sen-
sors will read
p(h
1
∧ h
2
) = p(h
1
)p(h
2
) .
A serious limitation of probabilistic logic, and bi-
nary logic alike, is expressed in (Jøsang, 2013): It is
impossible to express input arguments with degrees of
ignorance as e.g. reflected by the expression ”I don’t
know”. It led the authors to the search for probabilis-
tic distributions with limited support which can be
utilized for expression of that uncertainty (Dedecius
and Ettler, 2013). The winner - the beta distribution -
drove to the engagement of the subjective logic.
2.2 Subjective Logic
Subjective logic is a comprehensive methodology
for logic operations with uncertain propositions de-
scribed, e.g. in (Jøsang, 2013). Essentially, the theory
is based on definition of a probabilistic opinion about
a proposition h in the form of a quadruplet
ω
h
= (b, d, u, a) , (1)
where the components b, d, u, a are belief (amount
of h-supporting information), disbelief (the opposite),
uncertainty (amount of information insufficiency) and
base rate (prior information) respectively. It must
hold
b+ d + u = 1, b, d, u, a ∈ [0, 1] (2)
and the expected value can be expressed as
E
h
= b+ au . (3)
There exists a bijective mapping between an opin-
ion ω and the corresponding beta probability density
function for non-zero uncertainty u. For u = 0, the
function degenerates to the Dirac pdf concentrated at
a point between 0 and 1 given by the belief b.
Using the terms of the subjective logic, the above
mentioned example of health of two simultaneously
working sensors can be expressed as
ω
h
1
∧h
2
= ω
h
1
· ω
h
2
,
where operator of multiplication of opinions is de-
fined as the set of four equations for b, d, u and a
(Jøsang and McAnally, 2005). There exists a full set
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
128

of operators as counterparts to the binary logic and
probabilistic logic operators including deduction, ab-
duction, etc. Moreover, additional operators can be
used for various types of fusion and unfusion and for
the belief constraining.
The base rate a represent the prior amount of be-
lief and can be constructed from historical data or
based on experience of the user. A problem may arise
when evaluating the uncertainty u, as there do not ex-
ist plain rules for its determination. Several possibili-
ties how to quantify the uncertainty are offered in the
following text.
3 QUANTIFICATION OF
UNCERTAINTY
The potential of the subjective logic for the purpose
of condition monitoring is inspected in (Ettler and
Dedecius, 2014). The cited paper concerns propa-
gation of information in the grey part of the system
in Figure 1. The following sections present several
possibilities for quantification of uncertainty on the
lowermost level of the monitoring system represented
by green and blue blocks. Derived methods can be
considered independently or can be combined inside
a single block using various operators of the subjec-
tive logic calculus.
3.1 Respecting Signal Distribution
The basic possibility for quantification of u consists
in examination of the distribution of the signal x ∈ R
with respect to specified a priori specified boundaries.
Let X(t) be a moving window in time t
X(t) = [x(t), x(t − 1), . . . , x(t − m)] ,
where m is the window length and let suppose that
data in the window are approximately normally dis-
tributed (time indices are omitted in the following for
the sake of simplicity)
X ∼ N (µ
x
, σ
2
x
) ,
where µ
x
, σ
2
x
are mean and variance of window data
respectively. Then for x
+
being the positive limit for
x and using the three-sigma rule, the uncertainty u can
be expressed as
u =
(µ
x
+3σ)−x
+
3σ
if µ
x
∈ [x
+
, x
+
+ 3σ
x
)
x
+
−(µ
x
−3σ)
3σ
if µ
x
∈ [x
+
− 3σ
x
, x
+
)
0 otherwise
(4)
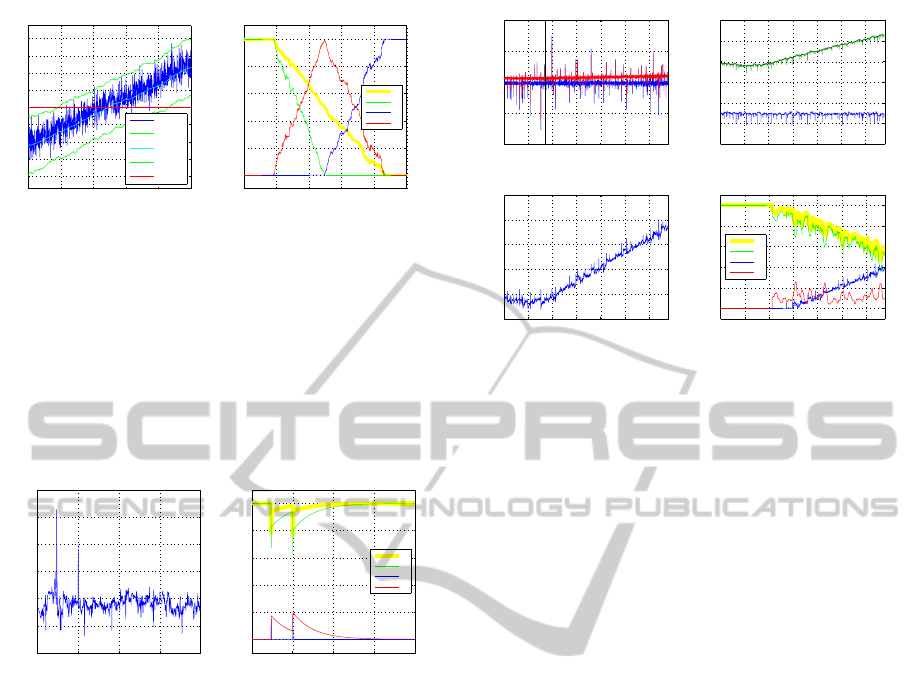
Figure 2 illustrates the situation belonging to the sec-
ond row of (4): the left plot depicts the location of the
data distribution with respect to the positive boundary
while the right plot shows the beta distribution cor-
responding to the opinion about health of the signal
x as for the signal range. Taking (2) into account,
b = 1− u and d = 0 for this case. The expected value
E
h
was evaluated according to (3) for a ”neutral” base
rate a = 0.5. The values of opinion components (1),
the corresponding beta distribution and the expected
value can be read in the right plot. Relations (4) can
be easily adapted for the case of the negative bound-
ary.
x+
0
µ−3σ +3σ
Signal range
Normal distribution of data
0 1
E
h
= 0.60
Beta distribution ∼ ω
h
b = 0.20
d = 0.00
u = 0.80
a = 0.50
Figure 2: Evaluation of uncertainty in the proximity of sig-
nal positive limit.
Obviously, there exist other possible approxima-
tions of the data distribution – for example (Pavelkov´a
and Jirsa, 2014) considers uniform distribution and
two-level boundaries while another approach (Jirsa
and Pavelkov´a, 2014) might employ Gaussian mix-
tures (K´arn´y et al., 2003) and more sophisticated dis-
tance measures.
3.2 Cautious Approach and Forgetting
There exist a class of signal failures which occur for
a very short time interval though often repeatedly. It
may be relatively straightforward to evaluate health h
and thus b and d in the moment of failure occurrence
but when it is over, the signal may seem to be perfect
again. In such a case caution is advisable which can
be expressed by increasing of the uncertainty in the
moment of recovery from the failure.
Let b(T) < 1, d(T) = 1 − b(T), u(T) = 0 be be-
lief, disbelief and uncertainty at time T in which a
failure is detected. Then, applying (3), it follows
E
h
(T) = b(T). In time T + 1 the failure is totally re-
covered and the signal might be evaluated as healthy.
However, the disbelief d(T) should be ”transformed”
into uncertainty so that the adjacent expected values
do not differ
E
h
(T + 1) ≈ E
h
(T) .
QuantificationofInformationUncertaintyforthePurposeofConditionMonitoring
129

Then, while respecting (2), considering time-invariant
base rate a and substituting b(T + 1) = 1 − u(T + 1),
the uncertainty immediately after the failure can be
expressed as
u(T + 1) = max
0, min
1,
b(T) − 1
a− 1
To allowrecovery of the health in finite time, some
kind of forgetting should be applied, either linear
u(t) = max(0, u(t − 1) + ∆
u
), ∆
u
∈ (−1, 0) ,
where ∆
u
is an empirically chosen decrement, or ex-
ponential
u(t) = λu(t − 1), λ ∈ (0, 1)
where λ is a forgetting factor. The latter option was
used for the treatment of outliers as depicted in Figure
4 in the section of examples.
3.3 Useful Results from Parameter
Estimation
Detection of unwanted deviations between two cor-
related signals can be based on modelling of relation
between the signals and the recursive estimation
of model parameters. Then, the properties and
deviations of parameter estimates or other results of
model identification can be transformed into opinion
about the health of the signals.
Let the relation of two signals x
1
(t) and x
2
(t) can
be approximately expressed by a linear model
x
2
(t) = P
′
(t)d(t) + e(t) ,
where
′
denotes transposition and d(t) is the data vec-
tor of the form
d(t) = [x
2
(t−1), . . . , x
2
(t−n
2
), x
1
(t), . . . , x
1
(t−n
1
), 1]
with n
1
≥ 0, n
2
≥ 0, P is the vector of unknown pa-
rameters and model noise is represented by the white
noise e(t) ∼ N (0, r) with unknown variance r.
The estimation in the RLS (Recursive Least
Squares) manner is based on the symmetric square
positive information (inverse covariance) matrix V(t)
of dimension 1 + dimd. Its recursive update reads
(Peterka, 1981)
V(t) = λV(t − 1) + [x
2
(t), d(t)]
′
[x
2
(t), d(t)] ,
where λ ∈ (0, 1) (close to 1) is the forgetting factor
allowing to track slowly varying parameters. Split-
ting the information matrix into blocks (time index is
omitted in the following for the sake of simplicity)
V =
V
x
2
v
′
v V ,
, V
x
2
∈ R
+
reveals the least-squares estimator of parameters,
ˆ
P = V
−1
v ,
where
ˆ
P stands for the parameter estimate.
For the real-time application, propagation of the
information matrix should be realized in the form of
matrix factorization of some kind, e.g. V
−1
= LDL
′
where L,D are lower triangular and diagonal matrices
respectively. This suppresses numerical difficulties
associated with potentially ill-conditioned matrices.
Unexpected changes of parameter estimates can
indicate oncoming failure of the signal. Parameter
estimates variance should then be transformed into
uncertainty u as illustrated in Figure 5 in Section 4.3.
Another possibility for quantification of uncer-
tainty consists in the use of associated estimation re-
sults such as the quality of the model expressed as the
estimate of variance r
ˆr =
V
x
2
− v
′
ˆ
P
κ
t
,
where κ
t
represents number of data samples in time t,
or the estimated parameter variance
ˆ
σ
2
p
i
= (V
−1
)
ii
where (V
−1
)
ii
denotes the element of V
−1
on posi-
tion (i, i).
A problem may occur with the unknown scale
of the above mentioned measures. Some form of
the logistic or another sigmoid function can be used
to transform the measure into the requested interval
u ∈ [0, 1].
4 EXAMPLES
4.1 Situation Near the Signal Boundary
The simulated example depicted in Figure 3 illustrates
the method from Section 3.1.
A noisy signal crosses its positive boundary x
+
= 10
in the left plot. Signal was constructed as the positive
trend
x(t) = 0.001· t + 5 + e(t)
where e(t) ∼ N (0, 1). The moving average regarded
as the mean µ
x
(t) of the signal was being evaluated
from the moving window of length m = 100 together
with the standard deviation σ
x
(t). The right plot
shows three components of the opinion ω
h
(t) about
signal health and its expected value E
h
(t). Neutral
base rate a = 0.5 was considered as time-invariant. It
can be seen that the highest point of u coincides with
the moment in which the moving average crosses the
boundary x
+
.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
130
0 200 400 600 800 1000
2
4
6
8
10
12
14
16
18
Signal range
Sample number
Noisy signal
x
µ
x
+3σ
x
µ
x
µ
x
−3σ
x
x
+
0 200 400 600 800 1000
0
0.2
0.4
0.6
0.8
1
Probability
Sample number
Progress of expected value E
h
based on opinion ω
h
E
b
d
u
Figure 3: Progress of ω
h
and E
h
for the simulated noisy
signal crossing its positive limit.
4.2 Influence of Outliers
Figure 4 illustrates the situation when outliers were
detected in the real measured signal. The example
comes from the metal-processing industry: the signal
in the left plot represents thickness deviation of the
metal strip entering a rolling mill.
0 200 400 600 800
−10
−5
0
5
10
15
20
Sample number
h
1
[µm]
Deviation of input thickness
200 400 600 800
0
0.2
0.4
0.6
0.8
1
Probability
Sample number
Progress of E
h
and ω
h
influenced by outliers
E
b
d
u
Figure 4: The real signal with outliers and progress of re-
lated ω
h
and E
h
.
Two positive outliers which were probably caused
by a dirt on the strip surface influenced expected value
E
h
of the signal health in the right plot. It can be
seen howthe disbelief which was increased in the mo-
ment of failure was transformed into uncertainty af-
terwards. Exponential forgetting enabled gradual re-
covery of health.
Similar method can be used when the FFT (Fast
Fourier Transform) analysis detects sudden peak cor-
responding to the momentary periodic disturbance.
Again, incurred uncertainty can be gradually dimin-
ished by the exponential forgetting.
4.3 Comparison of Parameter Estimates
Left plot in Figure 5 showstwo correlated real signals:
slide-valve position of the hydraulic servo valve and
its control signal. The servo valve controls flow of
oil into hydraulic actuator of a rolling mill. Peaks on
the signal correspond to wanted jerking of the servo
valve causing slight positional changes of the actuator
during rolling.
0.5 1 1.5 2 2.5 3
x 10
4
−40
−20
0
20
40
Slide valve position (red) and its control (blue)
[%]
← beginning of false trend
0.5 1 1.5 2 2.5 3
x 10
4
−1
0
1
2
3
4
5
Parameter estimates
0.5 1 1.5 2 2.5 3
x 10
4
2
2.5
3
3.5
4
4.5
Sample number
Difference of parameter estimates
0.5 1 1.5 2 2.5 3
x 10
4
0
0.2
0.4
0.6
0.8
1
Probability
Sample number
Progress of E
h
and ω
h
influenced by false trend
E
b
d
u
Figure 5: Progress of ω
h
and E
h
for the couple of related
signals.
In normal situation, relation of both signals can be
expressed by the model
x
2
(t) = p
1
x
1
(t − 1) + p
2
+ e(t) ,
where x
1
(t) represents the control signal and x
2
(t) the
controlled variable. The parameters p
1
, p
2
should
be constant except for small variations caused by the
simplification imposed by the model. An artificial
trend added to one of the signals simulates a creep-
ing failure in the hydraulic circuit. Beginning of the
trend is depicted by the vertical line in the upper left
plot in Figure 5. The trend was catched by one of the
parameter estimates (upper right plot in the same fig-
ure) and the difference of parameters (lower left plot)
was transformed into decreased health in the lower
right plot. The three-sigma rule was used to quantify
uncertainty of information about the failure.
5 CONCLUSIONS
There were introduced several methods for quantifica-
tion of information uncertainty when evaluating con-
dition/health of a measured signal or a pair of sig-
nals. Such knowledge about particular components
of the inspected control system can help substantially
in evaluation of health of a whole system if particular
pieces of information are compounded by the means
of the subjective logic.
Examples taken for this paper belong to the re-
search being accomplished in the framework of the in-
ternational project aiming to develop a practical con-
dition monitoring system based on probabilistic treat-
ment of information. Algorithms and methods are be-
ing developed in the Matlab environment using its ex-
isting OOP (Object Oriented Programming) features
QuantificationofInformationUncertaintyforthePurposeofConditionMonitoring
131

(Ettler and Puchr, 2013). Development of the pro-
duction version of the system in the appropriate OOP
framework is in progress now. The system will be
tested in a selected metal processing plant.
ACKNOWLEDGEMENTS
The research project is supported by the grant M
ˇ
SMT
7D12004 (E!7262 ProDisMon).
REFERENCES
Dedecius, K. and Ettler, P. (2013). Overview of bounded
support distributions and methods for Bayesian treat-
ment of industrial data. In Proceedings of the 10th
International Conference on Informatics in Control,
Automation and Robotics (ICINCO 2013), pages 380–
387, Reykjav´ık, Iceland.
Ettler, P. and Dedecius, K. (2014). Probabilistic reasoning
in service of condition monitoring. In Proceedings of
the 11th International Conference on Condition Mon-
itoring and Machinery Failure Prevention Technolo-
gies CM2014/MFPT2014, Manchester, UK.
Ettler, P. and Puchr, I. (2013). Utilization of Matlab classes
to streamline experimental software. In Proceedings
of the International Conference Technical Computing
Prague (TCP 2013), Prague, Czech Republic.
Jirsa, L. and Pavelkov´a, L. (2014). Testing of sensor con-
dition using gaussian mixture model. In Proceedings
of the 11th International Conference on Informatics
in Control, Automation and Robotics (ICINCO 2014),
Vienna, Austria.
Jøsang, A. (2013). Subjective logic (draft). University of
Oslo. Available on-line at
http://folk.uio.no/josang/papers/subjective
logic.pdf/.
Jøsang, A. and McAnally, D. (2005). Multiplication and
comultiplication of beliefs. International Journal of
Approximate Reasoning, 38(1):19–51.
K´arn´y, M., B¨ohm, J., Guy, T. V., and Nedoma, P. (2003).
Mixture-based adaptive probabilistic control. Inter-
national Journal of adaptive control and signal pro-
cessing, 17(2):119–132.
Kocjan, W. (2008). Learning Nagios 3.0. Packt Publishing.
Pavelkov´a, L. and Jirsa, L. (2014). Evaluation of sen-
sor signal health using model with uniform noise.
In Proceedings of the 11th International Conference
on Informatics in Control, Automation and Robotics
(ICINCO 2014), Vienna, Austria.
Peterka, V. (1981). Bayesian Approach to System Identifica-
tion In P. Eykhoff (Ed.) Trends and Progress in System
Identification. Pergamon Press, Eindhoven, Nether-
lands.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
132
