
A Necessary Test for Fixed-Priority Real-Time Multiprocessor Systems
based on Lazy-adversary Simulation
Romulo Silva de Oliveira, Andreu Carminati and Renan Augusto Starke
Department of Automation and Systems, UFSC, Florianopolis, Brazil
Keywords:
Operating Systems, Real-Time Systems, Embedded Systems.
Abstract:
Many embedded systems have real-time requirements which are sometimes hard and must be guaranteed at
design time, although most embedded systems have soft deadlines in the sense that they can be missed without
any catastrophe being caused by that. Scheduling simulations can be used as a necessary but not sufficient
schedulability test that is useful for both hard and soft real-time systems. They help to assess the pessimism
of formal analysis applied to hard real-time systems and they can be used as test-case generators during the
design of soft real-time systems. In this paper, we present a new adversary simulator for multiprocessors
with global task queue and fixed-priority scheduling. We consider sporadic tasks with constrained deadlines
(D ≤ T ). An adversary simulator uses the non-determinism in the arrivals of sporadic tasks to stress the
system scheduler with valid arrival patterns. The simulator proposed in this paper applies a lazy approach that
delays the arrival of high-priority tasks in order to form gangs that will preclude the execution of a victim task.
We show that the new lazy-adversary simulator presented in this paper outperforms the previously existing
necessary schedulability tests.
1 INTRODUCTION
Many embedded systems interact directly with the
physical world and present real-time requirements.
In hard real-time systems, there may be catastrophic
consequences associated with missing a deadline.
Most embedded applications however are soft real-
time systems in the sense that they have timing re-
quirements but there is no catastrophic consequence
associated with missing a deadline.
Schedulability analysis is used to prove that a
hard real-time system will never miss a deadline. It
is based on sufficient tests that produce pessimistic
upper bounds on task response times. While many
schedulable task sets fail these sufficient but not nec-
essary tests, those that pass the test are guaranteed to
never miss a deadline. This kind of analysis is not
appropriate for soft real-time systems since it would
lead to over-designed systems and unnecessarily in-
creased costs.
Schedulability analysis is generally based on iden-
tifying the worst possible sequence of arrivals. Details
of different task models give rise to different possi-
bilities, with various scenarios. In the case of multi-
processors with a single global task queue, there are
several types of anomalies (Andersson and Jonsson,
2002) and that makes the determination of the worst
sequence of arrivals a combinatorial problem.
One difficulty in evaluating the efficacy of suffi-
cient schedulability tests is to distinguish the cause
when a task set fails the test. The task set may not be
schedulable, or it may actually be schedulable but the
test itself was too pessimistic. Necessary schedula-
bility tests are used to distinguish between these two
possibilities. A necessary but not sufficient schedula-
bility test is such that if a task set fails the test then
there is a non-zero probability of it missing dead-
lines, while nothing can be said when it passes the
test. Many papers use necessary tests when empiri-
cally evaluating new schedulability tests. Examples
can be found in (Bertogna et al., 2009), (Cirinei and
Baker, 2007), (Davis and Burns, 2011), (Bertogna and
Baruah, 2011), (Lee et al., 2011), (Burns et al., 2012),
and (Back et al., 2012).
The deadlines of soft real-time systems are usu-
ally not guaranteed at design time. Test cases are used
instead to assess the timing behaviour of the system.
The generation of appropriate test cases to stress the
system scheduling is not an easy task due to the com-
binatorial nature of the problem. In this context, a
necessary but not sufficient schedulability test is use-
ful since it can be seen as a test-case generator capable
321
Silva de Oliveira R., Carminati A. and Starke R..
A Necessary Test for Fixed-Priority Real-Time Multiprocessor Systems based on Lazy-adversary Simulation.
DOI: 10.5220/0005008903210329
In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),
pages 321-329
ISBN: 978-989-758-038-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

of generating stressing loads to the system scheduler.
Regarding multiprocessors, probably the most
used necessary test is the one described in (Baker and
Cirinei, 2006) for the feasibility of sets of sporadic
tasks executed on globally scheduled multiprocessor
systems. It is a feasibility test in the sense that if a task
set fails the test then it is not possible to guarantee its
deadlines regardless the scheduler used.
Another approach is to simulate the system and
to observe the simulated response times of each task.
One cannot guarantee that during the simulation it
will be observed the worst-case response time of each
task. But scheduling simulations can be used as a nec-
essary but not sufficient schedulability test since any
task set that misses a deadline shows that its dead-
lines are not guaranteed. It is impossible to simu-
late the entire space of possibilities even for systems
of moderate size. Any non-determinism must be re-
solved during simulation. For example, it is necessary
to define when sporadic tasks arrive, although with
a minimum time interval between arrivals. Classic
scheduling simulators simply generate as much load
as possible, as soon as possible, but that is not neces-
sarily the worst case for multiprocessors. An example
of the classic approach can be found in (Davis and
Burns, 2011).
In (de Oliveira et al., 2013), an adversary simula-
tor was used as a necessary but not sufficient schedu-
lability test. The adversary simulator generates a pat-
tern of arrivals that is valid, but that also increases the
response time of tasks, acting as an adversary to the
scheduler. The adversary simulator stresses the sys-
tem in such a way that it is a much tighter necessary
but not sufficient schedulability test than the classic
scheduling simulator. In (de Oliveira et al., 2013) it
was described an adversary simulator for multipro-
cessors with a single (global) task queue and FP (fixed
priority) scheduling. It applies a greedy approach that
works well with small systems, but that is not very
stringent as the number of tasks and processors in-
crease.
In this paper, we present a new adversary simu-
lator for multiprocessors with global task queue and
fixed-priority scheduling. We consider sporadic tasks
with constrained deadlines (D ≤ T ). This new simu-
lator applies a lazy approach that is much more effec-
tive for large systems than both the classic simulator
and the greedy-adversary simulator from (de Oliveira
et al., 2013). We compare the three simulators using
both deadline monotonic priority ordering (DMPO)
and deadline minus computation time monotonic pri-
ority ordering (DCMPO).
The remainder of this paper is organized as fol-
low. Section 2 lists the related work. The task model
is described in Section 3. In Section 4 we describe
three existing necessary but not sufficient schedula-
bility tests for sporadic-task sets running on multi-
processors. Section 5 describes a new lazy-adversary
simulator. Its performance is evaluated in Section 6.
Conclusions are presented in Section 7.
2 RELATED RESEARCH
In (Baker and Cirinei, 2007), Baker and Cirinei con-
sidered the schedulability of a set of sporadic hard-
deadline tasks on a multiprocessor. The test is based
on modelling the arrival and scheduling as a finite-
state system, and enumerating the reachable states.
The computational complexity of the test is too high
to be practical for most real systems.
In (Baker and Cirinei, 2006), it is described a
necessary test for the feasibility of sets of sporadic
tasks. It has pseudo-polynomial complexity and any
task set that fails this test is proved to be infeasible in
globally scheduled multiprocessor systems. This test
is based on concepts originally presented in (Fisher
et al., 2006). This is a feasibility test in the sense that
if a task set fails the test it is not possible to guaran-
tee its deadlines regardless the scheduling algorithm
used.
In (Samii et al., 2008), it is proposed a simulation-
based method for worst-case response time estima-
tion of distributed real-time systems. The simulator
chooses the execution times of the jobs by exploring
the space of execution times so that it maximizes the
response times. In order to guide the execution-time
space exploration, the authors developed optimiza-
tion strategies based on three meta-heuristics: Sim-
ulated Annealing, Tabu Search, and Genetic Algo-
rithms (GAs) (Reeves, 1993). The authors used the
GA-based approach to estimate the pessimism of two
response-time analysis approaches for distributed em-
bedded systems considering two automotive commu-
nication protocols: CAN and FlexRay. The parame-
ters of the heuristic were tuned experimentally.
In (G. Thaker and Price, 2004), it is used simula-
tion to estimate the pessimism in different schedula-
bility tests for end-to-end distributed periodic tasks.
They compared values observed in simulation with
values computed using multiple scheduling theory
techniques. Regarding the simulations, the only deci-
sion was the phase for the first release of each periodic
task in a system.
An early work on a similar problem was presented
in (Baruah et al., 1991), but it considers the upper
bound for the cumulative value obtained through the
on-line scheduling of soft real-time aperiodic tasks
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
322

running on uniprocessor and dual processors.
The concept of an adversary simulator was used
by (de Oliveira et al., 2012) to stress the system in
such a way that the simulation will generate tighter
lower bounds for the maximum response time. This
concept was applied to multiprocessors using global
scheduling and fixed priority. The adversary simu-
lator resolves any non-determinism against a victim
task, which results in a valid timeline with a high re-
sponse time for the victim task. The adversary al-
gorithm is specific to each scheduling solution. In
(de Oliveira et al., 2012), an adversary for global
fixed-priority scheduling was presented for two pri-
ority assignment policies: deadline minus compu-
tation time monotonic priority ordering (DCMPO)
and deadline monotonic priority ordering (DMPO). In
(de Oliveira et al., 2013), an adversary simulator for
global fixed-priority until zero-laxity scheduling was
also described.
In this paper we present a new adversary simulator
for fixed-priority multiprocessor systems that applies
a lazy approach and is more effective for large task
sets than those presented in (de Oliveira et al., 2012)
and (de Oliveira et al., 2013).
3 TASK MODEL
We assume a homogeneous multiprocessor system
comprising m identical processors. There is a static
set τ of n sporadic tasks {τ
1
,...,τ
n
}. Each task gives
rise to a potentially infinite sequence of jobs. Each
job of a task may arrive at any time once a minimum
inter-arrival time has elapsed since the arrival of the
previous job of the same task. Tasks are independent
and can not voluntarily suspend themselves.
Each task τ
i
is characterized by its relative dead-
line D
i
, worst-case execution time C
i
, and minimum
inter-arrival time or period T
i
. The utilization U
i
of
each task is given by C
i
/T
i
and we assume D
i
≤ T
i
.
The worst-case response time R
i
of task τ
i
is defined
as the longest time from a job of the task arriving to
its complete execution.
A global queue exists for all processors. Accord-
ing to global fixed priority pre-emptive scheduling
(FP), the jobs with the m highest priorities execute. As
a result of pre-emption and subsequent resumption, a
job may migrate from one processor to another. The
cost of pre-emption, migration, and the run-time op-
eration of the scheduler is assumed to be either negli-
gible, or subsumed into the worst-case execution time
of each task.
We will consider two popular priority assignment
policies for the fixed-priority global scheduling of
multiprocessors: deadline monotonic priority order-
ing (DMPO) and deadline minus computation time
monotonic priority ordering (DCMPO).
4 EXISTING NECESSARY BUT
NOT SUFFICIENT TESTS
In this section we briefly describe the three most
used necessary but not sufficient schedulability tests
for multiprocessor systems when fixed-priority global
scheduling is applied. These three tests will be com-
pared to the new test described in Section 5.
4.1 Feasibility Test
We use as baseline the necessary feasibility test de-
scribed in (Baker and Cirinei, 2006), which is often
used in empirical evaluations in order to eliminate
task sets that are certainly not schedulable. It uses
the concepts of processor demand bound function and
processor load.
The processor demand bound function h(t) cor-
responds to the maximum amount of task execution
that can be released in an interval [0,t) and also has to
complete in that interval.
h(t) =
n
∑
i=1
max(0,
t −D
i
T
i
+ 1)C
i
(1)
The processor load is the maximum value of the
processor demand bound divided by the length of the
time interval.
load(τ) = max
∀t
(
h(t)
t
) (2)
Baruah and Fisher observed in (Baruah and Fisher,
2005) that a task set cannot possibly be schedulable
according to any algorithm if the total execution that
is released in an interval and must also complete in
that interval exceeds the available processing capac-
ity. The processor load provides a simple necessary
condition for task set feasibility: load(τ) ≤ m, where
m is the number of processors.
In 2006, Baker and Cirinei (Baker and Cirinei,
2006) defined the modified processor load (load
∗
) as
the processor load including task execution that must
unavoidably take place within an interval [0,t), even
though the release time or deadline is not actually
within the interval. The necessary feasibility test be-
comes load
∗
(τ) ≤ m.
Baker and Cirinei showed that an upper bound on
the modified processor load
∗
can be found by consid-
ering a synchronous arrival sequence, with the modi-
fied processor load calculated from the modified pro-
cessor demand bound function for each task:
ANecessaryTestforFixed-PriorityReal-TimeMultiprocessorSystemsbasedonLazy-adversarySimulation
323

h
∗
(t) = h(t) +
n
∑
i=1
max(0,t −max(0,
t −D
i
T
i
+ 1)T
i
− D
i
+C
i
) (3)
4.2 Classic Scheduling Simulation
The task model based on sporadic tasks defines a min-
imum interval of time between two arrivals of the
same task, but there is no maximum interval. The first
arrival of each task is not defined. Also, the execution
time of each individual job can be any value smaller
than or equal to the worst-case execution time of the
respective task.
When simulation is used to evaluate the schedu-
lability of sporadic task sets running on multipro-
cessors, it is necessary to resolve issues of non-
determinism of the system, since it is impossible to
simulate the entire space of possibilities.
Most simulations in the literature employ a classic
heuristic to define the behaviour of the system. The
classic scheduling simulation assumes that the greater
the workload offered to the system, the higher the re-
sponse times. Thus, the simulator tries to increase the
workload as much as possible, as quickly as possible.
We will adopt the behavior described in (Davis and
Burns, 2011) as an example of the classic approach.
In (Davis and Burns, 2011) each simulation runs
for a time interval equal to ten times the longest pe-
riod of any task in the task set. Each simulation starts
with the synchronous release of the first job of each
task. Subsequent jobs are released as early as possi-
ble. That means that the minimum inter-arrival time
is always used. Each job requires its worst-case exe-
cution time. The simulation deems a task set schedu-
lable by a given algorithm if it did not find a deadline
miss during the time interval simulated, or any un-
avoidable deadline miss for any job that had execution
time remaining at the end of the interval.
4.3 The Greedy-Adversary Simulator
In the classic approach, given the possibility of a job
to arrive sooner or later, the simulator always opts for
having the job arriving as soon as possible. It makes
sense for uniprocessor but this heuristic does not al-
ways performs well on multiprocessors.
In the case of multiprocessors, the worst scenario
for a victim job J
v
is obtained when jobs with higher
priority than J
v
occupy all processors. Since task pri-
orities can not be manipulated by the simulator, the
only way to manage the execution order is to control
the arrivals. The goal of an adversary simulator is
not to maximize the processing demand from higher
priority tasks but to organize this demand so higher-
priority tasks hold all processors simultaneously for
as long as possible.
The adversary simulator designed for global
fixed-priority multiprocessor scheduling presented in
(de Oliveira et al., 2012) and (de Oliveira et al., 2013)
chooses a specific job from a specific task to be the
victim job. It manipulates non-determinisms in the
task model in an attempt to generate the worst pos-
sible case for the victim. The only source of non-
determinism explored is the arrival time of sporadic
tasks, since the execution time of each task is always
set to its worst-case execution time. Each task is tried
once as the victim.
Let τ
v
denote the victim task and J
v
the victim
job. HP(τ
v
) represents the set of tasks with a prior-
ity higher than or equal to the priority of τ
v
. The first
job of the victim task is the victim job and it is the
first job to arrive at t = 0. The adversary heuristic de-
scribed in (de Oliveira et al., 2013) is based on the
following ideas:
• The arrival of jobs associated with tasks in HP(τ
v
)
is postponed until the arrival of J
v
.
• The arrival of jobs associated with tasks in HP(τ
v
)
is postponed unless there are enough jobs from
HP(τ
v
) to prevent the execution of J
v
.
• Jobs from a task in HP(τ
v
) arrive as soon as pos-
sible, as long as this task is capable of generating
more jobs before the deadline of J
v
.
• When a task in HP(τ
v
) is such that it will be able
to generate only a single last job before the abso-
lute deadline of J
v
, this last job will arrive only
when this is necessary to prevent the execution of
J
v
. If there are more than one job that satisfies this
condition, they arrive in the descending order of
their execution times.
• Any arbitrary tie-break is against the victim task
whenever possible.
This adversary simulator is greedy in the sense
that as soon as there are enough tasks to prevent the
execution of the victim, all enabled tasks are imme-
diately released. It might not be the best approach.
For instance, by waiting a little longer, the adversary
simulator might release a larger number of tasks that
would keep all processors busy for a longer time in-
terval, creating a worse scenario for the victim task.
The exact arrival pattern that will lead to the worst-
case response time of the victim is unknown due to
the combinatorial nature of the problem.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
324

5 THE LAZY-ADVERSARY
SIMULATOR
In this section, we present a lazy-adversary simula-
tor that also manipulates non-determinisms in the task
model to generate the worst possible case for the vic-
tim task. The only source of non-determinism is again
the arrival time of sporadic tasks, since the execution
time of each task will always be its respective worst-
case execution time. This adversary simulator also
chooses a specific job from a specific task to be the
victim job.
The lazy-adversary simulator postpones the re-
lease of enabled tasks in order to form larger gangs
of tasks. A task gang is a set of tasks that have higher
priority than the victim task and execute simultane-
ously in order to occupy all processors and prevent
the victim job from executing. The collective release
of the tasks of the gang creates a busy interval where
task τ
v
cannot execute. It is important to notice that
the same task may appear more than once in the gang
when its period is smaller than the busy interval cre-
ated by the gang.
Let τ
v
and J
v
denote the victim task and the victim
job, respectively. HP(τ
v
) and LP(τ
v
) are the sets of
tasks with a priority respectively higher than or equal
to and lower than the priority of τ
v
. The first job of
the victim task is released at time t = 0 and this is the
victim job. D
v
is the relative deadline of τ
v
and also
the absolute deadline of J
v
since it arrives at t = 0.
The lazy-adversary simulator is based on the fol-
lowing ideas:
• The arrival of tasks from HP(τ
v
) is organized in
gangs.
• No task from HP(τ
v
) arrives until a gang is
formed.
• No gang is formed until the arrival of J
v
.
• A gang is formed by at least m tasks from HP(τ
v
)
that can release a job immediately.
• Even when m or more tasks from HP(τ
v
) can re-
lease a job immediately, the gang formation will
be postponed if the following is true: the time un-
til the next task from HP(τ
v
) completes its mini-
mum time interval between arrivals is less than the
remaining execution time of J
v
and it is also less
than the execution time of this task from HP(τ
v
).
• Once a gang is formed, tasks from this gang arrive
only when this is necessary to prevent the imme-
diate execution of J
v
.
• Tasks of the gang arrive in the descending order
of their execution times.
• More tasks from HP(τ
v
) can be included in the
gang while the gang is executing.
• When there are not enough tasks from HP(τ
v
)
to prevent the execution of J
v
then tasks from
HP(τ
v
) are no longer released until a new gang
can be formed.
• Any arbitrary tie-break is against the victim task
whenever possible. The most obvious example is
when two tasks have the same priority.
At each moment of the simulation, set
waitingTasks contains all tasks that still have to
wait for the minimum time interval between arrivals
before generating a new job. Set enabledTasks
contains all tasks capable of immediately generating
a new job, because it already satisfied the minimum
time interval between arrivals since its last arrival.
All tasks enter set enabledTasks at t = 0. Set
enabledTasks is kept sorted by decreasing execution
times.
At any moment, availableProcessors(J
v
) returns
how many processors are available for job J
v
. That
depends on the total number of processors and the
number of jobs released but not finished that have a
higher priority than J
v
. This value can be obtained
from the global ready queue. Also, e
v
represents the
amount of processing time still needed to finish J
v
.
At any time t, nextDelta represents the time in-
terval until the next task from set waitingTasks will
be capable of generating a new job and then be trans-
ferred to enabledTasks. nextComp represents the ex-
ecution time of that task. If waitingTasks is empty
then nextDelta = ∞ and nextComp = 0.
The lazy-adversary simulator alternates between
two states: waiting the formation of a new gang
(waitingGang is true) and releasing tasks from a
formed gang (waitingGang is f alse). The first gang
is formed at t = 0 and includes all tasks from HP(τ
v
).
Initially, waitingGang is set to f alse, since the
victim job has not arrived yet. The first time the vic-
tim job is about to execute, tasks from the first gang
begin to be released. When there are no more tasks
in set enabledTasks to preclude τ
v
from executing,
this gang is finished and waitingGang is set to true.
waitingGang is set to f alse again when a new gang is
formed.
The heuristic described is used by the adversary
simulator when it has to decide whether a task must
be released or not. This happens when a task becomes
capable of generating a new job (becomes enabled)
and when the victim job is about to receive a pro-
cessor. Algorithm 1 is used whenever a task τ
i
be-
comes enabled (job J
k
i
may arrive). Algorithm 2 is
used when job J
v
is about to receive a processor.
ANecessaryTestforFixed-PriorityReal-TimeMultiprocessorSystemsbasedonLazy-adversarySimulation
325

Algorithm 1 When τ
i
becomes enabled
if τ
i
= τ
v
and t = 0 then
{Victim job arrives at t=0}
J
v
from τ
v
arrives now
exit
end if
if τ
i
belongs to LP(τ
v
) then
{Jobs of lower priority than J
v
are just ignored}
exit
end if
{Task of higher priority than J
v
becomes enabled}
insert τ
i
into set enabledTasks
if waitingGang ∧ size(enabledTasks) ≥ m then
if nextDelta < e
v
∧ nextComp ≥ nextDelta then
{Wait a little longer before starting a gang}
exit
else
{Start a gang right away}
while availableProcessors(J
v
) > 0 do
extract τ
j
from set enabledTasks
J
k
j
from τ
j
arrives now
end while
set waitingGang to f alse
end if
end if
Algorithm 2 When J
v
is about to execute
if ¬waitingGang then
if size(enabledTasks) ≥ availableProcessors(J
v
) then
{Release the necessary jobs from enabledTasks}
while availableProcessors(J
v
) > 0 do
extract τ
j
from set enabledTasks
J
k
j
from τ
j
arrives now
end while
else
set waitingGang to true
end if
end if
In this paper we assume a task model where D
i
≤
T
i
. When the deadline does not have to be equal to
the respective task period it is not simple to determine
which task has the biggest chance of missing its dead-
line. In order to avoid having to choose a single vic-
tim task, each task is tried once as the victim. Once a
task misses its deadline, it is proved that the task set is
not schedulable. The algorithm of the lazy-adversary
simulator is very fast, so it is feasible to run the simu-
lator once for each task.
6 EVALUATION OF THE LAZY
ADVERSARY
In order to evaluate the lazy-adversary described in
Section 5, we implemented using the programming
language C all three simulators: the classic, the
greedy-adversary and the new lazy-adversary. The
scheduling of many task sets with different sys-
tem utilizations were simulated considering different
numbers of processors. This empirical experimenta-
tion attempts to compare how many systems are de-
clared schedulable by each simulator.
Since all three simulators are driven by heuristics,
they can only obtain a lower bound for the maximum
response time of each task. The main goal is to de-
termine which one is the more challenging, the one
that will be more effective as a necessary schedulabil-
ity test by generating the most demanding test cases.
We also implemented the necessary feasibility test de-
scribed in (Baker and Cirinei, 2006) as a baseline.
6.1 Simulation Conditions
In order to evaluate the proposed lazy-adversary sim-
ulator, we use here the same conditions described in
(Davis and Burns, 2011) as a representative example
of the conditions generally used in empirical investi-
gations of this kind.
Task utilization’s were generated using the UUni-
fast Discard algorithm (Davis and Burns, 2009), giv-
ing an unbiased distribution. It is based on the UU-
nifast algorithm of Bini and Buttazzo (Bini and But-
tazzo, 2005) adapted to generate task sets with total
utilization greater than one as it happens in multipro-
cessor systems. The minimum time interval between
arrivals were generated according to a log-uniform
distribution with a factor of 1000 difference between
the minimum and maximum values, from 1 ms to 1
second. The log-uniform distribution was used be-
cause it generates an equal number of tasks in each
time band (e.g. 1-10ms, 10-100ms, etc).
Constrained deadlines were assigned according to
a uniform random distribution, in the range [C
i
,T
i
].
Task execution times were set based on the utiliza-
tion and the minimum time interval between arrivals
selected: C
i
= U
i
× T
i
.
In each experiment, the task set utilization (x-axis
value) was varied from 0.025 to 0.975 times the num-
ber of processors. For each utilization value, 1000
valid task sets were generated and the schedulability
of those task sets determined using the classic and the
two adversary simulators. We also used the necessary
feasibility test described in (Baker and Cirinei, 2006)
as a baseline. We considered three system sizes: 20
tasks running on 4 processors, 80 tasks running on 16
processors and 160 tasks running on 32 processors.
For each system size and each utilization, we are in-
terested in the number of task sets that were approved
by each test. The best necessary test is that one that
approves the minimum number of task sets.
The lines in each graph give the total number of
task sets at each utilization level that was approved
by the respective algorithm. Scheduling is always
based on global FP. Two priority assignment policies
were studied. Deadline monotonic priority ordering
(DMPO) was used because it is the most used order-
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
326

ing when D ≤ T . Deadline minus computation time
monotonic priority ordering (DCMPO) was also used
because, according to simulation studies, it is more
effective than DMPO (Davis and Burns, 2009).
6.2 Simulation Results
Figure 1 shows the results for 160 tasks on 32 pro-
cessors when DMPO is used. We can see that the
new lazy-adversary simulator is a better necessary but
not sufficient test than the previously existing simula-
tors. All simulators are more effective than the nec-
essary feasibility test for multiprocessors. Figure 2
also clearly shows that the lazy-adversary simulator
is a better necessary test when deadline minus com-
putation time monotonic priority ordering (DCMPO)
is used to assign priorities to tasks.
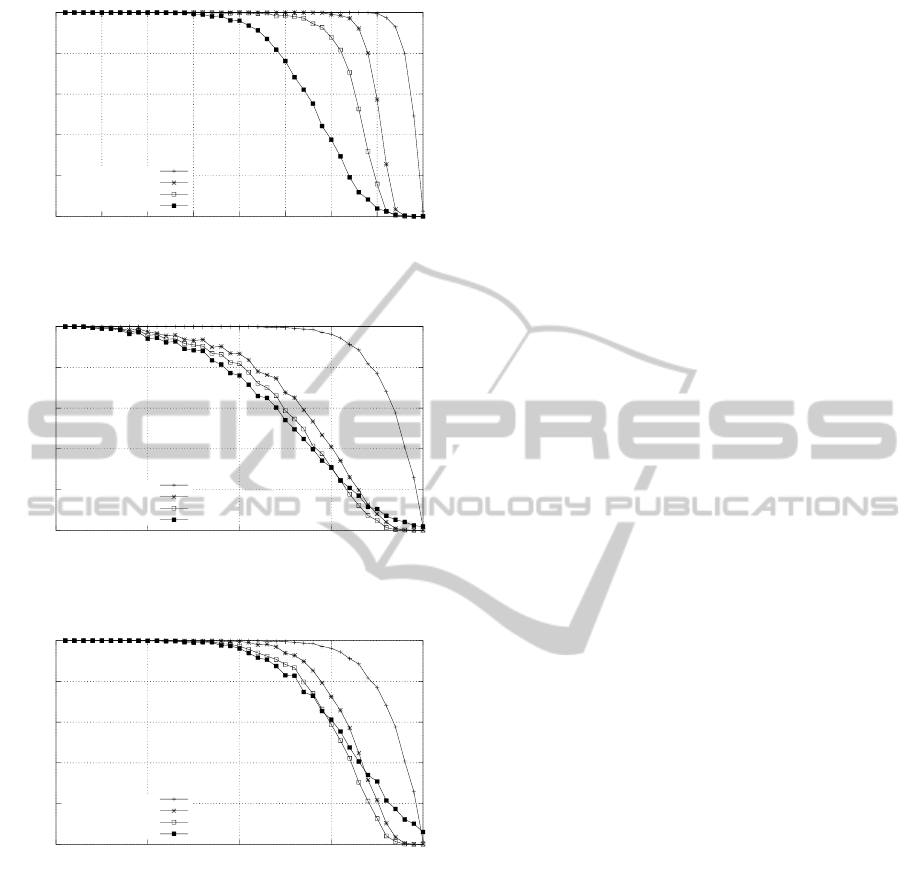
Figure 3 shows the results for 80 tasks on 16
processors scheduled by fixed priority assigned by
DMPO. Again the graph clearly shows that the lazy-
adversary simulator provides tighter lower bounds
for maximum response times than those generated
by both the classic and the greedy-adversary simula-
tors. Let’s consider for instance an utilization of 10.0.
The classic simulator finds 43% of all task sets to
be schedulable, the greedy-adversary finds 32% to be
schedulable, while the lazy-adversary simulator pro-
posed in this paper finds only 13% of all task sets to be
schedulable. Figure 4 shows similar results for when
DCMPO is used.
Figure 5 shows the results for 20 tasks on 4
processors and DMPO. The lazy-adversary and the
greedy-adversary simulators are better tests than the
classic simulator and the generic feasibility test. But
the lazy adversary is not always better than the greedy
adversary. While the lazy adversary is indeed bet-
ter for low utilization, the greedy adversary is still
better for small systems with high utilization. That
is because fewer tasks generates less opportunities to
form the big higher-priority task gangs that will pre-
vent the execution of the victim task. In this scenario
the greedy approach is capable of rejecting a larger
fraction of task sets. We arrive at these same con-
clusions when DCMPO is used instead of DMPO to
assign priorities to sets with 20 tasks (Figure 6).
All figures show that the necessary feasibility test
rejects a small number of task sets when compared to
any simulator. That can be explained in part because
the necessary feasibility test only reproves task sets
that can not be scheduled by any scheduler. While the
result of the necessary feasibility test is more general,
when one wants to consider a specific scheduling al-
gorithm, simulators are better necessary schedulabil-
ity tests, and the lazy-adversary simulator is the best
one. Regarding the classic simulator, it is a better test
than the feasibility test, but it is a worse test than both
greedy-adversary and lazy-adversary simulators.
All figures also show that DCMPO always en-
hances the schedulability of the system comparing
with DMPO. This is true regardless system size and
adversary simulator used.
0
200
400
600
800
1000
0 4 8 12 16 20 24 28 32
Schedulable Task Sets
Utilization
Feasibility
Classic
Greedy-Adversary
Lazy-Adversary
Figure 1: Global DMPO, 32 processors, 160 tasks
0
200
400
600
800
1000
0 4 8 12 16 20 24 28 32
Schedulable Task Sets
Utilization
Feasibility
Classic
Greedy-Adversary
Lazy-Adversary
Figure 2: Global DCMPO, 32 processors, 160 tasks
0
200
400
600
800
1000
0 2 4 6 8 10 12 14 16
Schedulable Task Sets
Utilization
Feasibility
Classic
Greedy-Adversary
Lazy-Adversary
Figure 3: Global DMPO, 16 processors, 80 tasks
The time to run a simulation depends on whether
a deadline is missed or not. When the system is
not schedulable the simulation is stopped once a task
misses its deadline so the execution time is very small.
It takes longer to run the simulators when all dead-
lines are met. The classic simulator makes a single
ANecessaryTestforFixed-PriorityReal-TimeMultiprocessorSystemsbasedonLazy-adversarySimulation
327
0
200
400
600
800
1000
0 2 4 6 8 10 12 14 16
Schedulable Task Sets
Utilization
Feasibility
Classic
Greedy-Adversary
Lazy-Adversary
Figure 4: Global DCMPO, 16 processors, 80 tasks
0
200
400
600
800
1000
0 1 2 3 4
Schedulable Task Sets
Utilization
Feasibility
Classic
Greedy-Adversary
Lazy-Adversary
Figure 5: Global DMPO, 4 processors, 20 tasks
0
200
400
600
800
1000
0 1 2 3 4
Schedulable Task Sets
Utilization
Feasibility
Classic
Greedy-Adversary
Lazy-Adversary
Figure 6: Global DCMPO, 4 processors, 20 tasks
run for each system, no matter how many tasks it has.
But it simulates the system for a total simulated time
equal to 10 times the longest period of the task set.
It takes around 0.5 seconds on an ordinary desktop
computer to make a classic simulation of a system of
80 tasks. Both adversary simulators must simulate the
system once for each task, but it simulates the system
only to the point in time equal to the deadline of the
first job of the victim task. Those features balance
each other and execution times of all simulators are
not very different. It takes around 0.1 seconds on an
ordinary desktop computer to make a lazy-adversary
simulation of a system of 80 tasks.
7 CONCLUSIONS
In hard real-time systems, formal analysis provides
guarantees for the deadlines, but these analyses are
extremely pessimistic for complex architectures. In
this case, a necessary but not sufficient test is used to
evaluate the pessimism level of the formal analysis,
by differentiating unschedulable task sets from task
sets that can not be proved to be neither schedulable
nor unschedulable.
In this paper we presented a new necessary but
not sufficient schedulability test for this task model.
The new test is based on the concept of an adversary
simulator, but it improves on previously existing algo-
rithms. Like any adversary simulator, it manipulates
the non determinism of load generation in order to
increase the response time of a victim task. But the
new simulator was called a lazy-adversary simulator
because it delays the arrival of high-priority tasks in
order to form gangs that will preclude the execution
of the victim task for a longer time.
Experiments showed that the new lazy-adversary
simulator is a much more effective necessary test
than the previously existing ones when considering
large systems (80 and 160 tasks). For small systems
(20 tasks), the new lazy-adversary simulator is bet-
ter than the classic simulator and the feasibility test,
but it is not better than the previously existing greedy-
adversary simulator for all system utilizations.
The complexity of real-time systems grows each
day, which makes the formal analysis necessary to
guarantee deadlines at design time every more pes-
simistic. We plan to expand the existing adversary
simulators to deal with more complex task models.
ACKNOWLEDGMENTS
The authors would like to thank CAPES and
CNPq for the partial funding of this research.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
328

REFERENCES
Andersson, B. and Jonsson, J. (2002). Preemptive multi-
processor scheduling anomalies. In Proceedings of
the 16th IEEE International Parallel and Distributed
Processing Symposium, pages 12–19.
Back, H., Chwa, H. S., and Shin, I. (2012). Schedu-
lability analysis and priority assignment for global
job-level fixed-priority multiprocessor scheduling. In
Real-Time and Embedded Technology and Applica-
tions Symposium (RTAS), 2012 IEEE 18th, pages 297
–306.
Baker, T. P. and Cirinei, M. (2006). A necessary and some-
times sufficient condition for the feasibility of sets of
sporadic hard-deadline tasks. In Real-Time Systems
Symposium, 2006. RTSS ’06. 27th IEEE International,
pages 178 –190.
Baker, T. P. and Cirinei, M. (2007). Brute-force determina-
tion of multiprocessor schedulability for sets of spo-
radic hard-deadline tasks. In Proceedings of the 11th
International Conference on Principles of Distributed
Systems, pages 62–75. Springer-Verlag.
Baruah, S. and Fisher, N. (2005). The partitioned multipro-
cessor scheduling of sporadic task systems. In Real-
Time Systems Symposium, 2005. RTSS 2005. 26th
IEEE International, pages 9 pp.–329.
Baruah, S., Koren, G., Mao, D., Mishra, B., Raghunathan,
A., Rosier, L., Shasha, D., and Wang, F. (1991). On
the competitiveness of on-line real-time task schedul-
ing. In Proceedings of the IEEE Real-Time Systems
Symposium, pages 106–115.
Bertogna, M. and Baruah, S. (2011). Tests for global edf
schedulability analysis. J. Syst. Archit., 57(5):487–
497.
Bertogna, M., Cirinei, M., and Lipari, G. (2009). Schedu-
lability analysis of global scheduling algorithms on
multiprocessor platforms. IEEE Transactions on Par-
allel and Distributed Systems, 20(4):553–566.
Bini, E. and Buttazzo, G. C. (2005). Measuring the per-
formance of schedulability tests. Real-Time Systems,
30:129–154.
Burns, A., Davis, R., Wang, P., and Zhang, F. (2012). Parti-
tioned edf scheduling for multiprocessors using a c=d
task splitting scheme. Real-Time Systems, 48:3–33.
Cirinei, M. and Baker, T. (2007). Edzl scheduling anal-
ysis. In Real-Time Systems, 2007. ECRTS ’07. 19th
Euromicro Conference on, pages 9 –18.
Davis, R. I. and Burns, A. (2009). Priority assignment for
global fixed priority pre-emptive scheduling in mul-
tiprocessor real-time systems. In Proceedings of the
30th IEEE Real-Time Systems Symposium, pages 398–
409.
Davis, R. I. and Burns, A. (2011). Fpzl schedulability anal-
ysis. In Proceedings of the 17th IEEE Real-Time and
Embedded Technology and Applications Symposium,
pages 245–256.
de Oliveira, R. S., Carminati, A., and Starke, R. A. (2012).
On using adversary simulators to obtain tight lower
bounds for response times. In Proceedings of the
27th Annual ACM Symposium on Applied Computing,
pages 1573–1579.
de Oliveira, R. S., Carminati, A., and Starke, R. A. (2013).
On using adversary simulators to evaluate global
fixed-priority and fpzl scheduling of multiprocessors.
Journal of Systems and Software, 86(2):403 – 411.
Fisher, N., Baker, T., and Baruah, S. (2006). Algorithms for
determining the demand-based load of a sporadic task
system. In Embedded and Real-Time Computing Sys-
tems and Applications, 2006. Proceedings. 12th IEEE
International Conference on, pages 135–146.
G. Thaker, P. Lardieri, D. K. and Price, M. (2004). Em-
pirical quantification of pessimism in state-of-the-art
scheduling theory techniques for periodic and spo-
radic dre tasks. In Proceedings of the 10th IEEE
Real-Time and Embedded Technology and Applica-
tions Symposium, pages 490–499.
Lee, J., Easwaran, A., Shin, I., and Lee, I. (2011). Zero-
laxity based real-time multiprocessor scheduling. J.
Syst. Softw., 84(12):2324–2333.
Reeves, C. R., editor (1993). Modern heuristic techniques
for combinatorial problems. John Wiley & Sons, Inc.,
New York, NY, USA.
Samii, S., Rafiliu, S., Eles, P., and Peng, Z. (2008). A sim-
ulation methodology for worst-case response time es-
timation of distributed real-time systems. In Proceed-
ings of Design, Automation and Test in Europe, pages
556–561.
ANecessaryTestforFixed-PriorityReal-TimeMultiprocessorSystemsbasedonLazy-adversarySimulation
329
