Describing Functionalities and Reactions of Cars and Managing

Their Feature Interactions

Ahmed Khoumsi

and Zohair Chentouf

Department of Electrical & Computer Engineering, University of Sherbrooke, Sherbrooke, Canada

Department of Computer Science, King Saud University, Riyadh, Saudi Arabia

Keywords: Automotive Reaction System (ARS), Car State and Functionality Descriptions, Car Reaction Description,

Conflicting Actions and Rules, Feature Interaction (FI) Detection and Resolution.

Abstract: We develop an Automotive Reaction System (ARS) framework to support cars by capabilities to react to

various situations. With ARS, the states and actions of a car are designed as objects of a high level object-

oriented language, called ARS-language. ARS permits also to design the reactions of a car to various

situations by an ARS-specification consisting of rules “conditionaction”. The ARS-objects and ARS-

specification are implemented in a car to provide her with capabilities to function and react online. ARS

permits also to model certain actions of a car at a high abstraction level by an ARS-model consisting of

rules “condition→operation”. With ARS, we are confronted to conflicts (or feature interactions) which

denote situations where an ARS-specification implies simultaneous executions of incompatible actions. We

propose an approach to detect and resolve feature interactions.

1 INTRODUCTION

We develop an Automotive Reaction System (ARS)

to support cars by capabilities to react in various

situations. We first develop a high level object-

oriented language, called ARS-language, which is

used to design the states and functionalities (or

actions) of a car by objects. Then, we propose a

formalism to design the car reactions by an ARS-

specification consisting of rules “condition 

action”. The ARS-objects and ARS-specification

must be implemented in a car to provide her with

capabilities to function and react online.

With ARS, we are confronted to feature

interactions (FI), where an ARS-specification

implies executions of incompatible actions.

FIs have been studied in telecommunications

since the 80s, for example in the workshops (Bouma

and Velthuijsen, 1994; Cheng and Ohta, 1995; Dini

et al., 1997; Kimbler and Bouma, 1998; Calder and

Magill, 2000; Amyot and Logrippo, 2003; Reiff-

Marganiec and Ryan, 2005; du Bousquet and

Richier, 2007; Nakamura and Reiff-Marganiec,

2009), where the term feature may denote not only a

basic service (or action), but also a complex service

which combines several simpler services.

For FI detection purpose, we model certain

actions at a high abstraction level by so-called ARS-

models consisting of rules “condition → operation”.

The proposed FI detection procedure is based on

combining adequately ARS models.

Here is the structure of the article: We first

present the three parts of ARS: the states and actions

of the car are designed as objects (Sect. 2), its

reactions are designed as rules “conditionaction”

(Sect. 3), and some actions are modeled as rules

“condition→operation” (Sect. 4). Then, we study

how an ARS-specification is translated into

executions of actions, while detecting (Sect. 5) and

resolving (Sect. 6) FIs. Sect. 7 is related to the

validation of our work. Sect. 8 presents related work

and highlights the relevance of using ARS. We

conclude in Sect. 9.

2 DESIGNING STATES AND

FUNCTIONALITIES OF A CAR

In the first part of ARS, a car is designed as an

object of a class car with attributes and methods.

The attributes specify the current state of the car,

while the methods specify actions of the car. Due to

space limit, we present a small portion of the class

147

Khoumsi A. and Chentouf Z..

Describing Functionalities and Reactions of Cars and Managing Their Feature Interactions.

DOI: 10.5220/0005010501470155

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 147-155

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

car, but which is sufficient to give a good idea of

how to model the states and actions of a car.

2.1 Portion of the Class Car

A portion of the class car is outlined below. To

distinguish types and classes from attributes and

objects, the latter are in italic while the former are in

bold. The class car uses methods and two categories

of attributes: basic and complex attributes.

Class car

// basic attributes of the class car

double time, maxSpeed, minSpeed

boolean downtown, dark, headlights

// complex attributes of the class car

position Position

speed Speed

school School //attribute describing school

neighborhood

stop Stop //attribute describing approached stops

obstacle Robs, Lobs, FLobs, FRobs //attrib. desc. obst.

// methods of the class car

void decel(), accel(), stop(), park(),

uTurn(), honk(), set(any, any)

not(any()), yes(any()), prepare(any())

boolean neighborhood(localizable), approach(localizable)

reach(localizable), close(moving)

void avoid(obstacle)

2.2 Basic Attributes in Car

Basic attributes have a basic type like double or

boolean, they are named in italic with the first letter

non-capitalized, while their types are named in bold.

The basic attributes given in the class car are: time,

the current time; maxSpeed, minSpeed, the current

max and min speed limits; downtown, it is true if the

car is in downtown; dark, it is true in darkness;

headlights, it is true if the headlights are on.

2.3 Complex Attributes in Car

a) Attributes: Position, Speed

Position: it is an object of a class position; it

specifies a circle that approximates a zone occupied

by the car. For example, the object Position has 3

basic attributes: longitude and latitude for the center

of the circle, and size for the radius of the circle.

Speed : it is an object of a class speed; it

specifies the linear speed vector of the car. For

example, Speed has two basic attributes: module and

angle, for the module and the direction of the speed.

b) Class localizable is a class with the attribute

Position.

c) Attribute School: The class school inherits

from localizable, and hence a school object has an

attribute Position of the class position. The attribute

School is a school object which is automatically

created when the car enters a school neighborhood,

and automatically destroyed when the car leaves the

school neighborhood. When School exists, its

attribute Position specifies a circular school

neighborhood.

d) Attribute Stop: The class stop inherits

from localizable. By inheritance, a stop object is a

localizable object, which hence has an attribute

Position of the class position. The attribute Stop is a

stop object which is created when the car starts

approaching a stop sign whose neighborhood

contains the car position, and destroyed when the car

starts going away from the stop sign. When Stop

exists, its attribute Position specifies a circular stop

neighborhood centered in the stop location.

e) Class moving: it inherits from the class

localizable and has the attribute Speed. Hence,

moving has at least two attributes: Position and

Speed, and the class car could be designed as a class

inheriting from moving.

f) Attributes of obstacle: The class obstacle

inherits from moving. By inheritance, an obstacle

object is a moving object which hence has attributes

Position and Speed of the classes position and

speed, resp. An obstacle object specifies an obstacle

which is close to the car and possibly moving.

obstacle has an attribute side which specifies in

which side of the car the obstacle is located. Four

obstacle attributes are defined in car (the complete

version of car contains other obstacle attributes):

Robs, Lobs, FRobs, FLobs, that correspond to

obstacles respectively at the right, left, front-right

and front-left of the car. Consider for example

FRobs, which is created when the car detects a close

obstacle at her front-right, and destroyed when the

obstacle is no more detected. When FRobs exists, its

attribute FRobs.Position specifies a circular

approximation of the zone occupied by the obstacle,

FRobs.Speed indicates the speed of the obstacle, and

FRobs.side that it is a front right obstacle.

2.4 Methods of Car

In Sect. 2.1, we represented methods of car by their

signature (name, types of parameters, and type of

returned value). any means any type. Let us present

each method.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

148

a) Methods without Parameter, which

return no Value

decel(), accel(), stop(), park(), uTurn() and

honk(): they execute the actions of accelerating,

decelerating, stopping, parking, making a U-turn and

honking, respectively.

b) Setter Methods, which return no Value

set(x, a): it is used with two parameters x and a

of the same type (which can be any type). For

example, set(maxSpeed, 50) sets the attribute

maxSpeed to 50.

c) Methods whose Parameter is a Method

Consider the expression p(m()), where m() is a

method used as parameter of a method p(). This

expression represents an action related to the action

of m(). Below are methods we have defined in car.

not(m()):

it sets the execution of m() to a forbidden

state. For

example, after the execution of not(park()),

park() is not executed when it is invoked.

yes(m()): it cancels the effect of not(m()), hence

m() is forbidden between not(m()) and yes(m()).

prepare(m()): it executes some actions in

preparation to the execution of a method. For

example, prepare(stop()) means to execute action(s)

in prevision to the execution of stop() that is

anticipated; example of action: decel().

d) Getter Methods whose Parameter is a

Localizable Object

neighborhood(N): it indicates if the car is in the

neighborhood of a localizable object N. For

example, neighborhood(School) returns true when

the car is in a school neighborhood.

approach(A):it indicates if the car is approaching

a localizable object A. Example, approach(Stop)

returns true if the car is approaching a stop sign.

reach(A): it indicate if the car has reached a

localizable object A. For example, reach(Stop)

returns true if the car has reached a stop sign which

it was approaching.

e) Methods whose Parameter is a moving

Object

close(M): it indicates if the car is too close to a

moving object M. For example, close(Lobs) returns

true if there is a close obstacle at the left of the car.

avoid(O): it executes the procedure to avoid an

obstacle specified as O.

2.5 The Environment of the Car in the

Class Car

The class car has attributes which contain

information about entities in the environment (e.g.

darkness, speed limits) or about relationships

involving the car (e.g. schools, obstacles).

3 DESIGNING CAR REACTIONS

Sect. 2 showed how to describe the states and

functionalities of a car in her environment by using

objects. Let us present the 2

part of ARS, called

ARS-specification, which consists of a set of rules in

the form “condition  action” meaning that action

must be taken whenever condition is satisfied. The

conditions and actions of rules describing a car are

constructed from attributes and methods of the

objects describing the car and its environment of the

part. condition is a passive boolean expression,

where by passive we mean that the expression does

not modify any attribute. condition may be

expressed by using attributes, methods and common

mathematical operators (e.g., logical, arithmetical).

action is a method call m(x) where m is a method

and x consists of none, one or more arguments. m(x)

and m(y) are considered as two distinct actions when

x and y have not the same value. In the following

examples of rules, all attributes and methods belong

to an object Car of the class car. For conciseness,

we omit to precede them by “Car.”.

Example 3.1. “downtown set(maxSpeed, 50)”

and “downtown set(minSpeed, 30)”. The car speed

in downtown must be ≥30 and ≤50 km/h.

Example3.2. “neighborhood(School)

(time

[7;19])  set(maxSpeed, 30)” and

“neighborhood(School)

(time [7; 19]) 

set(minSpeed, 15)”. The car speed must be

≥15 and

≤30km/h in a school

neighborhood from 7am to 7pm

Example 3.3. “dark  set(headlights, true)”.

The car must set on her lights when it is dark.

Example 3.4. “(Speed.module>maxSpeed) 

decel()”. The car must decelerate when her speed is

> a max speed limit.

Example 3.5. (Speed.module<minSpeed) 

accel()”. The car must accelerate when her speed is

< a min speed limit.

Example 3.6. “close(FRobs)  avoid(FRobs)”.

The car must avoid a close obstacle in her front right

Example 3.7.

“approach(Stop)prepare(stop())”. The car must

prepare to stop when it is approaching a stop sign.

DescribingFunctionalitiesandReactionsofCarsandManagingTheirFeatureInteractions

149

Example 3.8. “approach(Stop) reached(Stop)

stop()”. The car must stop when it reaches a stop

sign it was approaching.

4 MODELING ACTIVE ACTIONS

Let us model each active action of an ARS-

specification at a high abstraction level by an ARS-

model which consists of one or several rules

“condition→operation”. The rules of the 2

and 3

parts of ARS are distinguished by a bold  and a

thin → respectively. Let us define the rules of the 3

part by stressing their differences with the rules of

the 2

part:

part: in a rule “condaction” of the ARS-

specification (Sect. 3), action is a method call. This

rule means that action should be executed whenever

cond (modeling a situation) evaluates to true.

part: The ARS-model of each active action a

contains rules “cond→operation”, where operation

is a basic operation applied to some attribute. This

rule means that operation is executed when the

action a is applied under condition cond.

“true→operation” means that operation is executed

whenever the action a is applied.

The basic operations we have considered are:

Set(x, v) which sets an attribute x to a value v, Inc(x)

and Dec(x) which increases and decreases an

attribute x respectively. Let us propose some hints

which should help the designer in the development

of an ARS-model for each active action. The

principle of “cond → operation” is to model the

influence of an active action on an attribute x.

Therefore, the first step should be to determine for

each action a, the set Attributes(a) of attributes that

are modified by a. This first step can be realized by

modeling the first part of ARS (Sect. 2) by UML

diagrams from which the sets Attributes(a) can be

derived. Then, for each active action a and attribute

x in Attributes(a), the objective must be to construct

one or more rules “cond→oper” where oper is a

basic modification of x performed by a. The idea is

to construct rules modeling our comprehension of

how a can modify x. For brevity, we will say

operation instead of basic operation.

Example 4.1: accel() increases the attribute

Speed.module. Therefore,

the ARS-model of accel()

contains the rule

“true→Inc(Speed.module)“.

Example

4.2: Consider the attribute Speed.angle

and the method avoid(FRobs) which avoids by the

left a front right obstacle. Since the car avoids the

obstacle by turning anticlockwise (its angle

increases),

the ARS-model of avoid(FRobs) contains

the rule

“true→ Inc(Speed.angle)”. Assuming that

obstacle avoidance requires a speed in an interval [ν,

μ], the ARS-model of avoid(FRobs) contains also

the rules “Speed.module<ν→ Inc(Speed.module)“

and “Speed.module>μ→Dec(Speed.module)“.

Example 4.3: The method stop() sets the attribute

Speed.module to 0. Therefore, the ARS-model of

stop() contains the rule “true→Set(Speed.module,0)”

5 FI DETECTION

5.1 Definitions and Notations

Enabled/Disabled: rule is said enabled when its

condition evaluates to true. Otherwise, it is said

disabled. An action or operation is said enabled

(resp. disabled) when it is the action or operation of

an enabled (resp. disabled) rule.

(In)compatible: Two actions or operations are

said incompatible when they cannot be executed

simultaneously. Otherwise, they are compatible. For

example, accel() and decel() are incompatible. Two

rules are said (in)compatible when their actions or

operations are (in)compatible.

Conflicting: Two actions are said conflicting

when they are at the same time enabled and

incompatible.

ARSmodel(a) is the ARS-model of an active

action a.

priority(a) is a priority associated to an active

action a. It is necessary for FI resolution.

Enabled/disabled, (in)compatible and conflicting

characteristics can change with time passing.

5.2 Global ARS-procedure for

Detecting and Resolving FI and

Executing Actions

An ARS-specification specifies how a car must react

continuously by executing adequate actions. It is

hence necessary to develop a so called ARS-

procedure that realizes the specified reactions. What

makes this task difficult is the presence of

conflicting actions (or feature interactions, FI) which

must be handled by the ARS-procedure outlined

below. Its inputs are an ARS-specification, and an

ARS-model and a priority for each active action that

is used in the ARS-specification. The off-line part

executes (when the car is not in use) preliminary

steps for FI detection. The on-line part executes

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

150

(repetitively while the car in use) three tasks: 1) FI

detection that identifies pairs of conflicting actions;

2) FI resolution that elects which actions to execute

so that conflicts are avoided; 3) the elected actions

are applied. The FI detection is detailed in Sects. 5.4

(off-line) and 5.5 (online). The online FI resolution

is detailed in Sect. 6.

ARS-procedure

Inputs: - ARS-specification

- For each active action a :

ARSmodel(a), priority(a)

Off-line part: // executed when the car is not in use

| Off-line part of FI detection // sect. 5.4

On-line part: //executed repetitively while the car is in

use

| On-line part of FI detection // sect. 5.5

| On-line FI resolution // sect. 6

| Apply the elected actions

5.3 Incompatible Operations,

Conflicting Actions

The objective of FI detection is to identify

conflicting actions, i.e. actions which are enabled (in

a rule ) and incompatible. We have investigated

many incompatible situations of cars and we have

found that they all occur when several actions

modify the same attribute in a contradictory way.

Therefore, we consider that two actions are

incompatible when and only when they modify the

same attribute in a contradictory way. To

characterize formally conflicting actions, we first

need to characterize incompatible operations. Recall

the three basic operations on an attribute x: Set(x, v),

Inc(x) and Dec(x). Two operations op

and op

are

said incompatible if there exists an attribute x which

is modified by op

and op

in one of the following

cases, where v

is the current value of x:

a. op

and op

increases and decreases x, resp.,

b. op

and op

set x to values v

and v

s.t. v

≠v

c. op

sets x to a value v

≥ v

while op

decreases x,

d. op

sets x to a value v

≤ v

while op

increases x.

We say that two active actions a and b are

conflicting when they are enabled (in rules ) and

their ARS-models contain respectively rules

“cond

→op

” and “cond

→op

” such that the

operations op

and op

are both enabled and

incompatible. Intuitively, situations where a and b

are conflicting imply the simultaneous executions of

incompatible operations, and hence must be avoided.

Let us give examples of conflicts which are

constructed from Examples of Sections 3 and 4.

Example 5.1: From Examples 3.5 & 3.8, accel()

and stop() are simultaneously enabled when the

condition C1: “Speed.module<minSpeed

approach(Stop)

reach(Stop)” is true. From

Example

4.1, the ARS-model of accel() contains

“true→Inc(Speed.module)”. From Example 4.3, the

ARS-model of stop() contains

“true→ Set(Speed.module,0)”. In these rules, the

operations Inc(Speed.module) and

Set(Speed.module, 0) are enabled (by condition

“true”) and incompatible (above case d). Therefore,

the actions accel() and stop() are conflicting when

the above condition C1 evaluates to true. Intuitively,

the car decides at the same time to accelerate

(because its speed is lower than the minimum speed

limit) and to stop (because it reaches a stop sign).

Example 5.2: From Examples 3.6 and 3.8,

avoid(FRobs) and stop() are simultaneously

enabled

when the condition C2: “close(FRobs)

approach(Stop)

reach(Stop)” is true. From

Example 4.2, the ARS-model of avoid(FRobs)

contains the rule “Speed.module < ν →

Inc(Speed.module)“. From Example 4.3, the ARS-

model of stop() contains the rule

“true→

Set(Speed.module,0)”. In these rules, the operations

Inc(Speed.module) and Set(Speed.module,0) are

simultaneously enabled when Speed.module<ν and

incompatible

(above case d). Therefore, the actions

avoid(FRobs) and stop() are conflicting when C2

Speed.module<ν evaluates to true. Intuitively, the car

decides at the same time to keep a non-null speed (to

avoid a close obstacle) and to stop (because it

reaches a stop sign.

5.4 Off-line Part of FI Detection

We adopt an online approach where FI detection and

resolution are executed repetitively. We must

minimize as much as possible the duration of each

iteration so that it is always shorter than the car

reaction time. For this purpose, preliminary steps for

FI detection will be executed off-line, and we will

execute on-line only the FI detection part that cannot

be done off-line.

FI detection means identifying conflicting

actions, i.e. actions that are enabled and

incompatible. Recall that actions a and b are

conflicting if their ARS-models contain rules R

and

whose respective operations are incompatible and

simultaneously enabled. Since “enabledness” of

actions and operations cannot be determined off-

line, the off-line part of FI detection is conservative,

DescribingFunctionalitiesandReactionsofCarsandManagingTheirFeatureInteractions

151

i.e. it proceeds as if all actions and operations are

enabled. More precisely, the off-line part of FI

detection (outlined below) constructs for every pair

of active actions (a,b), a set ARSmodel(a,b)

containing every pair (R

) where R

and R

are

rules of ARSmodel(a) and ARSmodel(b) respectively,

whose operations are incompatible. The intuition is

that a and b are potentially conflicting if

ARSmodel(a,b) is not empty. The procedure

constructs the following graph:

Graph

of potentially conflicting actions (GPCA)

Its nodes correspond to active actions and its edges

link every pair of nodes a and b for which

ARSmodel(a, b)≠Ø. An edge between a and b is

denoted (a, b, ARSmodel(a, b)) and called edge (a,

b) labeled by ARSmodel(a, b).

Example 5.3: In Example 5.2, we have seen that

actions a=avoid(FRobs) and b=Car.stop() have their

AR-models containing respectively the incompatible

rules R

= “Speed.module < ν → Inc(Speed.module)”

and R

= “true → Set(Speed.module,0)”. In the off-

line part of FI detection, the pair (R

, R

) is inserted

in ARSmodel(a,b) and GPCA receives the nodes a

and b and the edge (a, b) labeled by ARSmodel(a,b).

Intuitively, a and b are potentially conflicting, and

ARSmodel(a,b) will be used online to determine

when a and b are effectively conflicting.

Off-line part of FI detection

Inputs: Every active action a and its set ARSmodel(a)

Result: Graph of potentially conflicting actions (GPCA)

Procedure:

| // Let N be set of nodes and E be the set of edges of

GPCA

| Initialize N and E to empty

| for each pair (a, b) of active actions:

| | // Compute ARSmodel(a, b)

| | Initialize ARSmodel(a, b) to empty

| | for each R

ARSmodel(a) and R

ARSmodel(b)

| | | if R

and R

are incompatible

| | | | insert the pair (R

, R

) in ARSmodel(a, b)

| | if ARSmodel(a, b) )≠Ø:

| | | if a is not in N: insert a in N

| | | if b is not in N: insert b in N

| | | insert (a, b, ARSmodel(a, b)) in E

5.5 Online Part of FI Detection

The online part of FI detection (outlined below)

consists in determining which of the potentially

conflicting actions are effectively conflicting. More

precisely, for every pair (a, b) of actions which are

potentially conflicting (i.e. ARSmodel(a, b))≠Ø, a

and b are effectively conflicting when they are

enabled and ARSmodel(a, b) contains a pair (R

) of enabled rules. The procedure constructs the

following graph:

Graph of conflicting actions (GCA): It is a

restriction of GPCA in the sense that it is obtained

from GPCA by removing edges linking actions

which are not effectively conflicting. An edge

between a and b is denoted by (a, b).

On-line part of FI detection

Input: GPCA

Result: Graph of conflicting actions (GCA)

Procedure:

| Initialize GCA to GPCA

| for each edge (a, b, ARSmodel(a, b)) of GCA

| | if a or b are disabled or

| | | ARSmodel(a, b) has no pair of enabled rules:

| | | Remove the edge

| Redefine every edge (a,b, ARSmodel(a,b)) as (a,b)

Example 5.4: In Example 5.3, the resulting

GPCA of the off-line part of FI detection, contains

the edge (a, b) labeled by ARSmodel(a,b), for a=

avoid(FRobs) and b= stop() which are potentially

conflicting. In the on-line part of FI detection, the

obtained GCA contains the edge (a, b) when a and b

are effectively conflicting, i.e. close(FRobs)

approach(Stop)

reach(Stop)

Speed.module<ν

(from Example 5.2).

6 ONLINE FI RESOLUTION

FI resolution targets to find a solution to each pair of

conflicting actions a and b represented by an edge

(a, b) in GCA. Our FI resolution consists of a local

treatment followed by a global treatment.

6.1 Local Treatment of FI Resolution

We assume that a priority() function is given which

assigns priorities to active actions. Two sets are

used: the set of Elected Actions (EA) and the set of

Blocked Actions (BA). For each edge (a, b) in GCA,

the local treatment inserts the most and least priority

actions in EA and BA respectively. A problem arises

when EA∩BA≠Ø. Consider for example two edges

(a, b) and (a, c) of GCA, i.e. a is conflicting with b

and c. Assume that priority(b) < priority(a) <

priority(c). In (a, b), a

is elected and b is blocked. In

(a, c), c is elected and a is blocked.

Hence,

EA={a,c}, BA={a,b}, EA∩BA={a}≠Ø. A question

arises: should a be elected or blocked? If we apply a

conservative decision by blocking a, then both a and

b are blocked, while the reason why b has been

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

152

blocked is for executing a. Hence since a is blocked,

it is useless to block b. To recapitulate, the

conservative solution is to block a and b, while a

more permissive solution is to block only a.

Example 6.1. Consider the three actions

a=stop(), b=accel() and c=avoid(FRobs). We have

seen in Examples 5.1 and 5.2 that a is conflicting

with b and c under some conditions. Assume that

those conditions are satisfied, and

priority(b)<priority(a)<priority(c). With the local

treatment, we obtain EA={a, c} and BA={a, b}. If

we apply the conservative decision, only c is elected,

i.e. avoid the obstacle. A more permissive decision

is to elect a and c, i.e. avoid the obstacle and

accelerate. Considering that obstacle avoidance

requires Speed,module

[ν,μ]), this scenario holds if

it is possible to accelerate without exceeding the

speed μ.

6.2 Global Treatment of FI Resolution

After the local treatment to the example of Section

6.1, we obtained EA={a, c} and BA={a, b}, hence a

is at the same time elected and blocked. The global

treatment solves this problem as follows. It starts by

applying a conservative decision by blocking a.

Formally, a is removed from EA, i.e. EA = EA\BA

(the symbol \ means set subtraction). We obtain

EA={c} and BA = {a, b}. The conservative decision

needs improvement. Indeed, since a is blocked there

is no reason to block b (it was blocked to avoid the

conflict between a and b). Hence the global

treatment transfers b from BA to EA. Formally,

EA={c}

{b}={b, c} and BA={a, b}\{b}={a}.

Hence, only a is blocked.

In the general case, we transfer iteratively to EA

every action of BA which is not conflicting with any

action of the current EA. The transfer is ordered

from the most priority to the least priority actions. A

formal definition of such a transfer is given in the

last part of the resolution procedure of Sect. 6.3

(Global treatment: transfer actions from BA to EA).

CA(a) is the set of actions which are currently

conflicting with action a (i.e. which are linked to a

in GCA); X is the set of actions of BA which do not

conflict with any action of EA; maxPriority(X) is

the action in X

with the greatest priority.

6.3 FI Resolution Procedure

The FI resolution procedure given below

implements the treatments presented in Sections 6.1

and 6.2. Note the last line of the procedure which

consists in electing all actions which do not conflict

with any other action.

Online FI resolution

Inputs: - Graphs of conflicting actions (GCA)

- Priorities of active ctions

Result: - The set of elected actions (EA)

- The set of blocked actions (BA)

Procedure

| // Local treatment: Compute EA and BA

| Initialize EA and BA to empty

| for each edge (a, b) in GCA

| | if priority(a) > priority(b)

| | | insert a in EA and insert b in BA

| | else: insert b in EA and insert a in BA

| //Conservative decision: remove from EA the actions

of BA

| EA = EA \ BA

| // Global treatment: transfer actions from BA to EA

| Compute X = {a BA | CA(a ) EA = }

| while X ≠

| | EA = EA U maxPriority(X)

| | BA = BA \ maxPriority(X)

| | X = {a BA | CA(a) EA = }

| Insert in EA all actions which are not in GCA

7 VALIDATION

We have validated our approach in many scenarios.

For example, as inputs for the ARS-procedure of

Section 5.2, we have used: an ARS-specification that

includes the rules given in Examples 3.*; ARS-

models that include the rules given in Examples 4.*;

and the following priorities:

priority(decel()) > priority(accel()),

priority(stop()) > priority(accel()),

priority(avoid(FLobs)) > priority(avoid(FRobs)),

priority(avoid(Lobs)) > priority(avoid(FRobs)).

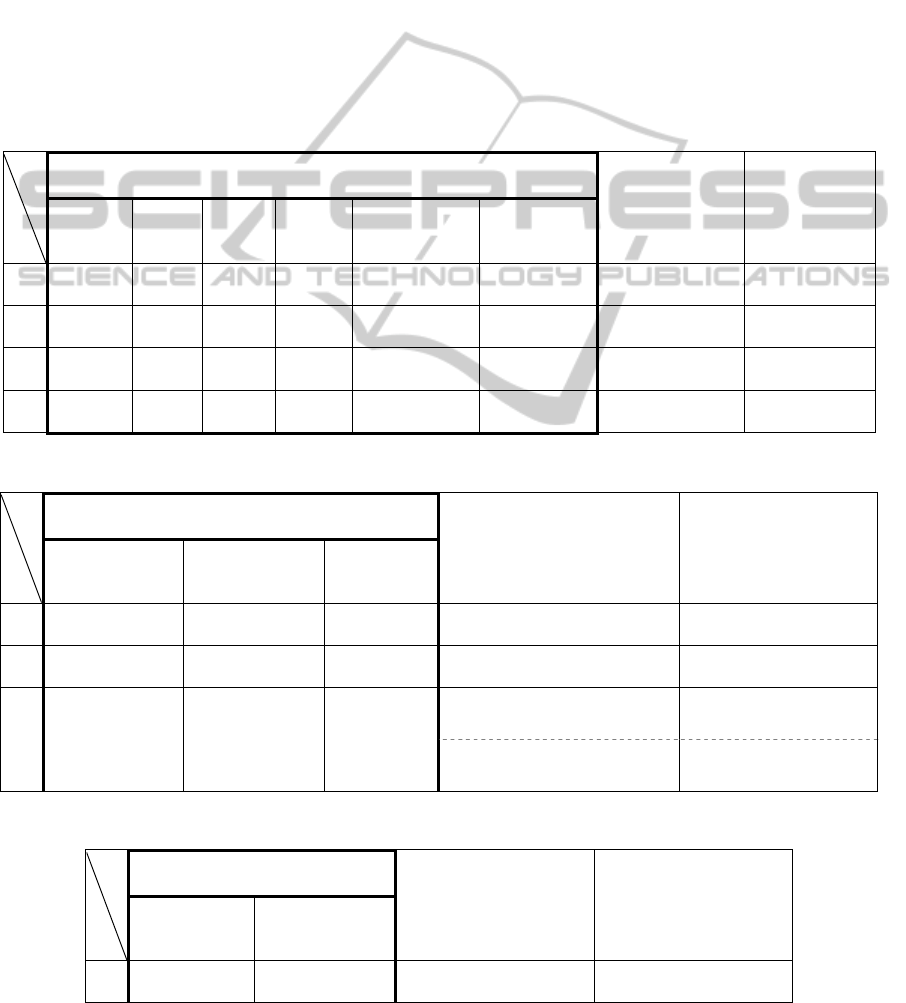
Table 1 represents examples of FI detection and

resolution involving the actions stop(), accel() and

decel(). Four configurations are considered which

are specified by the values (or intervals of values)

taken by the six parameters represented in columns

1-6 of Table 1: the current speed of the car, the car is

at downtown, the time is between 7am and 7pm, the

car is in a school neighborhood, the car is

approaching a stop, and the car has reached a stop.

All parameters are boolean, except the current speed

of the car which is of type double. Actually, each

configuration (corresponding to a row of the table)

abstracts several specific configurations, since it

specifies the values of only a part of the parameters.

In Table 1 (and also in Tables 2 and 3), the last two

columns represent the conflicting actions (FI

detection) and the elected action (FI resolution),

DescribingFunctionalitiesandReactionsofCarsandManagingTheirFeatureInteractions

153

respectively. In the “conflicting actions” column, are

indicated the column numbers (1 to 6) that have

implied each indicated action. For example,

accelerate (1,2) means that acceleration is implied

by each of the two facts: the car speed is < 30 (1),

and the car is in downtown (2).

Table 2 represents examples of FI detection and

resolution involving actions avoid(FRobs)

avoid(FLobs) and avoid(Lobs). Three configurations

are considered which are specified by the values

taken by the three boolean parameters represented in

columns 1-3 of Table 2: the car has a close obstacle

at her front right, the car has an a close obstacle at

her front left, and the car has a close obstacle in her

left side. Note the configuration 3 which generates

two FIs, due to the fact that avoid(FRobs) is

conflicting with avoid(FLobs) and avoid(Lobs).

Table 3 represents an example of FI detection

and resolution involving obstacle avoidance and

stopping.

8 RELATED WORK AND OUR

CONTRIBUTION

The method proposed in (Metger, 2004) for

managing FIs is conservative since it does not

consider the operational behavior of features. To our

knowledge, (Juarez-Dominguez et al., 2008b;

Juarez-Dominguez et al., 2008a; Juarez-Dominguez,

2008) present the most advanced automotive

framework dealing with FI detection. Below are

points by which we distinguish ourselves from the

latter references:

1. With ARS, a car is designed in three parts (Sects.

2-4). The fact of using several parts meets the

requirements of modularity and problem

decomposition.

2. We consider not only basic but also complex

actions. For example, “accelerate” and

“decelerate” are simple, while “make a U-turn”

and “avoid an obstacle” are complex.

3. We model actions at a high abstraction level (by

ARS-models), which permits to avoid state space

explosion (due to complex actions) in FI

detection and resolution.

4. We have opted for an on-line approach to

manage FIs, instead of an off-line approach using

model-checking.

5. In addition to FI detection, we study also FI

resolution.

6. In the 1

part of ARS, the car is designed as an

object depending on the elements of the car, and

on the environment that influences the car

behavior. Hence, the car environment can be

accessed from a single object.

Moreover, ARS contains the following specific

mechanisms which make it irreplaceable by other

systems:

a) The 1

part of ARS uses objects (such as School,

Stop, FRobs) which are automatically created

and destroyed under specific conditions.

Therefore, ARS must have a mechanism for such

automatic creation and destruction.

b) The 1

part of ARS uses methods (such as

not(park()), yes(park()), prepare(stop()) that

have a method as parameter. Therefore, the

compiler and code generator of ARS must have a

mechanism to such a type of methods.

9 CONCLUSIONS

We have developed a three-part Automotive

Reaction System (ARS) framework to provide cars

capabilities to react to various situations. Our

contributions and the relevance of ARS have been

highlighted in the previous Section 8. Here are some

points we plan to study for future work: the use of

variable priorities for FI resolution; FIs involving

more than two actions; FIs involving actions of

several cars; the scalability of our framework.

REFERENCES

Bouma, L. and Velthuijsen, H., editors (1994). 2

Int.

Workshop on Feature Interactions in Telecom. Syst.

(FIW), Amsterdam. IOS Press.

Cheng, K. and Ohta, T., editors (1995). 3

Int. Workshop

on Feature Interactions in Telecom. Syst. (FIW),

Kyoto. IOS Press.

Dini, P., Boutaba, R., and L, L., editors (1997). 4

Int.

Workshop on Feature Interactions in Telecom. Syst.

(FIW), Montreal. IOS Press.

Kimbler, K. and Bouma, L., editors (1998). 5

Int.

Workshop on Feature Interactions in Telecom. and

Soft. Syst. (FIW), Lund (Sweden). IOS Press.

Calder, M. and Magill, E. H., editors (2000). 6

Int.Workshop on Feature Interactions in Telecom. and

Soft. Syst. (FIW), Glasgow (Scotland, UK). IOS Press.

Amyot, D. and Logrippo, L., editors (2003). 7

Int.

Workshop on Feature Interactions in Telecom. and

Soft. Syst. (FIW), Ottawa (Canada). IOS Press.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

154

Reiff-Marganiec, S. and Ryan, M. D, editors (2005). 8

Int. Workshop on Feature Interactions in Telecom.

and Soft. Syst. (FIW), Leicester (UK). IOS Press.

du Bousquet, L. and Richier, J.-L., editors (2007). 9

Int.

Workshop on Feature Interactions in Software and

Comm. Systems (FIW). IOS Press.

Nakamura, M. and Reiff-Marganiec, S., editors (2009).

Int. Workshop on Feature Interactions in Soft. and

Comm. Syst. (FIW). IOS Press.

Juarez-Dominguez, A. (2008). FIs Detection in the

Automotive Domain. In IEEE/ACM Int. Conf. on

Automated Soft. Eng. (ASE).

Juarez-Dominguez, A., Day, N., and Fanson, R. (2008a).

Translating Models of Automotive Features in

MATLAB’s Stateflow to SMV to Detect FIs. In Int.

Systems Safety Conf. (ISSC).

Juarez-Dominguez, A., Day, N. and Joyce, J. (2008b).

Modeling Feature Interactions in the Automotive

Domain. In Int. Workshop on Models in Soft. Eng.

(MiSE).

Metger, A. (2004). Feature interactions in embedded

control systems. Computer Networks, 45(5):625–644.

APPENDIX

Table 1: First illustrative example of Section 7.

Parameters

FI detection:

Conflicting

actions

FI resolution:

Executed

action

Current

speed

Down-

town

time ∊

[7;19]

Near a

school

Approaching

a stop

Has reached

a stop

< 30 true true

accelerate (1,2)

stop (6)

stop

< 15 true True true

accelerate (1,3,4)

stop (6)

stop

< 30 true True

accelerate (1,2)

decelerate (5)

decelerate

< 15 true True True

accelerate (1,3,4)

decelerate (5)

decelerate

Table 2: Second illustrative example of Section 7.

Parameters

FI detection:

Conflicting actions

FI resolution:

Executed action(s)

Close to front

right obstacle

Close to front

left obstacle

Close to left

obstacle

true true false

avoid front right obs. (1)

avoid front left obs. (2)

avoid front left obs.

true false true

avoid front right obs. (1)

avoid left obs. (3)

avoid left obs.

true true true

avoid front right obs. (1)

avoid front left obs. (2)

avoid front left obs.

avoid front right obs. (1)

avoid left obs. (3)

avoid left obs.

Table 3: Third illustrative example of Section 7.



Parameters

FI detection:

Conflicting actions

FI resolution:

Executed action

Close to an

obstacle

Has reached

a stop

1

true true

avoid obstacle (1)

stop (2)

stop

DescribingFunctionalitiesandReactionsofCarsandManagingTheirFeatureInteractions

155