CloudaSec: A Novel Public-key Based Framework to Handle Data

Sharing Security in Clouds

Nesrine Kaaniche, Maryline Laurent and Mohammed El Barbori

Institute Mines Telecom, Telecom-SudParis, Paris, France

Keywords:

Cloud Storage Systems, Data Security, Access Control, Algorithm Veriﬁcation.

Abstract:

Recent years have witnessed the trend of leveraging cloud-based services for large scale content storage,

processing, and distribution. Data security and privacy are among top concerns for the public cloud envi-

ronments. Towards these security challenges, we propose and implement CloudaSec framework for securely

sharing outsourced data via the public cloud. CloudaSec ensures the conﬁdentiality of content in the public

cloud environments with ﬂexible access control policies for subscribers and efﬁcient revocation mechanisms.

CloudaSec proposes several cryptographic tools for data owners, based on a novel content hash keying system,

by leveraging the Elliptic Curve Cryptography (ECC). The separation of subscription-based key management

and conﬁdentiality-oriented asymmetric encryption policies uniquely enables ﬂexible and scalable deploy-

ment of the solution as well as strong security for outsourced data in cloud servers. Through experimental

evaluation, we demonstrate the efﬁciency and scalability of CloudaSec, build upon OpenStack Swift testbed.

1 INTRODUCTION

Recently, the US International Data Corporation

(IDC) proclaims that the digital universe will grow

by a factor of 300, up to 40 trillion gigabytes of repli-

cated data by 2020 (Gantz and Reinsel, 2012). This

explosive growth of data continues to rise the demand

for new storage and network capacities, along with

an increasing need for more cost effective architec-

tures. As such, recent years have witnessed the trend

of leveraging cloud data storage, since it provides ef-

ﬁcient remote storage services in pay per use business

model.

However, these promising data storage services

have brought many challenging design issues, consid-

erably due to the loss of control on outsourced data.

One of the biggest concerns is data conﬁdentiality

provisioning which remains a fundamental security

requirement in cloud storage services.

It is commonly agreed that data encryption at the

client side is a good alternative to mitigate such con-

cerns of data conﬁdentiality. Thus, the client pre-

serves the decrypting keys out of reach of the cloud

provider. Nonetheless, the conﬁdentiality preserva-

tion becomes more complicated with ﬂexible data

sharing among a group of users. First, it requires ef-

ﬁcient sharing of decrypting keys between different

authorized users. The challenge is to deﬁne a smooth

group revocation which does not require updating the

secret keys of the remaining users. So, the complexity

of key management is minimized. Second, the access

control policies should be ﬂexible and distinguish-

able among users with different privileges to access

data. That is, data may be shared by different users or

groups, and users may belong to several groups.

In this paper, we propose CloudaSec, a public key

based solution for improving data conﬁdentiality in

cloud storage environments and enhancing dynamic

sharing between users. CloudaSec applies the con-

vergent encryption concept (Wang et al., 2010) on

data contents. That is, the data owner uploads en-

crypted content to the cloud and seamlessly integrates

the deciphering key encrypted into the metadata to en-

sure data conﬁdentiality. In addition, CloudaSec in-

tegrates a conference key distribution scheme, based

on parallel Difﬁe Hellman exchanges, in order to

guarantee backward and forward secrecy (Burmester

and Desmedt, 2005). That is, only authorized users

can access metadata and decipher the decrypting data

keys. As such, user revocation is achieved without

updating the private keys of the remaining users.

Beyond these security properties, a deduplication

mechanism is deployed ensuringthat only one copy of

content is stored in cloud servers. This feature enables

the efﬁcient usage of storage capacities and achieves

fast data distribution.

Kaaniche N., Laurent M. and El Barbori M..

CloudaSec: A Novel Public-key Based Framework to Handle Data Sharing Security in Clouds.

DOI: 10.5220/0005010600050018

In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 5-18

ISBN: 978-989-758-045-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Paper Organization. The remainder of this work is

organized as follows: Section 2 presents security con-

siderations and design goals. Then, Section 3 de-

scribes the system model, reviews some preliminaries

and cryptographic primitives, details the framework

design, and describes the prototype and its different

procedures. In Section 4, rigorous security discus-

sions are given, and implementation results are dis-

cussed in Section 5. Finally, we review the related

work in Section 6, before concluding in Section 7.

2 PROBLEM STATEMENT

Providing data conﬁdentiality, in multi-tenant envi-

ronments, becomes more challenging and conﬂicting.

This is largely due to the fact that users outsource their

data on remote servers, which are controlled and man-

aged by possible untrusted Cloud Service Providers

(CSPs). That is why, it is compulsory to provide se-

crecy by encrypting data before their storage in cloud

servers while keeping the decryption keys out of reach

of CSP and any malicious user. Nonetheless, the con-

ﬁdentiality preservation becomes more complex with

resilient data sharing among dynamic groups. Hence,

secure data sharing should support ﬂexible security

policies including forward and backward secrecy.

• Forward Secrecy – this property requires that the

conﬁdentiality of previous encrypted data has to

be ensured even after the long-term secrets are ex-

posed. For example, a user cannot access stored

data before he joins a group.

• Backward Secrecy – this property means that a

compromise of the secret key does not affect the

secrecy of future encrypted data. As such, a re-

voked group member is unable to access data that

were outsourced after he leaves the group.

Therefore, the design of our protocol is motivated

by providing the support of both robustness and efﬁ-

ciency, while considering the limited storage and pro-

cessing capacities of user devices. It has to fulﬁll the

following requirements:

• Data Conﬁdentiality – our scheme has to protect

the secrecy of outsourced data contents against

both curious providers and malicious users.

• Flexible Access Control – CloudaSec should en-

sure ﬂexible security policies among users with

different granted privileges, belonging to differ-

ent groups. These access control policies should

guarantee backward and forward secrecy of out-

sourced data contents.

• Efﬁcient User Revocation – the revocation of a

group member should not affect the remaining

users. That is, contrary to traditional ﬁne-grained

access control schemes, the challenge is to de-

ﬁne a smooth group revocation which does not re-

quires updating the secret keys of the non-revoked

members.

• Low Computation Overhead – on one hand, for

scalability reasons, the amount of computation at

the cloud storage server should be minimized, as

the server may be involved in concurrent interac-

tions. On the other hand, the proposed algorithms

should also have low processing complexity, at the

client side.

• Low Communication Overhead – CloudaSec

should minimize the usage of bandwidth, relying

on low communication cost.

• Low Storage Cost – the limited storage capacities

of the user devices has a critical importance in de-

signing our solution. So, low storage cost at the

client side is highly recommended.

3 CLOUDASEC FRAMEWORK

This section presents CloudaSec architecture with

four different types of players. Then, it introduces

CloudaSec, a public key based framework to han-

dle data sharing security, and it highlights the cryp-

tographic assumptions that should be fulﬁlled by our

proposed framework.

3.1 System Model

Figure 1 illustrates a descriptive network architecture

for CloudaSec framework. It relies on the following

entities for the good management of client data:

• Cloud Service Provider (CSP): a CSP has signiﬁ-

cant resources to govern distributed cloud storage

servers and to manage its database servers. It also

provides virtual infrastructure to host application

services. These services can be used by the client

to manage his data stored in the cloud servers.

• Data Owner: a data owner makes use of

provider’s resources to store, retrieve and share

data with multiple users. A data owner can be ei-

ther an individual or an enterprise.

• Group Manager (GM): a group manager takes

charge of construction of a group, system param-

eters generation, user registration and user revo-

cation. Therefore, we assume that the group man-

ager is trusted by the other entities.

• Users: the users are able to access the content

stored in the cloud, depending on their access

SECRYPT2014-InternationalConferenceonSecurityandCryptography

Figure 1: CloudaSec architecture.

rights which are authorizationsgranted by the data

owner, like the rights to read, write or re-store the

modiﬁed data in the cloud. These access rights

serve to specify several groups of users.

In practice, the CSP provides a web interface for data

depositors to store data into a set of cloud servers,

which are running in a cooperated and distributed

manner. In addition, the web interface is used by the

users to retrieve, modify and re-store data from the

cloud, depending on their access rights. We assume

that there is an established secure channel between the

cloud user and the CSP. This secure channel supports

mutual authentication and data conﬁdentiality and in-

tegrity. It can be implemented through the Transport

Layer Security protocol (TLS) (Dierks and Rescorla,

2008), where the client can authenticate with a certiﬁ-

cate or password.

Next, we refer to these authorized user(s) as the

recipient(s) and to the data owner as the depositor.

We must note that our proposal does not require from

the recipients to be connected during the sharing pro-

cess. Indeed, recipients’ access rights are granted by

the data owner and managed by the CSP. That is, the

CSP is in charge of verifying each recipient access

permissions before sending him a redirected access

key element.

3.2 CloudaSec Overview

To protect outsourced data in public cloud servers

from unauthorized entities, CloudaSec provides sev-

eral cryptographic tools for the data owner in order

to guarantee the secrecy of his outsourced data and

to ensure that only authorized users are able to obtain

the decrypting data keys.

Our framework relies on the convergent encryp-

tion (Wang et al., 2010) which is a content hash key-

ing cryptographic system. That is, it presents two en-

cryption levels: data encryption level and key encryp-

tion level as follows.

• Symmetric Data Encryption Level – before out-

sourcing data to cloud servers, the depositor en-

crypts ﬁle contents, using a symmetric algorithm.

That is, the enciphering data key is derived, from

the ﬁle plaintext, using a one way hash function.

Hence, the choice of the convergent encryption is

multifold. First, storage capacity is preserved as

the same data encrypted by several users produce

the same encrypted data that need to be stored

once. As such, the number of redundant copies

is minimized in order to preserve the efﬁciency of

the storage service. Second, convergent encryp-

tion leads to a per-data enciphering key thus mit-

igating the usual key sharing problem when con-

tent sharing is needed. Third, the generation of the

deciphering data key is possible only if the plain-

text is known.

• Asymmetric Key Encryption Level – the depos-

itor enciphers the decrypting data key k, based

on an asymmetric algorithm, using the public key

of the recipient. Then, he includes this resulted

encrypted key in user metadata, ensuring ﬂexi-

ble access policies. Indeed, any authorized recipi-

ent may access to user metadata, in order to deci-

pher the encrypted data key, using his private key.

Then, he can decrypt the enciphered contents.

This dual encryption scheme on data then on the de-

crypting keys provides data conﬁdentiality, as well as

ﬂexible access control policies.

CloudaSec procedures involve two joint layers:

data layer and management layer. In the data layer,

we introduce the operations on data and the related

enciphering keys, namely GenerateParameters,

EncryptData, DecryptData, EncryptKey

OneToOne

EncryptKey

OneToMany

and ShrinKey. In the man-

agement layer, CloudaSec introduces procedures of

user revocation, when a group member leaves or is

revoked from the group, and user subscription, when

a new user joins the group.

CloudaSec supports ﬂexible access to encrypted

contents, by dynamically sharing a group secret key

within the group. That is, when the group state is

modiﬁed due to a user subscription or revocation, the

GM broadcasts the new group arrangement to autho-

rized members in order to generate the new secret

group key, based on the published public elements,

without updating the private keys of the remaining

users, as presented in Section 3.5.

CloudaSec distinguishes two different data shar-

ing scenarios. First, the data sharing one to one, pre-

sented in Section 3.4.1, where a data owner stores

for one CloudaSec user. Second, the data sharing

one to many, described in Section 3.4.2, where a

data owner shares data among a group of authorized

users. These scenarios encompass two different data

CloudaSec:ANovelPublic-keyBasedFrameworktoHandleDataSharingSecurityinClouds

key encryption algorithms EncryptKey

OneToOne

and

EncryptKey

OneToMany

The different notations used in this paper are listed

in Table 1.

Table 1: Our notations.

Notation Description

f ﬁle content

k data key

identity of a CloudaSec user U

private key of a CloudaSec user U

public key of a CloudaSec user U

private key of the CSP

public key of the CSP

d group secret key

3.3 Cryptographic Background

This section reviews a straightforward cryptographic

background, used in the design of our CloudaSec

framework.

3.3.1 Preliminaries

CloudaSec essentially relies on the use of one way

functions and bilinear maps, deﬁned as follows.

Collision Resistant Hash Functions (Boneh and

Boyen, 2006) – Let H : { 0,1}

∗

→ {0,1}

be a hash

function. H is a collision resistant function if no

efﬁcient algorithm can ﬁnd a pair M 6= M

′

∈ {0,1}

∗

such that H(M) = H(M

′

Bilinear Maps { (Regan, ), (Ratna et al., 2004)}

– an admissible symmetric pairing function ˆe from

× G

in G

has to be bilinear, non degenerate and

efﬁciently computable. G

is an additive subgroup of

the group of points of an Elliptic Curve (EC). How-

ever, G

is a multiplicative subgroup of a ﬁnite ﬁeld.

and G

have the same order q. In addition, G

and

are generated by P and the g = ˆe(P,P), respec-

tively.

3.3.2 Cryptographic Assumptions

Our proposal is based on two cryptographic assump-

tions, namely the Elliptic Curve Discrete Logarithm

Problem and the Computational Difﬁe Hellman

Problem.

Elliptic Curve Discrete Logarithm Problem

(ECDLP) – given an additive group G, a subgroup of

E(F

), which is generated by the point P of prime

order n, it is intractable to ﬁnd a, where Q = aP, and

P are known.

Computational Difﬁe Hellman Problem (CDH) –

given a cyclic group G of order p and generator g,

there is no efﬁcient algorithm to calculate g

, where

(g,g

) are known.

3.3.3 Group Key Distribution (GKD)

Burmester and Desmedt propose an unauthorized key

exchange protocol (Burmester and Desmedt, 2005).

It is a two round protocol that extends the concept of

the Difﬁe Hellman assumption.

Let G = {U

,...U

}, be a group of m users ar-

ranged into a cycle. To generate a group key, each

member U

, where i ∈ [1,m]

, ﬁrst selects a random

secret b

. Then, he broadcasts z

= g

, where g is

a generator of a multiplicative group G. Afterwards,

this latter publishes X

= (

i+1

i−1

)

. We must note that

the number of exponentiationsper user is constant and

each user U

computes K, as K ≡ g

+...+b

mod(p).

3.4 CloudaSec Data Layer Procedures

This section describes the different CloudaSec data

layer procedures. CloudaSec, ﬁrst, requires a sys-

tem setup procedure, ensured by the execution of

the GenerateParameters algorithm, before perform-

ing the sharing scenarios.

This CloudaSec GenerateParameters algorithm

initializes the system and generates the public param-

eters params, according to a required security param-

eter ξ, as presented in Algorithm 1. That is, the sys-

tem setup procedure generates the groups G

and G

and the pairing function ˆe from G

× G

in G

. G

is an additive subgroup of the group of points of an

Elliptic Curve (EC), where G

is a multiplicative sub-

group of a ﬁnite ﬁeld. G

and G

have the same order

n and are generated by P and g = ˆe(P,P), respectively.

After the speciﬁcation of the groups, CloudaSec

GenerateParameters procedure deﬁnes a secure one

way hash function H : E → {0,1}

, with respect to the

required security level, where E represents the ﬁnite

data domain and l is the length of the content encrypt-

ing key. In addition, it derivesan application F to bind

an element belonging to the multiplicative group G

∗

to a binary sequence of length l.

The groups G

and G

, the pairing ˆe, the point P,

the hash function H() and the application F form the

public parameters params as follows.

params = {G

,n, ˆe,g,P,H(),F}.

We must note that each user has to derive a pair of

public and private keys, with respect to the published

authentic public parameters params and the required

SECRYPT2014-InternationalConferenceonSecurityandCryptography

Algorithm 1: GenerateParameters.

1: Input: Security parameter ξ

2: Output: System parameters params =

, ˆe,P, g,H,F,n}

3: Choose an elliptic curve EC over an additive sub-

group G

of a prime order n, where BitLength (n)

> ξ and ECDLP is hard in G

;

4: Select P a generator of EC;

5: Choose a multiplicative subgroup G

of a prime

order n, where BitLength (n) > ξ and CDH is hard

in G

;

6: Select g a generator of G

;

7: Generate ˆe from G

× G

in G

an admissible

pairing map;

8: Generate a one way hash function H : E →

({0,1}

)

∗

, where E is the data space and l is the

length of the encrypting key;

9: Generate F : G

∗

→ {0, 1}

an application to bind

an element of G

∗

to a binary sequence of length l

10: return params = {G

, ˆe,P, g,H,F,n}

security level ξ. As such, a CloudaSec userU

is char-

acterized by his identity id

and the derived pair of

keys: his private key sk

, where sk

is a random secret

∈

and his public key as pk

= s

· P.

(id

, pk

,sk

)

In the following, we denote by · the scalar point mul-

tiplication in an additive group and by ⋆ two elements

multiplication belonging to a multiplicative group.

We consider a data sharing process, where the

client outsources his data to the cloud and authorizes

a group of users to access the data. This group may

be a duo group or a multi-user group.

3.4.1 CloudaSec One to One Sharing Scenario

The One to One scenario is deﬁned when a data owner

wants to share data with only one recipient user

. The depositor U

ﬁrst enciphers the data ﬁle f,

as presented in Algorithm 2, based on a symmetric

encryption scheme SymEnc, using a data enciphering

key k. Based on a convergent cryptographic solution,

the data key k is derived from the application of a one

way hash function over the original data ﬁle f. Sub-

sequently, U

stores the encrypted content f for the

recipient user U

, in remote servers. In order to as-

sign the access rights to the recipient, the depositor

enciphers the data decrypting key k using the public

key of the recipient pk

, as described in CloudaSec

EncryptKey

OneToOne

procedure (Algorithm 3). That

is, CloudaSec introduces a novel asymmetric key en-

coding, to ensure ﬂexible sharing of outsourced data.

Algorithm 2: EncryptData.

1: Input: { f,H,SymEnc}, where f is the data ﬁle,

H is a one way hash function and SymEnc is a

symmetric encryption algorithm

2: Output: < C

,k >

3: k = H( f);

4: C

= SymEnc( f,k);

5: return < C

,k >

For instance, the resulting enciphered key involves a

couple of elements < C

>. C

is included in the

user metadata, by the depositor U

. However, C

sent to the CSP, in order to grant additional access

veriﬁcations on the outsourced data and to generate a

redirected access key element. We assume in our ap-

proach that all key elements belong to a ﬁnite domain

space D. We denote each key element by key.elt as

deﬁned in Equation 1, where D can be either a user

metadata element space or a CSP metadata element

space.

key.elt

i∈{1,2,3}

= {C

,D(C

)}

i∈{1,2,3}

(1)

We must note that the CSP has a pair of private and

public keys as < sk

, pk

>, where sk

= s

∈

presents the provider private key and pk

= s

·P ∈ G

∗

is his related public key. When the CSP receives the

second key element C

, he runs the ShrinKey algo-

rithm in order to derive a redirected key element C

as presented in Algorithm 4. This latter enciphers C

using his secret key sk

and generates the correspond-

ingC

. Afterwards, when the CloudaSec recipientU

where j 6= i, wants to recover the outsourced data ﬁle,

he has to retrieve the encrypted data key < C

As such, the recipient user U

starts a data backup

scenario as follows.

Algorithm 3: EncryptKey

OneToOne

1: Input: {params,k, sk

, pk

}

2: Output: < C

3: Use a deterministic secure pseudo random num-

ber generator (SPRNG) with a random secret

seed to generate r ∈

;

4: C

= k⊕ F( ˆe(pk

, pk

)

);

5: C

= ˆe(pk

,r· P)

;

6: return < C

After successfully authenticating with the CSP, U

gets the redirected key element C

. Then, based on

the outsourced user metadata, the authorized recipi-

ent U

extracts the C

key element, which was enci-

phered, using his public key pk

by the depositor U

In the sequel, based on his local secret key sk

, the

CloudaSec:ANovelPublic-keyBasedFrameworktoHandleDataSharingSecurityinClouds

recipient U

performs the DecryptKey

OneToOne

proce-

dure, in order to decipher the encrypted data key k,

as presented in Algorithm 5. Finally, the recipient re-

trieves the data ﬁle content. That is, he locally runs

the CloudaSec DecryptData procedure, based on the

derived deciphering key k, using a symmetric algo-

rithm over encrypted data C

(cf. Algorithm 6).

Algorithm 4: ShrinKey.

1: Input: {C

,sk

}

2: Output: C

3: C

= (C

)

;

4: return C

Algorithm 5: DecryptKey

OneToOne

1: Input: {params,< C

>,sk

}

2: Output: Decrypting key k

3: C

⊕ F((C

)

);

4: return k

Algorithm 6: DecryptData.

1: Input: {C

,k,SymEnc}

2: Output: f

3: f = SymEnc(C

,k) ;

4: return f

3.4.2 CloudaSec One to Many Sharing Scenario

When a depositor U

intends to share data with a

multi-user group, he has to encipher the data decrypt-

ing key based on his public key pk

and a secret shared

group key d. The secret shared key is a private key,

only known to the authorized group members. It is

derived by performing the key agreement algorithm

(Section 3.3.3), based on parallel Difﬁe Hellman in-

stantiations (Burmester and Desmedt, 2005), as ex-

plained in Section 3.5.

The depositor executes the EncryptKey

OneToMany

procedure (cf. Algorithm 7), in order to encrypt the

deciphering data key. The resulting encrypted key in-

cludes a couple of elements < C

>, where C

integrated in user metadata by the depositor, and C

is sent to the cloud provider, in order to generate an

accessing keyC

element (Algorithm 4). When an au-

thorized group member wants to retrieve the data de-

crypting key, he has ﬁrst to send a request to the cloud

provider to access to the outsourced data. The CSP

veriﬁes the granted privileges of the requesting user.

Once accepted, the requesting group member receives

the redirected key elementC

obtained by performing

the ShrinKey procedure, as shown in Section 3.4.1.

Then, he runs the CloudaSec DecryptKey

OneToMany

procedure (cf. Algorithm 8) using the secret shared

group key d, in order to derive the deciphering data

key k.

Algorithm 7: EncryptKey

OneToMany

1: Input: {params,k, pk

,sk

,d, pk

}

2: Output: < C

3: Use a deterministic secure pseudo random num-

ber generator (SPRNG) with a random secret

seed to generate r ∈

;

4: C

= k⊕ F( ˆe(pk

,r· P)

);

5: C

= ˆe(pk

,r· P)

;

6: return < C

Algorithm 8: DecryptKey

OneToMany

1: Input: {params,< C

>,d}

2: Output: Decrypting key k

3: C

⊕ F((C

)

);

4: return k

3.5 CloudaSec Management Layer

Procedures

Efﬁcient data sharing between authorized cloud users,

among dynamic groups remains a challenging con-

cern. That is, it increases the computation complex-

ity and the bandwidth consumption, due to the shar-

ing of group secret keys. In addition, the heavy over-

head and the large size of outsourced data may reduce

the advantages of remote sharing services to resource-

constrained devices.

In order to tackle this challenging issue,

CloudaSec introduces the role of a group man-

ager (GM). This latter is responsible for elementary

procedures, namely the initialization of the group

parameters and the organization among authorized

registered group members. Then, the GM makes the

group parameters available by migrating them to the

cloud. Such a design can signiﬁcantly reduce the

computation overhead, at the CloudaSec user side.

Let us consider Gr = {{U

,id

},...,

N−1

,id

N−1

}} a dynamic group of N users.

These group members want to generate a common

secret d ∈ Z

. In the following, we denote by pubelts

the public elements of a CloudaSec registered group

member U

as described in Equation 2.

pubelts

=< id

, pk

> (2)

where i ∈ { 1,...,N − 1} and N is the number of group

users including the manager. As such, we note that

SECRYPT2014-InternationalConferenceonSecurityandCryptography

Algorithm 9: GenerateGroup.

1: Input: n, p,ξ

2: Output: < G,h >

3: Choose a multiplicative subgroup G of a prime

order n, where BitLength (n) > ξ;

4: Select h a generator of G, where h

≡ 1 mod p;

5: return < G,h >

the couple < id

, pk

> presents the public group el-

ements of the Group Manager (GM). First, the GM

runs a GenerateGroup procedure, in order to derive a

multiplicative group and makes public the output of

this algorithm, which is used to generate the secret

group key d (cf. Algorithm 9). We must note that

the order of the multiplicative group is strongly as-

sociated to the security level ξ of the cryptographic

algorithms.

Then, with respect to the published multiplicative

group G, each group user U

chooses a random b

and

locally runs the CloudaSec UserKeyShareElt proce-

dure in order to get his ﬁrst key share element h

, as

presented in Algorithm 10.

Algorithm 10: UserKeyShareElt.

1: Input: id

2: Output: < id

3: h

= h

∈ G

∗

;

4: return < id

The GM receives the public elements pubelts

each group member U

. Then, he updates a list of

non revoked users L

, which contains the public ele-

ments of all non revoked group users. This list sets

the authorized group members arranged into a cy-

cle. As such, each user can easily identify his pre-

decessor U

i−1

and his successor U

i+1

. Thus, using

the CloudaSec GenerateGroup and UserKeyShareElt

procedures, U

computes his group key share (h

as depicted in Equation 3.

) = (h

i+1

i−1

)

) (3)

Once computed, each user U

sends his group key

share to the GM. This latter publishes the received

key shares of the non revoked users, as presented in

Table 2. Afterwards, as presented in Section 3.3.3,

each user should derive the secret group key d, us-

ing the published elements in the L

list, while

respecting the ring construction of the group mem-

bers (Burmester and Desmedt, 2005).

Table 2: List of Non Revoked users L

Group id User Pubelts User Key Share

(id

, pk

) (h

)

(id

, pk

) (h

)

N−1

(id

N−1

, pk

N−1

) (h

N−1

)

3.5.1 User Subscription

When a new user {U

,id

} wants to join the

group Gr, presented by Gr = {{U

,id

},...,

N−1

,id

N−1

}}, where i /∈ {0,...,N − 1}, he ﬁrst

runs the UserKeyShareElt algorithm in order to get

his public key share element < id

>. Then, the

new group member computes and sends his key share

) to the group manager. Hence, The GM

sends a notiﬁcation message to the remaining group

members and updates the list of non revoked users

Afterwards, each group user computes the new se-

cret key d

, due to the group state modiﬁcation. Since

the derivation of the group secret key depends on

members’ identiﬁers, the computation of key shares

) may be restricted to the solicited members.

Consequently, CloudaSec signiﬁcantly saves the pro-

cessing time and storage cost at CloudaSec user side.

The user subscription operation prevents new

users from accessing to protected content, before join-

ing the group. As such, CloudaSec ensures the for-

ward security. In order to grant access privileges to

new subscribers to outsourced data, the sharing of a

secrets’ list L

is required.

Indeed, the group manager updates a list of previ-

ously used secrets L

by including the new group se-

cret key. Then, he sends it to the CSP in an encrypted

format by using symmetric encryption algorithm and

the derived secret group key d. In the sequel, any

authorized group member authenticates with the CSP

and uploads the encrypted list. So that, he can obtain

using the derived secret group key and the sym-

metric decryption algorithm.

3.5.2 User Revocation

When a group member U

leaves or is revoked

from the group Gr = {id

,id

,...,id

}, where j ∈

{0,1,...,k} , the group manager ﬁrst updates the list of

non revoked users L

. That is, he removes the pub-

lic elements < id

, pk

> and the key share (h

)

of the revoked member from the L

list. Then, he

sends a notiﬁcation message to other group users and

sends the updated list to the CSP. Each group user

computes a new secret key d

by running the Group-

Key algorithm.

CloudaSec:ANovelPublic-keyBasedFrameworktoHandleDataSharingSecurityinClouds

We note that the number of the revoked users RU

has to be strictly less than (N −1), in order to keep the

One To Many sharing scenario. In fact, we consider

two cases.

1. Case 1 – There are RU revoked users, where

1 ≤ RU ≤ N − 2. The group manager revokes

RU users, and updates the L

list. That is, he

withdraws the revoked users’ identities and reor-

ganizes the indexing system of the list. The group

manager optimizes the changes of the group list

based on a selection protocol, in order to save the

computation capacities of resource constrained

devices. As such, a non solicited group member

is requested to only compute the resulting group

key, using the published public group elements.

2. Case 2 – There are RU revoked users, where

RU ≥ N − 1. In this case, the group manager is

released from his role. As such, the multi-user

group becomes a duo group that shares data based

on a sharing One To One scenario.

4 SECURITY ANALYSIS

In the following security analysis, we discuss the re-

sistance of CloudaSec against two adversaries, based

on a realistic threat model. We brieﬂy present the se-

curity of our proposed framework in terms of access

control and data ﬁle conﬁdentiality.

4.1 Threat Model

For designing the most suitable security solutions for

cloud storage, we have to consider realistic threat

models. That is, we point out two adversaries: mali-

cious cloud user and honest but curious cloud server.

• malicious user adversary – an attacker can be

either a revoked user with valid data decryption

keys, an unauthorized group member or a group

member with limited access rights. As such, he

targets to get access to the outsourced shared data.

The objective of a malicious user is to convince

the cloud server that he is a legitimate data owner.

That is, we suppose that the adversary successes

to gain knowledge of an arbitrary part of the de-

crypting key.

• curious cloud server adversary – this storage

server honestly performs the operations deﬁned

by our proposed scheme, but it may actively at-

tempt to gain the knowledge of the outsourced

sensitive data.

CloudaSec must provide the capabilities to the clients

and the service provider to thwart the two threats men-

tioned above. To this end, our proposed framework

must enforce a mutual veriﬁcation of the actions con-

ducted by a CloudaSec client and the storage server.

4.2 Data Conﬁdentiality

In our model, data ﬁles are stored encrypted in cloud

servers using a symmetric encryption algorithm, and

the secret key is protected relying on an asymmetric

scheme, in order to ensure efﬁcient access control. As

such, the data conﬁdentiality preservation is tightly

related to security of the used symmetric algorithm

and the secrecy of the data key.

Theorem 4.1. Data Conﬁdentiality Preservation

The proposed framework supports data conﬁdential-

ity preservation.

Proof. The conﬁdentiality of data contents is twofold.

First, it depends on the security level of the encryption

algorithm. This latter is a recurrent concept in cryp-

tography. It permits to evaluate the hardness of break-

ing an encryption or a signature algorithm. That is,

the harder the level of security is, the harder the crypt-

analysis of the algorithm becomes. Our employed en-

cryption algorithm inherits the unforgeable property

from the selected scheme. Therefore, CloudaSec en-

sures the conﬁdentiality of encrypted content exposed

in public cloud servers.

Second, the conﬁdentiality of data relies also on

the secrecy of the deciphering key hosted in cloud

servers. The demonstration of this state is derived

from these two lemmas.

Lemma 4.2. Unauthorized users cannot decrypt the

deciphering data keys.

Proof. The proof of this lemma is equivalent to the

security of the key encryption algorithms and the cor-

rectness of the key decryption algorithms.

Let us suppose that an unauthorized user can be

a revoked group member or a malicious cloud user.

Thus, a brief security analysis can be done on the

three following cases.

• Case A – a revoked group member U

should not

be able to decrypt new data contents, using the

old group secret key d. This latter knows the pub-

lic elements of the non revoked users published

in L

and the previous organization of the group

arranged into a cycle. Moreover, he can merely

guess the solicited members after his revocation.

As such, taking advantage from published infor-

mation, U

tries to deduce the new group secret

SECRYPT2014-InternationalConferenceonSecurityandCryptography

key d

or to extract a data key after his revoca-

tion from the group. In this case, we may con-

sider two different sessions (α) and (β), where the

same data owner U

shares two different data ﬁles

and f

, after the revocation of U

. In the se-

quel, two key elements are deﬁned as follows:

(α)

= k

⊕ F( ˆe(pk

· P)

)

(β)

= k

⊕ F( ˆe(pk

· P)

)

On one side, knowing the public key of the de-

positor pk

, we state that the deduction of the new

group secret d

from C

(α)

cannot hold. Obvi-

ously, this is due to the usage of a random value

. We also state that our scheme inherits the

unforgeablility property from the Burmester key

distribution algorithm (Burmester and Desmedt,

2005). On the other side, U

cannot deduce se-

cret information from C

(α)

⊕ C

(β)

, mainly due to

the exclusive-or function.

As such, a revoked group member U

has no ad-

vantage to guess the new secret group, based on

the old group key d and the previously published

public elements. However, we must note that

CloudaSec does not prevent a revoked member

from decrypting previously shared contents.

• Case B – The main advantage of a malicious cloud

user is to deduce information from an unbounded

number of sessions, where the same data owner

shares different contents with legitimate group

members. As such, two different cases are ex-

posed as follows.

On one hand, in a one to many sharing scenario,

let us suppose that a user U

shares two data ﬁles

and f

, respectively enciphered based on two

different keys k

and k

, using the same random

r. That is, based on Equation 4 and Equation 5,

an attacker obtains indistinguishable data key ele-

ments key.elt

, as follows.

( f

)

= k

⊕ F( ˆe(pk

,r· P)

) (4)

( f

)

= k

⊕ F( ˆe(pk

,r· P)

) (5)

Hence, we notice that there is no polynomial-time

algorithm that can deduce secret information from

Equation 4⊕Equation 5 = k

⊕k

, due to the usage

of the exclusive-or function. As such, the secrecy

disclosure of the deciphering keys remains infea-

sible.

On the other hand, in a one to one sharing sce-

nario, we suppose that a depositor U

shares data

with one recipient U

, using the same random se-

cret r, in order to encipher different data decrypt-

ing key. Thus, based on two successive sessions

(α) and (β), the malicious cloud user gets the fol-

lowing key elements key.elt

(α)

= k

⊕ F( ˆe(pk

, pk

)

(α)

)

(β)

= k

⊕ F( ˆe(pk

, pk

)

(β)

)

Therefore, the deduction from the encipheredcon-

tents is protected, due to the usage of different

data encryption keys. In addition, the security of

metadata takes advantages from the properties of

the exclusive-or function which ensure the indis-

tinguishability of encryptions.

• Case C– Let us suppose that a depositor U

be-

longs to two different groups G

and G

. U

wants

to share the same data ﬁle f to these two groups.

and G

have two secrets d

and d

, respec-

tively. As such, we have two different key ele-

ments key.elt

, as follows:

(A)

= k⊕ F( ˆe(pk

· P)

) (6)

(B)

= k⊕ F( ˆe(pk

· P)

) (7)

We suppose that there a malicious group member

that belongs to the group of users G

. U

tries

to deduce the group secret key d

of G

From Equation 6, the recipient U

extracts the

data deciphering key k. In the sequel, from C

(B)

computes Equation 8 as follows:

(B)

⊕ k = k ⊕ F( ˆe(pk

· P)

) ⊕ k (8)

= F( ˆe(pk

· P)

) (9)

From Equation 7 and Equation 8, the mali-

cious recipient U

calculates ˆe(pk

· P)

⋆

[1/( ˆe(pk

·P)

)]. So that, U

executes the fol-

lowing steps:

ˆe(sk

· P, r

· P)

⋆ [

ˆe(sk

· P, r

· P)

] =

Knowing the group secret d

and the two quanti-

ties g

and g

, U

cannot extract the group

secret d

. Obviously, this contradicts the CDH as-

sumption.

Finally, as data may be shared by different depos-

itors or groups, and these depositors may belong

to several groups, our framework strongly ensures

the conﬁdentiality of outsourced contents, based

on the hardness of the CDH assumption.

Lemma 4.3. The CSP is unable to learn the content

of outsourced data ﬁles in his public servers, based

on the CDH assumption.

CloudaSec:ANovelPublic-keyBasedFrameworktoHandleDataSharingSecurityinClouds

Proof. A curious CSP tries to access to the stored data

contents. His main problem is that outsourced data

ﬁles are encrypted. However, the CSP tries to gain

knowledge of an arbitrary part of secret information.

That is, after each storage of data content, the CSP

receives the second key element key.elt

, from the de-

positorU

asC

= ˆe(pk

,r·P)

, where sk

∈ Z

is the

secret element of the depositor U

and pk

= sk

· P ∈

∗

is the public key of the storage provider. As such,

in order to extract secret information, the CSP com-

putes ˆe(pk

,P) = g

. This deduction cannot hold.

Clearly, this contradicts the CDH assumption.

Given the redirected key element C

= C

( ˆe(pk

,r · P)

)

, the CSP computes C

= ( ˆe(pk

,r ·

)

= ˆe(pk

,r· P). Then, he executes Equation 10

and Equation 11 as follows:

⋆ [

ˆe(pk

, pk

)

] =

= g

(10)

⋆ [

ˆe(pk

, pk

)

] =

(11)

From Equation 10 and Equation 11, this curious stor-

age server cannot extract the secret key of the depos-

itor sk

or the used random value r. As such, the stor-

age server cannot learn the content of the outsourced

data ﬁles, based on the hardness of the CDH assump-

tion.

4.3 Access Control

CloudaSec is designed to ensure forward and back-

ward secrecy. When a new user joins the group or a

group member is revoked, a notiﬁcation message is

sent to CSP and to the remaining members, in order

to adjust the access control lists.

On one side, when a new user U

joins the group,

he has to generate his own group public elements

pubelts

. These elements will be later used to derive

the new group key d

. On the other side, when a user

leaves the group, the GM updates the sharing lists,

in order to generate the new decrypting key. Conse-

quently, a new user cannot decrypt the old data ﬁles,

using the new derived key, and a revoked user cannot

decrypt new ﬁles, with the old deciphering key.

The access control preservation is ensured, based

on the following two lemmas.

Lemma 4.4. Key Decryption Correctness. Unre-

voked users are able to access the cloud.

Proof. The proof of this lemma is equivalent to the

correctness of the key decryption algorithms, on the

basis of the two sharing scenarios, as follows.

• One To One sharing scenario – the decryption

holds if, and only of the decrypting key k

∗

⊕ F((C

)

This veriﬁcation holds as follows. On one side,

the authorized recipient U

computes the data key

element included in user metadata as follows:

= k ⊕ F( ˆe(pk

, pk

)

= k ⊕ F( ˆe(sk

· P, sk

· P)

)

= k ⊕ F( ˆe(s

· P, s

· P)

)

On the other side, the cloud provider sends the

redirected key elementC

to the CloudaSec recip-

ient, which is computed as follows.

= (C

)

= ( ˆe(pk

,r· P)

)

= ( ˆe(sk

· P, r · P)

)

= ( ˆe(s

· P, r · P)

)

= ( ˆe(P, r · P)

)

In the sequel, given the non singularity property

of the bilinear functions, the veriﬁcation holds

if, and only if k

∗

= C

⊕ F((C

)

), where C

⊕

F((C

)

) is denoted by (E).

(E) = k ⊕ F( ˆe(sk

· P, sk

· P)

) ⊕ F( ˆe(P,r· P)

)

= k ⊕ F( ˆe(s

· P, s

· P)

) ⊕ F( ˆe(s

· P, r · P)

)

= k ⊕ F( ˆe(s

· P, s

· P)

) ⊕ F( ˆe(s

· P, s

· P)

)

= k

• One To Many sharing scenario – the decryption

holds if, and only of the data key k

∗

= C

⊕

F((C

)

). This veriﬁcation holds as follows.

On one hand, the authorized group member U

computes the data key elementC

included in user

metadata as follows:

= k ⊕ F( ˆe(pk

,r· P)

)

= k ⊕ F( ˆe(sk

· P, r · P)

)

On the other hand, the CSP executes the follow-

ing operations on key.elt

, in order to get the redi-

rected element C

= (C

)

= ( ˆe(pk

,r· P)

)

= ( ˆe(sk

· P, r · P)

)

= ( ˆe(s

· P, r · P)

)

= ( ˆe(P, r · P)

)

SECRYPT2014-InternationalConferenceonSecurityandCryptography

As presented in the One To One sharing scenario,

given the non singularity property of the bilin-

ear functions, the veriﬁcation holds if, and only if

∗

= C

⊕ F((C

)

), where C

⊕ F((C

)

) is de-

noted by (F).

(F) = k ⊕ F( ˆe(sk

· P, r · P)

) ⊕ F( ˆe(P,r· P)

)

= k ⊕ F( ˆe(s

· P, r · P)

) ⊕ F( ˆe(s

· P, r · P)

)

= k

We state that the authorized CloudaSec users are able

to decipher the decrypting data key, thanks to the cor-

rectness of the key decryption algorithms.

Lemma 4.5. Unauthorized entities are unable to ac-

cess the cloud.

Proof. The proof of this lemma is twofold.

On one side, after each group member U

revo-

cation, the group manager updates the list L

and

sends a notiﬁcation message to the authorized regis-

tered group members. Then, he communicates this

list to the cloud provider. This latter sends L

the remaining group members after a mutual authen-

tication, in order to verify the updated organization of

the group.Then, the remaining group members com-

pute the new secret group key d

by performing the

GroupKey algorithm. Therefore, the new data keys

are encrypted by using EncryptKey

OneToMany

algo-

rithm.

As discussed in Lemma 4.2 and Lemma 4.4, only

authorized recipients, knowing the new key d

, are

able to decrypt the enciphered data. However, the

CSP and the revoked users cannot extract the key

, based on the previously published public ele-

ments and the list of authorized members L

. This

is mainly due to the computation of the group secret

which requires the private secret key sk

of each de-

riving group member U

On the other side, when a group user wants to ac-

cess the cloud, the CSP has to verify the access con-

trol list. That is, the cloud provider gives or rejects

access to data contents, based on the granted privi-

leges of the requesting recipient.

5 PERFORMANCE EVALUATION

In this section, we ﬁrst present the context of

CloudaSec implementation with OpenStack Object

Storage, and then evaluate the system performances,

in terms of computation, communication and storage

costs.

5.1 Context

In order to evaluate the performances of our proposal,

we build a simulated CloudaSec framework, based

on OpenStack Storage system (Swift) (swi, ). Swift

is a cloud based storage system, which stores data

and allows write, read, and delete operations on them.

To achieve security enhancement of Swift, we extend

its functionalities with algorithms and protocols de-

signed in CloudaSec.

We have designed a simpliﬁed CloudaSec archi-

tecture, based on Swift. Indeed, our architecture con-

sists in dividing the machine drive into four physical

volumes. Then, each volume is divided into four log-

ical volumes. In total, we obtain sixteen partitions,

each one represents one logical storage zone.

The simulation consists of two components: the

client side and the cloud side. We implement

data layer cryptographic algorithms based on cryp-

tographic functions from the Open-SSL library (The

OpenSSL Project, 2003), the GMP library (et al.,

2002) and the Pairing Based Cryptography (PBC) li-

brary (Ben, 2007), with independent native processes.

We choose Advanced Encryption Standard (AES) as

our symmetric encryption algorithm and implement

the CBC mode of AES.

We have conducted a number of experiments to

evaluate CloudaSec in the system and cloud levels.

We study the client efﬁciency of the cryptographic

algorithms with different pairing types and the user

management costs for communication and storage.

5.2 Computation Cost Evaluation

In order to evaluate the performances at the client

side, we conduct data encryption and decryption tests

locally. For our tests, we used 1000 samples in or-

der to get our average durations. In addition, we con-

ducted our experiments on an Intel core 2 duo, started

on single mode, where each core relies on 800 MHz

clock frequency (CPU). Figure 2 shows the computa-

tion overhead of data encryption and decryption at the

client side, with different sizes of data contents. We

can notice that the data encryption takes less than 12

ms, in order to encrypt 1MB data ﬁle.

We can note that this computation cost remains

attractive, as it provides better security to outsourced

data and does not deserve the client resources.

Then, we perform the encryption of the decipher-

ing data key k. That is, as our proposed framework re-

lies on the use of bilinear maps, we choose two sym-

metric pairing functions from the PBC library (Ben,

2007), including type E pairing e.param and type A

a.param. Thus, we examine the impact of different

CloudaSec:ANovelPublic-keyBasedFrameworktoHandleDataSharingSecurityinClouds

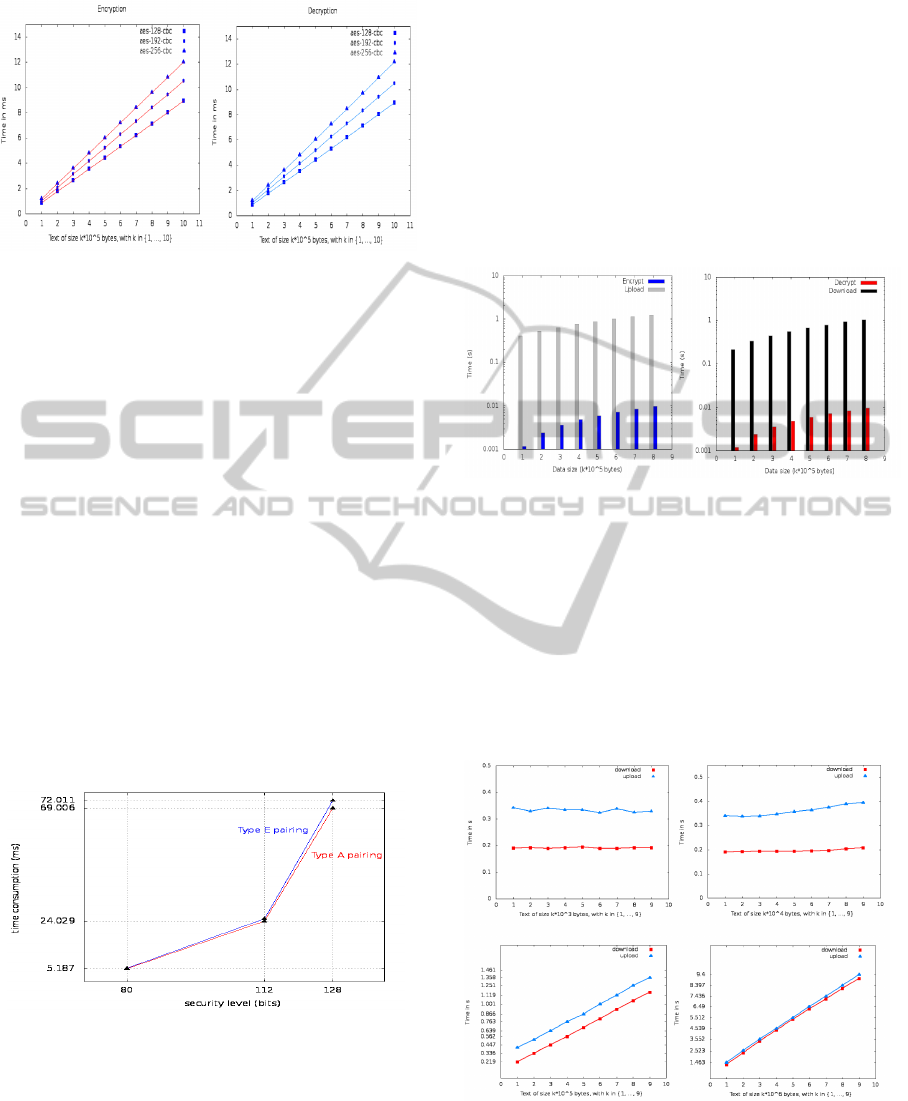
Figure 2: Computation overhead of data encryption and de-

cryption at the client side with different data size (from 10

to 10

bytes) (ms).

bilinear functions on the performances of CloudaSec,

while considering three different security levels (cf.

Figure 3).

In cryptography, the security level of a symmet-

ric encryption algorithm is deﬁned as the number of

operations needed to break the algorithm when a k-

bit key length is used. The security level in our pro-

posal depends on the security level of the bilinear

function in use ˆe, which is related to the hardness of

solving the ECDLP in G

. As such, it is closely re-

lated to the groups being selected. As shown in Fig-

ure 3, the encryption time increases along with the

security level, while there is a tiny difference between

the two symmetric pairing functions. As such, the

type of the pairing function should be taken into ac-

count, while implementing CloudaSec data layer pro-

cedures. We must note that the type of the pairing

function is bound to the choice of the elliptic curve,

where the bilinear map is computed.

Figure 3: Computation duration of Type A vs Type E pair-

ing functions (ms).

Finally, we investigate the impact of the cryp-

tographic operations, at CloudaSec client side. We

compare the encryption duration against OpenStack

upload and download duration, as depicted in Fig-

ure 4. In fact, we examine the encryption operations

vs Swift upload procedure and the decryption opera-

tions vs Swift download procedure. We must note that

the computation times include the key generation and

the data encryption with AES-256-CBC mode. We

notice that the cryptographic operations, at the client

side are acceptable compared to the upload operations

and do not carry exhaustive computation capacities.

For example, a 8 ∗ 10

bytes data size requires only

0.1 seconds to be enciphered, compared to 10 sec-

ond be uploaded. Therefore, the encryption proce-

dures involve 1% from the OpenStack upload over-

head. As such, CloudaSec does not deserve the client

resources, and presents an interesting processing cost

for resource constrained devices.

Figure 4: Impact of cryptographic operations on CloudaSec

at the client side (log

(ms)).

5.3 Communication Cost Evaluation

We investigate the communication overhead, when a

client stores his data ﬁle to remote servers and then

when he retrievesthe outsourced content. As such, we

conduct some experiments with different data sizes

and we evaluate the upload and download times of

encrypted contents, as shown in Figure 5.

Figure 5: OpenStack upload and download overhead with

different data size (ms).

We can notice that the average communication

times are merely stable, with small data sizes, for the

storage and backup scenarios. However, this overhead

gradually increases, when the client intends to store

SECRYPT2014-InternationalConferenceonSecurityandCryptography

large data contents. We also analyze the communica-

tion cost, due to a group update, namely when a new

user wants to join the group. In our tests, we are based

on pre-computed tables, in order to optimize the com-

putation cost to resource-constrained devices. Thus,

we consider that the group includes 10 members at

the beginning. Then, 10 users join the group simulta-

neously, until reaching 100 members. We recall that

the computation complexity of the group update in-

creases with respect to the number of new subscribers,

as presented in Section 3.3.

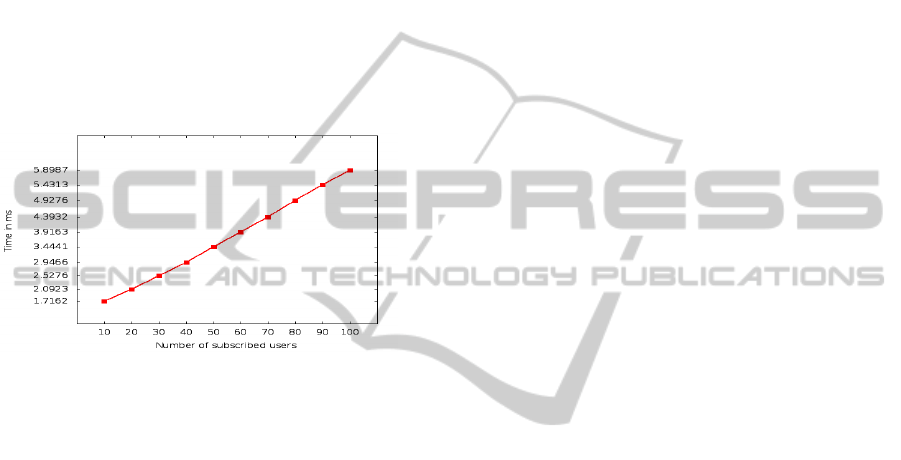
As depicted in Figure 6, the derivation of the new

secret group key takes less than 6 ms for 100 users.

This computation cost remains interestingly attrac-

tive, along with our broadcasting approach.

Figure 6: Computation complexity of a group update (ms).

5.4 Storage Cost Evaluation

We investigate the storage cost for the key manage-

ment operations at the client side. In order to main-

tain a group membership, a registered user has only to

keep the secret group key.

Let suppose that the security parameter ξ = 80

bits. We denoted by E(F

) the elliptic curve deﬁned

over the ﬁnite prime ﬁeld F

. Meanwhile, we de-

note ˆe : G

× G

−→ G

the bilinear function. G

corresponds to the q-torsion subgroups of E(F

) and

E(F

) where k is the embedding degree of the curve

E. G

is a multiplicative subgroup of F

of order q.

For example, according to the security parameter

ξ = 80, we set q = 160 bits and n = 512 bits length,

while the embedding degree is equal to 2. As such,

is a subgroup of F

which has a order 1024 bits

order. Therefore, a client has to locally keep a secret

d, where |d| = 160. As such, CloudaSec introducesan

attractive storage cost, especially for limited storage

capacities.

6 RELATED WORK

Several security solutions have been recently de-

veloped, in order to provide data conﬁdentiality in

public cloud storage environments { (Xiong et al.,

2012),(Zarandioon et al., 2011), (Yu et al., 2010),

(Zhou et al., 2011), (Liu et al., 2013),(Fugkeaw,

2012)}, while considering the group access control

issues.

In (Yu et al., 2010), Yu et al. proposed an attribute

based access control policy to securely outsource sen-

sitive client data to untrusted cloud servers. In this ap-

proach, data are encrypted using a symmetric encryp-

tion algorithm, while the enciphering key is protected

by a Key-Policy-Attribute Based Encryption scheme

(Goyal et al., 2006). In order to manage dynamic

groups, they delegate the key re-encryption proce-

dures to the cloud, without revealing the content of

outsourced data. As such, the membership revocation

mechanism brings additional computation overhead.

However, CloudaSec deﬁnes a new revocation system

based on (Burmester and Desmedt, 2005), without

updating the secret keys of the remaining group mem-

bers, in order to minimize the complexity of key man-

agement. That is, our design conveys performance

advantages for large scale sharing groups.

In addition, several storage systems are based

on the proxy re-encryption algorithms, in order to

achieve ﬁne grained access control {(Xiong et al.,

2012; Goyal et al., 2006),(Ateniese et al., )}. When

a recipient wants to retrieve outsourced data from the

depositor, he has ﬁrst to ask the cloud server to re-

encrypt data ﬁle using its public key and the pub-

lic master key, while considering the granted priv-

ileges. Ateniese et al. (Ateniese et al., ) propose

a proxy re-encryption scheme to secure distributed

storage systems and achieve efﬁcient access control

among dynamic groups. However, a collision at-

tack between the untrusted storage server and a re-

voked group member can be launched, which enables

to learn the decryption keys of all encrypted blocks.

In (Xiong et al., 2012), the authors design an end to

end content conﬁdentiality protection mechanism for

large scale data storage and distribution. They in-

clude many cryptographic mechanisms, namely the

proxy re-encryption and broadcast revocation. Unfor-

tunately, the subscription of a new user or the revoca-

tion of a group member requires the update of the en-

tire group with new parameters and secret keys. That

is, the complexity of user participation and revocation

in their approach is linearly increasing with the num-

ber of data owners and the number of revoked users,

respectively. To mitigate to such concern, CloudaSec

presents a ﬂexible revocation procedure, while con-

sidering a restricted member list, adapted to resource

constrained devices.

Recently, in order to achieve efﬁcient membership

revocation system, (Liu et al., 2013) adopts a group

CloudaSec:ANovelPublic-keyBasedFrameworktoHandleDataSharingSecurityinClouds

signature mechanism. They propose a multi-owner

data sharing scheme, MONA, for dynamic groups in

the cloud, while preserving identity privacy from un-

trusted servers. Nevertheless, MONA brings an extra

storage overhead at both the cloud and the group man-

ager side, for each outsourced data ﬁle.

In (Seo et al., 2013), Seo et al. propose an im-

proved mediated certiﬁcateless approach, in order to

secure data sharing in cloud servers. In fact, the ba-

sic concept of mediated cryptography is the usage of

a security mediator (SEM) which can control secu-

rity capabilities for the participating entities. Once

the SEM is notiﬁed that a group member is revoked,

it can immediately stop the user scenario. Unfortu-

nately, similarly to a proxy re-encryption scheme, this

approach involves a trusted third party, in order to

generate the partially decrypting keys. That is, it re-

quires additional storage capacities and computation

cost overhead, while considering ﬂexible user man-

agement mechanisms.

7 CONCLUSIONS

The growing need for secure cloud sharing services

and the attractive properties of the convergent cryp-

tography lead us to combine them, thus, deﬁning an

innovative solution to the data outsourcing security

and efﬁciencyissues. In this paper,we design a secure

data sharing scheme CloudaSec, for dynamic groups

in untrusted cloud storage environments. Our ap-

proach ensures the conﬁdentiality of outsourced data

in public untrusted cloud servers and deﬁnes a smooth

group revocation mechanisms. That is, ﬂexible access

control policies are enforced among users belonging

to separate groups with different privileges.

Our experimental results show the efﬁciency of

CloudaSec in scalable data sharing, while consider-

ing the impact of the cryptographic operations at the

client side.

REFERENCES

https://github.com/openstack/swift.

Ateniese, G., Fu, K., Green, M., and Hohenberger, S. Im-

proved proxy re-encryption schemes with applications

to secure distributed storage. ACM Trans. Inf. Syst. Se-

cur., 9:1–30.

Ben, L. (2007). On the implementation of pairing-based

cryptosystems.

Boneh, D. and Boyen, X. (2006). On the impossibility of ef-

ﬁciently combining collision resistant hash functions.

In In Proc. Crypto 06, pages 570–583.

Burmester, M. and Desmedt, Y. (2005). A secure and scal-

able group key exchange system. Inf. Process. Lett.,

94(3).

Dierks, T. and Rescorla, E. (2008). RFC 5246 - The Trans-

port Layer Security (TLS) Protocol Version 1.2. Tech-

nical report.

et al., T. G. (2002). GNU multiple precision arithmetic li-

brary 4.1.2.

Fugkeaw, S. (2012). Achieving privacy and security in

multi-owner data outsourcing. pages 239–244. IEEE.

Gantz, B. J. and Reinsel, D. (2012). The digital universe

in 2020: Big data, bigger digital shadows, and biggest

growth in the far east. IDC iView, (December):1–16.

Goyal, V., Pandey, O., Sahai, A., and Waters, B. (2006).

Attribute-based encryption for ﬁne-grained access

control of encrypted data. In Proceedings of the 13th

ACM conference on Computer and communications

security, CCS ’06, pages 89–98. ACM.

Liu, X., Zhang, Y., Wang, B., and Yan, J. (2013). Mona:

Secure multi-owner data sharing for dynamic groups

in the cloud. IEEE Trans. Parallel Distrib. Syst., 24(6).

Ratna, D., Rana, B., and Palash, S. (2004). Pairing-based

cryptographic protocols : A survey.

Regan, K. W. Minimum-complexity pairing functions.

Seo, S.-H., Nabeel, M., Ding, X., and Bertino, E. (2013).

An efﬁcient certiﬁcateless encryption for secure data

sharing in public clouds. IEEE Transactions on

Knowledge and Data Engineering, 99:1.

The OpenSSL Project (2003).

Wang, C., guang Qin, Z., Peng, J., and Wang, J. (2010). A

novel encryption scheme for data deduplication sys-

tem. pages 265–269.

Xiong, H., Zhang, X., Yao, D., Wu, X., and Wen, Y. (2012).

Towards end-to-end secure content storage and deliv-

ery with public cloud. CODASPY ’12, pages 257–

266. ACM.

Yu, S., Wang, C., Ren, K., and Lou, W. (2010). Achieving

secure, scalable, and ﬁne-grained data access control

in cloud computing. INFOCOM’10, pages 534–542.

Zarandioon, S., Yao, D. D., and Ganapathy, V. (2011). K2c:

Cryptographic cloud storage with lazy revocation and

anonymous access. In SecureComm, volume 96, pages

59–76. Springer.

Zhou, L., Varadharajan, V., and Hitchens, M. (2011). En-

forcing role-based access control for secure data stor-

age in the cloud. Comput. J., 54.

SECRYPT2014-InternationalConferenceonSecurityandCryptography