
Identification Technology of Mobile Phone Devices Using RFF
Saulius Japertas, Aurelijus Budnikas and Gedeiminas Činčikas
Department of Telecommunications, Kaunas university of technology, Studentų str. 50, Kaunas, Lithuania
Keywords: Rff, Wireless Devices Identification.
Abstract: The vulnerability of the device identifiers, such as IP and MAC addresses, IMEI and IMSI codes, etc.
creates threat to the information security, integrity and reliability. One of the solutions of this threat is usage
of Radio Frequency Fingerprinting (RFF) technology for identifying wireless devices based on their unique
radiation “fingerprint” as opposed to their addresses or codes. In this work identification problems of mobile
radio stations (from here in – mobile phones) are being analyzed and identification methodology for
identifying them based on the mathematical processing of front and rear fronts is proposed. All of this
provides new insight in the field of signal detection and identification, thus by using this method only the
original data is received. The purpose of this work is identification of a mobile phone, working on the DCS
(digital cellular service) frequency, based on the phone’s radiated signal time characteristics.
1 INTRODUCTION
The aim of this work is to explore the identification
possibilities of the mobile phone. Currently various
identification methods, such as identification of the
manufacturer’s model, according to the design of the
mobile phone, or identification according to the
physical and electrical parameters, or their entirety,
are being used. It is known, that each wireless device
has its own unique radiation characteristics (Danev
and Capkun, 2009), (Hall et al., 2003).
Identification of the wireless devices based on
the certain characteristics of the signal (phase, phase
and frequency errors, etc.) is proposed by other
authors (Hall et al., 2003), (Candore et al., 2009).
Technique to identify wireless device according
to its radiation characteristics is known as Radio
Frequency Fingerprinting. RFF are energy traces
that are left in the radio frequency spectrum. They
have certain characteristics that are emitted by every
transmitter. RFF allows to separate certain unique
characteristics that are radiated by every wireless
device even if several devices having the same
specifications are produced in the same plant (Danev
and Capkun, 2009), (Hall et al., 2003), (Danev et al.,
2012), (Danev et al., 2010). The essence of this
technique is that wireless devices are identified
according to the different radiation parameters such
as the phase characteristics of wireless device (Hall
et al., 2003), characteristics of various errors (Danev
et al., 2010), radiometric characteristics (Candore et
al., 2009). From these characteristics using various
mathematical models (such as Bayesian step change
detector (Hall et al., 2003) or Fisher linear
discriminant analysis (Danev and Capkun, 2009) the
certain parameters, that allow determining the
unique parameters of the transmitters, are calculated.
Identification is done by analyzing initial transient
signals.
By using RFF technique, identification system,
which can correctly determine the radio transmitter,
is formed. This system is an invaluable tool for
militaristic and civil purposes, where unauthorized
usage of electromagnetic specter is detected. It is
very useful to identify and localize the source of the
transmitted information. This system provides proof
that unsanctioned or illegal radio transmission is
being broadcasted (Shaw and Kinsner, 1997).
RFF technique is usually based on edge detection
and analysis of theirs various parameters, because
unique characteristics of every wireless device are
present within the boundary of these edges.
This technique is easily used to identify
transmitters, based on Bluetooth, 802.15.4 standard
(Danev and Capkun, 2009), WLAN 802.11 standard
(Danev and others, 2012), (Shaw and Kinsner,
1997), GSM (Zanetti and Lenders, 2012) and VHF
(Danev and others, 2012) standards.
Analysis of the aforementioned works shows that
practical usage of the identification techniques,
47
Japertas S., Budnikas A. and
ˇ
Cin
ˇ
cikas G..
Identification Technology of Mobile Phone Devices Using RFF.
DOI: 10.5220/0005011800470052
In Proceedings of the 11th International Conference on Wireless Information Networks and Systems (WINSYS-2014), pages 47-52
ISBN: 978-989-758-047-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

provided in these works, is met with certain
difficulties. The first problem is that it is quite
difficult to automate the identification process; the
second problem is the complexity of the
mathematical models, used in the identification
process (Danev and Capkun, 2009), (Hall et al.,
2003). In this work common math equations, which
can be easily implemented in the automated
identification system, are used. In this work, as well
as in many of the previous works, the identification
of the cell phone is based on the edge detection. In
this work is used a completely new methodology
based on discretization of the signals and description
on the shape of the edge by using mathematical
methods. In this paper we analyze the shape of the
signal amplitude in various aspects but do not
analyze characteristics of phase or errors.
2 EXPERIMENT AND
HARDWARE
This experiment was performed at Kaunas
University of Technology, Faculty of
Telecommunications, Radio Link laboratory. During
the experiment all mobile phones were functioning
on DCS frequency (1800MHz). All phones were
connected to the mobile network of the Tele2 Ltd.
(from herein after Tele2), one of the mobile
operators of Lithuania Republic. Algorithm of the
experiment is presented in Fig. 1.
This algorithm consists of three main parts.
1. Edge Detection. In the first part detection of
rising and falling edges is performed. This is
necessary to perform further calculations for
determining the edge curvature.
In this part the rising is detected. Firstly the
spectrum of the edge is calculated and 1ms length
part of the spectrum is taken. This part of the
spectrum is further discretized each 1µs. For each
discrete point the first derivative according to the
last discrete value is calculated. Rising edge
boundaries are detected according to the change of
this derivative.
After that boundaries of the falling edge are
detected according to the change of this derivative.
When change becomes significant enough, it is
considered, that the falling edge has begun. End of
the falling edge is considered as a point, when
change of derivative becomes low.
2. Calculation of Parameters. Calculation of
parameters is performed in the second part.
Calculation of the following rising edge
parameters is performed: the first and second
derivatives, curvature, slope coefficient. These
parameters are the central part of the work, since
they mathematically determine the shape of the
edge. If edge is a line, edge parameters of every cell
phone would be similar, but in reality they are
different.
3. Identification of the Device. In the third part
a matrix for identification of the device is created.
Figure 1: Algorithm of the experiment.
The following cell phones were tested: Nokia
X3, Nokia C3, Nokia 3600, Nokia 7260, two Nokia
6230i (further referred to as A and B), Samsung
E390.
During the work, spectrum analyzer
Rohde&Schwarz FSH8 was used. Its operating
frequency band is 9 kHz – 10 GHz. This device
ensures good sensitivity without additional amplifier
(up to – 141 dBm). Antenna used in this work was
omnidirectional and calibrated for 18700 MHz
frequency band.
During experiments in the laboratory, WLAN
networks were detected, but they did not interfere
with the experiments because their frequencies were
different (WLAN operates in 2400 MHz band and
experiments were performed in 1800 MHz band).
WINSYS2014-InternationalConferenceonWirelessInformationNetworksandSystems
48

Experiment was performed in strictly controlled
environment and on identical system settings.
During all experiments the same antenna, connector
cables and spectrum analyzer were used. To enhance
the transmitted signal and to avoid using additional
amplifying equipment we chose to use a small
distance between cell phone and spectrum analyzer
is 0.5 m. For each phone 80 measurements were
performed. Correlation coefficient of the
measurements was >95%, and error less than 8%.
Transmitted signal was initiated by call from the
mobile phone, thus monitored transmitting
frequency band was 1758-1782 MHz. Transmitted
signal frequency characteristics were collected from
3hr long calls by making a call each 2 minutes.
Results were collected on different days. No
significant differences were detected. Thus it can be
said that further experiments for certain band should
be easily performed. Stable conditions for all the cell
phones, which were used in the experiment, must be
assured. For the remaining part of the experiment a
certain frequency, in which all the following steps of
the experiment will be performed, is chosen. A 1765
MHz frequency was chosen, because signal
amplitude (strength) is strongest on this frequency.
3 RESULTS
As shown by the experiments, rising and falling
edges of all cell phones (power vs time), even of the
same brand (Nokia 6230i A and B), were different
(Fig. 2, 3).
Theoretically, duration of the rising and falling
edges are not accurately determined (but maximum
duration of the edge can be 28 µs), thus it can be
different (Molisch, 2011). Result analysis clearly
shows that longest duration of the edge change was
17 µs (Fig. 2). Thus it was decided that rising edge
will be sampled for a period of 17µs with a sampling
time of 1µs.
By sampling signal in the time axis, we obtain
specific signal amplitudes for each sampling step. In
this case we chose to discretize signal each 1 µs.
Falling edge of the signal is shown in Fig. 3. As
in the case of the rising edge, falling edges of all 7
cell phones are shown next to each other. Maximum
duration of the edge change was 16 µs, but, to meet
the identical conditions, discretization period was set
to 17 µs.
Figure 2: Rising edge.
Figure 3: Falling edge.
Average amplitudes of all rising edge signals are
shown in Fig. 4. Also noise level is addressed here.
It is obvious, that edge shapes of individual cell
phones are different. We can clearly see differences
between different mobile phones: their uniformity,
curvature, etc. In example, cell phone “Nokia X3”
has extra clear and wide signal edge curve. During
the experiment this was one of the most visually
apparent differences between rising fronts, created
by sending signals from this call phone. On the other
hand rising edge of the “Nokia C3” cell phone is
below the noise level until approximately 7 µs, thus
we can conclude that the rising edge of this cell
phone is shortest as well as steepest. Also rising
edge on a “Nokia 3600” cell phone was particularly
interesting: it has clear directivity and breaking
points.
‐70
‐65
‐60
‐55
‐50
‐45
‐40
‐35
‐30
‐25
‐20
0246810121416
Power, dBm
Time, µs
(Nokia X3)
(Nokia C3)
(Nokia 3600)
(Nokia 7260)
(Nokia 6230i A)
(Nokia 6230i B)
(Samsung E390)
Noise
Figure 4: Power of the rising edge of the cell phone signal
as function of time (averages).
Falling edges of 7 cell phones are shown in
Fig. 5. As we can see from the charts, as in the case
IdentificationTechnologyofMobilePhoneDevicesUsingRFF
49

of rising edge, “Nokia X3” has a clear breaking
point. Signal curve of cell phone “Nokia S3” is very
similar to the curve of “Nokia X3”.
Experiment results of two identical cell phones
“Nokia 6230i” should be specifically mentioned.
The first call phone was marked with letter “A”,
second – with letter “B”.
‐70
‐65
‐60
‐55
‐50
‐45
‐40
‐35
‐30
‐25
‐20
0246810121416
Power, dBm
Time, µs
(Nokia X3)
(Nokia C3)
(Nokia 3600)
(Nokia 7260)
(Nokia 6230i A)
(Nokia 6230i B)
(Samsung E390)
Noise
Figure 5: Power of the falling edge of the cell phone signal
as function of time (averages).
In references (Danev et al., 2010), (Shaw and
Kinsner, 1997) it is noted, that signal characteristics
of the cell phones of identical manufacturer and
brand should be quite similar or have slight
differences.
As we can see from Fig. 4 and 5, the difference
between such cell phones is not too big, but it is
quite significant. It will be later shown that this
difference, after mathematical processing, will
become much more apparent. Falling edge of the
cell phone “Nokia 3600”, as its rising edge, has an
apparent directional variation and several breaking
points during a 17 µs period. On the other hand
falling edge of the “Samsung E90” rapidly falls
down close to noise level but, as shown in the
diagram, later rises slightly after a rapid fall.
Duration of the falling edges is relatively slightly
shorter than the duration of the rising edges because
falling edges of most mobile phones drop down to
noise level after 14 -15 µs.
From Fig. 4 and 5 we can form an opinion that
GSM packets of a specific tested cell phone have
visually similar rising and falling edges. In example,
looking at “Nokia 3600” transmitted signal edges it
is visually apparent that shape of the falling edge is
similar to the shape of the rising edge – breaking
points and directional variations are clearly visible in
both rising and falling edges. The same applies to
both “Nokia 6230i” cell phones marked by orange
and yellow colors. It has to be said that in the cases
of other cell phones, i.e. “Samsung E930”, rising
edge is different from the falling edge. Despite that
later mathematical processing showed, that these
fronts are not their own “mirror images” according
to their shape.
As we can see from Fig. 2-5, rising and falling edges
of each phone are curves and they can be described
by the 1st and 2nd order derivatives, edge curvature
and edge slope coefficient.
The First Derivative. It is known that the first
derivative shows the speed of the functions quantity
change. Signal edges, obtained during this
experiment can be described by derivative, showing
the speed of the amplitude change. The higher this
number, the greater the change in comparison with
the previous value. As the derivative approaches
zero, the edge of the signal becomes straighter (the
form change stops). By using the results of the first
derivative we can detect the borders of the signal
edge, used to assure identical conditions to all tested
cell phones.
A combined chart of all 7 tested cell phones first
derivatives (in relative units) of the rising edge is
shown in Fig. 6.
0
1
2
3
4
5
6
7
8
9
10
11
0 2 4 6 8 10 12 14 16
The first derivative, r.u.
Time, µs
Nokia X3
Nokia C3
Nokia 3600
Nokia 7260
Nokia 6230i A
Nokia 6230i B
Samsung E390
Figure 6: The first derivative of the rising edge.
As we can see from the combined chart, the first
derivatives of each cell phone are different. It is
most visible with the cell phones “Nokia X3” and
“Nokia C3”. The first derivatives of other cell
phones are slightly lower, which means that the
changes of certain intervals are lower. A combined
chart of all 7 tested cell phones first derivatives of
the falling edge is shown in Fig. 7.
0
1
2
3
4
5
6
7
8
9
10
11
0246810121416
The first derivative, r.u.
Time, µs
Nokia X3
Nokia C3
Nokia 3600
Nokia 7260
Nokia 6230i A
Nokia 6230i B
Samsung E390
Figure 7: The first derivative of the falling edge.
Thus the charts of the first derivatives shows the
intensity of the function change over time. The
WINSYS2014-InternationalConferenceonWirelessInformationNetworksandSystems
50
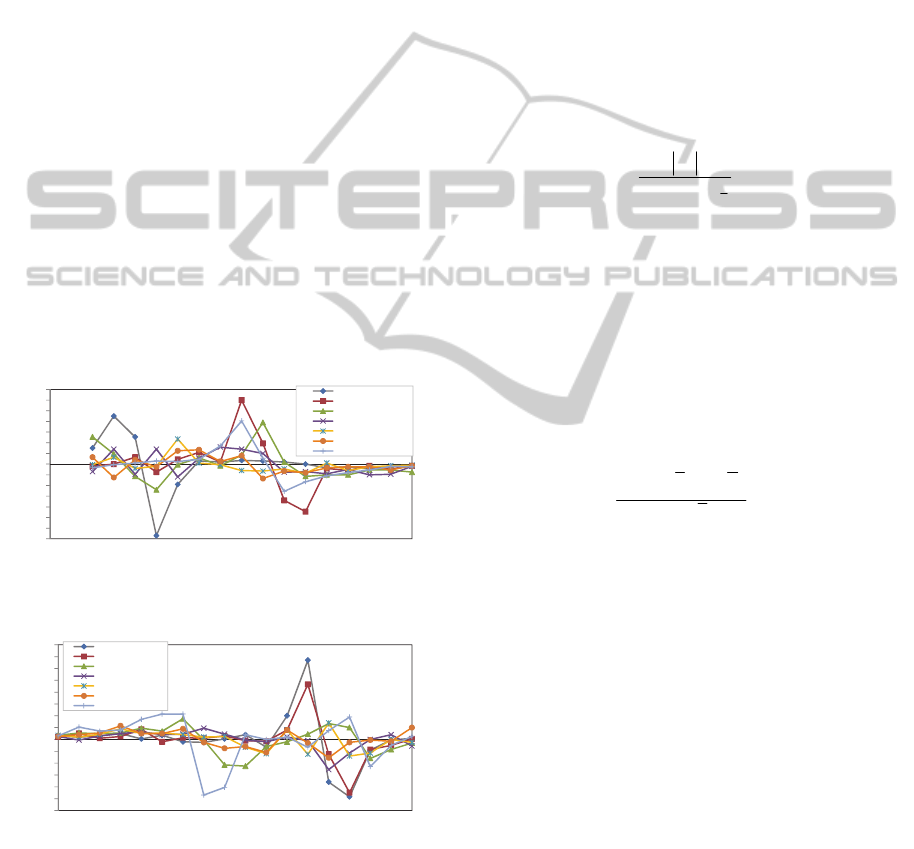
higher the intensity of this change results in higher
change of the amplitude and more apparent edge
curvature. In Fig. 6 and 7 we can see that derivatives
of the cell phones “Nokia X3” and “Nokia C3” are
the highest and in Fig. 4 and 5 we can see that the
edges of these phones are distinguished by their
individuality.
The Second Derivative. The second derivative
shows if a function has a breaking point (a point
where it’s direction changes) in the function change
interval. Existence of the breaking point is
considered the point where function of the second
derivative crosses zero axis. Results of the second
derivative of the rising edge are shown in Fig. 8 and
of the falling edge in Fig. 9.
Thus in these figures we can see a clear
differences between the second derivatives of the
edges of each phone. Changes of the second
derivative are especially clear in the case of a
“Nokia X3” with highest change being at 5 µs. Also
the value of the second derivative is big for the cell
phone “Nokia C3”. It is also apparent that the
second derivatives of various phones cross the y = 0
axis different number of times: 3 times for “Nokia
X3”, 4 for “Nokia C3” (Fig. 8). The time of these
crossings is different in each case as well.
‐7
‐6
‐5
‐4
‐3
‐2
‐1
0
1
2
3
4
5
6
7
0246810121416
The second derivative, r.u.
Time, µs
Nokia X3
Nokia C3
Nokia 3600
Nokia 7260
Nokia 6230i A
Nokia 6230i B
Samsung E390
Figure 8: The second derivative of the rising edge.
‐6
‐5
‐4
‐3
‐2
‐1
0
1
2
3
4
5
6
7
8
0 2 4 6 8 10 12 14 16
The second derivative, r.u.
Time, µs
Nokia X3
Nokia C3
Nokia 3600
Nokia 7260
Nokia 6230i A
Nokia 6230i B
Samsung E390
Figure 9: The second derivative of the falling edge.
The second derivatives of all phones first points
are not large, since as it is shown in Fig. 6, the
shapes of falling edges for all phones are bending
down slowly and do not change the direction of
approximately up to 10 s time interval. In this case,
mobile phone “Samsung E390” stands out, as the
second derivative here has a breaking point and
changes sign already at 7 µs. The highest points of
the second derivative are also at 12 µs of falling
edges curves for “Nokia X3” and “Nokia C3”
mobile phones. Curvature of these phones has been
observed at the first derivative as well.
Calculated the second derivatives of two mobile
phone signals for the same model “Nokia 6230i”
visually looks similar. However, under the analysis
it can be seen a sufficient difference. This difference
apparently could be influenced by a wider shape
(form) of mobile phone falling edge (Fig. 5).
Curvature and slope coefficient. The curvature K
of the curve can be calculated using the equation (1)
(Curvature definition, 2010):
3
2
2
''
1(')
y
K
y
(1)
where
'
y and ''y is first-and second-order
function's (in our case it is power) derivatives
respectively.
Slope coefficient b is an expression showing the
dependence of average of the random variable on the
other variable (several variables). Slope coefficient
is calculated using equation (2). It shows how the
signal edge steeply arises (or descends) (SLOPE
function definition):
2
()( )
()
x
xy y
b
xx
(2)
where x (in our case it is time) and y (in our case
it is power) are argument and function respectively.
Curvature is calculated using the first and second
derivatives. The curvature is calculated at each point
of the sampling and shows sharpness of the curve is
bending. In this case, the greater the curvature at that
point is the stronger deformation is observed. All
that is well seen by looking at the waveform.
Meanwhile, the curvature is less, the shape of signal
edge is straighter and smoother. Curvature is equal
to 0 if the waveform is straight. The curvature of
rising and falling edges are shown in Fig. 10. As it
can be seen from this figure, curvatures of different
edges are significantly different. “Nokia 3600” and
“Nokia X3” have large curvatures for the rising
edge, while phone model „Samsung E390“has the
largest curvature of falling edge. Curvatures of the
two mobile phones model of “Nokia 6230i” are also
clearly different.
IdentificationTechnologyofMobilePhoneDevicesUsingRFF
51

As mentioned above, the slope coefficient will
show the signal edge slope. This means that the
slope coefficient is higher, the mobile phone edge is
steeper. Slope coefficient is calculated from all
sampling points, i.e. using 18 points. In Fig. 11 we
can see that the lowest slope coefficient is in the
case of mobile phone “Nokia X3” raising edge.
Meanwhile, the highest slope coefficient is in the
cases of “Nokia C3” and “Samsung E390"signal
rising edges.
Thus, the presented results have shown that it is
possible to describe the rising and falling edges of
mobile phone transmitting signals using simple
mathematical categories. Following the creation of
corresponding matrix of such data, identification of
the mobile phones should be possible. The greater
number of parameters in a matrix, the higher
probability of the mobile phone identification.
However, the assessment of a larger number of
parameters and the formation of the matrix will be
done in subsequent works.
0,00
0,10
0,20
0,30
0,40
0,50
0,60
NokiaX3 NokiaC3 Nokia
3600
Nokia
7260
Nokia
6230(A)
Nokia
6230(B)
Samsung
E390
Averagecurvature,r.u.
Mobilephonemodel
RisingEdge
FallingEdge
Figure 10: Edges average curvature dependence on the
mobile phone model.
0,0
0,5
1,0
1,5
2,0
2,5
3,0
NokiaX3 NokiaC3 Nokia
3600
Nokia
7260
Nokia
6230(A)
Nokia
6230(B)
Samsung
E390
Slopecoefficient,r.u.
Mobilephonemodel
RisingEdge
FallingEdge
Figure 11: Edges slope coefficient dependence on the
mobile phone model.
Some issues are planned for further works: to
describe accurately identification algorithm for
mobile station, perform measurements with the
mobile station in further distance from the spectrum
analyzer, perform measurements with other wireless
devices.
4 CONCLUSIONS
Measurements have shown that rising and falling
edges of transmitted signal for different mobile
phones vary even when the phone models are the
same.
The experimental results of measurement are
estimated to not exceed 8% of the error; the
correlation coefficient of measurement results for
each model is > 0.95.
New digital wireless device identification
method based on assessment of signals rising and
falling edges form has been proposed. This method
is based on the calculation of rising and falling edges
parameters using mathematical methods – the first
and second derivatives, curvature and slope
coefficient.
Number of identification parameters will be
increased and the algorithm for the identification of
devices will be proposed in further works.
REFERENCES
Danev B., Capkun S., 2009. Transient-based Identification
of Wireless Sensor Nodes. IPSN’09, San Francisco,
California, USA.
Hall J., Barbeau M., Kranakis E., 2003. Proceedings of
IASTED International Conference on Wireless and
Optical Commnications (WOC), Banff, Alberta.
Candore A., Kocabas O., Koushanfar F., 2009. Robust
Stable Radiometric Fingerprinting for Wireless
Devices. IEEE International Workshop on Hardware-
Oriented Security and Trust, San Francisco, CA, USA.
Danev B., Zanetti D., Capkun S., 2012. On Physical-layer
Identification of Wireless Devices. ACM Computing
Surveys (CSUR).
Danev B., Luecken H., Capkun S., 2010. Attacks on
Physical-layer Identification. WiSec '10 Proceedings
of the third ACM conference on Wireless network
security.
Shaw D., Kinsner W., 1997. Multifractal Modelling of
Radio Transmitter Transients for Classification.
WESCANEX 97: Communications, Power and
Computing. Conference Proceedings., IEEE
Zanetti D., Lenders V., 2012. Exploring the Physical-layer
Identification of GSM Devices.
Molisch A. F., 2011. Wireless Communications, John
Wiley and Sons, 2nd Edition.
Curvature. Definitions and Examples. College of Science
and Mathematics 2010. URL: http://science.
kennesaw.edu/~plaval/math2203/curvature.pdf
SLOPE function definition on Microsoft Office support
resources. URL: http://office.microsoft.com/en-
au/excel-help/slope-HP005209264.aspx
WINSYS2014-InternationalConferenceonWirelessInformationNetworksandSystems
52
