Can Random Noise Injection Eliminate Noise?

Simulation and Hardware Implementation

Suleyman Kondakci

Faculty of Engineering & Computer Sciences, Izmir University of Economics, Izmir, Turkey

Keywords:

Signal Reconstruction, Evoked Potentials, Semi–digital Signal Processing, Simulation, Implementation.

Abstract:

Noise, found in all types of instrumentation and signal processing systems, has been a great challenge to

tackle, especially, in biomedical signal processing tasks. Often, low-frequency and low power measurement

signals are used in biomedical signal applications. This work is aimed at modeling and developing a simple,

efﬁcient, and inexpensive front end signal conditioner applying the cowpox approach to low-power analog

signal measurements. We focus here on the simulation and implementation of a signal conditioner for the

evaluation of its feasibility and efﬁciency based on the cost and accuracy constraints. As brieﬂy outlined

below, this article can serve as a model for facilitating the construction of semi–digital ﬁlters that can be

applied to denoising of signals with low-frequency and very weak amplitude levels.

1 INTRODUCTION

This article presents a framework comprised of a con-

cise theoretical background, simulations, optimiza-

tion, and implementation of a novel semi–digital

waveform denoising system that effectively enhances

signal-to-noise ratio (SNR) of highly noisy measure-

ments in real–time. The presented approach is based

on the idea of cowpox vaccination combined with

a recursive ﬁltering technique. In order to validate

the underlying method, we have built and evaluated

an experimental ﬁlter, which mainly decomposes the

noise–corrupted waveforms into a large number of

analog samples, generates random noise samples, and

injects the noise samples into the noise–corrupted

waveforms, and performs an an averaging process

in a recursive manner. The results obtained from

the implemented system comply with the results of

computer simulations and the underlying theoretical

method. Efﬁciency of the implemented system is op-

timized in terms of a desired noise reduction level,

number of recursions (waveforms), number of sam-

ples per waveform, and input noise level. There, ex-

ist several methods for ﬁltering the random noise in

biomedical instrumentations, e.g., (Guo, 2011; Os-

try, 2006a; Zerguine et al., 2011; Momot, 2009; Pal

and Mitra, 2012; Kamavuako et al., 2009; Durand

and Froment, 2001; Kadambe and Srinivasan, 2006),

and (Sharma et al., 2010) are the sources amongst a

number of them that suggest different techniques to

tackle the problem. The uniqueness of our approach

lies in the modeling of the entire process, which uses

cowpox vaccination combined with an analog register

to thwart random noise components in a signal in the

real-time. The analog register is modeled as a charge–

transfer device (CTD), which stores individual sig-

nal samples as charge units in the register, (Janesick,

2001; Pain and Fossum, 1991) and (Cain and Mor-

ling, 1977). CTD of the implemented system stores

1024 signal samples as charge units while they are

being transferred (shifted) from cell to cell in order to

avoid excessive leakage of the charges. Signal denois-

ing is done by a synchronized cowpoxing and averag-

ing technique during the charge transfer in a recursive

manner. That is, samples of the noisy signal are mixed

with random noise samples by a summation process,

the output of the summation circulates through charge

cells while being delivered to the output of the ﬁlter.

The ﬁlter output also circulates recursively through

additional cowpoxing and summation operations un-

til the desired reduction levelis achieved. The number

of recursions can be preset at the beginning of ﬁlter-

ing or it can be automatically determined by observ-

ing the mean value of the output signal whether the

mean value has reached the stationary state.

1.1 Outline of the Paper

The remainder of this paper is organized as follows.

Section 2 gives a brief review on some related work

604

Kondakci S..

Can Random Noise Injection Eliminate Noise? - Simulation and Hardware Implementation.

DOI: 10.5220/0005011906040611

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 604-611

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

and Section 3 presents the fundamental theory de-

scribing the model, which is used as the main ap-

proach for the realization of the proposed system.

Section 4 introduces the methods used for the design

of experiments and simulations used throughout the

paper. Section 5 deals with the system simulation and

discusses the dynamics of the presented algorithm.

Section 6 discusses the overall system efﬁciency and

derives the parameters for an optimum noise reduc-

tion. Section 7 introduces the realized hardware and

Section 8 concludes the paper.

2 RELATED WORK

There have recently been many attempts to remove

random noise from various types of signals using sta-

tistical inference methods mostly based on wavelet

statistical models and Bayesian estimation, (Sameni

et al., 2007). A survey of theoretical and practi-

cal aspects of hardware implementation of wavelet–

based denoising ﬁlters is presented in (Gavrincea

et al., 2007). Traditional ﬁlter implementations deal

with cutting of unwanted frequency components, typ-

ically using low–pass, high–pass, or band–pass ﬁlter-

ing conﬁgurations. Since the frequency range of ran-

dom noise covers the entire frequency bandwidth of

the processed signal, using the conventional pass/cut–

based ﬁltering method will also cut and distort the de-

sired signal while processing. The signal averaging

technique is an ideal solution to this essential prob-

lem, which recovers signal while quickly averaging

out random noise components.

The recursive semi-digital signal averaging

(RSDA) technique presented here bears also some

limitations compared to non–recursive or ﬁnite im-

pulse response (FIR) ﬁlters. Mainly, it can introduce

phase shifts cause also bandwidth limitations due to

the existence of feedback structures. This charac-

teristic can limit its applicability to measurements

involving very high frequency signal reconstruction

tasks. On the other hand, a non–recursive ﬁlter will

generally use more memory and CPU resources

for its applications, which makes its use difﬁcult

in real–time applications, and more costly as well.

Though most medical signal measurements operate

with narrow–band signals, narrow–band ﬁltering is

not considered by RSDA, however, (Choi and Cho,

2002) proposes a useful algorithm for the suppression

of narrow-band interference in direct sequence spread

spectrum systems, based on the open–loop adaptive

IIR notch ﬁltering.

The application of signal averaging techniques

are relatively old but steadily shows up in different

applications, algorithms, and modiﬁcations. For

example, as early as, (Bogdanov, 1997) has presented

a comparison of discrete and continuous average

techniques applied to multi–component force trans-

ducers. Most statistical algorithms are CPU–intensive

and require more memory usage. An algorithm for

robust weighted averaging with automatic adjustment

of insensitivity parameter is introduced in (Leski and

Gacek, 2004), where also the ensemble averaging

and weighted averaging techniques are discussed in

some context. The weighted signal averaging method

(Laciar and Jane, 2001), different from the sample–

based averaging presented here, is also sensitive to

the presence of outliers in the measurement data,

however, it has to perform intensive computations

in order to estimate the noise variance in all signal

cycles.

Adaptive ﬁltering, which has been a popu-

lar research ﬁeld for decades, is suitable for the

reconstruction of periodic signals with very low

frequencies. Though its efﬁciency is mainly based on

the recursive estimation of error–free denoising and

signal tracking parameters (Tichavsky and Handel,

1995), an adaptive ﬁlter can be effective for batch

processing, but relatively inefﬁcient in real–time

applications compared to the semi–digital averager

presented here.

Often, adaptive ﬁltering gives good performance

in low–amplitude signal measurements, e.g., an

adaptive scheme for ECG enhancement is presented

in (Almenar and Albiol, 1999). Inﬂuence of low

frequency noise in adaptive estimation using the

LMS algorithm is discussed in (Brito et al., 2009).

A relatively computation–intensive approach is pre-

sented in (Laguna et al., 1992). A noise–constrained

least mean fourth adaptive algorithm focusing on the

learning speed of the adaptive algorithm is discussed

in a newer work (Zerguine et al., 2011). Approaches

given in (Momot, 2009) deals with a comprehensive

study of weighted averaging of electrocardiogram

(ECG), which applies Bayesian inference to the

analysis of ﬁlter performance. Regarding the

electrocardiography, an alternative noise reduction

algorithm used for rhythmic and multitrial biosignals

is presented in (Celka et al., 2008).

Wavelet–based denoising using (soft) thresh-

olding involves several steps (Donoho, 1995); (1)

performing a linear forward wavelet transform of the

noisy data, (2) obtaining and performing a soft thresh-

olding of the wavelet coefﬁcients where the threshold

depends on the noise variance, and (3) the coefﬁcients

obtained from step (2) are then used to obtain the

signal estimate for the reconstruction of the signal

(linear inverse wavelet transform). Obviously, this

CanRandomNoiseInjectionEliminateNoise?-SimulationandHardwareImplementation

605

involves an excessive number of operations compared

to the sample–based averager presented here. Though

the wavelet–based methods have been relatively

successful in denoising of biological signals (Prasad

et al., 2008), RSDA offers cost–effective real–time

solutions to signal reconstruction tasks compared to

computationally intensive wavelet–based, digital IIR

and FIR approaches.

3 CONCISE DESCRIPTION OF

THE METHOD

In contrast to widely encountered approaches used for

signal denoising, we use a straightforward averaging

technique applying the cowpox approach. Therefore,

the theory behind this technique is trivial and the im-

plementation of an appropriate ﬁlter is quite uncom-

plicated. We ﬁnd several research done for denois-

ing and signal correction also applying statistical ap-

proaches, e.g., (Blanco-Velasco et al., 2008; Pal and

Mitra, 2012; Kabir and Shahnaz, 2012). For exam-

ple, (Blanco-Velasco et al., 2008) considers ECG sig-

nal denoising and baseline wander correction based

on the empirical mode decomposition, which decom-

pose a signal into a collection of AM–FM compo-

nents. Other known approaches, such as Fourier and

wavelet-based methods, use traditional data analysis

methods that require some predeﬁned preprocessing

functions to represent the signal. However, the tech-

nique presented here is uncomplicated, requires no

preprocessing, and especially efﬁcient in real-time de-

noising of evoked potentials an signals with some pe-

riodicity.

In the next section we use array notation for rep-

resenting the signal and noise samples, e.g., S[ ] and

RNG[ ] arrays. For convenience, we will use here the

vector notation to denote these quantities. The RSDA

algorithm decomposes the real–time input signal into

discrete samples represented in the form of time se-

ries consisting of the measurement signal components

(s) and independent random noise (n) components.

Thus, M × N noisy signal components are mixed to

construct a column vector space of M waveforms con-

sisting of N column vectors deﬁned as







(1,1)

(2,1)

(M,1)







, ...,c







(1,N)

(2,N)

(M,N)







. (1)

Mean value of each column vector can be obtained as

∑

r=1

(r,1)

,...,

∑

r=1

(r,N)

, (2)

where, r denotes the number of recursions, i.e., num-

ber of waveforms each with N samples. It is obvi-

ous that the average values c

,...,c

accomplish the

mean value of M waveforms into a single waveform

C, i.e., the wave sample space is now a column-wise

average of the input waveforms

C = {c

,. ..,c

As also supported by the simulation results, the higher

the number of waveforms the better denoising will be

achieved. This idea complies with the low of large

numbers, i.e., summing inﬁnitely many large random

numbers will tend to be zero, see also Borel’s low

of large numbers, (Wen, 1991). Similarly, with the

cowpox approach here, we recursively add as many

noise samples as possible to the noisy signal so that

the noise samples from the original signal will be sub-

stantially reduced. The larger the number of repeti-

tions, the better the approximation tends to be. It can

be easily veriﬁed that the above averaging process can

be expressed in terms of a recursive function

W =

∑

r=1

(r,n)

n=1,2,...,N

. (3)

Where,

(r,n)

denotes the average value of rth itera-

tion of the input signals each having n samples, where

n can be set to at least 256 or more (e.g., 8192), de-

pending on the sampling frequency and the quality of

denoising required.

4 TEST SETUP

In order to determine the major parameters needed for

an adequate system implementation a detailed simu-

lation and associated real-time experiments with the

implemented prototype system have been performed.

With the test diagram shown in Figure 1, two types

of signals, ECG signals and stimuli responses of elec-

trodermalmeasurements (i.e., skin conductance)were

experimented together with a white noise source.

Thoughwe apply a special form of the averagingtech-

nique to mostly periodic signals, we ﬁnd several dis-

tinctive approaches applied to different types of sig-

nals. The algorithm and source chosen for the gener-

ation of the random noise play an important role with

the cowpox method. Although we can ﬁnd several im-

plementations of random noise generators, e.g., (Lee

et al., 2006) and (Ostry, 2006b), we preferred using a

very special method due to its strengths underlined

below. Our random noise generator (RNG) gener-

ates a sequence of 24-bit real numbers with uniform

distribution and highly independent outcomes in the

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

606

Filter

Filtered

Output

Noise

Output

RNG

In(ωt)

∑

In(ωt)

remover

RNG = Random Noise Generator

Figure 1: Diagram of the simulation and experiment setup,

where RNG denotes the random noise generator and In(ωt)

denotes the noisy measurement signal.

generated bit sequence. That is, the frequency of oc-

currence of each number in the sequence is approx-

imately the same (uniformity), and no one value in

the sequence can be inferred from the others (inde-

pendence). Due to its strength and easy of imple-

mentation, we have used the Blum-Blum-Shub (BBS)

algorithm, (Blum et al., 1986), which is claimed to

be a cryptographically secure pseudo-random bit gen-

erator. Considering BBS as RNG for all practical

purposes, the generated bit sequence is unpredictable

(extremely random). The strength of such a pseudo-

random number generator is such that given the ﬁrst

k bits of the sequence, there is no practical algorithm

that can allow us to guess whether the next bit will

be 0 or 1 with probability greater than 1/2. Thus, the

RNG unit (Figure 1) generates 24-bit random noise

samples, which are further added to the noisy input

signal sample-by-sample. For the simulation real–

valued scalar quantities of clean input with a constant

gain K and a noise signal were generated by

S[ ] = K sin



2πn



, n = 0,1, ...,N, (4)

and

RNG[ ] = random(SNR,N); −60≤ SNR ≤ 0, (5)

respectively. Arranging the generated bits in the ar-

ray byte[ ] as a stream of 24-bit blocks (bytes each

having 24 bits) and passing the bit blocks byte-by-

byte through a 24–bit digital-to-analog (DAC) con-

verter produces a relatively high–resolution analog

data sample, which is stored in the random number

generator array RNG[ ]. That is, RNG[ ] is now an

array of N real numbers representing the noise sam-

ples. SNR denotes the signal–to–noise ratio in dB and

N denotes the number of samples for both input and

noise signals. As will be justiﬁed later, the higher the

number of samples, the better the noise reduction can

be achieved. Noisy input signal (w) to the averager

is constructed as sample–by–sample addition of the

elements of arrays S[ ] and RNG[ ]. The analog mem-

ory (CTD) used for the implementation of the ﬁlter

has a charge leakage factor that can diminish the sig-

nal level. The leakage factor can have a great impact

on the output if the number of recursions is extremely

high. Hence, the instantaneous level (ith sample) of

the signal measured at the output of the ﬁlter will cor-

respond to

A × (W

+ RNG

), A = e

−εrC



1−cos

2π



, (6)

where r denotes the current recursion count, A de-

notes the overall transfer function of CTD having C

memory cells, and ε stands for leakage factor for each

cell. In order to achieve higher accuracy, the transfer

function will be later (Section 5) modiﬁed with regard

to both signal and sampling frequencies and the num-

ber of recursions as well.

5 SIMULATION

In order to determine parameters for an optimum re-

source usage (CPU time and memory) and for the se-

lection of additional system components needed for

the realization of the system, we have simulated the

overall system with various conﬁgurations. In this

concise version of the paper, we present only a brief

formulation, related simulations, the implementation

of the simulated system, and results of experiments

with the implemented system. The simulation was

ﬁrst carried on with the straightforward addition of

waveforms sample–by–sample

(r,n)

= W

(r−1,n)

+ w

(r,n)

, (7)

which has gradually increased the amplitude of the

sum with the increased number of iterations. Indeed,

this approach constitutes the ”traditional averaging”

technique invented several decades ago.

Obviously, increasing the number of recursions of

ensemble averaging leads to instable outputs. Refer-

ring to the results from both simulations and real–time

experiments, we have observed a signiﬁcant level of

saturation in the output signal. If, after each recur-

sion, the output were scaled down by a certain factor,

the output could be kept at a stable level. Hence, Eq.

(7) has been experimentally modiﬁed to be

(r,n)

= A

(r−1,n)

(r,n)

− W

(r−1,n)

. (8)

Actual system parameters such as gain and charge

transfer leakage factor of the CTD used in the system

implementation were also modiﬁed in order to match

the simulation results. Most appropriately, the trans-

fer function

A = e

−εrC



1−cos

2πf



describing both the gain and the leakage factor of the

device chosen has been inserted into the averaging

CanRandomNoiseInjectionEliminateNoise?-SimulationandHardwareImplementation

607

function. Where, ε denotes the charge leakage factor,

r number of recursions, C gives the number of charge

cells, f and f

depict the signal and sampling frequen-

cies, respectively. Some results of the simulated ex-

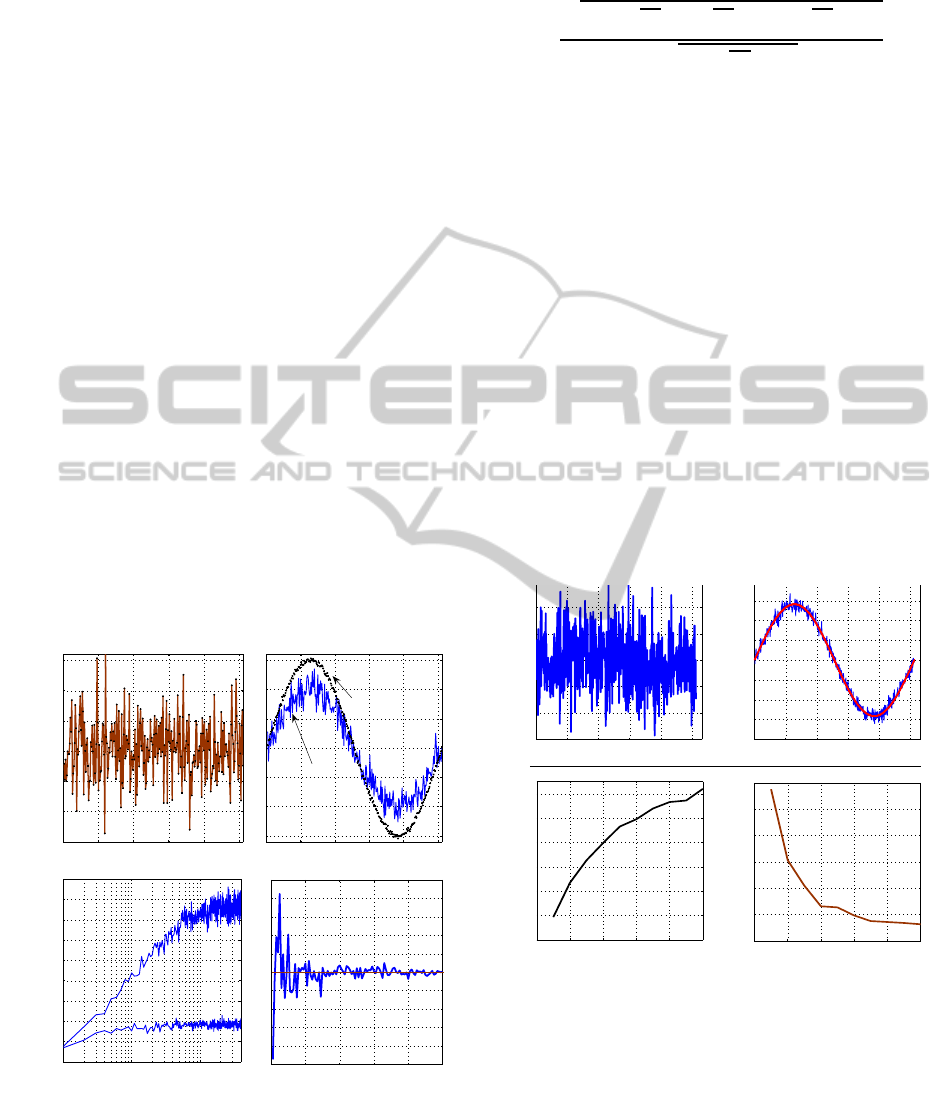
periments are shown both in Figure 2 and Figure 3.

6 EFFICIENCY AND

OPTIMIZATION

We strictly aim at ﬁnding an optimum recursion count

that minimizes the noise level to an acceptable level.

Thus, it is important to determine the optimum num-

ber of recursions (i.e., processing power) needed to

effectively reconstruct a noisy signal in terms of a

desired reduction factor. Figure 2 (a) and (b) show

the results from a simulated ﬁltering process, whereas

Figure 2 (c) depicts the noise reduction with respect to

the number of recursions and Figure 2 (d) illustrates

the mean value of the averaged signals at each itera-

tion. The normalized noise reduction factor R can be

parameterized as

R ≡ f (ψ,r,N,K),

which can be further expressed in terms of RMS

input–output ratio ψ combined with the number of

samples per waveform (waveform size N) and the

0 50 100 150 200 256

−300

−200

−100

100

200

300

Amplitude

(a) Noisy Input; SNR =−40dB, 256 samples

0 50 100 150 200 256

−1.5

−1

−0.5

0.5

1.5

(b) Reconstructed signals

10 100 1000

(Recursions)x10

Log (reduction)

0 20 40 60 80 100

−10

−8

−6

−4

−2

(Recursions)x100

(d) Means at different recursions

Output of −10 dB input

Output of −40 dB input

Figure 2: The tendency in the mean values and noise re-

duction of reconstructed waveform using 10.000 recursions:

(a) Noisy input with -40dB SNR, (b) Filtered signals with

-10dB and -40dB inputs, (c) Noise reduction versus recur-

sions, (d) Mean values of ﬁltered waveforms versus recur-

sions.

number of recursions r as

R =

∑

n=1



(r,n)

−

(r−1,n)



+ W

(r−1,n)

∑

n=1

(

(r,n)

)

. (9)

As depicted in Figure 2 (c), increase in the noise re-

duction is aligned with the theoretical description of

the input–output ratio ψ = RMS(In)/RMS(Out) and

the current number of recursions r until the estima-

tion parameters match the sample deviation and sam-

ple mean values, i.e., σ

≈ 1 and µ ≈ 0. The ef-

fect of the recursion count is illustrated in Figure 3,

where a 512 sample extremely noisy input signal, Fig-

ure 3 (a), was denoised using 4096 recursions, Figure

3 (b). The evolution of the cumulative reduction in

noise is shown in Figure 3 (c), and the corresponding

RMS values of the ﬁltered output at different recur-

sion counts are shown in Figure 3 (d). These results

comply with the theoretical analysis, which empha-

size the fact that the amount of random noise will

always tend to converge to zero with the increased

amount of injected noise quantity along with the in-

creased number of recursions. Figure 6 and 6 show

other results from the implemented system, which has

been tested with an extremely noisy sinusoidal stimu-

lus applied to a skin admittance measurement.

0 100 200 300 400 500

−30

−20

−10

(Samples)x8

Amplitude

0 100 200 300 400 500

−2

−1.5

−1

−0.5

0.5

1.5

(Samples)x8

Amplitude

0 2 4 6 8 10

(Samples)x400

20 log(RMS In/Out))

Noise Reduction

0 2 4 6 8 10

0.05

0.1

0.15

0.2

0.25

(Samples)x400

Mean value

Mean of averaged waveform

Figure 3: Effect of the injected white noise amount and the

recursion count varying from 64 to 4096 iterations.

7 PROTOTYPE

IMPLEMENTATION

We have designed and tested a relatively simple and

effective semi-digital system. A simpliﬁed block dia-

gram of the implemented system is shown in Figure

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

608

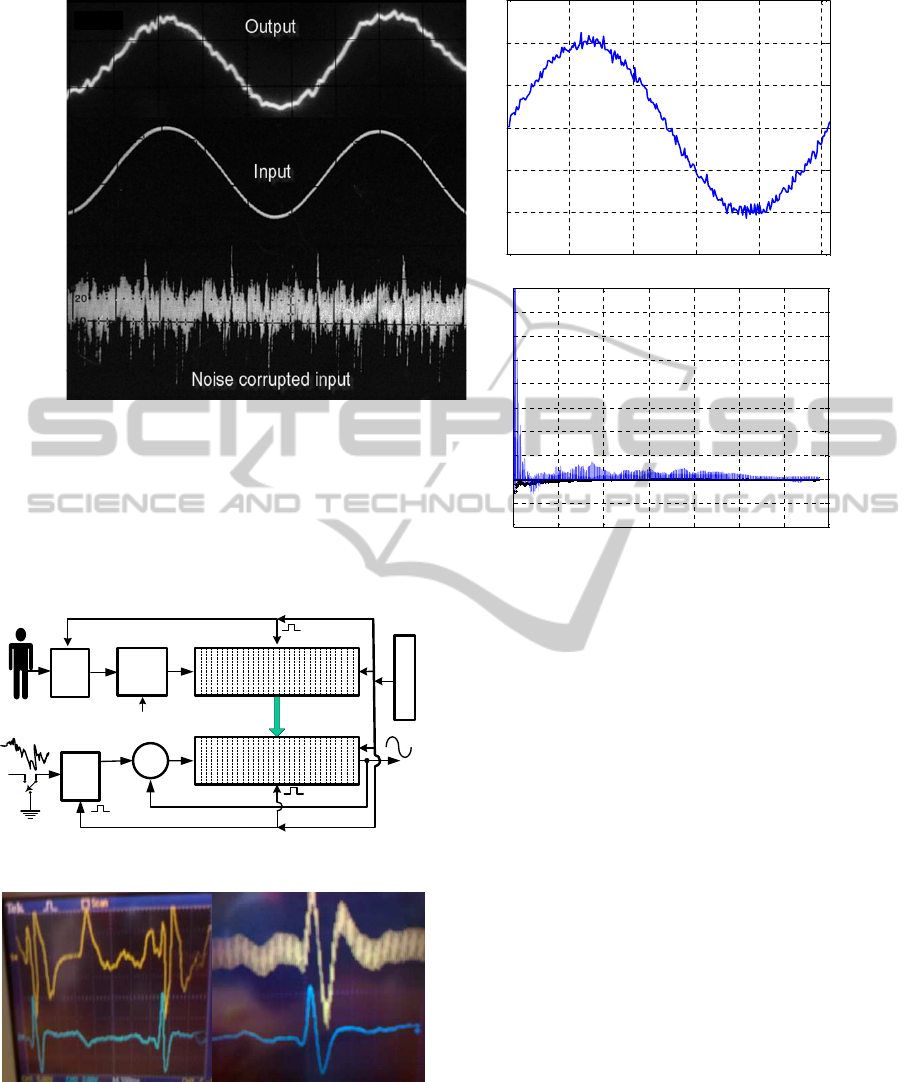
0 50 100 150 200 256

-1.5

-1

-0.5

0.5

1.5

0 1 2 3 4 5 6 7

x 10

-0.05

-0.025

0.025

0.05

0.075

0.1

0.125

0.15

0.175

0.2

Recursions

(a) Photo of the implementation result:

Oscilloscope screen of the real-time reconstruction

of extremely noisy input and denoised output using

68.000 recursions on the input with -40dB SNR.

(b) Simulation result of the same setup.

(b) Simulation

(a)

Figure 6: Oscilloscope snapshot of noisy and clean inputs and outputs of an experiment and its simulation results.

S/H

Front end CTD

CLK-1

∑

S/H

Filter

Output

Processor CTD

Shift

CLK-2

Outlier

reject

Trigger &

Gain set

Control logic

Random noise

Figure 4: Block diagram of the prototype system.

(a) (b)

Figure 5: Construction of corrupted ECG signals, (a) with

electrode motion artifact, (b) with addition of power-line

signal.

4. Its hardware implementation contains two charge

transfer devices (CTDs) each consisting of 1024 ana-

log memory cells. The CTDs are bucket brigade de-

vice, (Scott and Chamberlain, 1980), type analog de-

lay line circuits manufactured by EG & G Reticon

Results of an experiment with recording of a real–

time electrocardiogram (ECG) is shown in Figure 5,

where the ﬁrst ECG signal was corrupted due to elec-

trode motion artifacts and the second reading was su-

perimposed by 50 Hz power-line signal.

8 CONCLUSIONS

In this article, we described a simple and efﬁcient

method for signal reconstruction covering simulations

and design of a unique system that effectively en-

hances SNR in real–time. Basic theory of the pro-

posed system is already known from before, how-

ever, the approach and the design described here are

unique and efﬁcient. Random noise injection into

noisy measurements is the novelty of our approach

not shown elsewhere. It is shown here that apply-

ing this approach (cowpox) to noisy signals followed

by averaging process can perform a superior denois-

ing, given that the noise of the input signal is also

random. The results obtained from the simulations

and real–time experiments comply with the associ-

ated theoretical analysis of signal averaging. Due

to extensive resource usage, digital signal averaging

CanRandomNoiseInjectionEliminateNoise?-SimulationandHardwareImplementation

609

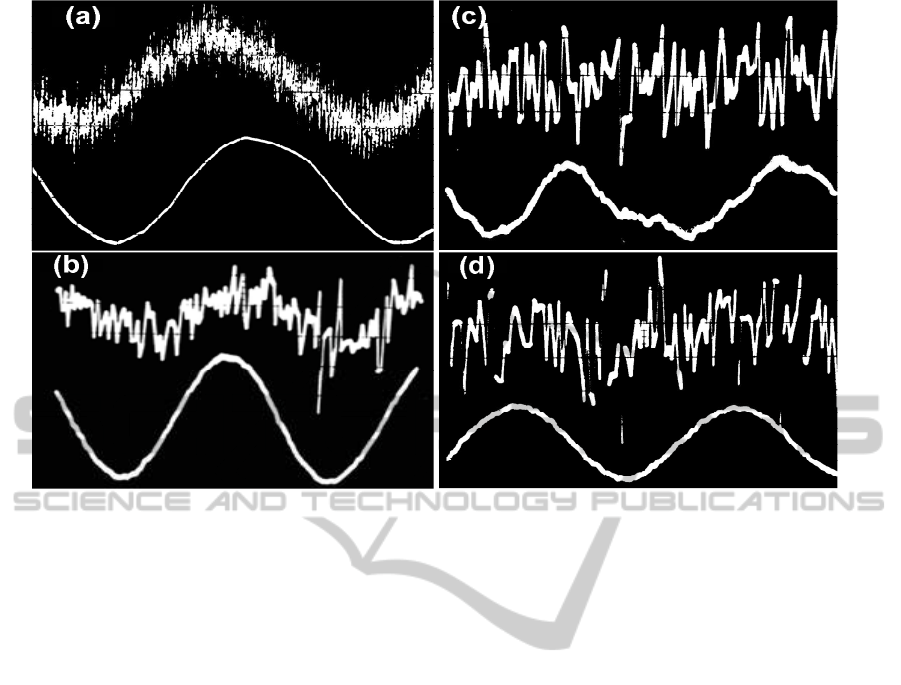
Figure 7: Oscilloscope snapshots of noisy inputs and denoised outputs.

technique is far more costly to implement compared

to its semi–digital counterparts. The unique design

presented here provides us a signiﬁcantly inexpensive

solution that can deal with noisy analog signals hav-

ing very low frequency and amplitude ranges.

REFERENCES

Almenar, V. and Albiol, A. (1999). A new adaptive scheme

for ecg enhancement. Signal Process., 75(3):253–263.

Blanco-Velasco, M., Weng, B., and Barner, K. E. (2008).

ECG signal denoising and baseline wander correction

based on the empirical mode decomposition. Comput-

ers in Biology and Medicine, 38(1):1 – 13.

Blum, L., Blum, M., and Shub, M. (1986). A simple un-

predictable pseudo random number generator. SIAM

J. Comput., 15(2):364–383.

Bogdanov, V. V. (1997). Comparison of the efﬁciency of av-

eraging the signal from multicomponent force trans–

ducers by direct and discrete methods. MECHANI-

CAL MEASUREMENTS, 4(7):646–651.

Brito, D. S., Aguiar, E., Lucena, F., Freire, R. C. S., Yasuda,

Y., and Barros, A. K. (2009). Fast communication: In-

ﬂuence of low frequency noise in adaptive estimation

using the lms algorithm. Signal Process., 89(5):933–

940.

Cain, G. and Morling, R. (1977). C.C.D. processor for

simultaneous time stretching and signal averaging.

Electronics Letters, 13(9):269–270.

Celka, P., Le, K., and Cutmore, T. (2008). Noise reduction

in rhythmic and multitrial biosignals with applications

to event-related potentials. Biomedical Engineering,

IEEE Transactions on, 55(7):1809–1821.

Choi, J. W. and Cho, N. I. (2002). Suppression of narrow-

band interference in ds-spread spectrum systems using

adaptive iir notch ﬁlter. Signal Process., 82(12):2003–

2013.

Donoho, D. (1995). De-noising by soft-thresholding. In-

formation Theory, IEEE Transactions on, 41(3):613–

627.

Durand, S. and Froment, J. (2001). Artifact free signal

denoising with wavelets. In Acoustics, Speech, and

Signal Processing, 2001. Proceedings. (ICASSP ’01).

2001 IEEE International Conference on, volume 6,

pages 3685–3688 vol.6.

Gavrincea, G., Tisan, A., Buchman, A., and Oniga, S.

(2007). Survey of wavelet based denoising ﬁlter de-

sign. In Electronics Technology, 30th International

Spring Seminar on, pages 112–116.

Guo, H. (2011). A simple algorithm for ﬁtting a gaussian

function [dsp tips and tricks]. Signal Processing Mag-

azine, IEEE, 28(5):134 –137.

Janesick, J. R. (2001). Scientiﬁc Charge–coupled De-

vices. SPIE Press Monograph Vol. PM83, Belling-

ham, Washington.

Kabir, M. A. and Shahnaz, C. (2012). Denoising of ECG

signals based on noise reduction algorithms in EMD

and wavelet domains. Biomedical Signal Processing

and Control, 7(5):481 – 489.

Kadambe, S. and Srinivasan, P. (2006). Adaptive wavelets

for signal classiﬁcation and compression. {AEU} -

International Journal of Electronics and Communica-

tions, 60(1):45 – 55.

Kamavuako, E. N., Yoshida, K., and Jensen, W. (2009).

Variance-based signal conditioning technique: Com-

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

610

parison to a wavelet-based technique to improve

spike detection in multiunit intrafascicular recordings.

Biomedical Signal Processing and Control, 4(2):118 –

126.

Laciar, E. and Jane, R. (2001). An improved weighted

signal averaging method for high-resolution ECG sig-

nals. Computers in Cardiology 2001, pages 69–72.

Laguna, P., Jane, R., Meste, O., Poon, P., Caminal, P.,

Rix, H., and Thakor, N. (1992). Adaptive ﬁlter for

event-related bioelectric signals using an impulse cor-

related reference input: comparison with signal av-

eraging techniques. Biomedical Engineering, IEEE

Transactions on, 39(10):1032–1044.

Lee, D.-U., Villasenor, J., Luk, W., and Leong, P. (2006).

A hardware gaussian noise generator using the box-

muller method and its error analysis. Computers,

IEEE Transactions on, 55(6):659 –671.

Leski, J. and Gacek, A. (2004). Computationally effective

algorithm for robust weighted averaging. Biomedi-

cal Engineering, IEEE Transactions on, 51(7):1280–

1284.

Momot, A. (2009). Methods of weighted averaging of ecg

signals using bayesian inference and criterion func-

tion minimization. Biomedical Signal Processing and

Control, 4(2):162 – 169.

Ostry, D. (2006a). Synthesis of accurate fractional Gaussian

noise by ﬁltering. Information Theory, IEEE Transac-

tions on, 52(4):1609–1623.

Ostry, D. (2006b). Synthesis of accurate fractional gaussian

noise by ﬁltering. Information Theory, IEEE Transac-

tions on, 52(4):1609 –1623.

Pain, B. and Fossum, E. (1991). Analog dynamic random-

access memory (ADRAM) unit cell implemented us-

ing a CCD with feedback. Electron Devices, IEEE

Transactions on, 38(1):178–179.

Pal, S. and Mitra, M. (2012). Empirical mode decompo-

sition based ECG enhancement and QRS detection.

Computers in Biology and Medicine, 42(1):83 – 92.

Prasad, V., Siddaiah, P., and Rao, B. (2008). Denoising of

biological signals using different wavelet based meth-

ods and their comparison. Asian Journal of Informa-

tion Technology, 7(4):146–149.

Sameni, R., Shamsollahi, M., Jutten, C., and Clifford, G.

(2007). A nonlinear bayesian ﬁltering framework

for ECG denoising. Biomedical Engineering, IEEE

Transactions on, 54(12):2172–2185.

Scott, D. and Chamberlain, S. G. (1980). Modeling and

experimental simulation of the low-frequency transfer

inefﬁciency in bucket-brigade devices. Electron De-

vices, IEEE Transactions on, 27(2):405–414.

Sharma, L., Dandapat, S., and Mahanta, A. (2010). Ecg sig-

nal denoising using higher order statistics in wavelet

subbands. Biomedical Signal Processing and Control,

5(3):214 – 222.

Tichavsky, P. and Handel, P. (1995). Two algorithms

for adaptive retrieval of slowly time-varying multiple

cisoids in noise. Signal Processing, IEEE Transac-

tions on, 43(5):1116–1127.

Wen, L. (1991). An analytic technique to prove borel’s

strong law of large numbers. The American Mathe-

matical Monthly, 98(2):146–148.

Zerguine, A., Moinuddin, M., and Imam, S. A. A. (2011). A

noise constrained least mean fourth (nclmf) adaptive

algorithm. Signal Process., 91:136–149.

CanRandomNoiseInjectionEliminateNoise?-SimulationandHardwareImplementation

611