Relationship between Simulink and Petri Nets

Debjyoti Bera

, Kees van Hee

and Henk Nijmeijer

Dynamics and Control, Department of Mechanical Engineering, TU Eindhoven, Eindhoven, The Netherlands

Information Systems, Department of Mathematics and Computer Science, TU Eindhoven, Eindhoven, The Netherlands

Keywords:

Petri Nets, Simulink, Colored Petri Nets, CPN Tools, Discrete Event Systems, Time Driven Systems, Model

Checking, Performance Analysis.

Abstract:

Matlab/Simulink is an industrial tool that is widely used to design and validate control algorithms for embed-

ded control systems using numerical simulation. A Simulink model of a control system typically deﬁnes one

or more control algorithms together with their environment. Such models exhibit both discrete and continuous

dynamics, simulated by discretizing time. On the other hand, a colored Petri net (CPN) is a well known for-

malism for modeling behavior of discrete event systems. In this paper, we give a formal semantics to Simulink

using the CPN formalism, by describing how Simulink models can be expressed as a CPN. We also show how

Petri nets can be simulated in Simulink. Finally, we show how a CPN model can be used for performance

analysis of a Simulink model.

1 INTRODUCTION

The use of Matlab/Simulink is one of the de facto

standards in the design of embedded control systems.

A Simulink model describes a time driven dynamic

system (Cassandras and Lafortune, 2006) as a set of

mathematical equations, evaluated at discrete points

in time. In general, a model of a control system con-

sists of a set of controllers and its environment (also

referred to as a plant). The goal is to deﬁne a mathe-

matical model of a controller, given a model of its en-

vironment and a set of requirements that a controller

must satisfy. Such models may contain both discrete

(difference equations) and continuous parts (differen-

tial equations). An exact solution of such a model

is in many cases not computable, therefore it is ap-

proximated by numerical simulation methods, i.e. by

discretizing time into time steps, whose minimum is

bounded by the resolution of the system. The results

obtained from numerical simulation are used as a ref-

erence to validate the behavior of both the model and

the implemented system (described in lower level lan-

guages like C).

An embedded control system is a discrete event

system (DES) (Cassandras and Lafortune, 2006)

whose state evolution depends entirely on the occur-

rence of discrete events (instantaneous) over time, like

”button press”, ”threshold exceeded” etc. The under-

lying time-driven dynamics (expressed as difference

and/or differential equations) of an embedded control

system are captured by the notion of time progression

in a state (i.e. the time elapsed between consecutive

event occurrences).

On the one hand, the formal speciﬁcation and ver-

iﬁcation of a DES is well studied in the context of au-

tomata theory (Hopcroft and Ullman, 1979) and Petri

nets (Reisig, 1985; Peterson, 1981). Both these for-

malisms have been extended with the notion of time

(Alur and Dill, 1994; Bowden, 2000) (e.g. Timed

Automata, time Petri nets) and support model check-

ing of timed properties expressed in temporal logics.

On the other hand, Simulink has only informal se-

mantics and of course an operational semantics in the

form of an implementation in software. So it is not

clear how a Simulink model can be incorporated into

a formal framework. Many attempts have been made

to address this shortcoming by proposing translations

of Simulink models into existing formal frameworks

(Agrawal et al., 2004; Denckla and Mosterman, 2005;

Tripakis et al., 2005; Tiwari, 2002; Zhou and Ku-

mar, 2012). However, most of these proposals re-

strict themselves to a subset of Simulink features and

do not formally capture the behavior of a simula-

tion run in Simulink. It is only in (Bouissou and

Chapoutot, 2012), that a formal operational semantics

of Simulink is deﬁned. Unlike other approaches that

focus on formalizing the solution method of equa-

tions encoded by a Simulink model, the semantics de-

Bera D., van Hee K. and Nijmeijer H..

Relationship between Simulink and Petri Nets.

DOI: 10.5220/0005012000120023

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),

pages 12-23

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

scribed here captures the behavior of the simulation

engine itself, describing the outcome of a numerical

simulation.

In this paper, we give a formal semantics to

Simulink models using the Petri net formalism. The

class of Petri nets present some inherent advantages

over automata: (a) Petri nets are graphically intuitive

and capture the structural information of a system,

(b) A ﬁnite automaton can be represented as a Petri

net but not vice versa; as a result Petri nets represent

a larger class of languages than the class of regular

languages, and (c) Structural analysis techniques of

Petri nets overcome the drawbacks of state space ex-

ploration techniques for analysis of behavior. Further-

more, there are many extensions of time in Petri nets

(van Hee and Sidorova, 2013) and their relationship

to Timed Automata is well studied (Bera et al., 2013;

Cassez and Roux, 2006). We focus on one such exten-

sion, namely Colored Petri nets (CPN) (Jensen et al.,

2007). A CPN is an extension of a Petri net with time

and data, and therefore an ideal choice for modeling

behavior of Simulink models. The state space reduc-

tion technique presented in (Bera et al., 2013; van Hee

and Sidorova, 2013) can be used to model check a

CPN (after discarding data). Furthermore, the mod-

eling and analysis of a CPN is well supported by the

popular CPN Tools. We also show how a Petri net

can be expressed as a Simulink model. Furthermore,

using a CPN model expressing a Simulink model, we

show how existing model checking techniques can be

used for performance analysis.

This paper is structured as follows: In the Sec. 2,

we present an informal description of Petri nets and

CPN. In the Sec. 3, we discuss the underlying con-

cepts of Simulink and show how a Simulink model

can be expressed as a CPN model. In the Sec. 4, we

show how a Petri net can be expressed as a Simulink

model. In the Sec. 5, we show how performance prop-

erties of a Simulink model can be veriﬁed. In the

Sec. 6, we present our conclusions.

2 CONCEPTS

A Petri net (PN) is a bipartite graph consisting of two

types of nodes, namely places (represented by a cir-

cle) and transitions (represented by a rectangle). We

give an example of a Petri net in the Fig. 1. The nodes

labeled P1 and P2 are called places and the node la-

beled A is called a transition. A place can be con-

nected to a transition and vice-versa by means of di-

rected edges called arcs. The notion of a token gives

a Petri net its behavior. Tokens reside in places and

often represent either a status, an activity, a resource

Figure 1: An example of PN and CPN.

or an object. The distribution of tokens in a Petri net

is called its marking or state. Transitions represent

events of a system. The occurrence of an event is de-

ﬁned by the notion of transition enabling and ﬁring.

A transition is enabled if all its input places have at

least one token each. When an enabled transition ﬁres

it consumes one token from each input place and pro-

duces one token in each output place, i.e. changes the

state. Apart from arcs between places and transitions

there are two other types of arcs, namely inhibitor and

reset arcs. An enabled transition having an inhibitor

arc (represented as an edge having a rounded tip from

transition A to place Q1) can ﬁre only if the place as-

sociated with the inhibitor arc does not contain con-

sumable tokens, i.e. place Q1. A transition connected

by a reset arc (represented as a dotted edge from tran-

sition A to place Q2) to a place, removes all tokens

residing in that place (i.e. Q2) when it ﬁres.

A colored Petri net (CPN) is an extension of a

Petri net with data and time. We give an example

of a counter modeled as a CPN in the Fig. 1. Each

place has an inscription which determines the set of

token colours (data values) that the tokens residing in

that place are allowed to have. The set of possible to-

ken colours is speciﬁed by means of a type called the

colour set of the place (for eg. the place counter has

a color set of type integer denoted by INT ). A token

in a place is denoted by an inscription of the form x‘y

(see token 1‘5), interpreted as x tokens having token

color y, i.e. as a multiset of colored tokens. Like in a

standard Petri net, when a transition ﬁres, it removes

one token from each of its input places and adds one

token to each of its output places. However, the col-

ors of tokens that are removed from input places and

added to output places are determined by arc expres-

sions (inscriptions next to arcs).

The arc expressions of a CPN are written in the

ML programming language and are built from typed

variables, constants, operators, and functions. An arc

expression evaluates to a token color, which means

exactly one token is removed from an input place or

RelationshipbetweenSimulinkandPetriNets

added to an output place. The arc expressions on input

arcs of a transition together with the tokens residing

in the input places determine whether the transition

is color enabled. For a transition to be color enabled

it must be possible to ﬁnd a binding of the variables

appearing on each input arc of the transition such that

it evaluates to at least one token color present in the

corresponding place. When the transition ﬁres with

a given binding, it removes from each input place a

colored token to which the corresponding input arc

expression evaluates. Firing a transition adds to each

output place a token whose color is obtained by eval-

uating the expression (deﬁned over variables of input

arcs) on the corresponding output arc. In our exam-

ple, the variables d1 and d2 are bound to the value

of the token (value 5) in place counter. When one of

the transitions, say add ﬁres, it produces a token with

value d1 + 1 = 6 in the place counter. Furthermore,

transitions are also allowed to have a guard, which is a

Boolean expression. When a guard is present it serves

as an additional constraint that must evaluate to true

for the transition to be color enabled. In our example,

the guard d1 < 10 ensures transition add can ﬁre if

the value of the token in place counter is less than 10.

In addition, tokens also have a timestamp that

speciﬁes the earliest possible consumption time, i.e.

tokens in a place are available or unavailable. The

CPN model has a global clock representing the cur-

rent model time. The distribution of tokens over

places together with their time stamps is called a

timed marking. The execution of a timed CPN model

is determined by the timed marking and controlled by

the global clock, starting with an initial value of zero.

In a timed CPN model, a transition is enabled if it is

both color enabled and the tokens that determine this

enabling are available for consumption. The time at

which a transition becomes enabled is called its en-

abling time. The ﬁring time of a timed marking is the

earliest enabling time of all color enabled transitions.

When the global clock is equal to the ﬁring time of a

timed marking, one of the transitions with an enabling

time equal to the ﬁring time of the timed marking is

chosen non-deterministically for ﬁring. The global

clock is not advanced as long as transitions can ﬁre

(eager semantics). When there is no longer an en-

abled transition at the current model time, the clock is

advanced to the earliest model time at which the next

transition is enabled (if no such transition then it is

a deadlock), i.e. the ﬁring time of the current timed

marking. The time stamp of tokens are written af-

ter the @ symbol in the following form x‘y@z, inter-

preted as x tokens having token color y carry a times-

tamp z. When an enabled transition ﬁres, the pro-

duced tokens are assigned a color and a timestamp by

evaluating the time delay interval, inscribed on out-

going arcs of a transition (see time interval @[a,b]).

The time stamp given to each newly produced token

along an output arc is the sum of the value of the cur-

rent global clock and a value chosen from the delay

interval associated with that arc. Note that the ﬁring

of a transition is instantaneous, i.e., takes no time.

3 EXPRESSING SIMULINK

MODELS USING PETRI NETS

In this section, we describe the basic concepts under-

lying a Simulink model, namely signals, blocks and

system. For these concepts, we give a formal seman-

tics using the CPN formalism. First, we show how a

Simulink block can be modeled as a CPN, which we

will call a P-block. A few simple rules describe how

a set of P-blocks can be connected to construct a sys-

tem, which we will call a P-system. The blocks of a

Simulink system are executed in a certain order called

the block execution order. We show how the block ex-

ecution order of a Simulink system can be modeled as

a CPN, on top of an existing P-system. The resulting

system describes fully the behavior of a simulation in

Simulink and we call it a C-system.

3.1 Signals, Blocks and System

Signals and Blocks are the two basic concepts of a

Simulink model. A signal is a step function in time,

representing the behavior of a variable. So only at

discrete points in time, the value of a variable may

change. Furthermore, a signal in Simulink can have

one of the following types: integer, real, complex or

its multi-dimensional variants.

A block deﬁnes a relationship between a set of

signals and possibly a variable representing its state

(state variable). If a block has a state variable then

it is a stateful block, otherwise it is a stateless block.

The set of signals belonging to a block are either of

type: input or output. A block can have zero or more

inputs and at most one output and one state variable.

A stateless block deﬁnes an output function f :

→ O, where I is the set of inputs, O is the set of

outputs and n is the number of inputs of the block. A

stateful block deﬁnes an output function f : I

× S →

O and an update function g : I

×S → S, where I is the

set of inputs, O is the set of outputs, S is the set of state

variables and n is the number of inputs of the block.

The output function of a stateful block must be evalu-

ated before its update function is evaluated. The result

of evaluating the update function of a stateful block

(say unit delay block as in the Fig. 2), updates its state

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

Figure 2: Commonly Used blocks in Simulink.

variable S which is expressed by S

, so S

= g(X, S).

Furthermore, the initial condition of a stateful block

is speciﬁed by the initial value of its state variable.

A block also has an associated sample time that

states how often a block should repeat its evaluation

procedure. The sample time of a block must be a

multiple of the time resolution of a system called the

ground sample time.

A Simulink model is a directed graph where a

node corresponds to a block represented as either a tri-

angle, rectangle or circle and a directed edge between

blocks corresponds to a signal. A signal models the

data dependency between the output of one block and

the input of another block. An output from a block

can be connected to input of one or more other blocks.

Note that the output of a block can be split into two

or more copies which serves as an input to multiple

blocks. However, the output signals of two or more

blocks cannot join to become one input for another

block. We call a network of blocks connected over

signals in this manner as a system. If all blocks of

a system have the same sample time then we call it

an atomic system. A subset of blocks belonging to a

system and having the same sample time is called an

atomic subsystem.

A mathematical model of a dynamic system is

a set of difference and differential equations. Such

equations can be modeled as a system in Simulink. A

simulation of such a system solves this set of equa-

tions using numerical methods. The state of a system

is deﬁned as the valuation of all its output variables

(signals) and state variables. So from an initial state

of the system the behavior in the state space is com-

puted in an iterative manner over discrete time steps

bounded by the ground sample time. A block hav-

ing a sample time equal to the ground sample time is

called a continuous block. All other blocks are dis-

crete blocks and have a sample time that is equal to

an integer multiple of the ground sample time. For

continuous integration, the whole simulation is re-

peated several times within one ground sample time

(depending on the numerical integration method, i.e.

solver type) to get a better approximation and detect

zero crossing events (Bouissou and Chapoutot, 2012).

Note that discrete blocks change their outputs only

at integer multiples of the ground sample time which

implies that the input to continuous integration blocks

remains a constant. However, we neglect the numeri-

cal reﬁnement of the ground sample time and consider

only one integration step per ground sample time.

The output and update functions of a block can be

programmed in Simulink using a low level program-

ming language such as C. However, some commonly

used constructs are available as predeﬁned conﬁg-

urable blocks in Simulink. In the Fig. 2, we give a

few examples of commonly used blocks in Simulink

consisting of ﬁve stateful blocks (unit delay, discrete

derivative, discrete integrator-A, discrete integrator-

I, continuous integrator) and three stateless blocks

(gain, add/sub and switch). We assume a ground sam-

ple time of h time units and k ∈ N.

The unit delay block is a stateful block having one

input signal X , a state variable S and one output signal

Y . A unit delay block serves as a unit buffer by delay-

ing the current value of its input signal by one sample

time, i.e. h.k time units in the following way: The

output function f assigns the current value of its state

variable to its output Y . The update function g copies

the current value of its input signal to its state vari-

able. After every h.k time units, the output function is

evaluated and then its update function.

The gain block is a stateless block that produces

as its output the current value of its input signal mul-

tiplied by some constant (speciﬁed as a block param-

eter). The add/sub block is a stateless block that pro-

duces as its output the sum/difference of the current

value of its input signals. The switch block is a state-

less block that produces as its output either the current

value of signal X or signal Y depending on the valua-

tion of the boolean expression deﬁned over signal C.

The continuous integrator block is a stateful block

that receives as its input (signal X) the derivative of

the state variable S (i.e. the rate of change of val-

uation of the state variable). The output function f

assigns the current value of its state variable S to its

output Y . The update function g, updates the value

of its state variable by integrating the product of the

derivative and the ground sample time. The discrete

integrator-I block is similar to the continuous integra-

RelationshipbetweenSimulinkandPetriNets

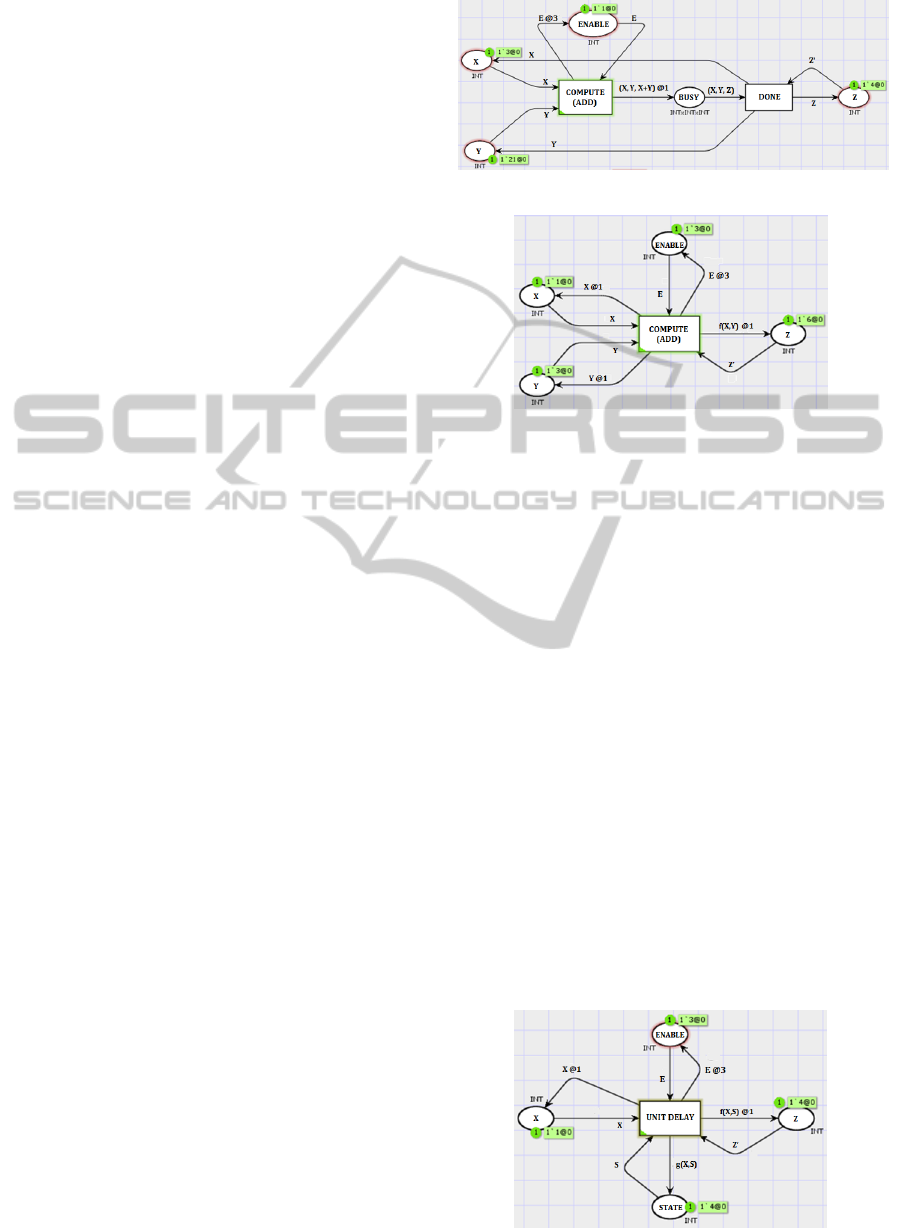
tor block. The only difference is that the sample time

of the block is an integer multiple of the ground sam-

ple time. The discrete integrator-A block accumulates

the sum of values of its input signal and updates its

state variable with this value. The output function of

this block copies the current value of its state variable

to its output. Note that Simulink blocks such as trans-

fer function and state space are similar to continuous

integrator blocks.

Modeling Simulink Blocks. In the Fig. 3, we

show with an example (add block) how a stateless

block can be modeled as a P-block. A signal is mod-

eled as a place having one colored token (see places

X, Y and Z). The valuation of this colored token is

a step function over time, i.e. its value maybe up-

dated by a transition at discrete points in time. A

stateless block has two transitions compute and done

connected over a shared place busy. The former tran-

sition has an incoming arc from each of its places

modeling its inputs and the latter is connected with

bi-directional arcs to the place modeling its output.

The availability of the token in place enable concerns

the sampling rate. The incoming arc to the place en-

able, speciﬁes the sample time of the block. In our

example, the add block has a sample time of 3, since

the token in the place enable is delayed by 3 time

units, each time the compute transition ﬁres. When a

compute transition ﬁres, it consumes one token each

from its inputs (X and Y ) and produces one token in

the place busy having a color value determined by

evaluating its output function. For an add block, the

output function f (X,Y ) = X +Y . The execution time

of the compute transition (called the block execution

time) is modeled as a delay along the outgoing arc

from the compute transition (see delay of 1 time unit

along the incoming arc to the place busy). Note that

it is also possible to specify the block execution time

as a time interval. When the token in the place busy

becomes available, transition done consumes this to-

ken and produces back one token in each of the in-

puts of the block (places X and Y with color value

unchanged) and updates the color value of the token

in its output with the computed result from the output

function. This way of modeling a P-block is good for

understanding its behavior. However, for a compact

representation, the model of a P-block can be simpli-

ﬁed by merging together the transitions compute and

done into one transition. In the Fig. 4, we show a sim-

pliﬁcation of the add block. However, such a model

can only be used if the block execution time is spec-

iﬁed as a ﬁxed point delay. This is because a time

interval specifying a block execution time allows dif-

ferent choices of timestamps for tokens produced in

the input and output places of the block. For the re-

Figure 3: An example of a Stateless Block (P-Block).

Figure 4: Simpliﬁcation of the P-Block (Stateless).

mainder of this section, we will consider block execu-

tion times as a ﬁxed point delay and use the simpliﬁed

model of a P-block to present our concepts.

The P-block of a stateful block has all the con-

cepts of a stateless block, and in addition is extended

in the following way: (a) add a special place state

containing one colored token representing the state of

the block and connect it with bi-directional arcs to the

block’s transition specifying the output function, (b)

deﬁne the update function along the outgoing arc to

place state. In the Fig. 5, we give an example of an

unit delay block modeled as a stateful P-block. The

update function g(X, S) = X is updating the state vari-

able and the output function f (X,S) = S is updating

the value of the token residing in the output place of

the block.

3.2 Modeling in Simulink

In the Fig. 6, we present an example of a cruise con-

trol system modeled in Simulink. The model is an

adaptation of the example in the paper (Bouissou and

Figure 5: An example of a Stateful Block (P-Block).

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

Figure 6: Simulink Model: Cruise Controller.

Chapoutot, 2012). We consider this example because

it is simple and covers all relevant modeling aspects

of Simulink. The system consists of three main parts:

(a) the plant (the device being controlled), (b) the PI

(proportional-integral) controller, and (c) the safety

mechanism. The plant approximates continuous be-

havior whereas the other parts are discrete. The safety

mechanism ensures that the velocity of the plant does

not exceed a speciﬁed limit.

The plant models continuous behavior of a vehicle

whose speed v and position x is given by the equation:

m ˙v = −b.v(t)+u(t) and ˙x = v(t), where m is the mass,

b is the friction coefﬁcient, ˙x and ˙v are the derivatives

of x and v w.r.t time t and u(t) is the power of the en-

gine over time. The above equation is implemented

in the Simulink model (see Fig. 6) region highlighted

as plant (continuous) consisting of one sum block,

two gain blocks that multiply their input by a factor

1/m and −b/m and one continuous integrator block

labeled dv. All blocks of the plant have a sample time

equal to the ground sample time h of the system.

A standard PI controller is modeled with its two

parts labeled proportional and integral. The goal of

the PI controller is to produce as output, the power de-

mand u(t) such that the the velocity of the plant v(t)

converges to the desired velocity, produced as output

of the switch block, as quickly as possible. Note that

the unit delay block acts as a unit buffer and serves

for discrete integration (Euler method). The remain-

ing blocks deﬁne the safety mechanism. The switch

block monitors the current velocity of the plant. If it

exceeds some speciﬁed threshold, then it produces as

its output, the output of the limit block, otherwise the

output of the set-point block is chosen. All blocks of

the PI controller and Safety are discrete and have a

sample time of h.k time units, where k is an integer.

Modeling Simulink System. Given a set of P-

blocks, we model a P-system by fusing the input

places of blocks with the output place of blocks, rep-

resenting the same signal (i.e. having the same place

label). Note that two or more blocks are not allowed

to have the same output place because in Simulink,

blocks have only one output and this is modeled in P-

blocks with a unique output place. To keep the ﬁgure

readable, we consider only the integral part of the PI

Figure 7: Dependency Graph: Cruise Controller.

controller (with h = 1 and k = 10) and model it as a

P-system in the Fig 9.

3.3 Execution of Simulink Models

The blocks of a Simulink model are executed in a

sorted order. To determine this sorted order, we dis-

tinguish between two types of blocks, namely inde-

pendent blocks and dependent blocks. If the output

function of a block is deﬁned over only its state vari-

able (i.e. does not depend on its inputs), then we call

it an independent block, otherwise we call it a depen-

dent block. The order in which independent blocks

are evaluated is not important. However, the order

in which the output of dependent blocks are evalu-

ated is important because the output of a dependent

block must be computed only after all other blocks

that produce an input to this block have been eval-

uated. This kind of dependency induces a natural or-

dering between blocks of a Simulink model which can

be represented as a directed graph (blocks as nodes,

dependency between blocks as directed edges) repre-

senting the order in which blocks of a Simulink model

must be evaluated, i.e. a directed edge from block A

to block B indicates that block A must be evaluated

before block B. We call this graph as the dependency

graph of a Simulink system. For the example pre-

sented in the Fig. 6, the dependency graph between

blocks is shown in the Fig. 7. The block sorted order

is a sorted sequence of blocks whose ordering satis-

ﬁes the dependency graph of a Simulink system. The

sorted order of a Simulink system is determined by

the simulation engine before the start of a simulation.

The simulation engine of Simulink executes the

contents of a Simulink model (blocks) according to

the block sorted order. Each execution of the block

sorted order is called a simulation step. In each simu-

lation step, every block occurring in the model is vis-

ited according to the block sorted order and the fol-

lowing condition is checked for each block: if the

time elapsed since this block’s last execution equals

its sample time, then the block produces its output,

otherwise the block execution is skipped, i.e. the

block’s functions are not reevaluated. The time that

is allowed to elapse between each simulation step is

a multiple of the ground sampling time called the

RelationshipbetweenSimulinkandPetriNets

Figure 8: Triggering Mechanism in P-blocks.

step size. The value of the step size for a given

Simulink model can be either speciﬁed explicitly or it

is determined by the simulation engine such that the

bounds on approximation errors of integrator blocks

are within some speciﬁed threshold.

The simulation engine of Simulink is able to ex-

ecute a model under two different simulation modes,

namely ﬁxed step solver and variable step solver. If a

ﬁxed step solver is chosen then a simulation step oc-

curs every step size time units. If a variable step solver

is chosen then a simulation step occurs at the earliest

time instant when at least one block in the model ex-

ists such that the time elapsed since its last execution

is equal to its sample time. The logic underlying the

variable step solver mode follows:

Given the initial conditions of a Simulink sys-

tem: initial condition of stateful blocks, current sim-

ulation time: t = 0, end time: t

, ground sample

time: h, initial step size: l = h.k, where k is an in-

teger, block sorted sequence: σ = hb

;...;b

i, where

| i ∈ 1 . . .k} is the set of k ∈ N blocks, the simula-

tion loop of a variable step is as follows:

• Loop until t ≤ t

– Evaluate output function of all blocks in the or-

der speciﬁed by σ;

– Evaluate update function of all stateful blocks;

– Detect zero crossing events (see (Bouissou and

Chapoutot, 2012));

– Update t = t + l; Determine the next simulation

step size l (an integer multiple of h);

In the ﬁxed step solver mode, the simulation step size

is a constant and zero crossing cannot be detected.

Modeling Simulink Control Flow. In the previous

section, we have seen how an arbitrary Simulink sys-

tem can be expressed as a P-system. The enabling of

P-blocks in a P-system is determined by their sam-

ple time (i.e. by the availability of token in the place

enable). This means that in each simulation step

of the model, multiple P-blocks with the same sam-

ple time can become enabled. In CPN semantics,

the choice of executing a P-block is done in a non-

deterministic manner. However, in a Simulink simu-

lation, the blocks of a Simulink model that can pro-

duce their output at a simulation step (determined by

their sample times), are evaluated according to their

block sorted order.

Consider the P-system of the integral part of the PI

controller in the Fig 9. This system has four blocks,

namely one sum block (sum2), two gain blocks (gain-

h and gain-ki) and one unit delay block. For this sys-

tem, one of the block sorted order satisfying the de-

pendency graph of the Fig. 7, is the sequence: hunit

delay; gain-h; sum2; gain-kii. The block execution

order of P-blocks of a P-system is modeled by ﬁrst

adding a trigger mechanism to each P-block and then

connecting the trigger mechanism of blocks accord-

ing to the block sorted order. We call the resulting

system a C-system.

The trigger mechanism is modeled on top of a

P-block by adding an input place trigger (labeled

trig), an output place acknowledge (labeled ack) and

a timed inhibitor transition (inhibitor arc that accounts

for the availability of token in place enable) called

skip. If the token in place trigger is available and

the token in place enable is unavailable, then the skip

transition is enabled due to the timed inhibitor arc.

Firing the skip transition does not progress time and

the execution of the block is skipped in the current

time step. If the skip transition is disabled (due to

an available token in place enable), then the block

transition (unit delay) ﬁres at its enabling time and

produces a token in the place acknowledge, delayed

by the execution time of the block (see inscription

CF@1). In both cases, one token is produced in the

place acknowledge. In the Fig. 8, we give an example

of a P-block, extended with a trigger mechanism.

Next, we model the block execution order of a

system by introducing a new transition called the

glue transition between the acknowledge and trigger

places of successive blocks as they occur in the sorted

order. The construction is carried out in the following

way: For each block occurring in the block execu-

tion order, we add one glue transition that consumes

a token from the place acknowledge of the preceding

block and produces a token in the place trigger of this

block. In this way, the C-System describes a simula-

tion run of the system. In order to allow for more than

one run of a simulation at a rate speciﬁed by the step

size: (a) we add a transition labeled closure that con-

sumes a token from the place acknowledge belonging

to the last block in the sorted order and produces a to-

ken in the place trigger corresponding the ﬁrst block

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

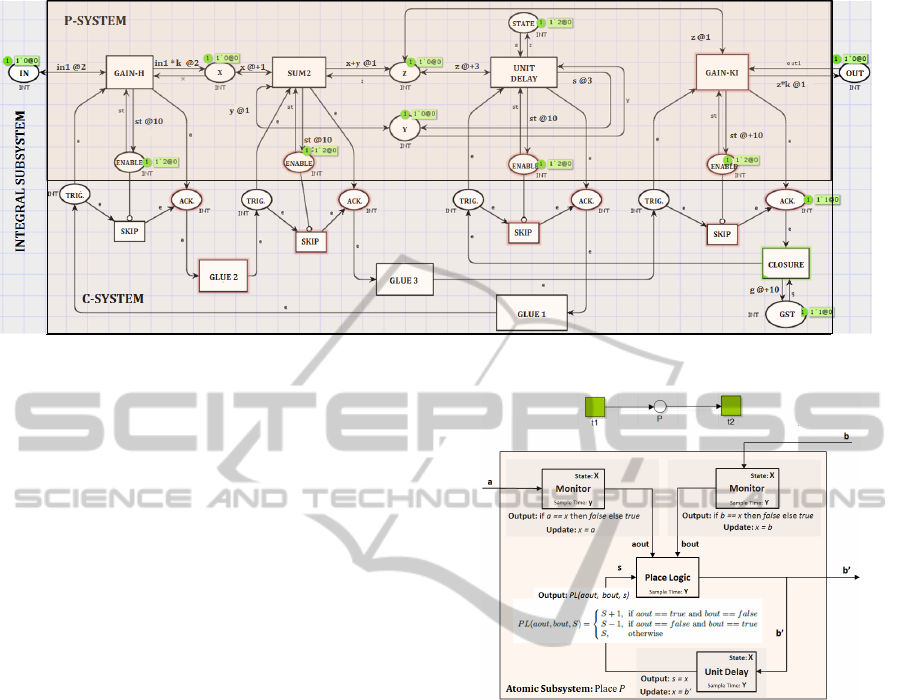
Figure 9: C-System: Integral Part (PI Controller).

in the sorted order, and (b) we initialize the place

acknowledge of the last block occurring in the block

sorted order with a token having a timestamp zero.

Furthermore, to this closure transition, we connect a

place called GST with bidirectional arcs and having

one token. On the incoming arc to the place GST , we

associate a delay corresponding the step size of the

simulation (multiple of ground sample time). As a re-

sult, a simulation run can only occur once every step

size time units. If the model has continuous blocks

then the step size must equal the ground sample time.

To simulate a variable step solver, the step size must

be equal to the least sample time of all blocks in the

system. In the Fig. 9, we describe the C-system of the

integral part of the PI controller having a step size of

10 time units.

4 EXPRESSING PETRI NETS

USING SIMULINK

In this section, we will express the semantics of a Petri

net as a Simulink system by modeling a place and a

transition as an atomic subsystem. The underlying

strategy is simple: The place subsystem keeps track

of the number of tokens and informs all successor

transitions about this value. When a transition sub-

system either consumes/produces a token, it indicates

the predecessor/successor place subsystem about the

occurrence of this event.

In the Fig. 10, we give an example of a Petri net

consisting of one place P, and two transitions t1 (pre-

transition) and t2 (post-transition), and show how the

place P of a Petri net can be modeled as an atomic

subsystem (place subsystem). The place subsystem

has two input signals (signals: a and b) and one out-

Figure 10: Modeling a Place in Simulink.

put signal (b

). The signals a and b are assumed to

be updated by the pre and post transitions t1 and t2,

respectively and the signals can either have a value

of 0 or 1. A change in the value of either of these

signals indicates that a transition has altered the num-

ber of tokens in the place. The output signal b

is an

input signal to transition t2 and has a data type inte-

ger, whose value represents the number of tokens in a

place subsystem. We call signals a and b as indication

signals and signal b

as a token signal.

The place subsystem has three stateful blocks (two

monitor blocks and a unit delay block) and one state-

less block (place logic). All the four blocks have the

same sample time equal to y time units. The input

monitor block receives an indication signal from a

pre-transition and the output monitor block receives

an indication signal from a post-transition. The two

monitor blocks compare the current value of their in-

put signal with the value recorded (i.e. state: x) from

the previous time step. If they are equal then the block

produces an output: false, otherwise it produces an

output true. The state of an unit delay block corre-

RelationshipbetweenSimulinkandPetriNets

Figure 11: Modeling a Transition in Simulink.

sponds the number of tokens in the place in the cur-

rent time step. At every time step, the unit delay block

produces as its output, the current value of its state

variable. The initial state of the unit delay block cor-

responds the initial number of tokens in the place. The

place logic block deﬁnes a function to compute the

number of tokens in the current time step depending

on the output of monitor blocks aout and bout and the

output of the unit delay block S. If either aout or bout

is true, then one of the transitions must have changed

the number of tokens in the place and the value of

signal b

must be updated (i.e. either increased or de-

creased by one), otherwise b

remains unchanged.

If a place subsystem has more than one pre-

transition, then we add for each pre-transition, one

indication signal (input) and a corresponding input

monitor block whose output is connected to the place

logic block. The logic underlying the place logic

block is extended to handle an additional input con-

dition. If a place subsystem has more than one post-

transition, then we add for each post-transition, one

indication signal (input) and a corresponding output

monitor block whose output is connected to the place

logic block. Additionally, the token signal (output) is

split as an input for each post transition.

In the Fig. 11, we give an example of a Petri net

consisting of one transition T and two places p1 (pre-

place) and p2 (post-place), and show how transition T

of a Petri net can be modeled as an atomic subsystem

(transition subsystem). The transition subsystem has

one input signal b

(token signal) as an output from

pre-place p1 and one output signal b (indication sig-

nal) that is split as an input to both its pre-place p1

and post-place p2. The current value of signal b

representing the number of tokens in the transition’s

pre-place p1. The signal b has either value 0 or 1.

The transition subsystem has two blocks having

the same sample time of z time units. The unit delay

block has a state either 0 or 1 and in each time step,

produces as its output the state of the block in the pre-

vious time step. The output of the unit delay block

is connected to the transition logic block. The tran-

sition logic block deﬁnes a function that produces as

its output a value of 0 or 1 depending on the value of

the token signal b

(from a pre-place) and the output

signal of the unit delay block. If the value of signal

is greater than zero, then it means there are enough

tokens and transition T can ﬁre. The ﬁring of a transi-

tion is indicated by a change in the value of the indi-

cation signal b such that it has a value that is not equal

to the output of the unit delay block.

If a transition subsystem has more than one pre-

place, then we add for each pre-place: one token sig-

nal as an input to the transition logic block, and split

the indication signal (output) as an input to the pre-

place subsystem. The logic of the transition logic

block is extended to change its value if and only if all

of its inputs have a value greater than zero. If a transi-

tion subsystem has more than one post-place, then we

split for each post-place, the indication signal (output)

as an input to the post-place subsystem.

An equivalent model for a network of places and

transitions can be obtained by connecting place sub-

systems to transition subsystems over their shared sig-

nals. In such a network, the place subsystems must

produce their outputs faster than transition subsys-

tems. If more than one transition shares the same pre-

place then they must have different sample times.

5 ANALYSIS

In this section, we discuss how timed properties of

a C-system can be veriﬁed by model checking tech-

niques using a simple example. In the Fig. 12, we

present an atomic subsystem modeling Euler integra-

tion with two blocks: unit delay and sum, both having

a sample time equal to 10 time units and a simula-

tion step size of 15 time units. The execution time

of the unit delay block lies in the interval of [1,3]

time units and the execution time of the sum block

is 2 time units. For analysis purposes, we modify the

C-system with one additional transition complete and

one place init (initialized with a token) with no de-

lays between them. If we consider the notion of col-

ored tokens in a state, then analysis is possible only

for a ﬁnite future (partial state space). If we drop the

notion of color from a CPN, then we obtain a sub-

class of Discrete Timed Petri nets (DTPN) (Bera et al.,

2013; van Hee and Sidorova, 2013). So for analysis

of a C-system, we will ignore color and discard places

modeling signals and states. As the state space of a

DTPN is inﬁnite because (a) time intervals on outgo-

ing arcs leads to an inﬁnite choice of timestamps for

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

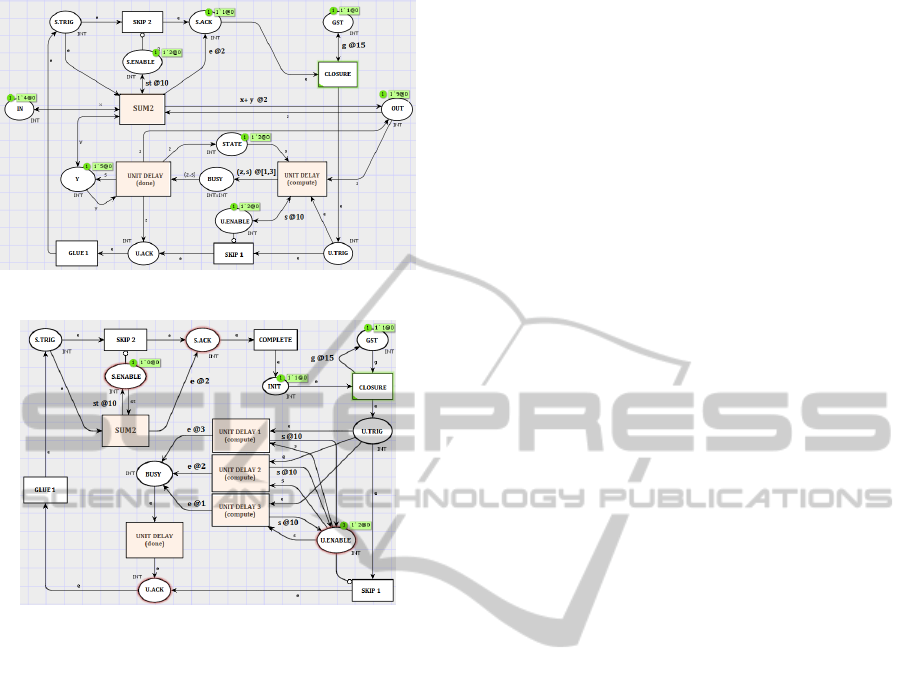
Figure 12: C-System: Euler Integration.

Figure 13: sDTPN of C-System.

newly produced tokens, and (b) time progression is

non-decreasing; model checking is not directly pos-

sible. For this a reduction method is proposed that

reduces the state space of a given DTPN into a ﬁnite

one. The reduction method progresses in two stages:

interval and time reduction.

The interval reduction step, replaces each time in-

terval on outgoing arcs of a DTPN with a set of ﬁ-

nite values in the following way: For each time in-

terval speciﬁed along an outgoing arc, construct a

set containing its lower bound, upper bound and a

ﬁnite number of equidistant points between the two

bounds such that the points are separated from each

other by a so called grid distance. The grid distance

is the least common multiple of the denominators of

all non-zero elements of the set consisting of all to-

ken timestamps in the initial marking, and the lower

and the upper bounds of all time intervals expressed as

non-reducible elements of the set of rational numbers.

The resulting net is called an fDTPN (preserves sim-

ulation equivalence). An fDTPN can be transformed

into a DTPN with outgoing arcs having only single-

ton delays by making copies of transitions and asso-

ciating each of their outgoing arcs with a unique ele-

ment from the ﬁnite set of delays associated with that

arc. The resulting net is called an sDTPN (preserves

strong bisimulation).

In our example, the C-System (DTPN) has a grid

distance equal to 1, so the time interval [1,3] associ-

ated with the outgoing arc from the unit delay transi-

tion is replaced by the ﬁnite set S = {1,2,3} and the

delay of 2 time units on the outgoing arc from the sum

transition is replaced by the singleton set {2}. The

resulting system is an fDTPN. Next, the choice of de-

lays represented by the set S on an outgoing arc from

one unit delay transition is simulated by three copies

of the unit delay transition (same preset and postset),

each having a unique delay from the set S speciﬁed

along its outgoing arc. The resulting sDTPN is shown

in the Fig. 13. Note that transitions unit delay 1, unit

delay 2 and unit delay 3 simulate the behavior of the

transition unit delay (compute).

The time reduction step, transforms a given

sDTPN into a ﬁnite transition system (rDTPN) by re-

ducing each timed marking of an sDTPN (concrete

marking) into a so called abstract marking. An ab-

stract marking represents a class of concrete markings

by aggregating them based on relative distances be-

tween timestamp of tokens. An abstract marking of a

concrete marking is obtained by subtracting the times-

tamps of all tokens in the marking by its ﬁring time.

This means the ﬁring time of an abstract marking is

zero. It turns out that for any bounded sDTPN there

exists a ﬁnite transition system (of abstract markings),

called an rDTPN (preserves strong bisimulation).

As all places have at most one token in any

reachable marking, we identify a token in a place

by the name of that place and deﬁne a marking

as a function that assigns to each token identity, a

timestamp. A marking is represented as a vector of

timestamps corresponding the ordered set of places:

[S.ENABLE; U.ENABLE; U.TRIG; BUSY; U.ACK;

S.TRIG; S.ACK; INIT; GST]. In the Fig. 14, we

present the rDTPN of our sDTPN. Consider the reach-

able concrete markings [11,10,−,−,−,−,−,3,15]

and [26,25,−,−,−, −, −,18,30] from the initial

marking of the sDTPN in the Fig. 13. From

both these markings, the earliest enabled transi-

tion is the closure transition at times 15 and 30,

respectively. So their abstract marking is L14 :

[(−4),(−5),−,−,−,−, −, (−12),0].

Timed Analysis. To analyse a C-system, we must

be able to compute the upper and lower bounds on

the time required to reach a marking m from its initial

marking m

, i.e. timed reachability.

First, we show how to compute the time taken

to execute a sequence of transitions σ = ht

;...;t

starting from the initial marking m

and leading to

marking m. Consider our sDTPN (see Fig. 13) and

its rDTPN (see Fig. 14). As all token timestamps are

RelationshipbetweenSimulinkandPetriNets

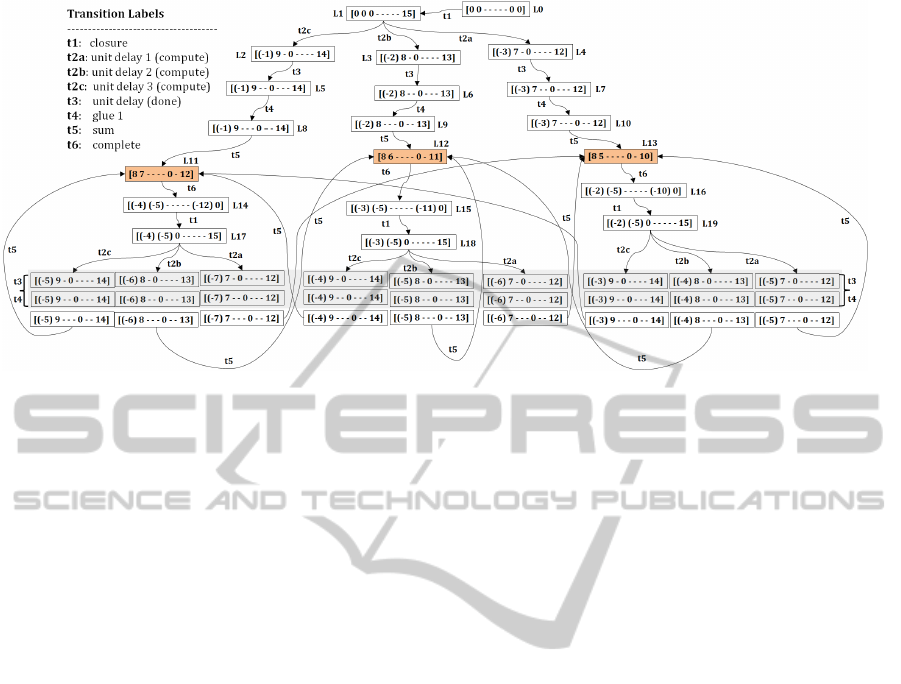
Figure 14: rDTPN.

zero in the initial marking m

, the initial marking l

of the rDTPN is an abstract marking of m

. Due to

bisimulation equivalence, the same sequence σ exists

from initial marking l

of the rDTPN, leading to a

marking l such that it is an abstract marking of m.

Then for each transition t ∈ σ, leading from an ab-

stract marking l

to the abstract marking l

, compute

the relative delay of marking l

in the following way:

Consider the marking l

as a concrete marking of the

sDTPN. From this marking, ﬁre the enabled transi-

tion t, leading to a marking, say ˜m. The ﬁring time of

marking ˜m (i.e. the earliest enabled transition) is the

relative delay of abstract marking l

. Note that the

relative delay of initial marking l

is always zero.

As an example, consider the marking L2 reach-

able from marking L1 over transition t2a. Consider

the marking L1 as a concrete marking of sDTPN. Fir-

ing transition t2a from this marking leads to marking

[0,10,−,1,−,−,−, −, 10] (in the sDTPN) with a ﬁr-

ing time 1. So the relative delay of L2 is 1.

The time taken to execute σ is the sum of all rela-

tive delays of all abstract markings visited by the tran-

sitions of this sequence. As an example, consider the

marking L12 reachable from L0 by the sequence of

transitions ht1;t2b;t3;t4;t5i. All the abstract mark-

ings visited by this sequence, except for L3 and L12

have a non-zero relative delay of 2 time units each. So

the time taken to execute this sequence is 4 units.

Next, the lower and upper bounds on the time re-

quired to reach marking m from marking m

in the C-

system corresponds the minimum and maximum of

execution times of all possible transition sequences

starting from marking l

and leading to marking l, re-

spectively. A desirable property of a well-deﬁned C-

system is formulated as: the upper bound of a run

of the block execution order must never be greater

than the simulation step size. As an example, con-

sider the set of shaded abstract markings called home

markings in our rDTPN. These markings correspond

the completion of a block execution order (token in

the place acknowledge of the sum block). So every

path starting from an initial marking or a home mark-

ing and leading back to a home marking represents

a run of the block execution order. For this, the up-

per and lower bounds of the time can be computed by

the techniques described so far. For our example, this

turns out to be in the interval of [3,5] time units. Note

that we have chosen a trivial example to present our

concepts. For a multirate system, the analysis and the

type of questions become more interesting.

An rDTPN can also be used to validate the timed

speciﬁcation of a Simulink model. Note that the unit

delay and sum blocks have the same sample time.

From its rDTPN, we verify that in every path between

home markings, one of the unit delay and sum tran-

sition always occurs. If the simulation step size is 10

time units then there exist paths between home mark-

ings where the skip transition of the sum block occurs.

Other interesting features of Simulink like deci-

sional constructs (if-then-else and switch) and loop

constructs (for and while) can also be veriﬁed using

the above techniques. These constructs can be mod-

eled in a C-system as a non-deterministic choice be-

tween triggering mechanisms of blocks (see Fig. 16).

In many Simulink systems, messages may have to

be exchanged over one or more communication chan-

nels (supported by UDP/TCP send-receive blocks).

Such a message passing mechanism is easily mod-

eled as a Petri net, which can in turn be expressed

as a Simulink system as a network of place and tran-

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

Figure 15: Petri net model of a Communication Channel.

Figure 16: Modeling Choices in C-System.

sition subsystems. In the Fig. 15, we give an example

of a Petri net modeling a communication channel with

buffer size 5. For a C-system with a communication

channel, interesting properties like buffer utilization

and system performance in the presence of communi-

cation delays may be analyzed.

6 CONCLUSIONS

Simulink is a graphical way of modeling a set of dif-

ference and differential equations whose result is sim-

ulated by discretizing time. We have shown how the

simulation behavior of Simulink models can be ex-

pressed using the formalism of CPN. As models of

this formalism can be model checked, the safety and

performance properties of a Simulink model can be

guaranteed. We also showed how Petri nets can be

simulated in Simulink. So the two formalisms are for-

mally equivalent in their expressive power. However,

the modeling comfort is different. Petri nets are a bet-

ter choice for modeling discrete events like message

passing, whereas Simulink has more built-in facilities

for numerical approximation of differential equations,

than existing tools for Petri nets. Furthermore, the

formal study of DES is deeply rooted in the theory of

Petri nets and automata theory. So the speciﬁcation

of both discrete and continuous parts of a Simulink

model using the same formalism, gives a better under-

standing of their behavior within the context of DES.

REFERENCES

Agrawal, A., Simon, G., and Karsai, G. (2004). Semantic

Translation of Simulink/Stateﬂow models to Hybrid

Automata using Graph Transformations. In Interna-

tional Workshop on Graph Transformation and Visual

Modeling Techniques, page 2004.

Alur, R. and Dill, D. L. (1994). A Theory of Timed Au-

tomata. Theoretical Computer Science, 126:183–235.

Bera, D., van Hee, K., and Sidorova, N. (2013). Dis-

crete Timed Petri nets. Computer Science Report 13-

03, Technische Universiteit Eindhoven, P.O. Box 513,

5600 MB Eindhoven, The Netherlands.

Bouissou, O. and Chapoutot, A. (2012). An Operational

Semantics for Simulink’s Simulation Engine. In Pro-

ceedings of the 13th ACM SIGPLAN/SIGBED Inter-

national Conference on Languages, Compilers, Tools

and Theory for Embedded Systems, LCTES ’12, pages

129–138, New York, NY, USA. ACM.

Bowden, F. D. (2000). A brief survey and synthesis of the

roles of time in Petri nets. Mathematical and Com-

puter Modelling, 31(10):55–68.

Cassandras, C. G. and Lafortune, S. (2006). Introduction to

Discrete Event Systems. Springer-Verlag New York,

Inc., Secaucus, NJ, USA.

Cassez, F. and Roux, O. H. (2006). Structural translation

from Time Petri Nets to Timed Automata. Journal of

Systems and Software, 79(10):1456–1468.

Denckla, B. and Mosterman, P. J. (2005). Formalizing

Causal Block Diagrams for Modeling a Class of Hy-

brid Dynamic Systems. In In IEEE CDC-ECC 05.

Hopcroft, J. E. and Ullman, J. D. (1979). Introduction

to Automata Theory, Languages, and Computation.

Addison-Wesley Publishing Company.

Jensen, K., Kristensen, L. M., and Wells, L. (2007).

Coloured Petri Nets and CPN Tools for Modelling and

Validation of Concurrent Systems. Int. J. Softw. Tools

Technol. Transf., 9(3):213–254.

Peterson, J. L. (1981). Petri Net Theory and the Modeling

of Systems. Prentice Hall PTR, Upper Saddle River,

NJ, USA.

Reisig, W. (1985). Petri nets: An Introduction. Springer-

Verlag New York, Inc.

Tiwari, A. (2002). Formal Semantics and Analysis Methods

for Simulink Stateﬂow Models. Technical Report, SRI

International.

Tripakis, S., Sofronis, C., Caspi, P., and Curic, A. (2005).

Translating Discrete-time Simulink to Lustre. ACM

Trans. Embed. Comput. Syst., 4(4):779–818.

van Hee, K. and Sidorova, N. (2013). The Right Timing:

Reﬂections on the Modeling and Analysis of Time.

In Proceedings of the 34th International Conference

on Application and Theory of Petri Nets and Concur-

rency, PETRI NETS’13, pages 1–20, Berlin, Heidel-

berg. Springer-Verlag.

Zhou, C. and Kumar, R. (2012). Semantic Translation of

Simulink Diagrams to Input/Output Extended Finite

Automata. Disc. Event Dyn. Sys., 22(2):223–247.

RelationshipbetweenSimulinkandPetriNets