Optimizing Camera Placement in Motion Tracking Systems

D´avid Szal´oki, Krist´of Csorba, G´abor Tevesz

Department of Automation and Applied Informatics, Budapest University of Technology And Economics,

Magyar Tud´osok k¨or´utja 2/Q., H-1117 Budapest, Hungary

Keywords:

Localization Accuracy, Multi-Camera System, Motion Tracking, Optimal Camera Placement.

Abstract:

This paper discusses the placement of cameras in order to achieve the highest possible localization accuracy.

It is reached by using several cameras with redundant ﬁelds of views. A camera model is introduced and the

components which cause the localization errors are identiﬁed. The localization accuracy measure is deﬁned

for one and for multiple cameras too. The problem of adding a new camera to the system in order to improve

the accuracy is formulated. The method for ﬁnding the optimal placement of this new camera is presented.

Some features are enumerated which can be applied for getting an advanced method.

1 INTRODUCTION

Object tracking is nowadays a very popular segment

of computer vision. There are application where mul-

tiple cameras are used to perform this task. The ap-

plications can be separated based on the common ﬁeld

of views of the cameras. The ﬁrst class contains ap-

plications with relatively few overlapping in the ﬁeld

of views. This class contains applications like video

surveillance systems where the observed area can be

maximized. With these systems the object tracking

has to be performed with low accuracy requirements.

Only the approximated trajectory is interesting like

in (Zhou and Aggarwal, 2006), not its accuracy.

The second class contains applications where the

localization accuracy can be helpful. There are a lot

of algorithms for the PnP problem which stands for

Perspective-n-Point problem meaning the estimation

of the pose of a calibrated camera from n 3D-to-

2D point correspondences. There are several papers

about the solution of the P3P, P4P or the general-

ized PnP problem. Some of them originate the PnP

problem in the simpler ones. There are given for this

estimation iterative (Oberkampf et al., 1996) and non-

iterative (Hesch and Roumeliotis, 2011) (Moreno-

Noguer et al., 2007) methods as well. In applications

using feature point-based camera tracking (Skrypnyk

and Lowe, 2004) (Lepetit and Fua, 2006) dealing with

hundreds of noisy feature points is required. Detailed

summary about the PnP can be found in (Wu and Hu,

2006). All of these generalized methods can be im-

proved if the nature of the noise is known. Thus our

ﬁrst goal is to determine the localization accuracy.

The calculated localization accuracy can be used to

validate the measured localization accuracy as pre-

sented in (Szal´oki et al., 2013a).

Another popular topic is the object tracking where

a high localization accuracy is required. There are ap-

plications where only the object locations are used.

If the variation of the localization could be supplied

the system performance could be improved. A typical

application is the robotic football contest (K¨appeler

et al., 2010). Here the ball is tracked with stereo cam-

eras. There are competitions where a prebuilt multi-

camera system can be used by the teams. With this

both the ball and the players can be recognized and

tracked. The information about the localization ac-

curacy could be useful for precision positioning and

aiming.

In (Ercan et al., 2007) a room is built with multiple

ﬁxed cameras. An object is tracked while it can be

hidden by some other objects from several cameras.

In this case the experimental result could be validated

with the theory of localization accuracy.

Assume that we have a camera system containing

ﬁxed and movable cameras. We would like to track

an object in the world as accurately as possible. The

movable cameras can be placed by the system opti-

mally so that the localization accuracy gets it’s high-

est possible value. The position and orientation con-

straints of the movable cameras are the limitations.

We would like to suggest a method for placing the

movable cameras in order to get the highest possible

localization accuracy.

288

Szalóki D., Csorba K. and Tevesz G..

Optimizing Camera Placement in Motion Tracking Systems.

DOI: 10.5220/0005012202880295

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 288-295

ISBN: 978-989-758-040-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

At ﬁrst a camera model has to be formulated. The

components which cause the localization inaccuracy

can be identiﬁed. The localization accuracy has to be

deﬁned and a measure has to be chosen. The nature

of these has to be examined for better understanding

their behavior. As a ﬁrst step they can be formulated

in 2D for one observed point. Later this model can

be generalized into 3D and for an observed area or

volume instead of one observed point. Finally, some

extra features can be included as the ﬁeld of view, the

dynamic constraints or the optimization of more than

one cameras together.

Please note that the presented algorithms and

methods are part of the Smart Mobile Eyes for Local-

ization (SMEyeL) system which is open-source and

is written in C++ using the popular OpenCV (Brad-

ski, 2000) computer vision library. The source code,

documentation and all the input data for the presented

measurements are available for download from our

homepage (SMEyeL, 2013).

2 LOCALIZATION ACCURACY

We assume that we use calibrated cameras. A cali-

brated camera represents a model, where the distor-

tions are identiﬁed and the pinhole camera model is

approximated during the mapping. Detailed informa-

tion about the camera model and the calibration pro-

cess can be found in (Bradski and Kaehler,2008). The

object localization has a ﬁnite accuracy, but then why

do we have localization error?

2.1 No Depth Information

One camera by itself can not provide depth informa-

tion. Based on the image of one camera only a half

line can be calculated on which the object is located.

Using every half line calculated from every camera

can be lead to localize the object. Of course in the

real world these half lines do not intersect in a sin-

gle point. Thus an optimal solution has to be found

which can be deﬁned as the object location. Detailed

calculations and experimental results can be found

in (Szal´oki et al., 2013a).

2.2 Detection Error

One camera can detect the tracked object on its own

image with an error. This is deﬁned as the detection

error. The further the object is, the larger the relative

error gets.

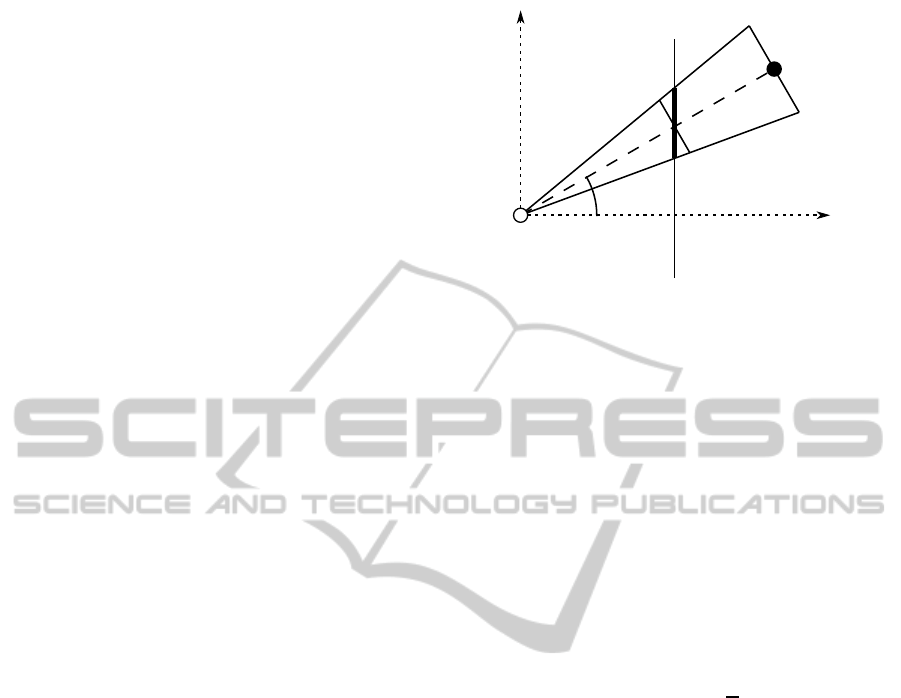
The derivation of the localization error in 2D can

be followed in Fig. 1. This ﬁgure is distorted for the

⟂

(c)

⟂

Figure 1: The derivation of the localization error from the

detection error. The camera is symbolized with the empty

circle. It is facing into the direction x and it has an imager

represented by a thin vertical line. f is the focal length. The

object is the ﬁlled circle which is located at the point x

(c)

in the camera coordinate system. The object is detected by

the camera at ϕ angle. The detection error e has a perpen-

dicular component e

⊥

. The perpendicular component of the

localization error is σ

⊥

sake of illustration, but in reality the focal length is

much larger than the detection error. This means that

the following assumption is a good approximation:

⊥

≈ e·cosϕ. (1)

This error is scaled up to the object location, so:

⊥

≈ d · cos

ϕ·

, (2)

where f is the focal length and e is the detection er-

ror of the camera. The distance of the object from

the camera is d. ϕ is the detection angle and σ

⊥

the perpendicular component of the localization er-

ror. Assuming that the camera is facing towards the

tracked object this means that the perpendicular com-

ponent of the standard deviation is proportional to the

distance of the object.

2.3 Covariance Matrix

Therefore, we can calculate the perpendicular compo-

nent of the localization error of one camera at a single

point. As shown in section 2.1 one camera can not

provide depth information. This means that the paral-

lel component of the localization error is:

→ ∞. (3)

For a point in the real world a matrix similar to

a covariance matrix can be formulated using (2) and

(3). This matrix is diagonal in the coordinate system

ﬁtted to the facing direction of the camera and it can

OptimizingCameraPlacementinMotionTrackingSystems

289

be easily transformed (rotated) into the world coordi-

nate system:

Σ = R



0 σ

⊥



, (4)

where α is the orientation of the camera and ϕ is the

detection angle. R

and R

are the rotation matrices

in 2D with angle α and ϕ respectively. σ

and σ

⊥

are the parallel and perpendicular components of the

localization error.

2.4 Using Multiple Cameras

It has been previously shown that the covariance ma-

trix for one camera observing one single point can

be calculated. If more than one camera is used, for

each camera its covariance matrix can be determined.

These matrices can be combined into one matrix con-

taining the variances of the resulting localization er-

ror. This can be achieved by applying the following

formulas incrementally:



−1

+ Σ

−1



−1

, (5)

= Σ



−1

+ Σ

−1



, (6)

where the two original densities are N (µ

, Σ

) and

N (µ

, Σ

), while the combined density is N (µ

, Σ

This is the so called product of gaussian densities.

0 50 100 150

−60

−40

−20

Figure 2: The derivation of the combined covariance ellipse.

Two cameras are observing one single point. The cameras

are represented with ﬁlled circles. The two larger ellipses

are the individual covariance ellipses of the cameras sepa-

rately. For better visualization their major axes are shrunk

so that not only two pairs of parallel lines can be seen. The

smaller ellipse is the combined covariance ellipse.

A simple example is shown in Fig. 2. The ﬁlled

circles are the cameras and the short line segments

symbolize their directions. The covariance ellipses

are drawn at a conﬁdence level of 95 %. The two

larger ones are the original ellipses of the cameras.

They are distorted, since the limit of their major axis

is ∞, but in the ﬁgure these axes are chosen in such

a way that not only two pairs of parallel lines can be

seen. The smaller ellipse is the resulting covariance

ellipse. This is not distorted and it can be observed,

that the large localization error of one camera disap-

peared, as the resulting ellipse is smaller.

It can be noticed that the original covariance ma-

trix of one camera contains an element which ap-

proaches ∞. Despite this, the inverse of this matrix

can be calculated and contains only ﬁnite elements.

According to (5) the inverse of the ﬁnal resulting co-

variance matrix is:

−1

∑

i=1

−1

, (7)

where n is the number of the cameras used for local-

ization and Σ

−1

is the inverse of the covariance matrix

of the i

camera. Since (7) contains only the inverse

matrices the inverse of the resulting matrix can be cal-

culated and it contains only ﬁnite elements. The de-

terminant of this matrix is zero if and only if there is

a speciﬁc direction in space in which the localization

has a variancewith unboundedlimit. This can occur if

the observed point and the centers of all the cameras

ﬁt on the same line. If the determinant of this ma-

trix is non-zero, the resulting covariance matrix can

be calculated and the localization has a ﬁnite variance

in every direction.

In Fig. 3 a camera conﬁguration and the resulting

covariance ellipses can be seen. The placement of the

ellipses is symmetric, since all the cameras have the

same parameters. It can be seen that the errors near

0 50 100 150

−60

−40

−20

Figure 3: The resulting covariance ellipses of the localiza-

tion using a speciﬁc camera conﬁguration.

the cameras are smaller and they have a larger vari-

ance in the y direction, while the distant ones have the

larger variance in the x direction.

The next step is to deﬁne a way to measure how

good the localization is if the tracked object is located

in a single observed point. This measure is the lo-

calization accuracy and it can be deﬁned in various

ways. In this paper two methods are discussed. In

both cases the accuracy is derived from the inverse of

resulting covariance matrix. The inverse is used be-

cause in some cases the inverse exists but the original

matrix does not.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

290

2.4.1 Determinant as Measure of Quality

First we can deﬁne the accuracy as the determinant of

the inverse covariance matrix:

det



−1



, (8)

where q

det

stands for quality using the determinant.

This measure has a physical meaning as it is inversely

proportional to the area of the covariance ellipse.

100

150

−50

0.5

1.5

2.5

x 10

Figure 4: The surface plot of the accuracy in 2D using the

previous camera conﬁguration (the same as in Fig. 3) and

the determinant measure. The measure is deﬁned in (8).

In Fig. 4 the accuracy is presented in the case of

the previous camera conﬁguration. It can be noticed

that the closer the observed point is, the better the ac-

curacy becomes. This occurs because the accuracy is

proportional to the inverse of the distance (d

−1

). Of

course an object can not be placed arbitrarily close to

one of the cameras because a camera has a physical

size and minimal focal distance.

2.4.2 Eigenvalue as Measure of Quality

Another possibility is to deﬁne the quality as the worst

case:

eig

= min



eig



−1



, (9)

where Σ

−1

is the inverse of the resulting covariance

matrix. q

eig

is the smallest eigenvalue of the inverse

matrix. This measure also has a physical meaning as

it is proportional to the largest axis of the ellipse.

In Fig. 5 the accuracy is presented in the case of

the previous camera conﬁguration using the smallest

eigenvalue of the inverse covariance matrix as mea-

sure. This is different from Fig. 4, where the deter-

minant was used as measure. Here the best quality is

achieved at a point where the detection directions of

the two cameras are perpendicular.

100

−60

−40

−20

Figure 5: The surface plot of the accuracy in 2D using the

previous camera conﬁguration (the same as in Fig. 3) and

the eigenvalue measure. The measure is deﬁned in (9).

3 ADD ONE CAMERA

Let there be given a set of ﬁxed cameras to deﬁne the

camera conﬁguration. These cameras are used for lo-

calization at a given point. We would like to add a

new camera to the system. The general problem is:

how should we place the new camera in order to in-

crease the accuracy as much as possible.

The common method is:

1. Calculate the covariance matrix of the localization

determined by the ﬁxed cameras at the observed

point.

2. Calculate the covariance matrix parametrized for

the new camera at the observed point.

3. Combine these two matrices using (5).

4. Calculate the objective function (q) deﬁned in (8)

or in (9).

5. Find the extremal points of this objective function.

Assume that the new camera is placed so that it is

facing into the direction of the observed point.

3.1 Using the Determinant Based

Measure

In this case the previously described method is used

with the determinant measure deﬁned in (8). The lo-

calization accuracy in the polar coordinate system ﬁt-

ted to the covariance ellipse generated by the ﬁxed

cameras is:

det

(α, d) = C+

B+ A· sin

, (10)

where α and d are the angle and distance in the po-

lar coordinate system. A, B and C are constant non-

negative values which are functions of the camera pa-

rameters and the ﬁxed cameras (Szal´oki et al., 2013b).

OptimizingCameraPlacementinMotionTrackingSystems

291

This means that if the new camera is placed at the

(α, d) point the localization accuracy at the origin is

equal to q

det

This formula can be easily converted into the

cartesian coordinate system:

det

(x, y) =

A· y

+ y

)

+ y

+C, (11)

where x and y are the coordinates of the new camera.

A, B and C are the previously mentioned constant val-

ues.

In Fig. 6 the contour of a speciﬁc case is plotted.

The same two cameras as in Fig. 3 observe the ori-

gin and a new camera is added. The curves are “iso-

accuracy” curves which means that if the new cam-

era is placed anywhere on a curve the resulting local-

ization accuracy becomes the same value. A curve

contained by another one has a higher localization ac-

curacy. It can be noticed from (11) that the plot has

reﬂectional symmetry with the x and y axes as well.

In this case the covariance matrix generated from the

ﬁxed cameras has two eigenvalues which rate is 1 to

3. If this rate is smaller than

, the contour plot be-

comes similar: q

det

has two local maxima, accord-

ing to the partial derivative by y. If the rate is larger

than

, the curves become convex ones and q

det

has

only one local maximum using a ﬁxed y. Detailed

calculations and experimental results can be found

in (Szal´oki et al., 2013b).

−60 −40 −20 0 20 40 60

−40

−30

−20

−10

Figure 6: The contours of the localization accuracy with the

newly added camera. The covariance matrix of the local-

ization generated by some ﬁxed cameras is known at the

origin. A new camera is added to the system. The value of

the localization accuracy with the new camera can be calcu-

lated. It is a function of the position of the new camera and

it has the same value along one curve. The closer the new

camera to the origin is, the higher the accuracy becomes.

3.2 Searching on the Boundary

Both of the partial derivatives of (11) equals zero only

at the origin, but a camera can not placed right at the

observed point. So this means that if a new camera is

placed with some constraints, the optimal placement

ﬁts on the constraint boundary. This simpliﬁes the

problem, since the extremal points of q

det

have to be

searched only on the boundary.

Another consideration can be that in the polar co-

ordinate system for any ﬁxed α

det

(α

, d

) ≥ q

det

(α

, d

) ⇐⇒ d

≤ d

(12)

This results in the optimal placement ﬁtting on the

constraint boundary since for any (α

, d

) point inside

the placing area there exists at least one point (α

, d

)

on the boundary where (12) is satisﬁed.

Assume that the boundary can be written as a

union of functions with one parameter:

[

{(x, y)|x = f

(t), y = g

(t), t ∈ [0..1]} (13)

If the extremal points are searched for on the i

boundary segment, the following has to be solved:

(opt)

= arg max

0≤t≤1

(t), (14)

where

(t) = q

( f

(t), g

(t)) = q

(x, y), (15)

which is the localization accuracy on the boundary

segment.

Unfortunately, on a boundary segment there can

be more than one local maximum even if the segment

is a simple line segment. So, global optimizers should

be started for every boundary segments. After that

the highest local maximum value can be chosen as a

global maximum.

Another possibility is to calculate the derivative

of Q

(t) on every boundary segment and ﬁnd every t

value where:

∂Q

(t)

∂t

= 0. (16)

This can be a complex task, but fortunately, if the

boundary segments are line segments, this is reduced

to simple solving of third-degree polynomials, which

can be performed analytically. In this case the plac-

ing area of the new camera is a polygon. This polygon

limitation is not too strong since most of the bound-

aries can be approximated with polygons.

3.3 Using the Eigenvalue Based

Measure

Another possibility is to deﬁne the localization accu-

racy as q

eig

in (9). The characteristic polynomial of

the inverse covariance matrix can be formulated. The

smaller root of this polynomial is the accuracy. This

has to be maximized. In this case, if a new camera is

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

292

added in the polar coordinate system, the localization

accuracy is:

eig

(α, d) =

D+

−

+ E

2EF

· cos(2α)

(17)

where D, E and F are constant non-negative values

which are functions of the camera parameters and the

ﬁxed cameras. This equation can also be easily trans-

formed into the cartesian coordinate system, but it

gets a little long and it is not so interesting. One might

assume that if d → 0 then q

eig

→ ∞, but it is not true.

If d → 0 the members in the square root with d in

the denominator get dominant and they eliminate the

member with d in the denominator outside the root.

With substitution of the constant values, the inverse

of the originally smaller variance (most accurate di-

rection) gets the upper limit. This can be achieved if

the facing direction of the new camera is perpendicu-

lar to the direction of the most inaccurate direction.

−50 0 50

−50

−40

−30

−20

−10

Figure 7: The contours of the localization accuracy with

the newly added camera. A curve contained by another one

has a higher localization accuracy. The camera conﬁgura-

tion and camera parameters are the same as in Fig. 6. The

difference is that here the measure deﬁned in (9) is used

instead of (8).

So the main difference from the previously dis-

cussed q

det

is that q

eig

has an upper limit while q

det

does not. While q

det

→ ∞ if d → 0, q

eig

has an up-

per limit. In Fig. 7 the contours of this function can

be seen. The camera parameters are the same as in

Fig. 6. The basic concept here is also correct that the

closer the camera is, the better the localization accu-

racy gets. However in this case it is more noticable

how powerful the angle is. If the new camera is placed

parallel to the most inaccurate direction, it improves

nothing, while with the determinant measure it does.

This behavior represents the real world better than the

determinant one.

In this case the optimal placement can also be de-

termined. A consideration similar to (12) can be for-

mulated here as well. This proves that if this line

segment and the placing area has no common point

it results that the optimum is situating on the bound-

ary. Unfortunately, the boundary can not be handled

so simply as in the determinant case because of the

square root in (17). This can be handled with global

optimization on the line segments. Although it is

resource-intensive, it is a simpliﬁed method since the

optimization has to be performed only on the line seg-

ments (1D) instead of the whole area (2D).

3.4 3 Dimensional Case

The previous sections focused on the 2D case. They

can be generalized to 3D by increasing the parame-

ter space. The result is that all the positions have

three coordinates instead of two. The orientation of

the camera is given with three angles rather than one,

thus the rotation matrices are the combination of three

rotations. There are two independent detection errors

and so two independent perpendicular components of

the localization accuracy. Thus the covariance matrix

is a 3-by-3 matrix instead of a 2-by-2 one. In 3D the

objective functions get more complex, specially the

measure with the eigenvalue. The optimization can

be done only numerically. A consideration similar to

(12) can be formulated here as well. This results in

the optimum lying on the boundary since the closer

point with the same orientation has a larger objective

funtcion value. Thus the optimization has to be per-

formed only on the 2D boundary instead of the whole

3D volume.

−40 −30 −20 −10 0 10 20 30 40

−30

−20

−10

Figure 8: The contours of the objective function deﬁned

with the eigenvalue in 3D on a general plane. It has two

peaks and a hollow space between them. It means that the

angle is powerful and it can radically change the objective

function value on a short distance.

In Fig. 8 the contours of the objective function de-

ﬁned with the eigenvalues can be seen on a general

plane. It has two peaks and a hollow space between

them. It means that there is a direction in which no

signiﬁcant improvement can be achieved but with a

little shift in the angle the objective function increases

strongly.

OptimizingCameraPlacementinMotionTrackingSystems

293

4 EXPERIMENTAL RESULTS

We have developed a measurement to conﬁrm the

localization accuracy theory presented in Section 2.

Three ﬁxed, calibrated cameras observe a marker ob-

ject. The marker is represented by a printed im-

age that contains easily recognizable ellipses. This

marker is moved with a precision robotic arm into

each vertex of a 3-by-3-by-3cubic grid. Tens of local-

izations are performed at every position on the grid.

The mean of these measurements are used as estima-

tions of the positions. The localization accuracy can

be characterized by the standard deviation of these es-

timated marker locations. Detailed calculations, ex-

perimental setup and results can be found in (Szal´oki

et al., 2013a). The standard deviation of marker loca-

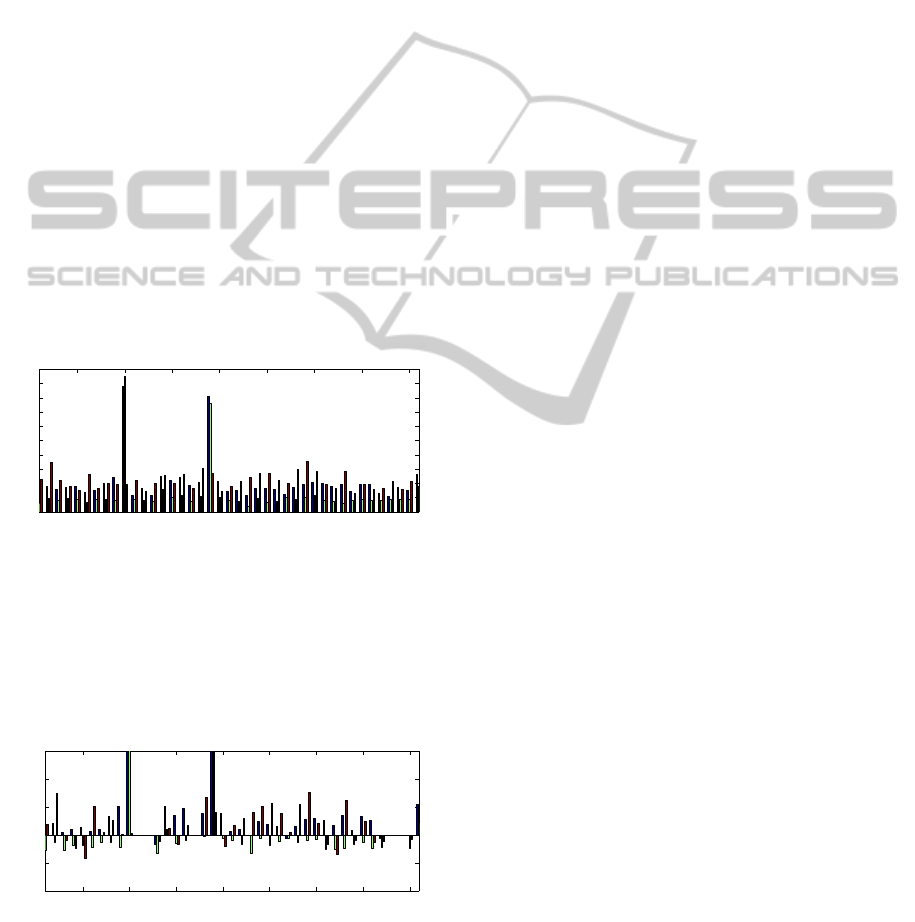
tion estimations can be seen in Fig. 9.

Fig. 10 shows the differences between the stan-

dard deviations of the theory and the measurement.

Based on our observations, the reprojection error sup-

plied by the OpenCV calibration method is a good

choice for estimating the detection error. The mea-

surement differs only with half of a millimeter from

the theory in most cases.

5 10 15 20 25 30 35 40

0.5

1.5

2.5

3.5

4.5

Location index

Standard deviation

Standard deviation (measurement)

Figure 9: Standard deviation of marker location estima-

tions, shown for the 3 axes separately. Differences are

caused by the varying view angles. The two large peaks

are measurement errors, they have to be ignored. The direc-

tion of the z axis is the nearest to the depth direction. This

conﬁrms that the largest inaccuracy can be found in this di-

rection.

5 10 15 20 25 30 35 40

−1

−0.5

0.5

1.5

Location index

Standard deviation

Standard deviation (measurement−theory)

Figure 10: The standard deviation differences of the mea-

surement and the theory in each locations for the 3 axes

separately. The two large peaks are measurement errors, as

it is mentioned in Fig. 9.

5 FUTURE PLANS

In this section some features are listed which could

be applied to the model. Some of them are easy to

include but some cases need large changings and de-

velopments.

5.1 Area Instead of a Single Point

In the previous sections there is only one observed

point where the localization has to be performed. The

more general case is that the localization is needed

in an area. Therefore a density function can be used.

Its value at a speciﬁc x

x point in space represents the

probability that the localization has to be done at that

point. In this case the objective function can be de-

ﬁned as the expected value of the accuracy:

(q(x

x)) =

Ω

q(x

x) f (x

x) dx

x, (18)

where Ω represents the whole space and f (x

x) is the

density function.

Another method for handling not only one ob-

served point is, when the worst case is used. This

means that the localization accuracy on an area is de-

ﬁned as the worst accuracy of its points.

5.2 Taking Field of View into Account

The ﬁeld of view of the cameras can also be taken into

account. This is only a 0-1 function which multiplies

its inverse covariance matrix, but it complicates the

optimization. An idea is that the space can be cut into

pieces with the boundaries of the ﬁelds of views. One

piece can be handled as described previously and all

the pieces has to be managed individually.

5.3 Utilizing Multiple Cameras

Together

If multiple cameras can be placed for localization ac-

curacy improvementthen applying the previous meth-

ods means that the cameras are placed incrementally.

The resulting localization accuracy can be increased

by optimizing the movable cameras together.

5.4 Rotation in 3D

In 3D if the camera is placed at a ﬁxed position so

that it is facing towards the observed point, then the

rotation around the facing direction can change the

objective function value. This rotation can also have

some constraints which have to be taken into account.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

294

5.5 Continuous Optimization for

Dynamic Environments

Since a moving object is tracked the optimal place-

ment of the movable cameras should be performed

continuously through time. One camera can be placed

closer to the object in order to have larger accuracy

improvement, but if the object is moving fast it can

occur that the camera can not follow it because of

its dynamic constraints. It can be a better solution

to place the camera further in order to be able to fol-

low the object on a longer path. These dynamic con-

straints of the movable cameras could be also taken

into account.

6 CONCLUSIONS

In this paper the multi-camera localization accuracy

and the optimal camera placement is examined. First

the camera model is formulated. The localization ac-

curacy is deﬁned for one camera observing one single

point. A method for calculating the localization ac-

curacy using multiple cameras is given. All the cal-

culations are performed in 2D and they are extended

later into 3D. Two measures are deﬁned. Their ben-

eﬁts and disadvantages are compared. In both cases

the objective function is calculated in case of adding

a new camera to the system. The optimization of the

placement of the new camera is discussed. The gen-

eral extension into 3D is described. Finally, the future

plans are formulated.

ACKNOWLEDGEMENTS

This work was partially supported by the Euro-

pean Union and the European Social Fund through

project FuturICT.hu (grant no.: TAMOP-4.2.2.C-

11/1/KONV-2012-0013) organized by VIKING Zrt.

Balatonf¨ured.

This work was partially supported by the Hungar-

ian Government, managed by the National Develop-

ment Agency, and ﬁnanced by the Research and Tech-

nology Innovation Fund (grant no.: KMR 12-1-2012-

0441).

REFERENCES

Bradski, G. (2000). The OpenCV Library. Dr. Dobb’s Jour-

nal of Software Tools.

Bradski, G. and Kaehler, A. (2008). Learning OpenCV.

O’Reilly Media Inc.

Ercan, A., El Gamal, A., and Guibas, L. (2007). Object

tracking in the presence of occlusions via a camera

network. In Information Processing in Sensor Net-

works, 2007. IPSN 2007. 6th International Sympo-

sium on, pages 509–518.

Hesch, J. and Roumeliotis, S. (2011). A direct least-squares

(dls) method for pnp. In Computer Vision (ICCV),

2011 IEEE International Conference on, pages 383–

390.

K¨appeler, U.-P., H¨oferlin, M., and Levi, P. (2010). 3d object

localization via stereo vision using an omnidirectional

and a perspective camera.

Lepetit, V. and Fua, P. (2006). Keypoint recognition using

randomized trees. IEEE Trans. Pattern Anal. Mach.

Intell., 28(9):1465–1479.

Moreno-Noguer, F., Lepetit, V., and Fua, P. (2007). Accu-

rate non-iterative o(n) solution to the pnp problem. In

Computer Vision, 2007. ICCV 2007. IEEE 11th Inter-

national Conference on, pages 1–8.

Oberkampf, D., DeMenthon, D. F., and Davis, L. S.

(1996). Iterative pose estimation using coplanar fea-

ture points. Comput. Vis. Image Underst., 63(3):495–

511.

Skrypnyk, I. and Lowe, D. G. (2004). Scene modelling,

recognition and tracking with invariant image fea-

tures. In Proceedings of the 3rd IEEE/ACM Interna-

tional Symposium on Mixed and Augmented Reality,

ISMAR ’04, pages 110–119, Washington, DC, USA.

IEEE Computer Society.

SMEyeL (2013). Smart Mobile Eyes for Localization

(SMEyeL).

Szal´oki, D., Kosz´o, N., Csorba, K., and Tevesz, G. (2013a).

Marker localization with a multi-camera system. In

2013 IEEE International Conference on System Sci-

ence and Engineering (ICSSE), pages 135–139.

Szal´oki, D., Kosz´o, N., Csorba, K., and Tevesz, G. (2013b).

Optimizing camera placement for localization accu-

racy. In 14th IEEE International Symposium on

Computational Intelligence and Informatics (CINTI),

pages 207–212.

Wu, Y. and Hu, Z. (2006). Pnp problem revisited. J. Math.

Imaging Vis., 24(1):131–141.

Zhou, Q. and Aggarwal, J. (2006). Object tracking in

an outdoor environment using fusion of features and

cameras. Image and Vision Computing, 24(11):1244

– 1255. Performance Evaluation of Tracking and

Surveillance.

OptimizingCameraPlacementinMotionTrackingSystems

295