Adaptive Filtering in Electricity Spot Price Models
Shin Ichi Aihara
1
and Arunabha Bagchi
2
1
Department of Computer Media, Tokyo University of Science Suwa, 5000-1 Toyohira, Chino, Nagano, Japan
2
Department of Applied Mathematics, Twente University, P.O.Box 217, 7500AE, Ensched, The Netherlands
Keywords:
Electricity Spot, Risk premium, Hyperbolic system, Kalman filter, Jump process, Parameter identification,
Parallel filter.
Abstract:
We study the adaptive filtering for risk premium and system parameters in electricity futures modes. Introduc-
ing the jump augmented Vasicek model as the spot price mode, the factor model of the electricity futures is
constructed as the stochastic hyperbolic systems with jumps. Representing the main spike phenomena of the
electricity spot price from one observed futures data by proxy, the filtering of the stochastic risk premium and
its system parameters are developed in a Gaussian framework. By using the parallel filtering algorithm, the
online system parameter estimation procedure is proposed.
1 INTRODUCTION
It is well known that the electricity is quoted same
as any other commodity, e.g. crude oil, gold, copper
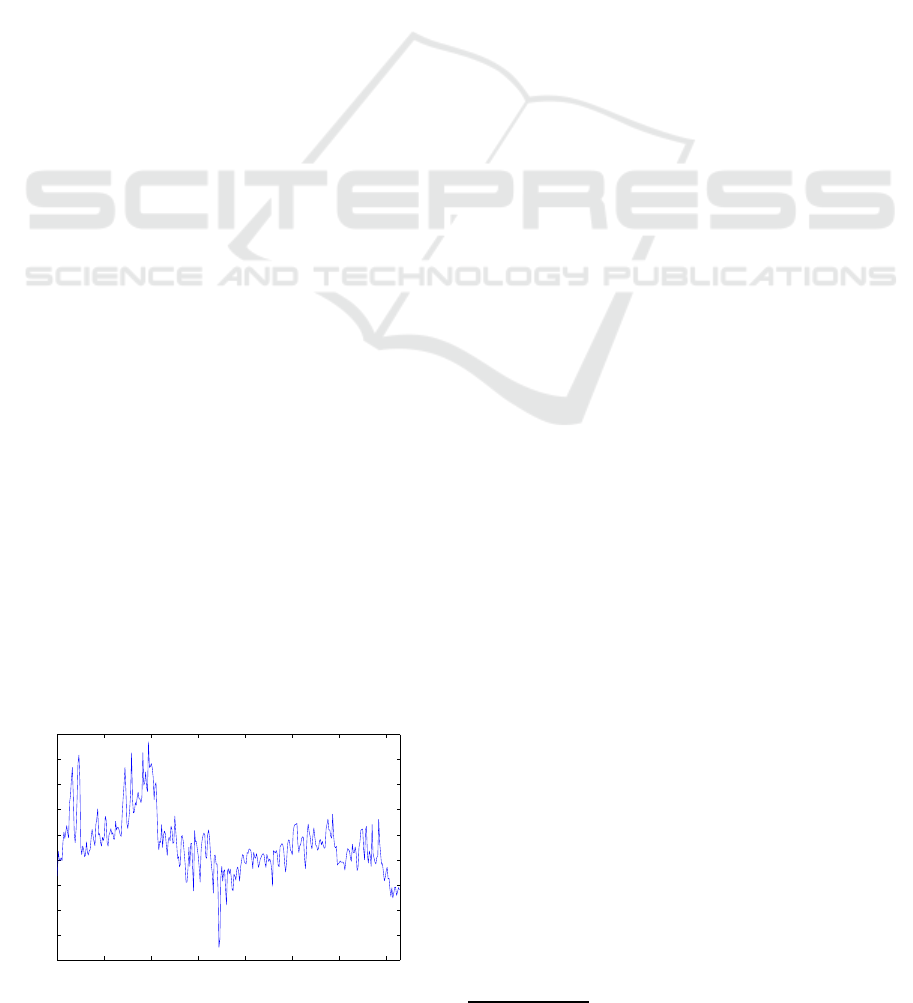
and others. As shown in Fig. 1, the electricity spot
prices present a higher volatility than equity prices
and its mathematical model is required for pricing of
electricity-related options, risk management and oth-
ers.
The peculiar characteristic of electricity is that one
can not store electricity, but there are many other char-
acteristics which distinguish electricity from other
commodities.
From Fig. 1, in which the spot price (a day-ahead
market) is shown, we observe the special behaviors
of electricity spot, i.e., many spikes frequently and
seasonal effect.
0 50 100 150 200 250 300 350
15
20
25
30
35
40
45
50
55
60
Time (day from 01/01/2013 to 31/12/2013)
Nord pool spot (EUR/MWh)
Figure 1: Nord Pool electricity spot price (day ahead im-
plicit auction market).
In this paper, instead of modeling this process
from the basic principle of supply and demand, the
simple mathematical model for this spot price is pro-
posed and leads to calibrate the model parameters
and price the options by using the stochastic sys-
tem approach. Along this line Schwartz and Smith
(Schwartz and Smith, 2000) proposed a two-factor
diffusion model and the system parameters are esti-
mated from M.L.E. (Maximum likelihood estimate)
by using Kalman filter. To apply this method one need
to add ad hoc observation noise in order to derive the
Kalman filter. This assumption has been made by nu-
merous authors, either in the commodity or interest
rate markets. The additional noise in the observa-
tion has been interpreted to bring into account bid-ask
spread, price limits or errors in the information. The
argument is clearly forced and unconvincing. By us-
ing the idea proposed by (Aihara and Bagchi, 2010),
we approach the modeling differently. In our setup,
on the one hand, the added measurement noise is
built in the model. On the other hand, the model-
ing of the correlation structure between the futures
(observation) is a natural component of our formu-
lation. Hence the model parameters can be calibrated
through the derived likelihood functional without any
ad hoc observation noise.
All the same, in these works, the important spikes
in the electricity prices could not be admitted, because
including jumps
1
means giving up on the closed-form
estimator like Kalman filter in (van Schuppen, 1977).
1
The closed-form formulae for forwards and options are
620
Aihara S. and BAGCHI A..
Adaptive Filtering in Electricity Spot Price Models.
DOI: 10.5220/0005014206200628
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 620-628
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Fortunately, for the term structure model in the elec-
tricity problem, we can represent the jump process for
the spike phenomena by using one observation com-
ponent and transform the Non-Gaussian estimation
problem into the Gaussian framework with correlated
noises.
In this paper, from the real data (Nord Pool elec-
tricity spot data ), the linear trend is firstly identified
by using a least squares method. After subtracting this
linear trend from the spot data and taking the FFT, the
prominent frequencyof the seasonality effect is inves-
tigated in Sec.2. We choose the spot price dynamics
as the jump-diffusionmodel proposed in (Duffieet al.,
2000). According to the idea in (Aihara and Bagchi,
2010), we construct the arbitrary free model of the
term structure, including jump-diffusion processes in
Sec.3. In the electricity market, the averaged-typefor-
ward and futures contracts are observed and are used
as the observation data for calibrating system param-
eters. After presenting this observation dynamics in
Sec.4, we derive the closed form filter for estimat-
ing the whole term structure. To derive this filter, we
choose one component of observation as the proxy for
the spike process of the spot price, say y
o
(t). Recon-
structing the spikes from y
o
(t) and plugging this into
observation and system equations, the filtering prob-
lem with jumps is converted to the Gaussian frame-
work in Sec.5. For figuring out the filtering problem,
we need to work under the real world measure. Hence
a suggested in (Carmona and Ludkovski, 2004), the
stochastic market price of risk is introduced as the lin-
ear Ito equation. This implies that our extended state,
including the stochastic market price of risk is still
Gaussian. Instead of the use of MLE, we suggest the
parallel filtering procedure in (Anderson and Moore,
1979) for obtaining the online state and parameter es-
timation. In the final section, some numerical exam-
ples are demonstrated.
2 IDENTIFICATION OF LINEAR
TREND AND SEASONALITY
2.1 Linear Trend
From Fig.1, we can observe a slight downward trend
in the spot data in 2013. A least squares fit gives the
trend line for the log price,
−6× 10
−4
t + 3.74.
Now we subtract off this linear trend from the data
shown in Fig.1 and obtain the data shown in Fig.2.
possible, even for the jump-diffusion and Levy processes in
(Benth et al., 2008).
0 50 100 150 200 250 300 350
2.8
3
3.2
3.4
3.6
3.8
4
day
log S(t)− trend
Figure 2: Log price (day ahead implicit auction market) mi-
nus the linear trend.
2.2 Seasonality
We take the FFT to the data shown in Fig.2 and obtain
the periodogram shown in Fig.3. From Fig.3, we can
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
0
2
4
6
8
10
12
14
16
18
20
Real magnutude
Frequency[Hertz
Figure 3: Periodogram of the log spot.
find big power points and zoom in on the plot and use
the reciprocal of frequency to label the x-axis in Fig.4.
365.0 182.5 121.7 91.2 73.0 60.8 52.1 45.6 40.6 36.5 33.2 30.4 28.1 26.1 24.3 22.8 21.5 20.3 19.2 18.2
0
5
10
15
20
25
days/cycle
power
Periodogram detail
Figure 4: Detail of periodogram.
The 365 days/cycle is not important, but we find
still three outstanding points; 182.5, 60.8 and 45.6
days/cycle. We also need to find phases at these points
(Red marks) in Fig.5.
AdaptiveFilteringinElectricitySpotPriceModels
621

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
−3
−2
−1
0
1
2
3
Angle
Frequency[Hertz
Figure 5: Angles at each frequencies.
Hence we find that
Se(t) = Linear trend + Seasonality
= −6× 10
−4
t + 3.74
+a
1
cos(2π × 16.4 × 10
−3
t − 2.8)
+a
2
cos(2π × 142.5 × 10
−3
t − 0.05)
+a
3
cos(2π × 284.9 × 10
−3
t + 2.11)(1)
The coefficients a
1
,a
2
and a
3
are identified to mini-
mize the |logS(t) − Seasonality - linear trend|
2
, i.e.,
a
1
= 0.114,a
2
= 0.006,a
3
= 0.042.
In Fig.6, we summarize the above results.
0 50 100 150 200 250 300 350
2.8
3
3.2
3.4
3.6
3.8
4
day
log S(t) − linear trend + 3.74
Seasonality
Log spot price − trend − seasonality
Log spot price − trend
Figure 6: Log price (day ahead implicit auction market)
with linear trend and seasonality.
3 SPOT RATE MODEL WITH
JUMPS
The spot price S(t) is set as
S(t) = exp(r(t)+ Se(t))
where Se(t) is identified by (1) and the short rate r(t)
is given by the jump augmented Vasicek model;
dr(t) = κ(¯r− r(t))dt + σ
r
dw
r
(t) +
Z
R
νp(dν, dt), (2)
where w
r
is a standard Brownian motion process
which is independent of the Poisson random measure
p and the compensated Poisson measure q
c
is is given
by
q
c
(dν, dt) = p(dν,dt) − (λ
+
ψ
P
(dν) + λ
−
ψ
M
(dν))dt
and where λ
+
(λ
−
) denotes the positive jump ( neg-
ative jump) time intensity and ψ
P
(ψ
M
) is a distribu-
tion of the positive (negative) jump size. In this paper
we more specify this jump process as the compound
Poisson processes:
Z
R
νp(dν, dt) = J
P
(t;ψ
P
)dN(t;λ
+
)
+J
M
(t;ψ
M
)dN(t;λ
−
),
where J
·
(t;ψ
·
) denotes the jump size with identically
distributed law ψ
·
and N(t,λ
·
) is a counting process
with parameter λ
·
. Here we shall present the simula-
tion results for these compounded Poisson processes:
0 0.2 0.4 0.6 0.8 1
−1.5
−1
−0.5
0
0.5
1
1.5
Time
Compound Poisson
Figure 7: Compounded Poisson process.
4 ELECTRICITY MODEL
By a basic no-arbitrage argument it follows that the
price of a futures contract F(t, T −t) which has payoff
S(T) at future time T equals to
F(t,T − t) = E{S(T)|F
t
},
with respect to the risk neutral measure. Hence we
can write the futures price as
F(t, T − t) = exp{A(t, T − t)+ B(t,T − t)r(t)}, (3)
where A and B satisfy deterministic equations. (See in
(Duffie et al., 2000) for details.) Although this model
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
622

is mathematically elegant, it is not consistent with the
forward curve as stated in (Carmona and Ludkovski,
2004). From the systems identification view points,
the observation futures data are summed to the artifi-
cial observation noises. In order to avoid this ambigu-
ity, we append the extra noise in (3) as used in (Aihara
and Bagchi, 2010). This noise represents the model
errors from the basic property of r(t). This will mean
that the corresponding futures price should be given
by a slight perturbation of (3),i.e.,
F(t, T − t) = exp{A(t, T − t) + B(t,T −t)r(t)
+
Z
t
0
σdw(s, T − s)}, (4)
where we use the same symbols in (3) and
Z
t
0
σdw(s, T − s) =
∞
∑
k=1
Z
t
0
σ
1
λ
k
e
k
(T − s)dβ
k
(s), (5)
and where e
k
(·) is a sequence of differentiable func-
tions forming an orthonormal basis in L
2
(0,T
∗
)
2
and
{β
k
(t)} are mutually independent Brownian motion
processes with
∑
1
λ
2
k
< ∞,i.e.,
σ
2
E{w(t,x
1
)w(t,x
2
)} = tq(x
1
,x
2
)
and
Z
T
∗
0
q(x,x)dx =
∞
∑
k=1
σ
2
λ
2
k
< ∞.
Setting
f(t,x) = A(t,x) + B(x)r(t)+
Z
t
0
σdw(s, x+ t − s), (6)
the futures contracts F(t,T − t) becomes
F(t, T − t) = exp( f(t,T − t)) (7)
with F(T,0) = exp( f(T, 0)) = S(T). Now we derive
the explicit forms of A and B so that F(t,T − t) is a
F
t
martingale in the risk neutral measure. Applying
the results by (Aihara and Bagchi, 2010), we get The
explicit form of (6) is a solution of
d f(t, x) =
∂f(t,x)
∂x
dt − ˜q
J
(x)dt + e
−κx
{σ
r
dw
r
(t)
+
Z
R
νq
c
(dν, dt)} + σdw(t,x) (8)
f(0,x) = ¯r(1− e
−κx
) +
σ
2
r
2κ
(1− e
−2κx
)
+
1
2
Z
x
0
q(z,z)dz+ Se(x) + e
−κx
r(0)
+
Z
x
0
(λ
+
C
P
(z) + λ
−
C
M
(z))dz, (9)
2
T
∗
denotes the longest future time in mind
where
˜q
J
(x) = σ
2
r
e
−2κx
+
1
2
q(x,x) + (λ
+
C
P
(x) + λ
−
C
M
(x))
and
C
•
(x) =
Z
R
exp(e
−κx
ν)ψ
•
(dν) − 1. (10)
5 REAL WORLD DYNAMICS
On the identification problem, we work in the real
world measure. For example, we add a simple risk
premium term to (8) . In this paper, we simplify the
position that the market price of risk Λ
w
(t) comes
mainly from w
r
(t) but this moves stochastically. We
set this term as
dΛ
w
(t) = κ
λ
(
¯
Λ− Λ
ω
(t))dt + σ
Λ
dw
2
(t), (11)
where the BMP w
2
is independent of w
r
. Now under
the real world measure the BMP ˜w
r
(t) is represented
by
w
r
(t) = ˜w
r
(t) −
Z
t
0
Λ
w
(s)ds.
Hence our system state [f(t, x) Λ
w
(t)] under the phys-
ical measure becomes
d f(t, x) =
∂f(t,x)
∂x
dt − ˜q
J
(x)dt
+e
−κx
{σ
r
(−Λ
w
(t)dt
+d ˜w
r
(t)) +
R
R
νq
c
(dν, dt)} + σdw(t,x)
dΛ
w
(t) = κ
λ
(
¯
Λ− Λ
w
(t))dt + σ
Λ
dw
2
(t).
(12)
6 OBSERVATION
Noting that electricity is essentially not storable, the
futures contracts are based on the arithmetic averages
of the spot prices over a delivery period [T
0
,T], given
by
1
T − T
0
Z
T
T
0
S(τ)dτ.
Now, for t < T
0
we can calculate the futures prices by
F(t, T
0
,T) = E{
1
T − T
0
Z
T
T
0
S(τ)dτ|S(t)}
=
1
T − T
0
Z
T
T
0
F(τ,t)dτ
=
1
T − T
0
Z
T−t
T
0
−t
exp[ f(t,x)]dx. (13)
In practice we adopt the geometric average as an ap-
proximation;
F(t,T
0
,T) ∼ exp[
1
T − T
0
Z
T−t
T
0
−t
f(t,x)dx]. (14)
AdaptiveFilteringinElectricitySpotPriceModels
623

By using this geometric approximation, the observa-
tion data for the futures price is set as
y
i
(t) =
1
T − T
0
Z
τ
i
+(T−T
0
)
τ
i
f(t,x)dx, (15)
where τ
1
< τ
2
< ··· < τ
m
.
Denoting
~
Y(t) = [y
i
(t)]
m×1
,
we have
d
~
Y(t) = H
δ
f(t,·)dt − H( ˜q
J
+ B(x)σ
r
Λ
w
(t))dt
+H[dw
M
(t,·)] + H[B
Z
R
νq
c
(dν, dt)], (16)
where B(x) = e
−κx
,
w
M
(t,x) = B(x)σ
r
w
r
(t) + σw(t,x), (17)
H(·) =
1
T − T
0
[
Z
τ
1
+(T−T
0
)
0
(·)dx, · · · ,
Z
τ
m
+(T−T
0
)
0
(·)dx]
′
and
H
δ
(·) = [
1
T − T
0
Z
G
(δ(η− (T − T
0
+ τ
i
))
− δ(η− τ
i
))(·)dη]
m×1
.
6.1 Reconstruction of Jump Process
Choosing one yield data for τ
0
< τ
1
,
y
0
(t) =
1
T − T
0
Z
τ
0
+(T−T
0
)
τ
0
f(t,x)dx, (18)
we have
dy
0
(t) = H
0
δ
f(t,·)dt − H
0
( ˜q
J
+ B(x)σ
r
Λ
w
(t))dt
+H
0
[dw
M
(t,·)] + H
0
[B
Z
R
νq
c
(dν, dt)],
where H
0
(·) =
1
T−T
0
R
τ
0
+(T−T
0
)
0
(·)dx, and
H
0
δ
(·) =
1
T − T
0
Z
G
(δ(η− (T − T
0
+ τ
0
))
−δ(η− τ
0
))(·)dη.
Hence it is possible to reconstruct the jump pro-
cess from y
0
(t) such that
Z
t
0
Z
R
νq
c
(dν, ds)
=
1
B
0
(y
0
(t) −
Z
t
0
H
0
δ
fds− H
0
w
M
(t,x))
+
Z
t
0
1
B
0
H
0
( ˜q
J
+ B(x)σ
r
Λ
w
(s))ds, (19)
where B
0
= H
0
B. Plugging (19) into (12), we have
d f(t, x) =
∂f(t,x)
∂x
dt − ( ˜q
J
(x) + B(x)σ
r
Λ
w
(t))dt
+dw
M
(t,x) +
B(x)
B
0
{dy
0
(t) − H
0
δ
fdt
+H
0
( ˜q
J
+ B(x)σ
r
Λ
w
(t))dt − H
0
dw
M
(t,x)} .(20)
We transform the above equation as the robust form
for jump term. Define
3
˜
f(t, x) = f(t, x) −
B(x)
B
0
y
0
(t). (21)
Hence we get
d
˜
f(t,x) = (
∂
∂x
− C
δ
)(
˜
f(t, x) +
B(x)
B
0
y
0
(t))dt
−(1− C
0
)( ˜q
J
(x) + B(x)σ
r
Λ
w
(t))dt
+ (1− C
0
)σdw(t,x), (22)
where
C
δ
=
B(x)
B
0
H
0
δ
, C
0
=
B(x)
B
0
H
0
. (23)
6.2 Reconstruction of Observed Yields
The original yield y
j
(t) becomes
4
y
j
(t) = H
j
f(t,·)
= H
j
˜
f(t,·) +
H
j
B
B
0
y
0
(t). (24)
Now we construct the new observation such that
˜y
j
(t) = y
j
(t) −
H
j
B
B
0
y
0
(t),
= H
j
˜
f(t, ·). (25)
Denoting
~
˜
Y(t) = [ ˜y
j
(t)]
m×1
,
and from (H − HC
0
)Bσ
r
Λ
w
= HBσ
r
Λ
w
−HBσ
r
Λ
w
=
0, we get
d
~
˜
Y(t) = (H
δ
− HC
δ
)
˜
f(t, ·)dt + (H
δ
− HC
δ
)
B
B
0
y
0
(t)dt − (H−HC
0
) ˜q
J
dt + (H − HC
0
)σdw(t,x).
(26)
3
We ued w
M
−
B
B
0
H
0
w
M
= (1−
B
B
0
H
0
)σw.
4
We used H
j
(·) =
1
(T−T
0
)
R
τ
i
+(T−T
0
)
τ
i
(·)dx.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
624

7 THE KALMAN FILTER
In (8), Poisson jump processes are included and this
is not a usual Kalman filter problem. There are many
articles for Non-Gaussian filtering problem by using a
martingale approach, e.g. (van Schuppen, 1977) and
however it is still difficult to derive the closed form
filtering algorithm. In our position, the transformed
system (22) with the observation (26) do not include
jump processes explicitly. Hence our estimation prob-
lem is in the Gaussian framework;
d
˜
f(t,x)
Λ
w
(t)
=
(
∂
∂x
− C
δ
) − (1−C
0
)
0− κ
λ
˜
f(t,x)
Λ
w
(t)
dt
+
(
∂
∂x
− C
δ
)
B
B
0
y
0
− (1− C
0
) ˜q
J
κ
λ
¯
Λ
dt
+ d
(1− C
0
)w(t, x)
w
Λ
(t)
. (27)
with
d
~
˜
Y(t) = (H
δ
− HC
δ
,0)
˜
f(t,x)
Λ
w
(t)
dt
+((H
δ
− HC
δ
)
B
B
0
y
0
(t) − (H − HC
0
) ˜q
J
)dt
+(H − HC
0
)dw(t,x). (28)
Denoting ˆ· = E{·|Y
t
}, for Y
t
= σ{
~
˜
Y(s),y
0
(s);0 ≤
s ≤ t}, we have
d
ˆ
˜
f(t,x) = (
∂
∂x
− C
δ
)(
ˆ
˜
f(t, x) +
B(x)
B
0
y
0
(t))dt
−(1− C
0
)(B(x)
ˆ
Λ
w
(t) + ˜q
J
(x))dt
+
˜
P
f f
(t)(H
δ
− HC
δ
)
∗
+(1− C
0
)Q(H − HC
0
)
∗
}
~
Φ
−1
×
(
d
~
˜
Y(t) − (H
δ
− HC
δ
,0)
ˆ
˜
f(t,x)
ˆ
Λ
w
(t)
!
dt
−((H
δ
− HC
δ
)
B
B
0
y
0
(t) − (H − HC
0
) ˜q
J
dt
,(29)
and
d
ˆ
Λ
w
(t) = κ
λ
(
¯
Λ−
ˆ
Λ
w
(t)dt
+
˜
P
Λf
(t)(H
δ
− HC
δ
)
∗
~
Φ
−1
×
(
d
~
˜
Y(t)− (H
δ
− HC
δ
,0)
ˆ
˜
f(t, x)
ˆ
Λ
w
(t)
!
dt
−((H
δ
− HC
δ
)
B
B
0
y
0
(t) + (H − HC
0
) ˜q
J
dt
,(30)
where Q =
R
q(x,z)(·)dz ,
~
Φ = (H − HC
0
)((H − HC
0
)Q)
∗
, (31)
and
∂
˜
P
f f
(t)
∂t
= (
∂
∂x
− C
δ
)
˜
P
f f
(t) +
˜
P
f f
(t)(
∂
∂x
− C
δ
)
∗
−
˜
P
fΛ
(1− C
0
)
∗
− (1− C
0
)
˜
P
Λ f
+ (1− C
0
)Q(1− C
0
)
∗
−
˜
P
f f
(t)(H
δ
−
HB
B
0
H
0
δ
)
∗
+ (1− C
0
)Q(H − HC
0
)
∗
~
Φ
−1
˜
P
f f
(t)(H
δ
−
HB
B
0
H
0
δ
)
∗
+ (1− C
0
)Q(H − HC
0
)
∗
∗
,
(32)
∂
˜
P
fΛ
(t)
∂t
= (
∂
∂x
− C
δ
)
˜
P
fΛ
(t) −
˜
P
fΛ
(t)κ
λ
−
˜
P
f f
(t)(H
δ
−
HB
B
0
H
0
δ
)
∗
+ (1− C
0
)Q(H − HC
0
)
∗
~
Φ
−1
˜
P
Λ f
(t)(H
δ
−
HB
B
0
H
0
δ
)
∗
∗
.
(33)
8 ADAPTIVE FILTERING
PROBLEM
8.1 Parallel Filtering
To construct the parameter estimation algorithm, we
confine the general jump process as the compound
Poisson process as stated in Remark, i.e., J
P
(t;φ
P
) =
Gaussian with mean m
P
J
and variance σ
P
J
and i.i.d for
each jump time and same as the negativejump. Hence
we have
C
P
(x) = exp[
Z
x
0
B(y)dy(m
P
+
1
2
(σ
P
J
)
2
)].
As used in (Aihara and Bagchi, 2010), we set the
function form q(x, x). Hence the unknown system pa-
rameters
5
θ = [κ ¯r σ σ
r
m
P
m
M
σ
P
J
σ
M
J
λ
+
λ
−
κ
λ
¯
Λ σ
λ
] ∈ Θ ⊂ R
13
,
where Θ is a known bounded set. Following from
(Anderson and Moore, 1979), the following parallel
filtering algorithm is made:
• Set candidates of unknown parameter θ such that
θ
( j)
∈ uniform random vectors in Θ, j = 1, ·, ·, m
p
.
• For each θ
( j)
, we solve the Kalman filter (29, 30)
for t
i
≤ t ≤ t
i+1
.
5
r is estimated from the initial forward cure. See (Aihara
and Bagchi, 2010)
AdaptiveFilteringinElectricitySpotPriceModels
625

• Calculate the posteriori probability,
p(θ
( j)
|
~
˜
Y(t
i
)
=
p(θ
( j)
|
~
˜
Y(t
i
))p(
~
˜
Y(t
i+1
)|θ
( j)
,
~
˜
Y(t
i
))
∑
m
k=1
p(
~
˜
Y(t
i+1
)|θ
(k)
,
~
˜
Y(t
i
))p(θ
(k)
|
~
˜
Y(t
i
))
,
where
p(
~
˜
Y(t
i+1
)|θ
( j)
,
~
˜
Y(t
i
)) ∝ exp
Z
t
i+1
t
i
~
˜
Y(s)
′
~
Φ
−1
×
(
d
~
˜
Y(t)− (H
δ
− HC
δ
,0)
ˆ
˜
f(t,x)
ˆ
Λ
w
(t)
!
dt
−((H
δ
− HC
δ
)
B
B
0
y
0
(t) − (H − HC
0
) ˜q
J
dt
• The estimates of f and θ are given by
ˆ
f(t
i+1
,x) =
m
p
∑
i=1
ˆ
f(t
i+1
,x;θ
( j)
)p(θ
( j)
|
~
˜
Y(t
i+1
))
ˆ
θ =
m
p
∑
i=1
θ
( j)
p(θ
( j)
|
~
˜
Y(t
i+1
)).
8.2 Resample Procedure for Parameters
The parallel filter algorithm is not sensitive for iden-
tifying many unknown parameters. In this paper, we
propose a new resampling procedure to increase the
diversity of parameter estimates.
• Set the resampling time period t
resamp
.
• At the time t
r
= (n−1)t
resamp
for n = 1,2, ···, cal-
culate
ˆ
σ
2
θ(i)
=
m
p
∑
j=1
{(θ
( j)
)
2
p(θ
( j)
|
~
˜
Y(t
r
)) −
ˆ
θ
2
(i)}
for i = 1, 2, · · · , 12.
• Construct the posteriori distribution by using the
Gaussian approximation:
P(θ(i)|
~
˜
Y(t
r
)) ∼ N (θ(i);
ˆ
θ(i),ε
i
ˆ
σ
θ(i)
),
where ε denotes a user defined parameter.
• Generate new samples θ
( j)
(i) in Θ from
P(θ(i)|
~
˜
Y(t
r
)). To get new samples in Θ, we use
the systematic resampling procedure.
• Reset p(θ
( j)
|
~
˜
Y(t
r
)) =
1
m
p
.
9 SIMULATION STUDIES
In this simulation study, we set the system parameters
in Table-1
Table 1: Systems parameters.
κ ¯r σ
r
σ m
P
J
λ
+
, σ
P
J
5.00 3.00 0.80 0.1 0.30 8.00 0.20
m
M
J
λ
−
σ
M
J
κ
λ
¯
Λ σ
λ
-0.30 8.00 0.20 6.00 0.40 2.00
Setting the seasonality and linear trend functions
are set in Sec.2, we simulate (12) by using the fi-
nite difference method with dx = 0.01, dt = 0.005 in
Fig.8.
We also generate the observation data
~
Y(t) =
[10y
i
(t)]
i
for i = 1,2, · · · , 7 with τ
1
= 0, τ
2
=
0.1, ··· , τ
7
= 0.6 shown in Fig.9.
0
0.2
0.4
0
0.5
1
2.5
3
3.5
4
4.5
Time(year)
Time−to−maturity
f(t, x)
Figure 8: f (t, x)- process.
0 0.1 0.2 0.3 0.4 0.5
0.24
0.26
0.28
0.3
0.32
0.34
0.36
Time(year)
Observation data y
Figure 9: Observed data
~
Y.
If all systems parameters are known, the Kalman
filter works good and such simulation results are
found in (Aihara et al., 2014). Here we shall look
into the feasibility of the proposed on-line algorithm.
Hence we set the upper and lower bounds for the un-
known parameters shown in Table-2 with the tuning
parameters ε
i
.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
626

Table 2: Upper and lower bounds for systems parameters.
κ ¯r σ
r
σ m
P
J
Upper 6.5 3.9 1.04 0.13 0.39
Lower 3.5 2.1 0.56 0.07 0.21
ε
i
1.05 1.05 1.05 1.05 1.05
λ
+
σ
P
J
m
M
J
λ
−
σ
M
J
Upper 10.4 0.26 -0.21 10.4.00 0.26
Lower 5.6 0.14 -0.39 5.6 0.14
ε
i
1.05 1.05 1.05 1.05 1.05
κ
λ
¯
Λ σ
λ
Upper 7.8 0.52 2.6
Lower 4.2 0.28 1.4
ε
i
1.05 1.05 1.05
The estimate
ˆ
f(t,x) is shown in Fig. 10.
0
0.2
0.4
0
0.5
1
2.5
3
3.5
4
4.5
Time(year)
Time−to−maturity
ˆ
f(t, x)
Figure 10: Estimated
ˆ
f(t,x).
The estimate of the market price of risk is demon-
strated in Fig.11.
0 0.1 0.2 0.3 0.4 0.5
−2
−1
0
1
2
3
4
Time(year)
True and estimated Λ
λ
Estimated
ˆ
Λ
λ
True Λ
λ
Figure 11: True and estimated Λ
w
(t).
Now we call demonstrate the estimates of un-
known parameters where we selected for κ, and ¯r in
Figs.12 and 13. The estimates of other parameters
have almost same beavers in these images.
0 0.1 0.2 0.3 0.4 0.5
3.5
4
4.5
5
5.5
6
6.5
Time (year)
True and estimated parameters
κ
Estimated value
Lower bound
Upper bound
True value
Figure 12: True and estimated κ.
0 0.1 0.2 0.3 0.4 0.5
2
2.2
2.4
2.6
2.8
3
3.2
3.4
3.6
3.8
4
Time (year)
True and estimated parameters
rb
Estimated value
Lower bound
Upper bound
True value
Figure 13: True and estimated ¯r.
10 CONCLUSIONS
Bringing in the compound Poisson jump process, the
stochastic model for the electricity futures has been
suggested. By using the idea proposed by (Aihara
et al., 2014) the original filtering problem is changed
to the Gaussian framework and its Kalman filter is de-
rived. In the adaptive filtering algorithm, the parallel
filtering method in (Anderson and Moore, 1979) is
used to obtain the on-line parameter estimates with
the new resampling procedure. From the proposed al-
gorithm, it is not possible to estimate the noise corre-
lation parameter, if it exits. The possible way to iden-
tify this parameter is to use the Rao-Blackwellized fil-
ter.
REFERENCES
Aihara, S. and Bagchi, A. (2010). Identification of affine
term structures from yield curve data. International
Journal of Theoretical and Applied Finance, 13:27–
47.
Aihara, S., Bagchi, A., and Imreizeeq, E. (2014). Filtering
and identification of stochastic risk premium for elec-
tricity spot price models. Proc. of 19th IFAC World
Congress, page to appear.
Anderson, B. and Moore, J. (1979). Optimal Filtering.
Prentice-Hall, Inc., Englewood Cliffs.
Benth, F.,
˘
S. Benth, J., and Koekebakker, S. (2008).
AdaptiveFilteringinElectricitySpotPriceModels
627

Stochastic Modelling of Electricity and Related Mar-
kets. World Scientific, Singapore.
Carmona, R. and Ludkovski, M. (2004). Spot convenience
yield models for the energy markets. In Mathematics
of finance, volume 351 of Contemp. Math., pages 65–
79. Amer. Math. Soc., Providence, RI.
Duffie, D., Pan, J., and Singleton, K. (2000). Transform
analysis and asset pricing fro affine jump-diffusions.
Econometrica, 68(6):1343–1376.
Schwartz, E. and Smith, J. (2000). Short-term variations
and long-term dynamics in commodity prices. Man-
agement Science, 46/7:893–911.
van Schuppen, J. (1977). Filtering prediction and smooth-
ing for counting process observations, a martingale
approach. SIAM J. Appl. Math., 32-2:552–570.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
628
