Real-time Super Resolution Equipment for 8K Video

Seiichi Gohshi

Kogakuin University, 1-24-2 Nishi-Shinjuku, Shinjuku-ku, Tokyo, 163-8677, Japan

Keywords:

Super Resolution, 8K, 4K, Real-time, Image Enhancement.

Abstract:

Resolution is one of the most important things when assessing image quality, and image quality improves in

proportion to resolution. Super Resolution (SR) is a resolution improving technology that is different from

conventional image enhancement methods. SR methods, of which there are many, typically have complex

algorithms that involve iterations, and it is not easy to apply them to video running in real time at 50 or 60

frames a second; i.e., each frame would have to be processed in 20 ms (50 Hz) or 16.7 ms (60 Hz). In this

paper, a simple form of SR that uses non-linear signal processing is proposed to cope with the difﬁculties in

real-time processing. Real-time hardware equipped with an FPGA (Field Programmable Gate Array) for 4K

and 8K video is shown and its SR capability is discussed.

1 INTRODUCTION

HDTV digital broadcasting started at the beginning of

this century and since has spread all over the world.

The resolution of HDTV is 1920 × 1080, ﬁve times

higher than analogue TV systems such as PAL, SE-

CAM, and NTSC. Although CRT displays were in the

mainstream at the beginning of HDTV broadcasting,

LCDs have become the common these days. LCDs

are cost effective, lightweight, and high in resolution.

Currently, almost all TV and computer displays are

LCDs. If we view digital HDTV broadcasting as

a paradigm shift, the spread of LCDs is surely an-

other one. Moreover, the resolution of LCDs has been

growing dramatically. In fact, 4K displays that have

four times higher resolution than HDTV are now on

the market. The problem is that there is no 4K broad-

casting. To ﬁll in for the dearth of 4K content, at-

tempts are being made to up-convert HDTV content

to 4K resolution and show it on 4K displays. Here,

the resolution of 4K is 3840 × 2160, so the HDTV

content has to be enlarged by double horizontally and

vertically.

Such enlargements always cause blur. Figure 1

is an enlargement made by cropping the white rect-

angle area in Figure 2 and blowing it up 1.3 times.

As one can see, it is very blurry compared with the

white rectangular area in Figure 2. This simple ex-

ample illustrates that images are easily degraded by

enlargement and suggests that up-converted 4K con-

tent from HDTV would look even worse, as the en-

largement factor would be 2, not 1.3. Moreover, it is

doubtful that Enhancer (Schreiber, 1970; Lee, 1980;

Pratt, 2001) would be a sufﬁcient means of enhanc-

ing such up-converted content. New technologies are

needed to deal with this problem.

Super Resolution (SR) is a technology that cre-

ates a high-resolution image from low-resolution ones

(Park et al., 2003; Farsiu et al., 2004; Eekeren et al.,

2010; Houa et al., 2011; Protter et al., 2009; Panda et

al., 2011; Matsumoto and Ida, 2010). The keyword

phrase ”Super resolution” gets about 190 million hits

on Google. Indeed, there are many SR proposals, but

most of them are complex algorithms involving many

iterations. Such algorithms are almost impossible to

into real-time hardware.

Figure 1: Enlarged image.

Figure 2: Original image.

149

Gohshi S..

Real-time Super Resolution Equipment for 8K Video.

DOI: 10.5220/0005014901490156

In Proceedings of the 11th International Conference on Signal Processing and Multimedia Applications (SIGMAP-2014), pages 149-156

ISBN: 978-989-758-046-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

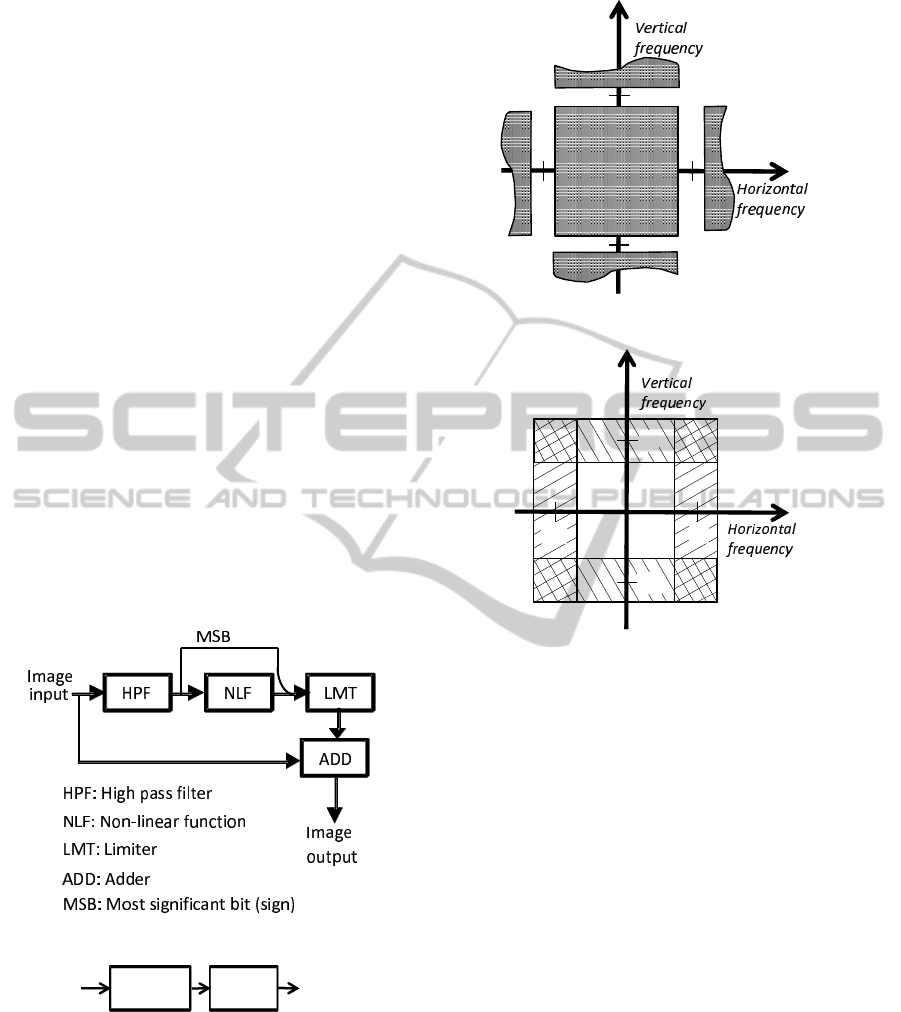
SR for TV should have low delay. In live

news broadcasts especially, conversations between

announcers in the TV studio and persons at the report-

ing point tend to be affected by delays. For viewers,

the superimposed time is not accurate on a TV screen

if the delay is longer than 60 seconds. For these rea-

sons, complex SR algorithms with iterations cannot

be used in TV systems.

Non-linear signal processing (NLSP) has been

proposed as an alternative to the conventional image

enhancement methods (Gohshi and Echizen, 2013),

and it has several advantages compared with them.

Since it does not use iterations or frame memories,

it is sufﬁciently lightweight to be installed in an

FPGA (Field Programmable Gate Array) for real-

time video processing. Furthermore, it can create

frequency elements that are higher than those of the

original image, as has been proven by performing

two-dimensional fast Fourier transform (2D-FFT) re-

sults(FFTs (Gohshi and Echizen, 2013). Although

there is real-time hardware that can process enlarged

images (Gohshi et al., 2013), its FPGA has a maxi-

mum speed of 30 Hz, far less than 60 Hz or 50 Hz

of video. In addition, certain frequency elements are

emphasized too much. In this paper, we present new

real-time NLSP hardware that is free of these prob-

lems.

Figure 3: NLSP algorithm.

Horizontal

NLSP

Input

Vertical

NLSP

Output

Figure 4: Sequential NLSP.

2 PREVIOUS RESEARCH ON

NLSP

The basic idea of NLSP is like that of the one-

dimensional signal processing shown in Figure 3

(Gohshi and Echizen, 2013). The input is distributed

Figure 5: 2D image spectra.

Figure 6: Enhanced areas in 2D.

to two blocks. The upper path creates high-frequency

elements that the original image does not have as fol-

lows. The original image is processed with a high

pass ﬁlter (HPF) to detect edges. The output of the

HPF is edge information that has a sign, i.e., plus

or minus, for each pixel. After the HPF, the edges

are processed with a non-linear function (NLF). If

an even function such as x

is used as the NLF, the

sign information is lost. To stop this from happen-

ing, the most signiﬁcant bit (MSB) is taken from the

edge information before the NLF and restored af-

ter the NLF. Non-linear functions generate harmon-

ics that can create frequency elements that are higher

than those of the original image. NLSP using a num-

ber of non-linear functions should be able to create

high-frequency elements. Here, we propose y = x

for plus edges and y = −x

for minus edges.

It is well known that images are expanded in a

Fourier series (Mertz and Gray, 1934).Here, we take a

one-dimensional image f(x) to make the explanation

simple. f(x) is expanded as follows.

f(x) =

∑

n=−N

cos(nω

) + b

sin(nω

) (1)

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

150

Here, ω

is the fundamental frequency and N means

a positive integer. The HPF attenuates low-frequency

elements including the zero frequency element (DC).

We denote the output of the HPF by g(x) and it be-

comes as follows.

g(x) =

−M

∑

n=−N

cos(nω

) + b

sin(nω

)

∑

n=M

cos(nω

) + b

sin(nω

) (2)

M is also a positive integer and N > M. The fre-

quency elements from −M to M are eliminated with

the HPF. DC has the largest energy in the images,

and it sometimes causes saturation whereby the im-

ages become either all white or all black. The square

function does not cause saturation by eliminating DC,

and it has the following effect. Edges are represented

with sin(nω

) and cos(nω

) functions. The square

function generates sin

(nω

) and cos

(nω

) from

sin(nω

) and cos(nω

). sin

(nω

) and cos

(nω

)

generate sin2(nω

) and cos2(nω

These NLFs create frequency elements that are

two times higher than the input (Gohshi and Echizen,

2013), and they can be used to double the size of the

images horizontally and vertically, such as in the con-

version from HDTV to 4K TV. It is necessary to apply

NLSP horizontally and vertically (Figure 4), since im-

ages and videos are two-dimensional signals. Com-

puter simulations based on Figure 4 have been pre-

sented (Gohshi and Echizen, 2013) and real-time (30

Hz) hardware based on Figure 4 has been developed

(Gohshi et al., 2013). However, these developments

pointed out two issues. Using the sequential NLSP

shown in Figure 4, speciﬁc frequency elements are

processed twice in a two-dimensional frequency do-

main ; this causes artifacts and increases noise. Fig-

ure 5 shows an example in the two-dimensional fre-

quency domain. The horizontal axis is the horizon-

tal frequency, and the vertical axis is the vertical fre-

quency. The origin of the axes is called direct current

(DC) since the frequency of DC is zero. In Figure 5,

the spectra around DC is fully presented. The same

spectra is repeated every 2π and parts of the spectra

from (2π, 0), (−2π, 0), (0, 2π), (0, −2π) are shown. π

on the horizontal axis and the vertical axis in Figure 5

are the horizontal and vertical Nyquist frequencies.

The ﬁrst issue is degradation of images whose

frequency components are processed twice. Figure

6 shows the areas in the spectra that are processed

by the sequential NLSP shown in Figure 4. The ar-

eas hatched with lines having positive slopes are sub-

jected to the horizontal signal processing, whereas

those areas hatched with lines having negative slopes

are subjected to the vertical signal processing. The

four corner areas are subjected to both horizontal and

vertical signal processing. These corner areas have

both horizontal and vertical high-frequency elements.

Yet by processing these areas twice, the corner areas

are emphasized in excess, and this degrades the video

quality. When dots in an image that have both hor-

izontal and vertical high-frequency elements move,

they cause ﬂicker. The NSLP emphasizes the ﬂick-

ers on the dots and degrades video quality. Noise that

also has both horizontal and vertical high-frequency

elements exists in these corner areas. If these dots that

have both horizontal and vertical high-frequency ele-

ments are processed with NLSP two times, the noise

will be emphasized. Noise always degrades video

quality.

The second issue is the speed of the FPGA. The

FPGA embodying the sequential NLSP shown in Fig-

ure 4 can only work at 30 Hz (Gohshi et al., 2013).

Although this is fast enough to work on 24 Hz movie

content, it is not fast enough for 50 Hz or 60 Hz video

content.

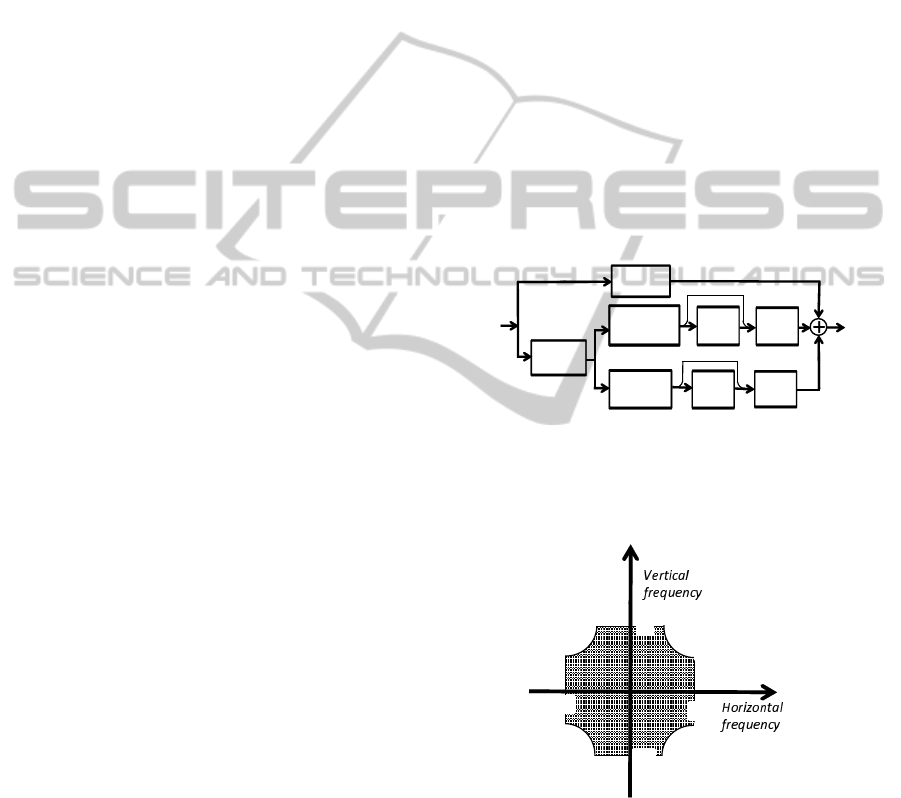
2D-LPF

Horizontal

HPF

Delay

Input

Vertical

HPF

Output

NLF

HPF: High pass filter

NLF: Non-linear function

LMT: Limiter

MSB: Most significant bit

LMT

NLF

LMT

MSB

Figure 7: Block diagram of real-time hardware.

Figure 8: Characteristics of 2D-LPF.

3 ADVANCED HARDWARE

ALGORITHM

Figure 7 is a block diagram of the real-time video pro-

cessing that is free of the issues discussed in section 2.

The input is distributed to two paths. The bottom line

Real-timeSuperResolutionEquipmentfor8KVideo

151

Figure 9: Appearance of real-time hardware.

includes a two-dimensional low pass ﬁlter (2D-LPF)

and a parallel NLSP part. The 2D-LPF decreases the

diagonal artifacts, and the parallel signal processing

enables the hardware to operate on 60 Hz moving im-

ages.

The input is distributed to the delay block and the

2D-LPF block. The delay path is the same as the in-

put, and the signal is delayed until the signal process-

ing on the other paths ends. The second path goes

to the 2D-LPF. The 2D-LPF reduces the diagonal is-

sue that is mentioned in section 2. Figure 8 shows

the two-dimensional frequency characteristics of the

2D-LPF. 2D-LPF passes the checker marked area and

eliminates the diagonal frequency elements, i.e., the

four corners shown in Figure 6. It also cuts the noise.

However, the human visual system is not so sensi-

tive to the horizontal and vertical high-frequency ele-

ments, i.e. the four corners shown in Figure 6 (Sakata,

1980). This means these frequency elements in the

NLSP video do not affect the perceived resolution.

Thus, to maintain the original diagonal resolution, the

original diagonal frequency elements are sent through

the delay line and added to the output.

The 2D-LPF eliminates diagonal frequency ele-

ments and splits the signal into two paths. The upper

path is the horizontal NLSP, and the lower path is the

vertical NLSP explained in section 2. The three video

paths are added together at the end to create the NLSP

video.

This parallel signal processing is fast. It reduces

the delay from input to output, as discussed in sec-

tion 1, and it can work at 60 Hz, unlike the sequential

NLSP shown in Figure 4. Figure 9 shows the NLSP

hardware. It up-converts full HDTV (1920× 1080) to

4K (3840× 2160), and it processes the up-converted

4K video with NLSP to increase the resolution at 60

Hz. The NLSP algorithm is installed in the FPGA,

which is located under the heat sink. Although there

are many parts on the circuit board, most of them are

input and output interface devices and electric power

devices.

Figure 10 shows an image processed with the

NLSP hardware shown in Figure 9. Figure 10(a) is

just an enlargement from HDTV to 4K, and it looks

blurry. Figure 10(b) shows the image processed with

NLSP after the enlargement. Its resolution is clearly

better than that of Figure 10(a). Figure 10(c) and

10(d) are the 2D-FFT results of Figure 10(a) and Fig-

ure 10(b). Figure 10(d) has horizontal and vertical

high-frequency elements that Figure 10(c) does not

have. This shows that real-time hardware works and

its function is the same as the simulation result.

4 EFFECT OF 2D-LPF

This section describes the effect of the 2D-LPF. Fig-

ure 11(a) shows the NLSP result when the 2D-LPF is

turned off, and Fig. 11(b) shows the result when the

2D-LPF is on. Comparing these two ﬁgures, we can

see there are artifacts around slanted lines that are the

diagonal frequency elements (Figure 11(a)). On the

other hand, artifacts are less evident in Figure 11(b).

This means that the 2D-LPF reduces the diagonal fre-

quency elements in Figure 6. Figures 11(c) and 11(d)

show the effect of the 2D-LPF on noise. Figures 11(e)

and 11(f) are enlargementscorresponding to the black

rectangular areas in Figure 11(c) and 11(d). A quick

comparison indicates that Figure 11(f) has less noise.

Slanted lines in an image have both horizontal and

vertical high-frequency elements. In the frequency

domain, slanted lines correspond to two of the four

cross-hatched corners in Figure 6. The lines in the

image that go upwards to the right correspond to the

cross-hatched areas in the ﬁrst and third quadrants in

Figure 6. The lines in the image that go downwards

toward the right correspond to the cross-hatched areas

in the second and fourth quadrants in Figure 6.

Dot-shaped noise in an image has frequency ele-

ments in the cross-hatched areas of all four quadrants

of Figure 6. The artifacts are reduced because the 2D-

LPF cuts off the frequency elements in these four cor-

ners.

5 FOCUSING EFFECT

Although ﬁlm cameras have been used in the movie

industry for a long time, most movies are made to-

day with more cost-effective HDTV cameras. These

professional HDTV cameras do not have auto focus

systems that commercial camcorders have. Produc-

tion zoom lenses are used to make TV content since

several scenes are shot in a single take. In these takes,

the camera focus is often changed from one object to

another. It is not easy, even for professional camera

persons, to adjust the focus with a small viewﬁnder.

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

152

(a) 4K image enlarged from HD (b) 10(a) with NLSP

Figure 10: Image processed with real-time NLSP.

Although TV content is often out of focus, we cannot

recognize this on a TV screen because of its relatively

small size. However, if that content were shown on

a large screen of a movie theater, it would appear as

blurry as content shot with a commercial camcorder’s

auto-focus. On the other hand, movies have high res-

olution and appear sharp on large screens in theaters.

That means although TV content and movie content

are shot with HDTV cameras, the difference between

them has to do with the lens focus. Single focus lenses

are used in the movie industry, whereas zoom lenses

are used to make TV content. Thus TV content is

affected by blurring caused by zoom lenses, while

movie productions face the difﬁculty of performing

multi-focus shots in a single take. These two aspects

of the gout-of-focus problemh are part of the topic

of image restoration, and many ideas have been put

forward to deal with them (Figueiredo and Nowak,

2003)(Pan and Blue, 2011)(Karungaru et al., 2009).

However, the methods presented so far need itera-

tions or parameter adjustments made under certain

hypotheses. It is not easy to use them in practical ap-

plications.

It would be useful if there were a technology that

could focus a shot after it has been made. Here, we

would like to point out that NLSP has a focusing ef-

fect. Figure 12(a) is a blurry image. The original im-

age is crisp (it is part of a test pattern), and it was pro-

cessed with an LPF to make it blurry. Figure 12(b) is

the result of processing Figure 12(a) with the NLSP

hardware. Comparing these ﬁgures, we can see that

the resolution of Figure 12(b) is better and the focus

looks adjusted. This effect is due to the character-

istics of NLSP. NLSP can generatee high-frequency

elements that the original image does not have, and

these high-frequency elements have a focusing effect.

6 4K TO 8K UP-CONVERTER

WITH NLSP

8K TV is currently under development. At the mo-

ment the baseband speed of 8K is four times higher

than 4K. At the same time 8K content is very rare.

4K content up-converted to 8K does not have satis-

factory resolution. However, if 4K content could be

up-converted with sufﬁcient resolution, it would be

very useful for 8K development.

The hardware up-converter with NLSP can pro-

cess HDTV and generate 4K in real time. Since the

pixel of 4K is 3820× 2080, it can be divided into four

HDTV video sections. Four 4K video sections can be

generated using the same hardware on each HDTV

section. These four up-converted 4K videos can then

be combined to create 8K video in real time. Figure

13 shows an example of 8K video up-converted from

4K. There are four pairs of images. The column (a)

images are the original 4K frames and the column (b)

ones are double enlargements 8K frames made with

Real-timeSuperResolutionEquipmentfor8KVideo

153

(a) NLSP with 2D-LPF off (b) NLSP with 2D-LPF on

(e) Noise without 2D-LPF (f) Noise with 2D-LPF

Figure 11: Effect of 2D-LPF.

(a) Blurry image (b) Focused image

Figure 12: Focusing effect.

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

154

(a) 4K ship (b) 8K ship

(e) 4K bus (f) 8K bus

(g) 4K roof (h) 8K roof

Figure 13: 4K and up-converted 8K images.

Real-timeSuperResolutionEquipmentfor8KVideo

155

NLSP in real time. The images enlarged with NLSP

do not show any blur. This means NLSP improves

resolution. The up-converter also works in real time

(60 Hz).

7 CONCLUSIONS

NLSP real-time hardware for 8K was presented.

Since the NLSP algorithm can create high-frequency

elements that the original image does not have, it can

create a high-resolution image in spite of the enlarge-

ment. Using parallel signal processing and a 2D-LPF,

it works in real time even on enlarged 8K video shown

at 60 Hz. The use of NLSP in up-conversion from 4K

to 8K removes the blur caused by the enlargement and

works in real time. It also has a focusing effect and

can be applied to defocused video in real time. The

papers on Super Resolution Image Reconstruction re-

ported the PSNR between the original image and SR

processed images since those studies used the origi-

nal images. However, there are no original 8K images

used in the examples of this paper. The subjective as-

sessment is the only assessment method, and it will

remain as future work to examine the possibility of

developing a more objective measure.

REFERENCES

W. F. Schreiber, ”Wirephoto Quality Improvement by Un-

sharp Masking”, J. Pattern Recognition, 2, 1970, pp.

111-121.

J-S. Lee, ”Digital Image Enhancement and Noise Filter-

ing by Use of Local Statistics”, IEEE Trans. Pattern

Analysis and Machine Intelligence, PAMI-2, 2, March

1980, pp. 165-168.

W. K. Pratt, ”Digital Image Processing (3rd Ed)”, John

Wiley and Sons, 2001, pg. 278.

S. C. Park et al., ”Super-Resolution Image Reconstruc-

tion: A Technical Overview”, IEEE Signal Processing

Magazine, 1053-5888/03, pp. 21-36, May, 2003.

S. Farsiu et al., ”Fast and Robust Multi-frame Super-

resolution”, IEEE Transactions on Image Processing

, vol. 13, no. 10, pp. 1327-1344, October, 2004.

A. W. M. van Eekeren et al., ”Multiframe Super-

Resolution Reconstruction of Small Moving Objects”,

IEEE Transactions on Image Processing, pp. 2901-

2912, Vol. 19, No. 11, November, 2010.

Xianghua Houa et al., ”Super-resolution Image Recon-

struction for Video Sequence”, 2011 International

Conference on Electronic & Mechanical Engineering

and Information Technology, pp. 4600-4603, 12-14

August, 2011.

Matan Protter et al., ”Generalizing the Nonlocal-Means

to Super-Resolution Reconstruction”, IEEE Transac-

tions on Image Processing, pp. 36-51, Vol. 18, No. 1,

Jan. 2009.

S. Panda et al., ”POCS Based Super-Resolution Image

Reconstruction Using an Adaptive Regularization Pa-

rameter”, IJCSI International Journal of Computer

Science Issues, Vol. 8, Issue 5, No. 2, September 2011,

ISSN (Online), 1694-0814.

P. Mertz and F. Gray, ”A Theory of Scanning and Its Rela-

tion to the Characteristics of the Transmitted Signal in

Telephotography and Television”, Bell System Tech-

nical Journal, Vol.63B, pp.464-515, (1934).

S. Gohshi and I. Echizen, ”Limitations of Super Resolution

Image Reconstruction and How to Overcome them for

a Single Image”, ICETE2013 (SIGMAP), Reykjavik,

Iceland , pp. 71-78, July, 2013.

N. Matsumoto and T. Ida, ”Reconstruction Based Super-

Resolution Using Self-Congruency around Image

Edges”, Journal of IEICE , Vol. J93-D, No. 2, pp. 118-

126, Feb. 2010 (in Japanese).

Seiichi Gohshi et al., ”Real-Time Up-Converter from HDTV

to 4K with Super Resolution”, 42.2, pp. 582-585,

0097-966X-13-4402, Society for Information Display

SID 2013 DIGEST, 23rd May 2013.

H. Sakata, ”Assessment of TV noise and Frequency Charac-

teristics”, Journal of ITE , Vol. 34, No. 3, pp. 239-245,

Mar. 1980 (in Japanese).

Seiichi Gohshi, ”Limitation of Super Resolution Image Re-

construction for Video”, Computational Intelligence,

Communication and Networks (CICSyN), Madrid,

Jun. 2007.

M. A. T. Figueiredo and R. D. Nowak, ”An EM algorithm

for wavelet-based image restoration”, IEEE Transac-

tions on Image Processing, vol. 12, pp. 906-916, Aug.

2003.

Hanjie Pan , Thierry Blu, ”Sparse Image Restoration us-

ing Iterated Linear Expansion of Thresholds”, Image

Processing (ICIP), pp. 1905 - 1908, 18th IEEE Inter-

national Conference, Sept. 2011.

Stephen Karungaru, Masakazu Sugizaki, Minoru Fukumi,

Yasue Mitsukura, and Norio Akamatsu, ”Out-of-

Focus Blur Image Restoration using the Akamatsu

Transform”, Industrial Electronics, IECON ’09. 35th

Annual Conference of IEEE, pp. 4257-4261, Nov.

2009.

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

156