Multi-cameras Visual Servoing to Perform a Coordinated Task using a

Dual Arm Robot

Renliw Fleurmond

1,2

and Viviane Cadenat

1,2

CNRS, LAAS, 7 avenue du Colonel Roche, F-31400 Toulouse, France

Univ. de Toulouse, UPS, LAAS, F-31400 Toulouse, France

Keywords:

Dual Arm Robots, Coordination, Vision-based control, Multi-cameras visual servoing.

Abstract:

This paper deals with the problem of coordinating a dual arm robot equipped with several cameras. Our goal

is to propose a vision-based control strategy allowing to realize a real cooperation of the two arms. The idea

is to sequence different vision based tasks built from visual features describing the relative pose between the

cap and the pen. Simulation results validate our approach.

1 INTRODUCTION

Dual arm manipulation has been studied since the

eighties (Caccavale and Uchiyama, 2008). At the be-

ginning, the objective was to enhance the range of re-

alizable industrial applications. It then became pos-

sible to carry heavy loads (Bonitz and Hsia, 1996),

manipulate ﬂexible objects (Zheng and Chen, 1993),

or assemble pieces (Yamada et al., 1995). Neverthe-

less, the recent development of service robots has led

to the design of new mobile robotic systems able to

help people in their daily life (co-worker, etc.) (Smith

et al., 2012). To complete such missions, these robots

must be able to perform complex manipulation tasks,

which requires to coordinate both arms motion. Ac-

cording to (Zollner et al., 2004), coordination tasks

can be divided into two classes : symmetric coordina-

tion when both arms manipulate the same object and

asymmetric coordination where they carry different

objects.

The coordination problem can be tackled at dif-

ferent levels and through many approaches (Smith

et al., 2012). In particular, it has been shown that

a pure position feedback is unable to deal with this

kind of problem because of its sensitivity to mod-

eling errors (Caccavale et al., 2001). Consequently,

other approaches using exteroceptive data have been

developed. Common solutions rely on hybrid po-

sition/force based control laws (Kraus and McCar-

ragher, 1997; Watanabe et al., 2005) or active compli-

ance control laws (Bonitz and Hsia, 1996; Albrichs-

feld and Tolle, 2002). However, other kinds of extero-

ceptive data such as vision can be exploited, the robot

being then controlled using visual servoing. This

kind of control offers two main advantages which ap-

pear to be quite interesting in the context of dual arm

manipulation. First, it can be realized using several

(embedded and/or external) cameras (Kermorgant and

Chaumette, 2011), which allows to beneﬁt from com-

plementary information on the task execution. Sec-

ond, visual servoing, especially image based control,

is known to offer nice robustness properties, which al-

lows to accurately perform the task (Chaumette and

Hutchinson, 2006). However, to the best of our

knowledge, there are only few works which have re-

ally dealt with dual arm visual servoing (Smith et al.,

2012). We present hereafter a brief overview. In

(Miyabe et al., 2003) 2D visual servoing is used to

simultaneously and independently control two arms

to capture an object. In (Hynes et al., 2006) the two

arms are alternatively controlled using visual servo-

ing to tie surgical knots. Finally, Vahrenkamp et al.

propose a 3D visual servoing to control the arms of a

humanoid robot in order to grasp the handles of a wok

or pour liquid from a bottle into a cup (Vahrenkamp

et al., 2009). Thus, in these works, the coordination

problem is not completely solved, the two arms being

often separately or alternatively controlled.

In this paper, we address the coordination prob-

lem from a control point of view. We aim at design-

ing a vision-based control strategy allowing to truly

coordinate the motions of a dual arm robotic system

equipped with several cameras. In other words, the

control will be deﬁned so that both arms simultane-

ously move to perform the desired task. Here, we

Fleurmond R. and Cadenat V..

Multi-cameras Visual Servoing to Perform a Coordinated Task using a Dual Arm Robot.

DOI: 10.5220/0005017700370044

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 37-44

ISBN: 978-989-758-040-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

have chosen to realize an asymmetric coordination

task consisting in recapping a pen. Our idea is to

build an image based visual servoing (IBVS) control

to beneﬁt from its good robustness properties with re-

spect to modeling errors (Chaumette and Hutchinson,

2006). This control law will be fed using the data

provided by two different cameras (a ﬁxed one and a

mobile one) mounted on the robot. We will then de-

velop a multi-camera visual servoing. To do so, as in

(Uchiyama and Dauchez, 1988; Dauchez et al., 2005),

we have considered the two arms as a single robotic

system to be controlled. Furthermore, (Dauchez et al.,

2005) and (Adorno et al., 2010) have shown that the

realization of a coordination task requires to deﬁne

it in terms of the relative pose between the two end-

effectors. Here, we have followed a similar reasoning,

except that our task will be directly expressed in the

image plane instead of the 3D space, which will lead

to the design of a more robust control law. This latter

will be obtained by regulating to zero a relative error

between the visual features describing the cap and the

pen provided by the cameras.

This paper is organized as follows: the two next

sections describe our contribution, namely the prob-

lem modeling and the proposed control strategy. Sim-

ulation results validating our approach are then pre-

sented while the last section is devoted to a conclusion

and some prospects.

2 MODELING THE PROBLEM

2.1 Robot Model

Our robotic platform is the PR2 developed by Wil-

low Garage. It consists of an omnidirectional mobile

base equipped with two 7-DOF robotic arms. We con-

sider that the mobile base and the head are ﬁxed in

this work. The robot has several cameras, and as ex-

plained before we will use the information provided

by two of them to perform the task. The ﬁrst one,

whose center is denoted by C

is ﬁxed on the head and

has a large ﬁeld of view. The second one, whose cen-

ter is denoted by C

, is located on the right forearm.

It gives us additional information on the scene which

will be useful when assembling the two objects.

We introduce the different frames which will

be necessary to model our problem (see ﬁgure 1).

) is ﬁxed and represents the world

frame. F

) and F

) are re-

spectively the frames linked to the left and right end

effectors. F

) and F

)

are respectively the frames attached to ﬁxed and mo-

bile cameras. We denote by q

and q

(respectively

˙q

and ˙q

) the joint coordinates (respectively the joint

velocities ) of the right and left arms.

Figure 1: The robotic platform and the different frames.

Using these notations, the kinematic screws of the

end effectors T

and T

, and of the mobile camera T

with respect to F

are given by the direct differential

kinematic model as follows:

= J

˙q

, T

= J

˙q

, T

= J

˙q

(1)

where J

, J

and J

are 6 × 7 matrices which have

been already determined. These kinematic screws are

respectively expressed in frames F

, F

and F

2.2 Modeling the Task

As previously mentioned, the task which is consid-

ered here consists in recapping a pen. To do so, we

ﬁrst introduce the two following hypotheses:

• Hyp 1: The cap and the pen are respectively

gripped by the right and left arms.

• Hyp 2: The two objects are modeled by two cylin-

ders as shown in ﬁgure 2. Furthermore, in the se-

quel, to avoid some singularities, we assume that

these objects are always seen as shown in this ﬁg-

ure.

Figure 2: Cap and pen model.

To recap the pen, the robot has to align both cylin-

ders before connecting them. But this movement can-

not be done directly. We then divide the task into the

three following subtasks as illustrated in ﬁgure 3

• Make both cylinders axes coplanar while ensur-

ing a sufﬁcient distance between the two objects.

The pen is shown as if it is ﬁxed for the sake of clarity.

But of course both objects are allowed to move.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

• Make both cylinders axes collinear while ensur-

ing a sufﬁcient distance between the two objects.

• Maintain the alignment and bring the cap near the

pen.

Figure 3: Steps to recap the pen.

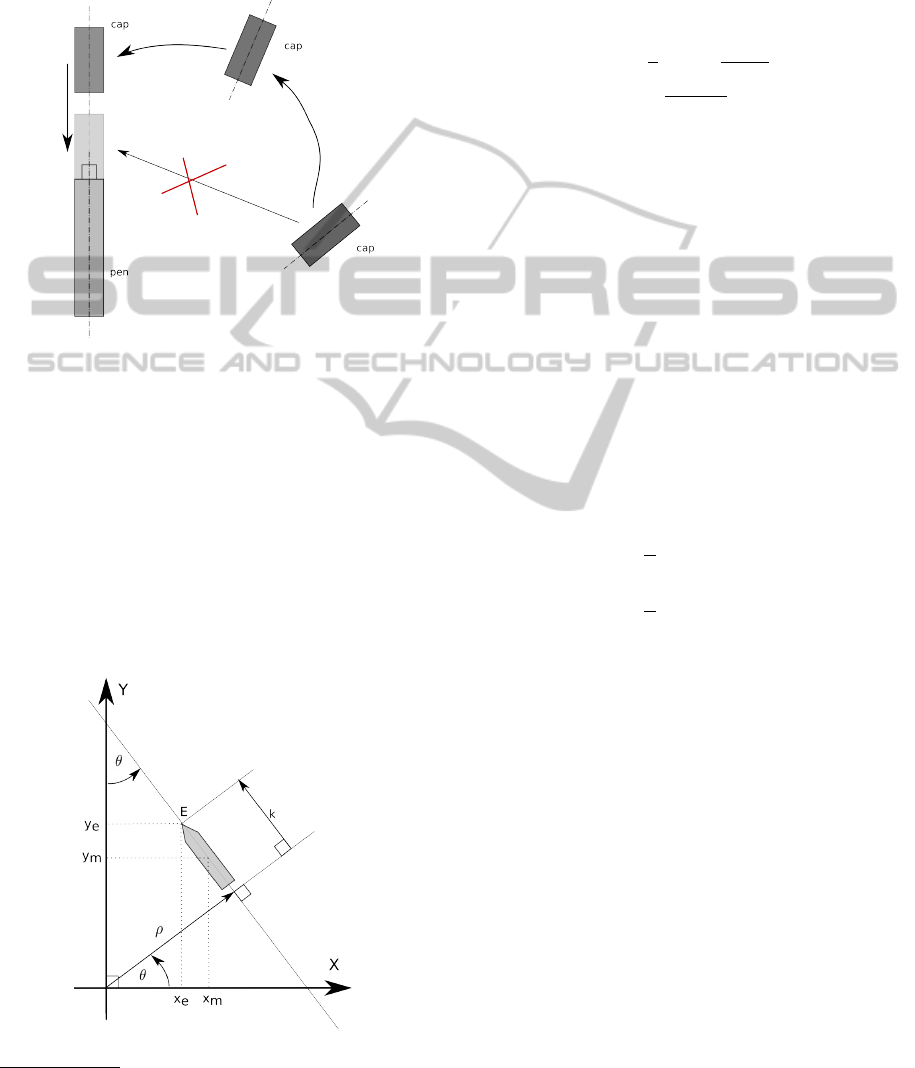
2.3 Visual Features

In this part, our goal is to choose visual features al-

lowing to represent the cap and the pen. Espiau et al.

(Espiau et al., 1992) have used two lines to deﬁne the

contour of the cylinder projection. Here we have cho-

sen to consider the projection of the cylinder axis on

the image plane. This straight line is obtained from

the axis of the grey area (cf. ﬁgure 4) corresponding

to the cylinder

in the image.

Figure 4: Visual features used: ρ, θ and k.

It is not an exact value of the projection of the axis but

it provides a good approximation.

We have then represented the line by using polar

parameters (ρ, θ) as in (Espiau et al., 1992). In this

representation, ρ is the distance between the line and

the center of the image, and θ is its relative orientation

with respect to the vertical axis (cf. ﬁgure 4). To com-

pute these features we have used the formulas given

in (Berry et al., 2000). We get:

θ =

atan



− I



ρ =

+ y

where (x

) is the center of mass of the area repre-

sented in grey in the ﬁgure 4.

However, with such a representation, two lines

which are symmetrical with respect to the origin are

characterized using the same parameters. To over-

come this ambiguity, we have allowed ρ to be positive

or negative as in (Espiau et al., 1992). We have cho-

sen to compute ρ by using this following expression:

ρ = x

.cos(θ) + y

.sin(θ) (2)

, I

and I

are the second order moments of this

area, and their well-known expressions are given by

(Chaumette, 2002a):

A =

∑

area

∑

area

∑

area

∑

area

(x − x

)

∑

area

(y − y

)

∑

area

(x − x

)(y − y

)

Parameters θ and ρ allow us to partially control

the orientation and the position of the objects. How-

ever, it is also necessary to monitor the translation of

a cylinder along its axis. To this aim, we introduce a

third parameter k which expresses the position of one

end point E (x

) of the cylinder on the straight line

(cf. ﬁgure 4). We get:

k = y

· cos(θ) − x

· sin(θ) (3)

Thus, the image of each cylinder is described by

three parameters. As we consider two cylindrical ob-

jects and two cameras, we deﬁne the four following

visual features vectors:

Multi-camerasVisualServoingtoPerformaCoordinatedTaskusingaDualArmRobot

Cap

Fixed camera Moving camera

f c

= [ρ

f c

,θ

f c

]

= [ρ

,θ

]

Pen

Fixed camera Moving camera

f p

= [ρ

f p

,θ

f p

]

= [ρ

,θ

]

Remark: A singularity occurs in the representation

of the visual features if the area is a disc because I

and I

= 0. However this case cannot happen here

thanks to hypothesis 2.

3 CONTROL STRATEGY

To perform our task, we have chosen to use visual

servoing which allows to control a robot using the vi-

sual informations provided by one or several cameras

(Chaumette and Hutchinson, 2006). Visual servoing

can be roughly speaking divided into three classes:

3D, 2D, 2D-1/2 (Chaumette and Hutchinson, 2006).

Here we have used the second approach also known

as image based visual servoing (IBVS), because of its

well-known properties of robustness with respect to

errors (Chaumette and Hutchinson, 2006).

To design our control law we have used the task

function approach (Samson et al., 1991) where the

task is described by a n-dimensional C

function

e(q,t), to be regulated to zero.

As classically done in the visual servoing area

(see for example (Espiau et al., 1992; Chaumette and

Hutchinson, 2006)), we impose an exponential decay

to make e(q,t) vanish. This controller is given by (Es-

piau et al., 1992) :

˙q = −J

λe (4)

where λ is a positive gain or a positive-deﬁnite matrix,

J the jacobian of the task function and J

its Moore-

Penrose inverse.

Our goal is to use this formalism to design our

control law. To this aim, we ﬁrst consider the two

arms as a single robotic system as in (Uchiyama and

Dauchez, 1988; Dauchez et al., 2005). The control

vector will then be composed of the joint velocities

of both arms: ˙q =



˙q



. Moreover, it is nec-

essary to deﬁne the task functions corresponding to

the above mentioned three tasks. In 2D visual ser-

voing e(q,t) is generally given by an error between

the current vector of visual features S and the de-

sired ones S

∗

, S

∗

being often constant. However, if

we follow this reasoning to deﬁne our task functions,

we will monitor the absolute pose of the two objects

with respect to the world frame, and the arms will be

separately controlled. Therefore, to really coordinate

the two arms, it is truly better to focus on the rela-

tive pose between the end effectors, as proposed in

(Adorno et al., 2010; Dauchez et al., 2005). Follow-

ing the same idea, we express the task functions as a

relative error between the visual features representing

to the cap and the pen.

3.1 The Task Functions

In this part, the aim is to model the previously men-

tionned subtasks by three task functions e

, e

. We

consider the ﬁrst one. To perform this substask, it is

necessary to constrain the two cylinder axes to belong

to the same plane. To do so, it sufﬁces to align their

projection in one image. We have chosen to use the

one provided by the mobile camera. The ﬁrst subtask

is then expressed as follows:





− ρ

− θ

− k

− d





(5)

where d is a constant value allowing to maintain a

given distance between the cap and the pen.

Now, we consider the second subtask. Its goal is to

align the axes of the two cylinders. At least two points

of view are necessary to guarantee that two straight

lines are aligned. Therefore we have to consider the

visual features provided by both cameras, which leads

to implement a multi-cameras visual servoing control

law. Our second subtask is deﬁned as shown below:





f c

− ρ

f p

f c

− θ

f p





(6)

Finally, our last subtask has to keep the axes

aligned while bringing the cap to the pen. We pro-

pose the following expression:



− S

f c

− S

f p



(7)

Taking into account the expressions of e

, e

, and

, it is possible to show that these subtasks can be

re-written as follows:

= H



− S

− A

f c

− S

f p



(8)

where H

is an activation matrix which allows to se-

lect only the necessary visual features. H

and A

are

deﬁned for each subtask e

as shown below:



3×3



and A

= [0,0, d]



5×5

5×1



and A

= [0,0, d]

= I

6×6

and A

= 0

3×1

Once the task functions are deﬁned, we now focus

on the control law allowing to regulate them to zero.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

3.2 Control Design

To design the control law, our idea is to use equation

(4). To this aim, we have to determine the jacobian of

each task function. Using the general formulation (8),

the time derivative of our subtasks e

is given by:

˙e

= J

˙q, ˙e

= H



−

f c

−

f p



(9)

Following (Chaumette, 2002b), the time deriva-

tive

S of a given visual features vector denoted by S

expresses as follows:

S = L · (T

− T

) (10)

where L is the interaction matrix, T

and T

are re-

spectively the kinematic screws of the camera and of

the mobile target with respect to the world frame F

They are expressed in the camera frame. Let us re-

call that we consider two cameras: a mobile one and

a static one. We have to express T

and T

in both

cases.

3.2.1 Fixed Camera

In this case, the camera kinematic screw T

is zero.

Thus it remains to compute T

. Here T

represents the

kinematic screw of the moving object (cap or pen).

This screw must be expressed at a particular point of

the object which coincides at every moment with the

ﬁxed camera center C

. To determine it, let us recall

the following well-known relation (P

erez, 1989):

where



3×3

[AB]

0 I

3×3



where T

and T

are the kinematic screws of two

points A and B belonging to the same mobile solid.

They are expressed with respect to a ﬁxed frame.

is the skew-symmetric matrix such as ∀

V ∈

, [AB]

V =

−→

AB ×

V .

Recalling that the cap is moved by the left end ef-

fector and the pen by the right one, and that T

must

be expressed in the camera frame F

, the following

expressions yield:

• For the cap



3×3



• For the pen



3×3



where

and

are respectively the rotation matri-

ces between F

and F

, and F

and F

Now combining these expressions and the equa-

tions (1) and (10), the time derivatives of S

f c

and S

f p

are:

f c

= −L

f c

˙q

(11)

f p

= −L

f p

˙q

(12)

where L

f c

and L

f p

are the interaction matrices corre-

sponding to S

f c

and S

f p

. Their expressions are de-

tailed in appendix A.

3.2.2 Moving Camera

In this case, the camera and the two objects are both

moving. We have then to determine the kinematic

screws T

and T

. The ﬁrst one is already known and

is given by T

(see equation (1)).

It then remains to compute T

. We follow the

same reasoning as previously, keeping in mind that

the kinematic screw must be expressed at the point

which coincides with the center C

of the mobile

camera. We ﬁnally obtain the following result:

• For the cap



3×3



• For the pen



3×3



where

and

are respectively the rotation ma-

trices between F

and F

Using (10) and (1), we obtain the time derivative

of S

and S

= L

˙q

−

˙q

) (13)

= L

˙q

−

˙q

) (14)

where L

and L

are the interaction matrices cor-

responding to S

and S

. Their expressions are de-

tailed in appendix A.

3.2.3 The Jacobian Matrix of Each Subtask

Finally we can deduce that the jacobian of each sub-

task e

is given by:

= H



−L

− L

−L

f c

f p

3×6







6×7





(15)

The control law corresponding to each subtask e

is then expressed as follows:

˙q

= −J

(16)

with i = {1,2, 3}.

Multi-camerasVisualServoingtoPerformaCoordinatedTaskusingaDualArmRobot

3.3 Transition Between Tasks

We have deﬁned three task functions. To recap the

pen, it is necessary to sequence them. In other words,

we need to sequence the control laws allowing to reg-

ulate them to zero, while preserving the smoothness

of the velocities applied to the robot.

This objective cannot be performed by consider-

ing the classical exponential decrease which is gener-

ally set to make the task function vanish. A ﬁrst so-

lution to this problem has been proposed in (Soueres

et al., 2003). The idea is to impose a second order

linear dynamic to make the task function vanish.

¨e + α ˙e + βe = 0

Thanks to this choice, it is possible to deﬁne the ini-

tial conditions on e and ˙e so that the control law

smoothness is guaranteed. A year later, (Mansard and

Chaumette, 2004) have proposed a particular choice

for alpha and beta, leading to the following linear dif-

ferential equation:

¨e + (λ + µ) ˙e + λµe = 0

The main advantage of this solution is that it allows

to separately choose λ and µ. If µ > λ > 0, the system

is stable and the transient time is set only by µ. So, to

switch from a task e

i−1

to another task e

at t

, the real

control ˙q sent to the robot is given by the following

expression:

˙q(t) = ˙q

(t) − exp(−µ(t − t

))( ˙q

) − ˙q(t

)) (17)

where ˙q

is the value computed by the formula (16)

and t

the switching time.

We switch from the current control law to the next

one when the norm of the current task function drops

below a given threshold.

4 SIMULATION RESULTS

We now present simulation results to validate our ap-

proach. A gaussian noise has been introduced on

the visual features (mean = 0, standard deviation =

2 pixels)

, on the joint coordinates q (mean = 0,

covariance = 7.6 × 10

−7

rad

) and on the veloci-

ties sent to the robot (mean = 0 rad/s, covariance =

7.6 × 10

−7

rad

). The control law is updated at

15 Hertz rate. Both arms trajectory has been recorded

and played

using ROS

on the Gazebo simulator

The sensor has the size of 4.51mm × 2.88mm with a

focal length of 2.5mm and provides an image of 752 × 480

pixels.

A video is available on

http://homepages.laas.fr/rﬂeurmo/.

http://www.ros.org/

http://gazebosim.org/

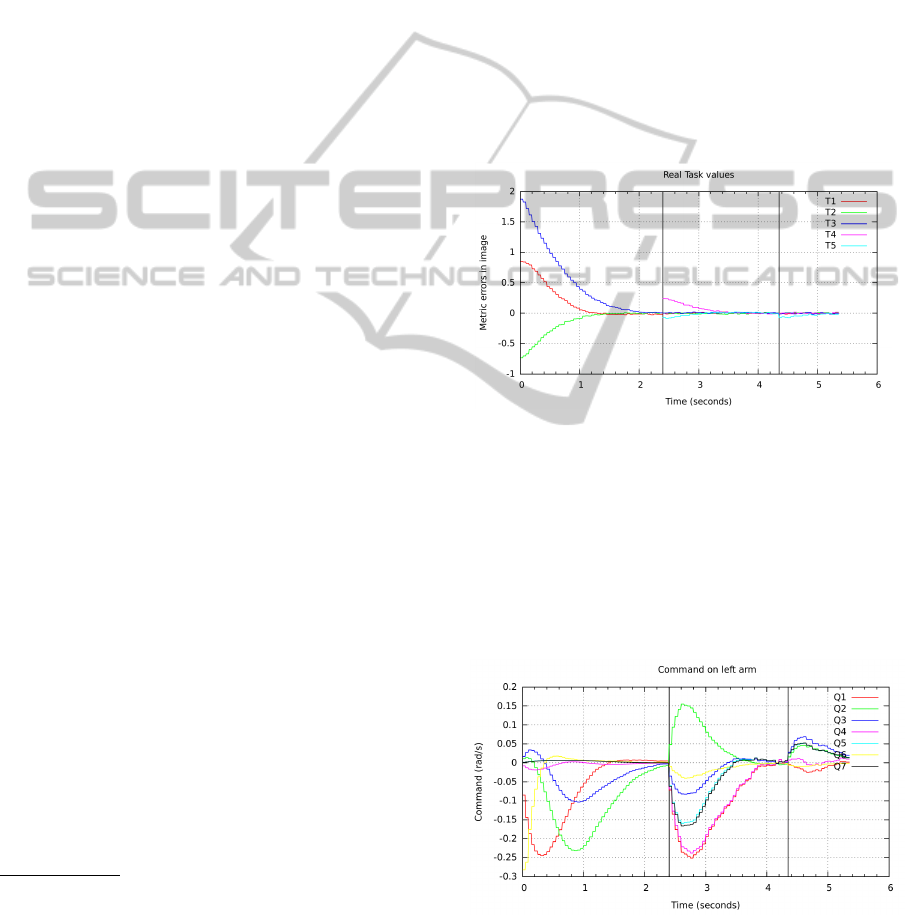
The evolution of the components T

of the three

task functions e

, e

and e

is presented on ﬁgure 5.

As we can see, all of them converge towards zero,

which shows that the corresponding tasks are success-

fully achieved. The ﬁrst subtask e

is active between 0

and 2.4 s: in this interval T

, T

and T

are respectively

deﬁned by ρ

− ρ

, θ

− θ

, and k

− k

− d.

At instant 2.4s, the norm of e

drops under a

threshold equal to 10

−2

, we start realizing the second

subtask. At this time, T

and T

are given by ρ

f c

−ρ

f p

and θ

f c

− θ

f p

. At t = 4.35s, the value of e

becomes

smaller than the chosen threshold and the last subtask

is launched. T

, T

and T

are then respectively de-

ﬁned by ρ

f c

− ρ

f p

, θ

f c

− θ

f p

and k

− k

. The two

switching instants are shown by two black lines on

ﬁgure 5.

Figure 5: Evolution of the task function.

Figures 6 and 7 show the evolution of the veloc-

ities sent to the two arms. As we can see, the con-

trol inputs applied to each of them appear to be sim-

ilar, which shows that both arms move to achieve the

task and that the coordination between them is prop-

erly performed. These ﬁgures also demonstrate the

efﬁciency of our smoothness strategy, as no sudden

jumps is registered.

Figure 6: Control sent to the right arm.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

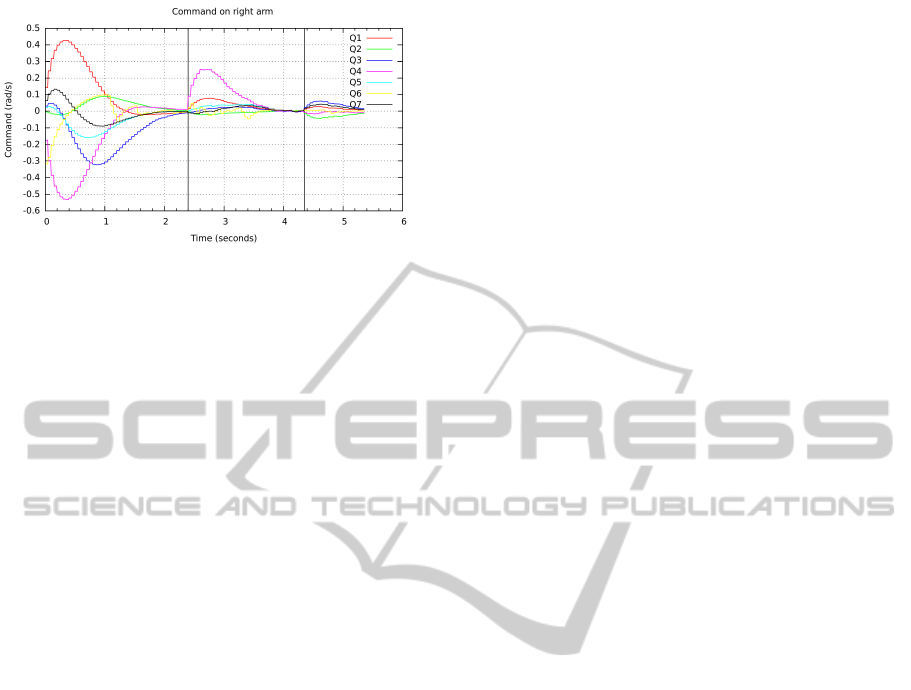
Figure 7: Control sent to the left arm.

5 CONCLUSION

In this paper, we have tackled the problem of coor-

dinating two manipulator arms from a control point

of view. We have proposed a vision-based control

strategy allowing to truly coordinate the motions of

a dual-arm robotic system. The task to be performed

has been described by a sequence of three subtasks.

Each of them is deﬁned by visual features character-

izing the relative pose between the end effectors so

that a true collaboration between both arms has been

achieved. A multi-cameras image based visual ser-

voing has then been designed. Finally, the proposed

control strategy has been validated and the obtained

simulation results have demonstrated its interest and

its efﬁciency.

Now, to go further and improve our approach, it is

necessary to take into account the unexpected events

which may occur during the task and hamper its exe-

cution (e.g., joint limits, singularities, collisions, oc-

clusions, etc.). Therefore, our next step will be to ad-

dress this problem by taking advantage of the system

redundancy. In addition to these theoretical improve-

ments, we also plan to experimentally validate our ap-

proach on the LAAS PR2 robot and to perform more

complex coordination tasks.

REFERENCES

Adorno, B., Fraisse, P., and Druon, S. (2010). Dual posi-

tion control strategies using the cooperative dual task-

space framework. In Intelligent Robots and Systems

(IROS), 2010 IEEE/RSJ International Conference on,

pages 3955–3960.

Albrichsfeld, C. V. and Tolle, H. (2002). A self-adjusting

active compliance controller for multiple robots han-

dling an object. Control Engineering Practice,

10(2):165 – 173.

Berry, F., Martinet, P., and Gallice, J. (2000). Turning

around an unknown object using visual servoing. In

Intelligent Robots and Systems, 2000. (IROS 2000).

Proceedings. 2000 IEEE/RSJ International Confer-

ence on, volume 1, pages 257–262 vol.1.

Bonitz, R. and Hsia, T. (1996). Robust internal-force based

impedance control for coordinating manipulators-

theory and experiments. In Robotics and Automation,

1996. Proceedings., 1996 IEEE International Confer-

ence on, volume 1, pages 622–628 vol.1.

Caccavale, F., Ciro, N., Siciliano, B., and Villani, L. (2001).

Achieving a cooperative behavior in a dual-arm robot

system via a modular control structure. Journal of

Robotic Systems, 18(12):691–699.

Caccavale, F. and Uchiyama, M. (2008). Cooperative ma-

nipulators. In Siciliano, B. and Khatib, O., edi-

tors, Springer Handbook of Robotics, pages 701–718.

Springer Berlin Heidelberg.

Chaumette, F. (2002a). A ﬁrst step toward visual servoing

using image moments. In Intelligent Robots and Sys-

tems, 2002. IEEE/RSJ International Conference on,

volume 1, pages 378–383 vol.1.

Chaumette, F. (2002b). La commande des robots manipu-

lateurs: Asservissement visuel, chapter 3, pages 101 –

151.

Chaumette, F. and Hutchinson, S. (2006). Visual servo con-

trol part 1: Basic approaches. IEEE Robotics and Au-

tomation Magazine, 13(4):82–90.

Dauchez, P., Fraisse, P., and Pierrot, F. (2005). A vi-

sion/position/force control approach for performing

assembly tasks with a humanoid robot. In 5th IEEE-

RAS International Conference on Humanoid Robots,

pages 277–282.

Espiau, B., Chaumette, F., and Rives, P. (1992). A new

approach to visual servoing in robotics. IEEE Trans-

actions on Robotics and Automation, 8(3):313–326.

Hynes, P., Dodds, G., and Wilkinson, A. J. (2006). Un-

calibrated visual-servoing of a dual-arm robot for mis

suturing. In The First IEEE/RAS-EMBS International

Conference on Biomedical Robotics and Biomecha-

tronics, pages 420–425.

Kermorgant, O. and Chaumette, F. (2011). Multi-sensor

data fusion in sensor-based control application to

multi-camera visual servoing. In IEEE International

Conference on Robotics and Automation, pages 4518–

4523.

Kraus, W., J. and McCarragher, B. J. (1997). Hybrid posi-

tion/force coordination for dual-arm manipulation of

ﬂexible materials. In Intelligent Robots and Systems,

1997. IROS ’97., Proceedings of the 1997 IEEE/RSJ

International Conference on, volume 1, pages 202–

207 vol.1.

Mansard, N. and Chaumette, F. (2004). Tasks sequencing

for visual servoing. In Intelligent Robots and Systems,

2004. (IROS 2004). Proceedings. 2004 IEEE/RSJ In-

ternational Conference on, volume 1, pages 992–997

vol.1.

Miyabe, T., Konno, A., and Uchiyama, M. (2003). Auto-

mated object capturing with a two-arm ﬂexible ma-

nipulator. In Robotics and Automation, 2003. Pro-

ceedings. ICRA ’03. IEEE International Conference

on, volume 2, pages 2529–2534 vol.2.

Multi-camerasVisualServoingtoPerformaCoordinatedTaskusingaDualArmRobot

erez, J. (1989). M

ecanique: points mat

eriels, solides, ﬂu-

ides : avec exercices et probl

emes r

esolus. Enseigne-

ment de la physique. Masson.

Samson, C., Borgne, M. L., and Espiau, B. (1991). Robot

control: the task function approach. Oxford engineer-

ing science series. Clarendon Press.

Smith, C., Karayiannidis, Y., Nalpantidis, L., Gratal, X.,

Qi, P., Dimarogonas, D., and Kragic, D. (2012). Dual

arm manipulationa survey. Robotics and Autonomous

Systems, 60(10):1340 – 1353.

Soueres, P., Cadenat, V., and Djeddou, M. (2003). Dynam-

ical sequence of multi-sensor based tasks for mobile

robots navigation. 7th Symposium on Robot Control

(SYROCO’03), 2:423–428.

Uchiyama, M. and Dauchez, P. (1988). A symmetric hybrid

position/force control scheme for the coordination of

two robots. In Robotics and Automation, 1988. Pro-

ceedings., 1988 IEEE International Conference on,

pages 350–356 vol.1.

Vahrenkamp, N., Boge, C., Welke, K., Asfour, T., Walter,

J., and Dillmann, R. (2009). Visual servoing for dual

arm motions on a humanoid robot. In 9th IEEE-RAS

International Conference on Humanoid Robots, pages

208–214.

Watanabe, T., Harada, K., Jiang, Z., and Yoshikawa,

T. (2005). Object manipulation under hybrid ac-

tive/passive closure. In Robotics and Automation,

2005. ICRA 2005. Proceedings of the 2005 IEEE In-

ternational Conference on, pages 1013–1020.

Yamada, Y., Nagamatsu, S., and Sato, Y. (1995). Develop-

ment of multi-arm robots for automobile assembly. In

Robotics and Automation, 1995. Proceedings., 1995

IEEE International Conference on, volume 3, pages

2224–2229 vol.3.

Zheng, Y. and Chen, M. (1993). Trajectory planning for two

manipulators to deform ﬂexible beams. In Robotics

and Automation, 1993. Proceedings., 1993 IEEE In-

ternational Conference on, pages 1019–1024 vol.1.

Zollner, R., Asfour, T., and Dillmann, R. (2004). Pro-

gramming by demonstration: Dual arm manipulation

tasks for humanoids robots. In IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems.

APPENDIX A

We brieﬂy present the computation of the interac-

tion matrix corresponding to the above mentioned vi-

sual features. Using the well-known pinhole camera

model, it is possible to express the projection of a

point M on the image plane as follows:

x = f X/Z, y = f Y /Z

where f is the focal length, (x,y) the coordinates of

the projected point in the image and (X,Y,Z) the co-

ordinates of M with respect to the camera frame. The

expression of the interaction matrix of a point is given

by:



− f /Z 0 x/Z xy/ f −( f + x

/ f ) y

0 − f /Z y/Z f + y

/ f −xy/ f −x



The interaction matrix L

ρθ

of a straight line described

by the parameter vector [ρ, θ]

has also already been

computed in (Chaumette, 2002b):

ρθ



−1 y

· cos(θ) − x

· sin(θ)

−1 y

· cos(θ) − x

· sin(θ)



−1



−cos(θ) −sin(θ) 0 0

0 0 −cos(θ) −sin(θ)







where L

and L

are the interaction matrices corre-

sponding to two distinct points A(x

), B(x

)

which belong to the line.

Finally, the interaction matrix L

relative to k can

be expressed using the previous formulas:



−sin(θ) cos(θ) 0 (−x

· cos(θ) − y

· sin(θ))





ρθ



where L

is the interaction matrix corresponding to

the point E.

The interaction matrix of the visual features vec-

tor, describing the cylinder is ﬁnally given by: L

cyl



ρθ



ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics