
Object Contour Reconstruction using Bio-inspired Sensors
Christoph Will
1
, Joachim Steigenberger
2
and Carsten Behn
1
1
Department of Technical Mechanics, Technische Universit
¨
at Ilmenau,
Max-Planck-Ring 12 (Building F), 98693 Ilmenau, Germany
2
Institute of Mathematics, Technische Universit
¨
at Ilmenau, Weimarer Straße 25, 98693 Ilmenau, Germany
Keywords:
Vibrissa, Mechanical Contact, Beam, Bending, Large Deflections, Profile Reconstruction.
Abstract:
This work is inspired and motivated by the sophisticated mammals sense organ of touch: vibrissa. Mammals,
especially rodents, use their vibrissae, located in the snout region – mystacial vibrissae – to determine object
contacts (passive mode) or to scan object surfaces (active mode). Here, we focus on the passive mode. In order
to get hints for an artificial sensing prototype, we set up a mechanical model in form of a long slim beam which
is one-sided clamped. We investigate in a purely analytical way a quasi-static sweep of the beam along a given
profile, where we assume that the profile boundary is strictly convex. This sweeping procedure shows up in
two phases, which have to be distinguished in profile contact with the tip and tangentially contact (between tip
and base). The analysis eventuates in a phase decision criterion and in a formula for the contact point. These
are the main results. Moreover, based on the observables of the problem, i.e. the clamping moment and the
clamping forces, which are the only information the animal relies on, a reconstruction of the profile is possible
– even with added uncertainty mimicking noise in experimental data.
1 INTRODUCTION
Rodents, like mice and rats, use tactile hairs in the
snout region (mystacial vibrissae) to obtain informa-
tion about the environment, whereby these vibrissae
are used in an active and passive mode. The vibris-
sae are supported in a compliant follicle sine complex
(FSC) as shown in Figure 1. The follicle sine com-
plex exhibits a large variety of mechanoreceptors, like
merkel cells, which detect the movement of the vib-
rissa base and convert this mechanical strain into sig-
nals to the central nervous system.
The main difficulty is the fact, that the animals get
only information about the environment from the pro-
cessing mechanoreceptors.
Inspired by this biological paragon and motivated
by its complex task to govern information, we focus
on a vibrissa in passive mode, i.e., object localiza-
tion. We set up a mechanical model in form of a plane
elastic bending rod for a quasi-static object scanning.
The exploitation of the corresponding mathematical
model is primarily not based on numerical methods,
but it relies on an analytical framework as far as pos-
sible. Before doing this, we focus on the state of art
to make a dissociation of the actual work in this field.
nerve to CNS
blood
sinus
Merkel cell
Merkel cell
Lancet
nerve ending
Paciniform
corpuscle
cirumferentially
oriented spiny
ending
vibrissal
shaft
Figure 1: Follicle sine complex (Behn, 2013b), arranged by
D. Voges (TU Ilmenau).
459
Will C., Steigenberger J. and Behn C..
Object Contour Reconstruction using Bio-inspired Sensors.
DOI: 10.5220/0005018004590467
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 459-467
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 STATE OF THE ART
Various approaches are done in literature to model
the biological paragon to get hints for a technical
implementation in, e.g., robotics for obstacle detec-
tion (Kim and M
¨
oller, 2006), (Pearson et al., 2011),
(Prescott et al., 2009).
First models, like the one presented in (Hirose
et al., 1989), consider long thin elastic beams for de-
tection of deformation caused by an obstacle contact.
If this “whisker-like” sensor perceives a deformation
of the beam (which has to be sufficiently large as to
exceed some given threshold), the actual position is
marked for further trajectory planning. Hence, the
pure existence of an obstacle is needed, no other in-
formation about the obstacle is requested (just detec-
tion).
Further approaches are given in (Kim and M
¨
oller,
2007) and (Tuna et al., 2012), which realize additional
information about the obstacle. In (Tuna et al., 2012),
a contact point with an obstacle is estimated using the
angle of deflection at the base (inspired by methods
in computer tomography, ray deflection). The authors
in (Kim and M
¨
oller, 2007) use the linear theory of
elasticity in application to large deflections of a beam.
In both methods, only the angle of deflection, neither
forces nor moments, are measured.
In (Birdwell et al., 2007), another model is given
which incorporates both small deformations and the
pre-curvature of the beam. This is done in adding the
pre-curvature to the linear deflection of the beam to
get the actual position of the beam. The achievable
accuracy of the model depends on the pre-curvature
of the beam, because the curvature is assumed to be
a function on the beam axis. For small radii of suf-
ficiently long beams, this method can fail due to the
cartesian coordinate system. Also, it is still unclear, if
the pre-curvature of the vibrissa results in a pre-stress.
An improved method for object localization and
shape detection is proposed in (Scholz and Rahn,
2004) for plane problems, in (Clements and Rahn,
2006) for spatial problems. In both works, the au-
thors switch from linear approximation of the curva-
ture to the description of the problem in natural coor-
dinates. This is a main improvement in comparison
to works presented above. Thus, they allow for large
deflections of the beam, which results in a clear for-
mulation of the boundary conditions. Further, exper-
imental data are used in a numerical reconstruction
algorithm in Simulink which results in the deformed
beam shapes and a numerical values for the contact
point. The entirety of all these beam shapes models
the shape of the object geometry.
Recent works, like (Pammer et al., 2013), approx-
imate the curvature of the beam in using finite differ-
ences. This gives the possibility to consider the curva-
tures of an undeformed vibrissa, but analytical equa-
tions with new insights do not exist due to numerical
simulations.
3 AIM AND SCOPE
In this paper, due to Section 2, we focus on an entire
analytical treatment of the scanning problem of an ob-
stacle via a beam vibrissa. Since we have to allow for
large deflections of the beam, we introduce the non-
linear Euler-Bernoulli theory of beam bending. More-
over, we set up a mechanical model and investigate
the quasi-static bending behavior, when the beam is
swept along an obstacle. In order to get information
about the obstacle, we determine both forces and mo-
ments at the base (here: a clamping of the beam) as
solutions of a boundary value problem (BVP). Re-
versely, we use them in an initial value problem (IVP)
to determine a contact point of the deformed beam
with the obstacle. The series of all contact points ex-
hibit the shape of the obstacle.
4 MODELING
The present paper deals with the problem what an an-
imal “feels” and perceives by means of a single vib-
rissa while moving along an obstacle, and which in-
formation it can get about the obstacle. As already
mentioned in Section 1, the only information is avail-
able at the support of the vibrissa.
4.1 Assumptions
In order to get further information, we treat the prob-
lem analytically to the greatest extent. The work is
based on (Steigenberger, 2013) and (Will, 2013). In
order to model the problem, the following assump-
tions are made:
• The problem is treated as a quasi-static one.
• We restrict the problem to an (x, y)-plane. The
(originally undeformed) vibrissa is vertical, its
base moves along the x-axis from the right to the
left.
• The vibrissa is assumed as a long, slim, straight
(until now, no pre-curvature is assumed) beam
with constant second moment of area I
z
, constant
Young’s modulus E and length L. Thus, ignoring
shear stress, the Euler-Bernoulli theory for large
deflections is applicable.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
460
• The stress of the beam is sufficiently small to use
Hooke’s law of linear elasticity.
• The support of the beam is a clamp.
Clearly, this does not match the reality of the vib-
rissa. In further works, we take a glimpse to an
elastic support due to the compliant properties of
the FSC, see Figure 1.
• The obstacle contour (i.e., its boundary) is a
strictly convex function g : x 7→ g(x), with g ∈
C
1
(R;R).
• The object contact is ideal, i.e., the deformation
of the beam is caused by a single contact force
perpendicular to the obstacle profile. Friction is
not taken into account.
4.2 Model
The starting point is
κ(s) =
M
bz
(s)
EI
z
, (1)
which is valid due to the assumptions in Section 4.1.
Here, M
bz
(·) denotes the bending moment with re-
spect to the z-axis, s ∈ [0, L] is the arc length of the
beam, and κ(·) represents the curvatures, see Figure
2. For the sake of brevity, we introduce dimension-
less variables. The units of measure are [length] = L,
[moments] = EI
z
L
−1
and [forces] = EI
z
L
−2
(for ex-
ample: s = Ls
∗
, s
∗
∈ [0, 1]).
s
E, I
z
, L
s
ϕ(s)
force
x
y
Figure 2: Euler-Bernoulli beam under large deflection.
As from now, all quantities are given in di-
mensionless representation, whereby the asterisk is
dropped. Then, (1) becomes
κ(s) = M
bz
(s) (2)
and the deformed beam is described by
d
ds
x(s) = cos(ϕ(s)) ,
d
ds
y(s) = sin (ϕ(s)) ,
d
ds
ϕ(s) = κ(s) ,
with initial conditions x(0) = x
0
, y(0) = 0 and
ϕ(0) =
π
2
(due to the clamping). Because of the strict
convexity of g, x and y are functions of the slope angle
α:
d
dx
g(x) = g
0
(x) = tan(α)
⇒ x = ξ(α)
:
= g
0−1
(tan(α)),
⇒ y = η(α)
:
= g(ξ(α)).
Now:
x, g(x)
7→
ξ(α), η(α)
.
To formulate the boundary conditions, we have to dis-
tinguish two configurations of contacting the profile,
see Figure 3:
• Phase A: Contact of beam tip and profile with
ϕ(1) ≥ α,
• Phase B: Contact of a point s
1
∈ (0, 1) and the
profile with equal angles ϕ(s
1
) = α.
−2 −1 0 1 2
0
0.5
1
(ξ(α), η(α))
x
y
Tip contact and deformed beams in phase A
Deformed beam in phase B
Phase change
Legend:
Figure 3: Profile with deflected beams.
In both phases, the contact point is given by the slope
angle α of the profile.
ObjectContourReconstructionusingBio-inspiredSensors
461

1.6
1.8 2 2.2 2.4
0
0.5
1
s
-
#„
F
α
x
y
Figure 4: Deflected beam in Phase A.
4.3 Phase A: Contact at the Tip
Using Figure 4, the bending moment is for s ∈ (0, 1):
M
bz
(s) = f
y(s) −η(α)
sin(α)
+
x(s) −ξ(α)
cos(α)
,
(3)
Decoupling of the bending moment from x(s) and
y(s), the derivative of (3) yields the following ODE
system (4) with boundary conditions (5):
(a) κ
0
(s) = f cos(ϕ(s) −α)
(b) ϕ
0
(s) = κ(s)
(c) x
0
(s) = cos(ϕ(s))
(d) y
0
(s) = sin(ϕ(s))
(4)
(a) ϕ(0) =
π
2
(b) y(0) = 0
(c) κ(1) = 0
(d) x(1) = ξ(α)
(e) y(1) = η(α)
(5)
This BVP splits into two separate problems:
{(4a,b),(5a,c)} and {(4c,d),(5b,d,e)}. The first one
has
κ
2
= 2 f (sin(ϕ −α) −sin(ϕ
1
−α)) (6a)
= 4 f sin
ϕ −ϕ
1
2
cos
ϕ + ϕ
1
−2α
2
. (6b)
as a first integral with ϕ
1
:
= ϕ(1).
Remark 4.1. The bending moment, considering the
lower part of the beam, depends on the clamp reac-
tions M
Az
, F
Ax
, F
Ay
, which results in a first integral of
the form:
κ
2
= 2 f sin(ϕ −α)−2 f cos(α) + M
2
Az
.
Because κ
2
(s) ≥ 0 has to be fulfilled, three cases
have to be discussed for (6b) with f > 0:
1. At least one factor is zero: hence κ(s) ≡ 0, and
the beam is not deformed at all.
2. Both factors are negative: The sine function is
positive on the interval (−π, 0) and negative on
(π, 2π). This results in the inequations
−2π < ϕ(s) −ϕ
1
< 0 ∨ 2π < ϕ(s) −ϕ
1
< 4π.
Hence ϕ(s) < ϕ
1
∨ ϕ(s) > 2π. This is a contra-
diction, because ϕ(s) ∈
ϕ
1
,
π
2
∀s ∈ [0, 1].
3. Both factors are positive: The sine function is pos-
itive on the domain (0, π), the cosine function on
−
π
2
,
π
2
. Therefore, it must hold:
0 < ϕ(s) −ϕ
1
< 2π ∧ −π < ϕ(s) + ϕ
1
−2α < π .
The first inequality contains no additional infor-
mation, the second one yields:
ϕ(s) + ϕ
1
< π + 2α ∀s
⇒ ϕ
1
<
π
2
+ 2α, since ϕ(s) ≤
π
2
.
Therefore, the angle ϕ
1
has to be in the domain
α < ϕ
1
< min
π
2
,
π
2
+ 2α
.
Due to the assumptions, the curvature is non-
positive along the solutions of (4a,b), which results
in, using (6a):
dϕ(s)
ds
= κ(s)
=−
p
2 f (sin(ϕ(s) −α) −sin(ϕ
1
−α)) (7)
as a ODE with separated variables for ϕ(s). Introduc-
ing H
A
:
H
A
: (t, u) 7→ F
sin
π
4
−
t
2
sin
π
4
−
u
2
, sin
π
4
−
u
2
!
, (8)
where F is the incomplete elliptic integral of first kind
according to the definition (Abramowitz and Stegun,
1972, 17.2.7)
F : (z, k) 7→
z
Z
0
1
p
1 −ψ
2
p
1 −k
2
ψ
2
dψ,
the separation of variables applied on (7) with initial
value (5a) yields:
p
f s = H
A
ϕ(s) −α, ϕ
1
−α
−H
A
π
2
−α, ϕ
1
−α
.
(9)
Hence, the contact force f can be expressed as
f (ϕ
1
, α)
:
=
H
A
(ϕ
1
−α, ϕ
1
−α)
−H
A
π
2
−α, ϕ
1
−α
2
.
(10)
Now, the only unknown parameter at this stage is the
angle ϕ
1
at the tip. To determine this parameter, (5b,e)
have to be used in the following two ways.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
462

4.3.1 Substitution of Variable
Here, y is given in dependence on ϕ:
dy(s)
ds
dϕ(s)
ds
=
dy(ϕ)
dϕ
=
1
κ(ϕ)
sin(ϕ) ,
with boundary conditions y(
π
2
) = 0 and y(ϕ
1
) = η(α).
At first, the first condition leads to
y(ϕ) = −
1
√
2 f
ϕ
Z
π
2
sin(τ)
p
sin(τ −α) −sin(ϕ
1
−α)
dτ.
The second boundary condition results in an implicit
expression for ϕ
1
∈
α, min
π
2
,
π
2
+ 2α
:
η(α)
p
2 f +
ϕ
1
Z
π
2
sin(τ)
p
sin(τ −α) −sin(ϕ
1
−α)
= 0.
(11)
Note that the integral (11) can be represented by
means of elliptic integrals and solved for ϕ
1
.
4.3.2 Shooting Method
Instead of substituting the variable, the problem can
efficiently be solved by applying a shooting method
for ϕ
1
, which can be both faster and more accurate.
Let ϕ
∗
1
∈
α + ε, min
π
2
,
π
2
+ 2α
−ε
be a valid
candidate for ϕ
1
. The corresponding deflection angle
ϕ(s) can be calculated from (9) using (10):
ϕ(s, ϕ
∗
1
) = α + H
−1
A
q
f (ϕ
∗
1
, α)s
+H
A
π
2
−α, ϕ
∗
1
−α
, ϕ
∗
1
−α
,
with
H
−1
A
(t, u)
:
= −
π
2
+ 2 arccos
JacobiSN
t,
cos
π
4
+
u
2
cos
π
4
+
u
2
from (8) and JacobiSN according to (Abramowitz and
Stegun, 1972, 16.1.3 and 16.1.5).
Now (4d) with (5b) yield
y(s, ϕ
∗
1
) =
s
Z
0
sin(ϕ(τ, ϕ
∗
1
))dτ,
which can be numerically computed. The shooting
value for ϕ
∗
1
is correct, if y(1, ϕ
∗
1
) −η(α) = 0.
0 0.2 0.4
0.6
0.8 1 1.2
0
0.1
0.2
0.3
0.4
s
1
s
-
#„
F
x
y
Figure 5: Deflected beam in Phase B, contact s
1
∈ (0, 1).
Summarizing, independent of the chosen method,
ϕ
1
is now known. The solution of (4c,d) is:
x = ξ(α) +
s
Z
1
cos(ϕ(τ))dτ, (12)
y = η(α) +
s
Z
1
sin(ϕ(τ))dτ.
4.4 Phase B: Tangential Contact
The bending moment is now, with yet unknown con-
tact point s
1
(see Figure 5):
M
bz
(s) =
f
y(s) −η(α)
sin(α)
+
x(s) −ξ(α)
cos(α)
, s ∈ (0, s
1
]
0 , s ∈ (s
1
, 1).
(13)
The related BVP with s ∈ (0, s
1
) is:
(a) κ
0
(s) = f cos(ϕ(s) −α)
(b) ϕ
0
(s) = κ(s)
(c) x
0
(s) = cos(ϕ(s))
(d) y
0
(s) = sin(ϕ(s))
(14)
(a) ϕ(0) =
π
2
(b) y(0) = 0
(c) κ(s
1
) = 0
(d) ϕ(s
1
) = α
(e) x(s
1
) = ξ(α)
(f) y(s
1
) = η(α)
(15)
A first integral of (14a) together with (14b) and
(15c) is
κ
2
= 2 f sin(ϕ −α)
⇒
d
ds
ϕ(s) = κ(s) = −
p
2 f
p
sin(ϕ(s) −α).
(16)
ObjectContourReconstructionusingBio-inspiredSensors
463
Equation (14b) with (16) and (15a) yield
p
f s = H
B
(ϕ(s) −α) −H
B
π
2
−α
,
which can be solved for ϕ(s):
ϕ(s) = α + H
−1
B
p
f s + H
B
π
2
−α
,
using
H
B
: t → F
√
2sin
π
4
−
t
2
,
√
2
2
!
,
with
H
−1
B
(t)=−
π
2
+ 2 arccos
√
2
2
JacobiSN
t,
√
2
2
!!
.
Since ϕ(s
1
) = α is known, the contact force can be
expressed as
p
f =
H
B
(0) −H
B
π
2
−α
s
1
. (17)
Again, considering the function y to get the last
missing parameter s
1
, condition (15b) results in:
y(s) =
1
√
f
√
f s+H
B
(
π
2
−α
)
Z
H
B
(
π
2
−α
)
sin
α + H
−1
B
(τ)
dτ. (18)
Summarizing, (17), (18) and (15f) yield
f (α) =
1
η(α)
H
B
(0)
Z
H
B
(
π
2
−α
)
sin
α + H
−1
B
(τ)
dτ
2
.
(19)
Now, (17) and (19) lead to the following equation
for the contact point s
1
:
s
1
(α) =
η(α)
H
B
(0) −H
B
π
2
−α
H
B
(0)
R
H
B
(
π
2
−α
)
sin
α + H
−1
B
(τ)
dτ
. (20)
The last integral of (14c) with (15e) is:
x(s) = x
0
+
1
√
f
√
f s+H
B
(
π
2
−α
)
Z
H
B
(
π
2
−α
)
cos
α + H
−1
B
(τ)
dτ,
whence, with s = s
1
, we obtain the foot coordinate
x
0
= ξ(α) −
1
√
f
H
B
(0)
Z
H
B
(
π
2
−α
)
cos
α + H
−1
B
(τ)
. (21)
Finally, for both phases, the footpoint x
0
is derived
using (12) and (21). Using (10) and (19) we can deter-
mine f and, hence, knowing α, also the contact force
#„
F . With f we get the clamping forces F
Ax
and F
Ay
, as
well as the clamping moment M
Az
using (3) and (13).
5 SIMULATIONS
Let us focus on the following two profile functions:
g
1
: x 7→
1
2
x
2
+
1
2
,
g
2
: x 7→
(
−
√
2
2
−x
2
+
5
2
, x > 0 ,
−
q
1
4
−x
2
+ 1, else.
Function g
1
is a parabola, and g
2
is a profile composed
of two circles, both shown in Figure 6.
−1.5
−1
−0.5
0
0.5
1
1.5
0
0.5
1
x
y
(a) Parabola profile g
1
−1.5
−1
−0.5
0
0.5
1
1.5
0
0.5
1
x
y
(b) Profile composed of two circles g
2
Figure 6: Profiles under consideration.
Computed observables for profile g
1
are exem-
plarily shown in Figure 7.
−1.5
−1
−0.5
0
0.5
1
1.5
0
1
2
x
0
M
Az
(a) Clamping moment M
Az
(maximum marked with )
−1.5
−1
−0.5
0
0.5
1
1.5
0
5
x
0
F
Ax
(b) Clamping forces F
A
( F
Ax
; F
Ay
)
Figure 7: Observables with profile function g
1
. marks the
change between Phase A and Phase B.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
464

The maximum clamping moment occurs in Phase
B, but besides a change of phase in M
Az
and F
Ay
. Ob-
viously, no direct information about the obstacle can
be extracted directly from the curve of the observ-
ables. We rather use the computed observables for
an object profile reconstruction in the next section.
6 RECONSTRUCTION OF THE
PROFILE
At this stage, we have the observables x
0
, F
Ax
, F
Ay
, M
Az
(values which are assumed that an animal can solely
rely on) numerically computed at hand. They repre-
sent the only information. In experiments these values
are produced by a measurement device.
We have to focus on a reconstruction procedure of
the obstacle profile, out of these “measured” values.
6.1 Analysis
Let us start with the following information at the base:
κ(0) = lim
s→0+
M
bz
(s) = −M
Az
,
ϕ(0) =
π
2
,
x(0) = x
0
,
y(0) = 0
and
α = −arctan
F
Ax
F
Ay
, f =
q
F
2
Ax
+ F
2
Ay
.
The main difficulty is to decide which phase the
beam actually undergoes. To solve this, let us focus
on the curvature (in Phase A, Phase B, or somewhere):
Ph. A: κ
2
A
(s) = 2 f (sin(ϕ(s) −α) −sin(ϕ
1
−α)) ,
(22)
any s: κ
2
R
(s) = 2 f (sin(ϕ(s) −α) −cos(α)) + M
2
Az
,
(23)
Ph. B: κ
2
B
(s) = 2 f sin(ϕ(s) −α). (24)
Obviously, it is Phase B iff ϕ
1
= α. Using (23), ϕ
1
can be determined by:
ϕ
1
= α −arcsin
M
2
Az
−2 f cos(α)
2 f
!
,
which results in the decision condition for Phase B
with only known parameters:
M
2
Az
−2F
Ay
= 0. (25)
If (25) is valid, the contact force is applied at s
1
∈
(0, 1) which can be computed:
s
1
=
H
B
(0) −H
B
π
2
−α
√
f
.
Else, if (25) does not hold, the contact force is applied
at s
1
= 1.
Now, the IVP is solved numerically using MAT-
LAB’s variable order Adams-Bashforth-Moulton
PECE solver:
ϕ
0
(s) = −
q
2 f sin(ϕ(s) −α)−2 f cos(α) +M
2
Az
,
ϕ(0) =
π
2
,
x
0
(s) = cos(ϕ(s)) , x(0) = x
0
,
y
0
(s) = sin(ϕ(s)) , y(0) = 0,
which results in the reconstructed contact point:
ξ(α) = x(s
1
), η(α) = y(s
1
).
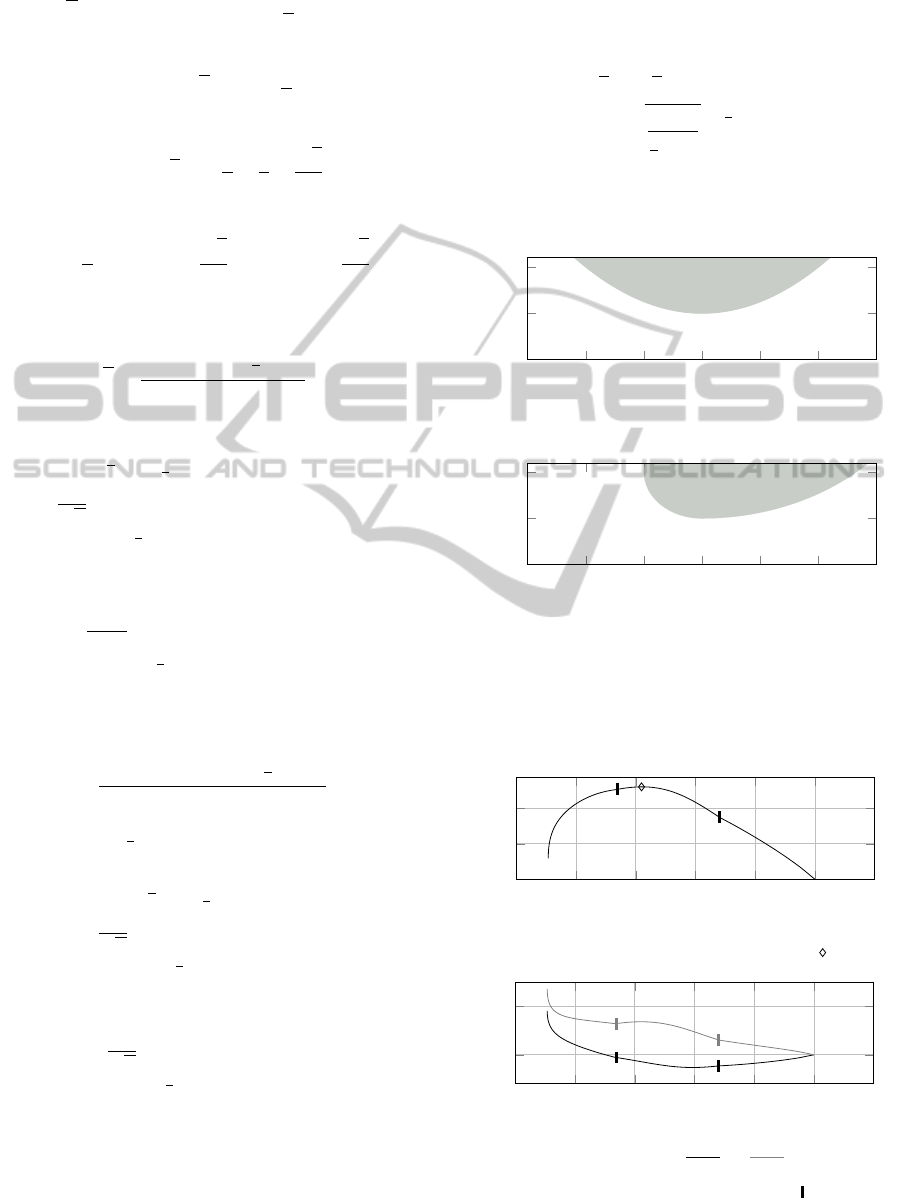
6.2 Numerics
During reconstruction, the error for each component
point k along the profile function g, shown in Figure 8,
is computed using the euclidian norm of the distance
between the given and the reconstructed contact point:
error
:
=
x
k
(s
1k
)
y
k
(s
1k
)
−
ξ(α
k
)
η(α
k
)
2
with s
1k
as reconstructed contact point, (x
k
(s), y
k
(s))
the reconstructed position of the beam in the plane
and (ξ(α
k
), η(α
k
)) the given contact point for com-
puting the observables.
−1.5
−1
−0.5
0
0.5
1
1.5
0
0.2
0.4
0.6
0.8
1
·10
−6
x
0
error
(a) Parabola profile g
1
−1.5
−1
−0.5
0
0.5
1
1.5
0
0.2
0.4
0.6
0.8
1
·10
−6
x
0
error
(b) Profile g
2
Figure 8: Reconstruction errors.
ObjectContourReconstructionusingBio-inspiredSensors
465

−1.2 −1 −0.8
−0.6
−0.4 −0.2 0 0.2 0.4
0.6
0.8 1
0
0.5
1
x
y
(a) Sweep along profile g
1
−1 −0.8
−0.6
−0.4 −0.2 0 0.2 0.4
0.6
0.8 1 1.2 1.4
0
0.5
1
x
y
(b) Sweep along profile g
2
−1.5
−1
−0.5
0
0.5
1
1.5
0
0.5
1
·10
−2
x
0
error
(c) Reconstruction error for profile g
1
−1.5
−1
−0.5
0
0.5
1
1.5
0
0.5
1
·10
−2
x
0
error
(d) Reconstruction error for profile g
2
Figure 9: Reconstruction with added noise.
6.3 Reconstruction under Uncertainties
Because of lack of experiments, we assume that the
computed observables underlie some measurement
noise like in real experiments. To generate some noise
to the observables, random uncertainty is added to
F
Ax
, F
Ay
and M
Az
. The scale of the added values is
1
20
rnd −
1
2
for forces F
Ax
, F
Ay
and
1
100
rnd −
1
2
for
moment M
Az
, rnd ∈(0, 1) according to technical data
sheet of a Schunk GmbH & Co. KG FT-Mini-40 force
and moment sensor.
Besides the error obtained by the noisy observ-
ables, the decision if a tuple of observables belongs to
Phase B or Phase A using (25) is very critical in the
process of reconstruction. During the reconstruction
using the computed observables,
M
2
Az
−2F
Ay
≤10
−4
was used as condition for Phase B. With the added
values, a higher tolerance gives better results, thus
M
2
Az
−2F
Ay
≤ 0.08 was used. As shown in Figure
9(c) and (d), the reconstruction error is increased by
four orders of magnitude if noise is added. For prac-
tical application, the profile is still sufficiently recon-
structed as shown in Figure 9.
Clearly, the shape of the deformed vibrissa is an
important part of the theory, but of little relevance in
the result of the practical reconstruction process. The
only important result is the sequence of the computed,
reconstructed contact points of the profile.
7 CONCLUSION
Analytical investigations have shown that it is pos-
sible to reconstruct a profile contour by one single
sweep of a thin elastic Euler-Bernoulli beam along it.
As a typical first step in modeling we determined
the “observables” (reactions of the clamping), which
an animal relies solely on, in a purely analytical way
because of lack of experiments, in contrast to (Scholz
and Rahn, 2004). But, the theoretical results showed
up a single equation for a decision of the contact be-
havior of the beam with the object: contact at the tip,
or contact between base and tip. This decision is new
in literature and provides an easier and faster com-
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
466

putation of the deformed vibrissa and reconstruction
of the profile as well. Furthermore, an explicit an-
alytical formula to determine the contact point out of
the “measured” values of the observables was derived.
Both will increase the efficiency in experiments in fu-
ture.
These results were obtained without assuming any
estimation or approximation of describing functions.
This is rather new in literature, in contrast to (Kim and
M
¨
oller, 2007), (Birdwell et al., 2007).
Further on, to mimick experimental data, a re-
construction based solely on the “observables” with
added random noise (uncertainty — mimicking noise
in experiments) is valid for various profiles. But, ob-
viously, the contact point approximation accuracy di-
minished from 10
−6
to 10
−2
(dimensionless), i.e., if
the vibrissa is 1 m long then the obstacle contact po-
sition can be determined in the plane with an accu-
racy of 1 cm by a single measuring point during ob-
stacle contour sensing. These results maintain the
hypothesis from biologists, that animals can navigate
by strongly relying on their mechanoreceptors at the
FSC.
Near future (theoretical) work is addressed to the
following investigations:
• analysis of the influence of an elastic support as in
the biological paragon (Behn, 2013a): This could
be needed to guarantee a bounded bending mo-
ment in controlling the support stiffness (i.e., the
vibrissa does not brake during sensing – just think
about a cat passing a fence).
• investigations on non-strictly convex profiles:
There can appear flat points and we have to ad-
just our theory.
• switching from investigations in the vertical x-y-
plane to a 3-dimensional sensing problem.
Intermediate future (experimental) work is addressed
to experiments. At present, we are working on a de-
sign of a prototype for sensing obstacles.
Far future work is addressed to an application of
such tactile sensors to mobile robotics (or a mouse-
like robot) for online object localization and different
tasks similar to the prototypes presented in (Kim and
M
¨
oller, 2006) and (Pearson et al., 2011).
REFERENCES
Abramowitz, M. and Stegun, I. A. (1972). Handbook
of mathematical functions: With formulas, graphs,
and mathematical tables, volume 55 of National Bu-
reau of Standards applied mathematics series. United
States Department of Commerce, Washington, DC,
10. print., dec. 1972, with corr edition.
Behn, C. (2013a). Mathematical Modeling and Control of
Biologically Inspired Uncertain Motion Systems with
Adaptive Features. PhD thesis, Technische Univer-
sit
¨
at Ilmenau, Ilmenau.
Behn, C. (2013b). Modeling the behavior of hair follicle
receptors as technical sensors using adaptive control.
In ICINCO (1), pages 336–345.
Birdwell, J. A., Solomon, J. H., Thajchayapong, M., Taylor,
M. A., Cheely, M., Towal, R. B., Conradt, J., and Hart-
mann, M. J. Z. (2007). Biomechanical Models for Ra-
dial Distance Determination by the Rat Vibrissal Sys-
tem. Journal of Neurophysiology, 98(4):2439–2455.
Clements, T. N. and Rahn, C. D. (2006). Three-dimensional
contact imaging with an actuated whisker. IEEE
Transactions on Robotics, 22(4):844–848.
Hirose, S., Inoue, S., and Yoneda, K. (1989). The whisker
sensor and the transmission of multiple sensor signals.
Advanced Robotics, 4(2):105–117.
Kim, D. and M
¨
oller, R. (2006). Passive sensing and active
sensing of a biomimetic whisker. In Rocha, L. M.,
editor, Artificial life X, A Bradford book, pages 282–
288. MIT Press, Cambridge, Mass.
Kim, D. and M
¨
oller, R. (2007). Biomimetic whiskers for
shape recognition. Robotics and Autonomous Systems,
55(3):229–243.
Pammer, L., O’Connor, D. H., Hires, S. A., Clack, N. G.,
Huber, D., Myers, E. W., and Svoboda, K. (2013).
The mechanical variables underlying object localiza-
tion along the axis of the whisker. The Journal of
neuroscience : the official journal of the Society for
Neuroscience, 33(16):6726–6741.
Pearson, M. J., Mitchinson, B., Sullivan, J. C., Pipe,
A. G., and Prescott, T. J. (2011). Biomimetic vib-
rissal sensing for robots. Philosophical Transac-
tions of the Royal Society B: Biological Sciences,
366(1581):3085–3096.
Prescott, T., Pearson, M., Mitchinson, B., Sullivan, J.
C. W., and Pipe, A. (2009). Whisking with robots:
From Rat Vibrissae to Biomimetic Technology for Ac-
tive Touch. IEEE Robotics & Automation Magazine,
16(3):42–50.
Scholz, G. R. and Rahn, C. D. (2004). Profile Sensing With
an Actuated Whisker. IEEE Transactions on Robotics
and Automation, 20(1):124–127.
Steigenberger, J. (2013). A continuum model of passive
vibrissae.
Tuna, C., Solomon, J. H., Jones, D. L., and Hartmann, M.
J. Z. (2012). Object shape recognition with artificial
whiskers using tomographic reconstruction. In IEEE
International Conference on Acoustics, Speech and
Signal Processing (ICASSP), pages 2537–2540, Pis-
cataway, NJ. IEEE.
Will, C. (2013). Anwendung nichtlinearer Biegetheorie
auf elastische Balken zur Objektabtastung am Beispiel
passiver Vibrissen mit unterschiedlicher Lagerung
(Application of non-linear beam theory for obstacle
detection with respect to the biological paragon of a
passive vibrissa using different supports). Master the-
sis, Technische Universit
¨
at Ilmenau, Ilmenau.
ObjectContourReconstructionusingBio-inspiredSensors
467
