Passivity Preserving Multipoint Model Order Reduction using Reﬂective

Exploration

Elizabeth Rita Samuel, Luc Knockaert and Tom Dhaene

Ghent University - iMinds, Gaston Crommenlaan 8 Bus 201, B-9050 Gent, Belgium

Keywords:

Model Order Reduction, Projection Matrix, Singular Values, Reﬂective Exploration, Passivity.

Abstract:

Reduced state-space models obtained by model order reduction methods must be accurate over the whole

frequency range of interest and must also preserve passivity. In this paper, we propose multipoint reduction

technique using reﬂective exploration for adaptively choosing the expansion points. The projection matrices

obtained from the expansion points are merged to form the overall projection matrix. In order to obtain a

more compact model the projection matrix is truncated based on its singular values. Finally, the reduced order

model is obtained, while ensuring that the passivity of the reduced system is preserved during the reduction

process.

1 INTRODUCTION

When analyzing and controlling large-scale systems,

it is extremely important to develop efﬁcient

modeling procedures. The design of a controller for a

high-dimensional system may be too time-consuming

to implement in practice. In fact it is important that

the key dynamic elements be identiﬁed and spurious

dynamic elements eliminated. Model reduction

techniques provide an extremely effective way to

address this requirement.

Model order reduction (MOR) techniques are now

standard for reducing the complexity of large scale

models and the computational cost of the simulations,

while retaining the important physical features of

the original system (Feldmann and R. Freund, 1995;

Gallivan et al., 1996; Odabasioglu et al., 1998;

Knockaert and De Zutter, 2000; Freund, 2000;

Phillips et al., 2003; Phillips, 2004; Knockaert

et al., 2011). Existing approaches based on Krylov

subspaces are very efﬁcient.

One of the main concerns regarding MOR

algorithms is that the model must be sufﬁciently

accurate not just at a single frequency point but

over a whole range of frequencies. This situation

typically arises when dealing with microwave

circuits. Reduction algorithms that address this

concern are the multipoint rational Krylov algorithm

(Gallivan et al., 1996; Silveira and Phillips, 2006;

Wang et al., 2012) and multipoint expansion using a

binary search (Ferranti et al., 2011), which are more

accurate but more expensive to set up.

Multipoint projections raise many practical

questions while implementation. In this paper, we

focus on three points namely;

• the order considered for each expansion point.

• adaptive frequency sampling using reﬂective

exploration (Beyer and

Smieja, 1996).

• obtaining a compact projection matrix.

In this paper, the projection matrices are computed

using the PRIMA technique (Odabasioglu et al.,

1998), which is known to be an efﬁcient technique for

the reduction of large systems. The expansion points

are selected adaptively using a reﬂective exploration

technique. It is a sequential sampling algorithm,

where the model is improved incrementally using

the best possible data at every time step with

additional properties allowing it to propose candidate

exploration points (Beyer and

Smieja, 1996). An

error-based exploration is implemented to ﬁnd the

expansion points. After obtaining the expansion

points the corresponding projection matrices are

computed using Krylov based MOR technique. The

projection matrices are then merged to obtain the

overall projection matrix. When the number of

expansion points increase, the merged projection

matrix also increases and might fail to provide a

satisfactory model dimension reduction. In this

paper, an adaptive truncation algorithm is proposed

to truncate the merged projection matrix based on its

singular values, thereby obtaining a more compact

483

Rita Samuel E., Knockaert L. and Dhaene T..

Passivity Preserving Multipoint Model Order Reduction using Reﬂective Exploration.

DOI: 10.5220/0005018804830491

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 483-491

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

reduced order model (ROM) which preserves the

system properties. Numerical results validate the

proposed technique.

2 BRIEF OVERVIEW OF

MULTIPOINT MOR

Here, the PRIMA algorithm (Odabasioglu et al.,

1998) is used for obtaining the projection matrices.

2.1 PRIMA

Consider a MIMO descriptor system of the form

E˙x(t) = Ax(t) + Bu(t)

y(t) = Cx(t) + Du(t). (1)

The transfer function is

H(s) = C(sE− A)

−1

B+ D. (2)

Let s

be a suitably chosen expansion point such

that the matrix s

E − A is nonsingular. Then the

transfer function can be rewritten as:

H(s) = C(s

E− A+ (s− s

)E)

−1

B+ D

= C(I+ (s− s

)M)

−1

R+ D (3)

where M = (s

E− A)

−1

E, R = (s

E− A)

−1

The q-th block Krylov-subspace is given by

(M,R) = colspan[R MR M

R ... M

(q−1)

R]. (4)

This yields the projection matrix V

, which is the

column orthogonal matrix computed from the Krylov

subspace K

(M,R), from which using congruence

transformation (5) the reduced state-space matrices

) are obtained as:

= V

, E

= V

B, C

= CV

, D

= D. (5)

2.2 Multipoint Projection Matrix

After model order reduction, the resulting model must

not only be accurate at a frequency point but over

the whole range of interest and must also preserve

passivity. For this the multipoint reduction algorithm

is used (Ferranti et al., 2011).

At each expansion point, the projection matrices

is computed as described in Section 2.1, i.e., for

N expansion points the corresponding projection

matrices V

(i = 1,2,... ,N) are merged to give;

comm

= colspan[V

... V

]. (6)

The merged projection matrix is not truncated

using its singular values during the iterative procedure

of the reﬂective exploration. But the matrix is

truncated after all the expansion points are adaptively

chosen which is described in the following section.

3 REFLECTIVE EXPLORATION

The process of selecting expansion points and

building the model in an adaptive way is referred

to as reﬂective exploration (Beyer and

Smieja,

1996). Reﬂectiveexploration is an effectivetechnique

when its very expensive to obtain the model from

Electromagnetic(EM) simulators. For the exploration

a reﬂective function is required to select a new

expansion point. The reﬂective function used for the

proposed multipoint MOR algorithm is the error norm

between the best model and the second best model.

As described in (Geest et al., 1999), the algorithm has

two loops: an adaptive modeling loop and an adaptive

sampling loop.

1. Adaptive Modeling Loop: The algorithm starts

with two expansion points selected at ω

min

and

max

of the frequency range of interest. It should

be noted that the initial number of sample points

that is uniformly distributed along the frequency

range of interest can be varied as needed, if prior

knowledge of the system is available.

The reduced order q at these points is equal to

the number of input ports of the system. Then

the reduced model is obtained with a common

projection matrix as explained in Section 2. If the

RMS error (7) between the two best models (I

and (I − 1)

) is more than a threshold δ

mod

, then

the reduced order q is increased by the number of

input ports again for all the expansion points. In

this paper the threshold is chosen to be 10

−3

Err

(I)

est

∑

k=1

∑

i=1

∑

out

j=1

I,(ij)

)−H

I−1,(i j)

)

(ij)

)

out

(ij)

) = |H

I,(ij)

. (7)

Here, K

, P

and P

out

are the number of frequency

samples considered on a dense grid, input and

output ports of the system, respectively.

2. Adaptive Sampling Loop: When the difference

in RMS error (7), between the two consecutive

models is very small i.e.,

Err

(I)

est

− Err

(I−1)

est

Err

(I−1)

est

< δ

samp

(8)

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

484

Figure 1: Reﬂective Exploration.

(in this paper the difference is considered to be

less than 10%), then a new expansion point is

selected. For selecting the new expansion point,

the error per frequency is ﬁrst computed by taking

the L1 norm of the frequency response of the best

model (H

) and the original model (H

act

), and

then the frequency at which Err

is maximum is

considered as the new expansion point.

Err

= kH

act)

) − H

)k;

k = 1, ...,K

. (9)

This process is iteratively repeated until the RMS

error between the original frequency response and the

reduced model is 10

−3

. Figure 1 shows a ﬂowchart of

the reﬂective exploration algorithm.

4 MODEL COMPACTING

After obtaining the best reduced order model from

the iterative procedure, it might be possible to further

compact the model with the information obtained

from the singular values Σ (10) of the V

comm

(6).

The economy-size svd is computed for the

common projection matrix V

comm

(6), to obtain the

singular values Σ of the merged projection matrix. In

matlab the economy-sized svd is computed as shown:

UΣV

= svd(V

comm

,0) (10)

Here, U and V are orthogonal matrices, which

are known as the left and right singular values. The

diagonal of Σ gives the singular values of the system.

σ = diag(Σ). (11)

The reduced order for the system is deﬁned based

on the ﬁrst q

comm

signiﬁcant singular values of V

comm

which is computed by adaptively setting a threshold

to the ratio of the singular values to the largest

singular value as shown in Fig.2. The ROM obtained

by the truncation of the merged projection matrix

with respect to the singular value, is compared with

the best model obtained from reﬂective exploration.

If the RMS error is less than 10

−4

, then we shall

truncate the singular values, else we keep the model

with the reduced order obtained using the reﬂective

exploration.

The compact projection matrix Q

comm

is equal

to the left singular value U where the column is

truncated to a size q

comm

based on the signiﬁcance of

the singular values.

comm

= U(:,1 : q

comm

). (12)

After truncation it can be noted that, on average

per expansion point an order of q

samp

(13) is required

to guarantee the desired accuracy at that expansion

point.

samp

= q

comm

/N. (13)

Here, n is the number of expansion points.

PassivityPreservingMultipointModelOrderReductionusingReflectiveExploration

485

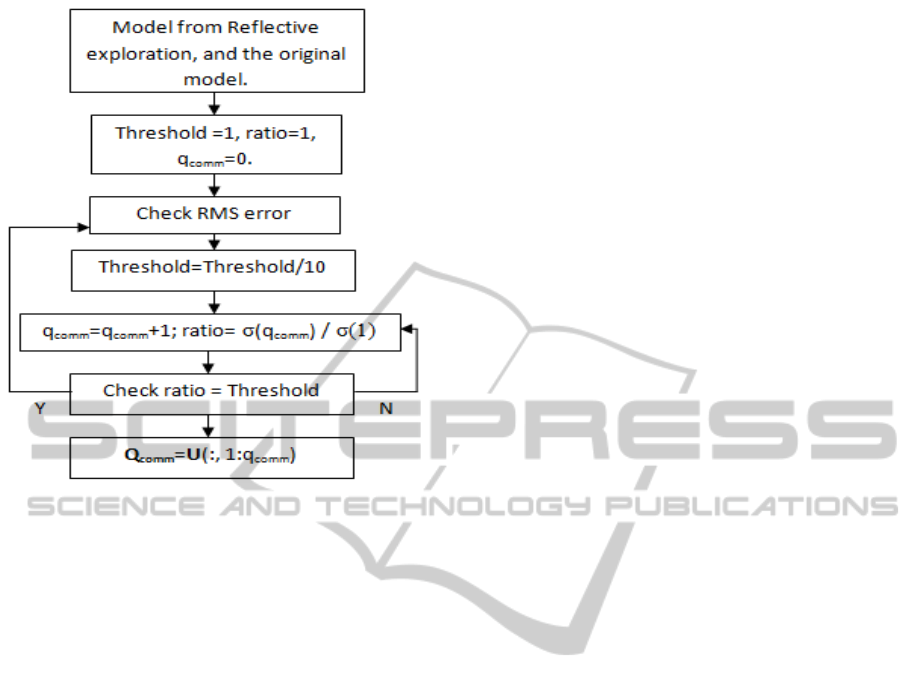
Figure 2: Truncation of the projection matrix.

Once the compact projection matrix Q

comm

computed, it is applied to the original system (1) and

a reduced system (5) is obtained through congruence

transformation.

5 PASSIVITY PRESERVATION

For transient behavior, stability and passivity are

the fundamental properties to be guaranteed by the

system, as known that, while a passive system is

also stable, the reverse is not necessarily true. A

passive system denotes a system that is incapable of

generating energy, and hence one that can only absorb

energy from the sources used to excite it (Anderson

and Vongpanitlerd, 1973). Passivity is an important

property to satisfy because stable, but not passive

macromodels can produce unstable systems when

connected to other stable, even passive, loads.

If the descriptor state space model in (1) satisﬁes

the following properties (Odabasioglu et al., 1998):

E = E

≥ 0

A+ A

≤ 0

B = C

, (14)

then it ensures the passivity of the admittance

model Y(s) = C(sE − A)

−1

B and with congruence

transformation the passivity of the model is preserved,

(g) = Q

comm

′

E(g)Q

comm

≥ 0

(g) = Q

comm

′

A(g)Q

comm

≤ 0

(g) = Q

comm

′

B(g)

(g) = Q

comm

C(g). (15)

If the system fails to have the state-space

properties described in (14) then the technique of

Linear Matrix Inequalities (LMI’s) (Knockaert et al.,

2011) has to be used, from which the solution

obtained fromLMI’s (Boyd et al., 1994; Gahinet and

Apkarian, 1993) gives a descriptor state space format

that preserves positive-realness and bounded realness

of the system.

Solving the LMI can be replaced by equivalently

solving an ARE, which is known to be a more efﬁcient

approach (Gahinet et al., 1995; Balas et al., 2005)

as the number of operations required to solve a

Riccati equation is O(n

), while the cost of solving

an equivalent LMI is O(n

). Thus for high orders it is

advisable to solve using ARE as it is computationally

cheaper in comparison with LMI.

6 NUMERICAL RESULTS

Some pertinent numerical examples are used to

demonstrate the accuracy and efﬁciency of the

proposed technique. The numerical simulations were

performed on a Windows 7 platform on Intel

(R)

Core

(TM)

2 Duo P8700 2.53 GHz machine with 2 GB

RAM and has been implemented in Matlab R2012b.

6.1 Example 1: Lossy Transmission

Line

For this example, a 1 cm long two conductor lossy

transmission line with the following per-unit-length

matrices

pul



75 15

15 75



Ω/m

pul



494.6 63.3

63.3 494.6



nH/m

pul



0.1 0

0 0.1



S/m

pul



62.8 −4.9

4.9 62.8



pF/m. (16)

for a frequency range of [1 Khz− 1 GHz], is modeled

as described in (Knockaert and De Zutter, 2000). The

original state-space order of the system is 1202 with

4 ports.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

486

0 0.2 0.4 0.6 0.8 1

x 10

−3

norm(H

act

−H

)

Frequency (GHz)

max(Err

=> new expansion point

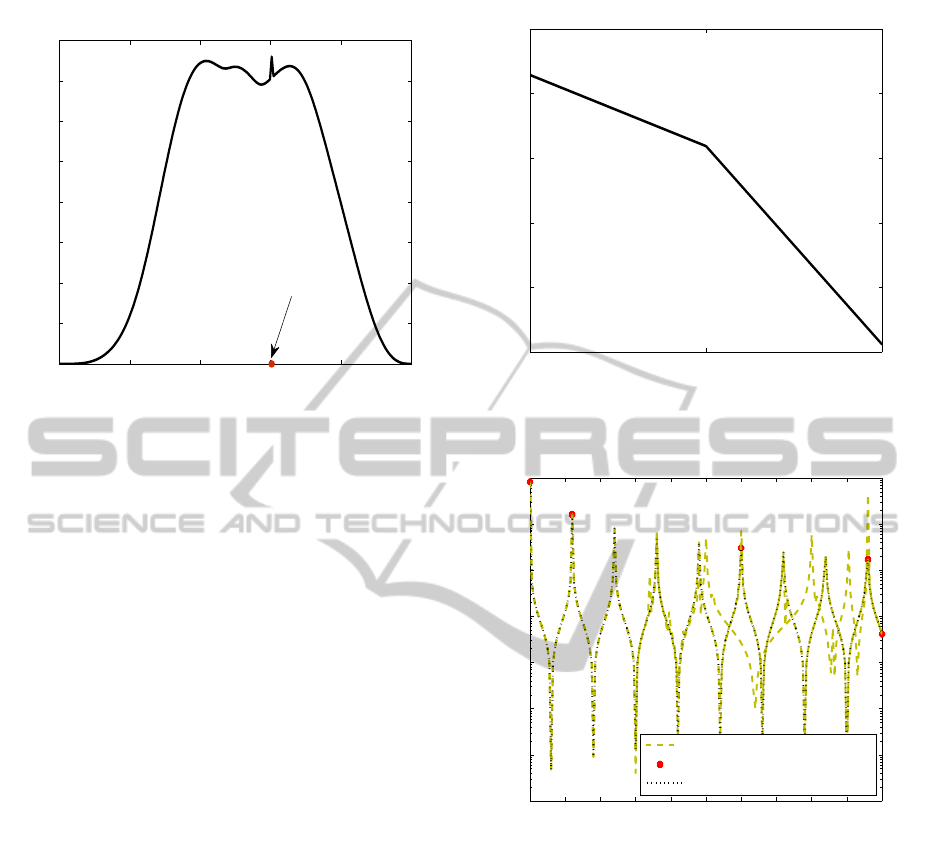
Figure 3: Example 1: Error per frequency used to select the

new expansion point for the adaptive sampling loop.

The sampling starts by considering two expansion

points at ω

min

and ω

max

. The reduced order for the

ﬁrst iteration is equal to 4, the number of ports of the

system. Then, as briefed in Section 3, the frequency

responses is computed using a merged projection

matrix (6) formed from the two expansion points. For

the next iteration, the frequency response is computed

for the same expansion points with an increased order

of 8, i.e.: it is increased by the number of ports. Then

the difference in response between the two models

is computed using (7). The error obtained is 2.147,

which is signiﬁcantly greater than 10

−3

, the threshold

set for the RMS error. Therefore, the algorithm

increases the order of the expansion points and again

computes the RMS error. Since the difference in the

RMS error in the successive iterations is less than

10%, the algorithm checks for the new expansion

point by computing the L1 norm of the best model

and the original model. As shown in Fig.3, the norm

of the frequency responses of the best model and the

actual response gives the error per frequency and the

new expansion point is considered at the frequency at

which the error is maximum.

Then, the frequency response which is the

admittance parameter Y(s), is again computed with

all the expansion points, with a reduced order of 12

per expansion point. Similarly in this manner the

sampling process is iterated till the RMS error (7) is

less than the 10

−3

, the accuracy threshold value set.

Figure 4 plots the RMS error (7) between the

iterated models when new expansion points are added

during reﬂective exploration.

Figure 5, shows the magnitude of the admittance

parameter Y

obtained during the reﬂective

1 2 3

0.5

1.5

2.5

Samples

RMS error

Figure 4: Example 1: RMS error between the iterated

models during the addition of new expansion points.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−6

−5

−4

−3

−2

−1

Frequency (GHz)

| (S)

Model obtained during each iteration

Expansion points chosen adaptively

Final reduced order model

Figure 5: Example 1: Magnitude of Y

for each iteration

with the adaptively chosen expansion points.

exploration for different iterations. A best model of

dimension 96 is obtained with 4 expansion points

within a CPU time of 15.23 secs.

Then the model is compacted based on the

truncation of the singular values of the common

projection matrix. With the truncation algorithm

described in Section 4, we obtain a model of order 85

by adaptively choosing a threshold of 10

−4

in 0.715

secs as shown in Table 1.

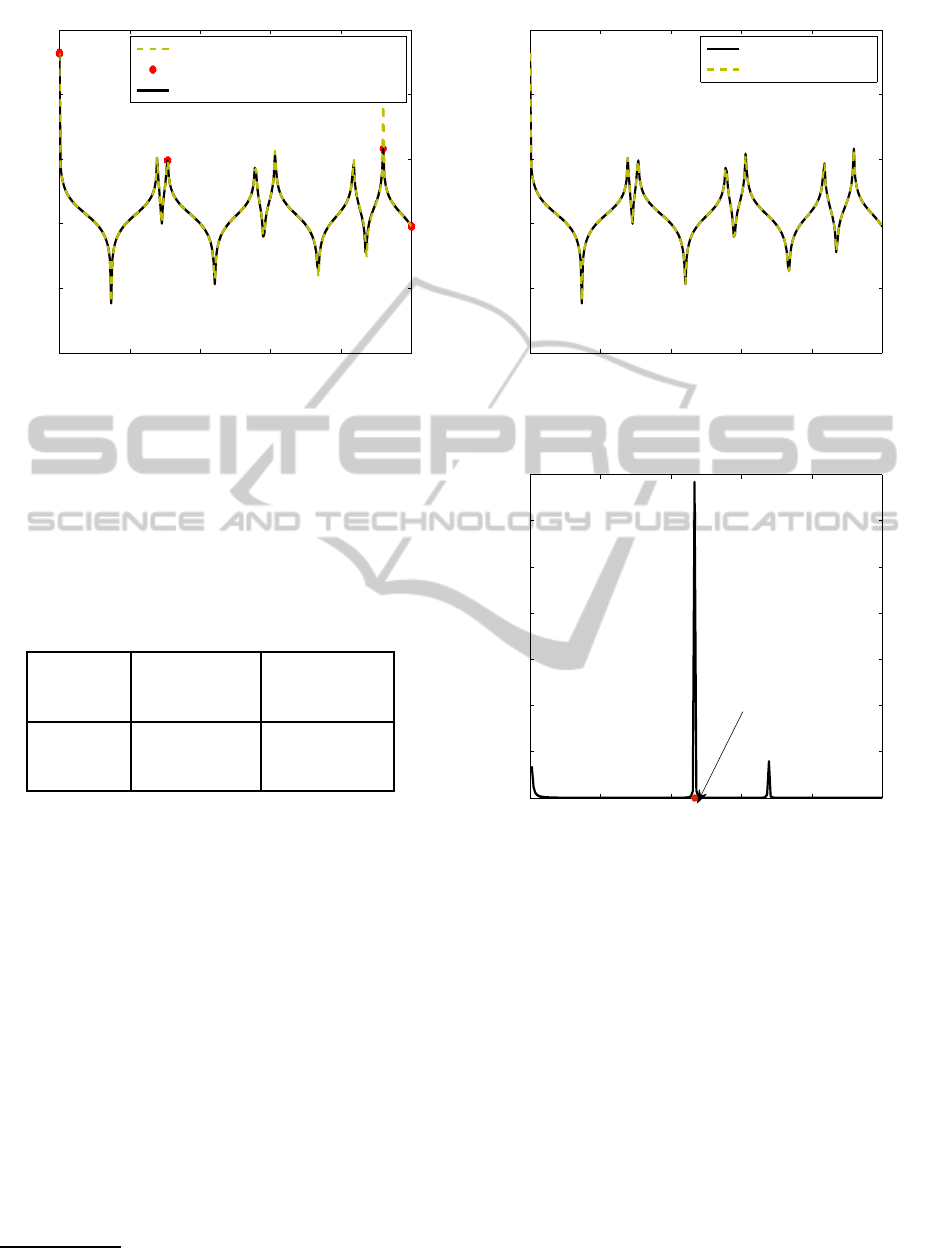
Figure 6 plots the magnitude of Y

for the

original and the reduced model using 4 expansion

points with a reduced order of 22 per expansion point.

PassivityPreservingMultipointModelOrderReductionusingReflectiveExploration

487

Table 1: Example 1: Adaptive truncation for model

compacting.

Threshold RMS Error Dimension of

ROM

−1

2.23× 10

−1

−2

1.703× 10

−1

−3

6.96× 10

−2

−4

9.72× 10

−4

0 0.2 0.4 0.6 0.8 1

−6

−5

−4

−3

−2

−1

Frequency (GHz)

| (S)

Original model

Reduced order model

Figure 6: Example 1: Magnitude of Y

after model

compacting.

6.2 Example 2: Lossless Transmission

Line

For this example, a 20 cm lossless uniform coupled

microstrip structure with two strips with the following

per-unit-length matrices (Khalaj-Amirhosseini,

2006),

pul



425.6 74.83

74.83 425.6



nH/m

pul



174.9 14.25

14.25 174.9



pF/m. (17)

for a frequency range of interest [1 KHz− 1 GHz], is

modeled. The original system has an order of 1604

with 4 ports.

Similar to Example 1, two expansion points at

min

and ω

max

are considered. The reduced order for

the ﬁrst iteration is equal to 4, the number of ports.

Then as briefed in Section 3, the frequency responses

are computed using a merged projection matrix (6).

Then similar to the previous case the difference in

0 0.2 0.4 0.6 0.8 1

Frequency (GHz)

norm(H

act

−H

)

max(Err

) => new expansion point

Figure 7: Example 2: Error per frequency used to select the

new expansion point for the adaptive sampling loop.

1 2 3

Samples

RMS error

Figure 8: Example 2: RMS error between the iterated

models during the addition of new expansion points.

response between the two models (7) is computed

and as the error is bigger than the threshold set, the

algorithm checks for the next expansion point using

the adaptive sampling loop as shown in Fig.11.

Similarly in this manner the sampling process is

iterated till the RMS error (7) is less than threshold

value of 10

−3

Figure 8 plots the RMS error (7) of the best

two models during each iteration of the reﬂective

exploration algorithm.

Figure 12, shows the frequency responses

obtained during the reﬂective exploration for different

iterations. The best model has dimension 64 and is

obtained with 4 expansion points within a CPU time

of 14.8 secs.

Finally, the model is compacted based on the

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

488

0 0.2 0.4 0.6 0.8 1

−6

−4

−2

Frequency (GHz)

| (S)

Models obtained during each iteration

Expansion points considered

Final reduced order model

Figure 9: Example 2: Magnitude of Y

for each iterative

step with the adaptively chosen expansion points.

truncation of the singular values of the common

projection matrix. With the truncation algorithm

described in Section 4, we obtain a model of order

35 by adaptively choosing a threshold of 10

−2

in 0.16

secs as shown in Table 2.

Table 2: Example 2: Adaptive truncation for model

compacting.

Threshold RMS Error Dimension of

ROM

−1

8.04 29

−2

8.645× 10

−4

Figure 13 plots the magnitude of Y

for the

original and the reduced model using 4 expansion

points with a reduced order of 9 per expansion point.

6.3 Example 3: Modiﬁed Nodal

Analysis

A modiﬁed nodal analysis (MNA) formulation for a

22 port circuit as given in the Niconet benchmark

collections

is considered for this example. The

original system has an order of 4863 with 22 ports

for a frequency range of interest [1 KHz− 5 GHz].

Similar to the previous examples, two expansion

points at ω

min

and ω

max

are considered. The reduced

order for the ﬁrst iteration is equal to 22, the number

of ports. Then as briefed in Section 3, the frequency

responses are computed using a merged projection

matrix (6). Then similar to the previous case the

http://www.win.tue.nl/niconet/niconet.html

0 0.2 0.4 0.6 0.8 1

−6

−4

−2

Frequency (GHz)

| (S)

Original model

Reduced order model

Figure 10: Example 2: Magnitude of Y

with the original

response after model compacting.

0 1 2 3 4 5

Frequency (GHz)

norm(H

act

−H

)

max(Err

) => new

expansion point

Figure 11: Example 3: Error per frequency used to select

the new expansion point for the adaptive sampling loop.

difference in response between the two models (7) is

computed and as the error is bigger than the threshold

set, the algorithm checks for the next expansion point

using the adaptive sampling loop as shown in Fig.11.

Similarly in this manner the sampling process is

iterated till the RMS error (7) is less than threshold

value of 10

−3

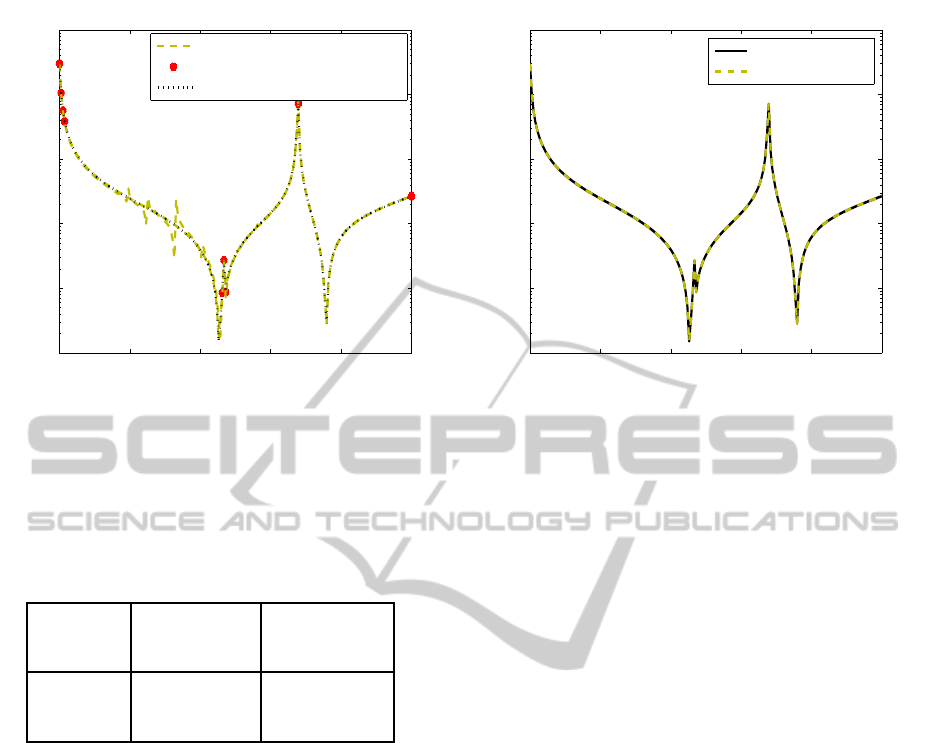
Figure 12, shows the frequency responses

obtained during the reﬂective exploration for different

iterations. The best model has dimension 1122 and is

obtained with 9 expansion points within a CPU time

of 2048.5 secs.

Finally, the model is compacted based on the

truncation of the singular values of the common

projection matrix. As shown in Table 3, with the

PassivityPreservingMultipointModelOrderReductionusingReflectiveExploration

489

0 1 2 3 4 5

−4

−3

−2

−1

Frequency (GHz)

(S)

Models obtained during each iteration

Expansion points chosen asaptively

Final reduced order model

Figure 12: Example 2: Magnitude of Y

for each iterative

step with the adaptively chosen expansion points.

truncation algorithm described in Section 4, we obtain

a model of order 202 by adaptively choosing a

threshold of 10

−2

in 4.38 secs.

Table 3: Example 3: Adaptive truncation for model

compacting.

Threshold RMS Error Dimension of

ROM

−1

15.09 88

−2

2.645× 10

−3

202

Figure 13 plots the magnitude of Y

for the

original and the reduced model using 9 expansion

points with a reduced order of 22 per expansion

point..

From the examples described it can be illustrated

that the proposed technique is able to capture

the behavior of the system accurately and is able

to preserve passivity of the original model by

construction.

7 CONCLUSION

For model order reduction its important that the

model is accurate over the whole frequency range of

interest and must also preserve passivity. Passivity

preservation is important since that interconnection

of merely stable systems does not necessarily yield

a stable system, while interconnection of passive

systems yield a passive and hence stable system. In

the literature several multipoint reduction algorithms

with passivity preservation has been proposed to

0 1 2 3 4 5

−4

−3

−2

−1

Frequency (GHz)

| (S)

Original model

Reduced order model

Figure 13: Example 3: Magnitude of Y

with the original

response after model compacting.

overcome this. In this paper, the adaptive selection

of expansion point is based on a reﬂective exploration

technique. The projection matrices obtained from

the expansion points are merged to obtain the overall

projection matrix for the system. To get a more

compact model the merged projection matrix is

truncated based on its singular values. Reduced order

models are obtained by a congruence transformation,

which preserves the passivity the system. The

numerical examples validate the proposed technique.

ACKNOWLEDGEMENTS

This work was supported by the Research

Foundation Flanders (FWO-Vlaanderen) and by

the Interuniversity Attraction Poles Programme

BESTCOM initiated by the Belgian Science Policy

Ofﬁce.

REFERENCES

Anderson, B. and Vongpanitlerd, S. (1973). Network

Analysis and Synthesis. Prentice-Hall, Englewood

Cliffs, NJ.

Balas, G., Chiang, R., Packard, A., and Safonov, M.

(2005). Robust Control Toolbox User’s Guide. The

MathWorks, Inc., Version 3.

Beyer, U. and

Smieja, F. (1996). Data exploration with

reﬂective adaptive models. Computational Statistics

& Data Analysis, 22(2):193 – 211.

Boyd, S., El Ghaoui, L., Feron, E., and Balakrishnan,

V. (1994). Linear matrix inequalities in system and

control theory.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

490

Feldmann, P. and R. Freund, W. (1995). Efﬁcient

linear circuit analysis by Pad`e approximation via

the Lanczos process. IEEE Transactions on

Computer-Aided Design of Integrated Circuits and

Systems, 14(5):639–649.

Ferranti, F., Nakhla, M., Antonini, G., Dhaene, T.,

Knockaert, L., and Ruehli, A. (2011). Multipoint

full-wave model order reduction for delayed peec

models with large delays. IEEE Transactions on

Electromagnetic Compatibility, 53(4):959–967.

Freund, R. W. (2000). Krylov-subspace methods for

reduced-order modeling in circuit simulation. J.

Comput. Appl. Math., 123:395–421.

Gahinet, P. and Apkarian, P. (1993). An LMI-based

parametrization of all H

∞

controllers with

applications. Proceedings of the 32nd Conference on

Decision and Control, pages 656–661.

Gahinet, P., Nemirovski, A., Laub, A., and Chilali, M.

(1995). LMI Control Toolbox User’s Guide. The

MathWorks, Inc., Version 1.

Gallivan, K., Grimme, G., and Dooren, P. (1996). A rational

Lanczos algorithm for model reduction. Numerical

Algorithms, 12(1):33–63.

Geest, J. D., Dhaene, T., Fach, N., and Zutter, D. D. (1999).

Adaptive CAD-model building algorithm for general

planar microwave structures. IEEE Transactions on

Microwave Theory and Techniques, 47(9):1801–1809.

Khalaj-Amirhosseini, M. (2006). Progress in

electromagnetics research. 60:107–117.

Knockaert, L. and De Zutter, D. (2000). Laguerre-SVD

reduced-order modeling. IEEE Transactions on

Microwave Theory and Techniques, 48(9):1469–1475.

Knockaert, L., Dhaene, T., Ferranti, F., and Zutter, D. D.

(2011). Model order reduction with preservation

of passivity, non-expansivity and Markov moments.

Systems & Control Letters, 60(1):53–61.

Odabasioglu, A., Celik, M., and Pileggi, L. (1998).

PRIMA: passive reduced-order interconnect

macromodeling algorithm. IEEE Transactions

on Computer-Aided Design of Integrated Circuits and

Systems, 17(8):645–654.

Phillips, J. (2004). Variational interconnect analysis via

PMTBR. pages 872 – 879.

Phillips, J., Daniel, L., and Silveira, L. (2003). Guaranteed

passive balancing transformations for model order

reduction. IEEE Transactions on Computer-Aided

Design of Integrated Circuits and Systems, 22(8):1027

– 1041.

Silveira, L. and Phillips, J. (2006). Resampling

plans for sample point selection in multipoint

model-order reduction. Computer-Aided Design of

Integrated Circuits and Systems, IEEE Transactions

on, 25(12):2775–2783.

Wang, H., Tan, S. X.-D., and Rakib, R. (2012).

Compact modeling of interconnect circuits over wide

frequency band by adaptive complex-valued sampling

method. ACM Trans. Des. Autom. Electron. Syst.,

17(1):5:1–5:22.

PassivityPreservingMultipointModelOrderReductionusingReflectiveExploration

491