
Efficient Construction of Infinite Length Hash Chains with Perfect
Forward Secrecy Using Two Independent Hash Functions
Sebastian Bittl
Fraunhofer ESK, Munich, Germany
Keywords:
Hash Chain Design, Perfect Forward Secrecy, One-time Password, Security, Privacy.
Abstract:
One-way hash chains have been used to secure many applications over the last three decades. To overcome the
fixed length limitation of first generation designs, so-called infinite length hash chains have been introduced.
Such designs typically employ methods of asynchronous cryptography or hash based message authentication
codes. However, none of the proposed schemes offers perfect forward secrecy, keeping former outputs secret
once the system got compromised. A novel algorithm for constructing infinite length hash chains with built-
in support for perfect forward secrecy is presented in this work. Thereby, the scheme differs significantly
from existing proposals by using a combination of two different hash functions. It avoids the computational
complexity of public-key algorithms, utilises well studied standard hash functions and keeps the benefits of a
hash chain without a length constraint.
1 INTRODUCTION
The idea of one-way hash chains (or simply hash
chains) was introduced in order to overcome the
weaknesses of password schemes using user chosen
passwords (Lamport, 1981). Thereby, the usage of
so called one time passwords (OTPs) was proposed.
Each OTP is only used once and its generation al-
gorithm should make it impossible for an attacker
to obtain the next password(s) from the current one
(Lamport, 1981). This issue is still an up to date
problem, as shown in (Florˆencio and Herley, 2007).
Thereby, it was found that many people use insecure
passwords, which are easy to obtain using a brute
force attack. Additionally, they often reuse passwords
multiple times for different services. Moreover, many
other use cases for hash chains were suggested in re-
cent years, like, e.g., micropayment schemes (Rivest
and Shamir, 1996).
Initial hash chain designs suffer from an a-priori
fixed length of the chain. After reaching its end, re-
initialisation of the system is required. Although the
concept allows the fixed number of entries N to be
chosen arbitrarily selecting high values for N is in-
feasible for systems with restricted amounts of com-
putational power and storage available. To overcome
this limitation, so called infinite length hash chains
have been introduced (Bicakci and Baykal, 2002).
These enable the chain to reach an arbitrary length
in real world applications. Thereby, they limit storage
requirements and necessary computational power to
generate an entry of the chain on demand in compar-
ison to the original proposal (Di Pietro et al., 2006;
Bicakci and Baykal, 2002). Thereby, existing ap-
proaches facilitate either public-key operations (Bi-
cakci and Baykal, 2002), hash based message authen-
tication codes (M’Raihi et al., 2005; M’Raihi et al.,
2011), or quite non-standard cryptographic primitives
(Di Pietro et al., 2005).
However, none of the published strategies pro-
vides perfect forward secrecy (Menezes et al., 1996),
i.e., past elements of the chain are not kept secret from
an attacker who obtains the current secret state of the
chain. To overcome this disadvantage, an algorithm
utilising a combination of two standard hash func-
tions (e.g., one from the SHA-2 and SHA-3 family
each (NIST, 2012; Chang et al., 2012; NIST, 2014))
to generate a hash chain is proposed in the following.
Thereby, the design offers built-in support for perfect
forward secrecy, while keeping requirements regard-
ing computational performance low.
The further outline is as follows. In Section 2, a
brief review of the theory in the area of hash chains
and published construction algorithms is given along-
side a selection of use cases. In Section 3 the new al-
gorithm for obtaining a hash chain is defined. Aspects
of security and implementation, like computational
performance, are also discussed there. Section 4 pro-
213
Bittl S..
Efficient Construction of Infinite Length Hash Chains with Perfect Forward Secrecy Using Two Independent Hash Functions.
DOI: 10.5220/0005020502130220
In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 213-220
ISBN: 978-989-758-045-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

vides a comparison of the suggested approach from
Section 3 to other proposed creation schemes. Fi-
nally, a conclusion about the obtained results is given
in Section 5.
2 STATE OF THE ART
In the following, state of the art strategies for obtain-
ing a hash chain as well as common use cases for the
concept of hash chains are described.
2.1 Common Creation Strategies
Common strategies to obtain hash chains can be dif-
ferentiated by the kind of limitation they impose on
the length of the chain. At first, the initial fixed length
design of hash chains is introduced. Afterwards, more
recent proposals enabling the construction of infinite
length hash chains are given.
2.1.1 Fixed Length Chains
The most popular concept of creating a hash chain has
been proposed in (Lamport, 1981). It is illustrated in
Figure 1.
generate
use
s
0
h(s
0
) = s
1
h(s
1
) = s
2
... h(s
j
) = s
j+1
Figure 1: Hash chain concept as proposed by (Lamport,
1981).
The system’s outputs s
j
(with j ≥ 0 a natural num-
ber) are used in the inverse order of calculation. In
Figure 1, the used hash function is denoted by h. Ev-
ery element s
j
of the hash chain (except the first one
s
0
, which is taken from a random seed) is obtained by
applying the hash function to its predecessor s
j−1
.
Since its proposal in (Lamport, 1981), many
strategies for optimised usage of this kind of hash
chains have been developed. Thereby, ways to re-
duce computational effort and storage requirements
have been studied in (Jakobsson, 2002; Coppersmith
and Jakobsson, 2002; Hu et al., 2005).
2.1.2 Infinite Length Chains
The advantages of infinite length hash chains have
been outlined in (Bicakci and Baykal, 2002) along-
side a feasible way of constructing such hash chains.
This strategy makes use of an arbitrary public-key al-
gorithm (e.g., based on RSA (Rivest et al., 1978) or
ECC (Miller, 1986; Koblitz, 1987)) in order to build
up the chain.
Another way to generate infinite length hash
chains using chaotic maps was proposed in (Xiao
et al., 2004). However, it was shown that the pro-
posed design is insecure (Bergamo et al., 2005). Fur-
thermore, (Di Pietro et al., 2005) and (Di Pietro et al.,
2006) suggested the usage of so called chameleon
functions for the same purpose. Details can be found
in (Di Pietro et al., 2005; Di Pietro et al., 2006).
Additionally, the Hash-based Message Authen-
tication Code (HMAC) based one time password
scheme from (M’Raihi et al., 2005) (HOTP) can also
be regarded as some kind of hash chain. It does not
use the former output of the system as the next in-
put as other approaches do. Instead it changes the
“message” after each round by increasing an embed-
ded counter value. For more details, the reader is re-
ferred to (M’Raihi et al., 2005).
Furthermore, the HOTP algorithm has been ex-
tended towards a time dependent variant (M’Raihi
et al., 2011) (TOTP). Thereby, the sequence counter
is simply replaced with the current timestamp. In
contrast to the other schemes described before, this
strategy requires time synchronization between cre-
ator and verifier of the hash chain’s output. More de-
tails can be found in (M’Raihi et al., 2011).
2.2 Use Cases
The probably oldest use case leading to the devel-
opment of the entire concept of hash chains is the
generation of OTPs for user authentication (Lam-
port, 1981). A possible implementation is described
in (Haller and Metz, 1996). Moreover, the extensi-
ble authentication protocol (EAP) can be used with
OTPs (Aboba et al., 2004). Additionally, the concept
of server-supported signatures relies on hash chains
(Asokan et al., 1996; Bicakci and Baykal, 2002).
Furthermore, non-communication oriented use
cases like micropayment schemes (like the ones ini-
tially proposed in (Rivest and Shamir, 1996)) are pop-
ular applications facilitating hash chains. Additional
use cases include the support for secure logs on un-
trusted machines (Schneier and Kelsey, 1998) as well
as stack and queue integrity on hostile platforms (De-
vanbu and Stubblebine, 1998).
3 HASH CHAIN FROM TWO
HASH FUNCTIONS
The basic idea of the generation algorithm for a one-
way hash chain built from two independent hash func-
tions (abbreviated by THF) providing perfect forward
SECRYPT2014-InternationalConferenceonSecurityandCryptography
214

secrecy is explained in the following. Thereby, a gen-
eral description is provided alongside with some ref-
erences to the use cases as given in Section 2.2.
3.1 Algorithm Design
A hash function is denoted by h
i
, with i ∈ I = {0;1}
being its identifying index. The generation procedure
of the hash chain starts with some random seed value
s
0
. The size of s
0
is chosen so big that it becomes
impossible for an attacker to try all possible values of
s
0
in reasonable time (e.g., 256 bit). The following
equations define the initial step of the system being
applied to s
0
.
h
0
s
0
= s
1
0
(1)
h
1
s
0
⊕ m
0
= s
1
1
(2)
The lower index i of s
j
i
shows which hash function
produced this result, while the upper index j ∈ J =
[0;∞[ gives the sequence number of the result. Hence,
j = 0 indicates the initial random seed value. Addi-
tionally, m
k
(k ∈ K = {0;1}) defines some bit mask,
which is fixed a-priori and is as long as s
i
. The value
of k is determined via k = j modulo 2. This means,
two independent values of the bit mask are used in an
alternating way. Its values can be chosen arbitrarily,
but as a recommendation they can be chosen to be the
ones defined in (Bellare et al., 1996) for opad (= m
0
)
and ipad (= m
1
). The motivation for using these bit
masks is described in detail in Section 3.2.2. More-
over, ⊕ denotes the standard XOR operation.
The result s
1
1
is the first usable output (e.g., the
first OTP), while s
1
0
has to be kept secret. When an
attacker gains access to s
j
0
the whole system has to be
regarded as broken and a re-initialization is necessary.
For each round following the initial one, the following
equations have to be solved.
h
0
s
j
0
= s
j+1
0
(3)
h
1
s
j
0
⊕ m
k
= s
j+1
1
(4)
The step counter j is incremented after each
round. It is not necessary to store the old values of
s
j
i
. Furthermore, to provide perfect forward secrecy
one has to securely delete the old values of s
j
i
.
An illustration of the whole process is given in
Figure 2. Due to the one-way characteristic of a hash
function, an attacker who has access to output s
j
1
(e.g.,
an OTP) cannot compute s
j−1
0
. Hence, he cannot ob-
tain s
j
0
being the current secret element of the system.
The algorithm itself does not depend on a certain
combination of hash functions. Desirable properties
of the used elements are outlined in the following.
3.2 Security Aspects
Different security aspects of the THF algorithm are
discussed in the following.
3.2.1 Perfect Forward Secrecy and Privacy
The one-way property of the hash function h
1
bans
an attacker from computing any future output of the
system after having intercepted one or multiple of the
system’s outputs. Thereby, the internal state of the
system is protected by the one-way property. More-
over, an attacker cannot generate past outputs of the
system. To do so, one would have to reverse not only
h
1
, but additionally one would be required to reverse
h
0
, which has the one-way property, too.
Please note that, even in case the attacker gets to
know the current internal secret s
j
0
, he can only com-
pute future outputs of the system. Due to the one-
way property of h
0
, he is not able to obtain past out-
puts. This means that forward secrecy even holds in
the case that the system cannot be used for any fu-
ture purposes before a re-initialization of s
0
was per-
formed. Therefore, the THF algorithm offers perfect
forward secrecy. Other state of the art hash chain al-
gorithms do not provide this property as discussed in
detail in Section 4.1. Such kind of security is typically
not required in a classical OTP use case, but other use
cases impose a perfect forward secrecy requirement
(Di Pietro et al., 2005).
An interesting side aspect of the perfect forward
secrecy property is that plausible denyability is pro-
vided to the user. This means that if s
j
1
was monitored,
it cannot be proven that the user with current internal
state s
k
0
(with k > j) was able to generate (and use) s
j
1
.
Furthermore, it even cannot be proven that multi-
ple outputs (s
k
1
being the first of them to be monitored)
of the same hash chain were really obtained from the
same hash chain as long as the attacker has no access
to any s
j
0
with j < k. Hence, in a multi-user system
with each user having his own hash chain as defined
by THF, the outputs of the systems (resp. the inputs
to the multi-user entity) cannot be used to reconstruct
which user provided a dedicated input (e.g., a log-in
via OTP only). Moreover, an attacker cannot even
determine the number of different users from the sup-
plied user inputs. In contrast, the multi-user entity can
identify each user unambiguously just given his input
defined by his individual current s
j
1
.
3.2.2 Sequential Use of Hash Functions
The algorithm from Section 3.1 uses two different
hash functions. Different possibilities to combine
EfficientConstructionofInfiniteLengthHashChainswithPerfectForwardSecrecyUsingTwoIndependentHash
Functions
215

generate
use
h
0
(s
0
) = s
1
0
s
0
h
0
(s
j
0
) = s
j+1
0
h
0
(s
1
0
) = s
2
0
h
1
(s
0
⊕ m
0
) = s
1
1
h
1
(s
j
0
⊕ m
k
) = s
j+1
1
h
1
(s
1
0
⊕ m
1
) = s
2
1
...
...
Figure 2: Creation of a one-way hash chain using two different hash functions.
these two functions exist. The most straight forward
one is a simple serial concatenation.
However, sequential usage of two hash functions
on a single input is the same as applying another hash
function h
2
given by h
1
(h
0
(s
j
)) = h
2
(s
j
). It has been
found that one has to be careful about such a de-
sign (Lehmann, 2010). One possible security flaw
created by such a combination is that after obtain-
ing a collision in h
0
, a collision in h
2
is automati-
cally obtained, too. Thus, it can be assumed that h
2
is more susceptible to collision attacks than h
0
and
h
1
individually (Lehmann, 2010). Multiple solutions
for solving this problem have been suggested. One
possibility is to use a so called secure hash function
combiner like C
4P&OW
from (Lehmann, 2010) at the
cost of increased computational effort. For details see
(Lehmann, 2010).
The HMAC design avoids direct concatenation by
the usage of additional bit masks of fixed value (Bel-
lare et al., 1996). As this has been shown to be an
effective and efficient approach (Bellare et al., 1996),
the design from Section 3.1 follows this outline.
Another possibility to avoid the risks imposed by
direct concatenation is to use the concept of a se-
quence counter being embedded into the hash chain as
introduced for HOTP (M’Raihi et al., 2005). Thereby,
one would replace Equation 4 by h
1
(s
j
0
| j) = s
j+1
1
,
with | denoting sequential concatenation.
While this would suffice to avoid the above de-
scribed weakness, there are two issues regarding this
kind of solution. At First, one has to store the value
of j, which is not required by the THF algorithm. The
second point is, that such kind of sequential concate-
nation requires the usage of a hash function h
1
with-
out length extension weakness to avoid possible se-
curity flaws introduced by this kind of design. Such
hash functions are available but currently they have
not been standardized (Chang et al., 2012).
3.2.3 Exploiting Collisions in Hash Functions
Another important aspect of the design is the resis-
tance to attacks monitoring the system’s output s
j
1
(multiple times) and trying to obtain the secret value
s
j
0
by finding collisions of hash function h
1
.
Assuming that an attacker monitored a single out-
put of the hash chain s
j
1
, he can try to find a value x
0
0
with h
1
(x
0
) = s
j
1
. In case such a value x
0
0
got obtained,
the attacker has no direct possibility to check whether
x
0
0
is equal to the real input for h
1
, which was s
j−1
0
.
Instead, the attacker has to perform the steps given
in Equations 3 and 4 with x
0
0
as the input. Thereby,
the attacker obtains assumptions h
0
(x
0
0
) = x
1
0
about the
real secret s
j+1
0
as well as h
1
(h
0
(x
0
0
)) = x
1
1
for the next
output s
j+1
1
. Afterwards, the attacker can perform ei-
ther
• a further monitoring step of the next output s
j+1
1
and check for equality with x
1
1
(passive attack)
1
or
• a direct try to use x
1
1
(e.g., as OTP) and checking
whether the communication partner accepts him
as an authenticated partner (active attack).
This shows that it is necessary to chose h
1
carefully
in order to make it as hard as possible for an attacker
to compute (multiple) collisions for h
1
given one or
multiple of its output(s) s
j
1
.
For a comparison of security aspects of the pro-
posed algorithm with regard to other published algo-
rithms given in Section 2.1 see Section 4.
3.3 Implementation Aspects
The kind of strategy suggested above requires the
availability of two different secure hash functions h
0
and h
1
. These functions should be as independent as
possible to avoid that a successful attack on h
1
also
leads to a successful attack on h
0
putting perfect for-
ward secrecy at risk. Fortunately, the algorithms from
the SHA-2 family (e.g., SHA-256) and SHA-3 pro-
posals (based on Keccak) have been designed based
on quite different concepts and currently both can be
regarded as being secure (Chang et al., 2012).
For performance reasons, it is beneficial to allow
the size of s
j
0
(potentially plus padding) to be equal to
the block size of both used hash functions. Common
block sizes are 512 and 1024 bits (NIST, 2012), and
as outlined in (Bertoni et al., 2011), Keccak being the
1
An attacker does not need to monitor the very next out-
put. It is sufficient to determine or (roughly) guess the
number of system outputs k between two monitored out-
puts. The attacker just has to perform the described steps
k-times (as the real user also did) before he can do a feasi-
bility check on his guess of the system’s secret.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
216

winner of the SHA-3 contest, can be easily tuned to
different block sizes. Furthermore, Keccak can gener-
ate an output of length 512 bit, which is an often used
block size, e.g., in SHA-256.
It is not required to compute the results of h
0
and
h
1
in parallel. Instead, one could first obtain the result
of h
1
in order to provide a usable output for the user
and compute h
0
afterwards to bring the system into a
state from which the next usable output can be gener-
ated. However, parallelization of the two calculations
is possible.
Furthermore, the amount of computational effort
necessary to compute the output of a hash function
is and was one of the core criteria in the selection
process of standardized hash functions (Chang et al.,
2012). Therefore, it can be assumed that the men-
tioned algorithms perform quite well with regard to
this criteria while simultaneously keeping necessary
security requirements.
The complexity of the proposed algorithm consid-
ering computational effort as well as storage require-
ment is both constant with O(1). During each step
(see Equations 3, 4), two hash functions are used and
the output of one of them has to be stored securely.
Thus, it can be claimed that the complexity of the
given design is very low.
A detailed comparison of the suggested approach
with other known hash chain designs will be given in
Section 4.
3.4 Computational Performance
As mentioned above, computational performance is
a key property of a hash chain generation algorithm.
Hence, the required runtime for generating one output
of the hash chain on demand (i.e., without precalcula-
tion of future outputs) is determined in the following.
Additionally, reference designs using standard
cryptographic primitives are measured in order to
compare their performance to the THF algorithm
from Section 3.1. Thereby, the concept of using a
public-key system (Bicakci and Baykal, 2002) as well
as the HOTP design (M’Raihi et al., 2005) are taken
into account.
3.4.1 Measurement Environment
To achieveresults applicable to a broad range of target
platforms, the two quite different processor technolo-
gies of an Intel Core i7-2640M (2.8 GHz) as well as
an AMD Geode LX (500 MHz) are used for measure-
ments. Details about these processors can be found in
references (Cor, 2013; Amd, 2014).
Algorithm runtime is determined with the help of
the POSIX standard clock
gettime() function using
clock ID CLOCK PROCESS CPUTIME ID (ISO,
2009). To avoid influence of out-of-order execution
disturbing the measurement results, advices from ref-
erence (Paoloni, 2010) have been followed. Thereby,
the instruction CPUID was used directly before and
after calling clock
gettime().
To implement the test sets, the well known
Crypto++ library (version 5.6.2) was used for all ba-
sic cryptographic algorithms (Dai, 2014). All tests
were carried out on a standard Debian Linux (stable
branch) operating system using GCC compiler ver-
sion 4.7.2 (deb, 2013; R. M. Stallman et. al., 2012).
3.4.2 Parametrization of Hash Chain Designs
The design from Section 3.1 uses the parameters
as described in Section 3.3, with SHA-256 being
used for h
0
and Keccak (512 bit block size and 256
bit output size, i.e., SHA3-256 (Dai, 2014; NIST,
2014)) for h
1
. Furthermore, two different implemen-
tation concepts of public-key cryptography are used
for the system from reference (Bicakci and Baykal,
2002). Thereby, RSA (in Probabilistic Signature
Scheme (PSS) mode) and ECC as Elliptic Curve Dig-
ital Signature Algorithm (ECDSA), being very pop-
ular public-key signature schemes, are taken into re-
gard. Additionally, HOTP is used with SHA-256 as
the underlying hash function. For details about these
standard cryptographic schemes the reader is referred
to (Paar and Pelzl, 2010).
Key lengths for RSA and ECDSA follow the rec-
ommendations given by the German Bundesamt f¨ur
Sicherheit in der Informationstechnik (BSI, 2014).
Therefore, for ECDSA the NIST P-256 curve (NIST,
2013) is applied and a 2048 bit length RSA key is
used. Moreover, a length of 256 bits for s
0
, i.e., the
initial random seed of the chains is used.
3.4.3 Performance Results
To conduct the following performance study the mea-
surement environment described in Section 3.4.1 was
used. Furthermore, the results were obtained by gen-
erating 10000 outputs of the hash chain algorithms
and taking the average of the individually measured
runtimes.
The obtained results for computational perfor-
mance of the different designs (parametrized as out-
lined in Section 3.4.2) are given in Figure 3. The
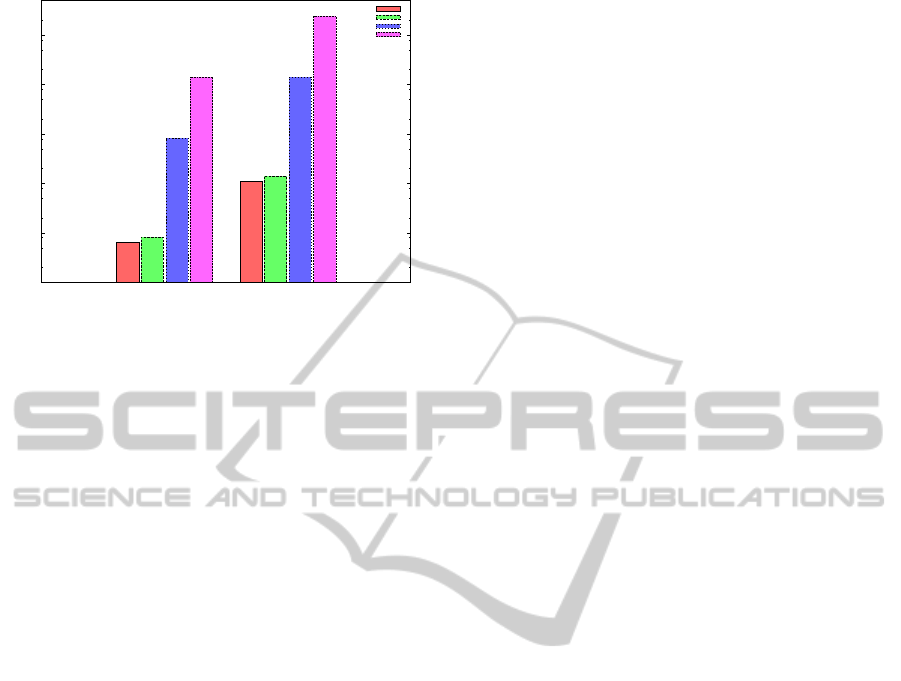
given runtime was measured in nanoseconds (ns).
Please note the logarithmic scale of the y-axis.
As one can see from the results in Figure 3, THF
requires less runtime than any of the other algorithms
on both platforms. Thereby, it significantly outper-
forms both schemes which are based on public-key
EfficientConstructionofInfiniteLengthHashChainswithPerfectForwardSecrecyUsingTwoIndependentHash
Functions
217
1000
10000
100000
1e+06
1e+07
1e+08
i7 Geode
runtime in ns
THF
HOTP
ECC
RSA
Figure 3: Runtime measurement results.
cryptography. This can be expected, as this kind of al-
gorithms are commonly known to require much more
computing power than the running of hash functions.
The runtime of all algorithms is much higher on
the used Geode processor (embedded systems do-
main) than on the i7 platform (desktop PC domain).
However, the relation between the runtimes of the in-
dividual algorithms is the same for both platforms.
Noticeably, the THF design slightly outperforms
the HOTP design, which consists of calculating a
HMAC and incrementing a counter. Thereby, the
HMAC design consists of sequentially executing two
hash functions, just as our design does. However,
HMAC also requires two XOR operations with a bit
mask, while our design requires only one such oper-
ation. Moreover, the incrementation operation from
HOTP is not needed by our design.
The amount of reduction in required computing
power from HOTP to THF is small and will depend
on the used combination of algorithms in practical ap-
plications. However, the THF design can be assumed
to offer a benefit regarding this important criteria.
Moreover, the standard deviation of the obtained
measurement results is quite low for all studied de-
signs. Hence, error bars are not displayed in Figure 3,
as they would be to small to be noticed. Hence, the
achieved results can be regarded as reliable.
A further in-detail comparison of computational
performance of different hash chain designs (includ-
ing not implemented ones) is provided in Section 4.2.
4 EVALUATION OF THE THF
ALGORITHM
The following detailed evaluation and comparison of
the THF design to other state of the art algorithms is
split into two parts for a more convenient presentation
of results.
At first, pure security properties of the systems are
taken into account. Afterwards, computational per-
formance and storage requirements are studied.
4.1 Security
None of the schemes from (Lamport, 1981; Bicakci
and Baykal, 2002; Di Pietro et al., 2006; M’Raihi
et al., 2005) has been targeted by any effective attack,
which would allow an attacker to determine a future
hash chain output from intercepted past output(s), as
long as the underlying cryptographic primitives have
been secure.
In the initial design from reference (Lamport,
1981), obtaining the result s
j
from step j of the chain
enables one to trivially compute all values s
k
with
k > j. While this is probably not a problem for an
OTP use case, it limits the usability to scenarios in
which it is not necessary to keep old results of the
chain secret (Di Pietro et al., 2005).
Additionally, such kind of forward secrecy is also
not provided by the approaches given in (Bicakci
and Baykal, 2002; Di Pietro et al., 2005). As both
schemes are based on asymmetric cryptography, the
knowledge of one hash chain output together with the
knowledge about the public key enables an attacker to
retrieve all previous states of the hash chain. There-
fore, they show the same characteristic regarding for-
ward secrecy as the fixed length design does.
In contrast, the HOTP approach (see (M’Raihi
et al., 2005)) provides forward secrecy (an attacker
cannot go back in the chain) like the algorithm from
Section 3 does. To calculate the past outputs of an
HOTP system an attacker has to obtain its private key,
which obviously also allows for the calculation of any
future steps of the chain. Therefore, past outputs can
be regarded as secure as future outputs.
However, HOTP does not provide perfect forward
secrecy. To fulfil this particular criteria, the system
should not allow an attacker to calculate past outputs
even if he is able to obtain the (current) private key.
Though, in a HOTP scheme, one can determine all
(prior) hash chain steps by adjusting the used counter
value when given the static secret key.
In contrast to prior work, the algorithm given
in Section 3 is able to provide perfect forward se-
crecy. This is done by protecting all the system out-
puts, which were generated before the private key is
obtained by the attacker. The only requirement to
achieve this is to use a secure hash function h
0
. In
order to obtain past outputs, the attacker has to invert
h
0
, which is regarded as infeasible. See Section 3.2.1
for more details.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
218

4.2 Computational Effort and Storage
Requirements
As outlined in Section 3.3, the suggested design has
computational complexity of O(1) and a constant
memory requirement of order O(1).
It has been found that for the traditional one-
way hash function from (Lamport, 1981) an opti-
mal trade-off between computational effort (neglect-
ing initialization effort) and required storage capacity
can be achieved (Jakobsson, 2002; Coppersmith and
Jakobsson, 2002). Thereby, the complexity regard-
ing computational effort as well as memory require-
ment is given by O(log(N)) (N is the fixed length of
the chain). Therefore, the algorithm from Section 3
clearly outperforms the design from (Lamport, 1981)
regarding computational and memory requirements.
(Di Pietro et al., 2006) provide a detailed analy-
sis of the computational effort required by the pro-
posed design. From Figure 2 of reference (Di Pietro
et al., 2006) one can see that for small numbers of
hash function runs the required computing power for
a chameleon function approach is higher than for the
algorithm using a hash function. Our approach uses
just two hash function runs. Thus, one can assume
that its execution time should be less than the one
from (Di Pietro et al., 2006)
2
.
Usage of public-key algorithms (e.g., RSA), as
done in the scheme from reference (Bicakci and
Baykal, 2002), typically requires high computational
effort. Reference (Di Pietro et al., 2006) points out
that using chameleon functions is more efficient than
this kind of calculations. As outlined before, our ap-
proach outperforms the one of (Di Pietro et al., 2006)
and therefore, it also clearly outperforms the one from
(Bicakci and Baykal, 2002) with regard to required
computing power. This is also shown by the results
given in Figure 3.
Approaches from (Bicakci and Baykal, 2002;
Di Pietro et al., 2006; M’Raihi et al., 2005) have stor-
age requirements of O(1) as the algorithm from Sec-
tion 3 has (see also Section 3.3).
4.3 Comparison Summary
The individual results from Sections 4.1 and 4.2 are
briefly summarized in Table 1. Thereby, the following
abbreviations are used.
The infinite length hash chain with two hash
functions from Section 3 is denoted by THF and
the fixed length hash chain (Lamport, 1981) by HC.
2
In (Di Pietro et al., 2006) SHA-1 was used. Although,
our approach requires two different hash functions, this
should not change the overall result of the comparison.
Moreover, the infinite length hash chain design uti-
lizing asymmetric cryptography (Bicakci and Baykal,
2002) (AC) and infinite length hash chains from
chameleon functions (Di Pietro et al., 2005) (CF) are
taken into regard. Finally, the HOTP scheme is in-
cluded (M’Raihi et al., 2005).
For detailed reasoning on the given results see
Sections 4.1 and 4.2.
Table 1: A brief comparison of hash chain designs.
THF HC AC CF HOTP
limited length no yes no no no
forw. sec. yes no no yes yes
perf. forw. sec. yes no no no no
comp. effort low med. high low low
storage req. low med. low low low
As one can see from Table 1, the proposed algo-
rithm from Section 3 (THF) performs well in com-
parison to the other given schemes. Thereby, it out-
performs all other designs with regard to at least one
of the chosen criteria. This is especially the case for
perfect forward secrecy.
5 CONCLUSIONS AND FUTURE
WORK
A novelalgorithm for generating one-way hash chains
has been proposed in this paper. The design provides
perfect forward secrecy, distinguishing it from pre-
ceding work. Thereby, it keeps prior states of the hash
chain secret, even if an attacker is able to recover the
current internal secret state of the cryptographic sys-
tem.
Furthermore, the given comparison to well known
approaches shows that the proposed algorithm per-
forms well with regard to several criteria. Thereby,
computational effort, storage requirement as well as
the usage of well studied cryptographic primitives
have been regarded.
Therefore, the proposed hash chain design is
ready to be used in a broad range of applications. One
important example being user authentication via one
time passwords.
Future work can study more use cases for the
given approach or extend the presented algorithm to
include time-based information. Thereby, some con-
cepts from the Time-Based One-Time Password Al-
gorithm (TOTP) (M’Raihi et al., 2011) could proba-
bly be reused.
EfficientConstructionofInfiniteLengthHashChainswithPerfectForwardSecrecyUsingTwoIndependentHash
Functions
219

REFERENCES
(2013). 2nd Generation Intel Core Processor Family,
Datasheet, Vol.1. Intel, 8th edition. Doc. No. 324641-
008.
(2013). Debian – The Universal Operating System. online:
http://www.debian.org/. retrieved: 04.2014.
(2014). AMD Geode LX Processor Family. AMD. Doc.
No. 33358E.
Aboba, B., Blunk, L., Vollbrecht, J., and Carlson, J. (2004).
Extensible Authentication Protocol (EAP). Technical
Report RFC:3748, IETF.
Asokan, N., Tsudik, G., and Waidner, M. (1996). Server-
supported signatures. In Computer Security - ES-
ORICS 96, volume 1146 of LNCS, pages 131–143.
Bellare, M., Canetti, R., and Krawczyk, H. (1996).
Keying Hash Functions for Message Authentication.
CRYPTO, LNCS, 1109:1–15.
Bergamo, P., D’Arco, P., De Santis, A., and Kocarev, L.
(2005). Security of Public-Key Cryptosystems Based
on Chebyshev Polynomials. IEEE Trans. on Circuits
and Systems I: Regular Papers, 52(7):1382 – 1393.
Bertoni, G., Daemen, J., Peeters, M., and van Assche, G.
(2011). The KECCAK SHA-3 submission. Technical
Report 3, STMicroelectronics and NXP Semiconduc-
tors.
Bicakci, K. and Baykal, N. (2002). Infinite Length Hash
Chains and their Applications. In Eleventh IEEE
International Workshops on Enabling Technologies:
Infrastructure for Collaborative Enterprises, 2002.
WET ICE 2002, pages 57–61.
BSI (2014). Kryptographische Verfahren: Empfehlungen
und Schl¨ussell¨angen.
Chang, S., Perlner, R., Burr, W. E., Turan, M. S., Kelsey,
J. M., Paul, S., and Bassham, L. E. (2012). Third
Round Report of the SHA-3 Cryptographic Hash Al-
gorithm Competition. Technical report, NIST.
Coppersmith, D. and Jakobsson, M. (2002). Almost Opti-
mal Hash Sequence Traversal. In Proc. of the Fourth
Conference on financial Cryptography, volume 2357
of LNCS, pages 102–119. Springer Berlin Heidelberg.
Dai, W. (2014). Crypto++ Library. online:
http://www.cryptopp.com/. retrieved: 04.2014.
Devanbu, P. T. and Stubblebine, S. (1998). Stack and Queue
Integrity on Hostile Platforms. In Proc. 1998 IEEE
Symposium on Research in Security and Privacy.
Di Pietro, R., Durante, A., Mancini, L., and Patil, V. (2005).
Practically Unbounded One-Way Chains for Authen-
tication with Backward Secrecy. In First International
Conference on Security and Privacy for Emerging Ar-
eas in Communications Networks, pages 400–402.
Di Pietro, R., Mancini, L. V., Durante, A., and Patil, V.
(2006). Addressing the Shortcomings of one-way
Chains. In Proc. of the 2006 ACM Symposium on
Information, computer and communications security
ASIACCS ’06, pages 289–296.
Florˆencio, D. and Herley, C. (2007). A Large-Scale Study
of Web Password Habits. In Proc. of the 16th interna-
tional conference on World Wide Web, pages 657–666.
Haller, N. and Metz, C. (1996). A One-Time Password Sys-
tem. Technical Report RFC:1938, IETF.
Hu, Y.-C., Jakobsson, M., and Perrig, A. (2005). Efficient
Constructions for One-way Hash Chains. In Proc. of
the Conference of Applied Cryptography and Network
Security (ACNS), pages 7–10.
ISO (2009). ISO/IEC 9945:2008 Information technology –
Portable Operating System Interface (POSIX
R
).
Jakobsson, M. (2002). Fractal Hash Sequence Represen-
tation and Traversal. In Proc. of the 2002 IEEE In-
ternational Symposium on Information Theory, pages
437–444.
Koblitz, N. (1987). Elliptic Curve Cryptosystems. Mathe-
matics of Computation, 48(177):203–209.
Lamport, L. (1981). Password Authentication with Insecure
Communication. Com. of the ACM, 24(11):770–772.
Lehmann, A. (2010). On the Security of Hash Function
Combiners. PhD thesis, Technische Universit¨at Darm-
stadt.
Menezes, A. J., van Oorschot, P. C., and Vanstone, S. A.
(1996). Handbook of Applied Cryptography. CRC
Press.
Miller, V. S. (1986). Use of Elliptic Curves in Cryptogra-
phy. In Williams, H. C., editor, Advances in Cryptol-
ogy - CRYPTO’85Proceedings, volume 218 of LNCS,
pages 417–426. Springer Berlin Heidelberg.
M’Raihi, D., Bellare, M., Naccache, D., and Ranen, O.
(2005). HOTP: An HMAC-Based One-Time Pass-
word Algorithm. Technical Report RFC: 4226, Net-
work Working Group, IETF.
M’Raihi, D., Machani, S., Pei, M., and Rydell, J. (2011).
TOTP: Time-Based One-Time Password Algorithm.
Technical Report RFC:6238, IETF.
NIST (2012). Secure Hash Standard (SHS).
NIST (2013). Digital Signature Standard (DSS).
NIST (2014). SHA-3 Standard: Permutation-Based Hash
and Extendable-Output Functions. draft.
Paar, C. and Pelzl, J. (2010). Understanding Cryptography.
Springer, 2nd edition.
Paoloni, G. (2010). How to Benchmark Code Execution
Times on Intel IA-32 and IA-64 Instruction Set Ar-
chitectures. White Paper 324264-001, Intel.
R. M. Stallman et. al. (2012). Using the GNU Compiler Col-
lection, For GCC version 4.7.2. Free Software Foun-
dation.
Rivest, L. and Shamir, A. (1996). PayWord and MicroMint:
Two simple micropayment schemes. In CryptoBytes,
pages 69–87.
Rivest, R., Shamir, A., and Adleman, L. (1978). A
Method for Obtaining Digital Signatures and Public-
Key Cryptosystems. Com. of the ACM, 21(2):120–
126.
Schneier, B. and Kelsey, J. (1998). Cryptographic Support
for Secure Logs on Untrusted Machines. In Proc. 7th
USENIX Security Symposium, San Antonio, Texas.
Xiao, D., Liao, X., Tang, G., and Li, C. (2004). Using
Chebyshev Chaotic Map to Construct Infinite Length
Hash Chains. In ICCCAS 2004, volume 1, pages 11–
12.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
220
