A Novel Approach to Model Design and Tuning through Automatic

Parameter Screening and Optimization

Theory and Application to a Helicopter Flight Simulator Case-study

Matteo Hessel

, Francesco Borgatelli

and Fabio Ortalli

Engineering of Computing Systems, Politecnico di Milano, Piazza Leonardo Da Vinci 32, Milano, Italy

TXT Next, TXT e-solutions, Via Frigia 27, Milano, Italy

Keywords: Model Tuning, Screening, Optimization, Machine-Learning, Adaptive Hill-Climbing, Sequential Masking.

Abstract: The aim of this paper is to describe a novel methodology for model-design and tuning in computer

simulations, based on automatic parameter screening and optimization. Simulation requires three steps:

mathematical modelling, numerical solution, and tuning of the model’s parameters. We address Tuning

because, at the state-of-the-art, the development of life-critical simulations requires months to appropriately

tune the model. Our methodology can be split in Screening (identification of the relevant parameters to

simulate a system) and Optimization (search of optimal values for those parameters). All techniques are

fully general, because they leverage ideas from Machine-Learning and Optimization Theory to achieve their

goals without directly analysing the simulator’s mathematical model. Concerning screening, we show how

Machine-Learning algorithms, based on Neural Networks and Logistic Regression, can be used for ranking

the parameters according to their relevance. Concerning optimization, we describe two algorithms: an

adaptive hill-climbing procedure and a novel strategy, specific for model tuning, called sequential masking.

Eventually, we show the performances achieved and the impact on the time and effort required for tuning a

helicopter flight-simulator, proving that the proposed techniques can significantly speed-up the process.

1 INTRODUCTION

Computer simulations have been one of the major

breakthroughs in the 20

century technology, with

previously unforeseeable theoretical and practical

implications. Simulations have shown how the

interaction among different entities/components with

non-trivial behaviour can result in an apparently

unpredictable dynamics, opening new perspectives

in the study of complex systems. In countless fields

of Science it is now a standard to resort to

simulations in order to test hypothesis or in order to

get a deeper insight in the dynamics of systems with

sensitive dependency on the initial conditions.

Concerning Engineering, simulations are essential

for both Testing and Training, and increasingly take

the place of traditional experimenting and

prototyping; this has dramatic impact on all

industries where safety and costs are critical factors

(such as the aerospace, bio-medical, pharmaceutical,

and military industries), and makes the development

of highly accurate simulators a life-critical activity.

For a very long time the Modelling and Simulation

techniques were developed independently by

different communities of Civil, Aerospace and Bio-

medical Engineers, and this led to much confusion

and lack of communication, hindering the

development of the sector. Only recently M&S was

recognized as a field on its own, with a well-

established methodology. In order to develop

effective and accurate computer simulations of

complex systems, three main steps are required:

1) Mathematical modelling of the agent(s), of the

environment, of the interactions between agents or

between agent and environment; 2) Numerical

solution of the model’s equations; 3) Tuning of the

model’s parameters. Much work has been done since

the 50s regarding the first steps. Depending on the

kind of simulation, Mathematical Modelling can rely

on principled results from Physics, Operational

Research and Game theory. Concerning the

Numerical solution of the model, beside to domain-

specific approaches (designed for particular

problems in CFD or computational electronics), also

efficient general-purpose techniques are now

Hessel M., Borgatelli F. and Ortalli F..

A Novel Approach to Model Design and Tuning through Automatic Parameter Screening and Optimization - Theory and Application to a Helicopter Flight

Simulator Case-study.

DOI: 10.5220/0005022600240035

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),

pages 24-35

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

available (e.g. FEM). Thanks to the advances in

these two steps it is therefore possible to model and

solve problems from virtually any application

domain. The third step of M&S, essential whenever

high accuracy is to be achieved, is Tuning; this is the

process of assigning precise values to the free

parameters of the mathematical model behind a

simulation (Even when it is possible to identify the

form of the functional relation among the different

variables of the system, it is seldom possible to set a

priori the exact values of all parameters). Tuning has

not seen in recent years the same development of the

first two steps of M&S, and is often the bottle-neck

of the process of building a simulator. This is the

case, for example, in the flight-simulators industry,

where tight regulatory constraints require a long

Tuning process in order to Certificate a simulator for

pilot Training; however, flight-simulations are not

the only example, and model tuning is even more

crucial in various medical contexts, such as

simulation-driven training (Morgan et al, 2006) and

accurate dose calculation in radiotherapy (which

relies on the ability of precisely modelling the

patient geometry using Computed Tomography

(Lewis et al, 2009)). In all these fields, the complex

tuning job is mostly carried out by hand, using a

trial and error approach in order to modify the huge

number of parameters until the required accuracy is

attained. This approach makes tuning a human-

intensive and time-consuming process (given the

high dimensionality of the solution space and the

complex interactions among parameters) and calls

for the development of automatic tools for model

tuning. In the following sections we begin formally

defining the tuning problem (section 2) and

providing a two-step decomposition of the problem,

heart of the proposed approach (section 3). In

sections 4 and 5 we present automatic techniques for

parameter Screening (i.e. identification of the most

relevant parameters for the effective simulation of a

system) and parameter Optimization (i.e. search of

the optimal values for those parameters); for each

step the state-of-the-art is discussed, highlighting the

major limits of currently used approaches, and

different alternatives are proposed, evaluating pros

and cons of each choice. Finally (section 6) we

validate the proposed techniques against a

Helicopter-simulator case study, comparing the

performances of our two-step approach with manual

tuning (taking TXT e-solutions data as benchmark):

we provide detailed results showing how the

combination of Screening and Optimization can

outperform manual tuning, in terms of speed,

accuracy and capability of dealing with high-

dimensional parameter spaces. It is important to

notice that, although validated against a specific type

of simulation, the proposed methodology is designed

to be as general as possible: our approach leverages

ideas from Machine-Learning and Optimization

Theory in order to achieve its goals treating the

simulator as a black-box, without relying on any

kind of domain knowledge or other a priori

assumptions.

2 THE TUNING PROBLEM

We now give a formal definition of the problem we

are facing, defining the terminology and notations to

be used in the rest of the paper; the elements here

presented can be specialized, depending on the

problem at hand; in section 6 we will see a

specification of all the following for a helicopter

flight simulator (case-study for validation). Let:

- P be a set of n parameters;

- A∈



be a generic assignment of parameters in P;

- Assign to each p

∈P a range 











,





;

- An assignment A is said consistent if 



∈



∀;

- A

denotes the initial consistent assignment,

randomly chosen or theoretically derived;

- Let S be a set of domain-specific performance

metrics, measuring different features of the output;

- S(A) represents the values of the performance

metrics computed when the simulation is executed

with the parameters’ assignment A;

- Ref is the set of expected values for the metrics

(ground-truth from observations);

- E(A) is a measure of the global simulation error

(combining errors on the different metrics).

→ The (full) tuning problem is the problem of

finding a consistent assignment A ∈



of all

parameters in P, such that the simulation error E(A)

is minimum.

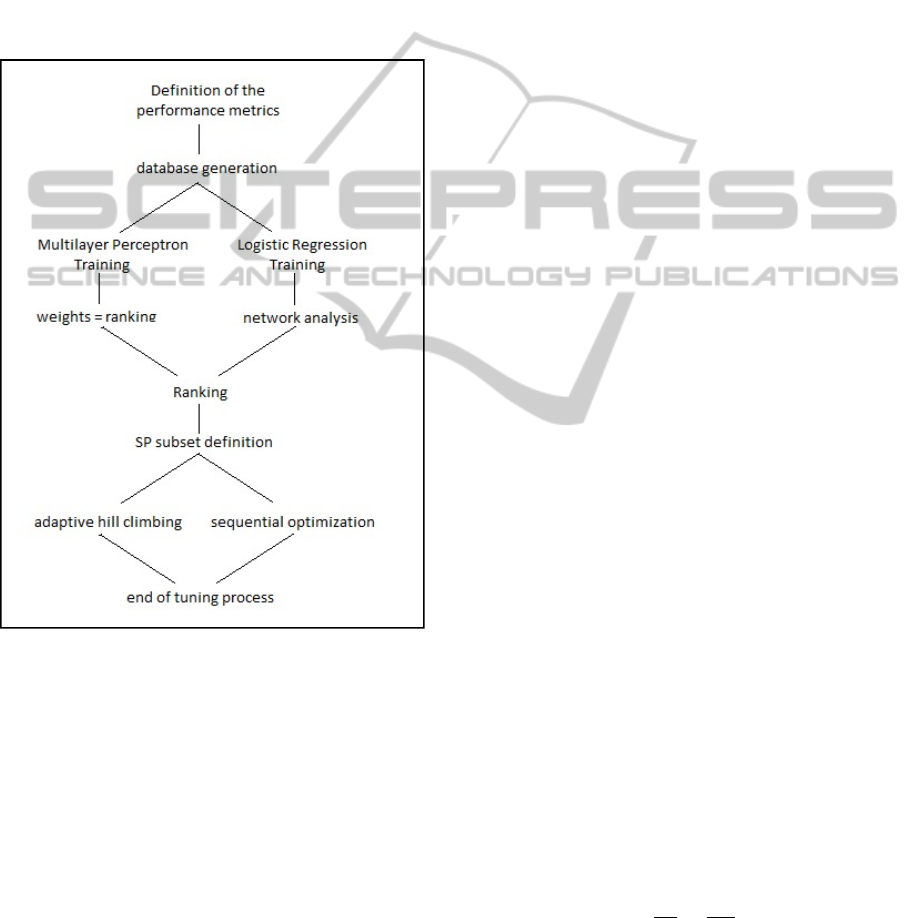
3 PROPOSED METHODOLOGY

As previously anticipated, the proposed

methodology decomposes the full tuning problem in

two sub-tasks. The two sub-problems can be solved

in sequence, exploiting the results of the first phase

in order to complete more efficiently the second:

→ The screening problem is the problem of ranking

the parameters according to their relevance and

defining a subset SP⊂P of most relevant parameters.

→ The restricted tuning problem requires to find the

ANovelApproachtoModelDesignandTuningthroughAutomaticParameterScreeningandOptimization-Theoryand

ApplicationtoaHelicopterFlightSimulatorCase-study

best consistent assignment A|

of parameters in SP,

exploiting the ranking of parameters in SP for

optimization, while assuming fixed the values of all

other parameters (those in P/SP).

If the Screening problem is effectively solved,

the restricted tuning problem should achieve the

same accuracy of the full tuning problem at a lower

cost and introducing less side-effects (issue that will

be explained in more details in section 6, devoted to

experimental results). The techniques for solving the

Screening problem are thus crucial for the entire

proposed approach to tuning.

Figure 1: The flow of the tuning process, highlighting the

available choices for screening and optimization.

4 SCREENING

Screening is a process with a long tradition in classical

statistics, and multiple methods are available to pursue

its goals. Most methods, though, make assumptions on

the distribution of data, require prior knowledge, or

have other disadvantages. One-factor-at-the-time

Designs (Zhang, 2007) require almost no interactions

among factors; Sequential Bifurcation (Bettonvil et al,

1997) requires the sign of the contributes of all factors

to be fixed and known; Pooled ANOVA (Last et al,

2008) requires to know the fraction of relevant factors;

Design Of Experiments (Fisher, 1935) requires to

evaluate an exponential number of configurations,

introducing scalability issues (fractional factorial

designs overcomes this problem through controlled

deterioration of the quality of results; however, the

fraction evaluated must decay with exponential speed

to keep constant the computational resources

required). SB and Pooled Anova assume further a low-

order polynomial relations between input and output

variables, and all previous approaches are usually

based on a two-level scheme (implicitly assuming

linearity - or at least monotonicity - for the functional

form of the output, and making the choice of the 2

levels a sensitive decision). When all assumptions are

satisfied and the required knowledge is available, these

methods can be very effective. However, in our

research, we were looking for a fully general approach

and we considered different Machine Learning

approaches in order to accomplish this goal. Feature

Selection, for example, is the classic area of Machine

Learning dealing with dimensionality reduction and

parameter identification; yet, this is NOT what we are

looking for because F.S. algorithms do not focus on

evaluating the impact of the different parameters on

the simulation’s output, trying just to eliminate

redundancy and relying mostly on learning the

statistical dependencies among factors (which, in our

context, are independent from each other). In order to

exploit Machine Learning for parameter screening we

have followed a completely different track: extracting

a feature ranking from a classifier trained on a

database of previously generated <parameter-set,

simulation error> tuples, and deriving the subset of

relevant parameters from such ranking.

4.1 Database Generation

In order to reduce as much as possible the bias

introduced during this critical phase, the database is

generated randomly using a normal distribution

centred in A

. The standard deviation depends on the

range R

of each parameter: it is a trade-off between

the necessity of exploration as much as possible of the

solution space and the need of remaining within the

ranges:













,∀1



(1)





~



0,







,













(2)



















(3)

Assuming the range symmetric with respect to the

initial assignment, with this policy about 1 out of 10

parameters will be sampled outside the range of

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

feasible values: outlier must be set on the boundary in

order to make all assignments consistent. After the

database set up, a simulation is executed for each

assignment A, and the error E(A) is stored as “class”

variable. The class variable is then discretized

(although this is compulsory only if Logistic

Regression is used in the proceedings). Discretization

can be done through a binomial partition (acceptable-

error, unacceptable-error), or a N bin partition with

equal frequency. Finally, how large must the whole

database be depends on which of the proposed ranking

algorithms is chosen in the following steps and on the

number of parameters (section 6).

4.2 Ranking: Logistic Regression

Logistic Regression (LR) is a classical classification

algorithm, very popular when dealing with discrete

class variables. We now give a brief presentation on

how to apply Logistic Regression and interpret the

results, discussing pros and cons of this choice in the

context of computer simulations. Implementations of

these ideas are available in most data analysis

packages (such as the Matlab Statistical Toolbox, or

its open source alternatives Weka and R). More

detailed information can be found in literature in

(Harrel, 2001) or in (Bishop, 2006).

4.2.1 The LR Model

Logistic Regression is the most famous and widely

used generalized linear model (Nelder et al, 1972)

with link-function given by the famous logit

function:









ln



1



(4)

Given a binomial class variable (Low_Error

High_Error) the LR model is described by the

following equations, where the coefficients grouped

in the vector β





are computed through either

maximum likelihood or maximum a posteriori

estimation:



_







∑





∗



(5)















(6)



_













(7)

The extension to a multinomial model is quite

straightforward; supposing K possible outcomes and

assuming the independence of irrelevant alternatives

a simple way to build the multinomial logit model is

to run independently K-1 binomial logistic

regressions, leaving out just the last outcome Y

ln























(8)

Then, by exponentiation of both terms, isolating the

different probabilities, and exploiting the fact that

probabilities of all outcomes must sum up to one:













∗















(9)









1

∑



















(10)

There are many extensions to this model, among

these we point out (Cessie et al, 1992) which uses

ridge estimators to improve accuracy high

dimensional parameter spaces. This slightly

modified Logistic Regression algorithm is the one

implemented in Weka, and the one used in our case-

study (section 6).

4.2.2 Parameter Ranking

If the LR approach is chosen it is easy to extract

measures of relevance for the parameters of the

model: the coefficients of the parameters already

provide such ranking. In general, this is not a

reliable measure if the different factors are highly

correlated, because multi-collinearity makes

computing the relevance of the single covariates

much more complex; therefore more sophisticated

metrics have been developed, which are capable of

producing valid results in such situations (among

these Dominance analysis, Likelihood ratio and

Wald statistics). However, multi-collinearity is not

an issue for us, because in computer simulations the

different parameters are independent and our

database is appropriately built in such manner; thus,

the ranking provided by the coefficients β

perfectly valid and there is no need to resort to more

complex procedures in order to obtain meaningful

results.

4.2.3 Pros and Cons of LR

The Logistic Regression model can achieve good

classification performance with a relatively low

amount of training data; most potential shortcomings

of this approach, such as the unreliability of the

coefficients as measure of relevance of the single

variables, are due to multi-collinearity, issue that, as

we have seen, is not present in our peculiar context.

The main problem with the use of Logistic

Regression for parameter ranking is that the

functional landscape that can be learned is limited;

therefore, very complex objective functions might

ANovelApproachtoModelDesignandTuningthroughAutomaticParameterScreeningandOptimization-Theoryand

ApplicationtoaHelicopterFlightSimulatorCase-study

require more powerful classifiers in order to be

properly modelled and offer a valuable insight on

the relevance of the different parameters. This is the

reason for introducing an alternative approach,

4.3 Ranking: Multilayer Perceptron

The Multilayer Perceptron (MP) is a feedforward

artificial neural network model, widely used in

classification problems, both for discrete and

continuous class variables. Therefore, we can train

the Multilayer Perceptron either on the original

database of simulations or on the version with

discrete class variable used for LR. Detailed

information on this topic can be found in (Haykin,

1998), and implementations of the ideas presented in

sections from 4.3.1 to 4.3.4 can be found in Weka

(Hall et al, 2009), in the RSNNS (Bergmeir, 2012),

and in the Matlab Neural Networks Toolbox. As

done for Logistic Regression, we now briefly

describe the model, discuss pros and cons of its

application to computer simulations, and finally

define the strategy that shall be used for parameter

ranking.

4.3.1 The MP Model

The perceptron was first proposed in (Rosenblatt,

1958) as the simplest model of the behaviour of

biological neurons. The perceptron maps N inputs

into a single binary or real-valued output variable y,

computed applying an activation function f to a

linear combination of the inputs and of a threshold

b, weighted by coefficients w

. Common activation

functions are the step function, the sigmoid functions

(such as the logit or the hyperbolic tangent), and the

rectifier/softplus functions.

Figure 2: this figure presents the pipelined structure of a

single perceptron, highlighting its main features.

A perceptron alone is quite limited and cannot be

used for non-linearly separable classification

problems. The combination of many perceptron in

an Artificial Neural Network, is instead extremely

powerful. The Multilayer Perceptron is an acyclic

layered directed graph of perceptrons with non-

linear activation function; the first layer (the input

layer) has |P| nodes, and the last layer (the output

layer) has as many nodes as the number of outcome

variables (for numeric classes) or as the number of

possible values of the outcome variable (for discrete

classes); other layers (called hidden layers) can have

any number of nodes.

Figure 3: the very common three layered MLP

4.3.2 Computation

Given L+1 node-layers (counting input, output and

hidden layers) and L edge-layers (the connection

layers between the node layers), the computation of

a multilayer perceptron can be described as a

sequence of non-linear transformations from x

to x





,



,











,



,







…





,



,







If N

is the number of nodes at layer j, x

∈





for

all j=0,…,L represents the input of layer j, and W

an N

×N

j-1

matrix for all j=1,…,L whose elements

h,k

represent the weight of the edge connecting

node h of layer j with node k of the previous layer j-

1. The output value is computed applying in order,

for all edge-layers for j=1 to j=L, the following

expression:















∑

























 (11)

This paradigm of computation is the reference that

must be kept in mind in order to understand how the

network is trained to learn the weights that best

approximate a target function.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

4.3.3 Topology

If a MP model is to be trained on our database, first

the structure of the network must be chosen; the

number of inputs and outputs is fixed thus the main

design choices are the number of hidden layers and

the number of nodes within those layers. The most

widely used network topology has just one hidden

layer. The reason is that convergence is usually

faster for shallow architectures and it has been

proved that the MP with a single hidden layer is a

universal approximator (Cybenko, 1989), thus any

function can be approximated with arbitrary

precision if the weights of edges are properly

chosen. In recent years, though, improvements in the

training of deep networks (Hinton et al, 2006) have

made other choices feasible, and some theoretical

results imply that the universal approximation

property of the three layered MP is achieved at the

cost of an exponential number of nodes with respect

to networks with more hidden layers. Therefore, our

approach to parameter ranking through the analysis

of a trained MP applies to networks with any

number of layers.

4.3.4 Training

Once the network’s topology has been devised, the

best values for the network’s weights must be found,

this is done with the iterative back-propagation

algorithm (Rumelhart, 1986) using the database of

pre-classified simulations. Let t be the iteration (also

called epoch) and η a parameter called learning rate;

if the database with continuous class variable is

used, training proceeds according to the following

rules, applied each iteration to all instances in the

dataset (discrete classes are dealt with likewise): 1)

compute the difference between the expected output

‘ex’ and the actual output ‘x

’; 2) propagate the error

across the network from output to input layer; 3)

update the weights and the thresholds values:







′















 (12)



















∑



















1 (13)

∆











,1 (14)

∆

















,1 (15)

This algorithm is the most widely used, although

convergence is quite slow it can be made more

efficient resorting to batching and multithreading.

It is proved equivalent to gradient descent applied to

an appropriate cost function and shares therefore the

known limits of such approach: convergence not

guaranteed and result possibly a local optimum.

4.3.5 Parameter Ranking

Extracting measures of relevance from a trained

Multilayer perceptron is a complex task and there is

no single way for doing so. Various approaches have

been proposed in the past, all with their specific pros

and cons; we present an alternative heuristic

approach that is easily applicable to MPs with any

number of hidden layers. Consider a network with

L+1 node-layers and L edge-layers, with a single

continuous outcome variable; given the previously

defined notations, and denoted as R the array of

length || containing the parameters’ ranks:





∶



 (16)









…





∏







 (17)

If the network was made of linear perceptrons

(having the identity function as activation function),

each element of R would represent exactly the

contribution to the outcome variable of the

associated parameter when it takes unitary value.

When applied to networks of non-linear perceptrons

the metric has just a heuristic value, yet it has

proved itself very effective in our experiments on

flight simulations, yielding to even better results

than LR (see section 6 for more details). The

extension of the method to N outcome variables or

to a discrete outcome having N possible values is

trivial (R is a matrix with obvious meaning).

4.3.6 Pros and Cons of MP

The multilayer perceptron’s main strength is its

representation power, due to its being a universal

function approximator. Furthermore, the MP can be

trained on the original simulation error values, and

does not require discretization as LR, although it is

still possible to train the network on the discretized

dataset. However this approach has one big

disadvantage when applied to our computer

simulated environment: it usually requires a larger

amount of data if compared to Logistic Regression.

This can be a problem because we are responsible of

generating all data to be analysed: computer

simulations can be computationally expensive and it

is not always possible to speed up computation just

adding resources. Indeed, this was the case in our

case-study for validation: being a training flight

simulator, was designed in such a way that

simulations could only be executed in real-time). If a

ANovelApproachtoModelDesignandTuningthroughAutomaticParameterScreeningandOptimization-Theoryand

ApplicationtoaHelicopterFlightSimulatorCase-study

single function evaluation (i.e. a single computation

of the simulation error for a given set of parameters)

takes very long we therefore advise to try Logistic

Regression first, and resort to the Multilayer

Perceptron if needed.

4.4 Computing SP

We use feature ranking algorithms to evaluate all

parameters of the model, assigning to each

parameter a weight, measuring its importance.

However in the subsequent phase we do not only

exploit the ranking among different parameters, but

execute the various optimization procedures

allowing them to modify only a subset SP of the

model’s parameters (restricted tuning problem).

Defining which parameters are the “most” relevant

and must be considered for tuning process is

somehow arbitrary, and requires to find a trade-off.

Considering for automatic tuning a high number of

parameter implies the exploration a large solution-

space and might introduce despicable side-effects

(which do not directly influence the performance

metrics but make the simulation less “natural” to a

human eye); Instead, considering a too small set of

parameters might make optimization impossible if

the optimum falls in the portion of spaces that

becomes unreachable once fixed the values of

parameters in P/SP. In order to use the ranks/weights

of parameters to take a good decision, we suggest to

sort the parameters according to their weights and

then draw the cumulative function: the parameter set

can be cut where the slope of the function slows

down and at least a given percentage of the total

weight is reached (e.g. at least 90-95%). An example

of this procedure is shown in section 6 both for the

Logistic Regression and for the Multilayer

Perceptron rankings (figures 5 and 6).

5 OPTIMIZATION

We have now reached the final step: the solution of

the (restricted) tuning problem through automatic

optimization procedures managing only the

parameters in the previously defined subset SP. We

present first a basic stochastic Hill Climbing

procedure (searching for optimal values of all

parameters in SP), then we describe two successive

refinements of the algorithm which have proved

themselves effective in a real tuning case-study. The

first refinement introduces adaptive variance, and

corresponds to a 1+1 evolutionary strategy. The

third algorithms, which is by large the most

efficient, is also capable of exploiting the ranking of

parameters in SP in order to tune an increasing

number of parameters at each iteration.

5.1 Local Optimization, Why?

All proposed approaches are local (and stochastic)

optimization strategies; this is no accident, and it is

appropriate for the following reasons:

1) Do we have any choice? Often we do not; global

optimization is more computationally demanding,

therefore, in M&S, it might simply be impossible.

The time for each function evaluation can be very

long; executing different simulations in parallel can

be unfeasible if all computational power available is

required for executing a single computer simulation;

finally, sometimes, e.g. in real-time simulations, no

speed-up of the single simulation is possible even if

more computational power is available.

2) If modeling is carried out in a sensible way, the

initial assignment A

is not a completely random

guess but a reasonable solution derived by physical

considerations, and is thus (hopefully) near to the

true optimal solution making local optimization less

at risk of remaining stuck in non-global optima.

3) When you recreate in a simulator some known

observed reality (which is typical of flight or other

life-critical simulations) you can recognize if you are

stuck in a local optima because you know which the

optimal value is (although you do not know where it

is located within the very large solution-space).

4) Concerning the choice of stochastic optimization

instead of deterministic procedures, there are two

elements to be considered: first, stochastic

procedures are less prone to getting stuck in local

optima, second, most stochastic algorithms needs to

know very little about the function (no need to

compute derivatives or similar). Having devoted so

much time to develop screening techniques capable

of treating the model just as a black box, we do not

want to start analyzing the equations now that

efficient black-box optimization techniques are

readily available.

5.2 Basic Stochastic Hill Climbing

The basic Hill climbing procedure we now present

in pseudo-code shall be thought of as a template to

be refined in the following. Therefore, it’s quite

impressing that, as we will see, even in this basic

form the procedure accomplishes a reasonably low

error, showing the power of Screening in making

tuning possible. The algorithms works exploring the

neighbourhood of the best solution up to a given

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

moment until a better one is found, then it moves to

the new location and continues:

01 best = A

02 A = A

03 min-err = execute(A

)

04 R = loadRange()

05 σ = computeStdDev(R)

07 while (error>threshold)

09 for (j=1 to |P|)

10 if(p

in SP)

11 A

= best

,+ σ

× N(0,1)

12 A

= setWithinRange(A

)

13 end-if

14 end-for

16 if(execute(A) < min-err)

17 min-err = execute(A)

18 best = A

19 end-if

21 end-while

best contains the best assignment found up to the

current iteration, min-err storing the corresponding

error. Exploration of the neighbourhood of best is

random: new assignments of each parameter 



SP are generated each iteration sampling from a

normal distribution centred in



. The function

computeStdDev(R) defines once for all the

value of the standard deviation used for each

parameter 



, which is proportional to the range 



;

the same precautions seen for the database

generation, to guarantee the consistency of all

assignments, are taken into account also in this

circumstance when defining the relation between

range and standard deviation (section 4.1). Function

execute(A) runs the simulation with

parameters’ values specified by A and computes the

simulation error E(A). Note that, as required, all

parameters in P/SP maintain their initial default, and

that as the number of iterations grows to infinity the

best parameter assignment eventually converges to

the global optimum with probability 1.

5.3 Adaptive Variance

In the hill climbing procedure of the previous

section, random mutations occur every iteration in

order to explore the neighborhood of the best

solution found; the parameter controlling such

mutations is the standard deviation of the normal

distribution used for sampling. As it is, this standard

deviation could be computed statically, depending

only on the range of the different parameters

considered; however, the optimal value of σ is not

the same throughout the execution of the

optimization procedure: indeed, it is intuitively clear

that the best value for σ should be greater when the

error is high and we are exploring the solution space

with a high success rate, while it should become

increasingly smaller when we are very near to the

optimum and very small corrections are needed in

order to improve our solution. This calls for a crucial

important modification of the procedure of section

5.1, allowing σ to adapt on-line during optimization.

There are two main approaches to achieve the

required capability: make the standard deviation

decrease along with the simulation error, or make it

increase or decrease dynamically depending on the

success rate (the fraction of mutations that are

successful, i.e. that improve the best solution). The

former approach still requires to define at design-

time the exact relation between error and standard

deviation, instead the latter is usually more powerful

because provides greater flexibility. A common

policy when the second approach is chosen is to

decrease σ when the success rate is below 0.2 and

increase it otherwise (this strategy is known as the

1/5 success rule; it can be proved optimal for several

functional landscapes and it is widely recognized to

give good results in practice in a wide range of

circumstances). Among the many implementations

of such rule, the simplest one (Kern et al, 2004)

accumulates the knowledge about success and

failure directly in the value of σ, substituting the if-

else clause of lines 16-19 with the following code:

18 if(execute(A) < min-err)

19 min-err = execute(A)

20 best = A

21 σ

= σ

 α

22 else

23 σ

= σ

 

/

24 end-if

Reasonable values of parameter α are between

/

and 2. This implementation requires to set only

1 parameter instead of the 3 (change rate, averaging

time to measure success rate, update frequency)

needed with classical implementations following

more narrowly the previous definition.

5.4 Sequential Masking

Although the hill climbing procedure, modified in

order to adapt online the parameter controlling the

entity of mutations, can already be used in practice

to solve the restricted tuning problem, performance

ANovelApproachtoModelDesignandTuningthroughAutomaticParameterScreeningandOptimization-Theoryand

ApplicationtoaHelicopterFlightSimulatorCase-study

can be further improved by the third algorithm,

Sequential masking, exploiting the ranking of

parameters in SP. This third approach to automatic

tuning works as follows:

1) A sequence of subsets, and thus of restricted

tuning problems, SP

 SP

 …  SP is generated

incrementally from the ranking of parameters in SP.

2) the hill climbing procedure with adaptive variance

is executed for a fixed number of iterations for each

sub-problem, starting from the smallest (simplest)

problem and using the result of each problem as

initial guess of the subsequent problem.

Figure 4: Sequential masking with four sub-problems.

The idea is that challenges of increasing complexity

are faced starting from increasingly good initial

assignments. The increasing complexity is due to the

fact that an increasing portion of the solution space

is reachable. In conclusion, as shown in figure 4,

starting from assignment A

we compute a sequence

of solutions converging to the final solution



the restricted tuning problem with parameters SP.





→



→





…



→



→



... 





→→



The execution of the algorithm is controlled by two

user defined parameters: the number of restricted

tuning problems, which we can call the granularity

of the algorithm, and the maximum number of

iterations for each phase of the procedure. The max

number of iteration can be different for each of the

problems (higher for those considering more

parameters).

6 CASE-STUDY

Our case-study for validation is the tuning of an

industrial level flight-simulator of our_company in

order to accurately simulate the take-off of a

helicopter with one engine inoperative (breaking

down during the execution of the procedure). This

case-study is a classic example of simulator with

severe accuracy requirements, as flight simulators

must be certificated by flight authorities of different

countries, verifying that the execution of a certain

set of flight procedures is adherent to the observed

behavior of the aircraft. There are 2 main procedures

for take-off: Clear area TO and Vertical TO. We

here analyse only the clear area procedure, showing

the results of the screening and optimization

algorithms (however the techniques have been

applied to both). In the following P is a set of 47

parameters, each associated to a range symmetric

with respect to the initial assignment A

. The

relevant performance metrics in S are three: CTO

distance (distance from starting point to take-off-

decision-point), GP1 (average climb in 100 feet of

horizontal motion during the 1

phase), and GP2

(average climb in 100 feet of horizontal motion

during the 2

phase). Expected values Ref of such

metrics are specified on the helicopter’s official

manual. The global error E(A) is the sum of the

squared relative errors with respect to the three

performance metrics.

6.1 Screening

A database of 1200 simulations has been generated

with the rules established in section 4.1,

appropriately discretizing the values of the global

simulation error. Then both the logistic regression

and the neural network based approach to parameter

ranking are applied, using the implementations

available in the open source machine-learning

package Weka (And choosing the classic three

layered topology for the MP). Results were largely

consistent: if the set of 10-20 most relevant

parameters for LR is compared to the corresponding

set within the MP ranking, about, about 85% of the

parameters figure in both sets. The main difference

is a single small group of parameters, having similar

physical meaning, in which all parameters are

ranked very low by LR while MP seems to be able

to discriminate more effectively between relevant

and not relevant parameters. If the cumulative

functions of the two approaches are compared

(Figure 7 and 8), this difference among the results is

reflected in a steeper curve for the LR-based

ranking, which concentrates most of the weight on

fewer parameters (trend confirmed by other flight

procedures). The resulting set SP of the most

relevant parameters is thus smaller for LR than it is

for MP.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

Figure 5: Cumulative weight-function, LR ranking.

Figure 6: Cumulative weight-function, MP ranking.

6.2 Evaluating Screening

In the next section we will go into details in the

comparison of the performances of adaptive hill

climbing and sequential masking, but, before, we use

the basic optimization procedure in order to provide

the reader with an intuitive proof of the impact of

the previous screening techniques; In figure 7 four

executions of the basic HC procedure are compared;

the horizontal axis identifies the number of

simulations executed, while the vertical axis

measures the minimum error up to the given

iteration. In all four cases the algorithm has gone

through 100 iteration: the solid lines represent the

execution of the algorithm considering the results of

screening (through LR and MP respectively); the

dotted line, that converges to a relatively high

simulation error and then stops improving, represent

the execution of the procedure with SP=P (i.e. the

procedure if applied directly to the full tuning

problem with no screening); the dashed line, that

shows no improvements at all, represent the

execution using only parameters in P/SP

Figure 7: Execution of the basic hill climbing optimization

with different screening policies.

In conclusion, figure 7 shows that LR and MP based

rankings truly identify the relevant parameters: if

optimization is allowed to modify only low-ranked

parameters no improvement is achieved; if instead

only high-ranked parameters can be modified, the

restricted tuning problem is solved faster than the

full problem and a lower error is reached: the

algorithm with P=SP keeps an acceptable rate only

for the first 10 iterations, then it almost stops and

maintains a constant almost imperceptible

improvement rate.

6.3 Optimization

We now show the results of applying the two

proposed optimization algorithms to our case-study.

Both converge to an error many orders of magnitude

lower than the one achieved by the basic hill

climbing procedure, and they also do so significantly

faster. In order to make the results understandable

the vertical axis is now the (base 10) logarithm of

the error.

The comparison of the two algorithms in figure 8

shows that they both are able to keep the error

decreasing at a good, almost constant, average rate.

Sequential masking achieves particularly impressive

performances, however both algorithms proved

themselves effective, significantly improving the

basic Hill climbing procedure, in figure 7, which

instead, whether screening is used or not, hits sooner

or later a wall, becoming unable of further

improvements, or capable of doing so only at an

unacceptable slow rate.

ANovelApproachtoModelDesignandTuningthroughAutomaticParameterScreeningandOptimization-Theoryand

ApplicationtoaHelicopterFlightSimulatorCase-study

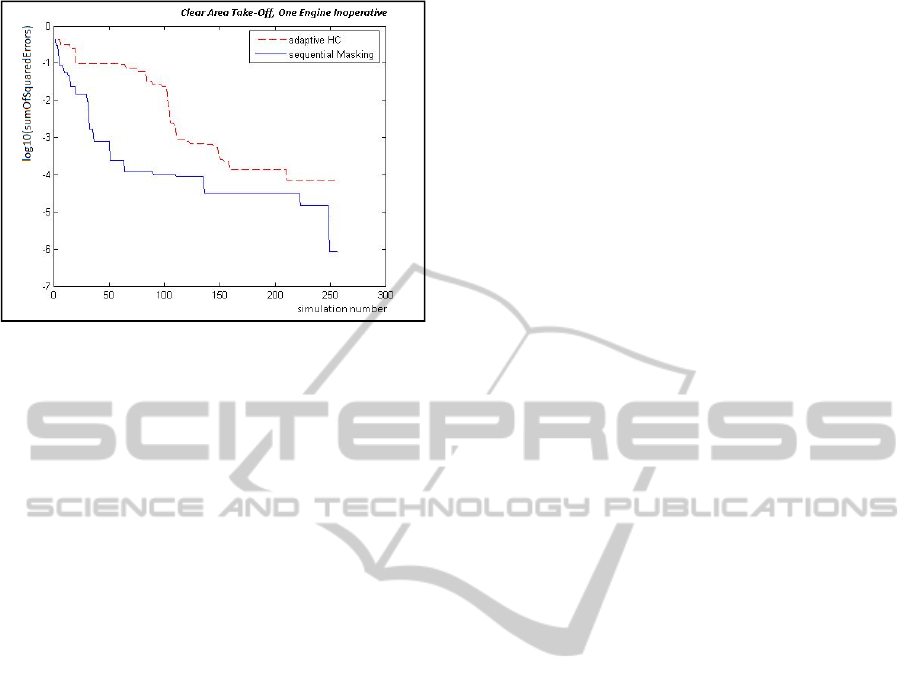
Figure 8: Comparison of sequential masking and adaptive

hill climbing optimization procedures.

6.4 Benchmarks and Conclusions

In conclusion our approach has been proved

effective in tuning a complex flight simulation

model finding the optimal values of 50 parameters

of the model. The entire process requires less than 2

days of machine-time on a single desktop computer

(with just a few hours actually dedicated to finding

those values, and most of the time devoted to

generating the database for parameter ranking). The

main benchmark against which this result must be

compared is manual tuning, which is still the state-

of-the-art in industrial applications. Our_company’s

experienced engineers would require from 10 to 20

days to accomplish the same result. Concerning

previous attempts to automatic tuning, there is little

work done for the tuning of industrial level

computer simulators, and to the best of our

knowledge, none in the area of flight simulations.

The best related work is in medical context (Vidal et

al, 2013): this paper presents an evolutionary

strategy for tuning, but the approach is used only for

lower dimensional problem with just 15 parameters.

Thanks to an integrated approach combining

screening and optimization (tightly coupled

especially in the sequential masking algorithm), our

methodology allows to significantly expand the

range of application of automatic techniques for

parameter tuning. When comparing to other attempt

of automatic tuning it is important to notice that

combining screening and optimization is not only

crucial in order to achieve fast convergence to a

really low simulation error, but it is also crucial in

order to avoid an issue we have anticipated in

previous sections of the paper: the introduction of

peculiar side effects that can make simulations

unrealistic to a human eye (such as odd small

oscillations and vibrations difficult to control). The

reason for such side-effects is that parameters that

have a low impact on the performance metrics and

thus on the global simulation error are free to deviate

randomly from their default values, because there is

no selective pressure capable of limiting their erratic

wandering. Our methodology solves the issue by

restricting tuning to the set of parameters with direct

impact on the performance metrics, so, during

optimization, all non-fixed parameters are directed

towards their optimal values instead of being free to

roam around. The proposed methodology is

therefore the first real alternative to manual tuning,

allowing an impressive speed up of the tuning

process while preserving high quality results.

Having applied the machine learning algorithms

without exploiting any prior domain knowledge we

also believe that is fully general, as future research it

would be therefore interesting to apply the proposed

technique to other application domains.

REFERENCES

Fisher, R.A., 1935, The design of experiments. Oxford,

England: Oliver & Boyd. xi 251 pp.

Rosenblatt F., 1958, The perceptron: a probabilistic model

for information storage and organization in the brain.

Psychological Review 65: 386—408.

Nelder J., Wedderburn R., 1972 Generalized Linear

Models, Journal of the Royal Statistical Society. Series

A (General) 135 (3): 370-384.

Rumelhart D.E., Hinton G.E., Williams R.J., 1986,

Learning representations by back-propagating errors.

Nature 323 (6088): 533–536. doi:10.1038/323533a0.

Cybenko G., 1989 Approximations by superpositions of

sigmoidal functions, Mathematics of Control, Signals,

and Systems, 2 (4), 303-314.

Le Cessie S., Van Houwelingen J.C., 1992, Ridge

estimators in Logistic Regression. Applied Statistics.

Bettonvil B., Kleijnen J.P.C., 1997, Searching for

important factors in simulation models with many

factors: Sequential bifurcation, European Journal of

Operational Research, Volume 96, Issue 1, Pages 180–

194.

Haykin S., 1998, Neural Networks: A Comprehensive

Foundation (2 ed.). Prentice Hall. ISBN 0-13-273350-

Harrel F., 2001 Regression Modeling Strategies, Springer-

Ve rl ag .

Kern S., Muller S.D., Hansen N., Büche D., Ocenasek J.,

Koumoutsakos P., 2004, learning probability

distributions in continuous evolutionary strategies – a

comparative review, Journal of Natural Computing

Volume 3 Issue 1, Pages 77 - 112.

Bishop C., 2006 Pattern Recognition and Machine

Learning, Springer Science+Business Media, LLC, pp

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

217-218.

Hinton G.E., Osindero S., Yee-Whye The, 2006, A fast

learning algorithm for deep belief nets, Neural

Computation, 18(7):1527–1554.

Morgan P.J., Cleave-Hogg D, Desousa S., Lam-

McCulloch J., 2006, Applying theory to practice in

undergraduate education using high fidelity

simulation, Med Teach, vol. 28, no. 1, pp. e10–e15.

Zhang A., 2007 One-factor-at-a-time Screening Designs

for Computer Experiments, SAE Technical Paper

2007-01-1660, doi:10.4271/2007-01-1660.

Last M., Luta G., Orso A., Porter A., Young S., 2008,

Pooled ANOVA, Computational Statistics & Data

Analysis, Volume 52, Issue 12, Pages 5215-5228.

Hall M., Eibe F., Holmes G., Pfahringer B., Reutemann P.,

Witten I., 2009 The WEKA Data Mining Software: An

Update; SIGKDDExplorations, Volume11, Issue1.

Lewis J. H., and Jiang S. B., 2009, A theoretical model for

respiratory motion artifacts in free-breathing CT

scans, Phys Med Biol, vol. 54, no. 3, pp. 745–755.

Bergmeir C., Benìtez J.M., 2012, Neural Networks in R

Using the Stuttgart Neural Network Simulator:

RSNNS, Journal of Statistical Software, Volume 46,

Issue 7.

Vidal F.P., Villard P., Lutton E., 2013, Automatic tuning of

respiratory model for patient-based simulation,

MIBISOC’13 - International Conference on Medical

Imaging using Bio-inspired and Soft Computing.

ANovelApproachtoModelDesignandTuningthroughAutomaticParameterScreeningandOptimization-Theoryand

ApplicationtoaHelicopterFlightSimulatorCase-study