
Linear Switching System Identification Applied to Blast Furnace Data
Amir H. Shirdel
1
, Kaj-Mikael Bjork
2,3
, Markus Holopainen
3
, Christer Carlsson
3
and Hannu T. Toivonen
4
1
Department of Chemical Engineering,
˚
Abo Akademi University, Biskopsgatan 8, FIN-20500 Turku, Finland
2
Arcada University of Applied Sciences, FIN-00550 Helsinki, Finland
3
Institute of Advanced Management Systems Research,
˚
Abo Akademi University, FIN-20520 Turku, Finland
4
Department of Information Technologies,
˚
Abo Akademi University, Joukahaisenkatu 3-5 A, FIN-20520 Turku, Finland
Keywords:
System Identification, Linear Switching System, Blast Furnace, ANFIS, Nonlinear System, Sparse Optimiza-
tion.
Abstract:
Switching systems are dynamical systems which can switch between a number of modes characterized by dif-
ferent dynamical behaviors. Several approaches have recently been presented for experimental identification
of switching system, whereas studies on real-world applications have been scarce. This paper is focused on
applying switching system identification to a blast furnace process. Specifically, the possibility of replacing
nonlinear complex system models with a number of simple linear models is investigated. Identification of
switching systems consists of identifying both the individual dynamical behavior of model which describes
the system in the various modes, as well as the time instants when the mode changes have occurred. In this
contribution a switching system identification method based on sparse optimization is used to construct linear
switching dynamic models to describe the nonlinear system. The results obtained for blast furnace data are
compared with a nonlinear model using Artificial Neural Fuzzy Inference System (ANFIS).
1 INTRODUCTION
An important goal of industries is to produce their
products with high quality and low costs. To reach
this goal, accurate models of industrial processes are
needed for monitoring and to maintain good quality
control. Data mining and modeling techniques can be
used to build predictive forecasting models, to find
alternative actions to be taken, or simply to gain a
deeper understanding of the underlying influencing
elements.
Having more precise mathematical modes of in-
dustrial processes allow engineers to have better con-
trol of the processes to improve production and win
the competition in markets. One of the industries fac-
ing fierce competition is the steel-making industry.
According to a review by the Association of Finnish
Steel and Metal Producers (Association of Finnish
Steel and Metal Producers, 2012), the ongoing polit-
ical and economic crisis in Europe has radically in-
creased price competition. In this paper, the blast fur-
nace for the steel making process is modeled. One
of the reasons which makes modeling of blast furnace
particularly complex is the fact that it is impossible to
directly observe the process inside the furnace. Op-
timization of this part is, however, essential for im-
provement in the overall process and quality of the
final product. Because of the very high temperature
environment, embedding sensors for gathering data
is impossible. Therefore, it is treated as a black-box
system, relying on experienced engineers for process
monitoring and control.
System identification can give mathematical mod-
els based on collected blast furnace data. The final
goal of the study reported in this paper is to opti-
mize the blast furnace process and, more specifically
to consider the quality indicator which describes the
gas utilization rate in the furnace, using external sen-
sor data and other process information for its estima-
tion.
Steel plants use the processed iron which pro-
duced in blast furnaces by reducing oxygen from the
iron. The process is run continuously, with iron-
bearing materials and coke being charged from the
top of the furnace (Geerdes et al. 2009). During the
reduction process, two kind of reaction, direct and in-
direct, take place in the furnace. The direct one takes
place in the lower part of the furnace and depends on
643
H. Shirdel A., Björk K., Holopainen M., Carlsson C. and T. Toivonen H..
Linear Switching System Identification Applied to Blast Furnace Data.
DOI: 10.5220/0005022806430648
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 643-648
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

consumption of coke. The indirect one occurs in top
part, where the gas removes oxygen from the ore. The
efficiency of the indirect reaction is often expressed
as the gas utilization rate, which is considered as an
important performance indicator of the furnace. The
process is highly complex from a chemical point of
view as it involves numerous factors, nonlinear rela-
tions and a certain level of randomness.
There are not many researches on modeling blast
furnace dynamics due its highly complex behavior.
Mathematical models for describing the process have,
for instance, been proposed in (Nath, 2002) and (Dan-
loy et al. 2001). Linear data-driven models have
been studied in (Saxn and stermark, 1996), (Korpi
et al. 2003) and (Bhattacharya, 2005). Nonlinear
soft computing techniques have been applied to blast
furnace process modeling in, among other: (Hao,
2004), (Helle and Saxn, 2005) and (Pettersson et al.
2007). A novel approach is presented in (Agarwal
et al. 2010) where they train a neural network us-
ing multi-objective genetic algorithms based on car-
bon dioxide content of top gas and silicon content in
the hot metal output. In (Bjork et al. 2013), AN-
FIS allows for customization regarding membership
functions, inputs and rules, an appropriate degree of
complexity is expected to be found.
Nonlinear systems with several operating regimes
can be modeled as switching systems, which switch
between a number of operational modes associated
with the various operating conditions. In this case
the mode is usually known or is a function of known
variables. In more general cases, the mode switches
may be random, or they may depend on variables
which are unknown. In this paper, a switching system
model is identified to estimate the gas utilization rate
of a blast furnace from available sensor data. Follow-
ing (Shirdel et al. 2014), the identification problem
is posed as a support vector regression (SVR) prob-
lem, and the models associated with the various op-
erational modes are found by solving a sequence of
sparse optimization problems techniques. The pre-
diction performance of the identified switching sys-
tem models of the blast furnace are compared with
results obtained with models constructed using Artifi-
cial Neural Fuzzy Inference Systems (ANFIS).
2 SWITCHING SYSTEM
IDENTIFICATION
Hybrid systems are a kind of switching systems char-
acterized by a logical dynamical component, which
determines the mode switches, and a continuous dy-
namical component, which determines the system be-
havior in the various operational modes. Hybrid sys-
tems can be categorized into five classes (Heemels
et al. 2001). Piece-wise affine (PWA) systems are
a class of hybrid systems whose state input domain
is partitioned into a finite number of non-overlapping
convex polyhedral regions, with linear or affine sub-
systems in each region (Sontag, 1981).Piece-wise-
linear functions are universal approximation of mul-
tivariate functions (Lin and Unbehauen, 1992). Due
to their approximate features, piece-wise affine hybrid
systems are useful for nonlinear system identification.
One approach to black-box identification of non-
linear dynamical systems using experimental process
input-output data is to identify a linear switching sys-
tem which describes the data. A special problem
in switching system identification is the fact that the
times of the mode switches may not be known. In
these cases the switching times between the vari-
ous modes should be identified simultaneously with
the individual models, which make the identification
of switching systems significantly more demanding
than standard system identification. Therefore, in
many studies of switching system identification var-
ious simplifying assumptions have been made.
In order to cope with the challenging problem of
simultaneous identification of system modes and pa-
rameters, a number of techniques have been devel-
oped (Saad et al. 2007), (Aliev et al. 2004). Segmen-
tation of time-varying systems and signals has been
discussed in (Ohlsson et al. 2010). Sparse optimiza-
tion which is based on finding each model sequen-
tially is proposed in (Bako, 2011). In (Shirdel et al.
2014), a method based on support vector regression
and sparse optimization techniques was proposed for
identification of switching systems. Recently in (Le
et al. 2013), an approach to identify hybrid systems
with unknown nonlinearities in the sub-models using
combination of sparse optimization and support vec-
tor machines was presented.
In this paper we consider a switching system de-
scribed by the time-varying linear model
y(k) = ϕ(k)
T
θ(k) + e(k) (1)
where y(k) is the output, e(k) is a disturbance, and
ϕ(k) is a state vector. The state vector consists of the
variables used to predict the output y(k). For exam-
ple, for autoregressive with exogenous terms (ARX)
mode, the state vector takes the form
ϕ(k)
T
= [y(k − 1), ..., y(k − r), u(k), ..., u(k − r)]
where u(k) is the exogenous input to the system.
It is assumed that the system dynamics switch be-
tween a number of modes, so that
θ(k) ∈
{
θ
1
, θ
2
, . . . , θ
M
}
(2)
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
644

where θ
i
is the vector of system parameters in the ith
mode, and M is the number of modes.
The switching system identification problem con-
sists of finding estimates of the parameter vec-
tors θ
i
from empirical process data {y(k), ϕ(k), k =
1, 2, . . . , N}. Notably, it is not assumed that the time
instants when the various modes have been active
are known. This implies that the identification is
essentially identical to a combinatorial optimization
problem. Although such problems are usually in-
tractable, the switching system identification problem
can often be solved with a high degree of accuracy
or even exactly via a sparse optimization formulation
and l
1
-relaxation (Bako, 2011), (Shirdel et al. 2014),
(Lughofer and Kindermann, 2010).
The approach used in this paper is based on the
fact that if mode i has been active at N
i
time instants,
then, assuming that e(k) ≤ ε, the inequality
y(k) − ϕ(k)
T
θ
i
≤ ε (3)
holds at these N
i
time instants. It follows that the
most commonly occurring mode and the associated
parameters θ
i
can be determined by finding the pa-
rameter vector
ˆ
θ
i
such that the number N
i
of time
instants for which the inequality (3) holds is max-
imized. This is a combinatorial optimization prob-
lem, which can be addressed using sparse optimiza-
tion techniques (Bako, 2011).
In (Shirdel et al. 2014), an approach was proposed
using the observation that the constraints (3) are iden-
tical with the ε-insensitive cost used in support vector
regression. The system parameters associated with a
given mode can then be found by solving the opti-
mization problem (Shirdel et al. 2014)
Minimize
ˆ
θ,ξ
+
,ξ
−
k
ˆ
θk
p
p
+
N
∑
k=1
C
k
(ξ
+
k
+ ξ
−
k
) (4)
subject to the ε-insensitive constraints
y(k) − ϕ(k)
T
ˆ
θ ≤ ε + ξ
+
k
−y(k) +ϕ(k)
T
ˆ
θ ≤ ε + ξ
−
k
(5)
ξ
+
k
, ξ
−
k
≥ 0
Here p = 1 or 2, corresponding to a linear or, re-
spectively, quadratic programming problem and C
k
is
trade off weight.
The problem of finding the mode which has been
active at the maximum number of time instants corre-
sponds to finding the parameters θ such that the max-
imum number of variables ξ
+
k
, ξ
−
k
are zero. This is
a sparse optimization problem, for which the second
term in (4) provides an l
1
-relaxation, and by iterative
reweighting applied to the weights C
k
the problem can
in many cases be solved with a high degree of accu-
racy (Bako, 2011), (Shirdel et al. 2014). In this way
the various system modes and the associated param-
eter vectors can be computed one by one. We have
the following algorithm (Bako, 2011), (Shirdel et al.
2014).
Algorithm. Identification of switching system.
Step 1. Initialization: set i = 1.
Step 2. Solve the SVR problem defined by (4), (5)
using iterative reweighting of C
k
to find a sparse so-
lution in the variables ξ
+
k
, ξ
−
k
. The solution gives a
parameter estimate
ˆ
θ
i
for mode i. Remove the data
pairs (ϕ(k), y(k)) at which mode i has been active.
Step 3. Check the reduced data set for convergence:
if all data pairs have been accounted for, stop. Other-
wise, set i := i +1 and continue from step 2 using the
reduced data set.
3 IDENTIFICATION OF BLAST
FURNACE
In this section the switching system identification
methods described in section 2 is applied to blast fur-
nace data. The goal of the model is to predict the gas
utilization as described by the carbon dioxide con-
tent of top gas as a function of measured variables
received from sensor data.
Table 1: Inputs.
Input No. Description
1 Pellets+sinter by total
2 Coke by total
3 Iron by total
4 Pellets+sinter by volume
5 GAS temp PCA
1
6 GAS temp PCA
2
7 GAS temp PCA
3
8 Burden height
9 Blast volume
10 Pressure by volume
11 Oxygen in blast
12 Hydrogen in top gas
13 Oil by blast volume
3.1 The Blast Furnace Data
In a complex plant like blast furnace, much redundant
affection can influence our major part of identification
which is measured data. For this study, three months
of detailed operational blast furnace data was used
for training. The final set of preprocessed data con-
sisted of data collected from 2208 hours of furnace
LinearSwitchingSystemIdentificationAppliedtoBlastFurnaceData
645

Table 2: Estimated parameters b
(i)
1,l
for input u
1
for various time lags l when using M = 4 modes.
Time lag 1 2 3 4 5 6 7 8
Input No. 1
Subsystem 1 0.000 0.000 0.979 1.075 0.000 -0.815 0.000 0.000
Subsystem 2 0.000 0.000 -0.623 0.000 0.564 0.000 0.816 -0.159
Subsystem 3 0.000 -1.854 0.000 0.000 0.000 0.000 0.000 0.000
Subsystem 4 0.000 0.000 -0.193 0.000 0.000 0.000 -0.396 0.147
operation. After consulting experts, it turned out that
many points of data are not sufficiently reliable and
should be removed. The final number of data points
was therefore 1800.
One of the most important performance indica-
tors of blast furnace is measuring the ratio of carbon
monoxide converted to carbon dioxide. This indicator
was chosen as the target series for the conducted anal-
ysis and modeling. It evaluates performance of the
data understanding indirect reduction reaction taking
place in the upper part of the furnace and controlling
this process by injecting oxygen, can allow furnace to
burn less coke and cost saving.
3.2 The Inputs
Input data entails charging data which are precise
amounts of burden materials and coke charged into
the furnace per time unit, continuous process data
from external sensors and data from analysis of hot
metal and some other variables. Top-gas exiting the
furnace can be considered as an input series. A
discussion of the role of hydrogen competing with
carbon monoxide in reducing oxygen is given in
(Geerdes et al. 2009). The inputs which are used in
the modeling of the blast furnace are shown in Table
1.
The output y(k) (carbon dioxide content of top
gas) was modeled as function of the input variables
u
j
(k) in Table 1. The model structure was
y(k) =
13
∑
j=1
b
j,1
(k)u
j
(k − 1) + ··· + b
j,13
(k)u
j
(k − 13)
where the parameters b
j,l
(k) ∈ {b
(1)
j,l
b
(2)
j,l
, . . . , b
(M)
j,l
}
belong to the set (2) associated with the system
modes.
Each input variable affect the process with a time
lag. Some of the variables affect the process rapidly,
such top gas-related variables, and some others have
a slower effect, like charging data. In the identifica-
tion method used here, the time lags of the various
process inputs were obtained as part of the identifi-
cation process, as the first term of the cost function
(4) forces parameter which do not affect the output to
zero, cf. (Shirdel et al. 2014), where the approach was
used to identify systems of unknown dimensions. Es-
timated time lags and parameters for modeling with
M = 4 subsystems for first input are shown in Table
2. It is seen that the time lag of the input is different
for different subsystems.
4 RESULTS
In this section, modeling by using the linear switch-
ing system identification approach is conducted. The
required data was taken from input series based on the
consultation of expert (Table 1). The maximum time
lag that we allowed our approach to have in this blast
furnace system is 8.
The result of each identified linear switching sys-
tem is given based on root mean square (RMS) error
between the estimated output and real output in Table
3. For comparison, the error of ANFIS model output
(Bjork et al. 2013) is shown in Table 4. It is seen that
the switching system model is slightly more accurate
than ANFIS model. A major difference is that in con-
trast to the approach considered here, in the ANFIS
modeling studied in (Bjork et al. 2013) it was not
possible to find the optimal time lags, or to include
all 13 input variables in the model due to a too heavy
computational burden. The output of a switching sys-
tem model is illustrated in Fig. 2, the mode switches
of a system with four modes are shown in Fig. 1.
Table 3: Root mean square error of estimated output of us-
ing identified switching system models.
Subsystem of
modes
RMSE
1 0.0840
4 0.0571
6 0.0537
8 0.0516
5 CONCLUSION AND
DISCUSSION
One application of switching system models is to rep-
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
646
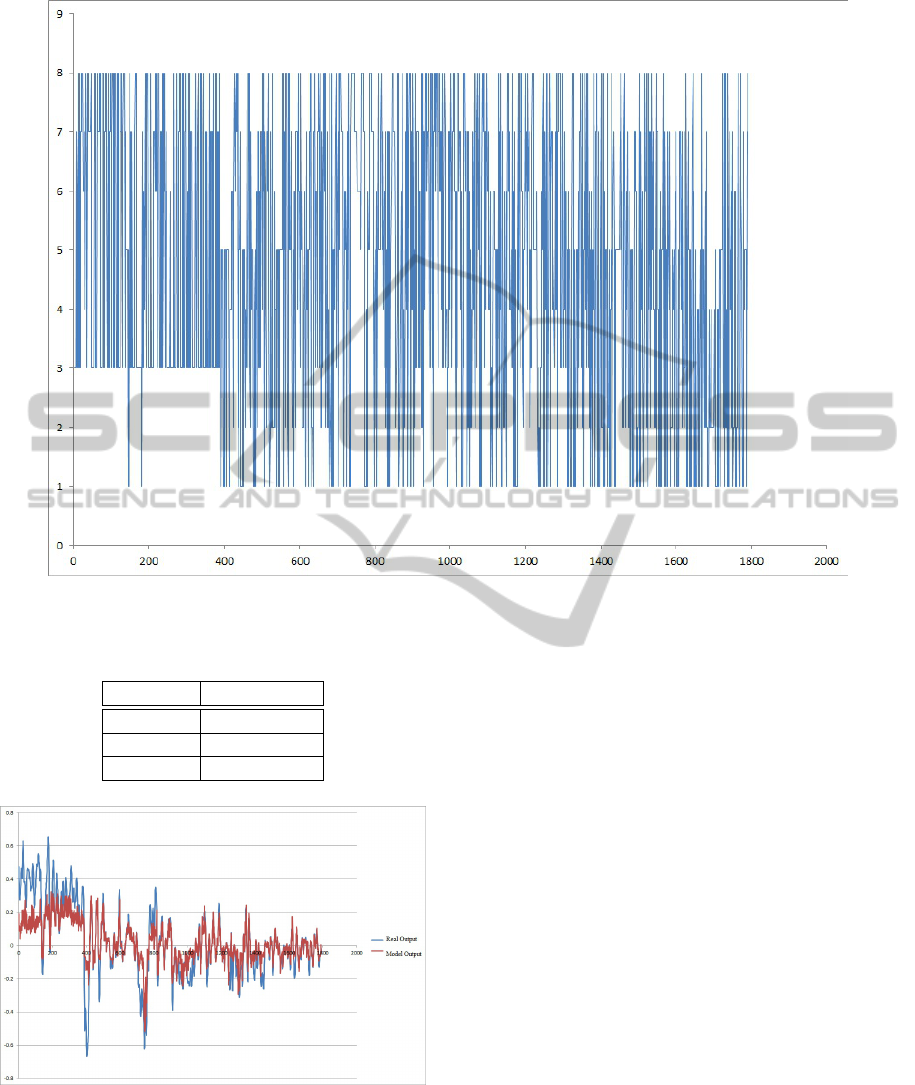
Figure 1: Mode switches of system with eight modes.
Table 4: Root mean square error of estimated output using
ANFIS model.
RMSE Input set
0.054 1,5,10,12,13
0.052 6,7,10,12,13
0.056 1,6,7,10,13
Figure 2: Normalized process output and model output
when using linear switching system with M = 8 modes.
resent complex systems with a number of simple lin-
ear subsystems. In this study, a switching system
model of a blast furnace process was identified from
experimental process data. The results show that with
a relatively few linear systems, quite good models can
be obtained, and by allowing more subsystems, the
nonlinearities are captured, even so that output is pre-
dicted slightly better than with the ANFIS method,
cf. Tables 3 and 4.
In future work, we will generalize the approach to
nonlinear switching systems for improved accuracy,
and also to test the method to other industrial pro-
cesses.
ACKNOWLEDGEMENTS
This work has been funded by the Foundation of bo
Akademi University and the center for optimization
and Systems Engineering at bo Akademi as well as
IAMSR at bo Akademi and the TUF foundation at
Arcada University of Applied Sciences.
REFERENCES
Bjork, K-M., Holopainen, M., Wikstrm, R., Saxen, H.,
Carlsson, C., Sihvonen, M.: Analysis of Blast Fur-
nace Time Series Data with ANFIS. TUCS Technical
Report 1094 ISBN 978-952-12-2986-2 (2013)
LinearSwitchingSystemIdentificationAppliedtoBlastFurnaceData
647

Shirdel, A. H., Bjork, K-M., Toivonen, H. T.: Identifica-
tion of Linear Switching System with Unknown Di-
mensions. In: 47 Hawaii International Conference on
System Sciences, HICSS-47 (2014)
The Association of Finnish Steel and Metal Pro-
ducers, Structure Review of Metal Refinement
(2012), http://www.teknologiateollisuus.fi/file/14190/
MJ rakennekatsaus212.pdf.html
Geerdes, M., Toxopeus, H. L., Van der Vliet, C.,
Chaigneau, R., Vander, T.: Modern Blast Furnace
Ironmaking: An Introduction. Ios PressInc, ISBN
9781607500407(2009)
Nath, N. K.: Simulation of gas flow in blast fur-
nace for different burden distribution and cohesive
zone shape. Materials and Manufacturing Processes,
17(5):671681 (2002). doi: 10.1081/AMP-120016090
Danloy, J., Mignon, R., Munnix, G., Dauwels, L., Bonte, L.:
A blast furnace model to optimize the burden distri-
bution. In: 60th Ironmaking Conference Proceedings,
pages 3748, Baltimore (2001)
Yu, Y., Saxn, H.: Experimental and dem study
of segregation of ternary size particles in a
blast furnace top bunker model. Chemical En-
gineering Science, 65(18):52375250 (2010). doi:
10.1016/j.ces.2010.06.025
Agarwal, A., Tewary, U., Petterson, F., Das, S.,
Saxn, H., Chakraborti,N.: Analysing blast fur-
nace data using evolutionary neural network
and multiobjective genetic algorithms. Ironmak-
ing and Steelmaking, 37(5):353359 (2010). doi:
10.1179/030192310X12683075004672
Saxn, H., stermark, R.: Varmax-modelling of blast furnace
process variables. European Journal of Operational
Research, 90(1):85101 (1996). doi: 10.1016/0377-
2217(94) 00304- 1
Korpi, M., Toivonen, H., Saxn,B.: Modelling and identifica-
tion of the feed preparation process of a copper flash
smelter. Computer Aided Chemical Engineering, El-
sevier (2003),(14):731-736, ISSN 1570-7946, ISBN
9780444513687
Bhattacharya, T.: Prediction of silicon content in blast fur-
nace hot metal using partial least squares (pls). ISIJ
International, 45(12):19431945, (2005)
Hao, X., Zheng, P., Xie, Z., Du, G., Shen, F.: A predic-
tive modeling for blast furnace by integrating neu-
ral network with partial least squares regression. In:
IEEE International Conference on industrial tech-
nology, volume 3, pages 11621167 Vol. 3,106-107
(2004). doi: 10.1109/ICIT.2004.1490724
Helle, M., Saxn, H.: A method for detecting cause-effects in
data from complex processes. In: Proceedings of the
International Conference in Coimbra, Pages 104107,
Portugal (2005)
Pettersson, F., Chakraborti, N., Saxn, H.: A genetic algo-
rithm based multi-objective neural net applied to noisy
blast furnace data. Applied Soft Computing, Volume
7, Issue 1, January 2007, Pages 387397
Heemels, W.P.M.H., De Schutter, B., Bemporad, A.: Equiv-
alence of hybrid dynamical models. Automatica, vol.
37, no. 7, pp. 10851091, (2001)
Sontag, E. D.: Nonlinear regulation: The piecewise linear
approach. IEEE Trans. Automatic Control, vol. 26, no.
2, pp. 346358, (1981)
Lin, J. N., Unbehauen, R.: Canonical Piecewise-linear
Approximations. IEEE Trans. Circuits Systems I-
Fundamental Theory and Applications, vol. 39, no. 8,
pp. 697699, (1992)
Saad, A., Avineri, E., Dahal, K., Sarfraz, M.: Soft Comput-
ing in Industrial Applications, Springer (2007)
Aliev, R. A., Fazlollahi, B, Aliev, R. R.: Soft Comput-
ing and Its Applications in Business and Economics,
Springer, edition 5 (2004)
Ohlsson, H.,Ljung, L., Boyd, S.: Segmentation of ARX-
models using sum-of-norms regularization. Automat-
ica, vol. 46, pp. 1107-1111 (2010)
Bako, L.: Identification of switched linear systems via
sparse optimization. Automatica, vol. 47, pp. 668-677
(2011)
Le, V. L., Lauer, F., Bako, L., Bloch. G.: Learning nonlin-
ear hybrid systems: from sparse optimization to sup-
port vector regression. In: HSCC - 16th ACM Inter-
national Conference on Hybrid systems: Computation
and Control - 33-42 (2013)
Lughofer, E. and Kindermann, S. (2010). SparseFIS: Data-
driven learning of fuzzy systems with sparsity con-
straints. Fuzzy Systems, IEEE Transactions on, 18(2),
396-411.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
648
