
Using a Hopfield Iterative Neural Network to Explain Diffusion
in the Brain’s Extracellular Space Structure
Abir Alharbi
Department of Mathematics, King Saud University, P.o Box 22452, 11495 Riyadh, Saudi Arabia
Keywords: Hopfield Neural Networks, Point Source Diffusion Equation, Finite Difference, Extracellular Space.
Abstract: Many therapies for drug delivery to the brain are based on diffusion, and diffusion in this extracellular space
is based on micro-techniques that can be modelled with classical differential equations such as the point
source diffusion equation. In this paper an energy function is constructed using a finite-difference
approximation to the governing diffusion equation and then minimized by a Hopfield neural network. The
synergy of Hopfield neural networks with finite difference approximation is promising. The neural network
approach is capable of giving insight to the complex brain activity better than any other classical numerical
method and the parallelism nature of the Hopfield neural networks approach is easier to implement on fast
parallel computers and this will make them faster than the traditional methods for modelling this complex
problem. Moreover, the effect of the involved parameters on the diffusion distribution and drug delivery in
the ECS is investigated.
1 INTRODUCTION
Diffusion plays a crucial role in brain function. The
space between cells, Extracellular space (ECS), is
like a foam and many substances move with in this
complicated region. Diffusion in this interstitial
space is modeled with classical differential
equations and quantified from measurements based
on micro-techniques. Theoretical and experimental
approaches rely on classical diffusion theory in
porous media. The brain is a very complex structure
of interwoven, intercommunicating cells, and is
considered an area of research in medical science
(Sykova, 1997). The classical laws of diffusion
applied in porous media theory can give an accurate
description of the way molecules are transported
through this tissue. Diffusing molecules have
random movements that cause collision with
membranes and affect their concentration
distribution (Nicholson and Tao, 1993). Diffusion is
an essential link in many processes, ranging from the
delivery of glucose to cells to intercellular
communication. Besides delivering glucose and
oxygen from the vascular system to brain cells,
diffusion also moves informational substances
between cells, a process known as volume
transmission (Nicholson, 2001). Diffusion is also
essential to many therapies that deliver drugs to the
brain. In treating brain disorders, where diffusion is
often compromised, understanding the transport of
molecules can be crucial to effective drug delivery
and treatment. The diffusion generated concentration
distributions of well-chosen molecules also reveal
the structure of brain tissue. This structure is
represented by the volume fraction represented by
(α), which is a dimensionless quantity and is defined
as the ratio between the volume of the ECS and the
total volume of the tissue. There is also the
tortuosity (λ) parameter, which is a hindrance to
diffusion imposed by local boundaries or local
viscosity. Analysis of these parameters also reveals
how the local geometry of the brain changes with
time or under pathological conditions. Experiments
has shown that the ECS in adult brain has α = 0.2
which is about 20% of the total brain volume, the
tortuosity is defined as
*/ DD
,
where D is a free diffusion coefficient and D* is the
apparent diffusion coefficient in the brain. As a
result of tortuosity, D is reduced to the apparent
diffusion coefficient D*=D/λ
2
. Thus, any movement
of a substance diffusing in the ECS is bombarded by
a number of obstacles or diffusion barriers.
Moreover, substances released into the ECS are
transported across membranes by concentration-
97
Alharbi A..
Using a Hopfield Iterative Neural Network to Explain Diffusion in the Brain’s Extracellular Space Structure .
DOI: 10.5220/0005029300970104
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 97-104
ISBN: 978-989-758-054-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

dependent uptake (k′) e.g., cellular uptake, loss
across blood vessels or washout from brain slices
(Sykova, 1997).
The diffusion of substances in a free medium is
described by Fick’s laws. In contrast to free
medium, diffusion in the ECS is hindered by the
presence of membranes, macromolecules of the ECS
and by cellular uptake. To take into account these
factors, it was necessary to modify Fick’s original
diffusion equations (Nicholson and Phillips, 1981;
Nicholson and Sykova, 1998) to include
macroscopic diffusion in a porous material which is
described by the same fundamental differential
equation as diffusion in a free medium (Fick’s
second law)
ck
s
r
c
D
t
c
'*
2
2
(1)
where c(r,t) is the concentration of the diffusing
substance, and s is the source density. Equation (1)
is a model of the concentration of the diffusing
molecules in the ECS at a radial distance r, it is a
parabolic partial differential equation studied in the
theory of some biological context (Berg, 1993).
Equation (1) plays an important role in drug therapy
and in curing major brain diseases such as
Parkinson’s and brain tumours, and solving it with
different approaches has been an appealing subject
to many researchers for many years and it proofed to
be not an easy task to do. Some researchers
presented analytic solutions as in ([Nicholson and
Freeman 1975, Saftenku, 2005), and some found
approximate solutions by numerical methods as in
(Nicholson 1985, Chen and Nicholson 2000). In this
paper Eq.(1) is solved by a numerical method based
on a neural network approach called the Hopfield
Finite Difference method (HFD) and that is because
neural networks are dynamic and were originally
designed to operate in a similar way as the brain
functions therefore this approach can give us insight
on the complex diffusion in the ECS of the brain
more than any other classical simple numerical
method. In section 2 a description of the governing
equation is given, and in section 3 the neural
network solution to this equation is presented. The
results will be given and examined in section 4
followed by conclusions and plans for our future
studies.
2 DIFFUSION EQUATION IN
THE ESC
Currently, the most widely used diffusion paradigm
is the release of a substance from a point source into
the ECS. In this study, the ion source which is an
ionophoretic electrode or pressure ejection
approximates a point source. Moreover, assuming
spherical symmetry and adopting the spherical
coordinate system, with the source density s = Q
(source strength in mol/s), Eq. (1) becomes the point
source equation as given in (Nicholson and Phillips,
1981)
ck
Q
r
rc
r
D
t
c
'
)(*
2
2
(2)
In the source term Q is characterized by Q = n I / F;
where I (amp) is the iontophoretic current, F is the
Faraday constant (96485 C/ mol), and n is the
transport number. Analytic solution to Eq. (2) is well
known and has the form (Crank, 1975)
)]'
2
(
)'
2
( rfc
*
'
exp[
8
*
'
*
*
*
tk
tD
r
erfce
tk
tD
r
e
D
k
r
rD
Q
c
D
k
r
(3)
in which erfc(.) is the complementary error function.
The common choice of ion for measuring diffusion
is TMA+ (Nicholson, 1993). One example of its use
is when research requires the use of experimental
models in which a defined population of cells can be
brought together into an epileptic state. One way to
do this is by locally injecting a drug that causes
seizure-like activity and after injection the drug will
diffuse in the ECS with the usual characteristics
determined by D, α and λ. This leads us to an
important question, what is the concentration
distribution that is required to produce an epileptic
focus? To resolve the distribution problem, two
types of information are required; the value of D and
D* for the drug used and a description of the
concentration distribution at the instant when nerve
cells begin seizure-like activity. Among agents that
produce epileptic models are penicillin, valproate
and pentylenetetrazol (PTZ). In principle, to
determine the concentration distribution that induced
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
98

seizure, one would employ appropriate drugs for the
epileptogenic agent, measure concentration at the
time that the cells began to display epileptic activity
and then calculate the drug distribution.
Unfortunately, such drugs do not perform well and
are fairly insensitive so they are not suitable for
work at the low concentrations that produce seizure.
Consequently, TMA+ was added to the
epileptogenic agent and both pressure ejected. Then
the distribution of the TMA+ could be measured
and, knowing the relative diffusion coefficients of
TMA+ and the drug, the drug distribution could be
calculated. It was also shown that values of λ,
obtained from D and D* from the combination of
TMA+ and the drug were similar to those previously
obtained with TMA+ alone. Using this approach
(Lehmenkuhler et al., 1991) were able to show that
neurons within a sphere of about 150 μm radius
must be exposed to penicillin to produce seizure.
Therefore, studying the diffusion of the ion TMA+ is
needed, and in our study we will present the solution
of the point source diffusion equation of the ion
TMA+ in the ECS of brain, together with an analysis
of all the involved parameters.
2.1 The Diffusion Equation in ECS by
the Hopfield Neural Networks
Continuous Hopfield neural networks were
developed by Hopfield and Tank to solve
constrained optimization problems. The nets are
recurrent where the weights are fixed to represent
the constrain and the quantity to be optimized. The
activations of the units iterate to find a pattern of
outputs that represent a solution to the problem and
correspond to the minimum of an Energy function
(Hopfield, 1982). Hopfield network can be easily
implemented on fast parallel computers, because of
its parallel nature. Therefore it is applied to many
optimization problems where complex computation
is needed, such as the traveling salesman problem,
map coloring, space allocation (Hopfield and Tank,
1985) and many more. Another area for using
Hopfield nets is combining it with the finite
difference method to solve partial differential
equations (PDE), this is done by minimizing an
energy function constructed to represent the total
squared error measuring how well the finite
difference quotients satisfy the PDE. This approach
is called the Hopfield Finite Difference method
(HFD), and it has the advantage of working in a
parallel mode and giving fast and accurate results.
The HFD method has been used to solve the
classical Wave, Heat (Diffusion), Poisson equations
(Alharbi, 1997, 2010, 2012), and to systems of PDEs
(Alharbi and Alahmadi, 2008).
We will use the HFD to solve the point source
diffusion equation in the ECS described in the last
section. However, before the method is applied there
are preliminary procedures to be done. First, a neural
representation of the problem is needed so that the
neurons in the network model the node points in the
mesh grid of the finite difference procedure, i.e. each
unit in the HFD neural net corresponds to a node
point in the mesh grid, and the activation of unit (i, j)
gives the approximate solution at (i∆r, j∆t) where i
and j are integers and ∆r, ∆t are the step sizes in r
and t respectively. Second, the Hopfield neural net is
designed to be a fully connected net with symmetric
weights. The weights are fixed to represent the
differential equation and the initial conditions. The
activation function is the identity function since
continuous range of outputs is desired. The design of
the HFD neural net goes through two stages: first,
the finite difference scheme for radial diffusion in
spherical coordinates is used on the grid points
denoted c
i,j
at (i∆r, j∆t), with the equations
])1(2)1[(
1)(
,1,,1
22
2
jijiji
ciicci
rirr
rc
for i≠0, and for i=0
2
1, 0,
22
() 6
( )
(r)
jj
rc
cc
rr
(4)
Substituting these equations in the diffusion
equation (2) and using the central finite difference
scheme for the time derivative we get
*
,1 ,
1, , 1,
2
,
[( 1) 2 ( 1) ]
'
ij ij
ij ij ij
ij
cc
D
ic ic ic
tir
Q
kc
(5)
Second, the finite difference method produces a
linear system of equations for i=1,2,…n, and
j=1,2,…,m. A design for the HFD net is made using
the energy function representing the total squared
error from the finite difference quotients, given by
2
2
11
,,1,
,1
2
*
,1,
'])1(2
)1[(
2
1
E
ck
Q
ciic
ci
ri
D
t
cc
E
n
i
m
j
jijiji
ji
jiji
(6)
where E
2
comes from the initial nodes with i=0,
UsingaHopfieldIterativeNeuralNetworktoExplainDiffusionintheBrain'sExtracellularSpaceStructure
99

2
1
,0
,0,1
2
*
,01,0
2
'
)(
6
2
1
m
j
j
jj
jj
ck
Q
cc
r
D
t
cc
E
(7)
We want to update the time step approximation unit
c
i,j
, therefore we differentiate the energy function
with respect to c
i,j
and consider only the closest
previously initialized units. The updating equations
for the activity of unit c
i,j
are given in Eq.(8).
The HFD net iterates to find the minimum of the
energy function given in equations (6) and (7) using
these updating equations given in (8). The net will
converge to a stable minimum of the Energy
function whenever the activity of each neuron
changes according to the equations of motion (8).
The parameters in the HFD net must be carefully
chosen to make sure the HFD finds the minimum of
E and captures all the dynamics of the diffusion in
the ESC. One of these parameters is the time step δ
which should be set to a small value, depending on
the parameters of the problem being solved, and
usually specified by trial and error. If we use a too
small value, the learning slows down, increasing the
number of epochs and the time needed to solve the
problem. Moreover, if we increase the grid size, then
δ must be accordingly decreased to maintain a
balanced updating of the activations.
c
i , j
( p1)
c
i, j
( p)
(
1
)[
c
i, j1
c
i, j
t
D
*
ir
2
[(i 1)c
i1, j
2ic
i, j
(i 1)c
i1, j
]
Q
k'c
i, j
]
c
0, j
( p1)
c
0, j
( p)
(
2
)[
c
0, j 1
c
0, j
t
6D
*
r
2
(c
1, j
c
0, j
)
Q
k'c
0, j
]
s.t.
1
(
1
t
2D
*
r
2
k'),
2
(
1
t
6D
*
r
2
k')
(8)
The choice of initial activations influences the
rate of convergence. Starting with a suitable range of
random initialized units decreases the number of
epochs the net needs to reach the desired activations,
hence reducing the time consumed in solving the
problem. On the other hand, choosing an initial state
that does not fall into the domain of any stable point
will cause the units to go through more epochs
seeking the closest minimum and converging. In our
case the net is initialized with zeros since the
concentration starts impulsively from rest, and then
activated seeking a minimum of the energy function,
by changing according to the updating equations (8).
The original Hopfield net described by Hopfield and
Tank uses random order to update the activations of
the neurons and this technique is utilized here too to
give the net its randomness similar to real neurons in
nature. An epoch consists of all units in the system
updating their activation. The net goes through as
many epochs as needed for it to converge to a
minimum, that is reaching a stable set of
activations, and hence finding the approximate
solution of the TMA
+
point source diffusion
equation.
3 DISCUSSION
The work done in this paper is theoretical and only
provides an approximate solution to the modelled
point source equation given in the last section from a
mathematical point of view, therefore the values of
the involved parameters in this model equation were
set according to an experiment conducted by
(Nicholson, 1993) in the specialized labs; where the
transport number of the electrode is 0.5 with the
effective diffusion coefficient used D* = 5.07 × 10
−6
cm
2
s
−1
, α = 0.2, k’ = 0.0025 s
-1
and λ=1.6. The
Hopfield neural network used in this study is
designed to minimize the energy function given in
Eq.(6) with parameters set as :m=15, n=20 , ∆t =10s,
∆r =10 m, δ =0.005, and Q=0.0005 nmol/s, and the
net is activated to update the neurons according to
Eq.(8). After only 500 epochs the net converges to a
stable set of activations and the approximate solution
describing the TMA+ concentration c (M) is shown
in Fig.1. As we can see the results are excellent in
terms of speed and accuracy compared to the exact
solution obtained from Eq.(3) and to results
published by Nicholson 1993. The total squared
error plot given in Fig. 2 confirms the HFD accuracy
after only 500 epochs. Table 1 compares results
obtained from the HFD approach described in this
work with numerical results obtained by the classical
finite difference method (FD).
As we can see in Table 1 the results are very
close in terms of accuracy and that makes the HFD
approach reliable even if it goes through more steps
and calculations because brain activity is a very
complex dynamic area and it needs a dynamic
approach such as neural networks to capture its
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
100
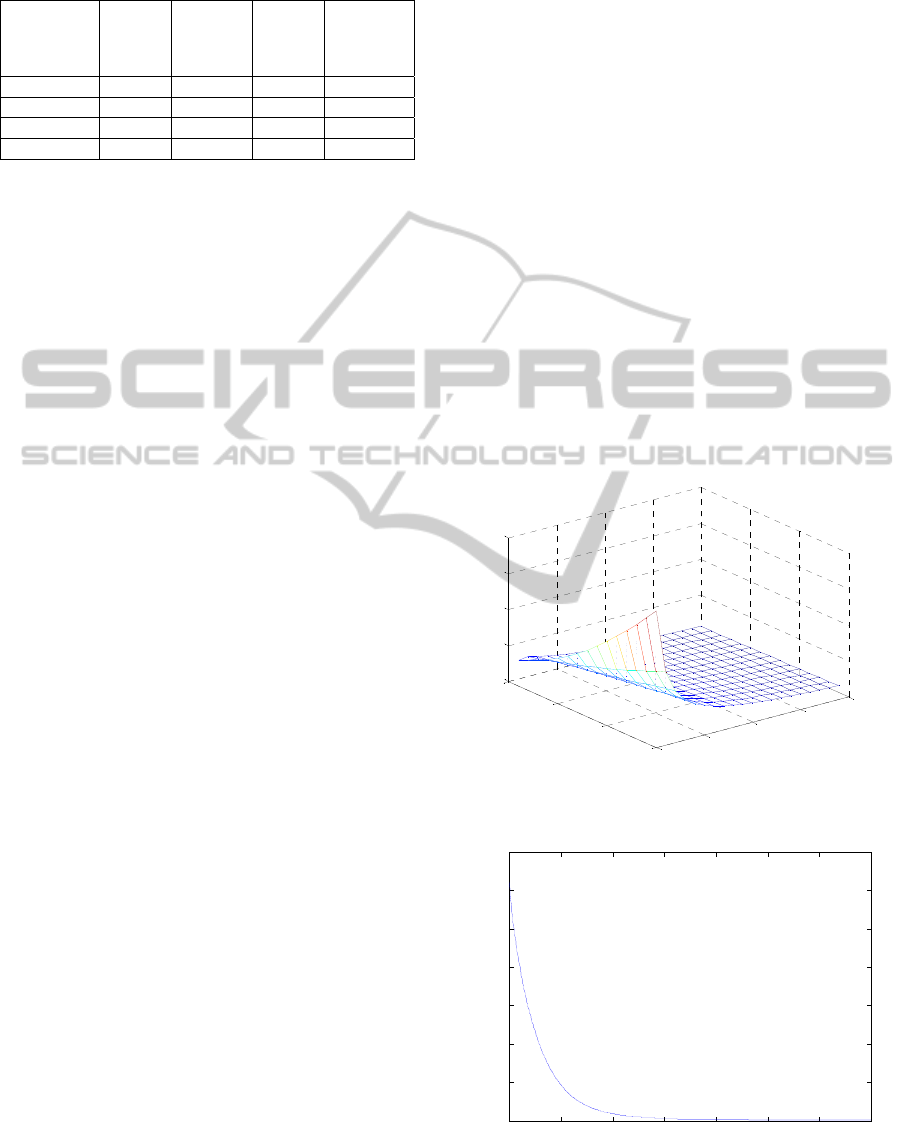
Table 1: Comparison of results from the Neural networks
HFD and the numerical method FD.
At t = 50 s
and
Selected
values of r
c(M)
in
HFD
Total
squared
Error in
HFD
c(M)
in
FD
Total
squared
Error in
FD
10 m
1.9625 5 x10
-4
1.9626 5.9x10
-4
50 m
0.3924 -1x10
-4
0.3923 -2x10
-4
100 m
0.1962 -1.5x10
-5
0.1963 5 x10
-5
150 m
0.1308 -1x10
-4
0.1306 -3.7x10
-4
behaviour rather than a simple classical
mathematical method such as FD. Neural networks
have the capability to accurately model the neural
activities and its different structures and tasks since
this was the original objective of creating neural
networks. Another feature of HFD that make it
exceed other classical numerical methods is that the
parallelism nature of the Hopfield neural networks
approach is easier to implement on fast parallel
computers and this will make them faster than the
traditional methods for modeling this complex
problem.
To look at the concentration of TMA+ as a
function of time t, Fig. 3 shows the concentration at
r= 100, 150, and 300 m. As we can see at closer
radial distances from the point source (r =100 m)
the concentration reaches higher values and then
gradually decreases to values still much higher than
all the other distances. Moreover, at farther radial
distances such as r =300 m the concentration does
not exceed 0.0654 M for all time periods, this
means if a drug is injected into the brain and allowed
to diffuse for a few seconds, at a location greater
than 300 m away from the source, the
concentration will be very low, and maybe too low
to activate any receptors or neurons there.
Figure 4 shows the concentration as a function of
radial distance r at times t = 20, 40, and 60s. As we
expect concentration has a higher value at earlier
times of the diffusion and gradually decreases as the
distance from the source grows further. Therefore, as
an example after just 150 seconds from injecting a
drug in the ECS at t =0, the drug will diffuse and the
concentration of the drug will be negligible at any
spherical distance from the source. The effect of the
initial concentration or source density on the
diffusion of TMA+ is shown on Fig.5, with D*=0.5
x10
-5
cm
2
/s, and r = 150 m. It is evident that the
higher the concentration initially released the higher
the values of the concentration at each t. This is
evident at the highest initial source Q =0.001 nmol/s,
where a higher concentrations for all t is reached and
manages to reach the farthest before all of the
TMA+ diffuses away.
To study the influence of different diffusion
coefficients on the concentration of TMA+ Fig.6
shows plots at Q=0.0005 nmol/s and r =150 m
away from the iontophoretic source for D* = 0.5,
0.7, and 0.2 x10
-5
cm
2
/s. As we can see the smaller
the diffusion coefficient the slower the concentration
reaches its highest and it takes longer time to
diffuse. It is also evident the larger D* reaches the
highest concentration earlier on and decreases
concentration faster. The diffusion coefficient
D*=0.7 x10
-5
cm
2
/s starts at a higher concentration
than the other two but drops faster to lower
concentrations.
From all the observations noted in the earlier
graphs, and if we consider different combinations of
initial density source and diffusion coefficients, we
can conclude that using D*=0.5x10
-5
cm
2
/s and
Q=0.0005 nmol/s starts low in concentration but
manages to give higher concentrations for a larger
radial diffusion distance. For that reason, we use this
combination in most of our study here. Hence, if our
analysis should present recommendations to efficient
0
50
0
150
200
0
50
100
150
0
1
2
3
4
t (s)
Approximate solution of Diffusion equation in the ECS of the brain
Figure 1: The approximate solution of diffusion equation
by HFD for r = 0 to 150 m and t = 0 to 200 s.
0 100 200 300 400 500 600 700
0
2
4
6
8
10
12
14
epoch
total squared error
Figure 2: The total squared error plot of the HFD solution
for the diffusion equation.
UsingaHopfieldIterativeNeuralNetworktoExplainDiffusionintheBrain'sExtracellularSpaceStructure
101

10 20 30 40 50 60 70 80 90 100
0
0.2
0.4
0.6
0.8
1
1.2
1.4
t (s)
Concentration of TMA+ function of time
r=150
r=100
r=300
Figure 3: The diffusion of TMA
+
at different radial
distances.
0 50 100 150 200 250 300
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Concentration of TMA+ function of r
t=40 (s)
t=20
t=60
Figure 4: The Diffusion of TMA
+
at different times.
0 10 20 30 40 50 60 70 80 90 100
0
0.2
0.4
0.6
0.8
1
1.2
1.4
t
(
s
)
Comparing Different source density values
Q=0,0001nmol/s
Q=0.0005
Q= 0.001
Figure 5: The concentration of TMA
+
at different source
density values.
0 10 20 30 40 50 60 70 80 90 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Comparing different diffusion coefficients
t (s)
D*=5x10
-
6 cm
2
/s
D*=2x10
-
6
D*=7x10
-
6
Figure 6: The concentration of TMA
+
with different
Diffusion coefficients.
drug delivery based on our results, then a carefully
chosen combination of D* and Q is needed for a
drug to reach neurons within a sphere of a specified
radius. Similarly, if the experiment combines the ion
TMA+ with another drug then a corresponding joint
D* and Q must be carefully chosen.
4 CONCLUSIONS
In this research a solution to the point source
diffusion equation in the ESC of the brain by a
Hopfield finite difference neural network. A finite
difference approximation in spherical coordinates is
used to form an energy function which represents
how well these approximations model the problem.
A Hopfield neural network is then designed to
minimize this energy function. Results obtained
from the Hopfield neural networks showed excellent
performance in terms of accuracy and speed. Our
study is done in a theoretical frame and is compared
to actual results published by Nicholson 1993, and
it needs to be extended by researchers in the drug
therapy field to conduct the actual experiments and
take these results to the next level of testing,
experimenting and reaching the desired
recommendations.
Our study of the effect of the parameters on the
solution showed that if a drug is delivered to the
brain by injection separately or with an ion, it will
diffuse in the region and activate all nearby neurons
with in a small sphere radius, and depending on the
concentration value needed to activate these
neurons. For example, if the ion TMA
+
was added to
the drug and both were pressure ejected. Then the
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
102

distribution of the TMA
+
could be measured and,
knowing the relative diffusion coefficients of TMA
+
and the drug, the drug distribution could be
calculated. From our results we showed that neurons
within a sphere less than 300 μm radius away from
the point source must be exposed to the drug and
they will produce a respond, and all neurons outside
this area will be exposed to almost negligible
concentrations and probably the drug will not show
an effect on them.
Therefore, our study may help doctors and
patients to attain efficient drug delivery, i.e. by
choosing the appropriate drug knowing its density
and diffusion factor and the location of the injection.
Apart from the clinical relevance of these studies,
they also provide a paradigm of how diffusion
analysis can be used to address other types of
question by using the co-diffusion of substances, one
of which has a ‘reporter’ role. A major reason for
introducing drugs is to fight cancerous tumors and
many studies have involved chemotherapy agents.
Tumors often have diffusion characteristics that
differ from normal tissue and this has made it
difficult to introduce many drugs that show an effect
on them, including large antibodies, that could
otherwise be effective agents (Lehmenkuhler et al.,
1991). The delivery of Dopamine to alleviate
Parkinson’s disease is another area where much
work has been done. Dopamine alleviates the effects
of Parkinson’s disease but, sadly, the treatment does
not offer a permanent cure because, for unknown
reasons, the treatment becomes ineffective after a
period of some months or years. This led to attempts
to implant sources of Dopamine in the brain directly,
most notably grafts of tissue or encapsulated
populations of dopamine-producing cells. Recently
there has been interest also in the delivery of
substances like nerve-growth factor (NGF) that may
be capable of reversing some of the effects of
Alzheimer’s disease (Krewson et al., 1995). All of
these reasons give us motivation for future work to
conduct more research on the diffusion equation in
the ECS, and on the concentration distribution with
different parameter values and with different drug
therapies and extend this work with specialists in the
drug therapy research labs to transform these
theoretical results to actual experimental results.
Furthermore, the neural networks are originally
designed to operate similarly to the brain’s functions
and that can give us more insight on diffusion in the
ECS of the brain than any other numerical method,
hence it will be beneficial in future work to use
different neural networks as models of the ECS
activities in the brain and fully make use of the
dynamics and full potentials of neural networks in
this area .
ACKNOWLEDGEMENTS
Special thanks to Dr. Guy Moss of the
Pharmacology Department at University College
London for suggesting the problem and the
constructive discussions.
REFERENCES
Abir Alharbi, 1997, A Neurocomputing Approach to
Solving Partial Differential Equations, Ph.D. thesis,
Florida Institute of Technology, Melbourne, Florida,
USA,.
Abir Alharbi, Alahmadi, E., 2008, A Neural Network
method for the unsteady flow past a circular cylinder,
FEJAM, 30, 2, 245 - 264.
Abir Alharbi, 2012, " A Solution to Neural Field
Equations by a Recurrent Neural Network Method ",
AIP American institute of Physics, ICNAAM, Greece.
Abir Alharbi, 2010, "An Artificial neural network method
for solving partial differential equations", AIP
American institute of Physics, ICNAAM, vol. 11281,
Greece.
Berg, H.C., 1993, Random Walks in Biology, Princeton,
NJ: Princeton University Press.
Chen, K.C., Nicholson, C., 2000, Changes in brain cell
shape create residual extracellular space volume and
explain tortuosity behavior during osmotic challenge,
Proc. Natl. Sci., USA, 97, 8306-8311.
Crank, 1975, The Mathematics of Diffusion, Oxford:
Clarendon.
Hopfield, J.J., 1982, Neural networks and physical
systems with emergent collective computational
abilities, National Academy of Science, USA, 79,
2554-2558.
Hopfield, J.J., Tank, D.W., 1985, Neural computation of
decisions in optimization problems, Biological
Cybernetics, 52, 141-152.
Krewson, C.E., Klarman, M.L., Saltzman, W.M., 1995,
Distribution of nerve growth factor following direct
delivery to brain interstitium, Brain Res., 680, 196–
206.
Lehmenkuhler, A., Nicholson, C., Speckmann, E.J., 1991,
Threshold extracellular concentration distribution of
penicillin for generation of epileptic focus measured
by diffusion analysis, Brain Res. 561, 292–8.
Nicholson, C., 1985, Diffusion from an injected volume of
a substance in brain tissue with arbitrary volume
fraction and tortuosity, Brain Res., 333, 325–9.
Nicholson, C., 1993, Ion-selective microelectrodes and
diffusion measurements as tools to explore the brain
cell microenvironment, J. Neuroscience. Methods, 48,
199–213.
UsingaHopfieldIterativeNeuralNetworktoExplainDiffusionintheBrain'sExtracellularSpaceStructure
103

Nicholson, C., 2001, Diffusion and related transport
mechanisms in brain tissue, Phys., 64, 815–884.
Nicholson, C., Freeman, J.A., 1975, Theory of current
source-density analysis and determination of
conductivity tensor for anuran cerebellum, J.
Neurophysiol. 38, 356–68.
Nicholson, C., Phillips, J. M., 1981, Ion diffusion
modified by tortuosity and volume fraction in the
extracellular microenvironment of the rat cerebellum,
J. Physiol. (Lond.), 321, 225–257.
Nicholson, C., Rice, M. E., 1986, The migration of
substances in the neuronal microenvironment, Ann. NY
Acad. Sci., 481, 55–71.
Nicholson, C., Sykova, E., 1998, Extracellular space
structure revealed by diffusion analysis, Trends
Neuroscience. 21,207–15.
Nicholson, C., Tao, L., 1993, Hindered diffusion of high
molecular weight compounds in brain extracellular
microenvironment measured with integrative optical
imaging, Biophys. J., 65, 2277–90.
Sykova, E., 1997, The extracellular space in the CNS: its
regulation, volume and geometry in normal and
pathological neuronal function, Neuroscientist, 3, 28–
41.
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
104
