
2-D Load Transfer Control Considering Obstacle Avoidance
and Vibration Suppression
Junichi Nakajima and Yoshiyuki Noda
Department of Mechanical Systems Engineering, University of Yamanashi,4-3-11, Takeda, Kofu, Yamanashi, Japan
Keywords:
Load Transfer Control, Trajectory Optimization, Vibration Suppression, Obstacle Avoidance, Overhead
Traveling Crane.
Abstract:
This paper is concerned with an advanced transfer control for load transfer machines such as a crane. In the
load transfer machine, it is required to carry the load efficiently and safety. In order to satisfy this requirement,
fast transfer of load, obstacle avoidance and vibration suppression have to be accomplished in the load transfer
system. Therefore in this study, the load transfer control system which the transfer trajectory on a plane is
optimized in consideration of the vibration suppression, obstacles avoidance and fast transfer is proposed.
Moreover, in order to optimize the trajectory in a short time, the fast solution approach is also proposed in
this study. The effectiveness of the proposed transfer control system is verified by the experiments using the
laboratory type overhead traveling crane system.
1 INTRODUCTION
In manufacturing and construction industries, a load
transfer machine such as an overhead traveling crane
and a gantry loader is used to carry a heavy load and
to support the assembly of components. These trans-
fer machines are required to reach at the target po-
sition in a short time and to avoid the obstacles on a
plane(Kawakami, et al., 2003), (Negishi, et al., 2013).
Furthermore, it is required to suppress the vibration of
the transfer object in the overhead traveling crane and
the gantry loader, because the next task after arriving
at the target position is delayed by the vibration oc-
curred. Therefore, there is a great hope that the load
transfer machine has the control functions of the ob-
stacles avoidance, the vibration suppression and fast
transfer(Yano, et al., 2002).
In order to fulfill the above requirements, the
transfer control systems have been proposed in the
previous studies. Especially, a lot of transfer con-
trol systems for an overhead traveling crane have been
proposed. The vibration suppression control to the
load of the overhead crane using optimal control the-
ory was proposed(Al-Garni, et al., 1995). The gain-
scheduled control was applied for suppressing the vi-
bration of the load with rope length varying(Takagi
and Nishimura, 1998), (Harald and Dominik, 2009).
The acceleration of the cart was shaped for elimi-
nating the natural frequency element of the vibra-
tion(Murakami and Ikeda, 2006). However, these
control systems are only for the swaying suppression
of the load. In the 2-D load transfer system such as the
overhead traveling crane without the vertical transfer,
a path planning with obstacles avoidance is needed.
In studies of the path planning for transfer system,
the path of the transfer object was derived by the po-
tential method(Branner,et al., 2012), the probabilistic
road map method(Yu-Cheng, et al., 2012), and pre-
dicting the action of the moving obstacle(Tamura, et
al., 2013). In the study(Suzuki and Terashima, 2000),
the potential method is used for deriving the path with
obstacle avoidance, and the path is reshaped for sup-
pressing the vibration. Since the reshaped path differs
from the path for avoidance of obstacle derived from
the potential method, the transfer object is in danger
of collision with obstacle.
Therefore in this study, the 2-D load transfer con-
trol using the trajectory planning approach consider-
ing the obstacles avoidance, the vibration suppression
and the fast transfer is proposed for the load transfer
machine on a plane. In this approach, the trajectory of
the cart can be derived by the optimization problem
which minimizes the integral square error of the cart
position and the target position, and energy of desired
frequency bands. The natural frequencies of the vi-
bration are assigned to the frequency bands in the cost
function for vibration suppression. The optimization
problem has the constraints on the acceleration, the
653
Nakajima J. and Noda Y..
2-D Load Transfer Control Considering Obstacle Avoidance and Vibration Suppression.
DOI: 10.5220/0005030806530660
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 653-660
ISBN: 978-989-758-040-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

velocity, and the position of the cart. The obstacles
are given as the constraints of the cart position. More-
over, in order to derive the trajectory in a short time,
the fast solution of the trajectory planning is also pro-
posed in this study. The effectiveness of the proposed
transfer control system is verified by the experiments
using the laboratory overhead traveling crane system.
2 REPRESENTATION OF LOAD
TRANSFER SYSTEM
The load transfer system in this study consists of two
position feedback control systems to the 2-D transfer
machine with an input and state constraints as shown
in Figure 1. These position feedback control systems
are assigned orthogonally in the 2-D load transfer ma-
chine. P(s) is shown as the transfer machine with vi-
bration elements, K(s) is shown as the feedback con-
troller, and r, z
u
and z
x
are shown as the target po-
sition, the control input and the controlled variables,
respectively. The observed variable y is the cart po-
sition which measured by the sensor such as a rotary
encorder.
Figure 1: Position feedback control system in load transfer
system
The model to transfer on X-axis in the orthogonal
arrangement is described by the discrete time system
as
x
x
(k + 1) = A
clx
x
x
(k) + B
clx
r
x
(k), (1)
z
x
(k) = C
zclx
x
x
(k) + D
zxlx
r
x
(k), (2)
y
x
(k) = C
yclx
x
x
(k) + D
yclx
r
x
(k). (3)
Similarly, that on Y -axis is described as
x
y
(k + 1) = A
cly
x
y
(k) + B
cly
r
y
(k), (4)
z
y
(k) = C
zcly
x
y
(k) + D
zxly
r
y
(k), (5)
y
y
(k) = C
ycly
x
y
(k) + D
ycly
r
y
(k). (6)
where x
x
(k) ⊂ R
n
and x y(k) ⊂ R
n
are shown as
the state vectors of each feedback system, and z
x
(k)
and z
y
(k) are shown as the control variables with the
constraints on each axis. The equation (1) is the
state equation to transfer on X -axis. The equation (2)
is output equation about controlled variable, and the
equation (3) is the observation equation. The transfer
on Y -axis is described similarly. The initial condition
is as x(0) = 0 becouse of the transfer from a stationary
state, and z
x
(k) and z
y
(k) has to be filled restrictions
as
z
x
(k) ∈ Z
x
= {z || z
x
|≤ z
xc
},∀k, (7)
z
y
(k) ∈ Z
y
= {z || z
y
|≤ z
yc
},∀k, (8)
where z
xc
and z
yc
are the boundary parameters of the
constraints.
3 TRAJECTORY PLANNING
APPROACH
We propose the trajectory planning method with the
time-series information by the optimization problem
which is considered reaching a target position in a
short time, suppressing the vibration, filling the con-
straints of the transfer machine, and obstacles avoid-
ance for the load transfer system.
3.1 Cost Function
One of the purpose in this study is to minimize the
cost function with the integral square error of the cart
position y and the target position r
0
in order to trans-
fer the target position in a short time, and the en-
ergy of the frequency bands to the varying natural fre-
quency of the vibration in order to suppress the vibra-
tion which the naturel frequency is changed. The cost
function is shown as
J=w
1
N−1
∑
k=0
| r
0x
(k) − y
x
(k) |
2
+w
1
N−1
∑
k=0
| r
0y
(k) − y
y
(k) |
2
+w
2
∫
v
2
v
1
| z
ux
(v) |
2
dv + w
3
∫
v
2
v
1
| z
uy
(v) |
2
dv. (9)
In this cost function, r
0x
and r
0y
are the target position
on X- and Y -axes, respectively. The first term in right
side has the integral square error of the cart position
y and the target position r
0
, additionally the second
term and the third term are the integral energy of the
frequency bands (v
1
to v
2
) on the control input on X-
and Y -axes, respectively. And, w
1
≥ 0, w
2
≥ 0 and
w
3
≥ 0 are the weight coefficients of scalar. Here,
the control input and the controlled and observation
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
654

valuables can be derived from the equations (2) and
(3) as
z
x
(k) =
k−1
∑
i=0
C
zclx
A
k−i−1
clx
B
clx
r
x
(i) +D
zclx
r
x
(k), (10)
y
x
(k) =
k−1
∑
i=0
C
yclx
A
k−i−1
clx
B
clx
r
x
(i) + D
yclx
r
x
(k). (11)
Here, the vectors of the input and the controlled vari-
able are defined respectively as
Z
u
= [z
u
(0) z
u
(1) · ·· z
u
(n − 1)]
T
,
Z
x
= [z
x
(0) z
x
(1) · ·· z
x
(n − 1)]
T
. (12)
Moreover, R
x
CR
0x
and Y
x
are the vectors consists of
the elements r
x
(k)Cr
0x
(k) and y
x
(k), (k =0,1,·· ·,n-1).
Therefore, the equations (10) and (11) can be repre-
sented as
Z
x
= M
zx
R
x
, Y
x
= M
yx
R
x
, (13)
where M
zx
and M
yx
are shown as
M
zx
=
D
zclx
0 · · · 0
C
zclx
B
clx
D
zclx
· · ·
.
.
.
.
.
.
.
.
.
.
.
.
0
C
yclx
A
n−2
clx
· · · C
zclx
B
clx
D
zclx
,
D 0 · · · 0
ɼ
ɼ
(14)
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
ɼ
ɼ
are constant.
Therefore, they are omitted from the cost function.
and these transposes are same
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
(14)
· · ·
M
yx
=
D
yclx
0 · · · 0
C
yclx
B
clx
D
yclx
· · ·
.
.
.
.
.
.
.
.
.
.
.
.
0
C
yclx
A
n−2
clx
· · · C
yclx
B
clx
D
yclx
.
ɼ
ɼ
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
ɼ
ɼ
are constant.
Therefore, they are omitted from the cost function.
and these transposes are same
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
∆ ∆
∆
(15)
Moreover, M
zy
and M
yy
on Y -axis can be derived
by similar process to the derivation on X-axis. There-
fore, the first term without the weight coefficient of
the cost function as shown in the equation (9) can be
represented as
J
1
= R
T
0x
R
0x
− R
T
x
M
T
yx
R
0x
− R
T
0x
M
yx
R
x
+R
T
x
M
T
yx
M
yx
R
x
+ R
T
0y
R
0y
− R
T
y
M
T
yy
R
0y
−R
T
0y
M
yy
R
y
+ R
T
y
M
T
yy
M
yy
R
y
. (16)
In the equation (16), R
T
0x
R
0x
and R
T
0y
R
0y
are constant.
Therefore, they are omitted from the cost function.
And, R
T
i
M
T
yi
R
0i
(i = x,y) and these transposes are same
value because of scalar. Therefore, the equation (16)
can be organized as
J
1
= (R
T
x
M
T
yx
M
yx
R
x
− 2R
T
x
M
T
yx
R
0x
)
+(R
T
y
M
T
yy
M
yy
R
y
− 2R
T
y
M
T
yy
R
0y
). (17)
The second term in right side without the weight co-
efficient w
2
in the cost function as shown in the equa-
tion (9) can be represented by using discrete Fourier
transform as
J
2
=
∫
v
2
v
1
| z
ux
(v) |
2
dv =
∫
v
2
v
1
|
N−1
∑
k
=
0
z
ux
(k)e
− jv∆T k
|
2
dv
=
∫
v
2
v
1
N−1
∑
k=0
z
ux
(k)e
− jv∆T k
∗
N−1
∑
k=0
e
jv∆T k
z
ux
(k)dv, (18)
where ∆T is a sampling period. By using the equation
(12), the cost function J
2
can be represented as
J
2
=
∫
v
2
v
1
Z
T
ux
EE
∗
Z
ux
dv, (19)
where E is as
E = [1 e
− jv∆T
···e
− jv∆T (n−1)
]
T
. (20)
E
∗
is the conjugate transpose matrix of E. Then, the
equation (19) can be represented as
J
2
= Z
T
ux
∫
v
2
v
1
EE
∗
dvZ
ux
= Z
T
ux
M
e
Z
ux
, (21)
where M
e
is as
M
e
=
∫
v
2
v
1
EE
∗
dv
ɼ
ɼ
(14)
(15)
-axis can be derived by
-axis. There-
, the first term without the weight coefficient of
the cost function as shown in the equation (9) can be
=
v
2
− v
1
e
jv
2
∆T
−e
jv
1
∆T
j∆T
−
e
jv
2
∆T
−e
jv
1
∆T
j∆T
v
2
− v
1
.
.
.
.
.
.
−
e
jv
2
∆T (n−1)
−e
2 jv
1
∆T (n−1)
j∆T
· · ·
· · ·
e
jv
2
∆T (n−1)
−e
2 jv
1
∆T (n−1)
j∆T
.
.
.
.
.
.
.
.
.
e
jv
2
∆T
−e
jv
1
∆T
j∆T
−
e
jv
2
∆T
−e
jv
1
∆T
j∆T
v
2
− v
1
. (22)
M
e
in the equation (21) can be replaced to the sym-
(22)
M
e
in the equation (21) can be replaced to the
symmetric matrix M
e
shown as
J
2
= Z
T
ux
M
e
Z
ux
= Z
T
ux
(
M
e
+ M
T
e
2
)Z
ux
= Z
T
ux
M
e
Z
ux
(23)
where M
e
is shown as
ɼ
ɼ
are constant.
Therefore, they are omitted from the cost function.
and these transposes are same
value because of scalar. Therefore, the equation (16)
(17)
The second term in right side without the weight co-
in the cost function as shown in the equa-
tion (9) can be represented by using discrete Fourier
M
e
=
v
2
− v
1
sinv
2
∆T −sin v
1
∆T
∆T
sinv
2
∆T −sin v
1
∆T
∆T
v
2
− v
1
.
.
.
.
.
.
sinv
2
∆T (n−1)−sin v
1
∆T (n−1)
∆T (n−1)
· · ·
sinv
2
∆T (n−1)−sin v
1
∆T (n−1)
∆T (n−1)
.
.
.
.
.
.
.
.
.
sinv
2
∆T −sin v
1
∆T
∆T
sinv
2
∆T −sin v
1
∆T
∆T
v
2
− v
1
. (24)
(24)
2-DLoadTransferControlConsideringObstacleAvoidanceandVibrationSuppression
655

Z
ux
can be represented as Z
ux
= M
zux
R
x
from the
equation (13). Therefore, the second term J
2
in the
cost function as shown in the equation (9) can be rep-
resented as
J
2
= R
T
x
M
T
zux
M
e
M
zux
R
x
. (25)
Going through the same procedure as J
2
, the third
term J
3
in the equation (9), which is the integral en-
ergy on the frequency bands (v
1
to v
2
) in Y -axis, can
be derived as
J
3
= R
T
y
M
T
zuy
M
e
M
zuy
R
y
. (26)
Summarizing the equations (17), (25) and (26), the
cost function in the equation (9) can be represented as
min
R
x
,R
y
J=min
R
x
,R
y
(w
1
J
1
+ w
2
J
2
+ w
3
J
3
)
=min
R
x
,R
y
{−2w
1
(R
T
x
M
T
yx
R
0x
+ R
T
y
M
T
yy
R
0y
)
+R
T
x
(w
1
M
T
yx
M
yx
+ w
2
M
T
zux
M
e
M
zux
)R
x
+R
T
y
(w
1
M
T
yy
M
yy
+ w
3
M
T
zuy
M
e
M
zuy
)R
y
}. (27)
This cost function has the dynamics of the transfer
system as represented in equation (13).
3.2 Input and State Constraints on
Transfer System
From the equations (7) and (8), the input and state
constraints of the 2-D load transfer machine can be
represented as
| M
zxx
R
x
|≤ Z
xxc
,| M
zux
R
x
|≤ Z
uxc
, (28)
| M
zxy
R
y
|≤ Z
xyc
,| M
zuy
R
y
|≤ Z
uyc
, (29)
where Z
xxc
, Z
xyc
, Z
uxc
and Z
uyc
are the input and state
constraints as
Z
xxc
= [z
xc
··· z
xc
]
T
, Z
xyc
= [z
yc
··· z
yc
]
T
,
Z
xuc
= [z
uxc
··· z
uxc
]
T
, Z
uyc
= [z
uyc
··· z
uyc
]
T
. (30)
The trajectory planning in this study is performed on
the finite time interval. In order to reach the transfer
object to the target position (r
0x
, r
0y
) with stationary
at the final time, the following equality constraints are
given.
M
f x
R
x
= Z
f x
, M
f y
R
y
= Z
f y
, (31)
where M
f x
, M
f y
, Z
f x
and Z
f y
are as
M
f x
=
C
yclx
A
N−2
clx
B
clx
···C
yclx
B
clx
D
yclx
C
zclx
A
N−2
clx
B
clx
···C
zclx
B
clx
D
zclx
, (32)
M
f y
=
C
ycly
A
N−2
cly
B
cly
···C
ycly
B
cly
D
ycly
C
zcly
A
N−2
cly
B
cly
···C
zcly
B
cly
D
zcly
, (33)
Z
f x
=
r
0x
0
, (34)
Z
f y
=
r
0y
0
. (35)
The first, second and third rows in the equation (31)
are for the terminate constraints of the cart position,
velocity and acceleration, respectively. The reference
trajectory optimization using the equations (27), (28),
(29) and (31) is performed by a quadratic program-
ming. However, since the reference trajectories on
X- and Y -axes are designed independently, it does not
include the function of the obstacle avoidance. In
next section, we introduce the function of the obstacle
avoidance.
3.3 Obstacle Represented by Constraint
Condition
If we try to apply for the load transfer system such
as an overhead traveling crane with some obstacles
in the transfer space, we should design 2-D transfer
trajectory which avoids the obstacles and does not ex-
cite the vibration. Therefore in this study, the obsta-
cle area are defined as inequality constraints in the
quadratic form, and they are given into the optimiza-
tion problem shown in the previous section for plan-
ning the trajectory with the obstacles avoidance.
Figure 2: Path planning with obstacle avoidance.
In this approach, the obstacle is covered in the
ellipse as shown in Figure 2. The inside of the el-
lipse is the no penetration area for planning the trajec-
tory. Therefore, the following inequality constraint is
given.
(y
x
(k) − x
s
)
2
a
2
+
(y
y
(k) − y
s
)
2
b
2
− 1 ≥ 0, (36)
where (x
s
,y
s
) is shown as the center position of the
ellipse, and a and b are shown as the length of the X-
and Y -directions on the ellipse. For matrix represen-
tation of the equation (36), the following inequality
equation is defined.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
656

(e
1
M
yx
R
x
− e
1
X
0
)
T
(e
1
M
yx
R
x
− e
1
X
0
)/(a
2
)
+(e
1
M
yy
R
y
− e
1
Y
0
)
T
(e
1
M
yy
R
y
− e
1
Y
0
)/(b
2
) − 1
= (R
T
x
M
T
yx
e
T
1
e
1
M
yx
R
x
− 2X
T
0
e
T
1
e
1
M
yx
R
x
+X
T
0
e
T
1
e
1
X
0
)/(a
2
) + (R
T
y
M
T
yy
e
T
1
e
1
M
yy
R
y
−2Y
T
0
e
T
1
e
1
M
yy
R
y
+Y
T
0
e
T
1
e
1
Y
0
)/(b
2
) − 1 ≥ 0, (37)
where e
1
= [1,0, 0,0, ··· , 0] ∈ R
1×n
, X
0
=
[x
0
,x
0
,· ·· ,x
0
]
T
∈ R
1×n
, Y
0
= [y
0
,y
0
,· ·· ,y
0
]
T
∈ R
1×n
.
The equation (37) shows the inequality equation at
k = 1. At k = 2, e
2
= [0,1,0, 0,· ·· ,0] ∈ R
1×n
is applied as the equation (37). Therefore,
e
i
= [0,·· · ,0,1, 0,· ·· ,0] ∈ R
1×n
is defined for
applying all of trajectory. The inequality constraint
for obstacle avoidance is represented as
(R
T
x
M
T
yx
ηM
yx
R
x
− 2X
0
ηM
yx
R
x
+X
0
ηX
0
)/(a
2
) + (R
T
y
M
T
yy
ηM
yy
R
y
−2Y
0
ηM
yy
R
y
+Y
0
ηY
0
)/(b
2
) −
˜
η ≥ 0, (38)
where,
η = [e
T
1
e
1
···e
T
k
e
k
···e
T
n
e
n
]
T
, (39)
˜
η = [e
1
e
T
1
···e
k
e
T
k
···e
n
e
T
n
]
T
. (40)
Organizing the equation (38) into a quadratic form,
the following equation can be derived.
R
T
x
(
1
a
2
M
T
yx
ηM
yx
)R
x
+ R
T
y
(
1
b
2
M
T
yy
ηM
yy
)R
y
−(
2
a
2
X
0
ηM
yx
)R
x
− (
2
b
2
Y
0
ηM
yy
)R
y
≥ −
1
a
2
X
0
ηX
0
−
1
b
2
Y
0
ηY
0
+
˜
η (41)
By adding the equation (41) into the trajectory opti-
mization in the previous section, the 2-D trajectory
with function of the obstacles avoidance can be de-
rived.
Therefore, the trajectory planning problem of the
2-D load transfer machine that is concerned with fast
transfer control with vibration suppression and ob-
stacles avoidance to a transfer object is resulted a
quadratic programing problem with quadratic con-
straints. This quadratic programming problem can
be solved by a sequential quadratic programming
method.
4 FAST SOLUTION OF
TRAJECTORY PLANNING
In this trajectory planning method proposed in this
study, the calculation takes immense amount of time,
Figure 3: Iteration for fast solution of transfer trajectory.
because the trajectory represented by the sample num-
ber n should be solved by the quadratic programming
problem with the quadratic constraints. In order to
solve the problem in a short time, we propose the fast
solution of the trajectory planning.
The calculation time for planning the trajectory
is decreased with decreasing the sample number n.
Therefore, the fast solution method as shown in Fig-
ure 3 is proposed. In this method, the trajectory with
the long sampling period is derived by the trajectory
planning proposed in the previous section. Then, the
discrete trajectory with the long sampling period is
linearly-interpolated, and the interpolated trajectory is
discretized with the shorter sampling period than that
of the previous optimized trajectory. The trajectory
optimization is performed with the discretized trajec-
tory as the initial trajectory. By iterating the proce-
dure as shown in Figure 3, the trajectory with a lot
of sample number n can be optimized in a short time.
The terminal condition in the iteration is given as
| J
s
(i − k) − J
s
(i − k − 1) |< ξ, k = (0, 1,2), (42)
where,
J
s
= J/n. (43)
J is the cost function as shown in the equation (27).
n is the sample number. Here, the relation between
the evaluation value J
s
and the sampling period ∆t
is shown in Figure 4. As seen from Figure 4, the
evaluation J
s
is converged with decreasing the sam-
pling period ∆t. Therefore, the trajectory is optimized
quickly by giving the appropriate finish condition. In
this study, we define the finish condition with ξ = 0.1,
that is selected by the relation between the evaluation
J
s
and the sampling period ∆t as shown in Figure 4.
2-DLoadTransferControlConsideringObstacleAvoidanceandVibrationSuppression
657

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−5
0
5
10
15
20
25
30
35
40
Sampling Period[s]
Evaluation Js
Figure 4: Relation between evaluation J
s
and sampling pe-
riod.
Figure 5: Overhead traveling crane system.
5 EXPERIMENTAL VALIDATION
USING OVERHEAD
TRAVELING CRANE
The effectiveness of the proposed method is validated
by the experiments using laboratory overhead travel-
ing crane as shown in Figure 5. The load as the trans-
fer object is suspended to the cart by the rope. The
travel range of the cart on X- and Y -axes are 1.2[m]
and 0.5[m], respectively. And the maximum rope
length is 0.85[m]. The cart traveled on X- and Y -axes
is driven by a servomotor and a belt-and-pulley mech-
anism on each axis. The rope is reeled by a servomo-
tor and a pulley. The cart position can be detected by
rotary encoders attached to the servomotor on each
axis. The rope length can also be detected by a rotary
encoder attached the servomotor. The sway angle of
the rope with the load can be detected by a laser range
sensor system. The constraints to the cart transfer are
shown in Table 1. The time constants and the gains
of the motors represented as a first order delay system
are shown in Table 2. The position feedback control
systems are constructed to the motors on X- and Y -
axes, respectively. The proportional control with the
both gains, K
p
= 100 are applied to the position feed-
back control systems.
Table 1: Constraints of transfer system.
Table 1: Constraints of transfer system
X-axis Y-axis
Velocity[m/s] ±0.35 ±0.35
Acceleration[m/s
2
] ±0.5 ±0.5
Input voltage[V] ±10 ±10
5 EXPERIMENTAL VALIDATION
Table 2: Parameters of motors.
Table 2: Parameters of motors
X-axis Y-axis
Gain[m/s/V] 0.0361 0.0358
Time constant[s] 0.011 0.015
The experimental conditions to the laboratory
overhead traveling crane system are shown as follows.
• Target position of the cart transfer is located as
1.0[m] and 0.4[m] on the X- and Y -axes, respec-
tively.
• The range of the rope length while the cart trans-
fer is between 0.3[m] and 0.7[m]. Therefore, the
natural angular frequency of the load vibration is
varied between 3.74[rad/s] and 5.72[rad/s]. The
frequency band for suppressing the vibration is set
to the range between 3.74[rad/s] and 5.72[rad/s]
in the trajectory planning of the cart transfer on
X- and Y -axes.
• Two obstacles covered into the ellipses are put
into the transfer space. The size of the obstacles
are same as 0.08[m] length of ellipse on X -axis
and 0.25[m] length on Y -axis. The center posi-
tions of the ellipses are located on [0.35 0] and
[0.75 0.4].
• The weight coefficients are given as w
1
= 1, w
2
=
1 and w
3
= 1 in case of the trajectory considering
with the vibration suppression. For comparison,
another experiment with the weight coeffieients
w
1
= 1, w
2
= 0 and w
3
= 0, is performed. It is
not considered with the vibration suppression.
• The transfer time is set to 6[s], and the sampling
period on the transfer control is 0.01[s].
In the procedure of the fast solution as shown in Fig-
ure 3, the series of the sampling period for optimizing
is given as ∆t = [1 0.5 0.25 0.1]. And in the terminal
condition shown in the equation (42), the evaluation
is selected as k = 0.
The experimental results of the cart transfer on X -
and Y -axes are shown in Figures 6 and 7, respectively.
In these figures, (a), (b), (c) and (d) show the cart posi-
tions, the velocities, the accelerations and the control
inputs, respectively. In (b) and (c), the broken lines
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
658

0 1 2 3 4 5 6
0
0.5
1
Position[m]
Time[s]
0 1 2 3 4 5 6
−0.5
0
0.5
Velocity[m/s]
Time[s]
0 1 2 3 4 5 6
−2
−1
0
1
2
Acceleration[m/s
2
]
Time[s]
0 1 2 3 4 5 6
−5
0
5
10
Control input[V]
Time[s]
Constraints
Constraints
(a)
(b)
(c)
(d)
Figure 6: Experiment results on X-axis.
0 1 2 3 4 5 6
0
0.2
0.4
Position[m]
Time[s]
0 1 2 3 4 5 6
−0.5
0
0.5
Velocity[m/s]
Time[s]
0 1 2 3 4 5 6
−2
−1
0
1
2
Acceleration[m/s
2
]
Time[s]
0 1 2 3 4 5 6
−10
−5
0
5
10
Control input[V]
Time[s]
Constraints
Constraints
(a)
(b)
(c)
(d)
Figure 7: Experiment results on Y-axis.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
x−position
y−position
Trajectory of cart
Start position
Target position
Obstacles
No penetrations
Figure 8: Experiment results in transfer trajectory.
Table 3: Calculation times.
Computation time[s]
Conventional solution 1484.00
(Once optimization)
Fast solution proposed 5.85
in this study
are the constraints to each state. The control inputs
are within the constraints. However, the velocities
and the accelerations are exceeded. In this approach,
since the sample period in the trajectory derived from
the terminal condition in the fast solution is longer
than that of the transfer control, the sample period of
the trajectory is adjusted to that of the controller by
the linear-interpolation method. By this procedure,
the velocities and the accelerations can be exceeded.
In order to solve this problem, interpolating smoothly
the trajectory will be required in the future.
The trajectory on X- and Y -axes is shown in Fig-
ure 8. In Figre 8, the blue bold line is the trajectory
of the transfer object, and the red thin lines are the
no penetration areas. The black broken lines show
the edges of the obstacles. As seen from Figure 8,
the transfer object avoids the obstacles, and reachs
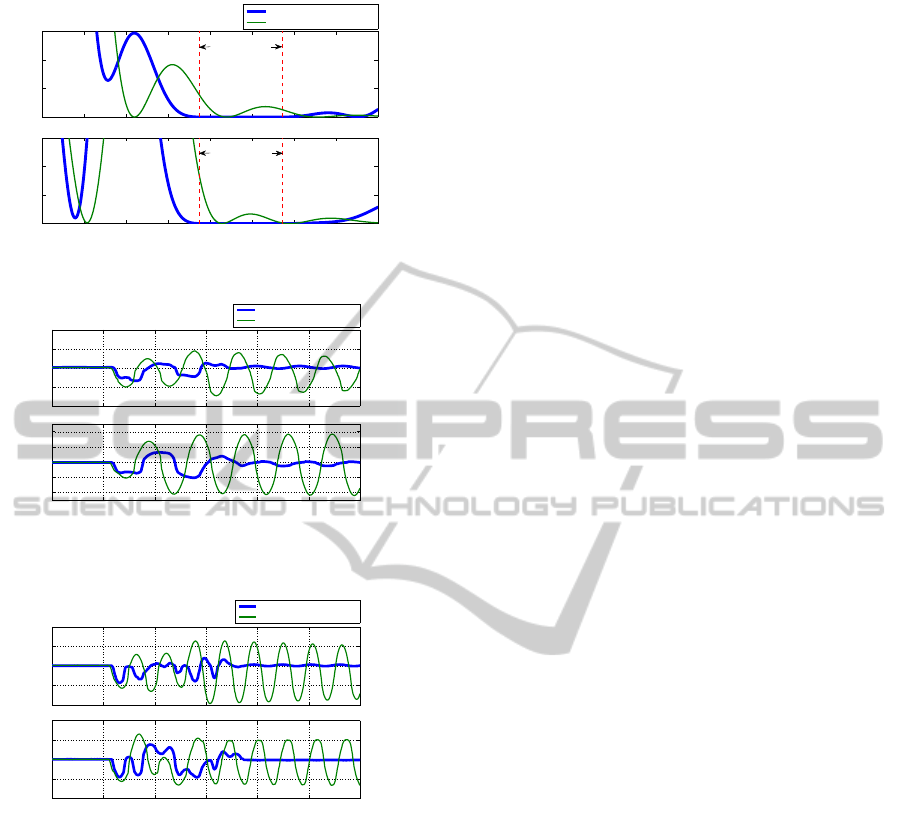
the target position. The power spectrum of the in-
put control is shown in Figure 9. The blue bold lines
show the control input considering the vibration sup-
pression, and the green thin lines show the that with-
out the vibration suppression. In the power spectrum
of the frequency bands 3.74[rad/s] to 5.72[rad/s], the
spectrum with considering the vibration suppression
is reduced. Therefore, the vibration considered in the
proposed method can not be excited. The experimen-
tal results of the vibrations with the natural angular
frequencies 3.74[rad/s] and 5.72[rad/s] are shown in
Figures 10 and 11, respectively. The blue bold lines
show the results by the proposed method considering
vibration suppression, and the green thin lines show
the results without vibration suppression. In Figures
10 and 11, it is seen that the vibration is suppressed
by the proposed method. The calculation time com-
pared between the fast solution proposed in this study
and the conventional solution which the trajectory op-
timization is performed only once by the sample pe-
riod 0.01[s], as shown in Table 3. The proposed opti-
mization process is much faster than the conventional
optimization process.
6 CONCLUSIONS
We proposed the trajectory planning method for 2-
D load transfer machine including vibration element.
2-DLoadTransferControlConsideringObstacleAvoidanceandVibrationSuppression
659
0 1 2 3 4 5 6 7 8
0
5
10
15
Power spectrum on X− axis
With vibration suppression
Without vibration suppression
0 1 2 3 4 5 6 7 8
0
5
10
15
Power spectrum on Y− axis
Frequency[rad/s]
Suppression band
Suppression band
Figure 9: Power spectrums of control inputs.
0 2 4 6 8 10 12
−0.4
−0.2
0
0.2
0.4
Sway angle (X−axis) [rad]
With vibration suppression
Without vibration suppression
0 2 4 6 8 10 12
−0.4
−0.2
0
0.2
0.4
Time [s]
Sway angle (Y−axis) [rad]
Figure 10: Experiment results of vibration with natural an-
gular frequency 3.74[rad/s] (Rope length:0.7[m]).
0 2 4 6 8 10 12
−0.4
−0.2
0
0.2
0.4
Sway angle(X−axis) [rad]
With Vibration suppression
Without vibration suppression
0 2 4 6 8 10 12
−0.4
−0.2
0
0.2
0.4
Sway angle(Y−axis) [rad]
Time [s]
Figure 11: Experiment results of vibration with natural an-
gular frequency 5.72[rad/s] (Rope length:0.3[m]).
The proposed method makes the transfer object avoid
the obstacles, the motion suppress the vibration in the
transfer object, and the state and the control input
keep under the constraints. Moreover, the fast solu-
tion which shorten the calculation time of the trajec-
tory optimization has been proposed in this study. In
the experiments for validating the proposed method, it
was seen that the vibration suppression, the obstacles
avoidance are accomplished. In the future works, we
will discuss the smooth interpolation method so that
the velocity and the acceleration of the transfer object
fall within the constraints.
REFERENCES
Kawakami, S, Miyoshi, T and Terashima, K, Path Planning
of Transferred Load Considering Obstacle Avoidance
for Overhead Crane, System Integration Division An-
nual Conference, p.640-641, 2003
Negishi, M, Masuda, H, Ohsumi, H and Tamura, Y, Eval-
uation of overhead crane trajectory, JSME Confer-
ence on Robotics and Mechatronics, p.1A2-p19(1)-
(4), 2013
Yano, K, Eguchi, K and Terashima, K, Sensor-Less Sway
Control of Rotary Crane Considering the Collision
Avoidance to the Ground, Transactions of the Japan
Society of Mechanical Engineers, Series(C), Vol. 68,
No. 676, p.146-153
A. Z. Al-Garni, K. A. F. Moustafa and S. S. A. K. Javeed
Nizami, Optimal Control of Overhead Cranes, Con-
trol Eng. Practice, Vol.3, No.9, p.1277-1284, 1995
Takagi, K, and Nishimura, H, Gain-Scheduled Control of A
Tower Crane Considering Varying Load-Rope Length,
Transactions of the Japan Society of Mechanical En-
gineers, Series(C), Vol. 64, No. 626, p.113-120
Harald, A and Dominik, S, Passivity-Based Trajectory Con-
trol of and Overhead Crane by Interconnection and
Damping Assignment, Motion and Vibration Control
, p.21-30, 2009
Murakami, S and Ikeda, T, Vibration suppression for High
Speed Position Control of overhead Traveling Crane
by Acceleration Inputs, Dynamics & Design Confer-
ence, p.128(1)-(6), 2006
Brunner, M, Bruggemann, B, and Schulz, D, Autonomously
Traversing Obstacle: Metrics for Path Planning of
Reconfigurable Robots on Rough Terrain, Proceed-
ings of 9th International Conference on Informatics in
Control, Automation and Robotics, p.58-69, 2012
Yu-Cheng, C, Wei-Han, H, Shin-Chung, K, A fast path
planning method for single and dual crane erections,
Automation in Construction, Volume 22, p. 468-480,
2012
Tamura, Y, Hamasaki, S, Yamashita, A and Asama, H,
Collision Avoidance of Mobile Robot Based on Pre-
diction of Human Movement According to Environ-
ments, Transactions of the Japan Society of Mechani-
cal Engineers, Series(C), Vol. 79, No. 799, p.617-628
Suzuki, M and Terashima, K, Three Dimensional Path
Planning using Potential Method for Overhead Crane,
Journal of Robotics Society of Japan, Vol.18, No.5,
p.728-736, 2000
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
660
