A Neural Model of Moral Decisions

Alessio Plebe

Department of Cognitive Science, University of Messina, Messina, Italy

Keywords:

Cortical Model, Moral Cognition, Emotion Modeling, Decision Making.

Abstract:

In this paper a neural model of moral decisions is proposed. It is based on the fact, supported by neuroimaging

studies as well as theoretical analysis, that moral behavior is supported by brain circuits engaged more gener-

ally in emotional responses and in decision making. The model has two components, the ﬁrst is composed by

artiﬁcial counterpart of the orbitofrontal cortex, connected with sensorial cortical sheets and with the ventral

striatum, the second by the ventromedial prefrontal cortex, that evaluate representations of values from the

orbitofrontal cortex, comparing with negative values, encoded in the amygdala. The model is embedded in

a simple environmental context, in which it learns that certain actions, although potentially rewarding, are

morally forbidden.

1 INTRODUCTION

Despite the extraordinarily inﬂuential role of neural

computation in the investigation of many human be-

haviors and capacities, no neural model for morality

has yet been developed. It is not surprising, since until

recently the coverage of empirical brain information

about moral cognition was scarce and patchy. Since

(Greene et al., 2001) directed neuroimaging studies

explicitly to moral cognition the situation has signiﬁ-

cantly improved, and the current knowledge, although

far from complete, is sufﬁcient for starting a project

of moral modeling. It is the purpose of this work.

It will start to ﬁll a gap inside the current trend in the

study of human morality, where traditional philosoph-

ical speculation has been supplemented by a plurality

of perspectives: from psychology, economics, neu-

roscience, anthropology, sociology. Neural computa-

tion was still missing.

This unparalleled shift in the study of morality

has been described by more than one philosopher as

the “empirical turn” (Nichols, 2004; Doris and Stich,

2005; Prinz, 2008), and several scholars are fostering

an even more radical approach to the science of moral

behavior, rooted in the understanding of the relevant

brain mechanisms (Verplaetse et al., 2009; Church-

land, 2011).

Two of the most important realizations to emerge

from all the empirical studied done so far, are that

there is no unique moral module, and that relatively

consistent set of brain areas that become engaged dur-

ing moral reasoning are also related to emotions, and

decision making (Greene and Haidt, 2002; Moll et al.,

2005; Casebeer and Churchland, 2003).

Decisions are continuously faced by the brain in

everyday life, from simple motor control up to long

term planning, and few of them speciﬁcally involve

moral judgments. Even between actions that we may

judge as “wrong” or “good”, to establish a clear cut

between moral norms and social conventions is not a

simple and straightforward task (Kelly et al., 2007).

The theoretical view embraced by this model is neo-

sentimentalism. It is a view within a philosophical

tradition that goes back to (Hume, 1740), which re-

lates moral properties to certain emotions in an essen-

tial way, and construes morality as a set of prescrip-

tive sentiments, where sentiment denotes the disposi-

tion of the subject to the relevant emotion (Nichols,

2004; Prinz, 2008).

For this reason the model here proposed is based

on circuits that encode emotions, and that performs

decisions on value-based representations. While neu-

rocomputational approaches to morality are still lack-

ing, there are indeed a number of existing models

that verge on emotions and decision making, which

have been a guiding reference for the development

here presented. The GAGE model (Wagar and Tha-

gard, 2004) assembles groups of artiﬁcial neurons

corresponding to the ventromedial prefrontal cortex,

the hippocampus, the amygdala, and the nucleus ac-

cumbens, in implementing the somatic-marker effect:

encoding of feelings that have become associated

111

Plebe A..

A Neural Model of Moral Decisions.

DOI: 10.5220/0005032001110118

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 111-118

ISBN: 978-989-758-054-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

through experience with the predicted long-term out-

comes of certain responses (Damasio, 1994). In the

ANDREA model (Litt et al., 2008) the orbitofrontal

cortex, the dorsolateral prefrontal cortex, and the an-

terior cingulate cortex interact with basal ganglia and

the amygdala in reproducing the human hypersensi-

tivity to losses over equivalent gains (Kahneman and

Tversky, 1979). The overall architecture of these

models shares similarities with those of (Frank and

Claus, 2006; Frank et al., 2007), in which the or-

bitofrontal cortex interacts with the basal ganglia to

produce dichotomic on/off decisions.

The proposed model is made of several simulated

cortical and subcortical areas, described in detail in

§2. It is embedded in a simpliﬁed world, which can

be experienced through vision and taste. There are

two possible kinds of objects in the scene, only one

is edible, like a fruit. Collecting fruits is not allowed

everywhere, there are areas where it is forbidden, and

any violation will call into action an angry face, visi-

ble in the scene. Results about the ability of the model

to learn this simple moral rule, and act accordingly,

will be shown in §3.

2 DESCRIPTION OF THE MODEL

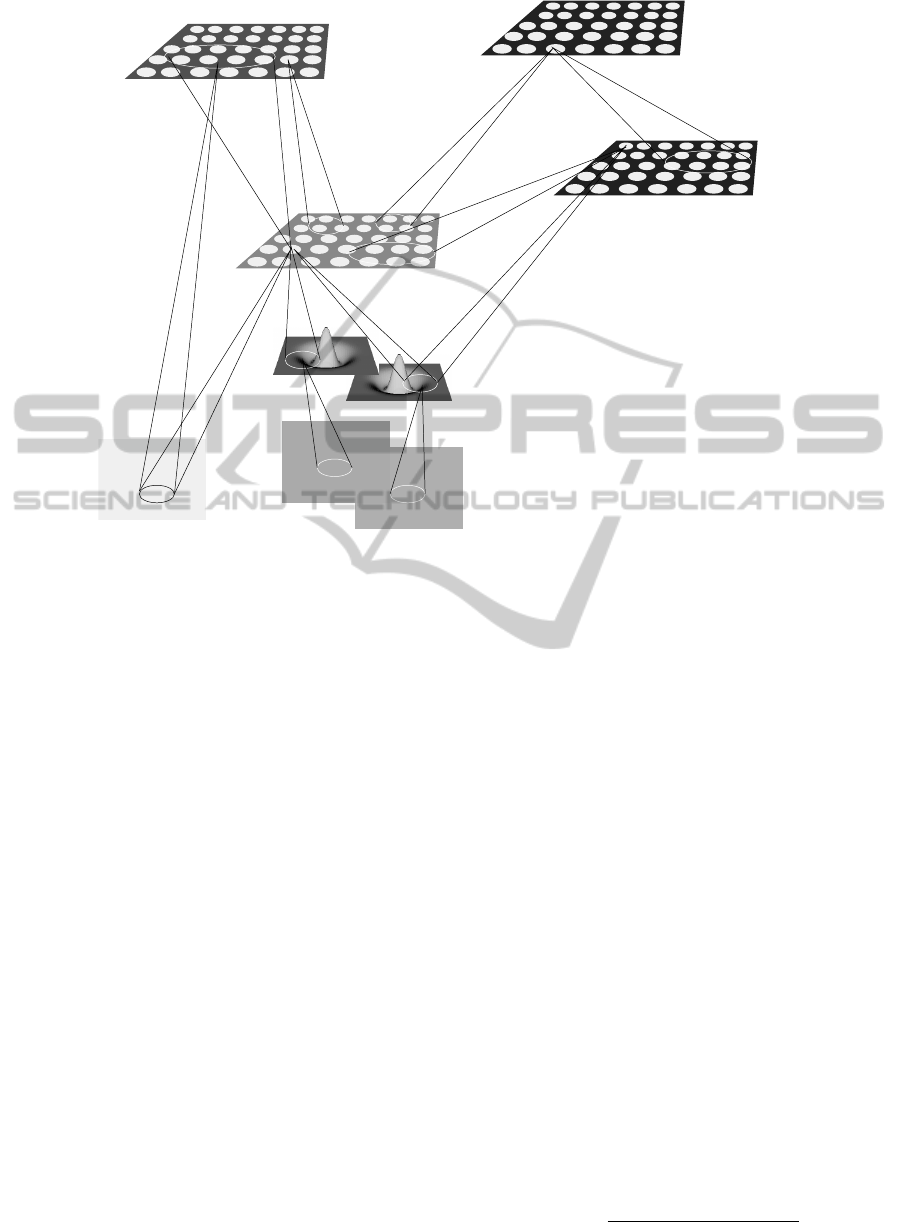
The overall model is shown in Fig. 1. It is composed

by a series of sheets with artiﬁcial neural units, la-

beled with the acronym of the brain structure that is

supposed to reproduce. It is implemented using the

Topographica neural simulator (Bednar, 2009), and

each cortical sheet adheres to the LISSOM (Laterally

Interconnected Synergetically Self-Organizing Map)

concept (Sirosh and Miikkulainen, 1997). In a LIS-

SOM sheet of neurons, the activation of each neuron

is due to the combination of afferents and excitatory

and inhibitory lateral connections, as detailed below.

There are two main circuits that learn the emo-

tional component that contributes to the evaluation

of potential actions. A ﬁrst one comprises the or-

bitofrontal cortex, with its processing of sensorial in-

formation, reinforced with positive perspective values

by the loop with the ventral striatum. The second

one shares the representations of values from the or-

bitofrontal cortex, which are evaluated by the ventro-

medial prefrontal cortex against conﬂicting negative

values, encoded by the closed loop with the amygdala.

The subcortical sensorial components comprise LGN

at the time when seeing the main scene, the LGN de-

ferred in time, when a possibly angry face will appear,

and the taste information.

2.1 Equations at the Single Neuron

Level

The basic equation of the LISSOM describes the ac-

tivation level x

of a neuron i at a certain time step

(k)

= f



·~v

+ γ

·~x

(k−1)

− γ

·~x

(k−1)



(1)

The vector ﬁelds ~v

, ~e

, ~x

are circular areas of ra-

dius r

for afferents, r

for excitatory connections,

for inhibitory connections. The vector ~a

is the

receptive ﬁeld of the unit i. Vectors~e

and

are com-

posed by all connection strengths of the excitatory or

inhibitory neurons projecting to i. The scalars γ

, γ

, are constants modulating the contribution of affer-

ents, excitatory, inhibitory and backward projections.

The function f is a piecewise linear approximation of

the sigmoid function, k is the time step in the recur-

sive procedure. The ﬁnal activation of neurons in a

sheet is achieved after a small number of time step

iterations, typically 10.

All connection strengths adapt according to the

general Hebbian principle, and include a normaliza-

tion mechanism that counterbalances the overall in-

crease of connections of the pure Hebbian rule. The

equations are the following:

∆a

+ η

− a

, (2)

∆e

+ η

− e

, (3)

∆i

+ η

− i

, (4)

where η

{A,E,I}

are the learning rates for the afferent,

excitatory, and inhibitory weights, and k · k is the L

norm.

2.2 Orbitofrontal Circuit

The ﬁrst circuit in the model learns the positive re-

ward in eating fruits. The orbitofrontal cortex is the

site of several high level functions (Rolls, 2004), in

this model information from the visual stream and

taste have been used. There are neurons in the or-

bitofrontal cortex that respond differentially to visual

objects depending on their taste reward (Rolls et al.,

1996), and others which respond to facial expressions

(Rolls et al., 2006), involved in social decision mak-

ing (Damasio, 1994; Bechara et al., 1994). For (Prehn

and Heekeren, 2009) the role of the orbitofrontal cor-

tex in moral judgment is the representation of the ex-

pected value of possible outcomes of a behavior in

regards to rewards and punishments.

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

112

LGN

taste

vmPFC

Amygdala

OFC

retina

retina’

LGN’

Figure 1: Overall scheme of the model, composed by LGN (Lateral Geniculate Nucleus), V1 (Primary Visual Area), OFC

(OrbitoFrontal Cortex), VS (Ventral Striatum), Amyg (Amygdala), vmPFC (ventromedial PreFrontal Cortex).

In all the subsequent equations the superscript of

time step sk will be omitted, for sake of readability,

and substituted by the name of the sheet, using the

abbreviations L and L

for, respectively, the output of

the LGN at the time when seeing the main scene, and

the output of the LGN deferred in time, and the ab-

breviation T for the taste signal.

The equation of the activation of a neural unit in

the OFC layer is the following:

(OFC)

= f



(OFC←V1)

·~v

(V1)

(OFC←L

)

(OFC←L

)

·~v

)

(OFC←T)

·~v

(T)

(OFC←VS)

(OFC)

·~v

(VS)

(OFC)

·~x

(OFC)

−

(OFC)

·~x

(OFC)



(5)

which is a specialization of the general equation (1).

Here, for better readability, the unit index i and time

step k have been omitted. There are three sensorial

afferents: ~v

(V1)

from the visual cortex V1, ~v

(L)

from

the lateral geniculate nucleus of the thalamus, and

the taste sensorial input ~v

(T)

, each in a sensorial area

corresponding to the receptive ﬁeld of the unit in

OFC. The fourth afferent, ~v

(VS)

, is the backprojection

from the VS loop that will be described next. The vi-

sual pathway is simpliﬁed in a single area, V1, with

the following equation:

(V1)

= h



(V1←L)

·~v

(L)

+ γ

(V1)

·~x

(V1)

−

(V1)

·~x

(V1)



(6)

which differs from equation (1) in that the nonlinear

function h has an adaptive threshold θ, dependent on

the average activity of the unit, using:

(k)

= θ

(k)

+ λ



¯x

(V1)

− µ



(7)

where ¯x

(V1)

is a smoothed exponential average in time

of the activity, and λ and µ ﬁxed parameters. This

feature simulates the biological adaptation that al-

lows the development of stable topographic maps or-

ganized by preferred retinal location and orientation

(Stevens et al., 2013). The output of LGN is given

by:

(L)

= f







(σ

)

−~g

(σ

)



·~v

r,c

β + γ

(σ

)

·~x

(L)





(8)

ANeuralModelofMoralDecisions

113

approximating the combined contribution of ganglion

cells and LGN with a positive center and negative

surround, by differences of two Gaussian ~g

(σ

)

and

(σ

)

, with the denominator term acting as contrast-

gain control (Stevens et al., 2013). The bidimensional

coordinates r and c refers to the retinal photorecep-

tors, and ~x

(L)

are the suppressive connection ﬁeld of

the given unit. It holds σ

< σ

OFC has forward and feedback connections with

the Ventral Striatum, VS, which is the crucial center

for various aspects of reward processes and motiva-

tion (Haber, 2011). VS in the model is a crude simpli-

ﬁcation of this complex area, and does not reproduce

the details of its direct and reciprocal connection with

the dopaminergic neurons centers. It is implemented

by the following equation:

(VS)

= f



(VS←OFC)

·~v

(OFC)

(VS←T)

·~v

(T)

(VS)

·~x

(VS)

− γ

(VS)

·~x

(VS)



(9)

The afferent signals ~v

(OFC)

come from equation (5),

(T)

is the taste signal. The output x

(VS)

computed in

(9) will close the loop into the prefrontal cortex with

equation (5).

2.3 Ventromedial Circuit

The second main circuit in the model is based on the

ventromedial prefrontal cortex, vmPFC, and its con-

nections from OFC and the amygdala. The ventrome-

dial prefrontal cortex is long since known to play a

crucial role in emotion regulation and social decision

making (Bechara et al., 1994; Damasio, 1994). More

recently it has been proposed that the vmPFC may

encode a kind of common currency enabling consis-

tent value based choices between actions and goods of

various types (Gl

ascher et al., 2009). It is involved in

the development of morality, in a study (Decety et al.,

2012) older participants showed signiﬁcant stronger

coactivation between vmPFC and amygdala when at-

tending to scenarios with intentional harm, compared

to younger subjects. The amygdala is the primary

mediator of negative emotions, and responsible for

learning associations that signal a situation as fearful

(LeDoux, 2000). In the model it is used speciﬁcally

for capturing the negative emotion when seeing the

angry face, a function well documented in the amyg-

dala (Boll et al., 2011).

vmPFC is implemented in MONE using the stan-

dard equation (1), as follows:

(vFC)

= f



(vFC←OFC)

·~v

(OFC)

(vFC←Amy)

·~v

(Amy)

(vFC)

·~x

(vFC)

−

(vFC)

·~x

(vFC)



(10)

The afferent signals ~v

(OFC)

come from equation (5),

while~v

(Amy)

, the connection from Amygdala, is given

from the following equation:

(Amy)

= f



(Amy←OFC)

·~v

(OFC)

(Amy←L

)

(Amy←L

)

·~v

)

(Amy)

·~x

(Amy)

−

(Amy)

·~x

(Amy)



(11)

The afferent signals ~v

(OFC)

come from equation (5),

while ~v

)

is a direct reading of face from the vi-

sual afferents in the thalamus, delayed in time with

respect to the ordinary visual scene. The activation

given from equation (11) will loop inside the vmPFC

by equation (10).

2.4 Decisions in the Ventromedial Area

A method of analysis has been carried out for the

identiﬁcation of decisions as population coding of

neural activation in the vmPFC map. Let us introduce

the following function:

(e) : E ∈ E → R; s ∈ E ∈ E , (12)

that gives the activation x of a generic neuron i in

vmPFC in response to an environmental condition e.

This condition is an instance of a class E, belonging

to the set of all classes of conditions E . In this exper-

iment E =

{

}

, where E

is the set of situa-

tions where an eatable object is freely available in the

scene, in E

a fruit is still in the scene, but forbidden,

in E

there is a neutral object in the scene. For a class

E ∈ E we can deﬁne the two sets:

E,i



) : e

∈ E



; (13)

E,i



) : e

∈ E

6= E ∈ E



. (14)

We can then associate to the class E a set of neurons

in the map, by ranking it with the following function:

r(E,i) =

E,i

− µ

E,i

, (15)

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

114

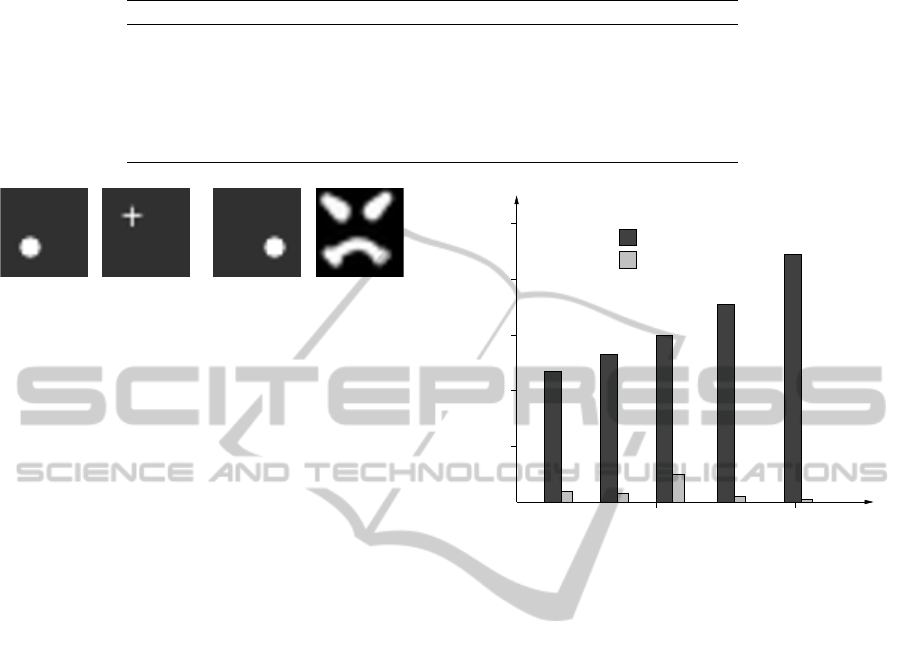
Table 1: Main parameters of all model maps. Radius values are normalized in range [0...2].

layer size r

LGN 24 × 24 0.3 - - - - - - - -

V1 22 × 22 0.1 - 0.8 0.4 2.0 - 1.0 0.3

OFC 16 × 16 0.4 0.1 0.1 0.5 0.8 0.4 1.4 1.6

VS 8 × 8 0.5 0.3 0.6 0.3 0.6 0.4 1.4 0.4

Amyg 8 × 8 0.6 0.5 0.5 0.6 0.6 0.3 0.5 1.5

vmPFC 12 × 12 0.4 0.5 0.4 0.2 2.0 −0.5 1.2 1.7

Figure 2: The visual inputs of the model. From the left to

the right: an edible object, possibly an apple, a + shaped

neutral object, the edible object in the forbidden area (the

bottom right quadrant of the scene), which is followed by

the sad and angry schematic face.

where µ is the average and σ the standard deviation of

the values in the two sets, and | · | is the cardinality of

a set. Now the following relation can be established

as the population code of a condition class E:

p(E) : E →

,·· · ,i

r(E, i

) > r(E,i

) > ·· · > r(E,i

)

}

(16)

where M is a given constant, typically one order of

magnitude smaller than the number of neurons in the

map The population code p(E) computed with (16) is

used to take a decision d ∈ D according to the status e

of the environment. In this experiment D =

{

}

where d

is the decision to collect and eat the object,

is the decision to ignore it.

d(e) = m

argmax

E∈E

(

∑

j=1···E

p(E)

(s)

, (17)

where p(E)

denotes the j-th element in the ordered

set p(E); α is a constant that is close, but smaller, than

one; m(·) is a mapping function from environmental

categories to decision:

→d

;

→d

;

→d

(18)

3 RESULTS AND DISCUSSION

The artiﬁcial moral brain architecture just described

is exposed to a series of situations that simulate

highly simpliﬁed contexts, and the appropriate ac-

tion is gradually learned. Some actions are charged

plus

apple

% of grasping decisions

learning epochs

100

100005000

Figure 3: Percentage of grasping actions selected by the

vmPFC model map, for the apple and the + shaped neutral

object, at different epochs of the development.

with important survival reward, but in some cases may

cause detriment to others. Their angry reaction will

lead to learn that that action is “wrong”.

The main input to the model is a visual scene, ex-

amples are shown in the Fig. 2. Our artiﬁcial sub-

ject is unfamiliar with the objects, she can realize how

pleasant fruits are to eat, thanks to its taste perception.

This sensorial input is simply a matrix 2 × 2, in which

the ratio of the upper row to the lower row signal how

pleasant the taste is. Fruits in the bottom right quad-

rant may belong to a member of the social group, and

to collect these fruits would be a violation of her/his

property, that would trigger an immediate reaction of

sadness and anger. This reaction is perceived in the

form of a face with a marked emotion, as the one in

the rightmost position in Fig. 2

3.1 First Learning Stage

This phases of development includes an early stage of

formation of V1, the visual system, with elongated

patterns as inputs, followed by item the good food

recognition stage, in which the stimuli are the two

types of objects, in all possible positions, and their

taste.

Learning is always ruled by equations (2), (3),

ANeuralModelofMoralDecisions

115

100

30001000 2000

forbidden

% of grasping decisions

learning epochs

free

Figure 4: Percentage of grasping actions selected by the

vmPFC model map for the apple, placed in the free, or om

the forbidden places, ad different epochs of the develop-

ment.

and (4). applied to the relevant connections. The

development of V1, involving equation (6) only,

setup the main systems of organization in the pri-

mary visual cortex, with arrangement of orientation

tuned neurons, similar to that described in (Plebe and

Domenella, 2007).

Then the OFC, VS, and vmPFC areas of the model

become plastic, and learn their connections of equa-

tions (5), (9), and (10). This set of equations is an

implicit reinforcement learning, where the reward is

not imposed externally, but acquired by the OFC map,

through its taste sensorial input. The amygdala has no

interaction during these stages.

The coding in vmPFC model map is the decision

made to grasp or not to grasp the object, the percent-

age of decision to grasp, at various learning steps, is

shown in Fig. 3. When the object is an apple, grasping

gradually become the prevailing choice, that reaches

to 60% after 5000 learning epochs, and to 90% at the

end of this learning phase. Occurrence of grasping

is instead low for the non rewarding object, and be-

come meaningless, below 5%, at the end of the learn-

ing phase.

3.2 Moral Learning

In this second phase the model receives additional ex-

periences, that of the moral emotion learning, with

the objects as stimuli, followed by an image in which

there could be the angry face. This face will pop up

only when an object of the ﬁrst kind, the apple, ap-

pears in the right bottom quadrant in the scene. This

is a sort of private property, and the owner reacts with

sadness and anger when his fruit has been grasped.

Now the amygdala gets inputs from both the OFC

map and directly from the thalamus, when the angry

face appears, as from equation (11), and learns its

connections. In this case, there is an implicit rein-

forcement learning as well, with the negative reward

embedded in the input projections to the amygdala.

In Fig. 4 there are the percentages of decisions

to grasp the apple fruit, decoded as before from the

vmPFC map. In this case, the samples of the edible

object have been divided in two groups, depending

on the position in the scene. It can be seen how the

model develops a strong inhibition to grasp the edi-

ble objects when placed in the forbidden sector. At

the end of this development phase the cases of trans-

gression have dropped below 1%. The percentage of

decisions to collect fruits inside the free area of the

scene are always high in all this phase, with values

above 90% at the end of the development. It can be

claimed that the model has learned a moral rule, as an

imperative inhibition to perform certain actions.

3.3 Conclusions

We have described a ﬁrst attempt to simulate moral

cognition in a neurocomputational model. It has sig-

niﬁcant limitations, and we think its contribution to

the progress of moral science will be modest. First,

the model is able to simulate only one kind of moral

situation, the temptation of stealing food, and the po-

tential consequent feelings of guilt. Since morality

is a collection of several, partially dissociated mech-

anisms, a model must necessarily, at least in its ﬁrst

implementation, choose a speciﬁc one to target. Sec-

ond, even in the single case of stealing, and conse-

quent guilt, the model is missing many brain areas

that are potentially involved, like the cingulate cortex

and the hippocampus, to name few.

Both the design of the moral situation, and the ar-

chitecture of the brain areas, derive from a compro-

mise between manageability of the model, and the

level of knowledge of the functions in brain areas po-

tentially involved. The food stealing situation offers

the advantage of adopting external signals, visual and

of taste, with a well established connections in cru-

cial areas included in the model, like the orbitofrontal

cortex and the amygdala.

While the schematic external world of the model

is a pale resemblance of a typical real situation of hu-

man moral decision, it is a major advance with re-

spect to any existing neural model of decisions. For

example, in the ANDREA model (Litt et al., 2008)

there is only a single input that signals a gain when

positive and a loss when negative; in the models of

Frank and co-workers the input is a combination of

4 possible abstract cues (Frank and Claus, 2006). In

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

116

this model the brain circuits for decisions and emo-

tions have been complemented by a visual system and

a simpliﬁed taste input, allowing the simulation of a

schematic worlds where moral relevant events take

place.

Therefore, even in its crudely simpliﬁed form, the

model simulates a typical moral situation, using the

relevant stimuli, and plausible neural mechanisms, in

a hierarchy of areas that capture the essence of the

moral decision to be done. We believe that the neu-

rocomputational approach is an additional important

path in pursuing a better understanding of morals, and

this model, despite the limitations here discussed, is a

valid starting point.

REFERENCES

Bechara, A., Damasio, A. R., Damasio, H. R., and Ander-

son, S. W. (1994). Insensitivity to future consequences

following damage to human prefrontal cortex. Cogni-

tion, 50:7–15.

Bednar, J. A. (2009). Topographica: Building and analyz-

ing map-level simulations from Python, C/C++, MAT-

LAB, NEST, or NEURON components. Frontiers in

Neuroinformatics, 3:8.

Boll, S., Gamer, M., Kalisch, R., and B

uchel, C. (2011).

Processing of facial expressions and their signiﬁcance

for the observer in subregions of the human amygdala.

NeuroImage, 56:299–306.

Casebeer, W. D. and Churchland, P. S. (2003). The neu-

ral mechanisms of moral cognition: A multiple-aspect

approach to moral judgment and decision-making. Bi-

ology and Philosophy, 18:169–194.

Churchland, P. S. (2011). Braintrust – what neuroscience

tells us about morality. Princeton University Press,

Princeton (NJ).

Damasio, A. (1994). Descartes’ error: Emotion, reason

and the human brain. Avon Books, New York.

Decety, J., Michalska, K. J., and Kinzler, K. D. (2012). The

contribution of emotion and cognition to moral sensi-

tivity: A neurodevelopmental study. Cerebral Cortex,

22:209–220.

Doris, J. M. and Stich, S. P. (2005). As a matter of fact:

Empirical perspectives on ethics. In Jackson, F. and

Smith, M., editors, The Oxford Handbook of Contem-

porary Philosophy. Oxford University Press, Oxford

(UK).

Frank, M. J. and Claus, E. D. (2006). Anatomy of a de-

cision: Striato-orbitofrontal interactions in reinforce-

ment learning, decision making, and reversal. Psycho-

logical Review, 113:300–326.

Frank, M. J., Scheres, A., and Sherman, S. J. (2007). Un-

derstanding decision-making deﬁcits in neurological

conditions: insights from models of natural action se-

lection. Philosophical transactions of the Royal Soci-

ety B, 362:1641–1654.

ascher, J., Hampton, A. N., and O’Doherty, J. P. (2009).

Determining a role for ventromedial prefrontal cortex

in encoding action-based value signals during reward-

related decision making. Cerebral Cortex, 19:483–

495.

Greene, J. D. and Haidt, J. (2002). How (and where) does

moral judgment work? Trends in Cognitive Sciences,

6:517–523.

Greene, J. D., Sommerville, R. B., Nystrom, L. E., Darley,

J. M., and Cohen, J. D. (2001). fMRI investigation of

emotional engagement in moral judgment. Science,

293:2105–2108.

Haber, S. N. (2011). Neural circuits of reward and deci-

sion making: Integrative networks across corticobasal

ganglia loops. In (Mars et al., 2011), pages 22–35.

Hume, D. (1740). A Treatise of Human Nature. Thomas

Longman, London. Vol 3.

Kahneman, D. and Tversky, A. (1979). Prospect theory:

An analysis of decisions under risk. Econometrica,

47:313–327.

Kelly, D., Stich, S., Haley, K. J., Eng, S. J., and

Fessler, D. M. T. (2007). Harm, affect, and the

moral/conventional distinction. Minds and Language,

22:117–131.

LeDoux, J. E. (2000). Emotion circuits in the brain. Annual

Review of Neuroscience, 23:155–184.

Litt, A., Eliasmith, C., and Thagard, P. (2008). Neural affec-

tive decision theory: Choices, brains, and emotions.

Cognitive Systems Research, 9:252–273.

Mars, R. B., Sallet, J., Rushworth, M. F. S., and Yeung,

N., editors (2011). Neural Basis of Motivational and

Cognitive Control. MIT Press, Cambridge (MA).

Moll, J., Zahn, R., de Oliveira-Souza, R., Krueger, F., and

Grafman, J. (2005). The neural basis of human moral

cognition. Nature Reviews Neuroscience, 6:799–809.

Nichols, S. (2004). Sentimental rules: On the natural foun-

dations of moral judgment. Oxford University Press,

Oxford (UK).

Plebe, A. and Domenella, R. G. (2007). Object recognition

by artiﬁcial cortical maps. Neural Networks, 20:763–

780.

Prehn, K. and Heekeren, H. R. (2009). Moral judgment

and the brain: A functional approach to the question

of emotion and cognition in moral judgment integrat-

ing psychology, neuroscience and evolutionary biol-

ogy. In (Verplaetse et al., 2009).

Prinz, J. (2008). The Emotional Construction of Morals.

Oxford University Press, Oxford (UK).

Rolls, E. (2004). The functions of the orbitofrontal cortex.

Biological Cybernetics, 55:11–29.

Rolls, E., Critchley, H., Browning, A. S., and Inoue, K.

(2006). Face-selective and auditory neurons in the

primate orbitofrontal cortex. Experimental Brain Re-

search, 170:74–87.

Rolls, E., Critchley, H., Mason, R., and Wakeman, E. A.

(1996). Orbitofrontal cortex neurons: Role in olfac-

tory and visual association learning. Journal of Neu-

rophysiology, 75:1970–1981.

Sirosh, J. and Miikkulainen, R. (1997). Topographic recep-

tive ﬁelds and patterned lateral interaction in a self-

organizing model of the primary visual cortex. Neural

Computation, 9:577–594.

ANeuralModelofMoralDecisions

117

Stevens, J.-L. R., Law, J. S., Antolik, J., and Bednar, J. A.

(2013). Mechanisms for stable, robust, and adaptive

development of orientation maps in the primary visual

cortex. JNS, 33:15747–15766.

Verplaetse, J., Schrijver, J. D., Vanneste, S., and Braeck-

man, J., editors (2009). The Moral Brain Essays on the

Evolutionary and Neuroscientiﬁc Aspects of Morality.

Springer-Verlag, Berlin.

Wagar, B. M. and Thagard, P. (2004). Spiking Phineas

Gage: A neurocomputational theory of cognitiveaf-

fective integration in decision making. Psychological

Review, 111:67–79.

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

118