
Self-Organising Fuzzy Logic Control with a New On-Line Particle
Swarm Optimisation-based Supervisory Layer
M. Ehtiawesh and M. Mahfouf
Department of Automatic Control and Systems Engineering, University of Sheffield, Sheffield, U.K.
Keywords: Fuzzy Logic, Self-Organising, Uncertainty, Optimisation, Non-Linear, Robustness.
Abstract: The Self-Organising Fuzzy Logic Control (SOFLC) which is an extended version of the Fuzzy logic
controller was designed to make Fuzzy controllers work with less dependency on previous knowledge.
Since the introduction of the SOFLC, only a few attempts have been made to create a performance index
table that is responsible for the corrections of the low-level control ‘adaptable’ according to the dynamics of
the process under control. In this paper a new dynamic supervisory layer is proposed which enables the
controller to adapt its structure on-line to any given certain performance criteria. In this mechanism, the
controller starts from an empty rule-base and uses an on-line Particle Swarm Optimisation (PSO) algorithm
to adapt the cells of the performance index (PI) table while issuing control actions to the low-level fuzzy
rule-base. The Simulation results achieved when the proposed scheme was tested on a non-linear muscle
relation process showed that it is superior to the standard SOFLC scheme in terms of accurate tracking and
efficient fuzzy rule-base elicitation (a conservative number of fuzzy rules).
1 INTRODUCTION
The concept of fuzzy logic was first introduced to
deal with uncertainties surrounding real-world
problems. Although Fuzzy Logic Controllers (FLCs)
have been successfully applied to various complex
applications, their structure in most cases must be
defined a-priori; among the usual design issues to be
resolved when fuzzy logic controllers are used
include: the determination of suitable membership
functions, the definition of a suitable rule-base size
and the derivation of fuzzy rules. In order to tackle
this issue and work with less dependent a priori
design information, Procyk and Mamdani (1979)
introduced the self-organising fuzzy logic controller
(SOFLC). The architecture of the SOFLC is shown
in Figure 1.
The SOFLC performs two functions while
operating. First, it issues the appropriate control
actions while observing the environment. Second, it
modifies the rules of the lower-level fuzzy logic
rule-base based on the observed environment. The
rule-base of the first level is adapted through the
self-organising part based on observation of the
response of the process being controlled.
Implicated control rules are modified if any
deviation from the desired (optimal) path occurs.
The self-organising mechanism allows the controller
to effectively control non-linear, mathematically ill-
understood, time-varying and uncertain systems.
However, SOFLC-based systems can also suffer
from drawbacks such as high memory storage
requirement and high computational burden
especially when the scheme is applied to
multivariable systems. The performance index (PI)
table is the main part of the adaptation process; it
normally issues the number of correction needed by
the system based on its evaluation of the control
action. Due to design difficulties, the PI table has
been left practically unchanged in most applications
since the original SOFLC scheme was introduced in
1979, where the performance index depended
entirely on predefined design information (Procky
and Mamdani, 1979).
A new SOFLC scheme with a dynamic
supervisory layer is proposed in this paper. In this
algorithm, the consequent parts of the performance
index table of the SOFLC are modified via an on-
line Particle Swarm Optimisation (PSO) algorithm
with the assistance of the idea of credit assignment
and fitness estimation; this gives the controller the
ability to update both the PI table and the lower-
level fuzzy logic rule-base at each sampling instant
given certain performance criteria. The dynamic
95
Ehtiawesh M. and Mahfouf M..
Self-Organising Fuzzy Logic Control with a New On-Line Particle Swarm Optimisation-based Supervisory Layer.
DOI: 10.5220/0005033200950102
In Proceedings of the International Conference on Fuzzy Computation Theory and Applications (FCTA-2014), pages 95-102
ISBN: 978-989-758-053-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

supervisory layer gives more flexibility to the
controller and allows it to work with a wider range
of applications.
Figure 1: The basic structure of the SOFLC ( Procky and
Mamdani,1979).
The rest of this paper is organised as follows:
Section 2 gives an introduction to the standard
SOFLC scheme. Section 3 introduces the proposed
SOFLC scheme. The simulation study that evaluates
the new SOFLC scheme is presented in Section 4.
Finally, Section 5 summarises conclusions relating
to this new proposed algorithm and future work
plans.
2 THE STANDARD SOFLC
ALGORITHM
The SOFLC scheme includes a policy that allows it
to adapt its structure with respect to the process
under control and the environment in which it is
operating. The SOFLC consists of two parts as
shown in Figure 1: Part ‘B’ which is the standard
Mamdani-type fuzzy logic controller, and Part ‘A’
which represents the self-organising mechanism that
monitors and evaluates the performance of the
controller. Part ‘A’ consists of: performance index
table, process model, state buffer, and rule modifier.
The input signals to the two levels are taken at
each sampling instant in the form of error (E), and
error change (CE), and they are both used to
evaluate the performance of the system. In order to
make the controller applicable with a wide range of
applications, Both E and CE are scaled through
tuning factors as shown in Figure 1, before being
sent to the controller. The output of the controller is
calculated with respect to the input signals according
to the fuzzy control rules issued by Part ‘A’.
Another tuning factor is used to scale the output
control signals before they are sent to the process.
The fuzzy rules are modified through the
following strategy; it is assumed that for a system
with a time lag of m samples, the control action
applied at ‘nT-mT’ is the most responsible for an
undesirable response at the sampling instant ‘nT’.
Hence, the adjustment rule reads as follows:
→
→
(1)
Where P
i
(nT) is the modification value issued by
the PI table.
The process model in Part ‘A’ of the controller is
used to reflect the degree of coupling between the
input and the output signals. This is crucial when the
SOFLC is used to control multivariable systems, for
instance, if the process to be controlled is a multi–
input / multi-output process, the rules modifications
are given as:
(2)
Where
.
.
.
,
.
.
.
P
o
(nT) is the correction issued by the PI table tables,
Pi(nT) is the manipulated input variable to the
process and M is an incremental model of the
process.
A gain of 1 is assigned in the model if the
SOFLC is used to control a SISO process. The state
buffer records the values of error, change of error,
and output signals to enable the rule modifier to
determine the rules responsible for any undesirable
trajectories. The performance index table is derived
based on the knowledge of the expert, or the
operator, and is normally constructed from standard
linguistic statements. The PI table can be
represented by a ‘look up’ table if the inputs are
assumed to be fuzzy singletons (Procyk and
Mamdani, 1979). Table 1 shows a typical
performance index table.
Table 1: A typical performance index table.
NB: negative big, NS: negative small, ZO: zero,
PS: positive small, PB: positive big.
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
96

In the next section, the idea behind the proposed
algorithm that uses a dynamic performance index
table will be outlined.
3 A DYNAMIC SUPERVISORY
LAYER USING THE ON-LINE
PARTICLE SWARM
OPTIMISATION ALGORITHM
The PSO is used in the proposed algorithm to
modify the performance index table of the SOFLC at
every sampling instant with only one particle from a
population being evaluated at that instant. The other
particles in the PSO population are then estimated
based on their relationship to the one applied to
process (optimal one); Figure 2 shows the structure
of the proposed scheme.
3.1 The PSO Process Encoding
In the proposed algorithm, the rules of the
performance index table are optimised by ‘N’ sets of
the PSO algorithm, where the number of these sets
‘N’ is decided by the number of cells in the PI table.
Each PSO set is independent and does not depend on
other PSO sets and only includes a small size of
particles. At each sampling instant, particles of the
set that represents the consequence of the PI table
will carry out one iteration ( equations 3 and 4) to
generate new particles and velocities , the remaining
‘N-1’ PSO sets in the other cells are kept unchanged.
Various PI tables with different sizes were tried
and good results are achieved when a PI table with
25 cells was used and was therefore adopted in this
paper; the inputs of the PI table are taken as the
tracking error and the change of error, while the
output of the table is rule modification value
P
i
(nT)
of the low-level basic fuzzy logic controller. Each
rule of the PI table is optimised through a PSO set
which consists of 5 particles. With such a population
size, a fast convergence is achieved, thus making the
optimisation process computationally inexpensive.
In the first generation, the 5×25 particles and
velocities are randomly generated, all particles are
given the same fitness values and a random particle
is selected in each set to fill the corresponding cell
of the PI table.
Figure 3 shows an example of how PI rules are
updated in the proposed algorithm and how the low-
level fuzzy logic controller is modified. At the
sampling instant ‘nT’, the cell ‘F24’ which produced
the modification value P
i
(nT-mT) at the sampling
instant ‘nT-mT’ is recalled again. All the 5 particles
in this cell experience one iteration of the PSO-
based operations after being given various rankings
based on the estimated fitness values, resulting in
new particles and velocities in this cell. If this cell
‘F24’ is visited again by the SOFLC algorithm, the
shaded particle ‘0.6’ in part B, for instance, with the
highest fitness (optimal particle), will be selected to
generate the modification value. In the meantime ,
the cell ‘F41’ is responsible for providing the lower-
level fuzzy logic rule-base with the modification
value
P
i
(nT) .The shaded particle ‘0.2’ in set A is the
one with the highest fitness and will be selected to
produce the modification value.
The new generated fuzzy rules are stored in a
rule bank and are added to this bank according to
this mechanism: a new rule can be added to a
particular cell of the rule bank if there is no rule in
this cell, otherwise the existing rule will be replaced
by the new one.
Figure 2: The detailed structure behind the proposed
SOFLC algorithm.
3.2 The on-Line PSO Algorithm
PSO has been classically developed for use in off-
line optimisation. In this technique, the social
behaviour among particles flying through a
multidimensional search space is simulated using
equations 3 and 4. In the off-line schema, swarms
which represent sets of solutions evolve for a
number of generations in order to produce the best
solution which is used as the system output. For
instance, when the PSO is used to tune a PID
controller (Oi et al., 2008), the optimisation is
carried out off-line based on a mathematical model
that represents the process to be controlled. At each
iteration, all the particles in the swarm are tested
through a fitness function to evaluate their suitability
to control the process; the best obtained solution is
then used in the real system afterwards.
Self-OrganisingFuzzyLogicControlwithaNewOn-LineParticleSwarmOptimisation-basedSupervisoryLayer
97

1
11
22
(3)
1 1
(4)
where Xi and Vi are the positions and the velocities
of the particles respectively. p
i
is the best position to
the time t, while p
g
is the global best position. W is
the inertia weight which usually decreases linearly
from 0.9 to 0.4; c
1
and c
2
are known as the
acceleration coefficients, and are usually set to 2.0;
while r
1
and r
2
are random numbers in the range
[0, 1].
The above process cannot be implemented if the
PSO is used to tune the PID parameters on-line due
to various issues that normally arise. First, during
on-line optimisation there is no model-based
evaluation techniques which can be used to assign
fitness values to each particle, hence, the fitness
values may be given based on noisy feedback
signals. Second, in on-line optimisation, only one
particle can be evaluated at each iteration as the PSO
must provide an appropriate control action at every
sample instant. Third, PSO normally needs a few
iterations before it converges and this is sometimes
not possible due to the limitation on the allowed
amount of computation that can be done between
sampling instants.
Figure 3: The self-organised information flow in the new
proposed algorithm.
To overcome the constraints stated above, a new
version of the PSO is proposed in this paper that
allows on-line optimisation, where only one particle
of the swarm is measured while the remaining
particles are estimated via a credit-assignment
mechanism according to their relationship with the
optimal particle. To the best knowledge of the
authors, such a mechanism that allows the PSO to
operate successfully on-line has never been
proposed before in the literature.
3.3 Evaluation of Trials
3.3.1 Performance Assessment
In order to improve the performance of the system,
the controller needs to update itself at each sampling
instant, and this can be achieved through two main
strategies. First, there are global criteria, such as
‘integral of the absolute error’ (IAE), which
measures the performance of the system over a
complete response trajectory. This type of evaluation
is not sufficient for the on-line PSO as it does not
provide accurate evaluation of the contribution of
each individual to every control action. Hence, this
type of measure can be used in most cases for off-
line performance measurement.
An alternative type of performance measure is a
local criterion which evaluates the performance of
the system over only limited neighbour states. The
predictive error function can then be used to predict
the future tracking points so that corrective actions
are taken in advance to avoid any undesirable
deviations from the target.
The polarity of the predictive error function can
be used to provide a performance evaluation in the
form of binary ‘good’ or ‘bad’ (Linkens and
Nyongesa, 1995). Although satisfactory results are
normally achieved with this technique, the modified
type of this local criterion proved to give better
results (Lu and Mahfouf, 2005) and was adopted in
this work. In this assessment type, a straightforward
ternary representation was used instead of the binary
performance evaluation where the cases that the
output responses can take are classified into three
groups as shown in figure 4. The output response is
considered ‘satisfactory’ if the current tracking error
is larger than the predicted tracking error, regardless
of the trend, while it is considered as ‘overshoot’ if
the trajectory passes across the target, and is
considered as ‘moving away’ if the response is
moving away from the set-point.
Figure 4: The classification of the performance; ‘sgn’
refers to the polarity of the signal.
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
98

The predictive error function is normally expressed
by the simple expression as follows (Linkens and
Nyongesa, 1995):
̂
(5)
Where
and
are the error and the
velocity of the process respectively at the sampling
instant ‘nT’, k is the number of steps predicted
ahead.
However, it was found that adding the error
acceleration
to the expression above results in
a more accurate estimation.
3.4 Credit Assignments
In Section 3.3.1 the performance assessment is used
as a mechanism for measuring the performance of
the particle X
j
that is applied to the system. In order
to compare the fitness values of all the particles in
this generation, it is also important to rate the
usefulness of the other four particles in this activated
set F
ij
. This task is carried out through the credit
assignment using the reward/penalty mechanism (Lu
and Mahfouf, 2005). The idea of ‘reinforcement
learning’ (Linkens and Nyongesa, 1995) is used as
the criterion, which states: ‘if a particular action is
associated with a satisfactory state of affairs then the
tendency to reproduce that action in a similar
situation should be enhanced’.
Since different particles in one generation
represent different modification values and results
therefore in different responses, the possible
performances (satisfactory, moving away or
overshoot) of the remaining four particles X
k
(k=1,2,..,, i-1,i+1,..,M) from the particle X
j
can be
inferred, where M is the population size in each PSO
set, which is 5. With such an inferred performance,
each individual can be assigned a reward or a
penalty (punishment); the degree of punishment or
reward depends entirely on the difference between
these individuals and the optimal individual that is
applied to the system as shown in Figure 5.
Punishments and rewards in this mechanism are
made with respect to making the tracking error
converge to ‘zero’.
4 SIMULATION RESULTS
4.1 Biomedical System
In order for patients to have a predefined degree of
paralysis during operations, they are given muscle
relaxant drugs through a certain dose. This is
normally done by an anaesthetist who sometimes
fails to maintain a steady level of relaxation.
Another safer method is to replace the
anaesthetist with a closed-loop infusion controller
which can be tested by applying it to a mathematical
model that represents a patient.
Figure 5: The credit assignment mechanism used to
estimate the PSO individuals.
4.1.1 Muscle Relaxant Model
The human muscle relaxation can be expressed by
the following linear transfer function (Mahfouf and
Linkens, 1998):
1
1
4
1
1
1
(6)
With the following nonlinearity:
.
.
0.404
.
(7)
Where K
1
=1; T
1
=34.4 min; T
2
=4.8 min; T
3
=3.08
min; T
4
=10.65 min; X
E
is the drug concentration in
the blood and X
eff
is the actual output which is the
muscle relaxation.
A step length of 0.1 and sampling interval of 1
are used for the simulation study, and the initial
conditions of the muscle relaxant model are zero. In
an equally portioned universe of discourse, five
Gaussian membership functions are used for both
input signals E and CE: negative big (NB), negative
small (NS), zero (ZO), and positive small (PS),
positive big (PB).
A set point profile of 85%, 65% and then 85%
muscle relaxation is used. The cells of the
performance index were optimised on-line through
the algorithm summarised in Section 3.4.
Figure 6 and Table 2 show the simulations
results of the proposed SOFLC scheme and the
standard SOFLC scheme that has a fixed
performance index table. The PI table used for the
Self-OrganisingFuzzyLogicControlwithaNewOn-LineParticleSwarmOptimisation-basedSupervisoryLayer
99
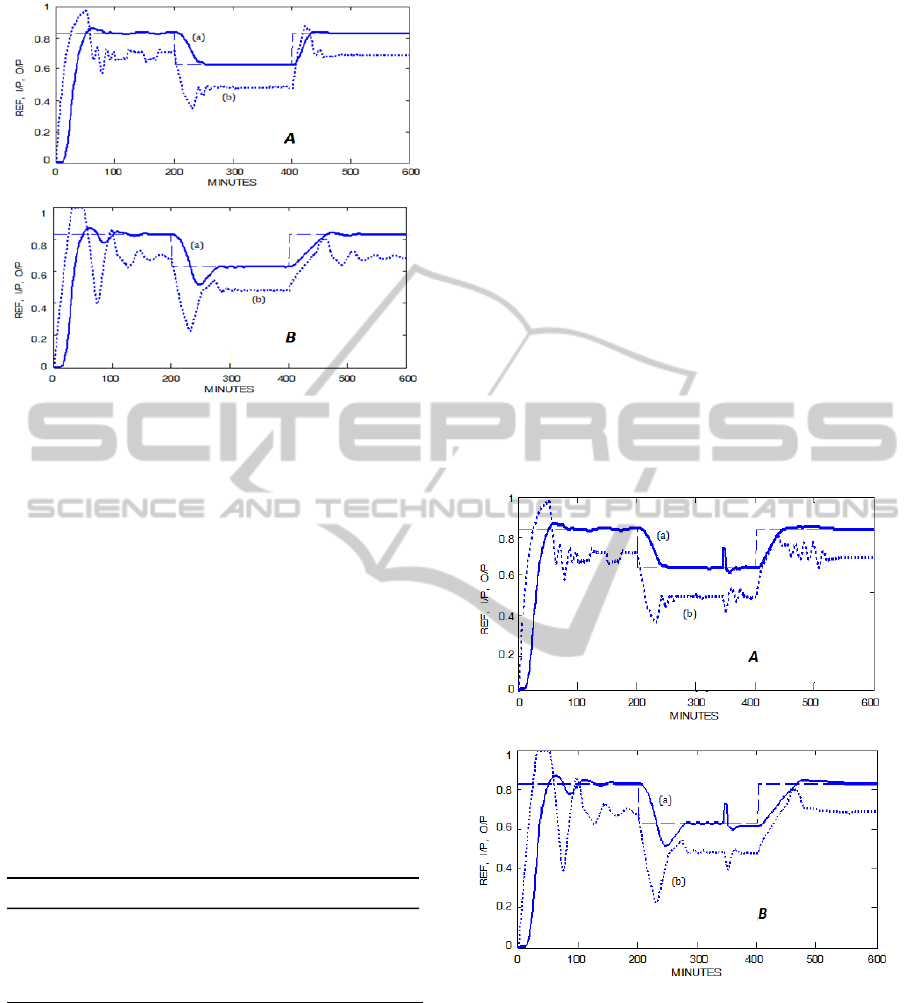
(a) Output signal (O/P); (b) input signal (I/P)
Figure 6: Simulation result of the proposed scheme (A);
and the standard scheme (B).
standard SOFLC is shown in Table 1. It can be seen
from the simulation results that the proposed SOFLC
scheme outperforms the standard SOFLC in terms of
making the system track the set-point (REF)
effectively with less undershoot, and how the
number of generated fuzzy rules in the low-level
FLC via the self-organising mechanism is smaller in
the proposed algorithm which leads to a lower
computational burden. It is concluded from the
results that the proposed SOFLC scheme has a more
accurate modification mechanism which has a lesser
degree of dependency on the operator/expert
knowledge.
Table 2: Summary of performance criteria of the proposed
SOFLC and the standard SOFLC.
Criteria Proposed SOFLC Standard SOFLC
IAE 345.849662 423.5136
ISE 177.1556 199.6294
Rule number 15 21
4.2 Robustness to Sudden Disturbances
In order to investigate how well the proposed
SOFLC scheme responds to on-line parameters
changes without the need for re-tuning, the output of
the process (muscle relaxation) is disturbed by 10%
at 345 min.
It can be seen from Figure 7 how the SOFLC
with fixed PI table fails to re-track the set-point after
the sudden disturbance for nearly 150 minutes. On
the other hand, the proposed algorithm manages to
bring the system output to track the target. Table 3
also shows how the proposed algorithm performs
better under the IAE and ISE criterion and how it
controls the system with a lower number of fuzzy
rules.
4.3 Robustness to Variable System
Dynamics
According to the nature of the human body, not all
bodies have the same characteristics. Hence, the
muscle relaxation process that represents a patient
differs from one person to another.
In order to test the capability of the proposed
algorithm to control different muscle relaxation
processes, the controller was applied to two different
models which consider the ratio of parameter change
in biomedics.
(a) Output signal (O/P); (b) Input signal (I/P)
Figure 7: Simulation result of the proposed scheme (A);
and the standard scheme (B) when undertaking a
disturbance of 10%.
The system response and the performance indices
are shown in Figures 8 and 9 and Table 4.
The simulation results show that the new
proposed scheme provides a good system
performance in terms of accurate tracking and
efficient fuzzy rule-base elicitation even when new
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
100
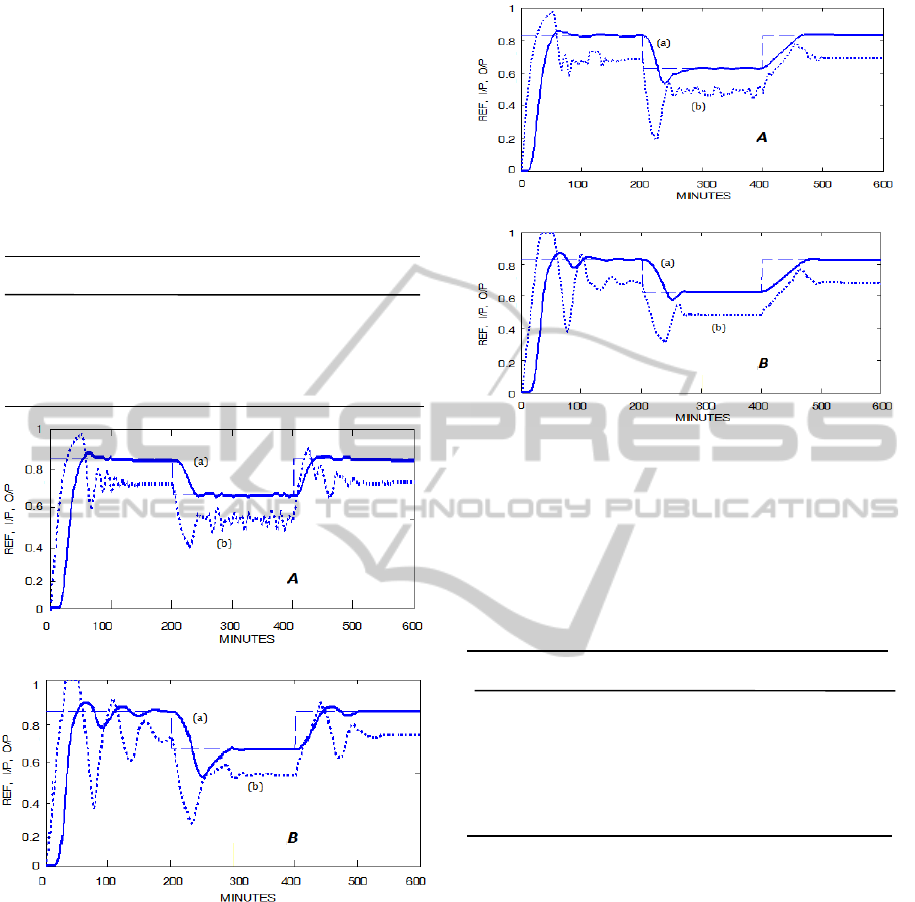
sets of model parameters are used. Conversely,
residual errors are noticeable in both Figures when
the standard SOFLC Scheme that uses a fixed
performance index table was applied, especially as
in Figure 8. This shows that the proposed controller
leads to superior performances when compared with
the standard scheme.
Table 3: Summary of performance criteria of the proposed
SOFLC and standard SOFLC while undertaking a
disturbance of 10%.
Criteria Proposed SOFLC Standard SOFLC
IAE 371.0260 446.4187
ISE 179.2902 201.9575
Rule number 19 23
(a) Output signal (O/P); (b) Input signal (I/P)
Figure 8: Simulation result of the proposed scheme (A);
and the standard scheme (B) using a new set of system
parameters: T1=29.36min, T2=3.1min, T3=4.2min,
T4=7.65min.
5 CONCLUSIONS
A new SOFLC scheme with a dynamic layer has
been designed in this paper; a new PSO algorithm is
applied to make the PI table dynamic to allow the
controller to adapt its structure depending on the
system under control. The simulation results relating
(a) Output signal (O/P); (b) Input signal (I/P)
Figure 9: Simulation result of the proposed scheme (A);
and the standard scheme (B) using a new set of system
parameters: T1=29.36min, T2=2min, T3=4.2min,
T4=5.65min.
Table 4: Summary of performance criteria of the proposed
SOFLC and the standard SOFLC with new set of system
parameters.
Criteria Proposed Standard
SOFLC SOFLC
Figure 7 IAE 360.3904 434.3420
ISE 185.9737 211.0548
Rule number 16 22
Figure 8 IAE 182.6875 204.7288
ISE 384.8043 424.5817
Rule number 17 23
to a non-linear system show that good performances
are achieved even when the controller starts with an
empty fuzzy rule-base. The proposed architecture
outperformed the standard SOFLC scheme in terms
of quick convergence, computational complexity as
well as robustness against disturbances and system
parameter variations. Future research will include
the use of type-2 sets instead of type-1 sets to allow
for better generalisation properties as well as the
extension of this controller to a multivariable case.
REFERENCES
Linkens, D. A. and Nyongesa, H. O. (1995), Genetic
algorithms for fuzzy control part 2: online system
Self-OrganisingFuzzyLogicControlwithaNewOn-LineParticleSwarmOptimisation-basedSupervisoryLayer
101

development and application. IEE Proceedings:
Control Theory and Applications, 142, 177-185.
Lu, Q. and Mahfouf, M. (2005), A new efficient self-
organising fuzzy logic control (SOFLC) algorithm
using a dynamic performance index table. 16
th
IFAC
World Congress, Prague, Czech Republic, pp. 40-45.
Mahfouf, M. and Linkens, D. A. (1998), Generalised.
Predictive Control and Bioengineering, London:Taylor
and Francis.
Mahfouf, M., King, O., Denai, M., Ross, J. J. and LU, Q.
(2011), A hierarchical self-organising fuzzy logic-
based on-line advisor for the management of cardiac
septic patients. 18
th
IFAC World Congress, Milano,
Italy, pp.575-580.
OI, A., Nakazawa, C., Matsui, T., Fujiwara, H.,
Matsumoto, K. and Nishida, H. (2008), PID optimal
tuning method by Particle Swarm Optimisation. SICE
Annual Conference, 3470-3473.
Procyk, T. J and Mamdani. E. H. (1979), A linguistic
self-organising process controller, Automatica, 15(1),
pp 15-3.
Zadeh, L.A.(1965), Fuzzy sets. Information and Control,
1965. 8(3): pp. 338-353.
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
102
