
Evolutionary Inheritance in Workflow Scheduling Algorithms within
Dynamically Changing Heterogeneous Environments
Nikolay Butakov, Denis Nasonov and Alexander Boukhanovsky
e-Science Research Institute, ITMO University, Birzhevaya liniya 4, Saint-Petersburg, Russia
Keywords: Genetic Algorithm, HEFT, Evolution, Workflow Scheduling, GAHEFT.
Abstract: State-of-the-art distributed computational environments requires increasingly flexible and efficient
workflow scheduling procedures in order to satisfy the increasing requirements of the scientific community.
In this paper, we present a novel, nature-inspired scheduling approach based on the leveraging of inherited
populations in order to increase the quality of generated planning solutions for the occurrence of system
events such as a computational resources crash or a task delay with the rescheduling phase .The proposed
approach is based on a hybrid algorithm which was described in our previous work and includes strong
points of list-based heuristics and evolutionary meta-heuristics principles. In this paper we also
experimentally show that the proposed extension of hybrid algorithms generates more effective solutions
than the basic one in dynamically heterogeneous computational changing environments.
1 INTRODUCTION
Today, scientific progress dramatically depends on
the achievements of high performance
computational (HPC) researches. One of the most
important aspects of HPC environment operability is
task-scheduling management. There are several
features which commonly have to be taken into
consideration for almost all HPC environments
during the task-planning operation, they are: (a)
distributed infrastructure peculiarities, (b)
heterogeneity of computational resources,
computational models, and storage nodes, (c) price
policies, and (d) dynamically variable system state
during run-time. Because of the fact that most
present scientific problems require complicated
complex multistep computations, the workflow
formalism is chosen as an easy-to-use and
convenient way to represent scientific tasks in the
executed HPC environments. Currently, a lot of
workflow management systems exist in the scientific
field (Xhafa et al. 2008, Yang and Xin 2008) and all
of them include task scheduling functionality. A
commonly used form of scientific workflow
representation is a directed acyclic graph (DAG). In
DAG, nodes correspond to computational tasks that
should be executed in the system and edges
correspond to data dependencies (due to data
transfers). Further information and the detailed
definition of the DAG workflow formalism can be
found in Sinnen (2007). As optimal workflow (task)
scheduling is an NP-complete problem, the scientific
community is motivated to investigate new
approaches for more efficient planning in HPC
environments.
The main criterion in workflow-scheduling
optimization that should be minimized is makespan,
i.e. overall execution time (Casanova et al.).
Moreover, during makespan optimization the
scheduling algorithms must take into account many
aspects, such as data transfer overheads,
dynamically changing workload, and the user’s
specified constraints. Data transfer overheads are
especially significant for data-intensive
computations. This may lead to situations in which
one less-powerful resource used for the execution of
two or more related tasks can overcome several
powerful separated resources because of a reduction
of data-transfer cost. Constraints which may be
required by users can include limitations on cost of
transfer and computations, deadlines (especially for
early warning systems), resource preferences, and
different priorities.
State-of-the-art distributed computational
environments increases the complexity of scheduling
algorithms by including the heterogeneous aspects
of the resources employed, such as computational
160
Butakov N., Nasonov D. and Boukhanovsky A..
Evolutionary Inheritance in Workflow Scheduling Algorithms within Dynamically Changing Heterogeneous Environments.
DOI: 10.5220/0005035201600168
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 160-168
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

performance, network bandwidth, access policies for
different users, and installed software. Moreover,
sets of resources may change during the execution
process, i.e. some failures can occur or new
resources can be added or excluded from the
environment. Also the stochastic nature of the
computational environment makes it impossible to
predict precisely the amount of computational or
transfer time, even for a single task.
As mentioned previously, the goal of the
scheduling is to minimize makespan. In our previous
work, we identified the following requirements for
workflow scheduling(Nasonov et al. 2014): (a)
processing of dynamic workload without pausing for
rescheduling of operations, (b) consideration of extra
scheduling for incoming workflows without
changing the existing applied plan, (c) operation in a
dynamic distributed environment where resources
can be added at runtime and crashes can occur, (d)
consideration of task execution delays, (e)
processing of workflows’ priorities, and (f)
providing a better solution than traditional heuristics
can generate.
In order to satisfy these requirements,
traditionally two classes of algorithms are used. The
first class is a list-based heuristic such as HPS,
CPOP, PETS, or HEFT(Arabnejad, 2013 and
Topcuoglu, 2002). With some differences, all of
these algorithms of this class perform two main
steps: prioritize and sort all workflow tasks and then
schedule them in ‘task-by-task’ manner according to
assigned priority. The fact that speed of execution
and satisfied quality of solution can be addressed is
one of the advantages of this class.
The second class is meta-heuristics algorithms
such as GRASP, GA, PSO, and ACO (Singh, Singh,
2013). They search through all of solution space and
thus are able to generate final solutions with much
higher quality than list-based heuristics (Rahman et
al., 2013), but in contrast to the previous class they
require much more time to generate solutions with
better quality than list-based algorithms can propose
in similar situations.
The hybrid algorithm proposed in our previous
work combines the advantages of both classes but
still needs to improve convergence in order to be
able to generate better solutions in a hard-limited
time. The extended algorithm will be described in
detail later. Our goal in this work is to investigate
and demonstrate how the convergence and the
performance can be improved with a proposed
novel, nature-inspired approach based on reusing the
inherited population in subsequent runs of the
scheduling algorithm. It is inspired by the idea of
inheritance and survival of populations in the natural
environment when subject to different changes. We
have extended our previously developed hybrid
algorithm with this technique and use multiple
population in order to improve the quality of
generated solutions and to leverage possibilities for
parallelization and increased reliability of GA.
This paper is organized into the following
sections. In Section 2 a review of related works is
presented. Section 3 is concerned with a description
of GAHEFT, the new approach and its application to
the workflow scheduling problem; the multi-
population modification of GAHEFT algorithm
called MPGAHEFT, which leverages potentialities,
is presented there. Section 4 contains an
experimental study of the proposed approach and the
performance of the MPGAHEFT algorithm. In
Section 5 conclusions and future works are
discussed.
2 RELATED WORKS
By our investigations, at the present time, there is no
research that has been completed in the field of
scheduling algorithms in which was addressed the
reuse of inherited populations with an inconsistency
that was produced by some system changes, such as
computational resource fail. We made a review of
works which are the most closely related to our
work.
Rahman et al. (2013) investigated how different
topologies of workflow influence performance of
different kinds of algorithms, including list-based
and meta-heuristics. The authors proposed the idea
of a hybrid algorithm which uses GA to correct the
deadlines of single tasks before DCP-G start, than
DCP-G corrects scheduling during the execution
process; however, there has not been any
experimental study of this technique. There is no
further improvement on the runtime of the generated
solution by the meta-heuristic algorithm.
Xhafa et al. (2008) presented a modification of
cellular memetic algorithm (cMA) to deal with
rescheduling. The algorithm shows good quality of
generated solutions and short execution time that can
be considered suitable for the rescheduling
procedure. But, the proposed approach is adapted
only for batch jobs and can't be applied for
workflows. Also, the executing process pauses each
time there scheduling procedure is performed.
Liu X. et al.(2010) proposed a modification of
ant colony-based(ACO) method and use this strategy
for rescheduling under temporal violations. The
EvolutionaryInheritanceinWorkflowSchedulingAlgorithmswithinDynamicallyChangingHeterogeneousEnvironments
161

rescheduling procedure is applied only for the part
of the workflow that has been affected by the
system. The approach does not take into
consideration the entire structure of the workflow; in
some situations it may show worse performance than
rescheduling with the rest of the workflow. Also, the
rescheduling procedure is not immediate that leads
to execution process pausing. Also, ACO
rescheduling may take a prolonged period which
means significant loss of time and delays in
execution of workflows.
Jakob et al.(2013) proposed a hybrid two-stage
scheme for workflow rescheduling. But,
ideologically, it is absolutely different from the one
we use. The authors apply several simple heuristics
to form an initial population for an evolutionary
algorithm and search for the solution while the
execution process is stopped. By comparison, we
almost immediately create and apply an initial
planning solution generated by the HEFT heuristic.
Then we form several populations (a population
generated by a random heuristic, an adapted
inherited population, and a HEFT-based initial
population) to improve the proposed solution of the
remaining part of the queued-for-execution tasks in
the hard-limited time. Such approaches release us
from task-execution interruptions that can be
unacceptable in some cases of real workload: for
example, for workflows with small execution time.
In this case, very frequent interruptions due to the
rescheduling procedure may lead to resource
underutilization.
Cochran et al. also use a two-stage approach for
scheduling. The distinguishing feature of this work
is using regular GA for the first stage and then using
a final population in multi-population GA for
exploring different areas of solution space.
Compared with our approach, this work operates
only with batch jobs and does not employ
rescheduling at all. The usage procedure for the
inherited population is significantly different from
ours, since the authors do not anticipate multiple
runs caused by changing environment events, for
which inherited populations have to adapt to these
changes.
In the field of evolutionary dynamic
optimization, there are works dedicated to reusing
individuals and to population management.
Rohlfshagen and Xin (2010) investigate reusing
previously found global optima in order to acquire a
closer starting point than random populations can
provide toward the new global optimum. But the
main goal of the authors is to study how genotype
distance impacts the performance of a solution that
is applied on the set of test problems, while our goal
is to create a practical approach for solving a
discrete optimization problem in the workflow-
scheduling field. Also, the authors do not consider a
situation when the previously found optimal solution
is no longer valid, whereas our work proposes an
approach to make the solutions consistent and reused
in the next generation. The paper does not contain
any experimental study of the discrete dynamic
optimization problem.
Yang and Xin(2008) proposed an associative
memory-based scheme in order to record good
solutions in different points of the search space and
recall the values when the environment changes.
Compared to our work, the paper does not consider
preparation of invalidated previous solutions for the
next generation.
Given this analysis of prior works, there is no
existing approach that can efficient satisfy the
proposed above requirements for the rescheduling
procedure.
3 ALGORITHM SCHEME
3.1 Problem Definition
The workflow scheduling problem can be
formulated in the following way. Let us assume that
we have a workflow W(T, E) that consists of a set of
tasks T = {T
1
, T
2
, … T
n
} and set of dependencies
between tasks E = {<T
a1
, T
b1
>,…,< T
ak
, T
bk
>}. Each
task requires computational time to be executed.
Given the set of available computational resources R
= {R
1
, R
2
, …, R
m
} we build a mapping among tasks
and resources (T and R) in the form of a schedule,
where each task T
i
will be executed on a resource R
j
;
it also has a start time and includes an estimated end
time. The final mapping must accept all
dependencies of E, and execution intervals of
different tasks that are scheduled on the same
resource should not overlap each other and should
have makespan as minimal as possible. Also, there
can appear different violations such as are (a)
resource crash, (b) adding a new resource to the
system, and (c) workload changes, all of it need to
be handled by a scheduler with
rescheduling(recreating previously generated
schedule). Finally, we have a NP-complete single-
objective optimization problem.
3.2 GAHEFT Scheme
In our previous research (Arabnejad, 2013) we
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
162
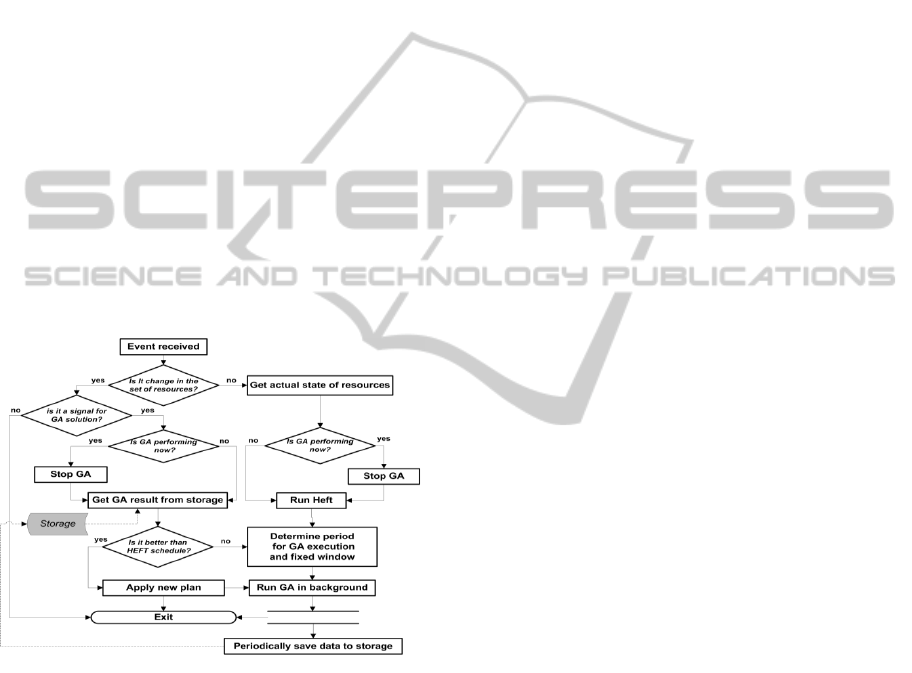
proposed a hybrid algorithm called GAHEFT which
combines, on the one hand, small execution time for
the generation of an initial suitable solution and, on
the other hand, tries to improve it with the use of a
meta-heuristic in a dynamically recalculated period
of time. The conceptual scheme of GAHEFT can be
viewed in Fig. 1.
GAHEFT consists of two main stages:
generation of the initial solution with a fast, list-
based heuristic and improving it with a more precise
meta-heuristic while the first part of the generated
schedule on the first stage is executing. The whole
procedure is the following. When rescheduling is
needed because of the generation of some event,
such as resource crash (the ‘Event received’ block in
Fig 1.), the scheduler updates information about the
state of the environment (‘Get actual state of
resources’), then it executes HEFT which generates
an initial solution (‘Run HEFT’). There are
situations when GA has been started because of a
previous event occurrence and has not reached a
sufficiently good solution at the present time; in this
case we interrupt its execution (‘Stop GA’) and run
the HEFT procedure (‘Run HEFT’).
Figure 1: GAHEFT scheme.
HEFT execution is a very cheap operation in
terms of execution time and takes almost nothing in
comparison with meta-heuristics like GA. On the
next step, the scheduler applies HEFT’s plan to
workflows execution, determines the time available
for GA performance, sets the state to unchangeable
for all the tasks which are started in the determined
time window(‘Determine period for GA execution
and fixed window’),and runs GA to improve the
schedule for the tasks out of the fixed window(‘Run
GA in background’). With the term ‘fixed window’
we mean the time interval which starts with the
resuming of interrupted workflow execution until
the point of some task finishing. It should be noted
that GA is running in the background, i.e. in parallel
with the execution of computational tasks on
resources, and every iteration it saves the best found
solution to storage(‘Periodically save data to
storage’) as it can be interrupted in the middle of the
current generation computation because of the end
of the fixed window. In this case, an appropriate
event will be generated and the algorithm will pass
by the block ‘Is it a signal to GA solution?’If a fail
occurs during execution of any fixed task in the
fixed window, GA will be interrupted and the
scheme will be started again (as explained
previously).When the final task of the fixed window
is finished, GA is stopping and the best solution is
extracted from storage (‘Get result of GA from
storage’). It will be applied if it is better than the
HEFT solution generated during the first stage. As it
was shown in our previous work, use of this hybrid
algorithm may lead to makespan improvement up to
25% in comparison to standard HEFT algorithm and
up to 10% in comparison to GA. For GA, we use
two-dimension chromosomes. The first dimension
represents computational resources where tasks of
the workflow have to be executed and the second
dimension is the order sequence of the workflow
tasks. Because of the existence of the tasks’
precedence order and transfer costs between related
tasks, it is important to have representation of a
second dimension and be able to manage it. Detailed
information about chromosome structure and other
genetic operators can be found in Yu and Buyya
(2006).
3.3 IGA
Despite all of the advantages of the proposed
GAHEFT algorithm, there remains a critical point to
provide a better solution as quickly as possible.
Since GA has only hard-limited time to find
improved solutions and may be interrupted on any
iteration when this time is expired, it must be revised
in order to increase convergence speed to deliver a
more suitable solution faster. To resolve this
problem we propose the following nature-inspired
approach. Different kinds of environmental changes
— e.g., failures of resources, task fails, adding new
resources, and excess of estimated execution or
transfer times — can be seen as disasters of different
scales like ones that occur in nature. Populations in
nature under such circumstances, and depending on
the scale of a disaster, either adapt to new conditions
and change, lose features of their individuals or get
EvolutionaryInheritanceinWorkflowSchedulingAlgorithmswithinDynamicallyChangingHeterogeneousEnvironments
163

replaced by populations of other more fit
species(Graham, 1994). An example of the first way
in nature is described in (Zimmer and Douglas,
2013),. The essence of it is the following. The
poison for defence of seeding from insects kills huge
amounts of insects, but there is some amount of the
insects that do not get enough of the poison to be
killed or which have specific genes to effectively
resist the poison. Such individuals of the population
will gain a significant edge on their fellows and
increase their proportion in the population in
subsequent generations, providing a resistance to the
poison. For the second way there is the classic
example of dinosaurs and mammals. Graham (1994)
highlights that survived dinosaurs could not find
their usual food to eat after the meteor strike because
it had been destroyed; whereas mammals could eat
insects and aquatic plants, which were relatively
intact.
So, in our case we can take the last population
from the previous run of the algorithm and try to
adapt it to new conditions. When changes are not so
dramatic— for example, we lose resources with a
relatively small number of scheduled tasks — it may
happen that a modified inherited parent is closer to
the optimal solution than the new generated ones. It
means that acceptable-by-quality solutions can be
found in several generations and provides significant
performance for algorithm execution time. In
contrast, if resource with many tasks fails, then this
procedure will serve as a randomized heuristic for
creating an initial population. Currently, we do not
consider impact of workflow structure on the
performance of this procedure and leave that to our
future works. Pseudo code of our adaptation
procedure for resource failures and our proposed
approach are shown on Fig. 2.
INPUT: storage s, finished tasks fsts , failed tasks flts, alive
nodes alns, added nodes addns, failed nodes fns.
OUTPUT: initial population for the next run.
# get the population of previous GA execution
GET inherited population ip FROM s;
FOREACH individual ind IN ip DO:
REMOVE fsts and flts FROM ind;
# handle the nodes which didn’t exist
in resource set for previous GA run
FOREACH node n IN addns DO:
ADD n to the chromosome of ind
# move left tasks from failed nodes to available nodes
FOREACH node n IN fns DO:
tasks = GET all tasks scheduled TO n
FOREACH task IN tasks DO:
K = RANDOM node FROM alns or addns;
M = RANDOM new place IN order seq of node K;
MAP task to node K IN position M;
RETURN inherited population;
Figure 2: Chromosome adaptation procedure.
Depending on the circumstances of the
environment at the moment of the failure, it may
happen that the time available for rescheduling is
enough to run GA without providing temporary
solutions. An example of such situation is illustrated
on Fig. 3. In the end of T9 task execution, the R2
resource crash has occurred and tasks T7 and T10
have to be remapped on other computational
resources as their resource is no longer available.
The algorithm has determined the duration of a fixed
window from the red line to the green line(the block
‘Determine period for GA execution and fixed
window’ in Fig. 1) that is illustrated in Fig. 3. In this
time interval no task will be finished so the
algorithm can run GA without generating a temporal
HEFT schedule.
Figure 3: Rescheduling example without HEFT.
3.4 IGAHEFT Scheme
As described earlier, adaptation can be applicable
for the GAHEFT algorithm, too. Indeed, in order to
make it possible to use the proposed procedure for
GAHEFT, we only need to account for changes
made by HEFT’s fixed window. In order to do this,
we have to remove all tasks of HEFT’s fixed
window from chromosome of each individual of the
inherited population and account for tasks which
have been scheduled by HEFT to newly added
resources. The modified adaptive procedure is
presented in Fig. 4.
INPUT: storage s, finished tasks fsts , failed tasks flts,
alive nodes alns, added nodes addns, failed nodes fns,
heft’s fixed window hw.
OUTPUT: initial population for the next run.
# get the population of previous GA execution
GET inherited population ip FROM s;
FOREACH individual ind IN ip DO:
REMOVE fsts and flts FROM ind;
REMOVE all tasks OF hw FROM ind;
SAVE info about scheduled tasks FROM hw to account it by
fitness function;
# handle the nodes which didn’t exist in resource set for previous GA run
FOREACH node n IN addns DO:
ADD n to the chromosome of ind
# move left tasks from failed nodes to available nodes
FOREACH node n IN fns DO:
tasks = GET all tasks scheduled TO n
FOREACH task IN tasks DO:
K = RANDOM node FROM alns or addns;
M = RANDOM new place IN order sequence of node
K;
MAP task to node K IN position M;
RETURN inherited population;
Figure 4: Chromosome adaptation for GAHEFT.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
164

This approach is based on the following rationale. If
workload is large enough and HEFT’s fixed window
touches only a relatively small amount of tasks, then
the impact produced by HEFT may be relatively
small and adaptation of chromosomes of the
inherited population will not change it too much.
Applicability of this scheme may be higher if we
have workload consisting of several different
workflows.
3.5 MPGAHEFT Scheme
During our investigations we also tried to reduce
algorithm execution time and increase the reliability
of the scheduling process from failure of
computational resources where the scheduler is
executed. Also, Nguyen et al. (2012) highlight that
multi-populational schemes are increasing in
popularity and receiving much attention from the
scientific community of evolutionary dynamic
optimization.
Figure 5: MPGAHEFT scheme.
Firstly, we divide the whole population of GAHEFT
into three subpopulations and evaluate them
separately from each other. Using this approach
provides a possibility to parallelize GA through
several computational resources and allow the whole
evolution process to continue its running if any
failure occurs. Also, it may help to discover different
areas of searched space and make the final solution
better; i.e., it can serve the purpose of increasing an
individual’s diversity. Randomly chosen 5% of
individuals for every subpopulation migrate each 10
generations. Secondly, we made the initial
generation for every subpopulation different. The
first subpopulation is randomly initialized as it is
done in the GAHEFT algorithm. The second
subpopulation is initialized from adapted best
individuals of the inherited population. The inherited
population for every algorithm’s run is formed by
the following scheme: all final subpopulations are
collected in one, then the individuals are sorted by
decreasing fitness values and the best representatives
are taken to the new run. For the third
subpopulation, we take the solution generated by
HEFT and apply random mutations. The scheme of
the modified algorithm is presented in Fig. 5.
The scheme is almost the same as for the
regular GAHEFT case, but several blocks are added.
After the end of the first stage (‘Determine period
for GA execution and fixed window’) MPGAHEFT
gets new populations from initializers which run in
parallel and create populations in the separated
islands (‘Determine initializers’, ‘Random
initializer’, ‘Inherited population initializer’, and
‘HEFT-based initializer’). The rest of the scheme is
the same as GAHEFT's one.
4 EXPERIMENTS
In order to verify our approach, three experiments
were done for the case of resource crashing as it is
the most frequent reason of changes in such
environments. GA parameters are: population
size,50; generations count, 100; crossover
probability, 0.8; replacing mutation probability, 0.5;
sweep mutation probability, 0.4; selection,
tournament 4 individuals. We tested our algorithms
on the well-known Montage workflow (Deelman et
al., 2004) with different task counts: 35, 50, 75, 100.
For our experimental study we determine
computational cost of every task in the workflow as
a content of runtime attribute from the xml
multiplied by a constant value (20). For any two
different resources, transfer cost is a constant greater
than zero. No one task can be parallelized; it is
computed only on one computational resource at one
single moment of time. Every computational
resource has a predefined value of power in flops
unit per unit of time. For experiments, the set of
resources consists of four resources with the
following characteristics of computational power:
10, 15, 25, and 30. The specification of the computer
used for the experimental study is: Intel core 2
Q6600 2.4 GHz, 6GB RAM, Windows 7 64bit.
4.1 GA and IGA Case
In the first experiment, we compared the GA
algorithm with IGA, which uses inherited population
EvolutionaryInheritanceinWorkflowSchedulingAlgorithmswithinDynamicallyChangingHeterogeneousEnvironments
165

for initialization step. The results are presented in
the Fig.6.a. In this experiment, Montage with 100
tasks (m100) was used. Several tasks of m100 were
chosen (0, 10, 20, 40, 50, 70, 90) and failures of
random computational resources were simulated.
Every point on the presented graphs corresponds to
the average value of 100 runs.
Figure 6.a: IGA makespan improvement in comparison
with regular GA (ID 00-70).
Figure 6.b: IGA(red) and GA(green) makespans.
The graphs show that IGA has a higher
convergence rate than regular GA provides. The
results generated by IGA on the 20th iteration are
better in most cases than the same generated by
regular GA. On the other hand, solutions generated
by IGA even on the 5th–10th iteration can be
applied to the scheduling by acceptable makespan
values (see Fig.6.b). It has more than 97% of the
optimal value for the ID00 case and more than
98.5% for ID20. For the failed ID00 case, the result
of GA becomes close enough to the IGA solution
only on the 50th iteration. For the ID70 case, the
result achieves the same values only on the 90th
iteration; for the ID40,after the 30th iteration. For
failures simulated on the ID90 step, GA-generated
results are better than IGA has, but the final
difference is approximately1–2%and IGA results are
still good enough to be used. This can be explained
by the fact that, when failure occurs on the ID90,
there are only a few tasks that still should be
rescheduled and random diversity in the initial
population can produce closer solutions to the
optimal one than the population with inheritance.
The generation of initial solutions and adapting of
inherited population take small time in comparison
with the evolution process and equals approximately
50–100 ms. For example, for ID00(Fig. 6.a) it can be
seen that the performance of GA and IGA becomes
equal only approximately 18–20 s from the start.
Thus, the result gained by IGA with 25 iterations
after 8.2 s can be achieved by GA only with 60
iterations after 19.8 s .Execution time decreases with
increasing task number because of the fact that it
depends on the count of tasks that need to be
scheduled.
For an experiment with a bigger workflow
Montage with 250 tasks we used a different
configuration of computational resources: 2x10,
2x15, 2x25, and 2x30, due to the fact that a crash of
any resource in the previous configuration leads to
very dramatic changes in the schedule because of the
workflow size.
Figure 7: IGA makespan improvement in comparison with
regular GA(Montage 250).
The approach shows better performance in
comparison with regular GA (see Fig. 7).
4.2 GAHEFT and IGAHEFT Case
In the second experiment, the GAHEFT algorithm,
which uses a randomly generated initial population,
and modified GAHEFT, which takes a previously
generated population for its initialization, are
compared. The results are presented in Fig.8
For the GAHEFT algorithm, the high speed of
convergence is an important aspect. So, it is
preferred to generate as good a result as possible on
the first iterations. The experiment shows that the
results which are generated by GAHEFT with the
inherited population (IGAHEFT) on the 20th
iteration are better than the ones generated by
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
166

GAHEFT. Also, for most cases GAHEFT could
achieve as good a result as IGAHEFT only on the
25
th
–30th iteration. GAHEFT with random initial
population generates better results for the ID00 case.
The final difference is about 5%, so the results
on this task generated by IGAHEFT are still good
enough to be used. As in the previous experiment,
for the ID90 case IGAHEFT does not outperform
GAHEFT because of the relatively small search
space, where the randomized heuristic output is
closer to the optimal one.
Figure 8: IGAHEFT makespan improvement in
comparison with regular GAHEFT(ID 00–70).
The results of makespan improvement for
IGAHEFT in most cases are worse than the ones for
GAHEFT, especially for the tasks that are closer to
the beginning of workflow execution. This can be
explained by the fact that when the failures of the
resource occur at the beginning of the workflow
there is a high possibility that many other tasks have
been scheduled on the failed resource. In contrast,
when a resource with the task from the middle of
workflow execution fails, fewer tasks need to be
moved to the other resources. In the case of
GAHEFT we have a “fixed window, which can be
dynamically or statically set. In the case of a
predefined static interval equal to 6, the results
show3.5–4 % of profit on ID 10, 20, 40, 70 against
regular GAHEFT in this limited time. Also, if the
interval is shorter, then the profit is higher.
For demonstration purposes we allowed the
evolution process to continue for 100 iterations. On
ID 50 (as well as ID 90), the difference between
IGAHEFT and GAHEFT at the point of deadline is
not sufficient. But, in the case of a dynamic “fixed
window,” when the interval depends on the
remaining part of work, it can decrease and provide
better performance in comparison with regular
GAHEFT too.
For larger workflow Montage with 250 tasks we
got better performance too (see Fig. 9).
Figure 9: IGAHEFT makespan improvement in
comparison with traditional GAHEFT(Montage 250).
4.3 Multi-populational Case
Also, we compared our multi-populational algorithm
with regular GAHEFT. We chose several tasks and
simulated failures of random resources and applied
the both algorithms to reschedule. The notation
AxB, for example 20x3, means that MPGAHEFT
uses 3 subpopulations and each one has 20
individuals whereas GAHEFT uses a single
population with 60 individuals. The simulation was
repeated 100 times for every chosen task for each
workflow and then the mean value of all obtained
results for every workflow is calculated. The
migration scheme is circular with random choice of
migrants. The results are on Fig.10. MPGAHEFT
shows improvement for all cases varying from
4.15% to 16.42%. The experiment demonstrates an
efficient growing trend with decreasing of number of
tasks in the workflow: from m100 (max=7.95%) to
m35 (max=16.42%). This can be explained by the
fact that the dimension of the solution space is
smaller for workflow with 35 tasks and it is easier to
find a better solution. The second emphasized trend
is increase of the makespan improvement with the
decrease of the count of individuals.
Figure 10: MPGAHEFT makespan improvement in
comparison with regular GAHEFT.
EvolutionaryInheritanceinWorkflowSchedulingAlgorithmswithinDynamicallyChangingHeterogeneousEnvironments
167

For the 50x3 configuration, with a total 150
individuals, the improvement ranged from 4.15% to
11.25% while for 20x3 configuration the
improvement ranged from 7.95% to 16.42%. By our
investigations, this fact is also connected with the
dimension of searching space and size of generated
populations.
5 CONCLUSION
In this paper, various hybrid algorithm schemes for
workflow scheduling in dynamically changing
distributed computational environments are
presented. They are modifications of GAHEFT
hybrid algorithm, combining the best features of a
list-based heuristic HEFT and meta-heuristic GA.
The experiments show that the new algorithms are
more effective than basic GAHEFT and can achieve
better results up to16%. The experiments show that
our nature-inspired approach based on reusing of
inherited populations may lead to speed up in
convergence and even help to generate better results.
High rate of convergence is especially required in
hard-limited time constraints, for example, in early
warning systems scenarios.
ACKNOWLEDGEMENT
This paper is supported by Russian Scientific
Foundation, grant #14-21-00137 "Supercomputer
simulation of critical phenomena in complex social
systems". The research is done in Advanced
Computing Lab (ITMO University), which is opened
in frame of 220 Decree of Russian Government,
contract #11.G34.31.0019.
REFERENCES
Arabnejad, Hamid. "List Based Task Scheduling
Algorithms on Heterogeneous Systems-An overview."
(2013)
Casanova, Henri, et al. "Heuristics for scheduling
parameter sweep applications in grid environments."
Heterogeneous Computing Workshop, 2000.(HCW
2000) Proceedings. 9th. IEEE, 2000.
Cochran, Jeffery K., Shwu-Min Horng, and John W.
Fowler. "A multi-population genetic algorithm to
solve multi-objective scheduling problems for parallel
machines." Computers & Operations Research 30.7
(2003): 1087-1102.
Deelman, Ewa, et al. "Pegasus: Mapping scientific
workflows onto the grid." Grid Computing. Springer
Berlin Heidelberg, 2004.
Graham, R.W. Dinosaurs: old bones and living animals.
Living Museum 56:35–37. 1994.
Jakob, Wilfried, et al. "Fast rescheduling of multiple
workflows to constrained heterogeneous resources
using multi-criteria memetic computing." Algorithms
6.2 (2013): 245-277.
Liu, Xiao, et al. "Handling recoverable temporal violations
in scientific workflow systems: a workflow
rescheduling based strategy." Proceedings of the 2010
10th IEEE/ACM International Conference on Cluster,
Cloud and Grid Computing. IEEE Computer Society,
2010.
Nasonov, Denis, et al. "Hybrid Evolutionary Workflow
Scheduling Algorithm for Dynamic Heterogeneous
Distributed Computational Environment."
International Joint Conference SOCO’14-CISIS’14-
ICEUTE’14. Springer International Publishing, 2014.
Nguyen, Trung Thanh, Shengxiang Yang, and Juergen
Branke. "Evolutionary dynamic optimization: A
survey of the state of the art." Swarm and
Evolutionary Computation 6 (2012): 1-24.
Rahman, Mustafizur, et al. "Adaptive workflow
scheduling for dynamic grid and cloud computing
environment." Concurrency and Computation:
Practice and Experience 25.13 (2013): 1816-1842.
Rohlfshagen, Philipp, and Xin Yao. "On the role of
modularity in evolutionary dynamic optimisation."
Evolutionary Computation (CEC), 2010 IEEE
Congress on. IEEE, 2010.
Singh L., Singh. S A Survey of Workflow Scheduling
Algorithms and Research Issues. - International
Journal of Computer Applications. –V.74, No 15. –
2013.
Sinnen, Oliver. Task scheduling for parallel systems. Vol.
60. John Wiley & Sons, 2007.– p. 108.
Topcuoglu, Haluk, Salim Hariri, and Min-you Wu.
"Performance-effective and low-complexity task
scheduling for heterogeneous computing." Parallel and
Distributed Systems, IEEE Transactions on 13.3
(2002): 260-274.
Xhafa, Fatos, et al. "Efficient batch job scheduling in grids
using cellular memetic algorithms." Metaheuristics for
Scheduling in Distributed Computing Environments.
Springer Berlin Heidelberg, 2008. 273-299.
Yang, Shengxiang, and Xin Yao. "Population-based
incremental learning with associative memory for
dynamic environments." Evolutionary Computation,
IEEE Transactions on 12.5 (2008): 542-561.
Yu, Jia, and Rajkumar Buyya. "Scheduling scientific
workflow applications with deadline and budget
constraints using genetic algorithms." Scientific
Programming 14.3 (2006): 217-230.
Zimmer Carl, and Douglas John Emlen. Evolution:
Making Sense of Life. Roberts, 2013.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
168
