Finding Optimal Exact Reducts

Hassan AbouEisha

Computer, Electrical and Mathematical Sciences and Engineering Division, King Abdullah University of Science and

Technology, KAUST, Thuwal 23955-6900, Saudi Arabia

Keywords:

Exact Reducts, Covering, Dynamic Programming, Knowledge Reduction, Feature Selection.

Abstract:

The problem of attribute reduction is an important problem related to feature selection and knowledge dis-

covery. The problem of ﬁnding reducts with minimum cardinality is NP-hard. This paper suggests a new

algorithm for ﬁnding exact reducts with minimum cardinality. This algorithm transforms the initial table to a

decision table of a special kind, apply a set of simpliﬁcation steps to this table, and use a dynamic program-

ming algorithm to ﬁnish the construction of an optimal reduct. I present results of computer experiments for a

collection of decision tables from UCI ML Repository. For many of the experimented tables, the simpliﬁcation

steps solved the problem.

1 INTRODUCTION

The problem of constructing a reduct with minimum

cardinality for a given decision table is one of the

key problems in the rough set theory (Pawlak, 1992;

Pawlak and Skowron, 2007; Skowron and Rauszer,

1992). It is also related to knowledge discovery, fea-

ture selection and data mining. It is well known

that this problem is NP-hard (Skowron and Rauszer,

1992). Different approximate approaches for ﬁnd-

ing minimal reducts have been presented in literature

(Hoa and Son, 1996; Wroblewski, 1995). However,

based on results of Feige for the set cover problem

(Feige, 1998), it is possible to show that, under some

natural assumptions about the class NP, the approxi-

mation ratio of the best approximate polynomial time

algorithm for reduct optimization is near to the nat-

ural logarithm on the number of pairs of rows (ob-

jects) with different decisions in the decision table

(Moshkov et al., 2008). Therefore, the improvement

of exact algorithms for reduct optimization continues

to be an important issue.

In this paper, I propose an algorithm which trans-

forms the initial decision table T into a new table T

(1)

with the same set of reducts. After that, the algo-

rithm simpliﬁes the table T

(1)

by removal of some

rows and columns (there are some analogies between

this part of the algorithm and attribute reduction al-

gorithms using discernibility matrix (Skowron and

Rauszer, 1992)). As a result, we have a new deci-

sion table T

(2)

and a subset A of the set of removed

attributes. The union of A and an arbitrary reduct

with minimum cardinality for T

(2)

is a reduct with

minimum cardinality for T. The problem of reduct

optimization for T

(2)

is equivalent to the problem of

minimization of decision tree depth for T

(2)

. The last

problem can be resolved by a dynamic programming

algorithm (Alkhalid et al., 2011).

A similar approach but with essentially more com-

plicated simpliﬁcation part (transformation of T

into

) was introduced in (AbouEisha et al., 2013). This

approach has more reduction rules that are continu-

ously executed until none of them can be applied.

In this paper, I consider a number of decision ta-

bles from UCI ML Repository (A. Asuncion, 2007)

and construct, for these tables, reducts with minimum

cardinality using the proposed algorithm.

The paper consists of four sections. In Section

2, the algorithm for reduct optimization is described.

Section 3 contains results of computer experiments,

and Section 4 provides a short conclusion.

2 MINIMIZATION OF REDUCT

CARDINALITY

In this section, I consider basic notions and describe

the algorithm for reduct optimization.

A decision table T is a rectangular table with n

columns labeled with conditional attributes f

, . . . , f

Rows of this table are ﬁlled by nonnegative inte-

gers which are interpreted as values of conditional at-

149

AbouEisha H..

Finding Optimal Exact Reducts.

DOI: 10.5220/0005035501490153

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2014), pages 149-153

ISBN: 978-989-758-048-2

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

tributes. Rows of T are pairwise different and each

row is labeled with a nonnegative integer (decision)

which is interpreted as value of the decision attribute.

The description above allows only consistent decision

tables. We say that an attribute f

separates two rows

of different decisions if the value of the attribute at

one of those rows is different than the other.

A test (superreduct) for T is a subset of columns

(conditional attributes) on which any two rows with

different decisions are separated by an attribute from

this subset. A reduct for T is a test for T for which

each proper subset is not a test for T. In other words,

a reduct is a minimal (with respect to set inclusion)

test. We denote by R(T) the minimum cardinality of

a reduct for T. Reducts for T with cardinality R(T)

will be called optimal. By P(T) I denote the number

of unordered pairs (ρ

′

, ρ

′′

) of rows of T with different

decisions.

For a = (a

, . . . , a

), b = (b

, . . . , b

) ∈ {0, 1}

, we

will write a ≤ b if a

≤ b

, . . . , a

≤ b

We now describe an algorithm for the construction

of an optimal reduct.

First, the algorithm transforms the decision table

T into a decision table T

(1)

which has n columns la-

beled with the conditional attributes f

, . . . , f

, and

P(T) + 1 rows. The ﬁrst P(T) rows r

, . . . , r

P(T)

are

ﬁlled with 0 and 1, and correspond to unordered pairs

(ρ

′

, ρ

′′

) of rows of T with differentdecisions. The row

of T

(1)

corresponding to a pair (ρ

′

, ρ

′′

) contains 1 at

the intersection with the column f

, i = 1, . . . , n, if and

only if ρ

′

and ρ

′′

have different values in the column

. The last row r

P(T)+1

in T

(1)

is ﬁlled with 0s. The

last row is labeled with the decision 2. All other rows

are labeled with the decision 1.

Each reduct of this table T

(1)

must contain an at-

tribute that separates each row r

, 1 ≤ i ≤ P(T) from

P(T)+1

. Since the value of all attributes on the row

P(T)+1

is zero, then any reduct of T

(1)

contains one

or more attributes with value 1 for all other rows. The

following statement is almost obvious.

Proposition 2.1. Decision tables T and T

(1)

have the

same set of reducts.

The next step of the algorithm (see Algorithm 1)

is to apply two reduction rules in the following order.

1. Reduction rule R

: For each pair of columns f

and f

of T

(1)

such that i 6= j and f

≤ f

, remove

column f

2. Reduction rule R

: For each row r

of T

(1)

, 1 ≤

i ≤ P(T) that is separated from the last row by

a unique attribute f

′

, add this attribute f

′

to the

partial reduct A and remove all of rows that are

separated by this attribute from row r

P(T)+1

Algorithm 1: Simpliﬁcation algorithm.

Input: A decision table T

(1)

with m = |P(T)| +

1 rows r

, . . . , r

and n conditional attributes

, . . . , f

Output: A subset A of conditional attributes and a

decision table T

(2)

A ←

(2)

← T

(1)

for each column f

of T

(2)

for each column f

of T

(2)

if i 6= j and f

≤ f

then

remove column f

from T

(2)

end if

end for

for each row r

of T

(2)

if i 6= m and there is a unique column f

of T

(2)

separating r

from r

then

A ← A∪ { f

}

remove all rows of T

(2)

that f

separates from

the last row

remove f

from T

(2)

end if

end for

We consider both rules in this order as the appli-

cation of R

may introduce more applications of R

but not vice versa. R

states that if an attribute f

sep-

arates all pairs of rows separated by f

then we can

replace f

by f

in any reduct containing f

and we

still have a reduct. R

describes the fact that if a pair

of rows are separated by only one attribute then this

attribute must belong to any reduct.

It is clear that the space complexity of this step

of the algorithm is O(|P(T)| × n) where |P(T)| is the

number of unordered pairs of rows of T with differ-

ent decisions and C = n is the number of conditional

attributes of T. The ﬁrst rule of the simpliﬁcation al-

gorithm has time complexity of O(|P(T)| × n

) while

time complexity of the second rule is O(|P(T)| × n).

Hence, the time complexity of the simpliﬁcation al-

gorithm is O(|P(T)| ×C

I denote by T

(2)

the table obtained after the appli-

cation of R

and R

. It is clear that this table contains

the row r

P(T)+1

. One can prove the following state-

ment.

Proposition 2.2. The union of each optimal reduct

for T

(2)

with the set A obtained after the application

of R

and R

is an optimal reduct for the table T.

The last step of the algorithm is the construction,

for the decision table T

(2)

, a decision tree Γ with min-

imum depth. It is not difﬁcult to prove the following

statement.

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

150

Proposition 2.3. The set B of attributes attached to

the path in Γ from the root to a terminal node which

accepts the row r

P(T)+1

is an optimal reduct for the

table T

(2)

Therefore the set A∪ B is an optimal reduct for T.

Figure 1 presents an example of a decision table

that we use to illustrate the notions and algorithm.

0 1 0 0

1 0 0 0

1 1 1 1

Figure 1: Decision table

This decision table contains three rows, three

conditional attributes f

, f

and f

in addition to the

decision attribute d. We have here two reducts only:

{ f

, f

} and { f

}. The set of tests (superreducts)

is {{ f

, f

}, { f

, f

}, { f

, f

}, { f

, f

}, { f

}}.

P(T) = {{r

, r

}, {r

, r

}} where r

denotes the ith

row of T and |P(T)| = 2.

Let us illustrate the algorithm by applying it to the

decision table in Figure 1. The algorithm transforms

this decision table into a new decision table T

(1)

pre-

sented in Figure 2.

1 0 1 1

0 1 1 1

0 0 0 0

Figure 2: Decision table T

(1)

The algorithm then applies the reduction rule R

twice and remove the columns f

and f

as f

≤ f

and f

≤ f

. Finally, R

is applied only once where

the attribute f

is added to the partial reduct A so that

A = { f

}. In the end, we obtain the decision table T

(2)

that does not contain any conditional attributes and

only one row with the decision 0. A decision tree Γ

with minimum depth for T

(2)

contains only one node

labeled with the decision 0. Hence, a reduct with min-

imum cardinality for table T is { f

To construct Γ, I use a dynamic programming al-

gorithm implemented in the system Dagger (Alkhalid

et al., 2011) which ﬁnds a subset of the set of all de-

cision trees with minimum depth for a given decision

table. As subproblems of the initial problem (decision

table) this algorithm uses subtables of this table given

by conditions of the kind “attribute = value”. I call

these kind of subtables separable subtables. The run

time of this algorithm is polynomial in the number of

separable subtables of the input table. In the worst

case, this algorithm has exponential time complexity

relative to the size of decision table. However, it is

applicable, usually, to medium size decision tables.

3 RESULTS OF EXPERIMENTS

In this section, I present experimental results for 23

datasets (decision tables) from UCI ML Repository

(A. Asuncion, 2007). I perform a set of preprocessing

steps on these datasets in order to handle problems

such as: inconsistencies and missing values. Some

tables contain missing values so I ﬁll each such value

with the most common value of the corresponding at-

tribute. Inconsistencies with the decision table may

appear when a group of identical rows are labeled

with different decisions. In that case, such group is

represented by a single row labeled with the most

common decision of this group. Finally, redundant

attributes that have the same value for all rows of the

table are removed.

Table 1 contains information about decision tables

and results of experiments:

• name of initial decision table T;

• size of decision table T – the number of condi-

tional attributes #atts and rows #rows;

• number P(T) such that the number of rows in T

(1)

is equal to P(T) + 1 (the number of attributes in

(1)

is the same as in T);

• size of ﬁnal decision table T

(2)

– the number of

conditional attributes #atts and rows other than the

last row #rows;

• cardinality |A| of the set of attributes A con-

structed during the simpliﬁcation of T

(1)

;

• minimum cardinality R(T) of a reduct for T;

• Time

is the time in seconds taken for creating

(1)

from T and then transforming it into T

(2)

;

• Time

is the time taken in seconds for ﬁnding op-

timal reducts in T

(2)

with Dagger.

A Mac Pro desktop with 16 GB of RAM memory

and dual Intel(R) Xeon(R) processors of 2.67 GHz is

used for the experiments. Both phases of the algo-

rithm are run sequentially. The time of each phase is

measured on average of ten executions of this stage

for each data set.

For 15 out of the 23 considered data sets, the re-

duction rules in the simpliﬁcation part of the algo-

rithm managed to ﬁnd the optimal reduct. It also re-

duced the number of attributes of other data sets dra-

matically such as: kr-vs-kp and soybean-small. Data

sets solved by the simpliﬁcation part of the algorithm

FindingOptimalExactReducts

151

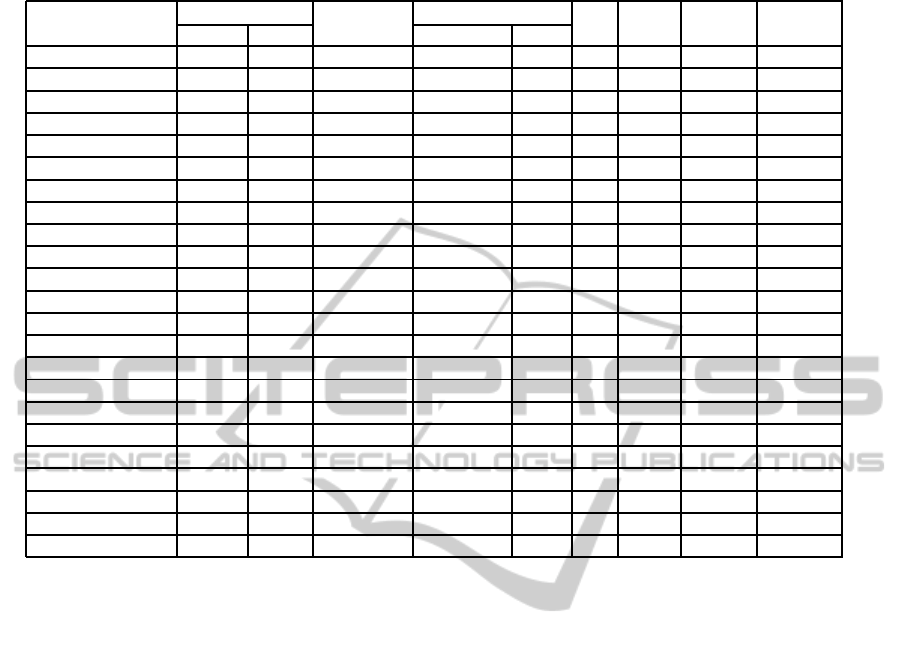
Table 1: Characteristics of decision tables and results of experiments.

Decision table T Size of table T P(T) Size of table T

(2)

|A| R(T) Time

Time

#rows #atts #rows #atts

adult-stretch 16 4 48 0 2 2 2 0.001

balance-scale 625 4 111168 0 0 4 4 0.036

breast-cancer 266 9 14440 0 1 8 8 0.007

cars 1728 6 682721 0 0 6 6 0.312

hayes-roth-data 69 4 1548 0 0 4 4 0.001

house-votes-84 279 16 17204 4 6 10 11 0.012 0.137

kr-vs-kp 3196 36 2548563 18 9 27 29 6.168 0.196

lenses 24 4 155 0 0 4 4 0.006

lymphography 148 18 5801 5801 18 0 6 0.003 33.653

monks-1-test 432 6 46656 0 3 3 3 0.021

monks-1-train 124 6 3844 0 3 3 3 0.002

monks-2-test 432 6 41180 0 0 6 6 0.016

monks-2-train 169 6 6720 0 0 6 6 0.002

monks-3-test 432 6 46512 0 3 3 3 0.011

monks-3-train 122 6 3720 0 2 4 4 0.001

mushrom 8124 22 16478528 16478528 19 0 4 75.026 329.542

nursery 12960 8 57319460 0 0 8 8 78.86

shuttle-landing 15 6 54 0 1 5 5 0

soybean-small 47 35 810 810 14 0 2 0.002 0.727

spect-test 169 22 1288 11 14 8 11 0 0.185

Teeth 23 8 253 0 2 6 6 0

tic-tac-toe 958 9 207832 207832 9 0 8 0.08 2.937

zoo-data 59 16 1405 105 14 2 5 0.002 0.43

have zero as the number of rows and/or columns.

Some data sets have zero rows and more than zero

columns as our implementation of the algorithm ﬁn-

ishes its work once no more rows need to be separated

from the last row.

The simpliﬁcation phase of the algorithm

achieved fast runtime for most of the data sets with

exception of mushroom and nursery due to the

huge size of the table T

(1)

. A simple brute force

algorithm may ﬁnd optimal reducts by considering

each possible subset and testing whether it form a

reduct or not. Such brute force algorithm would

have complexity of Ω(2

× P(T)) on table T with

n conditional attributes. It will be very difﬁcult to

apply this algorithm on data sets such as: kr-vs-kp,

mushroom, nursery and soybean-small.

Note that the dynamic programming algorithm is

used if |A| < R(T). If |A| = R(T) then an optimal

reduct A for T is constructed during the simpliﬁcation

of the table T

(1)

. In such cases, the value of the cell

Time

for this data set is empty.

The dynamic programming algorithm solved T

(2)

in a considerably fast time for all data sets with excep-

tion of lymphography and mushroom due to the large

number of separable subtables of each.

4 CONCLUSION

We considered a new algorithm for reduct cardinal-

ity minimization. Results of experiments for decision

tables from UCI ML Repository showed that this al-

gorithm is applicable to medium size decision tables.

One bottleneck of our algorithm is the memory

used to store the table T

(1)

as for large data sets the

size of T

(1)

may not accommodate the main memory.

This challenge may be studied in future work by de-

veloping an external memory algorithm to deal with

large tables. Another interesting possibility is a com-

parative study with other algorithms for ﬁnding exact

optimal reducts.

REFERENCES

A. Asuncion, D. N. (2007). UCI machine learning reposi-

tory.

AbouEisha, H., Farhan, M. A., Chikalov, I., and Moshkov,

M. (2013). An algorithm for reduct cardinality mini-

mization. In GrC, pages 1–3.

Alkhalid, A., Amin, T., Chikalov, I., Hussain, S., Moshkov,

M., and Zielosko, B. (2011). Dagger: A tool for analy-

sis and optimization of decision trees and rules. Com-

KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

152

putational Informatics, Social Factors and New Infor-

mation Technologies: Hypermedia Perspectives and

Avant-Garde Experiences in the Era of Communica-

bility Expansion, pages 29–39.

Feige, U. (1998). A threshold of ln n for approximating set

cover. J. ACM, 45(4):634–652.

Hoa, N. S. and Son, N. H. (1996). Some efﬁcient algorithms

for rough set methods. Proceedings of the sixth Inter-

national Conference on Information Processing Man-

agement of Uncertainty in Knowledge Based Systems,

pages 1451–1456.

Moshkov, M. J., Piliszczuk, M., and Zielosko, B. (2008).

Partial Covers, Reducts and Decision Rules in Rough

Sets - Theory and Applications, volume 145 of Studies

in Computational Intelligence. Springer.

Pawlak, Z. (1992). Rough Sets: Theoretical Aspects of

Reasoning About Data. Kluwer Academic Publishers,

Norwell, MA, USA.

Pawlak, Z. and Skowron, A. (2007). Rudiments of rough

sets. Information Sciences, 177(1):3–27.

Skowron, A. and Rauszer, C. (1992). The discernibility

matrices and functions in information systems. In In-

telligent Decision Support, pages 331–362. Springer

Netherlands.

Wroblewski, J. (1995). Finding minimal reducts using ge-

netic algorithms. In Proccedings of Second Joint An-

nual Conference on Information Sciences, pages 186–

189.

FindingOptimalExactReducts

153