
Multi-Agent Intention Recognition using Logical Hidden
Semi-Markov Models
Shi-guang Yue, Ya-bing Zha, Quan-jun Yin and Long Qin
College of Informaiton System and Management, National University of Defense Technology, Changsha, HN, China
Keywords: Multi-Agent Intention Recognition, Probabilistic Graphical Models, First Order Logic, Duration Modeling,
Logical Semi-Markov Models.
Abstract: Intention recognition (IR) is significant for creating humanlike and intellectual agents in simulation systems.
Previous widely used probabilistic graphical methods such as hidden Markov models (HMMs) cannot
handle unstructural data, so logical hidden Markov models (LHMMs) are proposed by combining HMMs
and first order logic. Logical hidden semi-Markov models (LHSMMs) further extend LHMMs by modeling
duration of hidden states explicitly and relax the Markov assumption. In this paper, LHSMMs are used in
multi-agent intention recognition (MAIR), which identifies not only intentions of every agent but also
working modes of the team considering cooperation. Logical predicates and connectives are used to present
the working mode; conditional transition probabilities and changeable instances alphabet depending on
available observations are introduced; and inference process based on the logical forward algorithm with
duration is given. A simple game “Killing monsters” is also designed to evaluate the performance of
LHSMMs with its graphical representation depicted to describe activities in the game. The simulation
results show that, LHSMMs can get reliable results of recognizing working modes and smoother probability
curves than LHMMs. Our models can even recognize destinations of the agent in advance by making use of
the cooperation information.
1 INTRODUCTION
Intention recognition (IR) in simulation is to identify
the specific goals that an agent or agents are
attempting to achieve (Sadri, 2011). Since goals are
always hidden in mind, they can only be inferred by
analysing the observed agents’ actions and/or the
changes in the state (environment) resulting from
their actions. IR is significant for creating human-
like and intellectual agents in real time strategy
games, artificial societies and other simulation
systems. Agents who recognize intentions of
opponents and/or friends can make counter and/or
cooperative decisions efficiently.
As an intersection of psychology and artificial
intelligence, the IR problem has attracted many
attentions for decades (Schmidt et al., 1978). Hidden
Markov models (HMMs), which are special cases of
dynamic Bayesian networks (DBNs), have been
widely used to recognize intentions in different
scenarios. For example,
Zouaoui-Elloumi etc. built an
autonomous system to detect suspicious ship in a
port based on HMMs (Zouaoui-Elloumi et al.,
2010). Dereszynski etc. learnt probabilistic models
of high-level strategic behaviour and recognized the
adversarial strategies in a real-time strategy game
(Dereszynski et al., 2011).
One problem of HMMs is that the Markov
assumption cannot always been satisfied. Thus,
some refined models are proposed by modelling
duration and transition of hidden states more
accurately, or introducing hierarchical structures.
For example, hidden semi-Markov models (HSMMs)
improve the recognition performance by modeling
duration explicitly (Yu, 2010). They have been used
to infer complex agent motions from partial
trajectory observations in the IR domain (Southey et
al., 2007). The typical refined hierarchical models
include hierarchical HMMs (Fine et al., 1998) and
abstract HMMs (Bui et al., 2002). Thi Duong et al.
further proposed Coxian switching hidden semi-
Markov model, which both built a hierarchical
structure and introduced Coxian distribution
modeling the duration of states to recognize human
activities of daily living (Duong et al., 2009).
701
Yue S., Zha Y., Yin Q. and Qin L..
Multi-Agent Intention Recognition using Logical Hidden Semi-Markov Models.
DOI: 10.5220/0005036707010708
In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),
pages 701-708
ISBN: 978-989-758-038-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Another problem of HMMs is that they are
actually propositional, which means they handle
only sequences of unstructured symbols. Therefore,
Kersting et al combined HMMs and first order logic
and proposed Logical hidden Markov models, which
belong to statistical relational learning methods
(Kersting et al., 2006). Comparing with HMMs,
LHMMs can infer complex relations and have fewer
parameters by adding instantiation process. However,
they do not consider relaxing Markov assumption,
which will lead to a similar performance decline
when long-term dependences between hidden states
exist as HMMs. Thus, we presented logical hidden
semi-Markov models (LHSMMs) by using the idea
of HSMMs (Zha et al., 2013). Even though our
previous work has proved the achievement of
applying LHSMMs in IR, we only consider
intentions of one single agent. However, most
complex tasks have to be done by one or more
teams. Agents always play different roles and
cooperate to achieve their common goals. In this
case, multi-agent intention recognition (MAIR)
problems have to be solved, which means that we
need to recognize not only the intentions of every
agent, but also the composition and cooperation
mode of teams (Pfeffer et al., 2009).
Since LHSMMs inherit advantages of LHMMs
and relax the Markov assumption, we will use
LHSMMs to solve MAIR problem, as an extension
to our previous work. Besides considering intentions
of more than one agent, we will refine the previous
models further in three aspects. First, logical
predicates and connectives are used to present the
working modes of the team. Second, Conditional
transition probabilities are applied which make
transition probabilities depend on previous
observations. Third, the alphabet of instances are
changeable during the inference, because the number
of simulation entities may change because of dying,
escaping and reinforcement. The former forward
algorithm with duration variable (LFAD) which is
the core of the inference is also adjusted according
to the modification of models. A simple virtual game
“Killing monsters” is designed to evaluate the
performance of LHSMMs in MAIR. In this game,
two warriors move around and kill monsters on a
grid map, they can both act individually and
cooperatively. In the simulation, we use lognormal
distribution to model the duration of working modes
(abstract hidden states), and compute the
probabilities of working modes, monsters being
chosen at each time. We will show that LHSMMs
can correctly recognize working modes and
intentions of warriors in the game. Additionally,
LHSMMs can even recognize the destinations of the
agent in advance by making use of the cooperation
information.
The rest of the paper is organized as follows: the
next section will gives the formal definition of
LHSMMs, the inference algorithm, and a directed
graphical representation of a game is presented.
Section 3 presents the simulation and results.
Subsequently, we have a conclusion and discuss the
future work in Section 4. In this paper, we will apply
LHSMMs to recognize intentions of two agents and
their working modes in a simple virtual game.
2 LOGICAL HIDDEN SEMI-
MARKOV MODELS
This section will introduce the LHMMs, which will
be used to recognize intentions of agents and the
working mode. We will give a formal description of
models and the inference process in 3.1 and 3.2
respectively. A multi-agent game is also designed to
evaluate the models in 3.3.
2.1 Model Definition
LHSMMs extend LHMMs by modelling the
duration of the hidden abstract states just as HSMMs
extend HMMs. In this paper, we further refine our
former models by redefining the logical alphabet,
the selection probability and the transition matrix.
A LHSMM is a five-tuple
,,,,Ms ΣμΔ D
,
the
{}
t
Σ records possible instances for the
variables in every abstract state at every time. Since
the number of simulation entities may change
because of dying, escaping or reinforcement, the
Σ
depends on observations available up to time t, (
t
is the logical alphabet at time t given
1: 1 2
,,,
tt
OOOO
).
{}
t
μ
is a selection
probabilityset over
Σ
,thus it is also a function of
1:t
O
.
Δ
is the transition matrix defining transition
probabilities between abstract states. Abstract
transition are expressions of the form
:
O
pH B
where
0,1p
,
B
,
H
and
O
are logic sentences
which represents hidden states. A
is a substitution,
and
B
B
is one state of
GB
, where
GB
represents the set of all ground or variable-free
atoms of
B
over the alphabet
, so are
H
and
O
.
We also use the idea of logical transition in
Natarajan et al.’s LHHMMs (2008) and let the value
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
702

of
p
in
Δ
depend on instances and observations.
Figure.1 gives an example of conditional transition
probabilities from the abstract states A(X).
1
() ()
1
() ()
2
() ()
2
() ()
:()
1,
:()
()
:()
2,
:()
AX BY
AX CZ
AX BY
AX CZ
p
BY
if condition then
p
CZ
AX
p
BY
if condition then
p
CZ
Figure 1: An example of conditional transitions from an
abstract state.
A(X), B(Y) and C(Z) are abstract states, X, Y
and Z are objects in these predicates,
1
() ()AX BY
p
,
1
() ()AX CZ
p
are the probabilities of states switching
from A(X) to B(Y) and C(Z) respectively when
condition 1 is satisfied by current observations. The
meanings of
2
() ()AX BY
p
and
2
() ()AX CZ
p
are similar.
Let
B
BGB
,
B
HB
HGH
and
BHO BH
OGO
. Then the model makes a
transition from state
B
B
to
B
H
H
and emits
symbol
B
HO
O
with probability
||
BH B BHO BH
pH H O O
(1)
is a set of abstract transitions encoding a prior
distribution, which has a similar representation as
Δ
,
except that any
B
in
is the start state with no
instance. In addition, any self-transition probability
in
Δ
is forced to be 0, and the duration distribution
of hidden states will be defined in
D
. Let B be the
set of all atoms that occur as body parts of
transitions in
Δ
,
D
define the duration distribution
and the corresponding emissions of every atom in B.
Elements of
D
are representations :
d
d
pB B
O
,
where
d
O is the set of 1d observations emitted
between
B
(
B
appears d times in this duration).
In this paper, we will define
1
()
d
d
d
pj fxdx
,
1, 2,d ,where
f
x
is the probability density
function of the lognormal distribution
log ( , , )norm
,
and
indicate the mean and
standard variance of
log x
respectively. And
they both depend on
j
s
, which is a instantiated
hidden state.
is the threshold and we make it 0.
Since
d
pj
is usually small when d is far from its
expectation for
j
s
, lognormal distribution is more
suitable to represent the lasting time of an intention
than the geometric distribution.
LHSMMs inherit the graphical representation
from LHMMs. Every node in the directed graph
represents an abstract state which is a predicate with
one or more terms. The transition will begin from
the Start node according to
. After reaching an
abstract state, the node has to be instantiated using
Σ
and
μ
. There are three kinds of edges representing
transitions: the solid, the dotted and dashed ones.
The detailed and formal descriptions of graphical
models can be found in reference (Kersting, 2006)
Actually, LSHMMs are special cases of LHMMs,
when
D
only contains geometric distributions.
2.2 Inference
Online intention recognition is a filter problem
computing
1:
Pr | ,
tjt
SsOMs
, where
j
s
is the
instantiated hidden abstract state at time
t . The
notion of
j
s
is similar with nodes in HMMs. It
indicates the abstract state and corresponding
instantiated results. The
M
s
is the parameter set.
Since
M
s
is known in the process of inference, it
will be neglected in this part for simplicity. And we
can compute the posterior probability by
1:
1:
1:
1:
1:
Pr ,
Pr |
Pr
Pr ,
Pr ,
tjt
tjt
t
tjt
tjt
j
SsO
SsO
O
SsO
SsO
(2)
For simplicity of notation in the following
section, we also denote:
12
[, ]tt j
Ss
,
j
s
starts at time
1
t and ends at
2
t with
duration
12
1dtt
. This also implies that the
state at time
1
1t
and
2
1t
can not be
j
s
.
12
,]tt j
Ss
,
j
s
starts before time
1
t and ends at
2
t
with duration
12
1dtt. This also implies that
1
1tj
Ss
the state at time
2
1t can not be
j
s
.
12
[,tt j
Ss
,
j
s
starts at time
1
t and will not end at
2
t with duration
12
1dtt. This also implies that
2
1tj
Ss
the state at time
1
1t can not be
j
s
.
Since we do not know whether
j
s
will end at time
t , we have to compute the
1:
Pr ,
tjt
SsO
by
Multi-AgentIntentionRecognitionusingLogicalHiddenSemi-MarkovModels
703

1: ] 1:
max
[, 1] 1:
12
Pr , Pr ,
Pr ,
tjt t jt
td
tt d j t
tdtt
SsO S sO
SsO
(3)
The first part is the probability that the hidden state
.the probability of this part will be 0;
In LHSMMs,
1
S is always the start state, whose
duration is 1, so we can make 1t
and compute the
[, 1] 1:
Pr ,
tt d j t
SsO
by
[, 1] 1:
1] 1: 1
[, : 1] 1: 1
Pr ,
Pr ,
Pr , | ,
tt d j t
tit
i
tt j tt t i t
SsO
SsO
SsOS sO
(4)
The meaning of
1] 1: 1
Pr ,
tit
SsO
is similar with
]1:
Pr ,
tjt
SsO
, and
[, : 1] 1: 1
Pr , | ,
tt j tt t i t
SsOS sO
means that the
hidden state switch
i
s
to
j
s
at time 1t
and the
j
s
will last to time 1t at least with observations
:tt
O
.Since both
:tt
O
and
[,tt j
Ss
are only
determined by
1]ti
Ss
, we only need to compute
[, : 1]
Pr , |
tt j tt t i
SsOS s
as follows:
[, : 1]
11
:
11:
1
Pr , |
||
1|
O
tt j tt t i
tj Bt t BH
pH B
d
dtttj
d
SsOS s
psH OO
pj O s
(5)
B
and
H
are results of
,
i
mgu B s
and
,
j
mgu H s
respectively, where
mgu
is the most general unifier
(MGU) operation in first-order logic.
11
||
tj Bt t BH
psH OO
is the
probability that
i
s
transfers to
j
s
and emits
t
O
,which
is similar with equation (1),
11:
1
1|
d
dtttj
d
pj O s
is the probability
that
j
s
lasts for more than d times and emits
1:tt
O
.Then, we will sum all
B
which satisfies
i
s
in
Δ
.
Thus, the key problem is to compute
]1:
Pr ,
tjt
SsO
, which can be solved using a
logical forward algorithm with duration (LFAD). In
the LFAD, the forward variable
[1,] 1:
Pr ,
td t j t
SsO
is represented as
,
t
id
, and
,
j
d
p indicates the probability of duration d for
j
s
.
The pseudo-code of LFAD is given in Figure 2.
After using LFAD,
]1:
Pr ,
tjt
SsO
can be obtained
by
,
t
d
dj
.
2.3 Graphical Representation
To evaluate the performance of LHSMMs using in
MAIR, we design a simple game named “Killing the
monsters”. There are 2 warriors and 4 monsters on a
grid map. The warriors know the locations of
monsters, and warriors’ mission is to find the
shortest path to the chosen monster, get there and
kill it. The map and location information can be
0
:1
1:
2: 1,2, ,
3: 1:
4:
5:
6: max. . : .. ,
7: ..
8:
9:
10 : ,
td
t
jtd
O
Bj
iBH Btdt BH
it
tt i
t
SStart
for t T do
for d t do
S
foreach s S do
f
oreach spec p H B s t mgu s B exists do
foreach s H G H s t O unifies with O
if s S then
SS s
id
,:1
1:
0
11: , , , | |
t t td jd td i B td tdt B H
dtd
id id jd p p s H O O
Figure 2: The pseudo-code of the LFAD.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
704

found in Figure 3
Figure 3: Initial positions in the grid map.
The red points are locations of monsters that will
stay there and not move around. The green points
are start points of the warriors, in each step, warriors
may go into one of the four adjacent places or stay at
current one. However, a warrior cannot get through
the place where a live monster stands, except that
the monster is chosen to be killed by him.
WAGo(MX) and WBGo(MX) are predicates
which mean Warrior A and Warrior B go to the
destination MX respectively. Re(MX) is a function
which returns the resembling point adjacent to MX.
The abstract state 3 represents warriors act
individually. The dotted lines from state 3 have the
same meaning as they are in LHMMs, these lines
imply that the abstract state from 4 to 5 cannot stay
for a moment, their functions are changing the
instance of destinations when state 3 terminates. The
abstract state 2 means that warriors will go towards
assembling points together. However, it is notable
that results of Re(MX) are uncertain and are
sampled from a known distribution. The conditional
transitions are depicted in Figure 4(a)and Figure 4(b).
Figure 4(a): Conditional transitions from abstract state 3.
(, ,Re( )) 1: 7
2
1: 3
if IsReached A B MX then
else then
Figure 4(b). Conditional transitions from state 2.
(, )
I
sKilled A MX is a predicate which means
Monster MX is killed by Warrior A. And
(,,Re( ))
I
sReached A B MX means both A and B have
reached the resembling point before going to kill
their target MX. The observations are position series
of warriors which can be used to judge whether the
transition conditions are satisfied. The directed
graphical representation of our game is depicted in
figure 5.
3 SIMULATION
To evaluate the performance of LHSMMs using in
MAIR, we set parameters manually and run the
game. Since learning algorithm is not discussed in
this paper, these parameters will be used directly.
The conditional transition probabilities are given in
Table 1.
Table 1: The conditional transition probabilities.
1
3,4
p
1
3,2
p
1
3,6
p
2
3,2
p
0.6 0.4 0.6 0.4
1
3,5
p
2
3,2
p
2
3,4
p
3
3,2
p
0.6 0.4 0.6 0.4
When the warrior is moving towards his
destination, there may be more than one shortest
path, and the warrior will choose one of them with
an equal probability. Similarly, the assembling point
is chosen by a uniform distribution. It is also
assumed that the duration of abstract state 2 and
state 3follow the same distribution.We collect the
duration data and learn parameters of the
log ( , , )norm
using distribution fitting tool.
Then, the abstract self-transition probability
p
in
LHMMs can be made equal to
1/
, since the
expectation of
g
eo p
is 1/ p .
We select one typical set of traces of the warriors
after several runs. The warriors both executed
missions individually and cooperatively, and the
working mode has even been terminated twice
before the chosen monster was killed. The detailed
information is shown in Table 2.
1
3,4
12
1
3,2
1
3,6
11
2
3,2
1
3,5
22
2
3,2
2
3,4
3
3,2
:4
(, ) (, )
:2
:6
(, )
:2
3
:5
(, )
:2
:4
:2
p
if IsKilled A M IsKilled A M then
p
p
if IsKilled A M then
p
p
if IsKilled A M then
p
p
else then
p
Multi-AgentIntentionRecognitionusingLogicalHiddenSemi-MarkovModels
705

Figure 5: The directed graphical representation of the game.
Table 2: The set of traces.
No. Durations
Abstract
states
Instances Interrupted
1
1,1t
Start None No
2
2,8t
State 2 M3: 4 Yes
3
9,13t
State 3
M1: 2,
M2: 3
No
4
14,17t
State 3
M1: 1,
M2: 4
Yes
5
18,25t
State 2 M3: 3 No
6
26,26t
State 7 M3: 3 No
7
27,27t
End None No
The first working mode chosen is working
together and their target is the monster No. 4, but
warriors changed their minds and decide to go to
No. 2 and No. 3. After Warrior A completed his
mission, their abstract state changed to state 6,
which meant that both of them would have a new
target. However, since state 6 could not stay and had
to transfer to state 3, the records showed that
warriors were staying in state 3. The fourth mission
were interrupted again at t=17, and warriors decided
to go to the monster No.3 together. In this time, the
place which is in the north of the monster No.3 is
regarded as the assembling point. According to the
records, the Warrior B reached there earlier and he
waited for Warrior B for 5 steps. Then, they went to
kill the monster No.3 together and finished the
game. We used LHSMMs and LHMMs to compute
the probabilities of abstract state at each time
respectively. The results are shown in Figure 6 and
Figure 7.
Figure 6: Probabilities of abstract states computed by
LHSMMs.
Figure 7: Probabilities of abstract states computed by
LHMMs.
We only show the probabilities of abstract state
2, 3 and 7, because state 1 and 8 only exist at the
first and the last step, state 4, 5 and 6 have
transferred to state 3 during inference. The results
prove that both of models can recognize the abstract
at most times, but LHSMMs generally had a better
performance: probabilities change more smoothly
and LHMMs have a failed recognition at t=14. We
also use LHSMMs to recognize monsters being
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
706
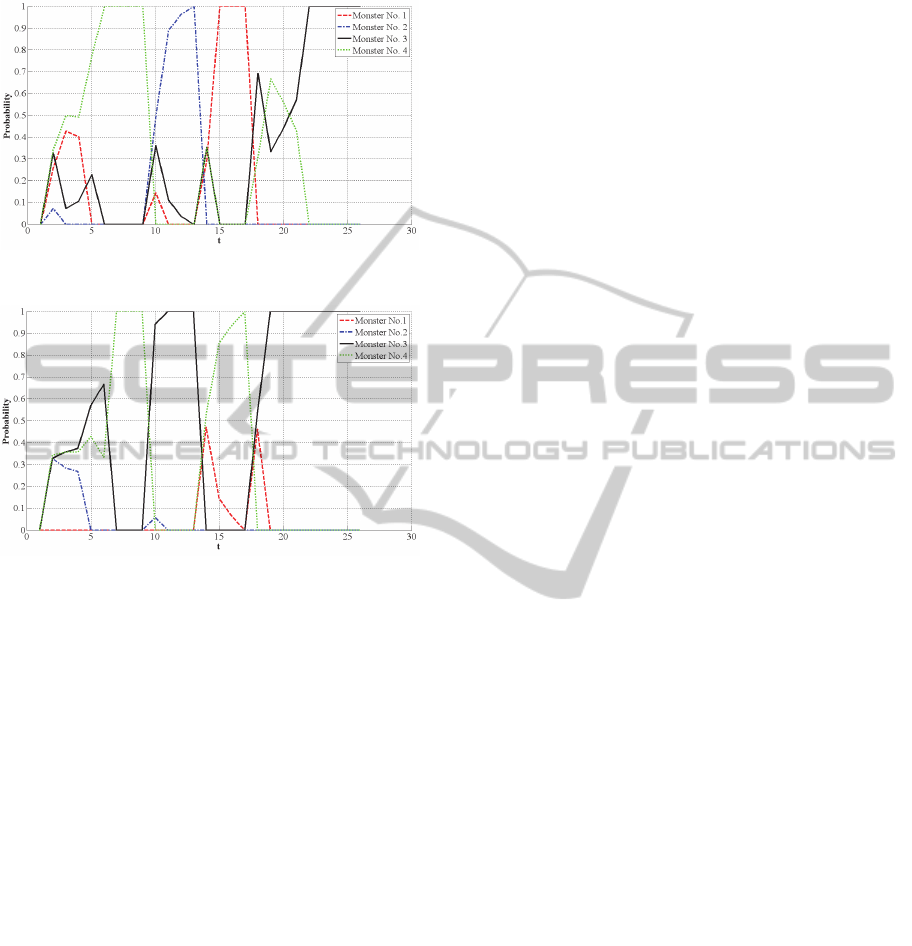
chosen by two warriors. The results are shown in
Figure8 and Figure 9.
Figure 8.Probabilities of monsters chosen by Warriors A.
Figure 9: Probabilities of monsters chosen by warriors B.
Comparing recognition results shown in Figure 8
with the instance information in Table 2, we can find
that LHSMMs have quite good performance to find
the real monster chosen by Warrior A. Although
there is a shake before t=20, the probability of
Monster increases very fast and reach 1 at t=22, that
is exactly the time when Warriors B is waiting him
at the assemble point. Thus, even though Warrior A
has not reach the assemble point we can still
recognize his destination accurately. Figure 9 also
shows the efficiency of recognizing intentions of
Warrior B using LHSMMs.
4 CONCLUSIONS
In this paper, we analyze the history of intention
recognition methods and advantages of LHSMMs
using in MAIR. We further refine our former models
by adding conditional transition probabilities and
making the alphabet of instances changeable.
According to these modifications, the inference
process of MAIR based on the LFAD is depicted.
We also design a simple game to evaluate the
performance of LHSMMs. After using first order
logic to describe the abstract states of the two
warriors, we give the directed graphical
representation of the game. The simulation results
show that LHSMMs have a good performance on
recognizing both working modes and missions of
every warrior. In addition, we also find that the
probability curves of abstract states computed by
LHSMMs are smoother than LHMMs, and the result
of working mode recognition is quite helpful to
identify the goal of members in the team. In the
future, we may do some research on modifying
Viterbi and Baum-Welch algorithm in LHSMMs.
Approximate inference algorithm which may need
less computing time is also absorbing.
REFERENCES
Bui, H. H., Venkatesh, S. & West, G. (2002), Policy
recognition in the abstract hidden Markov models,
Journal of Artificial Intelligence Research, 17, 2002,
451–499.
Duong, T., Phung, D., Bui, H., Venkatesh, S. (2009),
Efficient duration and hierarchical modeling for
human activity recognition, Artificial Intelligence,
173(7-8), 830–856.
Dereszynski, E. Hostetler, J., Fern, A. & Dietterich, T.,
Hoang, T. & Udarbe, M. Learning Probabilistic
Behavior Models in Real-time Strategy Games, In
AIIDE’2011, Proc. of the 7th In Artificial Intelligence
and Interactive Digital Entertainment, 20-25. AAAI
Press.
Fine, S., Singer,Y., & Tishby, N. (1998), The hierarchical
hidden Markov model: Analysis and applications,
Machine Learning, 32(1): 41-62.
Kautz, H. A. & Allen, J.F., Generalized plan recognition,
In AAAI’1986, Proc. of the 5
th
National Conference
on Artificial Intelligence, 32-37.AAAI Press.
Kersting K., De Raedt L. & Raiko T. (2006).Logical
hidden Markov models. Journal of Artificial
Intelligence Research, 25, 425–456.
Natarajan, S., Bui, H. H. &Tadepalli, P., et al.
2008.Logical hierarchical hidden Markov models for
modeling user activities. In ILP’2008, LNCS 2008,
192-209.Springer Heidelberg
Pfeffer, A., Das, S. & Lawless, D., et al. (2009) Factored
reasoning for monitoring dynamic team and goal
formation. Information Fusion, 10(1), 99-106.
Sadri, F. (2011). Logic-Based Approaches to Intention
Recognition. In N. Chong, & F. Mastrogiovanni (Eds),
Handbook of Research on Ambient Intelligence and
Smart Environments: Trends and Perspectives,
Hershey, PA: Information Science Reference, 346-375.
Schmidt, C. F., Sridharan, N. S. & Goodson J. L.
(1978).The plan recognition problem: an intersection
of psychology and artificial intelligence. Artificial
Intelligence, 11(1-2), 45-83.
Multi-AgentIntentionRecognitionusingLogicalHiddenSemi-MarkovModels
707

Southey, F. Loh, W. & Wilkinson, D, Inferring Complex
Agent Motions from Partial Trajectory Observations
,In IJCAI’2007, Proc. of the 20
th
International Joint
Conference on Artificial Intelligence, 2631-2637.
AAAI Press.
Yu, S. Z. (2010). Hidden semi-Markov models, Artificial
Intelligence, 174, 215–243.
Zha, Y. B., Yue, S. G. &Yin, Q.J.,et al., 2013, Activity
recognition using logical hidden semi-Markov models,
In ICCWAMTIP’2013, Proc. of 10
th
International
Computer Conference on Wavelet Active Media
Technology and Information Processing, 77-84,
UESTC Press.
Zouaoui-Elloumi, S., Roy, V. &Marmorat J P, et al.
Securing harbors by modeling and classifying ship
behavior. In BRIMS’2011, Proc. of 20
th
Annual
Conference on Behavior Representation in Modeling
and Simulation, 114-121, Curran Associates.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
708
