
Reactive Embedded Device Driver Synthesis
using Logical Timed Models
Julien Tanguy
1,2
, Jean-Luc Béchennec
2
, Mikaël Briday
2
and Olivier-H Roux
2
1
See4sys Technologie, Espace Performance La Fleuriaye, 44481 Carquefou CEDEX, France
2
LUNAM Université, Ecole Centrale de Nantes,
IRCCyN UMR CNRS 6597 1 rue de la Noë, 44321 Nantes, France
Keywords:
Real-Time Systems, Formal Modeling, Control, Logical Time, Software Synthesis.
Abstract:
The critical nature of hard real-time embedded systems leads to an increased usage of Model Based Design to
generate a correct-by-construction code from a formal specification. If Model Based Design is widely used at
application level, most of the low level code, like the device drivers, remains written by hand. Timed Automata
are an appropriate formalism to model real time embedded systems but are not easy to use in practice for two
reasons i) both hardware and software timings are difficult to obtain, ii) a complex infrastructure is needed
for their implementation. This paper introduces an extension of untimed automata with logical time. The new
semantics introduces two new types of actions: delayed action which are possibly avoidable, and ineluctable
action which will happen eventually. The controller synthesis problem is adapted to this new semantics. This
paper focuses specifically on the reachability problem and gives an algorithm to generate a controller.
1 MOTIVATION
Nowadays embedded systems realize many critical
functions. From avionics to automotive electronics
control systems, the software has grown in size and
its complexity has become more important.
The increasing number of functions and complex-
ity of such systems make software development very
difficult due to a high level of concurrency and to the
hard real-time context. Many safety-critical systems
now cooperate in real-time on several ECUs across
many communication links.
Due to the critical nature of these systems, soft-
ware vendors have to prove the functional safety of
their systems. Unit and functional tests are common
requirements, but they do not guarantee the software
is bug free. The automotive community is now push-
ing for a more formal verification of the systems’ be-
havior.
Model Based Design (MBD) methodologies are
now widely used in the industry and are a way to
address the complexity of these systems. Instead of
writing the code by hand the engineer models the sys-
tem to control and builds a model of the application.
The models can be tested and simulated. They can
also be verified if their spatial and temporal complex-
ity and their size remain practicable. At last the code
is generated automatically from the model.
In the automotive industry the AUTOSAR stan-
dard (Kirschke-Biller, 2011) proposes a framework
for MBD. It specifies an architecture and a method-
ology for the design of such systems, based on
current development methods, design best practices
and applicable international standards (such as the
ISO26262 norm (The International Organization for
Standardization, 2011)).
However if MBD is used at the application level,
basic software especially device drivers remain coded
by hand and are more prone to have bugs. For ex-
ample in the AUTOSAR standard the basic software
is a set of modules. These modules are usually de-
fined as a core of basic functionalities which can do
everything and some configuration code which selects
or refines the previously defined behaviors and wrap-
per code to encapsulate the module functionalities in
APIs — see Figure 1. The configuration code is usu-
ally generated at compile-time and compiled along
the core code, but the specification allows a post-
compilation configuration which is passed to the core
code by pointers.
This high level of configurability at every level in-
creases greatly the complexity of such systems; they
usually require multiple modules and abstraction lev-
els. It can also result in a lot of dead code and if
163
Tanguy J., Béchennec J., Briday M. and Roux O..
Reactive Embedded Device Driver Synthesis using Logical Timed Models.
DOI: 10.5220/0005040101630169
In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),
pages 163-169
ISBN: 978-989-758-038-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
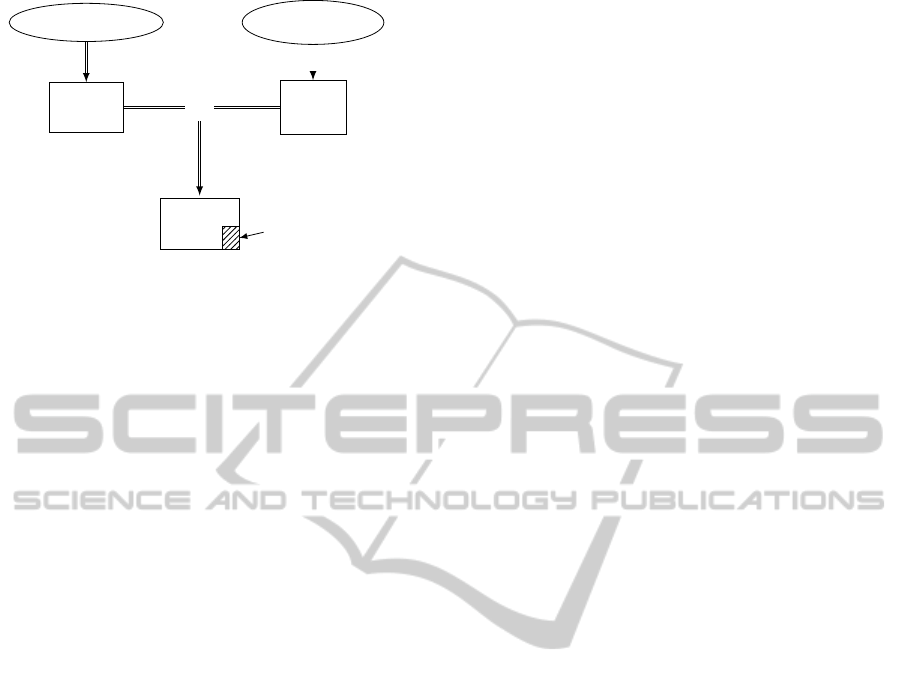
Core Model
Cfg Model
Core
Cfg
+
bin Dead code
Figure 1: Current development methodology.
the configuration is not perfectly tuned to the appli-
cation demands, so that unnecessary behaviors make
it into the code and may be executed. This comes at
the cost of decreased performance and greater mem-
ory footprint, in terms of stack size, ROM and RAM
usage. The consistency of the configuration must also
be checked in order to be sure that the driver cannot
behave in an unspecified way.
The proposed approach. Instead of doing complex
verification on existing systems, we propose to use an
MBD approach to generate the device driver. How-
ever, to reduce the flaws of the current methodology,
we combine the use of formal models, the lifting of
configuration at the model level and well-known con-
troller synthesis techniques (Ramadge and Wonham,
1989) to generate correct-by-construction software.
Given the real-time nature of these systems, the
model of timed automata (Alur and Dill, 1994) and
timed games (De Alfaro et al., 2003) is an appropri-
ate formalism to express and model the required timed
properties. In a timed game, we model two players,
the controller and the environment, playing moves at
a certain time on a shared model called the board. The
board represents all possible states of the two play-
ers and the possible actions available at all times. In
this case, the controller is the device driver, and the
environment is the hardware device along with its en-
vironment (communication bus, analog signals, etc.).
Moves played by the device driver are also known as
controllable actions and moves played by the hard-
ware device and its environment are known as uncon-
trollable actions.
Their level of expressiveness and well-known
controller synthesis techniques and tools (Behrmann
et al., 2007) allow the modeling of complex systems,
while providing a formal proof on the behavior of the
systems.
However, these timed models require a good un-
derstanding of all the components, including the
knowledge of the timings of both players. These tim-
ings are rarely known: the hardware timings are not
always described exhaustively, and the software exe-
cution times are rarely known precisely.
In addition, embedded systems hardware re-
sources (computing power, memory, etc.) are limited.
The basis of timed controlled, namely explicit clocks,
are very expensive to use in a critical embedded en-
vironment. Implementation wise, the infrastructure
needed to implement these clocks in a timed con-
troller is not acceptable for implementing real-time
systems at low level such as device drivers. In or-
der to function properly, a timed driver may need an
exact timing. These exact timings do translate into
low-level software to hardware clocks triggering in-
terrupts each time a controller needs to wait during an
arbitrary amount of time. Even with this, a controller
cannot guarantee all the timing constraints, because
interrupts might have been masked for a certain com-
putation.
Our contribution. In this paper, we explore an-
other way of modeling embedded systems, starting
from peripheral devices. We would like to derive a
controller — a device driver — without explicit timed
models. However, the untimed automata framework
does not have the necessary level of expressiveness in
order to generate useful drivers.
Beside the controllable and uncontrollable actions
used in untimed games, device drivers rely on addi-
tional behaviors of the device in order to work. These
behaviors can be reduced into two types of uncontrol-
lable actions:
• Delayed actions, that take time to complete or
cannot happen immediately, such as writing to an
external memory, sending a message on a bus,
performing a specific computation on a hardware
dedicated unit, etc. These actions come usually
with some kind of abortion mechanism, so they
are avoidable in a certain point of view. They are
modeled in an explicit timed context by guards
with lower bounds on clocks as constraints.
• Ineluctable actions, that are known to happen in
a nominal context: the end of a transmission or
a conversion, or more generally an acknowledge-
ment of the reception of a command. These can be
modeled using invariants on states, however in the
explicit timed context we need to know an upper
bound on the delay, which is not always possible
with a quantitative approach.
We propose to extend the semantics of untimed
games with two properties of uncontrollable actions:
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
164

avoidability — an avoidable action cannot disrupt the
behavior of the driver — and ineluctability — the
driver can rely on these actions to happen.
We will derive the traditional controller synthesis
problem for reachability games in this context.
2 LOGICAL TIMED GAME
AUTOMATA
In this section we propose a variant of the traditional
untimed game automata with new logical-timed se-
mantics. The modified semantics of actions let us ex-
press two important notions of timed automata: delay
and urgency. Without these notions, it is impossible
to write an untimed controller while keeping the ele-
ment of surprise. The element of surprise is necessary
in this context: a device driver should be able to react
to any hardware interrupt when it happens.
Without delays, we cannot express the fact that an
hardware action (such as analog conversions, or emit-
ting a message on a communication bus) takes times,
and as such the device driver can perform actions,
even aborting the current operation (see Figure 3).
Without urgency, we cannot model any predicted be-
havior of the device. In these kind of games, the de-
vice is expected to play every move at its disposal
to make the controller fail, including choosing not to
play, even if the controller cannot play any move in
the current state. As such, it would not make sense to
wait for something to happen (see Figure 4).
As we do not want real-valued clocks, we define a
logical time semantics for game automata. It is based
on the classical definition G = (Q,q
0
,A
C
,A
U
,δ)
where
• Q is a set of states
• q
0
∈ Q is the initial state
• A
C
and A
U
are two disjoint sets of actions for the
controller and the environment, respectively.
• δ : Q × (A
C
∪ A
U
) × Q a set of edges between
states. We denote q
a
−→ q
0
for (q,a,q
0
) ∈ E.
In addition to this definition, we also define A
a
U
⊆
A
U
and A
U
⊆ A
U
the subsets of avoidable and in-
eluctable actions, respectively. Note that these sub-
sets are independent, and may or may not intersect.
These subsets reflect a finer model of the environ-
ment: avoidable actions are actions which cannot hap-
pen instantaneously, such that we are able to avoid or
abort them before they have a chance to happen. In-
eluctable actions, on the other hand, can reasonably
expected to happen, unless a major failure occurs.
q
0
q
1
q
2
q
3
q
4
q
5
c
u
ua
ui
uai
Figure 2: Graphical notation example: Here q
0
is the initial
state, and c ∈ A
C
,u ∈ A
a
U
,ua ∈ A
a
U
,ui ∈ A
a
U
and uai ∈ A
a
U
.
q
0
q
1
q
2
q
3
start
recv
recv
recv
read
read
Figure 3: Rx part of a communication device: the uncon-
trollable actions recv represent the reception of a message.
In q
1
the data register is empty, in q
2
it is full and in q
3
it is overwritten. Because the transmission of a message
takes time, two immediate and consecutive receptions can-
not happen. In this situation, we are able to express the
ability for the driver to perform a read action between two
recv, and avoid q
3
.
For the rest of this paper, we will consider an arbi-
trary game G = (Q, q
0
,A
C
,A
U
,δ). For the following
figures, we will use the following notations:
• States are represented in circles, and the initial
state is denoted q
0
.
• Controllable transitions are represented in solid
arrows.
• Uncontrollable transitions are represented in
dashed arrows.
• Avoidable transitions start with a circle.
• Ineluctable transitions end with a double arrow-
head.
2.1 Definitions
For X ⊆ Q and Σ ⊆ A
C
∪ A
U
, we define the prede-
cessor and successor functions pre
Σ
: 2
Q
→ 2
Q
,suc
Σ
:
2
Q
→ 2
Q
: ∀q ∈ Q,q ∈ pre
Σ
(X) iff ∃a ∈ Σ and q
0
∈
X, s.t. q
a
−→ q
0
, and ∀q ∈ Q, q ∈ suc
Σ
(X) iff ∃a ∈
ReactiveEmbeddedDeviceDriverSynthesisusingLogicalTimedModels
165

q
0
q
1
send
end
Figure 4: Tx part of a communication device: the uncontrol-
lable action end represent the end of transmission interrupt.
Because of the way the bus may be structured, or saturated,
we do not know an upper bound on the reaction time, only
that it will happen eventually.
Σ and q
0
∈ X, s.t. q
0
a
−→ q. If Σ = A
C
∪ A
U
, we note
pre(X) and suc(X )
For i = C,U , we define Γ
i
: Q → 2
A
i
∪ {⊥}, with
⊥ /∈ A
i
the enabling conditions. For q ∈ Q, Γ
i
(q) is
the set of available moves for player i. The special
action ⊥ represents the act of choosing not to play in
this state.
We denote by ∆ the set {0,•}. It represents the
logical time at which an action is played. It can be
instantaneous (0), or unknown (•).
A run of a game structure is the sequence
q
0
,ha
1
,t
1
i,q
1
,ha
2
,t
2
i,q
2
,... with t
i
∈ ∆, such that
q
i
∈ Q and q
i
a
i
−→ q
i+1
for all i >= 0. Semantically,
ha,0i means that the action a is performed immedi-
ately, whereas in ha,•i, the action is performed at an
unknown time, possibly zero. We denote by R the set
of runs, and by R the set of finite runs.
For r ∈ R , we define First(r) the first state of
r, States(r) the set of states which appear in r, and
Act(r) the set of actions which appear in r. If r ∈ R ,
we define Last(r) the last state of r.
We define R
s
the set of reliable runs, which do not
depend on uncontrollable actions:
r ∈ R
s
⇔ Act(r) ∩ A
U
=
/
0
For R ⊆ R and X ⊆ Q, we denote by R|
X
the sub-
set of R such that ∀r ∈ R|
X
,States(r) ⊆ X.
3 CONTROLLER SYNTHESIS
In this section, we will solve the controller synthesis
problem using our modified semantics. The goal is
to derive a strategy for the controller to restrict the
behavior of the game.
A strategy s
i
for player i is a function s
i
: R →
2
A
i
∪ {⊥} × ∆. It is said to be memoryless if it only
depends on the current state of the run, i.e. s
i
: Q →
2
A
i
∪ {⊥} × ∆.
Let G = (Q,q
0
,A
C
,A
U
,δ) be a game structure,
and s
C
a strategy for the controller. We define the
outcome Outcome(q,s
C
) of a strategy the subset of R
defined inductively by:
• q ∈ Outcome(q,s
C
)
• If r ∈ Outcome(q,s
C
) is finite, r
0
= r
a
−→ q
0
∈
Outcome(q,s
C
) if r
0
∈ R and
– a ∈ A
a
U
;
– a ∈ A
a
U
and @(r
a
0
−→ q
00
s.t. ha
0
,0i ∈ s
C
(r)).
– a ∈ s
C
(r).
• An infinite run belongs to Outcome(q,s
C
) if all its
finite prefixes also belong to Outcome(q,s
c
)
If q = q
0
, we simply write Outcome(s
C
). The con-
trol synthesis problem can be declined into objectives,
or winning conditions. For a given game G, a winning
condition C
W
is a set of allowed runs. A strategy s for
the controller is winning if Outcome(s) ⊆ C
W
.
The result of applying a strategy on a game is also
a game whose set of runs is exactly the outcome of the
strategy. We will use both definitions indifferently.
Relation to timed Games It is possible to ex-
press some of our semantics using timed games, as
in (De Alfaro et al., 2003; Behrmann et al., 2007).
The avoidable actions for example, translate directly
into guards with a lower bound on clocks and vice
versa. However, the ineluctability cannot be trans-
lated as-is into and from timed automata. We can use
invariants on states to force the environment to play,
but as the model uses explicit clocks, we have to ex-
press an upper bound on the invariants. Our extension
here removes this need for explicits values or parame-
ters. It restricts only the behavior of the environment,
not of the controller, as it is in timed automata where
invariants apply to all players including the controller.
4 REACHABILITY GAMES
A reachability objective of the controller is to force
the game to reach a certain set of states. Formally:
Definition 1 (Reachability objective). Let G =
(Q,q
0
,A
C
,A
U
,δ) be a game, and Goal ⊆ Q a set of
goal states. A run r ∈ R is winning if it has a finite
prefix r
0
such that Last(r
0
) ∈ Goal. The set of winning
runs is denoted Reach(Goal).
q
0
q
1
G
w s
Figure 5: Example reachability game. The objective is to
reach the state G.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
166

4.1 Computing the strategy
The computation of the strategy is obtained from the
set of winning states. A state is winning for the con-
troller if it is possible to reach a goal state. The main
algorithm for computing winning strategies for reach-
ability games is a backwards fixed-point algorithm
over the controllable predecessor function.
Intuitively, a state s is a controllable predecessor
of X if the following conditions are met:
• there is an action which is guaranteed to happen
(either controllable or uncontrollable ineluctable);
• all other actions of the environment cannot pre-
vent the game to reach a state in X.
Definition 2 (Controllable predecessors). Let G =
(Q,q
0
,A
C
,A
U
,δ) be a game, and X ⊆ Q a set of
states. The controllable predecessors π(X) of X is
the subset of Q defined by:
π(X) = pre
C
(X) \ pre
U
a
(X)
∪ pre
U
(X) \ pre
U
(X)
(1)
The two parts of the formula represent two differ-
ent ways to win:
• if there is a controllable action from s to a state in
X, all uncontrollable actions must either be avoid-
able, or also lead to states in X
• if there is an ineluctable uncontrollable action, all
other uncontrollable actions must also lead to a
state in X.
The set of winning states is computed using a
backwards fixed-point algorithm.
Algorithm 3 Reachability computation algorithm
Require: Goal
Ensure: W
W ← Goal
while π(W ) 6= W do
W ← W ∪ π(W )
end while
if initial ∈ W then return Success
else return Failure
end if
From the set of winning and goal states, we can
derive a non-deterministic, memoryless strategy for
the controller. The canonical memoryless strategy s
m
c
:
W → (2
A
C
∪ ⊥, ∆) is defined by:
s
m
c
(q) =
(
⊥if @a ∈ A
C
,q
a
−→ q
0
,q
0
∈ W ,
{ha,di|a ∈ A
C
,q
a
−→ q
0
,q
0
∈ W },
where
d =
0 if ∃a
0
∈ A
a
U
,q
00
∈ Q \ W
such that q
a
0
−→ q
00
,
• otherwise.
(2)
4.2 Correctness of the computed
strategy
The partial definition of s
m
c
on W makes sense
because the strategy does not allow leaving W
(Lemma 5). Note that in the first case, the controller
waits for an uncontrollable ineluctable action to oc-
cur, which is bound to happen by definition of in-
eluctable actions, and because the current state is in
W . The second case just cuts off transitions which
would lead to loosing states.
The following lemmas and theorems hold if Al-
gorithm 3 returns successfully. To simplify the for-
mulation of the results we will always assume that it
returns successfully. For our game G, let us consider
a reachability condition in the form of Goal ⊆ Q. We
will assume that the algorithm returns successfully
and computes the set W of winning states.
Lemma 4 (Winning states). From all states in W ,
there is a sure run to a state in Goal, i.e. ∀s ∈ W ,∃r ∈
R
s
such thatFirst(r) = s and Last(r) ∈ Goal.
Proof. We will proceed by induction. We define the
following sequence:
W
k
=
(
Goal if i = 0,
W
i−1
∪ πW
i−1
otherwise.
It is trivial to see that for all states in W
0
, there is a
sure run for a state in Goal. If the property holds for
n ∈ N, we can show that it holds for n+1 by finding a
run from W
n+1
to a state in W
n
, from which we have
a sure winning run. From the definition of π, we can
see that, for all states q ∈ W
n+1
:
∃a ∈ A
C
,q
0
∈ W
n
such that ∃q
a
−→ q
0
and
@a
0
∈ A
a
U
,q
00
∈ W
n
,q
a
0
−→ q
00
,
(3)
or
∃a ∈ A
U
,q
0
∈ W
n
such that ∃q
a
−→ q
0
and
@a
0
∈ A
U
,q
00
∈ W
n
,q
a
0
−→ q
00
.
(4)
ReactiveEmbeddedDeviceDriverSynthesisusingLogicalTimedModels
167

Because the sequence is monotonic and the set of
states is finite, it necessarily converges to a limit,
W .
Lemma 5. Given s
m
c
defined by Equation 2, we have
Outcome(s
m
c
|
W
) = Outcome(s
m
c
). That is, the appli-
cation of the strategy does not leave W .
Proof. Let us procede by contradiction. Let’s
suppose that there is a run r ∈ Outcome(s
m
c
) \
Outcome(s
m
c
)|
W
. Assuming our hypotheses, that
means that there are one or several intermediate states
in r which are not an element of W . It cannot be first
because q
0
⊆ W by definition. Let’s take q the first
of these states, and denote by p the state just before q,
and a the action such that p
a
−→ q is an infix of r. We
have q ∈ W and p ∈ W . By definition, we also have
a /∈ A
U
. By definition of the outcome, we have one of
the following cases:
a ∈ A
a
U
(5)
a ∈ A
a
U
and @(p
a
0
−→ q
0
s.t. ha
0
,0i ∈ s
m
c
(p)) (6)
a ∈ s
m
c
(r). (7)
The case of 7 is not possible by definition of s
m
c
, and
because q /∈ W . This would lead to a contradiction of
the hypothesis.
If a ∈ A
a
U
(5), then by definition we have p ∈
pre
U
a
(W ), and p ∈ pre
U
(W ). By definition of π, we
have p /∈ π(W ), thus p /∈ W by definition of W . We
would have a contradiction too.
Let’s consider the case (6). The fact that there is
no possible move ha
0
,0i ∈ s
m
c
(p) implies that s
m
c
(p) =
⊥. Thus, we have p /∈ pre
C
(W ). Because a ∈ A
U
, we
have p /∈ π(W ), thus p /∈ W by definition of W .
Since all possible cases lead to a contradiction, the
hymothesis is false and thus the lemma holds.
Lemma 4, proves that the game is possibly win-
ning for the controller, with the right strategy.
We cannot prove that our generated controller in-
cludes all and only the winning runs, since it allows
infinite runs (see Figure 6).
q
0
G
a
b
Figure 6: Possibly infinite game: the canonical strategy al-
lows to do a infinitely many times before b.
We must however assure that the strategy is safe
and sound, in that it does not capture loosing runs,
and all winning runs are captured.
Theorem 6. For all r ∈ Outcome(s
m
c
),r ∈
R =⇒ ∃ρ ∈ R
s
s.t. rρ ∈ Reach(Goal)and rρ ∈
Outcome(s
m
c
)
Proof. If any finite run r does not leave W , we
have Last(r) ∈ W . Thus, by Lemmas 4 and 5
there is a finite winning run r
0
∈ R
s
such that r
0
∈
Reach(Goal), and rr
0
∈ Outcome(s
m
c
). Formally, ∀r ∈
Outcome(s
m
c
),States(r) ∩W =
/
0.
Lemma 7. For all r ∈ (Reach(Goal) ∩ R
s
)|
W
, we
have either
r ∈ Outcome(s
m
c
), or
∃r
0
∈ Outcome(s
m
c
),
such that r ∈ (Reach(Goal) ∩ R
s
)|
W
.
Sketch of proof. From Theorem 6, we know
that Outcome(s
m
c
) ⊆ R
s
|
W
. For a given run
r ∈ (Reach(Goal) ∩ R
s
)|
W
, it can either be in
Outcome(s
m
c
) or not. In the latter case, the run has
been cut at a certain point because a different action
from the environment could have spoiled the outcome
of the game (see Figure 7).
q
0
q
1
W
q
2
a
c
b
d
Figure 7: Example of a winning run cut by our strategy.
The winning run bc is cut because the controller takes a
immediately in order to prevent the environment to take d.
Because Algorithm 3 returns successfully, we can
construct a sure winning run from every state in W ,
so there is another winning run.
As a consequence, we can state the following the-
orem about the existence of solutions and our ability
to capture them.
Theorem 8. If Reach(Goal) 6=
/
0, then
Outcome(s
m
c
) 6=
/
0.
5 CONCLUSION
In this paper, we have presented a semantic extension
of untimed automata to introduce a model based de-
sign methodology in the conception of low level soft-
ware for embedded systems. This extension intro-
duces two uncontrollable actions’ properties that ex-
tend the model of the environment:
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
168

• the delayed action cannot happen instantaneously
so that the device driver can perform another ac-
tion if needed.
• the ineluctable action is guaranteed to happen
eventually, and on which the driver can rely.
This model combines some of the expressiveness
of timed games, with the simplicity of untimed au-
tomata. It allows an easier implementation of these
models, more suitable to embedded real-time sys-
tems.
We have adapted the notion of control and reacha-
bility games for this extension and defined and proved
an algorithm to solve these problems in the general
case.
However, the generated strategy can be non-
deterministic, and allows infinite runs (one can switch
infinitely many times between two states before
reaching the goal). In practice, we need to find a de-
terministic implementation of the strategy that finds
the shortest path and eliminating loops.
The goal of this work is to provide the complete
toolchain to model, configure and generate the de-
vice driver code for any given system. In order to do
so, we must extend the controller synthesis to safety
games, which deals with avoiding bad states. We will
also propose a generic implementation of the result-
ing controller to complete the methodology.
REFERENCES
Alur, R. and Dill, D. L. (1994). A theory of timed automata.
Theoretical Computer Science, 126(2):183–235.
Behrmann, G., Cougnard, A., David, A., Fleury, E., Larsen,
K. G., and Lime, D. (2007). Uppaal-tiga: Time for
playing games! In Computer Aided Verification, pages
121–125. Springer.
De Alfaro, L., Faella, M., Henzinger, T. A., Majumdar, R.,
and Stoelinga, M. (2003). The element of surprise in
timed games. In CONCUR 2003-Concurrency The-
ory, pages 144–158. Springer.
Kirschke-Biller, F. (2011). Autosar – A worldwide
standard current developments, roll-out and outlook.
www.autosar.org.
Ramadge, P. J. and Wonham, W. M. (1989). The control
of discrete event systems. Proceedings of the IEEE,
77(1):81–98.
The International Organization for Standardization (2011).
ISO/DIS 26262 - Road vehicles - Functional safety.
ReactiveEmbeddedDeviceDriverSynthesisusingLogicalTimedModels
169
