Sensor Reduction on EMG-based Hand Gesture Classification

Giovanni Costantini

, Gianni Saggio

, Lucia Quitadamo

, Daniele Casali

Alberto Leggieri

and Emanuele Gruppioni

Departement of Electronic Engineering, University of Rome “Tor Vergata”, Rome, Italy

Centro protesi INAIL, Budrio, Bologna, Italy

Keywords: Neural Networks, EMG, Hand-Gesture, Classification, Feature Selection.

Abstract: This work concerns a system based on EMG sensors, signal conditioning circuitry, classification algorithm

based on Artificial Neural Network, and virtual avatar representation, useful to identify hand movements

within a set of five. This is to potentially make any trans-radial upper-limb amputee able to drive a virtual or

real limb prosthetic hand. When using six EMG sensors, the system is able to recognize with an accuracy of

88.8% the gestures performed by a subject, and replicated by an avatar. Here we focused on differences

resulting with the adoption of a different number of sensors and therefore, by means of a very simple

heuristic method, we compared different subsets of features, excluding the less significant sensors. We

found optimal subsets of one, two, three, four and five sensors, demonstrating a decrease of the performance

of only 0.8% when using five sensors, while with three sensors the accuracy can be as high as 81.7%.

1 INTRODUCTION

The electrical activity of a muscle can be detected by

sensors able to convert electro-myogram (EMG)

signals into electric ones. Surface and intramuscular

EMGs differ from invasiveness and feasibility, and

we deal with the surface one for practical reasons.

In the recent years, different systems were

proposed to use surface EMG (sEMG) signal

acquired on human forearms as input data to control

a real prosthesis (Matrone et al., 2010) or a virtual

device (Li et al., 2010), either for interactive or

clinical/rehabilitative (Scheme and Englehart, 2011)

purposes.

Most of the EMG-controlled device users are

radial upper-limb amputees, i.e. amputation occurred

below elbow. For these people, the replacement of

missing arm functionalities could be a significant

improvement to their quality of life. Moreover

research showed that the visual-sensorial feedback

provided by following the prosthetic or virtual hand

movements can be useful to alleviate the phantom

limb pain (Castellini et al., 2009, Alphonso et al.,

2012), an invalidating condition that affects between

50% and 80% of amputees (Flor H, 2002).

Standard EMG-controlled devices have usually

relied on the detection of weak/strong contractions

of just two forearm muscles to perform very simple

movements (e.g. hand opening and closing) and this

has restricted their usability by amputees (Zlotolow

and Kozin, 2012). To avoid these limitations, pattern

recognition on multiple forearm muscle signals has

been proposed to discriminate hand movements

(Chowdhury et al., 2013). Extracted patterns of

EMG activity, which are different for each hand

movement, allow to increase the amount of usable

information and to realize a more natural, and hence

satisfactory, reproduction of the gestures. A pattern

recognition-based system is tipically structured in

three main steps:

1. EMG signal acquisition and condition by means

of an array of sensors and electronic circuitry;

2. feature extraction, consisting in the calculation

of relevant characteristics from the signals, e.g.

mean, energy, waveform length, etc.

(Phinyomark et al. 2012)

3. feature translation, or classification, to assign

the extracted features to the class (gesture) they

most probably belong to.

Once the gesture attempted by the user of the

system is recognized, it can be mapped towards the

controlled device.

In order to develop a fully reliable system to

classify the intended hand gesture of the amputee, it

seems reasonable to utilize as many EMG sensors as

138

Costantini G., Saggio G., Quitadamo L., Casali D., Leggieri A. and Gruppioni E..

Sensor Reduction on EMG-based Hand Gesture Classiﬁcation.

DOI: 10.5220/0005040501380143

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 138-143

ISBN: 978-989-758-054-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

possible. But this is untrue for several reasons,

among which:

 Limited space: the sensors must be arranged

around the stump socket of the forearm, so that

their maximum number is fixed by their physical

dimensions;

 Calibration procedure: the EMG sensors need to

be manually and exactly calibrated in analog

voltage gain, which is a time-expensive

procedure, even for a skilled personnel;

 Cost: efficient circuitry-integrated EMG sensors

are quite expensive, which means a reduced

number means a significative cost reduction for

the patient;

 Comfort: greater pressure assures optimal

contact for signal extraction, but this implies that

a great number of sensors produces higher

discomfort for the patient;

 Reliability: unlike what one can think, a greater

number of EMG sensors can produce lower

realibility. This is because it is necessary a

higher number of electric contacts, that are the

first carrier for the sweat to reach the electronic

circuitry, so potentially give raise to electrical

malfunctions.

In this work we use a low density sEMG-based

system for the recognition of hand gestures to be

further replicated via a virtual limb in 3D computer

graphics (avatar), useful in rehabilitation of

amputees. For the aforementioned reasons, here we

intend to find the best trade-off between accuracy

and the optimal number of EMG sensors.

The system was tested with 20 able-bodied

subjects, 10 males and 10 females. A comparison of

classification accuracy obtained by feeding the

classification algorithm with different feature

vectors was performed. The different feature subsets

were chosen in order to determine what sensors can

be excluded without excessive degradation of the

performance.

2 MATERIALS AND METHODS

An experiment was carried out with a dataset

acquired from 20 subjects. The system was trained

off-line. The described validation, compared with

different sets of sensors, was entirely off-line. The

whole cross-validation, including repeated training

and test of the network takes about 20 seconds per

subject on Pentium 4, while the classification of a

single window takes about 100 sec, which means

that it can be done in real-time. The system has also

been tested in real-time, but only using 6 sensors.

2.1 Subjects

Testers were twenty able-bodied subjects, ten males

and ten females, free of known muscular and/or

neurological diseases, with an average age of 32

years. Each subject gave informed consent before

performing experiments. Eighteen subjects were

right-handed and two left-handed. For every subject

we considered both a session with the right hand and

a session with the left hand.

b) c) d)

Figure 1: Positioning of the EMG sensors and bracelet. a)

the six sensors equally spaced in the bracelet; final

bracelet dimensions are 51.3xLx7 mm where L depends

on subject’s forearm diameter b) sensor 1 positioning; c)

sensor 6 positioning; d) bracelet positioning on the

forearm.

2.2 Setup

Six commercial active sEMG sensors (Ottobock

13E200=50, 27x18x9.5 mm) were placed on the

subjects’ forearm using a silicone bracelet, as

depicted in Fig.1 a-d. Sensors were placed equally

spaced in the bracelet (Fig. 1a), so that the first

sensor was placed on the flexor carpi-radialis muscle

(Fig. 1b) and the sixth sensor on the brachio-radialis

muscle (Fig. 1c). The bracelet was placed around the

forearm, 5cm below the elbow (Fig. 1d). This

configuration was chosen to simulate the positioning

of the prosthesis sensors on amputees’ forearms.

Sensors operated in 0÷5V range with a bandwidth of

90-450Hz and a Common-Mode Rejection Ratio

(CMRR) >100dB. Data were collected using a

purpose-built acquisition system (12 bits A/D

converter, 1 kHz sampling frequency) and USB-

transmitted to the PC.

SensorReductiononEMG-basedHandGestureClassification

139

2.3 Experimental Procedure

The subjects were sitting in a comfortable chair in

front of a PC monitor, where the gestures to be

performed were depicted as follow (see Fig. 2):

1) Rest: hand relaxed.

2) Fist: hand with all fingers closed.

3) Pinch: hand with thumb and finger

touching as if picking a small

object.

4) Spread: hand open and stretched.

5) Pointing: hand with all fingers closed with

the index pointing.

We chose the aforementioned five gestures because

they are considered the most meaningful ones in

everyday life (Saggio et al. 2011).

Figure 2: The five hand gestures.

Every gesture was randomly repeated 10 times and

Recorded for 2s. We empirically determined

gestures duration by means of preliminary studies.

As steady-state sEMG signals are more robust than

transient signal for classification purposes

(Englehart et al., 2001, Oskoei and Hu, 2008)

transitions between gestures were not recorded.

The whole recording procedure was performed

twice, once with the dominant hand and once with

the non-dominant hand. Half the subjects, randomly

selected, started the recording session with the

dominant hand and the other half with non-

dominant hand.

2.4 Feature Extraction

After acquisition, raw EMG data were segmented

using the overlapped windowing technique (Oskoei

and Hu, 2008): the windows length was fixed to

256ms, with 64ms of overlap between two

successive windows. This timing was chosen in

order to fulfill the requirements of real-time

applications, such as the control of virtual hands or

real prosthesis. For each sensor and each window,

features were extracted; in particular, by indicating

with x

the i

time sample in a window and with N

the total length of the window (in samples), the

following time-domain features were used:

 Mean (M): it is defined in Eq. 1 and represents

the mean value of the EMG amplitude:

M 

i1



(1)

 Root Mean Square (RMS): it is defined in Eq. 2

and represents the mean power of the signal.

RMS 

i1



(2)

 Willison Amplitude (WA): it is defined in Eq. 3

and represents the number of counts for each

change in the EMG signal amplitude that

exceeds a predefined threshold, set to avoid

background noise-induced counts. It is related

to the level of muscle contraction.

WA 

f (| x

i1





 x

i1

f (x) 

1, x  threshold

0,otherwise







(3)

 Slope Sign Change (SSC): it is defined in Eq. 4

and represents the number of times the slope of

the EMG signal changes sign.

SSC 

f [(x

i2





 x

i1

)  (x

 x

i1

)]

f (x) 

1, x  threshold

0,otherwise







(4)

• Simple Square Integral (SSI): it is defined in

Eq. 5 and represents, similarly to Energy in

continuous-time signal, the area under the

curve of the squared signal:

SSI  x

i1



(5)

• Variance (V): it is defined in Eq. 6 and

represents a statistical measure of how signal

varies from its average value (Mean, as defined

in Eq. 1) during the observation:

V 

W 1

 M)

i1



(6)

• Waveform Length (WL): it is defined in Eq. 7 and

represents cumulative length of the EMG signal

waveform. WL is a measure of EMG signal

complexity:

WL  | x

i1

 x

i1





(7)

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

140

2.5 Classification

We implemented an Artificial Neural Network

(ANN) with 10 neurons in the hidden layer and

back-propagation training method. The number of

neurons of the hidden layer was empirically

determined in previous tests.

3 SENSOR SELECTION

When using all sensors, a 5-fold cross-validation to

measure the performance of every configuration

gives a mean accuracy among all subjects of 88.8%,

anyway there was a strong difference among

subjects, being the standard deviation 7.2%.

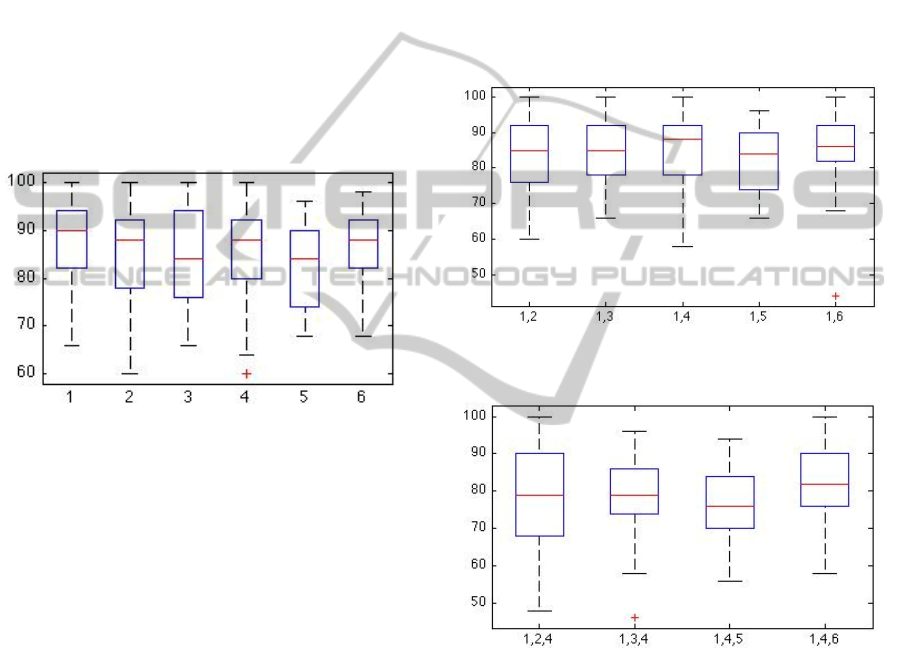
Figure 3: Accuracy (%) of the classifier when excluding

each one of the sensors.

In order to determine what sensors are more

important, we first repeated the whole test, with the

cross-validation, excluding sensor 1, i.e. considering

only the features based on sensors 2, 3, 4, 5, 6. Then

we excluded sensor 2, and cross-validated the

network using the features based on sensors 1, 3, 4,

5, 6. The same was repeated excluding, one at a

time, all the sensors.

We had to judge the configuration that gives the

best results. As we stated above, there is a big

variance among subjects, so the mean value is not

very significant: we should consider more robust

indicators, such as median (50

percentile), and

other percentiles. Figure 3 shows a box-plot of the

accuracy: on each box, the central mark is the

median, the edges of the box are the 25th and 75th

percentiles (1

and 3

quartiles), the whiskers

extend to the most extreme data points not

considered outliers. Outliers are individually plotted

as crosses.

By examining the graph, it is evident that the

best performance can be achieved by excluding

sensor 1: in fact it has higher median but also higher

and 3

quartiles, so we can deduce that the best

configuration if we want to use only five sensors is

when using sensors 2, 3, 4, 5, 6.

Next step is trying to use four sensors. In spite of

testing all the possible combinations of four sensors,

we made the test excluding sensor 1 and 2, then 1

and 3, until 1 and 6. This is because we are

exploiting the information acquired on previous

experiment, where we found that sensor 1 is the least

useful one. This is a heuristic method that allows us

to avoid the exploration of configurations that are

less likely to give the optimal solution. Results are in

Figure 4.

Figure 4: Accuracy (%) of the classifier when excluding

each couple of sensors reported on the column.

Figure 5: Accuracy (%) of the classifier when excluding

each triplet of sensors reported on the column.

Although it has a wider range, and for some

subjects it has an accuracy lower than 60%, the third

combination (1, 4) reached what can be considered

globally the best performance, because it has a

higher median and 3

quartile. Hence we can argue

that, if we want to classify with only four sensors,

best choice is more likely 2, 3, 5, 6, even if we

didn’t test all the possible configurations.

We now followed with the same procedure:

excluding sensor 1 and 4 together with every

remaining one. Result is shown in Figure 5.

In this case, the last trial, which is the one where

we excluded sensors 1, 4, 6, gave better results.

SensorReductiononEMG-basedHandGestureClassification

141

Therefore, if we want to use only three sensors the

best choice is to consider the numbers 2, 3, 5. Going

on, we excluded another sensor. Figure 6 shows the

best result achieved by excluding sensors 1, 3, 4, 6.

This means that if we want to use only two sensors

the best choice falls on sensors 2 and 5.

Figure 6: Accuracy (%) of the classifier when excluding

each 4-tuple of sensors reported on the column.

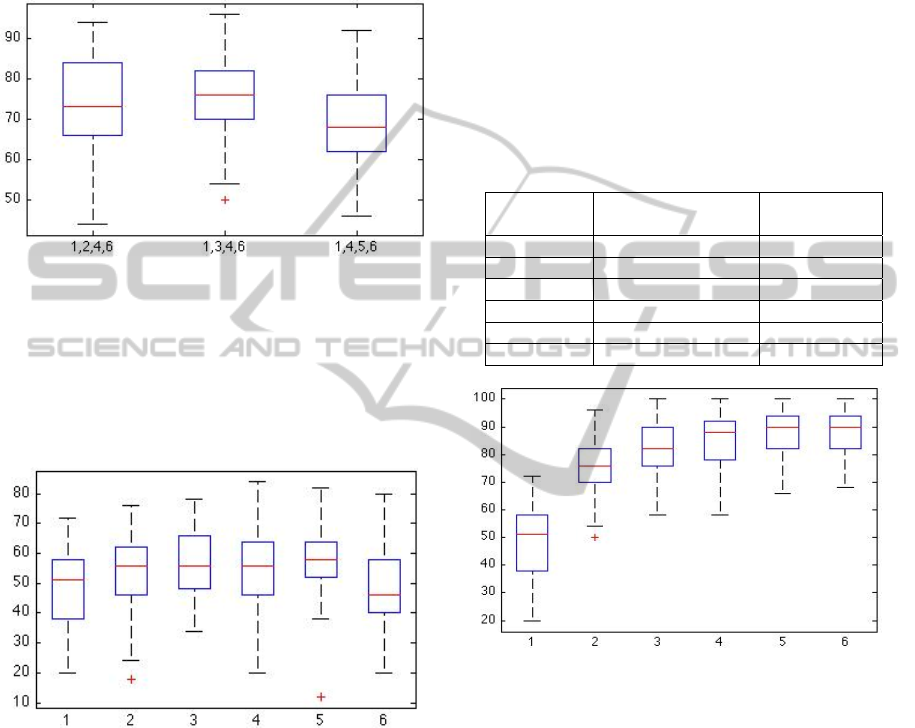
Finally, we considered the best solution when

adopting just a single sensor. In this occurrence, we

didn’t test only sensor 2 and sensor 5, but the entire

set of six, in order to give a validation of our

heuristic method as well.

Figure 7: Accuracy (%) of the classifier when using only

one sensor, reported on the column.

Results are reported in Figure 7, where we can see

that the best sensor, when used alone, is the number

5, which was one of our two candidates as the most

useful sensor. In addition, sensor 2 and 3 perform

relatively well when used alone, while sensor 1, 4,

and 6 are the worst when tested alone, and they

actually were the first ones that we excluded.

4 RESULTS

On Table 1, for every considered number of sensors

we resume the best combination of sensors and the

mean value of the accuracy. Moreover, for the

chosen combinations of sensors, on Figure 8 we

show the box-plot of the accuracy.

Results show that when the number of used

sensors grows, the accuracy increases, but with a

non-linear relationship. With only three sensors (2,

3, 5) it is possible to obtain a quite good level of

accuracy, with a mean value of 81.7%. With five

sensors (2, 3, 4, 5, 6) the accuracy is almost the same

as with all the six sensors, with a difference as little

as 0.8%.

Table 1: Mean accuracy and best combinations for every

considered number of sensors.

Number of

sensors

Sensor combination Accuracy

1 5 48.3 %

2 2, 5 70.0 %

3 2, 3, 5 81.7 %

4 2, 3, 5, 6 84.6 %

5 2, 3, 4, 5, 6 88.0 %

6 1, 2, 3, 4, 5, 6 88.8 %

Figure 8: Box-plot of the accuracy for every considered

number of sensors.

5 CONCLUSIONS

We propose a system composed of a bracelet with

six EMG sensors, a data condition circuitry, a

Neural Network classifier, adopted to recognize

hand’s gesture within a set of five. Our intent was to

investigate the possibility of reduction in the number

of sensors, to determine the optimal trade-off

between their number and the accuracy obtained in

the gesture classification. Mean accuracy resulted

from an unacceptable 48.3% in the case of only one

sensor, up to a useful 88.8% with the adoption of all

six sensors. From this value, the performance

degraded of a negligible 0.8% with five sensors,

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

142

while a significant 7.1% when using only three

sensors.

REFERENCES

Alphonso A.L., Monson B.T., Zeher M.J., Armiger R.S.,

Weeks S.R., Burck J.M., Moran C., Davoodie R.,

Loeb G., Pasquina P.F., Tsao J.W., (2012). Use of a

virtual integrated environment in prosthetic limb

development and phantom limb pain, Stud Health

Technol Inform vol. 181, pp. 305- 309.

Castellini C., Gruppioni E., Davalli A., Sandini G., (2009).

Fine detection of grasp force and posture by amputees

via surface electromyography, J Physiol Paris, vol.

103, no. 3-5, pp. 255-262.

Chowdhury R.H., Reaz M.B., Ali M.A., Bakar A.A.,

Chellappan K., Chang T.G., (2013). Surface

electromyography signal processing and classification

techniques, Sensors (Basel), vol. 13, no. 9, pp. 12431-

12466.

Englehart K., Hudgins B., Parker P.A., (2001). A wavelet-

based continuous classification scheme for

multifunction myoelectric control”, IEEE Trans

Biomed Eng, vol. 48, no. 3, pp. 302-311.

Flor H., (2002). Phantom-limb pain: characteristics,

causes, and treatment”, Lancet Neurol, vol. 1, no. 3,

pp. 182-189.

Li G., Schultz A.E., Kuiken T.A., (2010). Quantifying

pattern recognition- based myoelectric control of

multifunctional transradial prostheses, IEEE Trans

Neural Syst Rehabil Eng, vol. 18, no. 2, pp. 185-192.

Matrone G.C., Cipriani C., Secco E.L., Magenes G.,

Carrozza M.C., (2010) Principal components analysis

based control of a multi-DoF underactuated prosthetic

hand. J Neuroeng Rehabil, vol. 23, pp. 7-16.

Oskoei M.A., Hu H., (2008). Support vector machine-

based classification scheme for myoelectric control

applied to upper limb”, IEEE Trans Biomed Eng, vol.

55, no. 8, pp. 1956-1965.

Phinyomark A., Phukpattaranont P., Limsakul C., (2012).

Feature reduction and selection for EMG signal

classification, Expert Systems with Applications, vol.

39, no. 8, pp. 7420–7431.

Saggio G., Cavallo P., Casali D., Costantini G. (2011).

Complexity Reduction in Control of Human Hand

Prosthesis for a Limited Set of Gestures. Proceedings

of the 4th International Conference on Health

Informatics (HEALTHINF, part of BIOSTEC).

Scheme E. and Englehart K. (2011) Electromyogram

pattern recognition for control of powered upper-limb

prostheses: state of the art and challenges for clinical

use, J Rehabil Res Dev, vol. 48, no. 6, pp. 643-659.

Zlotolow D.A., Kozin S.H., (2012). Advances in upper

extremity prosthetics, Hand Clin, vol. 28, no. 4, pp.

587-593.

SensorReductiononEMG-basedHandGestureClassification

143