Means for Finding Meaningful Levels of a Hierarchical Sequence

Prior to Performing a Cluster Analysis

David Allen Olsen

Department of Computer Science and Engineering, University of Minnesota-Twin Cities, Minneapolis, U.S.A.

Keywords:

Intelligent Control Systems, Hierarchical Clustering, Hierarchical Sequence, Complete Linkage, Meaningful

Level, Meaningful Cluster Set, Distance Graphs, Noise Attenuation.

Abstract:

When the assumptions underlying the standard complete linkage method are unwound, the size of a hierarchi-

cal sequence reverts back from n levels to

n·(n−1)

+1 levels, and the time complexity to construct a hierarchical

sequence of cluster sets becomes O(n

). Moreover, the post hoc heuristics for cutting dendrograms are not

suitable for ﬁnding meaningful cluster sets of an

n·(n−1)

+ 1-level hierarchical sequence. To overcome these

problems for small-n, large-m data sets, the project described in this paper went back more than 60 years to

solve a problem that could not be solved then. This paper presents a means for ﬁnding meaningful levels of an

n·(n−1)

+ 1-level hierarchical sequence prior to performing a cluster analysis. By ﬁnding meaningful levels of

such a hierarchical sequence prior to performing a cluster analysis, it is possible to know which cluster sets

to construct and construct only these cluster sets. This paper also shows how increasing the dimensionality of

the data points helps reveal inherent structure in noisy data. The means is theoretically validated. Empirical

results from four experiments show that ﬁnding meaningful levels of a hierarchical sequence is easy and that

meaningful cluster sets can have real world meaning.

1 INTRODUCTION

Reasoning about hardware limitations while an ap-

plication is being developed is a key aspect of com-

putational thinking (Kirk and Hwu, 2013). This pa-

per presents the second part of a three-part research

project. The goal of this project was to develop a gen-

eral, simplistic, complete linkage hierarchical cluster-

ing method that 1) substantially improves upon the

accuracy of the standard complete linkage method

and 2) can be fully automated or used with minimal

operator supervision. The standard complete link-

age method (Sorenson 1948) was the ﬁrst of seven

standard hierarchical clustering methods to be devel-

oped during the late 1940’s to the mid-1960’s (Everitt

et al., 2011). At that time, clustering problems hav-

ing about 150 data points were viewed as moderately-

sized problems while problems having about 500 data

points were viewed as large. Cf. (Anderberg, 1973).

To accommodate the hardware limitations of that

time and solve these “large-scale” clustering prob-

lems, those who developed the standard hierarchical

clustering methods made several assumptions. They

assumed that cluster sets are nested partitions, i.e.,

that clusters are both indivisible and mutually exclu-

sive (Jain and Dubes, 1988). Making this assump-

tion reduces the size of a hierarchical sequence from

n·(n−1)

+ 1 levels to n levels (Berkhin, 2006), where

n is the number of data points in a data set. Fur-

ther, the number of combinations that need to be ex-

amined at each level of the hierarchical sequence be-

comes much smaller than complete enumeration (An-

derberg, 1973). Those who developed the standard

hierarchical clustering methods also assumed that no-

tions of distance between data points (“interpoint”

distances) can be generalized to notions of distance

between clusters of data points (“intercluster” dis-

tances). By making this assumption, proximity mea-

sures known as linkage metrics could be devised.

Linkage metrics are used to combine clusters of data

points or subdivide a cluster of data points at a time

(Berkhin, 2006). Once the cluster sets of an n-level

hierarchical sequence are constructed, a dendrogram

is used to visually represent the hierarchical sequence,

and post hoc heuristics for “cutting” dendrograms are

used to ﬁnd meaningful cluster sets. See, e.g., (Jain

and Dubes, 1988), (Johnson and Wichern, 2002), and

(Everitt et al., 2011).

The above-described assumptions sacriﬁce accu-

Olsen D..

Means for Finding Meaningful Levels of a Hierarchical Sequence Prior to Performing a Cluster Analysis.

DOI: 10.5220/0005040600210033

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 21-33

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

racy for efﬁciency when the inherent (hierarchical)

structure in a data set is not taxonomic. See (Lance

and Williams, 1967), (Olsen, 2014). The stan-

dard complete linkage method has the following four

weaknesses: First, when clusters are being combined

or a cluster is being subdivided, the standard com-

plete linkage method cannot resolve ties between in-

tercluster distances. Consequently, either one of the

distances is selected arbitrarily or alternative hierar-

chical sequences are constructed, and the results are

no longer deterministic. Second, because the stan-

dard complete linkage method uses intercluster dis-

tances to construct clusters, does not allow clusters

to overlap, and does not allow data points to migrate

between clusters (Lance and Williams, 1967), cluster

sets often are constructed inaccurately. Third, results

obtained from the standard compete linkage method

can depend on which end of a hierarchical sequence

is treated as the beginning. Consequently, the dendro-

grams for agglomerative hierarchical clustering and

divisive hierarchical clustering may be different, and

ﬁnding the cause(s) for the difference is both inconve-

nient and time-consuming. Fourth, the standard com-

plete linkage method does not ﬁnd meaningful levels

or meaningful cluster sets of hierarchical sequences

It still is necessary to construct a dendrogram and de-

termine where and how many times to cut the den-

drogram, and post hoc heuristics are computationally

expensive to run.

Because of these weaknesses, it can be difﬁcult

to interpret results obtained from the standard com-

plete linkage method. Consequently, it is underuti-

lized in automation and by intelligent control systems,

including supervisory functions such as fault detec-

tion and diagnosis and adaptation. Cf. (Isermann,

2006). When the standard complete linkage method is

used, stopping criteria often are used in place of post

hoc heuristics. Stopping criteria are predetermined.

If the model upon which they are based is inadequate

or changes, the stopping criteria lose their usefulness.

Moreover, the standard complete linkage method is an

updating method, so it uses information from previ-

ously constructed cluster sets to construct subsequent

cluster sets. It must construct the cluster set for ev-

ery level of an n-level hierarchical sequence until the

stopping criteria are met. See, e.g., (Jain and Dubes,

A “meaningful cluster set” refers to a cluster set that

can have real world meaning. Under ideal circumstances,

a “meaningful level” refers to a level of a hierarchical se-

quence at which a new conﬁguration of clusters has ﬁn-

ished forming. These deﬁnitions appear to be synonymous

for

n·(n−1)

+ 1-level hierarchical sequences. The cluster set

that is constructed for a meaningful level is a meaningful

cluster set, so these terms are used interchangeably.

1988), (Johnson and Wichern, 2002). These cluster

sets must be either materially accurate or, if possible,

amendable for material inaccuracies. See, e.g., U.S.

Patent No. 8,312,395 (defect identiﬁcation in semi-

conductor production; operators must ensure that the

results are 80 to 90 percent accurate). As much as 90

percent of the effort that goes into implementing the

standard complete linkage method is used to develop

stopping criteria or interpret results.

Notwithstanding these weaknesses, the standard

complete linkage method is an important clustering

method. The distributions of many real world mea-

surements are bell-shaped, so the standard complete

linkage method has broad applicability. Its simplic-

ity makes it relatively easy to mathematically capture

its properties. Of the standard hierarchical cluster-

ing methods, the standard complete linkage method is

the only method that is invariant to monotonic trans-

formations of the distances between the data points,

that can cluster any kind of attribute, that is not prone

to inversions, and that produces globular or compact

clusters (Johnson and Wichern, 2002), (Everitt et al.,

2011). Moreover, more sophisticated methods show

no clear advantage for many purposes. Thus, the need

exists to bring complete linkage hierarchical cluster-

ing over from the “computational side of things ... to

the system ID/model ID kind of thinking” (Gill, 2011)

as part of closing the loop on cyber-physical systems.

For the ﬁrst part of the project, a new, complete

linkage hierarchical clustering method was devel-

oped. See (Olsen, 2014). The new clustering method

is consonant with the model for a measured value that

scientists and engineers commonly use

, so it sub-

stantially improves upon the accuracy of the standard

complete linkage method. Further, it can construct

cluster sets for select, possibly non-contiguous levels

of an

n·(n−1)

+1-level hierarchical sequence. The new

clustering method was designed with small-n, large-

m data sets in mind, where n is the number of data

points, m is the number of dimensions, and “large”

means thousands and upwards (Murtagh, 2009).

The model for a measured value is measured value =

true value + bias (accuracy) + random error (statistical un-

certainty or precision) (Navidi, 2006). This model has sub-

stantially broader applicability than the taxonomic model

that is the basis for the standard complete linkage method.

These data sets are used by many cyber-physical sys-

tems and include time series. For example, a typical auto-

mobile has about 500 sensors; a small, specialty brewery

has about 600 sensors; and a small power plant has about

1100 sensors. The new clustering method may accommo-

date large-n, large-m data sets as well, and future work in-

cludes using multicore and/or heterogeneous processors to

parallelize parts of the new clustering method, but large-n,

large-m data sets are not the focus here.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

Because the computational power presently ex-

ists to apply hierarchical clustering methods to much

larger data sets than before, the new clustering

method unwinds the above-described assumptions.

However, by unwinding these assumptions and letting

the size of a hierarchical sequence revert back from n

levels to

n·(n−1)

+1 levels, the time complexity to con-

struct cluster sets becomes O(n

). This is large even

for small-n, large-m data sets. Moreover, the post hoc

heuristics for cutting dendrograms are not suitable for

ﬁnding meaningful cluster sets of an

n·(n−1)

+ 1-level

hierarchical sequence. For example, in (Tibshirani

et al., 2001), Tibshirani et al. present a gap statistic

for determining an “optimal” number of clusters for

a data set and use this technique to determine where

to cut a dendrogram. Because the technique selects

the number of clusters from a range of numbers, a

range of cluster sets must be constructed as opposed

to constructing only select cluster sets. Like other

post hoc heuristics, see, e.g., (Kim and Lee, 2000),

(Daniels and Giraud-Carrier, 2006), the gap statistic

is designed to ﬁnd only one or maybe a few clus-

ter sets. Further, it is not designed for hierarchical

sequences where clusters are not well-separated but

close together or overlap.

Thus, with today’s technology, the project went

back more than 60 years to solve a problem that could

not be solved then. For the second part of the project,

a means was developed for ﬁnding meaningful lev-

els of an

n·(n−1)

+ 1-level (complete linkage) hierar-

chical sequence prior to performing a cluster analy-

sis. By ﬁnding meaningful levels of such a hierarchi-

cal sequence prior to performing a cluster analysis,

it is possible to know which cluster sets to construct

and construct only these cluster sets. This reduces the

time complexity to construct cluster sets from O(n

)

to O(ln

), where l is the number of meaningful lev-

els. These are the cluster sets that can have real world

meaning. It is notable that the means does not depend

on dendrograms or post hoc heuristics to ﬁnd mean-

ingful cluster sets. The second part also looked at how

increasing the dimensionality of the data points helps

reveal inherent structure in noisy data, which is nec-

essary for ﬁnding meaningful levels.

2 OTHER RELATED WORK

Researchers have avoided developing clique detec-

tion methods for hierarchical clustering, and at least

one researcher has speciﬁcally taught away from us-

ing these methods (Jain and Dubes, 1988) (citing

(Matula, 1977)). In (Peay, 1974) and (Peay, 1975),

E.R. Peay presents a linkage-based clique detection

method and applies the method to hierarchical cluster-

ing. For each level of an

n·(n−1)

+ 1-level hierarchical

sequence for which a clique set is constructed, Peay’s

clique detection method recognizes every maximally

complete subset of data points as a clique, includ-

ing those from which the data points migrate. Be-

cause Peay’s clique detection method is an updating

method, it also constructs a clique set for every level

of such a hierarchical sequence. It cannot construct

only the clique sets that correspond to meaningful

levels of a hierarchical sequence. A similar prob-

lem holds for ﬂat clique detection methods. Without

knowing which levels of a hierarchical sequence are

meaningful, ﬂat methods are ineffective.

Within a framework based on ultrametric topology

and ultrametricity, F. Murtagh, in (Murtagh, 2009),

observes that it is easier to ﬁnd clusters in sparse or

high dimensional spaces. This work does not describe

how to ﬁnd meaningful levels of a hierarchical se-

quence. Also, it assumes that the mean values and

the standard deviations of all the dimensions of a data

point are the same.

3 NOISE ATTENUATION

The means for ﬁnding meaningful levels is based on

two assumptions. Let X = {x

,...,x

} be a data set

that contains a ﬁnite number of data points n, where

each data point has m dimensions. Further, suppose

that each data point is a sequence of samples and that

at any moment in time, with respect to each class or

source, all the samples have the same true values and

biases

. First, the means assumes that noise (random

error) is the only random component in a measured

value, that noise can be modeled as Gaussian random

variables, and that the noise that is embedded in each

dimension (sample) of each data point is statistically

independent. Second, the means assumes that the dis-

similarities between the data points are non-negative

values. This latter assumption is needed because p-

norm distance measures do not distinguish between

positive and negative correlation.

Within the context of the nearest neighbor prob-

lem for database search, where high(er) dimensional-

ity is considered to be a curse, Beyer et al., in (Beyer

et al., 1998), show that under broadly applicable con-

ditions, if

lim

m→∞

Var[

E[kY

]

] = 0, (1)

In real world terms, this is the same as calibrating the

sensors.

MeansforFindingMeaningfulLevelsofaHierarchicalSequencePriortoPerformingaClusterAnalysis

Figure 1: Exemplary results from a sensitivity analysis. The minimum distance and the maximum distance (not shown)

between data points from two different classes are calculated. Limits calculated with Equation 5 are very consistent with the

empirical results for STDDIST Normal. When noise is uniformly distributed, the results are analogous to those when noise is

normally distributed, indicating that the Gaussian random variable assumption is reasonable.

then for every ε > 0,

lim

m→∞

Prob[DMAX

≤ (1 + ε)DMIN

] = 1. (2)

is the difference between any independent data

point P

i,m

,i = 1, 2, ..., n, and Q

, a query point that is

chosen independently of all the data points; m is the

dimensionality of P

i,m

and Q

; DMAX is the distance

between Q

and the farthest away data point; DMIN

is the distance between Q

and the nearest data point;

and p is the index of the p-norm distance measure. In

(Hinneburg et al., 2000), Hinneburg et al. extend this

work by showing that

lim

m→∞

DMAX

−DMIN

1/p−1/2

] = C

, (3)

lim

m→∞

E[DMAX

−DMIN

] = C

·(m

1/p−1/2

). (4)

is a constant that depends on p.

For the purposes of cluster analysis, these equa-

tions hint that classes of noisy data points may be spa-

tially separable. However, they do not show how the

distances between data points from different classes

(“interclass” distances) relate to the distances be-

tween data points that belong to the same class (“in-

traclass” distances). Also, C

is unknown. A set of

theorems was proved to provide the missing pieces.

Theorem 1, below, pertains to the 2-norm distance

measure. Here, although it can have a much broader

scope, it is written speciﬁcally for Euclidean distance.

Since statistical independence is assumed only with

respect to the Gaussian random variables (noise), the

mean values (true values plus biases) may be highly

correlated.

Theorem 1. Let C

and C

be two clusters,

each of which is comprised of a ﬁnite set

of data points, i.e., C

= {x

1,1

1,2

,...,x

1,n

}

and C

= {x

2,1

2,2

,...,x

2,n

}. Let each data

point have m dimensions, each of which is

a statistically independent, Gaussian ran-

dom variable, i.e., X

1,i,k

∼ N(µ

1,i,k

,σ

1,i,k

) and

2, j,k

∼ N(µ

2, j,k

,σ

2, j,k

),i = 1, 2, ...,n

, j = 1, 2, ..., n

and k = 1,2,...,m. When Y

k,(i, j)

= (X

1,i,k

−X

2, j,k

k,(i, j)

∼ N(µ

k,(i, j)

,σ

k,(i, j)

). If σ

k,(i, j)

is bounded

from below by ε > 0 and above by a constant S,

and if |µ

k,(i, j)

| is bounded from above by a constant

M, then as m → ∞, the variance σ

m,(i, j)

of the

random variable Z

m,(i, j)

= (

∑

k=1

k,(i, j)

)

converges

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

Proof for Theorem 1. A sketch of the proof is in the

Appendix to this paper.

For Y

k,(i, j)

∼ N(0, 1), k = 1,2,...,m,

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

lim

m→∞

m,(i, j)

. For Y

k,(i, j)

∼ N(0, σ

k,(i, j)

) where

k,(i, j)

= σ

(i, j)

, k = 1,2, ..., m, lim

m→∞

m,(i, j)

(i, j)

. When σ

k,(i, j)

and µ

k,(i, j)

are chosen from

uniform distributions, the Monte Carlo method shows

that the limit in Theorem 1 converges from below

as the bound M on µ

k,(i, j)

increases. As

m increases, the standard deviation of this number

becomes smaller relative to its magnitude. When

k,(i, j)

= σ

(i, j)

, k = 1,2,...,m, the Monte Carlo

method shows that the limit in Theorem 1 con-

verges from below to mS

as the bound M on µ

k,(i, j)

increases. The standard deviation of this number de-

creases to zero absolutely. When σ

k,(i, j)

= σ

(i, j)

and

k,(i, j)

= µ

(i, j)

, k = 1,2,...,m, the result in Theorem 1

becomes

lim

m→∞

m,(i, j)

(i, j)

2(1 +

(i, j)

)

(i, j)

(1 +

(i, j)

)

. (5)

If σ

(i, j)

is held constant and µ

(i, j)

is allowed to vary

between 0 and |µ

(i, j)

|  σ

(i, j)

, σ

m,(i, j)

is a constant

between

(i, j)

and σ

(i, j)

. The graph for the ﬁrst term in

Equation 5 is monotonically decreasing while that for

the second term is monotonically increasing. More-

over, as Fig. 1 shows, limits calculated with Equation

5 are very consistent with the empirical results from a

sensitivity analysis.

4 FINDING MEANINGFUL

LEVELS AND CLUSTER SETS

Often, as the dimensionality of the data points in-

creases and the 2-norm interclass distances become

larger, the standard deviations of the 2-norm inter-

class distances, i.e., σ

m,(i, j)

, nonetheless remain rel-

atively small or constant. When σ

k,(i, j)

= σ

(i, j)

and

k,(i, j)

= µ

(i, j)

, k = 1,2,...,m, this is certainly so, be-

cause Equation 5 shows that σ

m,(i, j)

is a constant. In

particular, when the distribution of the noise that is

embedded in each dimension of each data point does

not change, σ

m,(i, j)

is a constant between

(i, j)

√

and

(i, j)

. As the Monte Carlo simulations show, this also

is so when the 2-norm interclass distances grow at an

expected rate that is much faster than

√

)

√

When this scenario holds, data points that belong

to the same class link at about the same time even

at higher dimensionalities. As Fig. 2(a) depicts,

classes of data points can be close together at lower

dimensionalities. When they are, the magnitudes of

many intraclass distances and interclass distances are

about the same, so the two kinds of distances com-

mingle. However, as Fig. 2(b) depicts, the classes of

data points are farther apart at higher dimensionali-

ties, so the intraclass distances and the interclass dis-

tances segregate into bands. Thus, higher dimension-

alities can attenuate the effects of noise

that preclude

ﬁnding meaningful levels of a hierarchical sequence

at lower dimensionalities and distinguish between the

classes. Moreover, as Figs. 2(b) and (c) show, this

pattern repeats itself as clusters become larger from

including more data points.

Consequently, as the dimensionality of the data

points increases, the distance graphs for a data set

can exhibit identiﬁable features that correlate with

meaningful levels of the corresponding hierarchical

sequences. These levels are the levels at which multi-

ple classes have ﬁnished linking to form new conﬁg-

urations of clusters. In particular, assuming that the

data set has inherent structure, a distance graph takes

on a shape whereby sections of the graph run nearly

parallel to one of the graph axes. Where there is very

little or no linking activity, the sections run nearly ver-

tically. Where there is signiﬁcant activity, i.e., where

new conﬁgurations of clusters are forming, the sec-

tions run nearly horizontally. Thus, portions of the

graph that come after the lower-right corners and be-

fore the upper-left corners indicate where new con-

ﬁgurations of clusters have ﬁnished forming. As the

schematic in Fig. 2(c) shows, a distance graph can be

visually examined prior to performing a cluster anal-

ysis. Since a distance graph is used to ﬁnd meaningful

levels of a hierarchical sequence prior to performing

a cluster analysis, it is not a summary of the results

obtained from the analysis. Instead, it enables a user

to selectively construct only meaningful cluster sets,

i.e., cluster sets where new conﬁgurations of clusters

have ﬁnished forming.

Finding meaningful levels is remarkably easy:

Step 1. Calculate the dissimilarities between data

points x

and x

in data set X , i, j = 1, 2, ..., n, x

6= x

Then, calculate the lengths or magnitudes of the vec-

tors that contain the dissimilarities between the data

points. Here, the dissimilarity measures are simple

value differences, and the 2-norm is used to obtain

Euclidean distance.

Step 2. Construct ordered triples (d

i, j

,i, j) from

these distances and the indices of the respective data

points, sort the ordered triples into rank or ascending

order according to their distance elements, and as-

sign indices to the sorted ordered triples (the “rank

order indices”). The time complexity to calculate

the distances is O(

n·(n−1)·m

). If ordinary merge sort

Attenuating the effects of noise refers to reducing the

effects of noise on cluster construction.

MeansforFindingMeaningfulLevelsofaHierarchicalSequencePriortoPerformingaClusterAnalysis

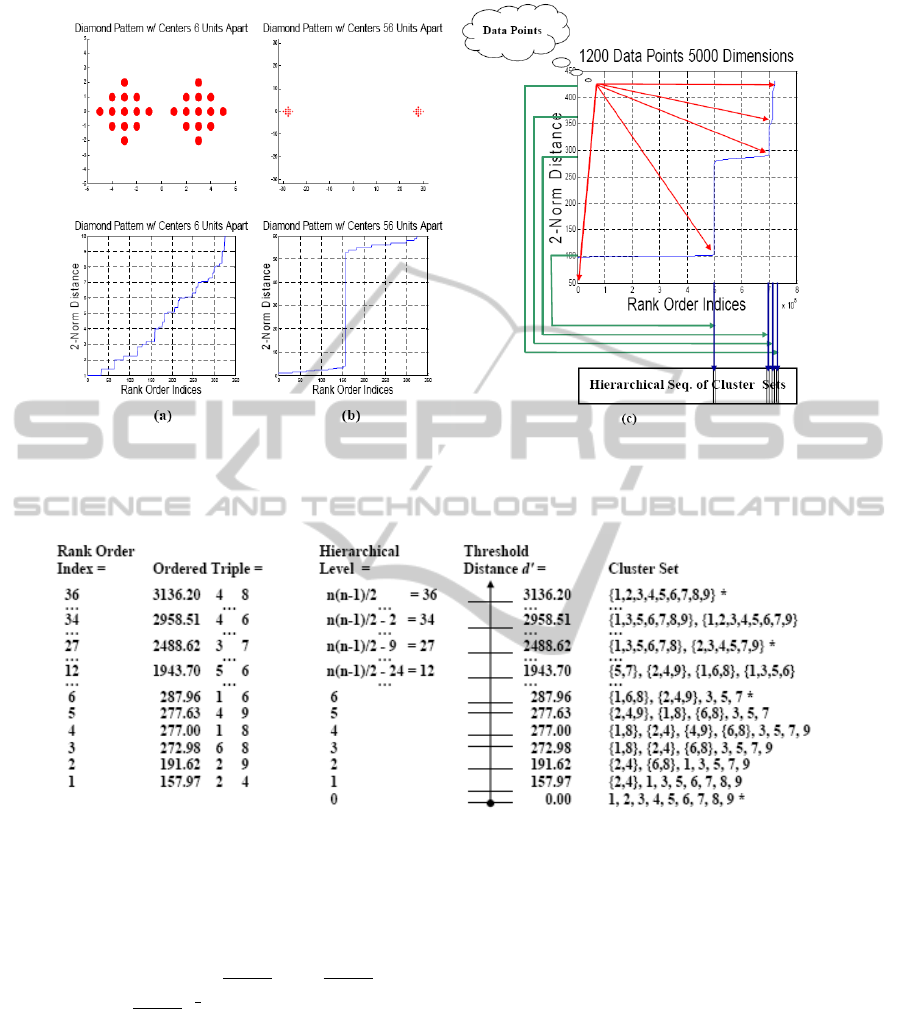
Figure 2: Simple illustration that shows how two classes of data points link as the distance between the classes increases (left)

and schematic for ﬁnding meaningful levels of a hierarchical sequence (right). Inherent structure is revealed through identi-

ﬁable features of the distance graph. These features correlate with those levels of the corresponding hierarchical sequence at

which multiple classes have ﬁnished linking to form new conﬁgurations of clusters.

Figure 3: Illustration that shows how rank order indices and distance elements align with levels and the respective threshold

distances d

of the corresponding hierarchical sequence. The data come from the nine motes experiment described in Subsec-

tion 5.3. The 2-norm distance measure was used to calculate the distances. The arrow in the column for the threshold distance

signiﬁes that threshold distance d

is a continuous variable. The meaningful cluster sets in the last column have asterisks.

(Cormen et al., 2004) is used, the time complexity to

sort the ordered triples is O(

n·(n−1)

·log(

n·(n−1)

)) =

O(n ·(n −1) ·log(

n·(n−1)

)

Step 3. Use the rank order indices and the ordered

triples to construct a distance graph. The distance

graph will remain smooth, regardless of the dimen-

sionality of the data points, when inherent structure is

absent. Assuming that the data set has inherent struc-

ture, increase the dimensionality of the data points

and repeat Steps 1 to 3 until the lower-right corners

have good deﬁnition (or as good as is practically pos-

sible).

Step 4. Along the axes of the distance graph, lo-

cate the rank order indices and/or the distance ele-

ments that correspond to where the lower-right cor-

ners appear in the graph. Under ideal circumstances,

these corners are nearly orthogonal. The rank order

indices and the distance elements coincide with the

meaningful levels and the respective threshold dis-

tances d

of the corresponding hierarchical sequence.

For an example that shows how these four vari-

ables align, see Fig. 3. As part of the cluster analy-

sis described in (Olsen, 2014), the ordered triples are

evaluated in ascending order for information about

linkage. As the distance elements become larger,

threshold distance d

increases implicitly from 0 to

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

the maximum of all the distance elements. Although

threshold distance d

is a continuous variable that can

vary from 0 (where each data point is a singleton) to at

least this maximum distance (where all the data points

belong to the same cluster), the only values that matter

are those

n·(n−1)

values that are equal to the distance

elements d

i, j

. Since the number of data points in a

data set is ﬁnite, the maximum number of levels of a

hierarchical sequence is ﬁnite and equal to the number

of ordered triples (distance elements) plus one. Thus,

the rank order indices, by virtue of the distance ele-

ments d

i, j

, coincide with the last

n·(n−1)

levels of the

hierarchical sequence.

Step 5. Use a complete linkage hierarchical clus-

tering method such as that in (Olsen, 2014) to con-

struct only the cluster sets for the meaningful levels.

By using a method that constructs cluster sets de novo

instead of using an updating method, it is possible to

construct only the cluster sets for meaningful levels

of a hierarchical sequence. The number of clusters in

a meaningful cluster set becomes an artifact of clus-

ter set construction. Finding meaningful levels of a

hierarchical sequence reduces the time complexity to

construct cluster sets from O(n

) to O(ln

5 EMPIRICAL RESULTS

The remainder of this paper describes the empirical

results from four experiments. The ﬁrst experiment

shows how the effects of noise are attenuated as the

dimensionality of the data points increases. The sec-

ond experiment looks at data sets having multiple at-

tributes and how meaningful cluster sets can have real

world meaning. The third experiment also shows how

meaningful cluster sets can have real world meaning.

The fourth experiment demonstrates other interesting

properties of the means for ﬁnding meaningful levels

of an

n·(n−1)

+1-level hierarchical sequence. The data

sets are representative of other data sets that have in-

herent structure. The 2-norm distance measure (Eu-

clidean distance) is used to calculate the distances.

level is a variable that is used to refer to individ-

ual meaningful levels, and d

refers to the respective

threshold distances d

5.1 Synthetic Data Sets–Nearly Ideal

Circumstances

This experiment shows how the effects of noise are at-

tenuated and inherent structure emerges as the dimen-

sionality of the data points increases. The heat map

in Fig. 4 was provided by the Hollings Cancer Cen-

ter at the Medical University of South Carolina. The

data sets constructed from this heat map include three

gene classes and four sample classes. The ratio for

the gene classes is 50:150:1000 while the ratio for the

sample classes is 25:25:10:40. The signal-to-noise ra-

tio for the gene classes is 1.29/1.87, where noise is de-

ﬁned as the pooled estimate of the standard deviations

for over (N(2,4

), mostly in red-orange (dark gray)),

under (N(−2,4

), mostly in yellow (light gray)), and

normally (N(0,1

), mostly in orange (medium gray))

expressed genes.

The mean values of the three gene classes are used

to construct a noiseless data set. As the ﬁrst graph in

Fig. 4 shows, inherent structure emerges immediately

for noiseless data. For the noisy data set, inherent

structure emerges as early as m = 5000 dimensions,

and the last graph suggests that the corresponding hi-

erarchical sequence has ﬁve meaningful levels: level

= 0 or d

= 0.00, level = 499,500 or d

= 105.28, level

= 699,500 or d

= 297.65, level = 711,900 or d

365.58, and level = 719,400 or d

= 429.81. The clus-

ter sets for these levels were constructed without con-

structing any of the other 719,396 cluster sets (which

also is 1195 fewer cluster sets than an n-level hierar-

chical sequence). The gene classes are discernible by

examining the meaningful cluster sets. The two tables

in Fig. 4 show that noise attenuation is not the same

as noise elimination.

5.2 Residential Heat Pump

This experiment looks at data sets that have multi-

ple attributes. Three data sets were provided by the

U.S. National Institute of Standards and Technology

(NIST). The data sets originally were collected for a

study described in (Kim et al., 2006). There, they

were used to analyze the performance of a residen-

tial heat pump that was operating in the cooling mode

when a single external fault was imposed. The data

sets are comprised of numerous kinds of measure-

ments that were collected at approximately 12 sec-

ond intervals for at least 17 minutes. While two of

the data sets were collected, the indoor air side ﬂow

rate ( f t.

/min., scfm) was changed from 1000 scfm to

500 scfm and from 1000 scfm to 1200 scfm, respec-

tively. Using no-fault, third-order polynomial corre-

lations as the basis for calculating residuals, the read-

ings for the most informative seven kinds of measure-

ments related to air ﬂow are excerpted from each data

set, and consecutive sequences of readings that in-

clude 15 consecutive time points are concatenated to

construct data points. In all, 11 data points having

105 dimensions (7 measurements x 15 time points)

are constructed from each data set, or 33 data points

MeansforFindingMeaningfulLevelsofaHierarchicalSequencePriortoPerformingaClusterAnalysis

Figure 4: Heat map, distance graphs, and meaningful cluster sets for the synthetic data sets. The ﬁrst graph pertains to the

noiseless data set while the next three graphs pertain to the noisy data set.

in total.

As the chart in Fig. 5 shows, the standard devi-

ations for all the measurements are relatively small.

Consequently, inherent structure emerges as early as

m = 105 dimensions. The graph in Fig. 5 suggests

that the corresponding hierarchical sequence has ﬁve

meaningful levels. The fault pattern for the 500 scfm

data appears at level = 407 or d

= 40.10 while that

for the 1200 scfm data appears at level = 286 or d

8.28.

5.3 Motes Sensing Luminescence

This experiment shows that meaningful cluster sets

can have real world meaning while other cluster sets

generally do not. Nine Crossbow



MicaZ motes

with MTS300CA sensor boards attached thereto are

conﬁgured into a 1x1 meter grid. The motes are pro-

grammed to take light readings (lux) of an overhead

light source every 1 second. After calibrating the

motes, canopies are placed over motes 1, 6, and 8 dur-

ing the entire experiment, so they are never exposed

to direct light (the “full shade” motes); canopies are

never placed over motes 2, 4, and 9, so they are al-

ways exposed to direct light (the “full sun” motes);

and canopies are placed over motes 3, 5, and 7 for 1.5

minutes out of every 3 minute cycle (collectively, the

“partial shade” motes). Further, the canopy for mote

3 is deployed at 30 seconds into each 3-minute cycle

and removed at 120 seconds, the canopy for mote 5 is

deployed at 60 seconds and removed at 150 seconds,

and the canopy for mote 7 is deployed at 90 seconds

and removed at 180 seconds. Data were collected for

15 minutes or 900 samples per mote (8100 samples

in total), out of which 893 samples per mote (8037

samples in total) were usable

Typical direct light readings were about 905 lux

while typical indirect light readings were about 813

lux. The standard deviations of the readings collected

by each mote are all less than 10 lux, so although

some corners of the distance graph are not nearly or-

thogonal, inherent structure emerges as early as m =

180 dimensions. The graphs in Fig. 6 suggest that the

corresponding hierarchical sequence has four mean-

ingful levels. At level = 6 or d

= 287.97 (m = 893),

the cluster set includes ﬁve non-overlapping clusters,

one for the full sun motes, another for the full shade

motes, and one for each of the partial shade motes.

At level = 27 or d

= 2488.63 (m = 893), the cluster

set includes two overlapping clusters, one for those

motes that were exposed to direct light during all or

part of the experiment (the full sun motes and the par-

tial shade motes) and the other for those motes that

were not exposed to direct light during all or part of

the experiment (the full shade motes and the partial

shade motes).

As the table in Fig. 6 illustrates, the cluster sets

for the meaningful levels have real world meaning.

The cluster sets for the other levels generally do not,

and the more so for levels that are not proximate to

the meaningful levels. When multiple classes of data

points have not ﬁnished linking to form a new conﬁg-

uration of clusters, the cluster sets are comprised of

overlapping clusters whose differences are not related

to inherent structure. These cluster sets are much less

transparent to domain experts.

Seven packets from mote 9 were dropped during trans-

mission.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

Figure 5: Mean values and standard deviations, distance graph, and meaningful cluster sets for the seven kinds of measure-

ments that were excerpted from the NIST data sets.

Figure 6: Conﬁguration, dendrogram, distance graphs, and exemplary cluster sets for the nine motes data set. The motes are

classiﬁed according to the data sequences that are collected. The different colors (gray scales) represent the different clusters

at level = 6. The meaningful cluster sets have asterisks.

The number of meaningful levels does not appear

to be a limiting factor. In experiments involving com-

plex geometric patterns, as many as 19 meaningful

levels have been found. In contrast, the post hoc

heuristics are designed to ﬁnd one or maybe a few

cluster sets. The gap statistic found the cluster set at

level = 6 but not that at level = 27, because the latter

cluster set includes overlapping clusters.

When the standard complete linkage method is

used to cluster a data set, some cluster sets that should

be meaningful are obscure. As the dendrogram in Fig.

6 shows, while mote 7 combines with the full sun

motes at d

= 2488.63, motes 3 and 5 combine with

the full shade motes. This disparity among the partial

shade motes is difﬁcult to understand without taking

into consideration how the standard complete linkage

method imposes taxonomic structure onto data sets.

MeansforFindingMeaningfulLevelsofaHierarchicalSequencePriortoPerformingaClusterAnalysis

Figure 7: ECG and distance graphs for the data that are

excerpted from ﬁle 16265 of the MIT-BIH Normal Sinus

Rhythm database.

5.4 Health Monitoring

The data used in this experiment come from ﬁle

16265 of the MIT-BIH PhysioNet Normal Sinus

Rhythm database (Goldberger et al., 2000). This ﬁle

contains ECG readings collected at 128 hertz. The

P,Q,R,S,T interval of each heart beat, illustrated by

the ﬁrst two graphs in the top row of Fig. 7, describes

how a heart pumps blood to other parts of a body.

Here, 25 samples per beat that include the Q,R,S com-

plex and at least the left side of the ST element are ex-

cerpted from the ﬁrst 300 consecutive beats of the ﬁle,

and the data set is divided into ten segments (approx.

25 seconds each). The last graph in the ﬁrst row of

Fig. 7 shows that this data set has almost no inherent

structure.

An elevating ST element is simulated by adding

a constant c

elevST

to samples 11-22 of the excerpts

in the last ﬁve segments. Increasing c

elevST

from 10

mV to 150 mV adds structure to the data set. The

graphs in the second row show that the elevating ST

is detectable as early as 80 mV, when the ﬁrst ﬁve

segments and the last ﬁve segments are grouped into

different clusters. The graphs in the bottom row show

how inherent structure emerges as the dimensionality

of the segments increases. Increasing the dimension-

ality of the segments does not add structure to the data

set, however, and the law of diminishing returns even-

tually sets in. At these elevations, the damage from

ischemia and the risk of sudden death still are low.

6 CONCLUSION

When the assumptions underlying the standard com-

plete linkage method are unwound, the size of a

hierarchical sequence reverts back from n levels to

n·(n−1)

+ 1 levels, and the time complexity to con-

struct a hierarchical sequence of cluster sets becomes

O(n

). Moreover, the post hoc heuristics for cut-

ting dendrograms are not suitable for ﬁnding mean-

ingful cluster sets of an

n·(n−1)

+ 1-level hierarchical

sequence. To overcome these problems, this paper

presents three contributions. First, using the 2-norm

distance measure as an example, it presents a means

for ﬁnding meaningful levels of an

n·(n−1)

+ 1-level

hierarchical sequence prior to performing a cluster

analysis. By ﬁnding meaningful levels of such a hier-

archical sequence prior to performing a cluster anal-

ysis, it is possible to know which cluster sets to con-

struct and construct only these cluster sets. This re-

duces the time complexity to construct cluster sets

from O(n

) to O(ln

). Second, it shows how increas-

ing the dimensionality of the data points helps re-

veal inherent structure in noisy data. Third, it pro-

vides working deﬁnitions for the notions “meaningful

level” and “meaningful cluster set”. The empirical re-

sults from four experiments show that ﬁnding mean-

ingful levels of a hierarchical sequence is easy and

yields results that can have real world meaning. Fu-

ture work includes mathematically capturing and in-

tegrating the means into the new clustering method,

so that the new clustering method is self-contained,

and working with more complex beta applications.

ACKNOWLEDGEMENTS

The author thanks Dr. Larry Gray, Department of

Mathematics, University of Minnesota, for his help

with the proof, and Dr. John Carlis, Department

of Computer Science and Engineering, University of

Minnesota, for his general guidance and advice on

technical writing. The author also thanks the paper’s

reviewers for reviewing the paper and for their helpful

feedback.

REFERENCES

Anderberg, M. (1973). Cluster Analysis for Applications.

Academic Press.

Berkhin, P. (2006). A survey of clustering data mining

techniques. In Kogan, J., Nicholas, C., and Teboulle,

M., editors, Grouping Multidimensional Data: Re-

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

cent Advances in Clustering, chapter 2, pages 25–71.

Springer-Verlag.

Beyer, K., Goldstein, J., Ramakrishnan, R., and Shaft,

U. (1998). When is “nearest neighbor”meaningful?

Technical report, Computer Sciences Department,

University of Wisconsin-Madison, Madison, WI.

Cormen, T., Leiserson, C., Rivest, R., and Stein, C. (2004).

Introduction to Algorithms. MIT Press, 2nd edition.

Daniels, K. and Giraud-Carrier, C. (2006). Learning the

threshold in hierarchical agglomerative clustering. In

Proceedings of the Fifth International Conference on

Machine Learning and Applications (ICMLA ’06),

pages 270–278, Orlando, FL.

Everitt, B., Landau, S., Leese, M., and Stahl, D. (2011).

Cluster Analysis. John Wiley and Sons, 5th edition.

Gill, H. (2011). CPS overview. In Symposium on

Control and Modeling Cyber-Physical Sys-

tems (www.csl.illinois.edu/video/csl-emerging-

topics-2011-cyber-physical-systems-helen-gill-

presentation), Champaign, IL.

Goldberger, A., Amaral, L., Glass, L., Hausdorff,

J., Ivanov, P., Mark, R., Mietus, J., Moody,

G., Peng, C., and Stanley, H. (June 13, 2000).

PhysioBank, PhysioToolkit, and PhysioNet:

Components of a New Research Resource

for Complex Physiologic Signals. Circulation

101(23):e215-e220 [Circulation Electronic Pages;

http://cir.ahajournals.org/cgi/content/full/101/

23/e215].

Hinneburg, A., Aggarwal, C., and Keim, D. (2000). What

is the nearest neighbor in high dimensional spaces? In

Proceedings of the 26th International Conference on

Very Large Data Bases (VLDB 2000), pages 506–516,

Cairo, Egypt.

Isermann, R. (2006). Fault-Diagnosis Systems: An In-

troduction from Fault Detection to Fault Tolerance.

Springer-Verlag.

Jain, A. and Dubes, R. (1988). Algorithms for Clustering

Data. Prentice Hall.

Johnson, R. and Wichern, D. (2002). Applied Multivariate

Statistical Analysis. Prentice Hall, 5th edition.

Kim, H. and Lee, S. (2000). A semi-supervised document

clustering technique for information organization. In

Proceedings of the 9th ACM International Conference

on Information and Knowledge Management (CIKM

’00), pages 30–37, McLean, VA.

Kim, M., Payne, W. V., and Domanski, P. (2006). Per-

formance of a residential heat pump operating in the

cooling mode with single faults imposed. Technical

report, U.S. National Institute of Standards and Tech-

nology, Gaithersburg, Maryland.

Kirk, D. and Hwu, W. (2013). Programming Massively Par-

allel Processors. Elsevier Inc., 2nd edition.

Lance, G. and Williams, W. (1967). A general theory of

classiﬁcatory sorting strategies ii clustering systems.

Computer J., 10(3):271–277.

Matula, I. (1977). Graph theoretic techniques for cluster

analysis algorithms. In Ryzin, J. V., editor, Classiﬁca-

tion and Clustering, pages 95–129. Academic Press.

Murtagh, F. (2009). The remarkable simplicity of very high

dimensional data: Application of model-based clus-

tering. J. of Classiﬁcation, 26:249–277.

Navidi, W. (2006). Statistics for Engineers and Scientists.

McGraw-Hill.

Olsen, D. (2014). Include hierarchical clustering: A hier-

archical clustering method based solely on interpoint

distances. Technical report, Minneapolis, MN.

Peay, E. (1974). Hierarchical clique structures. Sociometry,

37(1):54–65.

Peay, E. (1975). Nonmetric grouping: Clusters and cliques.

Psychometrika, 40(3):297–313.

Tibshirani, R., Walther, G., and Hastie, T. (2001). Es-

timating the number of clusters in a dataset via the

gap statistic. Journal of the Royal Statistical Society,

63(2):411–423.

APPENDIX

Proof for Theorem 1. (sketch only)

Assume that the stated conditions are true. The

second moment of

m,(i, j)

is E[Z

m,(i, j)

] = E[(

∑

k=1

k,(i, j)

)

·2

]

∑

k=1

E[Y

k,(i, j)

]

∑

k=1

E[(σ

k,(i, j)

+ µ

k,(i, j)

)

]

∑

k=1

E[(σ

k,(i, j)

)

+ 2σ

k,(i, j)

]

∑

k=1

E[(σ

k,(i, j)

)

] +

∑

k=1

E[2σ

k,(i, j)

] +

∑

k=1

E[µ

k,(i, j)

where W is a normally distributed random vari-

able. The expected value of the middle term in the

last expression equals zero and drops out, so

E[Z

m,(i, j)

] =

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

To ﬁnd the expected value E[Z

m,(i, j)

] in terms

of the standard deviations σ

k,(i, j)

and mean values

k,(i, j)

, Taylor’s series is used to expand E[Z

m,(i, j)

Let

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

)

and

h =

∑

k=1

2σ

k,(i, j)

MeansforFindingMeaningfulLevelsofaHierarchicalSequencePriortoPerformingaClusterAnalysis

Then,

E[Z

m,(i, j)

] = E[(

∑

k=1

k,(i, j)

)

]

= E[(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

+ 2σ

k,(i, j)

))

]

≈ E[(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

−

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

48(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

+ ...] (6)

≈ E[(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

] −E[

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

]. (7)

In Equation 6, 2σ

k,(i, j)

is symmetric, so E[

∑

k=1

((σ

k,(i, j)

)

+µ

k,(i, j)

))

] = 0 and drops out. As

m → ∞, the third-order term and all higher order terms converge to 0. Thus,

(E[Z

m,(i, j)

])

≈ (E[(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

])

−2(E[(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

]E[

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

])

+ (E[

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

])

. (8)

Using the dominated convergence theorem and Taylor’s series, where g =

∑

k=1

((σ

k,(i, j)

)

−σ

k,(i, j)

), the

ﬁrst term in Equation 8 evaluates to

(E[(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

])

≈

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

−

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

)

. (9)

When h

is expanded, the terms with (

∑

2σ

,(i, j)

)(

∑

2σ

,(i, j)

) in the numer-

ator drop out, leaving only those terms with 4

∑

k=1

(σ

k,(i, j)

)

in the numerator. Using the dominated

convergence theorem and Taylor’s series once more, where g =

∑

k=1

((σ

k,(i, j)

)

−σ

k,(i, j)

), the second term

in Equation 8 evaluates to

−2(E[(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

]E[

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

])

≈ −E[(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

]E[

∑

k=1

(σ

k,(i, j)

)

(

∑

k=1

((σ

k,(i, j)

)

+ µ

k,(i, j)

))

]

≈ −

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

. (10)

As m → ∞, the third term in Equation 8 converges to 0.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

Thus, the variance σ

m,(i, j)

of Z

m,(i, j)

= E[Z

m,(i, j)

] −(E[Z

m,(i, j)

])

≈

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

−(

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

−

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

)

−

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

∑

k=1

k,(i, j)

. (11)

QED

MeansforFindingMeaningfulLevelsofaHierarchicalSequencePriortoPerformingaClusterAnalysis