A Comparison Between a Deterministic, Compartmental Model and an

Individual Based-stochastic Model for Simulating the Transmission

Dynamics of Pandemic Inﬂuenza

Hung-Jui Chang

, Jen-Hsiang Chuang

, Tsurng-Chen Chern

, Mart Stein

, Richard Coker

, Da-Wei

Wang

, Tsan-sheng Hsu

Institute of Information Science, Academia Sinica, Taipei, Taiwan

Epidemic Intelligence Center, Centers for Disease Control, Taipei, Taiwan

National Institute for Public Health and the Environment (RIVM), Bilthoven, The Netherlands

Communicable Diseases Policy Research Group, London School of Hygiene and Tropical Medicine, Bangkok, Thailand

Keywords:

Agent-based Model, Equation-based Model, Model Comparison, Parameter Calibration.

Abstract:

Simulation models are often used in the research area of epidemiology to understand characteristics of disease

outbreaks. As a result, they are used by authorities to better design intervention methods and to better plan

the allocation of medical resources. Previous work make use of many different types of simulation models

with an agent-based model, e.g., Taiwan simulation system, and an equation-based model, e.g., AsiaFluCap

simulation system, being the two most popular ones. Some comparison studies has been attempted in the past

to understand the limits, efﬁciency, and usability of some model. However, there was little studies to justify

why one model is used instead of the other. In this paper, instead of studying the two most popular models one

by one, we try to do a comparative study between these two most popular ones. By observing that one model

can outperform the other in some cases, and vice versa, we hence study conditions that which one should be

used. Furthermore, previous studies show little results in the issue of allocating medical resources. Our paper

studies and compares the two models using medical resources allocation as one of our primary concerns. As a

conclusion, we come out with a general guideline to help model designers to pick one that ﬁts the given needs

better.

1 INTRODUCTION

Simulation models are often used in the research

area of epidemiology estimating the characteristics of

a speciﬁed disease outbreak, such as outbreak day,

peak day and prevalence rate (Diekmann and Heester-

beek, 2000). Simulation results can support govern-

ments in designing intervention methods to prevent

the spread of diseases (Tsai et al., 2010) or to estimate

the amount of medical resources needed (Krumkamp

et al., 2011; Rudge et al., 2012; Stein et al., 2012).

There are many different types of simulation mod-

els, such as homogeneous (Diekmann and Heester-

beek, 2000; Krumkamp et al., 2011) or heteroge-

neous (Garnett, 2002; Keeling and Danon, 2009;

Lunelli et al., 2009), deterministic (Diekmann and

Heesterbeek, 2000; Keeling and Danon, 2009) or

stochastic (Britton and Lindenstrand, 2009; Lunelli

et al., 2009), equation-based (Diekmann and Heester-

beek, 2000; Garnett, 2002) or agent-based (Berger,

2001; Davidsson, 2002; Macal and North, 2005;

Moss and Davidsson, 2001; Parker et al., 2003). The

major difference between homogeneous and hetero-

geneous model is a homogeneous model treats all the

people exactly the same way but in a heterogeneous

model, people are partitioned into different groups

according to their characteristic. In a deterministic

model, the number of newly infected people is always

the same for a given number of susceptible people and

infectious people. But in a stochastic model, the num-

ber of newly infected people is often different as this

number is chosen based on a random distribution. An

equation-based model is the one that utilizes numer-

ical time-stepping procedures to simulate the behav-

iors over time. And an agent-based models focuses on

the actions and the interactions among autonomous

agents.

586

Chang H., Chuang J., Chern T., Stein M., Coker R., Wang D. and Hsu T..

A Comparison Between a Deterministic, Compartmental Model and an Individual Based-stochastic Model for Simulating the Transmission Dynamics of

Pandemic Inﬂuenza.

DOI: 10.5220/0005040905860594

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),

pages 586-594

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

In 2009, the novel inﬂuenza H1N1 spread from

Mexico and caused over 18,000 deaths worldwide.

The AsiaFluCap project (AFC) (AsiaFluCap, 2009)

has focused on the medical resources issue in the

southeast Asia where infectious diseases similar to

H1N1 may break out. AFC has built a homogeneous

deterministic equation-based model (the AsiaFluCap

Simulation, AFC model) to simulate the disease trans-

mission behavior. This simulator has the same ba-

sis as the SEIR model described in Krumkamp et

al.(Rudge et al., 2012; Stein et al., 2012). In the

same time, Institute of Information Science (IIS)

of Academia Sinica cooperates with CDC in Tai-

wan (Tsai et al., 2010) has developed a heteroge-

neous individual based model (the Taiwan simulation

model, TW model) to simulate the disease transmis-

sion behaviors in order to design effective interven-

tion policies. Although the AFC model and the TW

model are different in design, they both model the

same disease namely pandemic inﬂuenza. Since the

two models modeled the same disease, a natural ques-

tion raised: How different are these two models and

how well does each model describe the same disease?

Previous studies have mentioned the relation-

ship between agent-based models and equation-based

models (Ajelli et al., 2010; Bobashev et al., 2007;

Connell et al., 2009; Rahmandad and Sterman, 2008).

These works focused on comparing the simulation re-

sults between the compartment model and individual-

based model (Connell et al., 2009; Rahmandad and

Sterman, 2008), trying to hybrid these two ap-

proaches (Bobashev et al., 2007) and giving the prin-

ciple of which models should be used based on the

policy designed (Rahmandad and Sterman, 2008), but

none of them focused on how to calibrate different

model by calibrating the parameters.

In this paper, we construct a series of methods to

calibrate parameters between these two models. In

order to compare and analyze the simulation results of

these two models, we use the same parameters setting

after calibration. We also give a guideline in choosing

a simulation model that best ﬁts a user’s needs.

2 METHODS

2.1 AsiaFluCap Simulation Model

The AFC model (AsiaFluCap, 2009) is a homoge-

neous and deterministic model which is base on the

Pandemic (H1N1) 2009 - update

112, published by WHO and available at

http://www.who.int/csr/don/2010

08 06/en/index.html

fundamental SIR model with three additional com-

partments, Prophylaxis (P), Exposed (E) and Asymp-

tomatic (A). The detail of the model is described in

the supporting text.

In this model, the setting of parameters is the same

for all people. The number of people being transited

from one compartment to the next compartment in

each time slice are given with differential equations.

For example, if the latency between E and A is x days

and the time slice is y steps per day then in every time

slice 1/(x× y) of the people in E are transited to A.

2.2 Taiwan Simulation Model

The TW model (Tsai et al., 2010) is a stochastic and

heterogeneous model. Each individual has his own

personal attributes such as age, gender, contact prob-

ability and daily activities. People with the same daily

actives are called in the same mixing group. The dura-

tion that an infected individual stays in a disease state

is selected according to a probability distribution and

individuals may have different disease courses.

2.2.1 Social Structure

In the TW model, the age of a person is the major fac-

tor that affects his behaviors such as daily activities

and contacts. The social structure basically follows

the one given in (Tsai et al., 2010). There are ﬁve age

groups in the TW model, namely c

(0-4 years), c

(5-

18 years), a

(19-29 years), a

(30-64 years) and a

(above 64 years). At the beginning of the simulation,

the age and gender of each person are stochastically

generated based on the demographic distributions ac-

cording to the real census data.

There are ten mixing groups in the TW model,

household (HH), household cluster (CL), neighbor-

hood (NB), community (CM), daycare center (DC),

play group (PG), elementary school (ES), middle

school (MS), high school (HS) and work group (WG).

Each household contains 1 to 7 people. The age, gen-

der and number of people in each household are also

generated according to the Taiwan census data. A

household cluster contains four households. A neigh-

borhood contains about 500 people, and a community

is formed by four neighborhoodsi.e., about 2000 peo-

ple. Each community has one high school, one mid-

dle school and two elementary schools. Each high

school and each middle school are shared by all four

2000 Taiwan census data published by Directorate-

General of Budget, Accounting and Statistics, Execu-

tive Yuan, Republic of China (Taiwan), available at

http://eng.stat.gov.tw/lp.asp?CtNode=1627&

CtUnit=777&BaseDSD=7&mp=5

AComparisonBetweenaDeterministic,CompartmentalModelandanIndividualBased-stochasticModelforSimulating

theTransmissionDynamicsofPandemicInfluenza

587

neighborhoods in the same community. Two neigh-

borhoods share one elementary school. Each neigh-

borhood has several daycare centers, playing groups

and working groups. The numbers of those groups

depend on the number of people in those groups in

that neighborhood.

Each day is divided into two periods, the day time

period (DP) and the night time period (NP). Each pe-

riod has 12 hours. In DP, the young children (c

) ei-

ther go to the daycare center or stay close to home in

a playing group with an equal probability. The school

age children (c

) go to schools, either ES, MS or HS,

depending on their ages with preset drop out rates.

The working adults (a

and a

) go to work in DP

with a given unemployment rate. All the elder adults

), the drop out students and the unemployed adults

stay at home during DP. In NP, people stay at home

within the correspondinghousehold cluster, neighbor-

hood and community.

2.2.2 Disease Transmission Model

Disease transmission behavior is mainly controlled

by two epidemiological parameters: contact proba-

bility (CP) and transmission probability (P

trans

). Con-

tact probabilities are given for people of speciﬁc age

group in a social mixing group, i.e., people in the

same age group and same mixing group have the same

contact probability. In any time period, a susceptible

person may be infected by an infectious person in the

same mixing group.

The TW model has four main states S, E, I and

R. Each state comprises several compartments. There

are two different compartments in E, namely Latency

(L) and incubation (In). For all people in E, only peo-

ple in In can infect others. I also contains two dif-

ferent compartments, namely asymptomatic (I

) and

symptomatic (I

). People in any compartment are

transited to the next compartment after one DP and

one NP, and they will be transited to either Recover

(R) or Death (D) after then.

3 CALIBRATION

We now provide a case study of the calibration be-

tween the AFC model and the TW model. We will

ﬁrst group parameters according to they are used in

only one model or in both models. For the parameters

used in both models, they are grouped according to

their representation.

3.1 General Descriptions of the

Parameters

In this subsection, parameters are classiﬁed accord-

ing to their attributes. The ﬁrst step is to distinguish

between shared parameters and individual parame-

ters. Shared parameters are those used by both mod-

els such as the transmission probability, the total num-

ber of people in the region. Individual parameters are

those only used by either one model. In the TW model

individual parameters are personal information such

as age, gender, household structure etc. Since the in-

dividual parameters only appear in one model, in the

calibration phase we only focus on the shared param-

eters. The shared parameters can also be classiﬁed

into three groups according to the possible range of

their values: ﬁxed-value, ﬁxed-probability and proba-

bility distribution. The tree structure of the parameter

groups is shown in Figure 1.

Parameters

Shared parameter Individual parameter

Fix-value

Fix-probability Probability distribution

Figure 1: Parameter usage and type of representation.

Shared parameters may use the same representa-

tion method, to calibrate them we simply assign the

same value. For shared parameters that belong to dif-

ferent groups in different models, we need to design

a method to transliterate their values.

Before we introduce how to calibrate shared pa-

rameters between the AFC model and the TW model,

we ﬁrst describe the different types of parameters and

how to group the parameters.

3.2 Individual Parameters

Individual parameters are those only used by either

one model. They describe details about the nature

of the disease and the human behavior. For exam-

ple, the compartment expose only appears in the AFC

model and the corresponding parameter also only ap-

pears in the AFC model. Similarly, the TW model

uses mixing group to describe the social structure, so

the corresponding parameters which denotes the dis-

tribution of household structure and the distribution

of age only appear in the TW model.

3.3 Shared Parameters

Shared parameters are those used in both models.

They usually refer to the natural history of disease

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

588

Table 1: Distribution of onset days.

Onset days 3 4 5 6

days

0.3 0.4 0.2 0.1

Table 2: Distribution of latency and incubation days.

Incubation (Latency) days 1 (1) 2 (1) 3 (2)

Latency,Incubation

= P

Latency

0.3 0.5 0.2

and the human behavior. For example, the number

of days of each state of disease and the transmission

probability and the efﬁcacy of vaccination belong to

the disease natural history. And the reduction of so-

cial contact due to government intervention measures

and the availability of medical resources belong to the

human behavior.

Parameters represented as ﬁxed values include the

parameters such as the total number of people, the

number of simulation days and the amount of avail-

able medical resources.

A parameter represented as a ﬁxed probability

means the probability of a particular event will hap-

pen e.g., the transmission probability of two people

have made an effective contact. Another example is

the probability that a patient becomes symptomatic or

asymptomatic.

Parameter represented as a probability distribu-

tion contains two parts: its sample distribution and

the probability space. For example in the section of

Taiwan Simulation Model, the number of infectious

days are 3-6 days with the corresponding probability

of 0.3, 0.4, 0.2 and 0.1 respectively. See Table 1 for an

illustration. Another example is shown in Table 2 to

illustrate the numbers of latency and incubation days

in the TW model.

3.4 Methods of Calibration

For each shared parameter, we ﬁrst decide whether

it belongs to the same group in the two models. We

reassign an equal value if they do. If the parameter

belongs to different groups, we design a formula to

transliterate the ‘values’ between the two models.

We ﬁrst consider how to transliterate between a

ﬁxed-value parameter in one model and a probability-

distribution one in another model. For example, the

number of incubation days is 1 day in the AFC model,

and it is from 1 to 3 days with probabilities 0.3, 0.5

and 0.2 respectively, in the TW model. To calculated

the expected number of incubation days in the TW

model, we simply sum the product of the number of

days and the corresponding probability, that is:

∑

D× Pr{Incubation is D days}. (1)

The expected number of incubation days is 1× 0.3+

2× 0.5 + 3 × 0.2 = 1.9, and the expected number of

onset days is 3 × 0.3 + 4× 0.4 + 2 × 0.5 + 6× 0.1 =

4.1. See Table 1 and Table 2 for details.

Now we consider the case of transliterating from

an expected value parameter in one model to a prob-

ability distribution in another model. We use either a

scaling or a geometric distributed methods.

In scaling method, the value of probability events

of a given distribution is multiplied with the ra-

tio of the given expected value over the expected

value of the given probability distribution. Consider

a distribution has expected number D

and sample

space D

,...,D

with corresponding probability

,...,P

respectively. If we want to scale this dis-

tribution’s expected value to D

′

, we ﬁrst calculate the

ratio RATIO = D

′

. Next, we multiply each sam-

ple space D

with RATIO and we have a new distri-

bution with expected value D

′

= D

× RATIO. For

example, the number of latency and incubation days

in the AFC model is 1.0 and the expected latency and

incubation days in the TW model is 1.9. We can scale

down the value of the probability distribution D

latency

in the TW model with 1.0/1.9 = 0.526.

In the above case, if we treat the number of days

as the expected number of a simple probability distri-

bution, then we can reconstruct the distribution by ﬁt-

ting a probability distribution to that expected value.

In the AFC model, each period of the disease course

is described as a geometric distribution. For example,

the number of latency day is 1.0, and the number of

time interval in a day is 15, then in each time interval,

1/15 of the people in E transit to A. Then we can cal-

culate the corresponding probability of the number of

day that a person remain in the same compartment by

P(t) = p(1− p)

t−1

(2)

where t is the number of time intervals and p is the

probability that person transits to the next compart-

ment. For example, the time interval in the TW model

is 2 and the latency period is 1.0 in the AFC parameter

setting, then 1.0/2 = 0.5 of the people transit from E

to A in one time interval, and the corresponding prob-

ability of people remain in the E is 0.5, 0.25 and 0.125

with 0.5, 1.0 and 1.5 day respectively.

3.5 Experiment design

In order to observe the outputs of the two models

under different data settings, we design two experi-

ments. One simulation comprises three major parts,

the simulation model, either the AFC model or the

TW model, the parameter setting, either the AFC data

setting or the TW data setting, and the size of regions.

AComparisonBetweenaDeterministic,CompartmentalModelandanIndividualBased-stochasticModelforSimulating

theTransmissionDynamicsofPandemicInfluenza

589

Table 3: Experiment scenarios for basic experiment.

Model Regions Size Parameter Setting

AFC Large AFC-setting

AFC Large TW-setting

AFC Small AFC-setting

AFC Small TW-setting

TW Large AFC-setting

TW Large TW-setting

TW Small AFC-setting

TW Small TW-setting

Table 4: Experiment scenarios for small region experiment.

Model Region Size Parameter Setting

TW 1. ..100 AFC-setting

TW 1. ..100 TW-setting

The experiment scenarios is detailed in Table 3 and

Table 4.

In the ﬁrst experiment, we examine the behaviors

of both models using different sizes of regions. We

denote the whole Taiwan as the large region and 1 CM

as the small region. For each model we run the sim-

ulation twice in both region sizes with the TW data

setting and the AFC data setting respectively. Note

that the AFC data setting has longer periods of states

in the disease course, the number of days one patient

is hospitalized is 12 days and the number of day one

patient uses a ventilation is 13 days, and also has a

larger number of expected contacts, 7.0, than that of

using the TW data setting, 4.19.

Since the prevalence of the AFC model is not af-

fected by changing the region size, and the TW model

is sensitive to the size of the region, the second exper-

iment focuses on observing the behavior of the TW

model with different sizes of regions. This experi-

ment uses both the AFC and the TW data settings as

parameter settings. The size of the region, i.e., the

number of CM variates from 1 to 100.

4 EXPERIMENTAL RESULTS

In this section, we introduce the experiment environ-

ments for implementing the AFC model and the TW

model. We show the data settings and the correspond-

ing experiment results.

The TW model is implemented using C++ (Tsai

et al., 2010) and the AFC model is implemented using

an Excel spreadsheet (Krumkamp et al., 2011). The

experiments were run on a server with dual Intel Xeon

X5482, quad-cores, 3.20 GHz CPU and 64GB DDR3

memory. Since TW is an agent-based simulation, for

each simulation of TW model we run 30 times and

take the average.

The ﬁrst experiment includes eight scenarios for

the combination of the AFC model and the TW

model, the AFC setting and the TW setting, and the

large region (entire Taiwan) and the small region (1

CM). The experiment results are shown in Figure 2

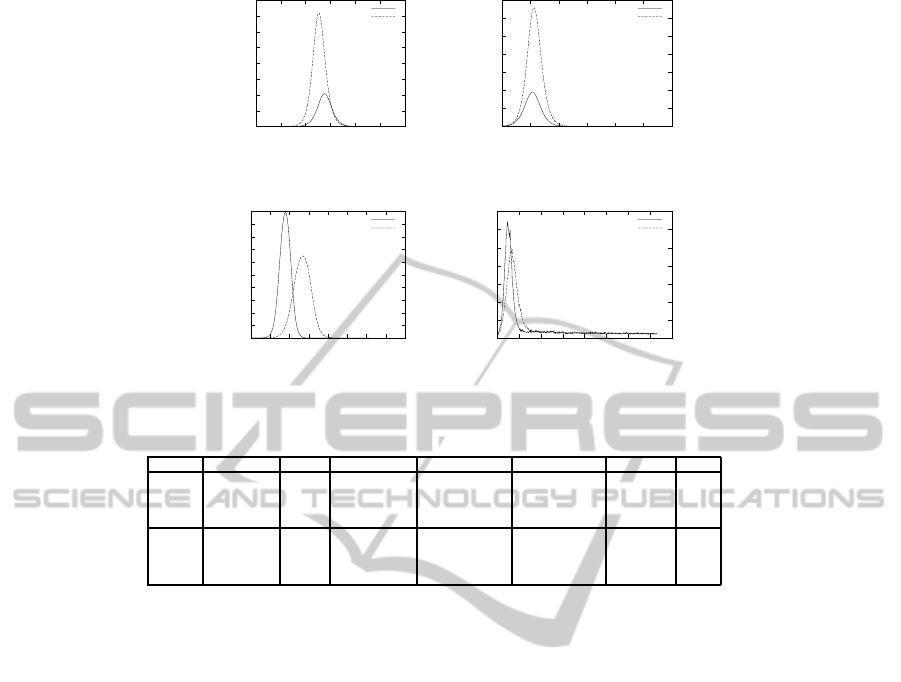
and the detail values are shown in Table 5. Figure 2

shows the number of daily cases with different size

of regions and different parameter settings. The

ﬁrst three columns in Table 5 denote the model used,

the data settings and the size of each region, respec-

tively. The three columns followed are the prevalence

of symptomatic cases, asymptomatic cases, and their

total. The last two columns denote the peak day and

the R

of each experiment. The peak day is the day

with the maximum average number of people that are

currently symptomatic. We ﬁrst calculate the average

number of symptomatic cases of all 30 simulations

and then choose the day with the largest number of

symptomatic cases as the peak day.

The basic reproduction number R

is derived for

each model. The AFC model calculates R

by multi-

plying the number of contacts with the transmission

probability and the number of days of the disease

course (Krumkamp et al., 2011).

The TW model calculates R

using a formula that

is similar to the one used in calculating the expected

number of contacts (Tsai et al., 2010). In each simu-

lation, we sample 2,000 individuals, i.e., the number

of people in 1 CM. We then calculate the expected

number of peoples that can be infected by each of the

sampled individuals. We calculate the probability that

one susceptible is infected by the indicated infectious

person minus the probability that this susceptible in-

dividual is not infected by that infectious person in all

of the mixing groups they shared.

Table 6: Simulation result in TW model with different num-

bers of CM.

AFC TW

CM All(%) Sym(%) Peak Day All(%) Sym(%) Peak Day

1 74.09 56.88 24 79.70 59.73 31

2 62.61 46.75 29 66.37 47.36 38

3 56.87 41.52 31 61.70 43.18 45

4 56.01 40.58 33 59.22 41.19 46

5 53.65 38.49 35 56.54 39.16 47

6 52.34 37.50 35 55.20 37.92 50

7 51.34 36.60 37 54.83 37.58 53

8 50.22 35.77 35 53.65 36.65 53

9 49.94 35.40 39 53.87 36.81 55

10 49.38 35.07 38 52.65 35.89 55

20 48.89 34.58 40 51.39 34.76 63

30 48.77 34.49 39 50.38 33.99 66

40 47.27 33.11 48 50.01 33.68 70

50 47.11 33.02 48 50.18 33.74 72

60 47.08 32.94 49 50.09 33.68 72

70 46.77 32.73 53 49.76 33.43 75

80 46.52 32.50 50 49.79 33.45 77

90 46.58 32.58 54 49.56 33.23 77

100 46.66 32.64 53 49.46 33.18 79

Taiwan 46.25 32.29 86 49.39 33.09 130

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

590

200000

400000

600000

800000

1e+06

1.2e+06

1.4e+06

1.6e+06

0 50 100 150 200 250 300

Number of Cases

Day

AFC-parameter

TW-parameter

(a)

100

120

140

0 50 100 150 200 250 300

Number of Cases

Day

AFC-parameter

TW-parameter

(b)

20000

40000

60000

80000

100000

120000

140000

160000

180000

200000

0 50 100 150 200 250 300 350 400

Nuber of Cases

Day

AFC-parameter

TW-parameter

(c)

0 50 100 150 200 250 300 350 400

Nuber of Cases

Day

AFC-parameter

TW-parameter

(d)

Figure 2: Basic experiments with two models, two parameter settings and different size of regions.

Table 5: Basic experiments with two models, two parameter settings and different size of regions.

Model Parameters Size Symptomatic Asymptomatic Prevalence All Peak Day R

AFC AFC large 31.32% 13.43% 44.75% 137 1.32

AFC small 31.41% 13.44% 44.85% 52 1.32

TW large 48.84% 24.42% 73.26% 125 1.78

TW small 48.71% 24.33% 73.04% 55 1.78

TW AFC large 32.29% 13.97% 46.25% 90 1.38

AFC small 56.88% 17.22% 74.09% 24 1.36

TW large 33.09% 16.30% 49.39% 136 1.43

TW small 59.28% 20.20% 79.48% 34 1.41

5 DISCUSSION

5.1 The Baseline Experiment

The ﬁrst observation is that the prevalence is not af-

fected by the region size in the AFC model and is af-

fected by the region size in the TW model. In the AFC

model, the region size affects the prevalence only

slightly, namely 0.1% for the AFC data setting and

0.2% for the TW data setting. In the TW model, ex-

periments using a large region size have much lower

prevalence than that of using a small region size. It is

46.25%, greatly reduced from 76.25%, for the AFC

data setting and from 79.48% down to 49.39% for

TW data setting.

Peak day in a large region setting is later than that

of the setting for a small region even using the same

model. When using the AFC model with the AFC

data setting, the peaks day for a large region setting

and a small region setting are 137 and 52 respectively,

and when using the AFC model with the TW data set-

ting, the peak day for a large region setting and a small

region setting are 125 and 55 respectively. When us-

ing the TW model with the AFC data setting, the peak

day for a large region setting and small region setting

are 90 and 24 respectively, and when using the TW

model with the TW data setting, the peaks day for

large region setting and small region setting are 136

and 34 respectively.

of the AFC data setting is almost identical us-

ing all 4 different settings, namely 1.32, 1.32, 1.38

and 1.36, but R

of the TW data setting deviates a lot,

namely 1.78, 1.78, 1.43 and 1.41.

The experiment results showthe prevalenceis sen-

sitive to the region size in the TW model and is not

sensitive in the AFC model with either data settings.

This is because AFC model is homogeneous,i.e., con-

tact probability is the same for all individuals. The

TW model is, on the other hand, heterogeneous based

on demographic statistics for the entire nation, i.e.,

an individual with in a given mixing group and has a

distinct contact probability with another individual in

another mixing group.

Both the AFC and TW data settings have a larger

prevalence in the TW model when using a smaller

region setting, and a smaller prevalence when using

a larger region setting. The TW model has similar

behaviors when regions of similar size are used even

when the values of other parameter are different.

Another important factor is that worker ﬂow is not

considered in the AFC model but may affect the ac-

curacy of simulation if there are a large number of

people commuting. Worker ﬂow is the only way two

AComparisonBetweenaDeterministic,CompartmentalModelandanIndividualBased-stochasticModelforSimulating

theTransmissionDynamicsofPandemicInfluenza

591

people in different communities may have a chance

to contact in the TW model. It takes more time for

the disease to spread to other CM when the number

of CM’s increases. This factor affects the peak day

and the prevalence in the TW model.

Although the AFC model is homogeneous, when

the size of regions increases, the peak day also de-

lays. This is because when the initial condition is the

same, the increasing rate of newly infected people re-

mains the same. As the number of susceptible people

increases, more time is needed to infect the same per-

centage of people.

The values of R

are similar for AFC model and

the TW model using the AFC data setting, but are

quite different when using the TW data setting. The

main reason is the disease courses used in the two

models are different. The TW model assumes that

asymptomatic patients and patients in the incubation

period only have half of the original transmission

probability. But in the AFC model, the transmission

probability is the same in all states. If we apply the

formula in the AFC model for the TW data setting and

replace the transmission probability for the asymp-

tomatic case and patients in incubation with half of

the original probability, then R

is 1.40. This value is

close to the R

values in the TW model using the TW

data setting which are 1.41 and 1.43, respectively.

5.2 The Small Region Experiments

This experiment focuses on the behavior of the TW

model using the AFC data setting and the TW data

setting when the size of regions is small.

The prevalence decreases as the region size in-

creases. The AFC data setting has a prevalence of

74.09% when the number of CM’s is 1, and becomes

46.66% when the number of CM’s is 100. The TW

data setting has a prevalence of 79.70% when the

number of CM’s is 1, and 49.46% when the number

of CM’s is 100. In the case of having 100 CM’s, the

prevalence is very close to that of the simulation result

with the entire nation.

The peak day of using a larger region setting is

later than the peak day of using a smaller region set-

ting. Although the peak day does not increase mono-

tonically as the number of CM’s increases, the peak

day of the AFC data setting increases from 24 to 53

and the peak day of the TW data setting increases

from 31 to 79 as the number of CM’s increases from

1 to 100.

Note there is no direct relationship between the re-

gion size and the expected number of contacts. How-

ever, when the number of CM’s increases, the disease

needs more time to transmit to other CM’s due to the

worker ﬂow being that the only way for people to

travel between CM’s. Since the worker ﬂow describe

the probability that a worker lives in a particular town

and works in other town, it only assigns workers to

the level of a town not to the level of a CM. The prob-

ability of a CM in the same town being chosen as a

worker works is uniformly distributed over all CM in

this town. As the number of CM’s in a town increases,

the probability of patients working in some indicated

CM decreases. Hence it is harder to spread over the

whole town and therefor the prevalence decreases.

Due to reasons similar to the above, as the num-

ber of CM’s increases, the disease needs more time

to spread from the original CM where the index cases

are to all other CM’s. Hence the peak day is further

delayed as the number of CM’s increases.

6 CONCLUSION

To analyze the trade-off between various simulation

models and establish a guideline for model selec-

tion, we ﬁrst introduced two different real instances,

namely the AFC model and the TW model. We

grouped the parameters used and introduced proce-

dures to transliterate parameters. We also described

procedure to perform calibration. We ran both mod-

els with the data settings calibrated between them. We

then analyzed the simulation results and gave the ad-

vantages and disadvantages of these models and pro-

vided a principle of model selection.

As a by-product of our study, we conclude the fol-

lowing recommendations when there is a choice be-

tween using a aggregative model and an agent based

one to study the same disease. According to the anal-

ysis result, we should select the model depending on

user requirements. Generally, if we want to build a

simulation model to observe the high-level disease

transmission behavior, to get a immediate simulation

results, or we have only a limited information about

the disease course, e.g., the average time of each du-

ration, we should choose the AFC model since it can

be built using relatively little information. If we want

to study how the heterogeneous social structure, e.g.,

schools and day care centers, affects the disease trans-

mission behavior, to predict the effect of interven-

tion policy on an individual basis, or to observe the

spatio-temporal spreading behaviors of the disease,

we should choose the TW model since it is geographic

based and can easily contain detail individual infor-

mation.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

592

ACKNOWLEDGMENTS

The AsiaFluCap project is coordinated by the London

School of Hygiene and Tropical Medicine with col-

laborators from the Hamburg University of Applied

Sciences (HAW), Netherlands National Institute for

Public Health and the Environment (RIVM), Inter-

national Health Policy Programme -Thailand (IHPP),

Taiwan Centers for Disease Control, University of In-

donesia Faculty of Public Health, Vietnam Ministry

of Science and Technology, Vietnam Military Med-

ical University, Lao PDR National Emerging Infec-

tious Diseases Coordination Ofﬁce, Lao PDR Univer-

sity of Health Sciences, Mahidol University Faculty

of Tropical Medicine, Cambodia Department of Com-

municable Disease Control, and Cambodia National

Institute of Public Health. We are grateful to the many

collaborators within this project consortium for their

contribution towards resource characterization, data

collection, and discussions at consortium meetings.

These include: Ly Khunbunn Narann and Chau Dara-

pheak (Cambodia); Sandi Iljanto, Noviyanti Liana

Dewi, Kamaluddin Latief, Amir Suudi, Lilis Much-

lisoh (Indonesia); Nyphonh Chanthakoummane, Sing

Menorath and Rattanaxay Phetsouvanh (Lao PDR);

Yu-Chen Hsu, Yi-Ta Yang, SteveKuo (Taiwan); Porn-

thip Chompook, Jongkol Lertiendumrong and Viroj

Tangcharoensathien (Thailand); Le Minh Sat and La

Thanh Nhan (Vietnam). Excellent administrativesup-

port from Nicola Lord and Wasamon Sabaiwan is

greatly appreciated. We also thanks for James W.

Rudge for revising this paper.

REFERENCES

Ajelli, M., Gonc¸alves, B., Balcan, D., Colizza, V., Hu,

H., J. J Ramasco, S. M., and Vespignani, A. (2010).

Comparing large-scale computational approaches to

epidemic modeling: Agent-based versus structured

metapopulation models. BMC Infectious Diseases 10,

190 (2010).

AsiaFluCap (2009). The AsiaFluCap Simulator.

http://www.cdprg.org/asiaﬂucap-simulator.php.

Berger, T. (2001). Agent-based spatial models applied to

agriculture: a simulation tool for technology diffu-

sion, resource use changes and policy analysis. Agri-

cultural Economics, 25(2-3):245 – 260.

Bobashev, G. V., Goedecke, D. M., Yu, F., and Epstein,

J. M. (2007). A hybrid epidemic model: combining

the advantages of agent-based and equation-based ap-

proaches. In WSC ’07: Proceedings of the 39th con-

ference on Winter simulation, pages 1532–1537, Pis-

cataway, NJ, USA. IEEE Press.

Britton, T. and Lindenstrand, D. (2009). Epidemic mod-

elling: aspects where stochasticity matters. Mathe-

matical Biosciences, 222(2):109–116.

Connell, R., Dawson, P., and Skvortsov, A. (2009). Com-

parison of an agent-based model of disease propaga-

tion with the generalised SIR epidemic model. Sci-

ence And Technology, 5(3):1–22.

Davidsson, P. (2002). Agent based social simulation: A

computer science view. J. Artiﬁcial Societies and So-

cial Simulation, 5(1).

Diekmann, O. and Heesterbeek, J. (2000). Mathematical

epidemiology of infectious diseases: model building,

analysis, and interpretation. Wiley series in mathe-

matical and computational biology. John Wiley.

Garnett, G. P. (2002). An introduction to mathematical

models in sexually transmitted disease epidemiology.

Sex Transm Infect, 78(1):7–12.

Keeling, M. J. and Danon, L. (2009). Mathematical mod-

elling of infectious diseases. British Medical Bulletin,

92(1):33–42.

Krumkamp, R., Kretzschmar, M., Rudge, J. W., Ahmad, A.,

Hanvoravongchai, P., Westenhoefer, J., STEIN, M.,

Putthasri, W., and Coker, R. (2011). Health service

resource needs for pandemic inﬂuenza in developing

countries: a linked transmission dynamics, interven-

tions and resource demand model. Epidemiology and

Infection, 139:59–67.

Lunelli, A., Pugliese, A., and Rizzo, C. (2009). Epidemic

patch models applied to pandemic inﬂuenza: contact

matrix, stochasticity, robustness of predictions. Math-

ematical Biosciences, 220(1):24–33.

Macal, C. M. and North, M. J. (2005). Tutorial on agent-

based modeling and simulation. In Winter Simulation

Conference, pages 2–15.

Moss, S. and Davidsson, P., editors (2001). Multi-Agent-

Based Simulation, Second International Workshop,

MABS 2000, Boston, MA, USA, July, 2000, Revised

and Additional Papers, volume 1979 of Lecture Notes

in Computer Science. Springer.

Parker, D. C., Manson, S. M., Janssen, M. A., Hoffmann,

M. J., and Deadman, P. (2003). Multi-agent systems

for the simulation of land-use and land-cover change:

A review. Annals of the Association of American Ge-

ographers, 93(2):314337.

Rahmandad, H. and Sterman, J. (2008). Heterogeneity and

network structure in the dynamics of diffusion: Com-

paring agent-based and differential equation models.

Management Science, 54:998–1014.

Rudge, J. W., Hanvoravongchai, P., Krumkamp, R., Chavez,

I., Adisasmito, W., Chau, P. N., Phommasak, B., Put-

thasri, W., Shih, C.-S., Stein, M., Timen, A., Touch,

S., Reintjes, R., Coker, R., and on behalf of the Asi-

aFluCap Project Consortium (2012). Health system

resource gaps and associated mortality from pandemic

inﬂuenza across six asian territories. PLoS ONE,

7(2):e31800.

Stein, M., Rudge, J., Coker, R., Weijden, C., Krumkamp,

R., Hanvoravongchai, P., Chavez, I., Putthasri, W.,

Phommasack, B., Adisasmito, W., Touch, S., Sat, L.,

Hsu, Y.-C., Kretzschmar, M., and Timen, A. (2012).

Development of a resource modelling tool to sup-

port decision makers in pandemic inﬂuenza prepared-

ness: The asiaﬂucap simulator. BMC Public Health,

12(1):870.

AComparisonBetweenaDeterministic,CompartmentalModelandanIndividualBased-stochasticModelforSimulating

theTransmissionDynamicsofPandemicInfluenza

593

Tsai, M., Chern, T., Chuang, J., Hsueh, C., Kuo, H., Liau,

C., Riley, S., Shen, B., Wang, D., Shen, C., and Hsu, T.

(2010). Efﬁcient simulation of the spatial transmission

dynamics of inﬂuenza. PloS ONE, 5(11):1–8.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

594