
A Real-time Motion Data Reduction and Restoration Compatible with
Robot’s Physical Limits
Doik Kim, Jung-Min Park and Seokmin Hong
Interaction and Robotics Research Center, KIST,
Hwarangno 14-gil 5, Seongbuk-gu, Seoul, 136-791, Republic of Korea
Keywords:
Data Reduction, Restoration, Hardware Limit, Convolution Interpolation.
Abstract:
In order to control a robot, motion data obtained from various interface devices such as haptic and tele-
operating interfaces, and a motion capture system, or from predefined parametric equations are needed. It is
hard to store and transmit the data because of their high control frequency and synchronization problem. In
addition, usually, all these data are only for one target robot system, i.e., it is hard to use them to other robot
system with different hardware limits. In order to solve the problems, the reduction of the original data is
conducted with two stage magnitude quantization and the restoration without violating the hardware limits,
such as maximum velocity, acceleration, etc., is conducted with the convolution interpolation, in this paper.
The proposed method can be used in on-line data transmission and for off-line data storage.
1 INTRODUCTION
A robot is controlled by motion data obtained from
various interface devices of tele-operation, haptics,
and motion capture system as well as parametric
equations for trajectory generation. If motion data are
to be stored for replaying later or to be transmitted to
remote devices in real-time, several problems need to
be considered. Especially the realtimeness, and target
system’s physical limits are essential to be considered
for stable and safe control.
Data size for controlling a robot is different
from robot to robot, according to its control Hz,
DOF(Degree of Freedom), control variables, etc. Ab-
solute size of motion data is less than other types of
data such as audio and video, but it must be guar-
anteed a real-time synchronization from sensors to
actuators through networks within its control sam-
pling time. This hard real-time condition makes
load of the network comparable to audio and video
data(Hinterseer et al., 2008).
In addition, the transmitted signal should not vi-
olate physical hardware limits such as velocity, ac-
celeration, jerk, etc. In many cases, the transmit-
ted data will be used for the same robot hardware
system, but if motion data are stored as reference
data, they can be applied to other robot hardware
systems as far as they are compatible to the original
robot. Compatibility can be qualified by consider-
ing workspace, DOF, structural similarity, and actu-
ation hardware limits, etc. For example, if two robots
have similar workspace and motion data for control
are composed of the position and orientation of the
end-effector, there is high possibility that the motion
data are compatible between two robots regardless of
their structures and DOF from the theoretical view-
point. However, in order to share the motion data
between real robot systems, the restored data should
not violate physical hardware limits of a target robot;
otherwise they make the robot unstable. Thus, non-
violation of physical hardware limits is a fundamental
condition for safe and stable control.
In order to solve the realtimeness, data reduc-
tion/restoration methods have been studied. Most re-
search is focused on the haptic data reduction and
transmission. DPCM(differential pulse code modu-
lation) related methods are used to reduce haptic mo-
tion data by (Shahabi et al., 2002; Kron et al., 2004).
Hirche, et al., proposed a psychophysically motivated
compression method with the deadband concept to re-
duce the haptic data(Hirche et al., 2007; Hirche and
Buss, 2007). If the difference between the current
data and the most recently transmitted data exceeds
a predefined perception threshold (the deadband), the
current data are transmitted, and otherwise the haptic
data are abandoned. It is extended to 3 DOF haptic de-
vices in (Hinterseer et al., 2008), and 6-DOF in (Sakr
et al., 2010; Sakr et al., 2011) A haptic data reduction
360
Kim D., Park J. and Hong S..
A Real-time Motion Data Reduction and Restoration Compatible with Robot’s Physical Limits.
DOI: 10.5220/0005041303600367
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 360-367
ISBN: 978-989-758-040-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

based on human perception is summarized in (Stein-
bach et al., 2011). All these are concerned on the real-
timeness by reducing motion data, especially in tele-
presence and tele-action system, and thus human per-
ception is an important aspect in reducing data. How-
ever, from the viewpoint of control, human percep-
tion is a sub-condition of motion data reduction, i.e.,
motion data can be reduced more beyond the human
perception to control a robot, and it has not been con-
sidered deeply.
In the case of restoration, physical hardware lim-
its are not considered importantly, because the data
is used for the same hardware. However, if a set of
motion data is transmitted to or stored for later us-
age of several different robots, physical hardware lim-
its must be considered for safe and stable operation.
This discordance between source motion data and tar-
get robots cannot be solved in all cases, but in many
cases, it can be relaxed and increase the compatibility
in restoration stage by considering hardware limits.
To solve these realtimeness and hardware com-
patibility problems, two-stage data reduction and
convolution-based data restoration are proposed as
follows: section 2 and 3 describe the reduction and
restoration method, respectively. Section 4 shows ex-
perimental results, and section 5 concludes this paper.
2 DATA REDUCTION WITH
MINIMAL SHAPE
INFORMATION
Motion data are considered as set of signals having
similar properties such as noise level, sampling time,
etc. Specifically, motion data such as position, orien-
tation, joint angles, which are mostly used for control-
ling a robot and feeding the status back to a user, are
considered in the paper and other kinds of data can
also be considered similarly without any problem.
+
Original Data
Stage 1
Anchor Point
g=1
Stage 2
Deadband
Reduced data
Change
Reduction level
0 <= g < 1
No
Yes
Ignore
Figure 1: Flow chart for data reduction: The original data is
reduced by two-stage process.
The reduction is conducted in two stages: the an-
chor point and the deadband as shown in Figure 1.
The first stage finding the anchor point is to preserve
the minimal shape of motion data and the second
stage is to reduce motion data by adjusting the dead-
band size.
Before reducing motion data, a critical length is
introduced to normalize the data for removing depen-
dency of kinematic differences. The max length, d
max
is defined as a constant critical length of a robot sys-
tem. It can be any value representing a maximum
magnitude of a signal. For example, a fully extended
link length of a robot can be one candidate for position
signal, and maximum joint angle can be a candidate
for joint angle signal. The max length d
max
will be
used as scale factor in reduction and restoration, and
thus it should not be changed in all process.
2.1 Anchor Point
With the points of zero velocity which will be called
the anchor point, we can obtain several information of
a signal such as direction change, start and stop point.
Set of anchor points are minimum set of motion data
to represent the overall shape of motion.
The anchor point can be obtained by finding a
point with zero velocity, but it is difficult to find the
point, because the original data are discretized. So,
the zero crossing condition is used to find an approx-
imate point of zero velocity as follows:
y
a
= x(k), if v(k) · v(k − 1) ≤ 0 (1)
where y
a
is an approximate anchor point. x(k) is a
point and v(k) is the velocity of the point x(k) of the
original data, respectively. If Eq. (1) satisfies, a point
somewhere between x(k −1) and x(k) has zero veloc-
ity, and thus the current point x(k) is chosen for an
approximate anchor point.
In addition, the velocity, v(k) in Eq. (1) is obtained
usually from the numerical differentiation of points
x(k), and this makes noise in velocity. To remove ef-
fects of the noise, the following condition is added
y
i+1
=
y
a
, if ky
a
− y
i
k ≥ d
min
none, otherwise
(2)
where d
min
is the minimum anchor distance between
the previous reduced point y
i
and the new reduced
point y
i+1
. Note that here the reduction point y
i
is
composed of only the anchor points, y
a
. The range of
the minimum anchor distance is 0 ≤ d
min
≤ d
max
.
From Eq. (2), we can set a minimum distance be-
tween adjacent anchor points. If d
min
= 0, all the an-
chor points, y
a
, in Eq. (2) will be the reduced point
y
i+1
, and if d
min
= d
max
, almost all the anchor points
will be abandoned and there will be the least reduced
point and loose the shape of data in most cases.
AReal-timeMotionDataReductionandRestorationCompatiblewithRobot'sPhysicalLimits
361

Velocity
Position
x(k)
x(k+1)
x(k+2)
x(k+3)
x(k+4)
x(k+5)
x(k+6)
v(k)
v(k+1)
v(k+2)
v(k+3) v(k+4)
v(k+5) v(k+6)
±d
min
0
time
time
Figure 2: The anchor point is defined a point with zero
velocity but for discretized points, an approximate anchor
point is obtained.
Figure 2 shows the relation of anchor points.
Somewhere between v(k) and v(k + 1) has zero ve-
locity and thus x(k + 1) is set as the anchor point,
represented as a black circle in velocity graph and
is assumed to be new reduced point represented as a
blue circle in position graph. The next v(k + 2) also
crossed zero, and thus x(k + 2) is a candidate of the
anchor point but it is within the boundary of d
min
, so
it is abandoned.
2.2 Point with Deadband
The basic idea of the deadband has been studied by
many researchers as in (Hirche et al., 2007; Hirche
and Buss, 2007). However, in this paper, previous
method is extended to adjust the reduction level from
no reduction to maximum reduction.
Position
x(k)=y
i
x(k+1)
x(k+2)=y
i+1
x(k+3) x(k+4)
x(k+5)
±δ
th
time
Figure 3: Reduction by deadband: If x(k + i) is within the
threshold, i.e., |x(k + i) − y
i
| ≤ δ
th
, it will be abandoned,
otherwise, it will set as new transmission point y
i+1
.
The reduction law is simple by quantization of
data with length comparison as follows:
y
i+1
=
x(k), if kx(k) − y
i
k ≥ δ
th
none, otherwise
(3)
where x(k) is the kth original data vector, y
i
is the
ith reduced data. Figure 3 explains the deadband ap-
proach. A blue circle represents reduced data, y
i
, and
white circle represents abandoned original data.
The threshold value is defined as
δ
th
= γd
max
(4)
The reduction level, γ is a value in the range of
0 ≤ γ ≤ 1 representing fraction of d
max
.
The threshold, δ
th
is automatically calculated by
the user adjusted reduction level γ and the max length,
d
max
. As shown in Eq. (3), a new reduced data y
i+1
is defined if an error between the current original data
x(k) and the current reduced data y
i
is larger than the
given threshold, δ
th
. Otherwise, no data will be stored
or transmitted.
Note that, the threshold represents the maximum
quantization error between the original and reduced
data. The reduced data y
i+1
has maximum error of
δ
th
, i.e., ky
i+1
− x(k)k ≤ δ
th
where x(k) is set of orig-
inal data between y
i
and y
i+1
.
By adjusting γ, a user can change relative reduc-
tion ratio which is related to the error range. If γ = 0,
i.e., δ
th
= 0, there is no error between the reduced data
and the original data, i.e., reduction is not occurred. If
γ = 1, i.e., δ
th
= d
max
, almost all data are vanished be-
cause d
max
is a maximum magnitude of a signal.
In the case of maximum reduction, γ = 1, it is,
however, inconvenient if no data are stored or trans-
mitted, because we don’t have any information of the
original data. To overcome this, the maximum reduc-
tion is slightly modified to represent set of data with
minimal information of the signal by using the anchor
point described in the previous section.
In summary, the proposed algorithm has three
user defined parameters, the maximum critical length,
d
max
, the reduction level, γ, and the minimum anchor
distance, d
min
. The maximum critical length, d
max
is a
constant and is related to the mechanical specification
of a robot system. This value is also used in restora-
tion stage. The reduction level γ is a user defined rel-
ative reduction ratio which related to the quantization
error between the original data and the reduced data.
The minimum anchor distance, d
min
is a user defined
value, and is mostly related to the signal properties
such as signal noise and numerical noise. The re-
duction level, and the minimum anchor distance can
be adjusted any time, even in running the algorithm.
Note that signals for the reduction are a position and
its derivative (velocity) and thus these signals should
be obtained appropriately before reduction.
3 DATA RESTORATION
WITHOUT VIOLATING
PHYSICAL LIMITS
In the previous section, motion data are reduced with
magnitude quantization. The restoration process is to
generate a trajectory satisfying the hardware system
of a target robot from randomly transmitted data in
real time.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
362

As shown in the previous works(Hinterseer et al.,
2008), they used a zero-order-hold strategy or the lin-
ear prediction method to restore reduction data. A
zero-order-hold strategy holds a received sample un-
til a new sample arrives, and the linear prediction
method uses an average change-of-rate from the pre-
viously received samples to extrapolate current sam-
ple. All these methods and other prediction methods
always give discontinuity when a new sample arrives,
since the prediction cannot predict future motion ex-
actly. From the aspect of control, discontinuity makes
system unstable.
In addition to this discontinuity one more severe
problem not mentioned in the previous research is that
the hardware limit. The reduced data can be applied to
any robot with different hardware specifications. For
example, two robots have the same mechanical struc-
ture but their actuator limits such as acceleration, ve-
locity and position limit can be different from each
other. In this case, the reduced data should be restored
to signals that are not violating the hardware limits of
each robot.
In order to solve these problems, a convolution
interpolation is proposed to obtain continuous and
hardware-compatible motion data in real time.
3.1 Convolution Interpolation to
Generate a Trajectory
The convolution interpolation has several useful as-
pects: it can generate continuously differentiable tra-
jectories without violating physical system limits by
applying successive convolution operation; a recur-
sive form of discrete convolution can reduce compu-
tational loads drastically. In this subsection, the con-
volution interpolation to generate a trajectory shown
in (Lee et al., 2011; Lee et al., 2012) is summarized
briefly.
Let us suppose that y
0
(t) is an non-convoluted in-
put function defined in [0,t
0
], h(t) is a rectangular
function of unit area defined in time duration [0,t
h
],
and y
1
(t) is the 1st output function convoluted by two
functions y
0
(t) and h(t). Then the convolution has
following properties:
1. The final time t
1
of y
1
(t) is the sum of both time
durations of y
0
(t) and h(t), i.e., t
1
= t
0
+t
h
.
2. The area of output y
1
(t) is always equal to that of
input, y
0
(t).
3. The maximum absolute value of y
1
(t) is always
less than or equal to that of y
0
(t). Especially, if the
input maintains a constant over the time duration
t
h
, then output reaches the input value.
S
n
S
0
S
1
S
2
v
0
y
0
(t)
t
0
t
*
1/t
1
h
1
(t)
t
1
t
v
1
y
1
(t)
t
0
+t
1
t
=
*
1/t
2
h
2
(t)
t
2
t
v
2
y
2
(t)
t
0
+t
1
+t
2
t
=
.
.
.
*
1/t
n
h
n
(t)
t
n
t
v
n
y
n
(t)
t
=
n
k
k
t
0
v
1
y
1
(t)
t
0
+t
1
t
S
1
S
n-1
v
n-1
y
n-1
(t)
t
1
0
n
k
k
t
Figure 4: The effect of the convoluted trajectory with non-
zero final condition is shown. The trajectory becomes
smoother with more convolutions.
S
b
S
t
S
n
v
n
v
f
y
n
(t)
t
n
k
k
t
0
t
0
v
i
=
v
n
-v
i
v
f
-v
i
y
n
(t)
t
n
k
k
t
0
t
0
n
+
y
n
(t)
n
k
k
t
0
v
i
n
t
Figure 5: A general trajectory with non-zero initial and final
velocity can be calculated by decomposing the trajectory
into non-zero initial and non-zero final condition.
With the above properties, convolution operation
can be used for generating a trajectory as shown in
Figure 4. The initial and the final velocity are as-
sumed zero, v
i
= v
f
= 0, and v
k
is the kth convoluted
velocity. S
k
are the area calculated with the kth convo-
lution and are equal regardless of k from the property
2. After the 1st convolution, the input y
0
(t) function
which is a class C
−1
function becomes a continuous
but not a differentiable function y
1
(t), i.e., y
1
(t) be-
comes a C
0
function. After the 2nd convolution, the
input y
1
(t) function becomes a function y
2
(t) which
has a continuous first-derivatives, i.e., a C
1
function,
and so on. Consequently, by increasing the number of
convolution, we can increase the order of differentia-
bility as many as we want, and it can be represented
as y
k
(t) is a C
k−1
function. In convolution, the com-
pletion time is also increased from the property 1.
Figure 5 shows the case of non-zero initial and fi-
nal velocity. The area S
n
is divided into two area:
a translated area S
t
n
with zero initial velocity and a
rectangular base area S
b
n
with the initial velocity, v
i
.
By adding two area, the entire area can be obtained,
AReal-timeMotionDataReductionandRestorationCompatiblewithRobot'sPhysicalLimits
363

S
n
= S
t
n
+ S
b
n
.
In order to guarantee that the resultant function
does not violate system limits, the time duration t
k
of
a unit-area function h
k
(t) becomes
t
k
=
v
k−1
max
v
k
max
for k = 1,2, ·· · ,n (5)
where v
k
max
denotes the system limits of kth convolu-
tion. For example, v
0
max
, v
1
max
, and v
2
max
denote the
maximum velocity, acceleration, jerk, respectively.
By using Eq. (5) and from property 3, we can guar-
antee the convolution interpolation does not violate
the system limits.
From Figure 5, total moving distance is repre-
sented as follows:
S
n
= S
t
n
+ S
b
n
= v
0
t
0
+
(v
f
+ v
i
)
2
n
∑
k=1
t
k
(6)
There are two cases in using Eq. (6) with known
S
n
: 1) if v
0
= v
0
max
, then the only unknown is t
0
, 2) if
the final time t
f
is known, then t
0
can be obtained from
property 1 and Eq. (5), and thus the only unknown is
v
0
. These relations can be solved as follows:
Max Velocity. If v
0
= v
0
max
, then we can arrive S
n
as
fast as possible and time t
0
for this can be obtained as
follows from Eq. (6)
t
0
=
S
n
−
(v
f
+ v
i
)
2
n
∑
k=1
t
k
!
/v
0
max
(7)
Known Final Time. If we know the final time, t
f
to
go, then t
0
can be obtained from Property 1 as follows:
t
0
= t
f
−
n
∑
k=1
t
k
(8)
Note that t
0
is equal to zero or negative if given time
interval, t
f
is too short. This means that it is impos-
sible to reach the target with the system limits within
the given time interval. For positive t
0
, v
0
is obtained
as follows:
v
0
=
S
n
−
(v
f
+ v
i
)
2
n
∑
k=1
t
k
!
/t
0
(9)
So far convolution operation is described in the
continuous time domain, but for fast and simple cal-
culation, it can be expressed in the discrete time do-
main as follows: The convolution sum considered
with nth unit-area function, h
n
[k] for 0 ≤ k ≤ m
n
− 1
can be expressed by a recursive form as follows:
y
n
[k] =
y
n−1
[k] − y
n−1
[k − m
n
]
m
n
+ y
n
[k − 1] (10)
where k and m
n
are positive integers satisfying k =
[t/T
s
] and m
n
= [t
n
/T
s
], respectively, with sampling
time T
s
and Gauss floor function [x] to denote the
largest integer not greater than x.
3.2 Continuously Restored Trajectory
with Convolution
In the previous subsection, a convolution interpola-
tion is introduced and will be used to restore the re-
duced motion data. Without loss of generality, we
only use the 1st convolution which preserves up to the
acceleration. If more hardware limits are supposed to
be satisfied, more order of convolution is needed, and
the relations can be obtained similarly.
v
i
v
i
v
f
Position
time
s
k
S
d
y
i
y
i+1
r
i
(1)
r
i
(2)
r
i
(0)
r
i
(n)
r
i+1
(0)
r
i+1
(k)
t
f
Predicted
trajectory
Original
Trajectory
Interpolated
Trajectory
Figure 6: When a new point is arrived, there is a gap, S
d
, be-
tween the predicted point, r
i
(n) and the arrived point, y
i+1
.
This gap is interpolated by using the convolution method as
fast as possible without violating system limits.
In restoring data, a linear prediction is used, i.e.,
when a reduced point is composed of the point x(i)
and the velocity v(i). With these information, the re-
stored point, r
i
(k) becomes
r
i
(k) = v(i) · (k∆t) + x(i) (11)
where i and k are indexes for the ith transmitted data,
and kth restored data, respectively. ∆t is the sam-
pling time which may be different from the reduction
side. In the case that the velocity is not available, the
last transmitted point can used for restored data, i.e.,
r
i
(k) = x(i), and this will give more errors than the
linear prediction case.
As shown in Figure 6, the gap between the cur-
rent predicted point to the newly transmitted point is
interpolated by the convolution method as fast as pos-
sible. In the figure, the linear prediction is used with
the transmitted instantaneous velocity. It is also pos-
sible to use a zero-order-holder strategy or any other
prediction methods, but the important thing is the gap
between the current point and the newly transmitted
point.
S
d
in Figure 6 is the distance between the current
point and the newly transmitted point, but it is hard to
reach on the newly arrived point within one sampling
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
364
time in general, and thus we need more time. For the
linear prediction case as shown in Figure 6, we need
to go more distance S
k
calculated as follows:
S
k
= S
d
+ v
f
t
f
(12)
where v
f
is the transmitted final velocity, and t
f
is
the time for reaching out to S
k
. The distance S
k
can
also be calculated as in Eq. (6) and by equating with
Eq. (12),
S
d
+ v
f
t
f
= v
0
max
t
0
+
(v
f
+ v
i
)
2
t
1
(13)
where v
0
in Eq. (6) is replaced with the maximum ve-
locity, v
0
max
, and t
f
= t
0
+t
1
from property 1. v
i
is the
velocity of the current point. Finally, by solving the
above equation, t
0
becomes
t
0
= (s
d
−
v
i
− v
f
2
t
1
)/(v
0
max
− v
f
) (14)
where t
1
= v
0
max
/v
1
max
as in Eq. (5). Note that if the
linear prediction is not used, then S
k
= S
d
and thus
the term for the linear prediction v
f
t
f
becomes zero
in Eq. (13).
Now, we know all variables to interpolate between
the current point, r
i
(n), and the newly transmitted
point, y
i+1
. By applying the convolution interpola-
tion, we can connect the points smoothly and quickly
without violating the hardware limits. Note that the
error between the current point and the newly trans-
mitted point is reduced as fast as possible with the
maximum velocity and acceleration. Note also that
the signal distortion almost always exists whenever a
new point is transmitted, and it is related to the thresh-
old value, δ
th
.
4 EXPERIMENTS
In order to verify the proposed reduction/restoration
method, real motion data are obtained from a 6 DOF
arm attached on the humanoid Mahru developed by
KIST. The maximum length d
max
is set to 1m for con-
venience although the actual length is 0.72m when the
arm is unfolded straightly.
Arbitrary motions are conducted to analyze the
performance. In this paper, we only considered the
position (x,y, z) of the end-effector. Other values such
as joint angles can be considered similarly.
4.1 Data Reduction
The position signal has three elements (x,y, z), but for
calculating the anchor points, each signal is calculated
independently, because the anchor point represents
the stationary point with zero velocity. If all three ele-
ments are considered together as a vector, each signal
loses its shape information. Figure 7 represents the
anchor points of the y element. The anchor points,
green points in the figure, indicate points where the
direction is changed and they are the minimum num-
ber of points to present the shape of original signal as
shown in the figure with the blue line. In calculating
the anchor point, The minimum anchor distance is set
as d
min
= 0.005m. The original data has 2078 points
and the number of anchor points is 10 for y element.
0.22
0.24
0.26
0.28
0.3
0.32
0.34
0.36
0.38
0.4
0.42
0 500 1000 1500 2000 2500
distance (m)
Sampling Number
original
connected anchor point
anchor point
Figure 7: Anchor points of y element. The red line rep-
resents the original signal and discontinuous points on the
blue line represent the anchor points.
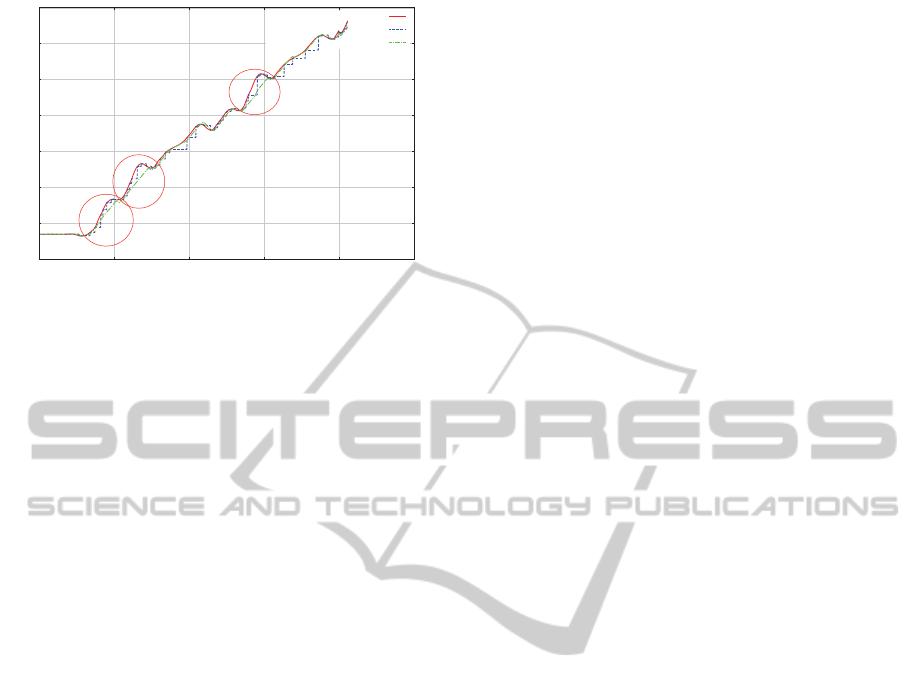
For the deadband approach, the distance is calcu-
lated with the position vector unlike the anchor point,
because relative relations of each element are impor-
tant. The blue line in Figure 8 represents the reduction
results. The reduction ratio for this case is 4.23% (88
/ 2078) with the linear prediction.
The error due to the reduction is shown in Fig-
ure 9(a). The error can be estimated by the reduction
level γ. In this case, γ = 0.01 is used and thus the
maximum error is γd
max
= 0.01m, which is valid as
shown in Figure 9(a).
4.2 Data Restoration
The green line of Figure 8 shows the restoration re-
sults with the convolution interpolation and the lin-
ear prediction. As shown in the figure, all the dis-
continuity points are connected smoothly. If more
smoothness is needed, we only need more convolu-
tions which need more delay in restoration.
The error level of the restored data shown in Fig-
ure 9(b) is similar to the reduction error shown in Fig-
ure 9(a). In most cases, the restoration error level is
equal to the reduction error, because the role of the
convolution interpolation is to connect the discontinu-
ity, i.e., it does not give additional error. However, in
AReal-timeMotionDataReductionandRestorationCompatiblewithRobot'sPhysicalLimits
365

0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0
500 1000 1500 2000 2500
Position (m)
Sample Number
original
received
linear prediction + convolution
(a) x
0.22
0.24
0.26
0.28
0.3
0.32
0.34
0.36
0.38
0.4
0.42
0 500 1000 1500 2000 2500
Position (m)
Sample Number
original
received
linear prediction + convolution
(b) y
0.51
0.52
0.53
0.54
0.55
0.56
0.57
0.58
0 500 1000 1500 2000 2500
Position (m)
Sample Number
original
received
linear prediction + convolution
(c) z
Figure 8: Results of data reduction and restoration. The red
line is for the original signal, the blue line for the reduced
signal and the green line for the restored signal.
some cases, there are larger errors. This comes from
the combination of wrong prediction, numerical error,
convolution interpolation, and different hardware lim-
its. For example, the convolution interpolation gives
a different trajectory from the original one in direc-
tion change to connect points smoothly. But in most
cases, the convolution interpolation gives desired re-
sults if the hardware limits are not so poor.
-0.01
-0.008
-0.006
-0.004
-0.002
0
0.002
0.004
0.006
0.008
0.01
0
500
1000 1500 2000
2500
error (m)
Sample Number
error x
error y
error_z
(a) reduction
-0.02
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0 500 1000 1500 2000 2500
Error (m)
Sample Number
error_x
error_y
error_z
(b) restoration
Figure 9: Error of data reduction(a) and restoration(b). All
errors in reduction and restoration are related the reduction
level γ and the maximum critical length d
max
.
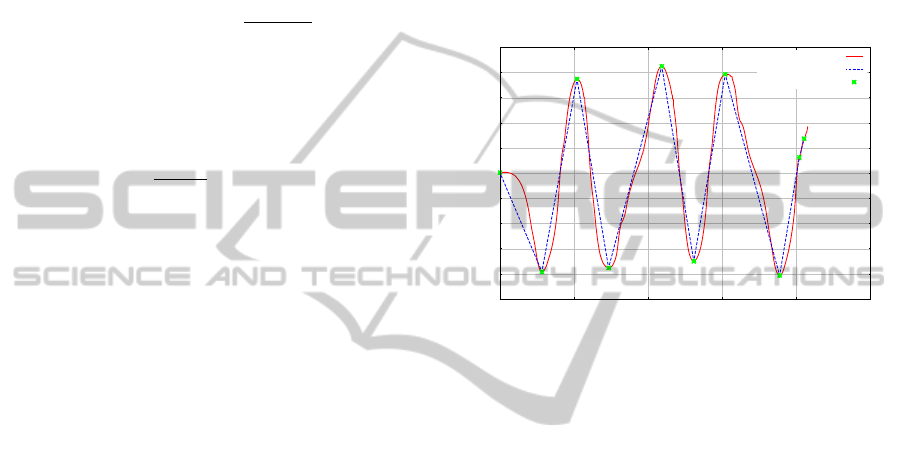
The green line in Figure 10 shows the result of the
convolution when the maximum velocity is 0.1 times
less than that of the original system. In this case, as
shown in the figure with red circles, the system cannot
follow the original signal because it has lower maxi-
mum velocity, but the restored trajectory is generated
with the maximum velocity to follow the given origi-
nal trajectory as fast as possible. The convolution in-
terpolation gives a smooth trajectory even in the case
of a low performance system, and this property is very
important for the safety aspect.
Note that the proposed method is to reduce and
restore a signal, and thus it does not have any limit
of signal type, but if a signal is nosy such as force
and acceleration, we need to choose parameters care-
fully. In addition, derivate of the signal is also needed
in reduction stage, and this magnifies the noise too.
Consequently, in order to improve the performance,
the relation between the parameters and signal noise
needs to be analyzed further.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
366
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0 500 1000 1500 2000 2500
Position (m)
Sample Number
original
received
linear prediction + convolution
Figure 10: Restoration results when the maximum velocity
is less than the original one. At several places enclosed by
red circles, the green line cannot follow the red line because
of the hardware limits.
5 CONCLUSIONS
In reduction and restoration of motion data, most re-
searchers focused on the reduction and not on the
restoration. However, the restoration is also impor-
tant because of the difference of hardware limits. In
the paper, we suggested a convolution based motion
data restoration method to restore data without vio-
lating the hardware limits and to generate a smooth
trajectory in real-time. In addition, we can expect
error level in reduction and restoration by using the
proposed method. With only 4.23% of the original
data, we can restore the signal with the error level
of 0.01m. The proposed method can be used in any
tele-operation and tele-presence system and for the
data storage. Especially, the proposed method is use-
ful for a poor communication environment, heteroge-
neous master-slave system, and simultaneous control
of multi-robot.
ACKNOWLEDGEMENTS
This work is supported by the KIST institutional pro-
gram (Project No. 2E24800).
REFERENCES
Hinterseer, P., Hirche, S., Chaudhuri, S., Steinbach, E., and
Buss, M. (2008). Perception-based data reduction and
transmission of haptic data in telepresence and tele-
action systems. IEEE TRANSACTIONS ON SIGNAL
PROCESSING, 56(2):588–597.
Hirche, S. and Buss, M. (2007). Transparent data reduction
in networked telepresence and teleaction systems. part
ii: Time delayed communication. Presence: Teleop-
erators Virtual Environment, 16(5):531–542.
Hirche, S., Hinterseer, P., Steinbach, E., and Buss, M.
(2007). Transparent data reduction in networked
telepresence and teleaction systems. part i: Commu-
nication without time delay. Presence: Teleoperators
Virtual Environment, 16(5):523–531.
Kron, A., Schmidt, G., Petzold, B., Zah, M. F., Hinter-
seer, P., and Steinbach, E. (2004). Disposal of ex-
plosive ordnances by use of a bimanual haptic telep-
resence system. In IEEE International Conference on
Robotics and Automation, pages 1968–1973.
Lee, G., Kim, D., and Choi, Y. (2012). Faster and smoother
trajectory generation considering physical system lim-
its under discontinuously assigned target angles. In
IEEE International Conference on Mechatronics and
Automation, pages 1196–1201, Chengdu, China.
Lee, G., Yi, B.-J., Kim, D., and Choi, Y. (2011). New
robotic motion generation using digital convolution
with physical system limitation. In IEEE Conference
on Decision and Control and European Control Con-
ference (CDC-ECC), pages 698–703, Orlando, FL,
USA.
Sakr, N., Georganas, N. D., and Zhao, J. (2010). Ex-
ploring human perception-based data reduction for
haptic communication in 6-dof telepresence systems.
In IEEE International Symposium on Haptic Audio-
Visual Environments and Games (HAVE), pages 1–6,
Phoenix, AZ.
Sakr, N., Georganas, N. D., and Zhao, J. (2011). Human
perception-based data reduction for haptic communi-
cation in six-dof telepresence systems. IEEE Trans.
on Instrumentation and Measurement, 60(11):3534–
3546.
Shahabi, C., Ortega, A., and Kolahdouzan, M. R. (2002).
A comparison of different haptic compression tech-
niques. In IEEE International Conference on Multi-
media and Expo (ICME ’02), pages 657–660.
Steinbach, E., Hirche, S., Kammerl, J., Vittorias, I., and
Chaudhari, R. (2011). Haptic data compression and
communication: A review of the challenges for telep-
resence and teleaction. IEEE SIGNAL PROCESSING
MAGAZINE, pages 87–96.
AReal-timeMotionDataReductionandRestorationCompatiblewithRobot'sPhysicalLimits
367
