Using Evolutionary Algorithms to Plan Automatic Minehunting

Operations

Nuno Abreu

1,2

and Aníbal Matos

1,2

INESC TEC, Campus da FEUP, Rua Dr. Roberto Frias, 378, 4200-465 Porto, Portugal

FEUP - DEEC, Rua Dr. Roberto Frias, s/n, 4200-465 Porto, Portugal

Keywords:

Evolutionary Algorithms, Neural Networks, Mission Planning, AUV, 3D Coverage, Minehunting.

Abstract:

While autonomous underwater vehicles (AUVs) are increasingly being used to perform mine countermeasures

(MCM) operations, the capability of these systems is limited by the efﬁciency of the planning process. In this

paper we study the problem of multiobjective MCM mission planning with an AUV. In order to overcome

the inherent complexity of the problem, a multi-stage algorithm is proposed and evaluated. Our algorithm

combines an evolutionary algorithm (EA) with a local search procedure based on simulated annealing (SA),

aiming at a more ﬂexible and effective exploration and exploitation of the search space. An artiﬁcial neural

network (ANN) model was also integrated in the evolutionary procedure to guide the search. The results show

that the proposed strategy can efﬁciently identify a higher quality solution set and solve the mission planning

problem.

1 INTRODUCTION

AUVs are able to perform underwater minehunting

missions with higher efﬁciency, reduced search time

and even with covert search capability when com-

pared to traditional methods. In order to quickly and

safely demine an area, the AUV needs to properly

navigate through that area. Hence, a path needs to be

carefully planned so all the region is sampled. There

is an abundance of path planning algorithms in liter-

ature and, for this speciﬁc application, a small subset

known as coverage path planning algorithms is usu-

ally used (Choset, 2001).

Solving a multiobjective path planning problem

is computationally very expensive. EAs have been

successfully used in the past for solving the multiob-

jective path planning problem (Fujimura, 1996; Xiao

et al., 1997). This approach is an alternative to classi-

cal optimization methods with the capability of solv-

ing problems involving a big search space quickly, al-

though not guaranteeing that an optimal solution is

found.

This article consists of four sections and is struc-

tured as follows. Section 2 presents our multiobjec-

tive mission planning problem and section 3 presents

an EA designed to solve it. Section 4 presents and dis-

cusses the obtained results. Finally, in the last section

we give some conclusions and ideas for future work.

2 MISSION PLANNING

The most popular approach used for underwater mine

hunting is performing complete coverage of the oper-

ational area with the robot’s sensors. When acquiring

data with a sonar-equipped vehicle, a lawn-mowing

search pattern (Land and Choset, 1998) with several

parallel tracks is standard if no prior information on

potential target locations is available.

In the underwater domain, coverage path planning re-

search has its most important application in the con-

text of MCM applications. (Stack and Smith, 2003)

presented a 2D coverage algorithm for MCM us-

ing cell decomposition. They investigate a planning

scheme for incomplete coverage, as it may not be fea-

sible in terms of time and energy costs to execute

complete coverage. This scheme divides the search

area into cells and surveys each cell using a conven-

tional line-sweep pattern with a row spacing that is

larger than the sensor footprint, exploring the fact that

mines are normally placed in lines. They assume that

if mines are evenly spaced, then randomly varying the

spacing between each row in the lawn-mowing pat-

tern will decrease the probability of missing an en-

tire mine line. An acceptable probability of detection

(POD) is ensured by establishing bounds on row spac-

ing. A perfect POD is assumed for any mine within

the sensor footprint.

228

Abreu N. and Matos A..

Using Evolutionary Algorithms to Plan Automatic Minehunting Operations.

DOI: 10.5220/0005043102280235

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 228-235

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

(Fang and Anstee, 2010) developed an algorithm

for 3D ofﬂine mission planning, combining Boustro-

phedon decomposition with the generalized Voronoi

diagram, to cover a well-known planar seabed using

an AUV ﬁtted with side-looking sonar. The vehicle

can navigate over terrain at constant altitude. They

consider both even and uneven lawn-mowing cover-

age patterns but the spacing is ﬁxed, proportional to

range setting. Since they assume a planar seabed, they

do not consider a complex topography and therefore

there was no need to implement variable spacing be-

tween the segments.

(Williams, 2010) presented an 2D ofﬂine coverage

algorithm for MCM that optimizes the spacing be-

tween parallel tracks in order to maximize POD, con-

sidering seabed type and range. Their track-spacing

algorithm consists of an exhaustive greedy search

for the best tracks. To further improve these se-

lected tracks a small geographical displacement of

each track is considered. The main disadvantage of

this greedy algorithm is that solutions are only locally

optimal.

2.1 Measures of Mission Performance

In order to assess the effectiveness of a MCM opera-

tion we need to be able to estimate the detection per-

formance that should be achieved in a speciﬁc mis-

sion.

2.1.1 Lateral Range

The concept of lateral range curve (LRC) was intro-

duced by (Koopman, 1999). Imagine a searcher fol-

lowing an inﬁnitely long, straight path, searching on

either side of that path. Lateral range refers to the

perpendicular distance an object is to the searcher’s

path. That searcher’s LRC p(x) is the probability of

detecting a stationary object that is at its closest ex-

actly a distance x from the searcher’s path. The LRC

is derived experimentally by moving a sensor through

an area, where objects are randomly placed (the po-

sitions are known), using parallel straight-line search

transects and then testing the detection system.

2.1.2 Probability of Detection

POD is an estimate of how likely it will be for a search

performed in a given area to ﬁnd an object, assuming

it is there. It is known that an overlap in area cover-

age can improve the detection performance. When it

is assumed that multiple searches are executed inde-

pendently of each other, the combined POD is given

by:

PODcum = 1 −

∏

i=1

(1 − POD

) (1)

If assuming complete correlation, the combined

POD is simply the higher of the two probabilities.

When there is an indeterminate amount of correlation

an accepted practice (Nash et al., 1982) is to aver-

age the probabilities obtained assuming complete in-

dependence. Given the risk involved in these opera-

tions, it is advisable to obtain conservative estimates

by assuming complete correlation between searches.

2.2 Covering with Different Sensors

The sidescan sonar uses one transducer on each side

to emit acoustic beams down towards the seaﬂoor,

across a wide angle perpendicular to the path of the

sensor through the water, and receives the echos of

those beams. All sidescan sonars suffer from an in-

ability to illuminate targets within the “nadir-gap”

area (section below the transducers).

The multibeam bathymetric sonar uses two or

more perpendicular transducer arrays to transmit and

receive the beams. Each received beam allows the es-

timation of the range (calculated from the time delay)

to the seaﬂoor. By combining data from consecutive

pings (range and angle of the received beam), a 3D

map of the seaﬂoor can be generated.

The most relevant feature to consider in mission

planning is the existence of the nadir gap in sonar

coverage, as illustrated in ﬁgure 1. The traditional

approach to compensate for this feature is to partially

overlap pairs of swaths so their nadir gaps are

covered, also known as uneven lawn-mowing.

2.3 Problem Statement

The principal problem under study in this paper is

how to design and implement a more ﬂexible 3D path

planning algorithm that enables an AUV to efﬁciently

cover the bottom of a submerged area with no missed

areas and with a speciﬁed minimum POD. The plan-

ner should identify a set of parallel transects, rep-

resenting sonar swaths, that maximize the estimated

performance of a MCM operation, using the available

knowledge and resources.

2.3.1 Decision Variables

• Mission Path

A mission path is represented by a set of consecutive

straight-line tracks, also referred as swaths (data ac-

UsingEvolutionaryAlgorithmstoPlanAutomaticMinehuntingOperations

229

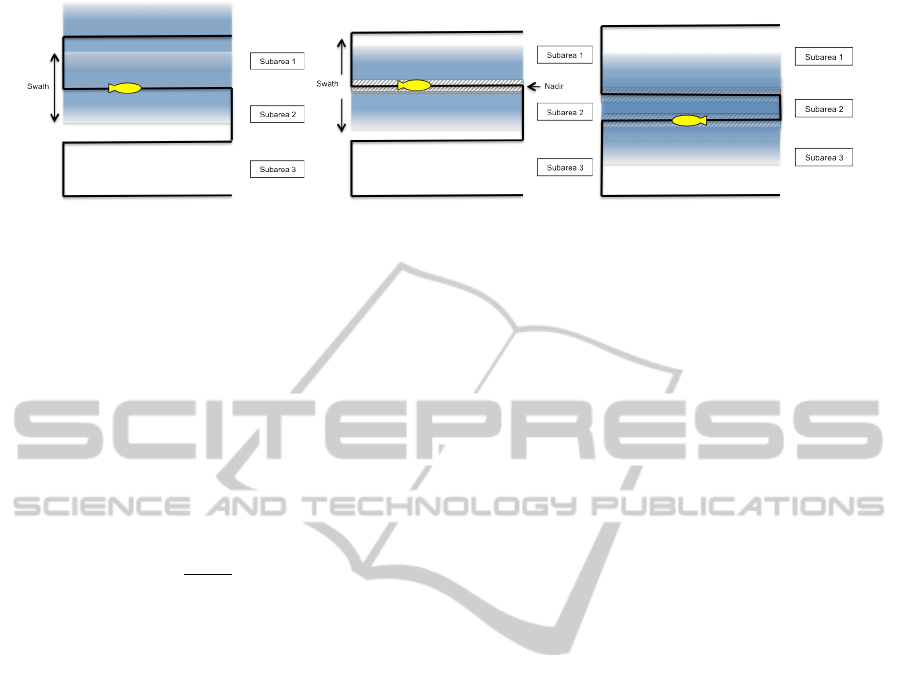
(a) Coverage with a multibeam sonar. (b) Coverage with a sidescan sonar. (c) Uneven lawn-mowing technique.

Figure 1: Different methodologies used in coverage problems.

quired by the sonar):

P = {s

, s

, ..., s

} (2)

• Vehicle Velocity

The AUV will follow the speciﬁed path with a con-

stant forward velocity relative to water equal to v

water

2.3.2 Objectives

• Maximize Probability of Detection

The MCM effectiveness is maximized by maximizing

the POD of the target on the survey area:

max

∑

POD

(S, P) (3)

• Minimize energy consumption

The amount of energy consumed by the vehicle de-

pends on its velocity, orientation and the actual path.

min E(P, v

water

) (4)

• Minimize time to complete the mission

The time required to execute the mission depends

only on the path and the component of velocity that

is parallel to the track direction.

min T (P, v

earth

) (5)

2.3.3 Constraints

Searching for a path requires the consideration of the

terrain topography, vehicle constraints (battery capac-

ity, maximum velocity and maximum steering angle),

sensor constraints (sonar maximum range and vertical

beam angle) and mission contraints (maximum time

available for the mission and minimum global POD).

3 METHODS

3.1 Multiobjective Problems

In a multiobjective optimization problem, the goal is

to ﬁnd a set of different solutions representing distinct

trade-offs among the different objectives. These so-

lutions are known as Pareto-optimal solutions (Deb,

2001). This set of solutions can be found using the

Pareto Optimality Theory (Deb, 2001).

The continuous improvement in hardware tech-

nology has allowed the use of algorithms with higher

complexity such as EAs, providing efﬁcient means

for addressing real world problems that traditional al-

gorithms were unable to conquer. These techniques

are based on the principles of natural evolution as

presented by (Darwin, 1859). Pareto dominance-

based techniques remain the most popular selection

scheme adopted by multiobjective evolutionary algo-

rithms (MOEAs), because of the several advantages

that it provides. The SPEA 2 (Zitzler et al., 2001) is

one of the most popular MOEAs used when compar-

ing a newly designed MOEA.

3.2 Proposed EAs for Mission Planning

Our approach is a a posteriori technique, more specif-

ically a Pareto-based approach. The mission planning

algorithm is an off-line planner that should be exe-

cuted before the vehicle is deployed in the target area.

3.2.1 Individual Representation

We consider an individual as a solution represented

by a vector of real valued parameters x ∈ R

. Thus, an

individual is represented by:

Ind ∈ (t, θ, d, a, v) (6)

where t is the track spacing, θ is the track direction,

d is the depth of the path (when planning with con-

stant depth), a is the altitude of the path relative to the

seaﬂoor (when planning with constant altitude) and v

is the vehicle velocity.

3.2.2 Informed EA

Our approach combines an EA with an approximation

technique, more speciﬁcally ANNs. EAs usually need

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

230

a sufﬁciently large number of function evaluations to

reach the optima of the problem. The approximate

model is used to reduce the number of expensive ex-

act function evaluations. The main task of the approx-

imate model is to capture the general trend of the ﬁt-

ness landscape and guide the search towards the better

regions while reducing the number of exact function

evaluations needed to ﬁnd the best solutions. This

guidance is executed by assessing the performance

of multiple candidate individuals using the approxi-

mate models, with a much smaller evaluation time,

and choosing only the best to integrate the next gen-

eration population. One of the challenges that arises is

the need to update the approximate model using new

information from exact function evaluations through-

out the execution of the algorithm, adding ﬁner details

to the ﬁtness landscape.

Initialisation

• Randomly generates N

individuals from a uni-

form distribution in decision space;

• Uses them to train the approximate model.

Neural Network Training

• Uses a classical multilayer feedforward ANN

using the standard error back-propagation algo-

rithm;

• The ANN receives in the input six parameters that

deﬁne an individual, and generates the estimated

objective function values at the output;

• Executed every n

generations;

• Since it is proven (Huang, 2003) that a ANN with

two hidden layers can approximate any function

with negligibly small error, we test networks with

different number of neurons in each layer and

choose the best topology (smaller mean square er-

ror in cross-validation).

Fitness Assignment

• Same procedure as in SPEA2.

Environmental Selection

• Uses variable archive and population sizes (avoids

creating clusters of individuals);

• Controls the individual’s density in the containers.

Termination

• The EA stops when a pre-speciﬁed number of

generations is achieved, when the maximum ex-

ecution time is achieved or when it converges.

Mating Selection

• Mating occurs between individuals in the archive

and between individuals in the archive and the

population;

• The pair should be close to each other in objective

space to minimize the randomization effect.

Recombination

• Evaluates candidate offspring using the approxi-

mate model (cheaper);

• Ranks them in terms of improvement over the less

ﬁt parent (choosing one objective function);

• Evaluates the best one using the exact objective

functions and adds it to the population;

• Should signiﬁcantly speed up the EA because we

can quickly test multiple candidate individuals.

Mutation

• Evaluates possible mutations using the approxi-

mate model (cheaper);

• Performs sensitivity analysis using the ANN, test-

ing different variations of the original individual

and analysing the estimated performance;

• Ranks them in terms of improvement over the

original individual;

• Evaluates the best one using the exact objective

functions and adds it to the population.

3.3 Local Optimization

Our local search stage, based on SA, has been de-

signed to optimize two distinct objectives, namely:

• Minimize the uncovered area;

• Maximize the average POD.

This is a combinatorial problem where we have to

choose the best set of inter track distances maximiz-

ing the coverage of an area characterized by a speciﬁc

topography. We use distinct strategies depending on

the type of sonar that is being used for seaﬂoor map-

ping, more speciﬁcally if using multibeam (no nadir

gap) or sidescan sonar (with nadir gap).

Strategy for the Case Without Nadir Gap

Initialization

• Determines the original spacing between tracks

(kept constant by the EA);

• Neighbourhood size is set to the initial spacing.

UsingEvolutionaryAlgorithmstoPlanAutomaticMinehuntingOperations

231

Evaluation

• Determines the insufﬁciently covered area per-

centage and the average POD (per subarea and to-

tal as seen in Figure 1);

• Accept the solution if better then the last or apply

the Metropolis criterion (Metropolis et al., 1953).

Check for termination

• Terminates when the temperature reaches a mini-

mum value or when it converges.

Mutation

• Selects the subarea between a pair of tracks with

lower coverage quality;

• Places two tracks closer together, achieving

higher coverage in the subarea in between;

• The amplitude of the mutation ∆

is obtained from

equation 8, where r is a random number between

-1 and 1, N is the neighborhood size and T is the

temperature of the process. It must be inferior to

the previous track spacing s

in subarea i;

• Update spacing s

(equation 7);

• Calculate the contribution (weights w

) of each

subarea ∆

( j 6= i) to compensate for ∆

(equations

12 and 10);

• If there are no uncovered areas (ucells = 0) then

maximize the average POD (avgpod) using a sim-

ilar procedure where track spacing is decreased in

the region where the average POD is lower;

• In this case the contribution of each region ∆

depends directly on the average POD in each of

those regions (equation 11).

= s

− ∆

(7)

∆

= rNT (8)

∆

= −

∑

j=1

j6=i

∆

(9)

ucells

(10)

= avgpod

(11)

∑

j=1

j6=i

(12)

∆

= w

× ∆

(13)

Strategy for the Case With Nadir Gap

The most used technique to handle this problem is the

uneven lawn-mowing coverage pattern, where con-

secutive pairs of tracks cover each other’s nadir. Here

we make the distinction between odd and even areas

because they are analysed differently. Even areas will

have smaller spacing since the adjacent tracks need to

be closer together in order to cover their nadir gaps.

This strategy differs from the previous one on the mu-

tation phase:

Mutation

• Similar to the previous one, except that adjust-

ing odd subareas only affects other odd subareas,

while adjusting even subareas only affects adja-

cent subareas.

• The purpose of controlling track spacing in even

subareas is mainly to cover their nadir gaps, there-

fore only the adjacent subareas should compen-

sate for the variation of track spacing.

• Even subareas should remain untouched when ad-

justing odd subareas so the nadir gaps remain cov-

ered.

4 RESULTS

With the following experiments we intend to:

• demonstrate that our multi-stage multiobjective

algorithm can solve the mission planning problem

successfully;

• show that the integration of our local search strat-

egy increases the efﬁciency of the search process.

4.1 Standard VS Informed EA

This experiment aims at proving the advantage of in-

tegrating the ANN in the EA. Table 1 shows the ob-

tained results. We can observe that at the initial stages

the Pareto set obtained by the informed EA is domi-

nated to a larger extent by the one obtained by the

standard EA (no ANN). This can be due to the longer

initialization phase that is executed on the former, as

the ANN needs to be trained, while the latter starts

the evolutionary process sooner. The increasing dom-

inance that the Pareto set generated by the informed

EA exhibits over time demonstrates that the ANN

is guiding the search to more promising regions, in-

creasing speed of convergence.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

232

Table 1: Comparison of the obtained non-dominated sets as the EAs are executed.

Time (min) 10 20 40 60

EA Std Inf Std Inf Std Inf Std Inf

% Dominated 2.70 26.67 10.11 18.60 23.71 12.50 30.39 4.76

Generations 6 4 15 14 26 31 37 50

Table 2: Design constraints used in this test.

Parameter Bounds

Battery capacity 800 Wh

Velocity relative to water 1 ≤ v ≤ 3

Sonar maximum range 80 m

Sonar vertical beam angle 10 ≤ α ≤ 70

Maximum operating time 10 h

Figure 2: Example of a Pareto Front containing several so-

lutions for the mission planning problem.

4.2 Mission Planning with EAs

It is important to exemplify what will be the typical

output of the execution of our planning algorithm. We

decided to stop the algorithm after 1 hour so we could

analyse its behaviour in detail. Our planning prob-

lem was subject to the constraints detailed in table 2.

We selected 5 distinct solutions from the Pareto front

shown in ﬁgure 2 and these are fully described in ta-

ble 3. They were chosen because they clearly demon-

strate the trade-offs between the objective function

values. We can observe that a higher detection per-

formance implies more time to complete the mission.

As expected, we can also observe that the detection

performance is better when using smaller track spac-

ing. The velocity also has considerable impact on per-

formance as the best solutions (in terms of detection

performance) use the minimum values for this vari-

able as the energy that is saved by doing so is being

used to increase the length of the path.

4.3 Local Optimization

Non-dominated solutions previously found by our in-

formed EA were used as initial solutions here. Table

4 presents descriptive statistics for the optimized set

of solutions for covering a given area with a sidescan

sonar. It shows the variation in the amount of insuf-

ﬁciently covered cells ("MinRatio") and the variation

in POD. In average we obtained approximately a de-

crease of 5% in the former and a increase of 0.6% in

the latter, clearly showing the improvement made by

local search in this scenario. This demonstrates the

need for uneven lawn-mowing coverage pattern when

using a sidescan sonar. The obtained results allowed

us to take some additional conclusions related to the

usefulness of this search process. As explained ear-

lier, it is required an even number of tracks to cover

the nadir gaps caused by the use of a sidescan sonar.

If the original number of tracks is odd, then we need

to add or remove a track in order to use our algorithm.

The simulations showed that while the performance is

positively affected by an addition of a track, it is nega-

tively affected by its removal. The local optimization

algorithm could not compensate the decrease in per-

formance caused by the removal of a track. Table 5

presents the descriptive statistics for the optimized set

of solutions excluding the ones where tracks were re-

moved. It can be seen that the average POD increases

and that the amount of cells with insufﬁcient cover-

age is reduced. In this scenario the preferred action is

to add a track, but since mission planing constraints

need to be respected, it may not be possible to do so.

Therefore we conclude that, in a time critical appli-

cation such as the one being addressed here, it may

be better to simply skip the local optimization of so-

lutions that required removal of a track since it is not

worth the extra computational time. Figure 4 shows

a graphical representation of a given solution before

and after the local optimization procedure was exe-

cuted. The improvement in this case was a decrease

of 14.0% in the amount of insufﬁciently covered cells

and an increase of 0.9% in the average POD. This is

visually identiﬁed by the almost inexistence of red re-

gions in the optimized solution plot. Notice that the

tracks were simply rearranged maintaining its direc-

tion and depth and that no tracks were added or re-

moved. This demonstrates the usefulness and com-

UsingEvolutionaryAlgorithmstoPlanAutomaticMinehuntingOperations

233

Table 3: Some distinct solutions in the Pareto Front.

s POD (%) Energy (Wh) Time (h:m:s) Depth (m) Altitude (m) Spacing (m) V Dir (◦)

A 95.65 728.80 6:59:20 - 13.24 41.13 1.07 91.44

B 89.72 537.04 4:31:11 - 11.63 63.26 1.14 32.31

C 90.33 723.73 4:07:59 82.38 - 57.46 1.34 259.87

D 94.08 656.93 5:22:51 81.24 - 50.96 1.15 16.70

E 86.75 500.53 3:55:52 - 18.00 72.31 1.18 201.79

(a) 2D coverage plot of original solution. (b) 3D coverage plot of original solution.

Figure 3: Original solution obtained by the EA using a sidescan sonar.

(a) 2D coverage plot of optimized solution. (b) 3D coverage plot of optimized solution.

Figure 4: 3D local optimization of the previous solution obtained by the EA using a sidescan sonar.

Table 4: Descriptive statistics of the complete set of solu-

tions obtained for the coverage problem using a sidescan

sonar.

∆

(%) ∆

POD

(%) Time (s)

Min -19.41 -8.84 24.00

Mean -4.99 0.59 64.74

Max 11.81 5.51 380.00

SD 5.80 1.76 67.04

plementarity of both our local optimization algorithm

and our EA.

Similar experiments were performed, but using a

multibeam instead of sidescan sonar. The improve-

Table 5: Descriptive statistics of the set of solutions exclud-

ing the ones where tracks were removed.

∆

(%) ∆

POD

(%) Time (s)

Min -19.41 -1.99 24.00

Mean -5.43 0.81 64.77

Max 2.09 5.51 380.00

SD 5.56 1.28 68.58

ments are considered negligible as they are smaller

by a factor of 5 then in the previous scenario, mean-

ing that the gains do not justify the extra processing

time.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

234

5 CONCLUSIONS

This paper introduced an multiobjective multi-stage

approach combining EA with simulated annealing for

planning minehunting operations in static 3D environ-

ment with predictable terrain. Our algorithm main-

tains a diverse population of feasible solutions in or-

der to explore the search space and uses simulated an-

nealing to improve the best solutions found and pro-

duce new solutions in the neighbourhood. Our exper-

iments showed that the integration an ANN model to

guide the search is beneﬁcial and that the proposed lo-

cal optimization phase signiﬁcantly helps to improve

the quality of the solutions, however at the cost of a

higher computational time. We also exempliﬁed what

would be the typical output of the execution of our

planning algorithm and demonstrated the role that the

decision maker may have to play when planning a

minehunting mission with an AUV.

In the near future we are going to explore mission

planning with distinct priorities for speciﬁc areas and

study mission replanning. The idea is to use these al-

gorithms to obtain a Pareto front for each area (when

replanning a mission these areas are automatically de-

ﬁned according to mission performance) an then to

efﬁciently try to interconnect the coverage paths, thus

becoming a variant of the travelling salesman prob-

lem.

ACKNOWLEDGEMENTS

This work is ﬁnanced by the ERDF – European Re-

gional Development Fund through the COMPETE

Programme (operational programme for competi-

tiveness) and by National Funds through the FCT

– Fundação para a Ciência e a Tecnologia (Por-

tuguese Foundation for Science and Technology)

within project FCOMP-01-0124-FEDER-037281.

REFERENCES

Choset, H. (2001). Coverage for robotics - a survey of re-

cent results. In Ann. Math. Artif. Intell. SCITEPRESS.

Darwin, C. (1859). On the Origin of Species by Means

of Natural Selection, or the Preservation of Favoured

Races in the Struggle for Life. John Murray, London,

UK.

Deb, K. (2001). Multi-objective optimization using evolu-

tionary algorithms. Wiley, UK.

Fang, C. and Anstee, S. (2010). Coverage path planning

for harbour seabed surveys using an autonomous un-

derwater vehicle. In OCEANS 2010 IEEE - Sydney,

pages 1–8. IEEE.

Fujimura, K. (1996). Path planning with multiple objec-

tives. Robot Autom. Mag., 3(1):33–38.

Huang, G. (2003). Learning capability and storage capac-

ity of two-hidden-layer feedforward networks. Neural

Networks, IEEE Transactions on, 14(2):274–281.

Koopman, B. (1999). Search and Screening: General Prin-

ciples with Historical Applications. The Military Op-

erations Research Society, Virginia, USA.

Land, S. and Choset, H. (1998). Coverage path planning for

landmine location. In 3rd International Symposium on

Technology and the Mine Problem.

Metropolis, N., Rosenbluth, A., Rosenbluth, M., Teller,

A., and Teller, E. (1953). Equation of state calcula-

tions by fast computing machines. J. Chem. Phys.,

21(6):1087–1092.

Nash, L., Hover, G., and Burns, R. (1982). Additional anal-

yses of probability of detection (pod) in search and

rescue (sar) project data. Technical report.

Stack, J. and Smith, C. (2003). Combining random and

data-driven coverage planning for underwater mine

detection. In OCEANS 2003. Proceedings, volume 5,

pages 2463–2468 Vol.5. IEEE.

Williams, D. (2010). On optimal auv track-spacing for un-

derwater mine detection. In Robotics and Automa-

tion (ICRA), 2010 IEEE International Conference on,

pages 4755–4762. IEEE.

Xiao, J., Michalewicz, Z., Zhang, L., and Trojanowski,

K. (1997). Adaptive evolutionary planner/navigator

for mobile robots. Evolutionary Computation, IEEE

Transactions on, 1(1):18–28.

Zitzler, E., Laumanns, M., and Thiele, L. (2001). Spea2:

Improving the strength pareto evolutionary algorithm.

Technical report.

UsingEvolutionaryAlgorithmstoPlanAutomaticMinehuntingOperations

235