Partial Fingerprint Identiﬁcation Through Correlation-based Approach

Omid Zanganeh, Nandita Bhattacharjee and Bala Srinivasan

Clayton School of Information Technology, Monash University, Clayton, Australia

Keywords:

Biometric, Partial Fingerprint, Identiﬁcation, Authentication, Local Correlation Matching Technique.

Abstract:

Partial ﬁngerprints are likely to be fragmentary or low quality, which mandates the development of accu-

rate ﬁngerprint veriﬁcation algorithms. Two ﬁngerprints should be aligned properly, in order to measure the

similarity between them. Moreover, the common ﬁngerprint recognition methods (minutiae-based) only use

the limited information that is available. This affects the reliability of the output of the ﬁngerprint recogni-

tion system, especially when dealing with partial ﬁngerprints. To overcome this drawback, in this research, a

region-based ﬁngerprint recognition method is proposed in which the ﬁngerprints are compared in a pixel-wise

manner by computing their correlation coefﬁcient. Therefore, all the attributes of the ﬁngerprint contribute

in the matching decision. Such a technique is promising to accurately recognise a partial ﬁngerprint as well

as a full ﬁngerprint compared to the minutiae-based ﬁngerprint recognition methods which only concentrate

on parts of the ﬁngerprint. The proposed method is based on simple but effective metrics that has been de-

ﬁned to compute local similarities which is then combined into a global score and then used to make the

match/non-match decision. Extensive experiments over FVC2002 data set has proven the superiority of our

method compared to the other well-known techniques reported in literature.

1 INTRODUCTION

Fingerprint is an impression left by the friction

ridges of a person’s ﬁngertip. It is one of the most

well-known biometrics due to its uniqueness and

consistency. Although the ﬁngerprint uniqueness is

accepted based on a manual inspection (by experts),

its consistency has been proven by morphogenesis of

friction ridge skin (Pankanti et al., 2002). Tradition-

ally, ﬁngerprint had been widely used and associated

with criminal investigation, but now it has become

more popular in other areas such as civil application

(access control, ﬁnancial security, etc.) as well

(Vaidehi et al., 2010). Although a lot of effort has

been put in the past 30 years to end up with a reliable

automated system, we are still far from the good.

A number of factors which cause bottlenecks

towards achieving desired system performance are:

lack of reliable feature extraction algorithms, difﬁ-

culty in accurately aligning the ﬁngerprints and also

in deﬁning a reliable similarity measurement between

ﬁngerprints (Vaidehi et al., 2010). In addition,

ﬁngerprint individuality is empirically accepted, but

ﬁngerprint recognition is a difﬁcult task, mainly

due to the large intra-class (a.k.a. within-ﬁnger)

variation and large inter-class (a.k.a. between-ﬁnger)

similarity in ﬁngerprints. Intra-class variation occurs

when ﬁngerprints are slightly different each time

they are captured. So different impressions of the

same ﬁnger are not identical; likewise, inter-class

similarity refers to quite similar ﬁngerprint impres-

sions which are from different ﬁngers (Maltoni et al.,

2009). Intra-class variation is mainly caused due to

partial overlap, non-linear distortion, sensor noise

(Nandakumar and Jain, 2004; Parziale, 2008; Labati

et al., 2014), and intentionally altering the ﬁngerprint

(Yoon et al., 2012). Non-linear distortion introduced

during ﬁngerprint sensing is certainly one of the

most critical intra-class variability (Maltoni et al.,

2009). It is produced by non-orthogonal pressure of

the ﬁnger against the ﬁngerprint scanner. The act

of sensing maps the 3-dimensional shape of a ﬁnger

onto the 2-dimensional surface of the sensor results

in non-linear distortion in successive acquisitions of

the same ﬁnger due to skin elasticity (Maltoni et al.,

2009). Presence of noise in the ﬁngerprint images

could be due to the dirty ﬁngers which also contribute

to the intra-class variations (Nandakumar and Jain,

2004). Intentionally altering the ﬁngerprint is usually

done by criminals to hide their identity (Soweon

et al., 2012).

Researchers proposed numerous ﬁngerprint

matching techniques which can be coarsely cate-

gorised into three major groups (Maltoni et al., 2009;

275

Zanganeh O., Bhattacharjee N. and Srinivasan B..

Partial Fingerprint Identiﬁcation Through Correlation-Based Approach.

DOI: 10.5220/0005045302750284

In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 275-284

ISBN: 978-989-758-045-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Donida Labati and Scotti, 2011): Minutiae-Based

( i.e. (Kovacs-Vajna, 2000; Tico and Kuosmanen,

2003; Chen et al., 2005; Liu et al., 2005; Gao et al.,

2011)), Non-Minutiae-Based (i.e. (Sha et al., 2003;

Yang et al., 2007; Lumini and Nanni, 2006; Qader

et al., 2007)), and Correlation-Based (i.e. (Lindoso

et al., 2007; Karna et al., 2008)). Also, researchers

proposed hybrid matchers which make use of more

than one of the above-mentioned approaches ( i.e.

(Nandakumar and Jain, 2004; Ross et al., 2002;

Benhammadi et al., 2007)). All the ﬁngerprint

matching methods can be roughly categorised into

the mentioned groups based on the features they

extract from the ﬁngerprints. Fingerprint features can

also be categorized into three major levels (Maltoni

et al., 2009; Donida Labati and Scotti, 2011; Yager

and Amin, 2004). Level-1 features (general patterns)

are the macro information on the ﬁngerprint such as

ridge ﬂow and ridge orientation. The level-1 features

are mostly used to categorize the ﬁngerprints into

speciﬁed classes or pattern type (loop, arch, tented

arch, etc.). Level-2 features are the minutiae, such

as ridge bifurcations and endings. Level-3 features

include all dimensional attributes of the ridge such

as ridge width, shape, pores, incipient ridges, breaks,

creases, scars, and other permanent details (Jain

et al., 2007).

Regarding ﬁngerprint features, it should be noted

that some features could be highly-discriminative

but are very sensitive to the quality of the images.

Usually, minutiae features have these types of prop-

erties(Maltoni et al., 2009; Pankanti et al., 2002).

Minutiae are deﬁned as the points that a ridge ends

or disjoints, therefore, minutiae extraction in low

quality images will lead to detecting false minutiae

due to the unclear ridges and valleys (Yager and

Amin, 2004). Although extracting the minutiae from

grey-scale image instead of skeleton image compen-

sate for detecting false and spurious minutiae (Yager

and Amin, 2004), designing a foolproof minutiae

extractor to reliably detect these features is still

an issue. Another disadvantage of Minutiae-based

approaches is that they only use limited available

information on the ﬁngerprint. Pankati et al. claimed

that extracted information in minutiae-based methods

is limited, and algorithm developers should explore

the use of non-minutiae based information as well

(Pankanti et al., 2002). This problem becomes more

serious when dealing with partial ﬁngerprints since

some of the remaining useful information is not used

by minutiae-based methods. Typically, in a small

area of a ﬁngerprint, only 4-5 minutiae may exist

and in that case, minutiae-based methods will not

work satisfactorily due to limitation in providing

ﬁngerprint discriminative information (Maltoni et al.,

2009).

On the other hand, correlation-based methods

directly use the grey-level information from the

ﬁngerprint image (Nandakumar and Jain, 2004;

Vaidehi et al., 2010; Lindoso et al., 2007). These

methods take into account all dimensional attributes

of a ﬁngerprint which include micro characteristics

such as minutiae, macro characteristics such as ref-

erence points, and also ridge shape, ridge thickness,

etc. A grey-level ﬁngerprint image contains richer

and more discriminatory information than only the

minutiae location. Furthermore, in correlation-based

methods false/missed minutiae do not decrease the

matching performance and even no hard decision

needs to be made on the searching for minutiae

pairs. Correlation-based methods are also capable

of dealing with low quality images. Although

Correlation-based methods have a higher reliability,

their main drawback is their high computational

cost (Nandakumar and Jain, 2004; Vaidehi et al.,

2010; Lindoso et al., 2007). To overcome this issue

different strategies have been proposed. One of these

strategies is to use an appropriate region selection

for comparison purposes (Lindoso et al., 2007).

Moreover, the computation required to compute

cross-correlation can also be achieved in Fourier

domain (Douglas A., 2010; Lindoso et al., 2007).

Finally, computing correlation of the local regions of

the images can be performed in parallel.

To improve the performance of correlation al-

gorithms, Karna et al. proposed a method based on

normalized cross-correlation (Karna et al., 2008).

Their method involves extracting the common region

between two ﬁngerprints (as one single region) and

computing the correlation of the common region. The

highest correlation coefﬁcient value is considered as

the degree of similarity between two ﬁngerprints.

The main limitation of this method is the alignment

algorithm. This process is done manually by select-

ing points of interest from the template and query

ﬁngerprints. By so doing, the accuracy of aligning

the ﬁngerprints improves signiﬁcantly. However,

such an alignment strategy is not practical in AFIS

(Automated Fingerprint Identiﬁcation System) which

requires processing large number of images. In

addition, accurately aligning the ﬁngerprints can

signiﬁcantly improve the system performance. An-

other drawback of this method relates to dealing with

non-linear distortion. If the similarity measurement

is not applied locally, the matching result will suffer

from non-linear deformation.

Nandakumar and Jain proposed a hybrid method

of minutiae and correlation (Nandakumar and Jain,

SECRYPT2014-InternationalConferenceonSecurityandCryptography

276

2004). Their method is based on computing the

correlation of small region around minutiae points

and takes the average of the correlation values as the

ﬁnal similarity degree of two ﬁngerprints. Although

their approach can sufﬁciently deal with non-linear

distortion, it suffers from being dependent on the

minutiae points. The two main problems of minutiae-

based methods (working on limited information and

detecting spurious/false minutiae) also prevents this

method from providing better result. Nandakumar

and Jain also stated that ”the grey-level information of

the pixels around the minutiae point contains richer

information about the local region than attributes of

the minutiae points”.

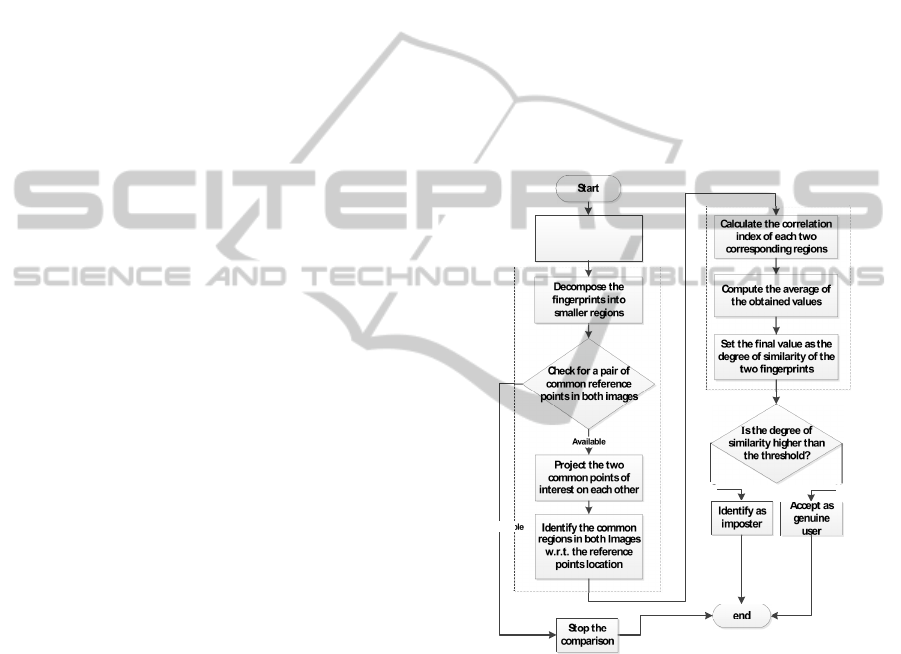
2 PROPOSED METHOD

The proposed correlation-based method consists of

the following major steps: ﬁngerprint alignment,

common region extraction, and computing the degree

of similarity. As in other methods, the ﬁngerprints are

enhanced and segmented as the preliminary steps of

the proposed method.

In a pixel-wise comparison of the images, the cor-

responding regions in two images need to be com-

pared. In order to compute the correlation of the same

regions, the translation difference can be taken care of

by applying the sliding window technique. Therefore

the images only need to be rotationally aligned. Rota-

tional alignment of two ﬁngerprints refers to rotating

the ﬁngerprints so they become as identical as possi-

ble in the orientation. In partial prints, there may be

a small overlap between the two ﬁngerprints, hence

a suitable strategy needs to be performed to align

them. In section 2.1, the alignment method is dis-

cussed which also addresses the alignment issues in

Karna et al.’s method (Karna et al., 2008).

After alignment step, in order to extract the com-

mon regions between two ﬁngerprints, ﬁrst they are

decomposed into smaller regions. Then, by project-

ing the common singular points of the two ﬁnger-

prints, the regions which are located at the same lo-

cation with respect to these points, are identiﬁed as

the common regions (section 2.2).

After identifying the common regions between the

two images, similarity of two ﬁngerprints is measured

(section 2.3). As discussed, there may be a small

overlap between two partial ﬁngerprints. Thus, in or-

der to utilise all the available information, correlation

of the overlapped regions is computed. Correlation

of each small regions in query image is computed

with respect to the corresponding one in registered

image. Dividing the ﬁngerprints into smaller regions

and computing the similarity of the ﬁngerprints lo-

cally will minimize the effect of the non-linear dis-

tortion (depending on choosing a reasonable size of

the regions). A large size region cannot properly han-

dle the non-linear deformation. On the contrary, cor-

relation of a small size regions are more affected by

the small distorted parts of that region (compared to

large size regions). Apart from these points, region

size should be small enough to cover most of the ﬁn-

gerprint information close to the borders. By comput-

ing the local similarities, all the attributes contained

in the ﬁngerprint is utilised. To obtain the ﬁnal simi-

larity score of two ﬁngerprints (global similarity), the

local similarities are averaged. The Block diagram

of the proposed method is presented in Figure 1. All

the steps is described in detail in the following sub-

sections.

Align the two

Fingerprints

Common Region Extraction

Yes

Not Availab

Computing Similarity Degree

A t

Figure 1: Block diagram of the proposed matching method.

2.1 Fingerprint Alignment

One of the intra-class variations is the rotation dif-

ference in two ﬁngerprints. In our proposed method a

pixel to pixel comparison of both images is computed,

therefore even a slight rotation difference between the

two images, could result in an inaccurate matching

decision. In other words, an accurate alignment lead

to reducing false rejection of the genuine users in the

system.

The previously developed ﬁngerprint alignment

methods, including minutia-based and non-minutia

feature based ones, are not completely suitable for

partial ﬁngerprints. One issue of applying these meth-

PartialFingerprintIdentificationThroughCorrelation-basedApproach

277

ods to partial prints is that the required features could

be very few on the fragments. Accordingly, they will

either lead to incorrect alignment or not being appli-

cable for partial ﬁngerprints (Zhao et al., 2010). For

instance, Khalili et al. have investigated on using ﬁn-

gerprint reference points to rotationally align the ﬁn-

gerprints (Khalil et al., 2009). However, it is likely

that reference points are not available in partial ﬁn-

gerprints. Therefore, it is critical to align the partial

ﬁngerprints only based on the available features.

This issue in partial ﬁngerprint alignment can be

reasonably overcome by using the remaining infor-

mation in the fragment. In addition, since the shape

of the partial ﬁngerprint is not ﬁxed, the ﬁngerprints

must be aligned adaptively to the partial print shape.

In alignment step, a new approach to align the ﬁn-

gerprints based on the correlation of ﬁngerprints (us-

ing the micro features, refer to section 2.1.1) and their

singular points (using macro features, refer to section

2.1.2) is applied. The resulting algorithm is not only

simple and intuitive, but is also robust and accurate.

2.1.1 Alignment based on Fingerprint Micro

Features

As discussed in section 1, the region-based compar-

ison include much richer information than minutiae-

features for matching while being more reliable with

respect to the image quality. The same discussion is

applicable for the features to use to align the ﬁnger-

prints.

The process starts with cropping a region from the

query ﬁngerprint. The size of the cropped region can

vary depending on the size of the valid ﬁngerprint re-

gions. In addition to the size of the region, it can be

cropped from different part of the query ﬁngerprint.

These two properties make this strategy suitable for

partial ﬁngerprints alignment. For each of the cropped

regions, the correlation of the cropped region and the

registered ﬁngerprint is computed for different rota-

tion angles. The rotation angle which gives the high-

est correlation value, is used to rotationally align the

two ﬁngerprints.

By aligning the ﬁngerprints in this way, partial ﬁn-

gerprints can be aligned even though there is no sin-

gular point available. In addition, the ﬁngerprints are

accurately aligned since the ﬁnger skin elasticity is

handled and the effect of distorted regions on the ﬁn-

gerprint is ignored, due to the point that different re-

gions (with different sizes) can be cropped from the

query ﬁngerprint. The result of aligning by this strat-

egy is shown in Figure 2. Although this strategy is

accurate, it is not efﬁcient in terms of computation

cost. Each cropped region is rotated by -35 to +35

degree till the rotation difference is found. In order

to increase the efﬁciency, the singular points position

(if available) on the ﬁngerprint is used as the second

strategy.

Figure 2: A pair of impression of the same ﬁnger being

aligned based on computing the correlation of their ridge

structure.

2.1.2 Alignment based on Fingerprint Macro

Features

The ﬁngerprints are generally 2-dimensional images

which could be rotationally aligned if two identical

points can be located in both images. Singular points

(if available) could be used to align the ﬁngerprints

efﬁciently based on this theory. In this study, the lo-

cations of singular points are detected based on the

method proposed by Wang et al. (Wang et al., 2011).

The ideal situation in intra-class cases is that the

location of any singular point in one image should

be identical to the location of corresponding singular

point in the other image. For instance, the difference

in the Euclidean distance between core and delta point

in two intra-class ﬁngerprints ”A”, and ”B”, should be

very small. If so, the idea of using the singular point

location for alignment is promising. Considering the

four types of singular points in a ﬁngerprint (upside

core, downside core, right delta, and left delta), there

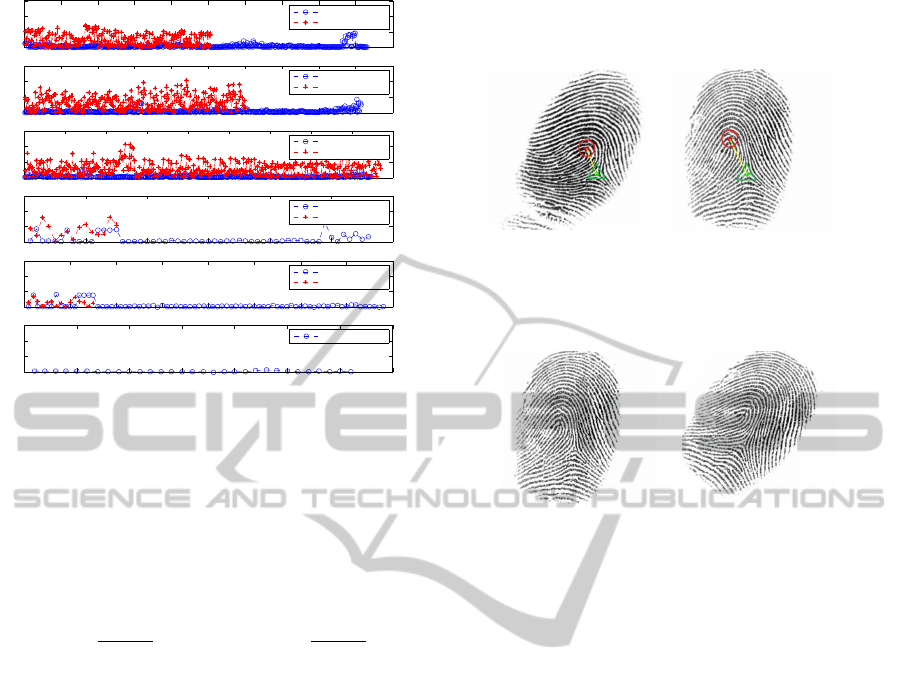
are six combinations of them. Figure 3 shows the plot

of subtracting the Euclidean distance between singu-

lar points of intra-class and inter-class ﬁngerprints.

The experiment is conducted on the public data set

FVC2002 DB1. As shown, generally the subtraction

between the Euclidean distance of the two pairs of

singular points locations in intra cases is much lower

than those in inter-cases (desired). On the other hand,

in some intra-cases, this value is more than the ones

in inter-cases due to the intra-class variation (unde-

sired). In this case, aligning the ﬁngerprints based on

the position of reference points will not be accurate,

but it still could be used for a coarse alignment (to

take advantage of the efﬁciency of this strategy).

Assume two pairs of the same reference points

exist in both ﬁngerprints. To align them based on

their position and angle with respect to x-axis, the

query image is rotated till the gradient of the two

common reference points are identical.If C

, y

)

and D

, y

) are core and delta points respec-

tively in registered ﬁngerprint, likewise C

′

, y

′

)

and D

′

, y

′

) are core and delta points respectively

SECRYPT2014-InternationalConferenceonSecurityandCryptography

278

0 50 100 150 200 250 300 350 400 450 500

100

200

300

Ucore & Dcore

Intra Comparisons

Inter Comparisons

0 50 100 150 200 250 300 350 400 450 500

100

200

300

Ucore & Ldelta

Intra Comparisons

Inter Comparisons

0 50 100 150 200 250 300 350 400 450

100

200

300

Ucore & Rdelta

Intra Comparisons

Inter Comparisons

0 10 20 30 40 50 60

100

200

300

Dcore & Ldelta

Intra Comparisons

Inter Comparisons

0 10 20 30 40 50 60 70 80

100

200

300

Dcore & Rdelta

Intra Comparisons

Inter Comparisons

0 5 10 15 20 25 30 35

100

200

300

Ldelta & Rdelta

Intra Comparisons

Figure 3: y-axis indicates the difference between the Eu-

clidean distance between each pair of singular points in in-

tra and inter class ﬁngerprints (in pixels), x-axis indicates

a comparison in inter/intra. Ucore = upside core, Dcore =

downside core, Ldelta = left delta, and Rdelta = right delta.

in query ﬁngerprint, the angle between (C

, D

), and

, D

), (θ

and θ

respectively) is computed as fol-

lows:

= tan

−1

(

− y

− x

), θ

= tan

−1

(

′

− y

′

− x

′

) (1)

angle = θ

− θ

(2)

Eq. 2 indicates the angle that query ﬁngerprint

must be rotated in order to be aligned with the regis-

tered ﬁngerprint.

Figure 4 illustrates an example of aligning the ﬁn-

gerprints based on the above process. Figures 4(a)

and 4(b) show the registered and query ﬁngerprints

respectively, which are different impressions of the

same ﬁnger. To align the query ﬁngerprint with the

registered one, the query ﬁngerprint should be rotated

clockwise. The red and green circles depict the lo-

cation of up-core and delta respectively on both of

the ﬁngerprints. According to the position of the core

and delta points on registered image and by using Eq.

1, θ

= +111

◦

and likewise θ

= +116

◦

. Then the

angle (Eq. 2) is −5

◦

which means the query image

should be rotated by 5

◦

(clockwise) to be aligned with

registered image (Figure 4(c)). In this case, the sin-

gular point detection method correctly identiﬁed the

position of the singularity, but due to the intra-class

variation, core and delta points changed their posi-

tion in two different impressions. In these cases us-

ing the position of the singular points will not result

in an accurate alignment. However, the ﬁngerprints

were coarsely aligned which signiﬁcantly improves

the alignment efﬁciency in total.

(a) Registered image. (b) Query image.

= +111, θ

= +116, angle = θ

− θ

= −5

tated by −5

◦

(d) Query image ro-

tated by −35

◦

Figure 4: Aligning the query ﬁngerprint (b) with respect

to registered ﬁngerprint (a), in (c) only ﬁst strategy used to

align the ﬁngerprints, in (d) alignment is done by combining

ﬁrst and second strategy

2.1.3 Alignment by Hybrid of Micro and Macro

Features

Considering these two strategies, combing the two

alignment strategies results in taking advantage of

accurately aligning by using micro features and ef-

ﬁciently aligning by using macro features. Figure

5 shows the ROC plot of the discussed alignment

method. Each curve shows the False Reject Rate

(FRR) versus False Accept Rate (FAR) (refer to (Cap-

pelli et al., 2006) for FAR and FRR explanation) for

different degree of rotation used in second strategy.

The red curve shows the system performance when

rotation angle is set to zero which is equivalent to only

applying the second alignment strategy (coarse align-

ment). As depicted, by increasing the rotation angle

(in ﬁrst strategy), the Equal Error Rate, EER (where

FAR = FRR, (Cappelli et al., 2006)) decreases.

Furthermore, the ROC curves associated with the

rotation angles of 0 and 5 shows signiﬁcantly higher

FAR and FRR compared to the ROC curves associ-

ated with the rotation angles 10, 15, 25, 35, and 45.

As mentioned in (Maio et al., 2002), the maximum

rotation difference between any two samples in this

dataset is a maximum of 35

◦

. This will lead us to the

PartialFingerprintIdentificationThroughCorrelation-basedApproach

279

1 2 3 4 5 6

False Accept Rate (FAR)

False Reject Rate (FRR)

Rotation Angle = 0

Rotation Angle = 5

Rotation Angle = 10

Rotation Angle = 15

Rotation Angle = 25

Rotation Angle = 35

Rotation Angle = 45

Figure 5: ROC of the proposed method by using different

rotation angles in second alignment strategy.

Figure 6: Block diagram of the proposed alignment method.

optimal rotation degree that can result in lowest FAR

and FRR. Considering that at this point ﬁngerprints

are coarsely aligned, there is not much difference be-

tween the curves for rotation angles of 15, 25, 35, and

45. This can be concluded that the rotation angle 15 is

the optimal degree of rotation needed for this dataset.

Block diagram of the proposed method for alignment

is presented in Figure 6.

There is one more step needs to be performed af-

ter ﬁngerprints are aligned to make sure the same re-

gions are compared between two ﬁngerprints. In next

section, how the common regions between two ﬁnger-

prints are extracted is discussed.

2.2 Common Region Extraction

Local matching techniques are proposed to overcome

the problems such as lack of robustness with re-

spect to the non-linear distortion in global match-

ing techniques (Cappelli et al., 2010). In order to

locally match the ﬁngerprints, they are decomposed

into smaller regions. The main reasons that the local

matching techniques perform better than the global

ones are:

• Their capability in handling the non-linear distor-

tion of the ﬁngerprints (refer to section 1 for non-

linear distortion deﬁnition).

• The effect of the distorted regions on the ﬁnal sim-

ilarity degree is reduced by dividing the images

into smaller regions (refer to section 2.3).

With regard to the size of the smaller regions, in

computing the correlation of two images, there is a

trade-off between size of the region and sensitivity to

distortion. If the selected region size is too small it

will not capture enough image information and will

be too sensitive to the distortion. This may result in

miscalculating the correlation of that region. On the

other hand, if the region size is too large, it becomes

less sensitive to the distortion (desired) but also less

sensitive to the actual variations of the ﬁngerprints

(not desired). Considering the resolution of the ﬁnger-

prints in the dataset, it is observed that the minimum

region size required for any feature to be extracted is

50 × 50 pixels (refer to section 3). Moreover, this size

is also used to extract the common regions between

the two ﬁngerprints.

In order to extract the common regions, at least

one common reference point needs to be located on

both ﬁngerprint. The query ﬁngerprint is projected

on to the registered ﬁngerprint by aligning their com-

mon reference points. Subsequently, the overlapping

regions are identiﬁed to be the common regions be-

tween the two ﬁngerprints.

2.3 Computing Degree of Similarity

Due to the small overlap in partial ﬁngerprint match-

ing, a similarity measure that can reﬂect all the distin-

guishing characteristic of a ﬁngerprint is essential. As

discussed in section 1, correlation coefﬁcient of two

ﬁngerprints reﬂects all the available features. There-

fore, the similarity of two ﬁngerprints is computed in

terms of their correlation coefﬁcient. In addition, as

discussed in section 1, the ﬁngerprints could suffer

from the distortion. The distortion on a ﬁngerprint

may not be uniformly distributed and different regions

may have different image quality levels. Thus, com-

puting the similarity of the ﬁngerprints locally (small

regions extracted in section 2.2) reduces the effect of

the distorted regions. In next section, the details of

computing the local similarities and why it tolerates

the effect of distorted regions on similarity degree of

the ﬁngerprints is discussed followed by computing

SECRYPT2014-InternationalConferenceonSecurityandCryptography

280

the global (ﬁnal) similarity degree through consoli-

dating the local similarities for comparison.

2.3.1 Local and Global Degree of Similarity

Conventionally, in correlation-based methods, the

whole ﬁngerprints were considered as one big single-

region. Accordingly, the degree of similarity was

computed based upon the correlation of the two

single-regions. In order to lower the effect of distorted

regions on ﬁngerprints, the similarity of two ﬁnger-

prints is computed locally (in small-region level) and

then the average value of local similarities is consid-

ered as the ﬁnal similarity score between the two ﬁn-

gerprints. Computing the similarities of each pair of

small-regions individually and then averaging them

to obtain the global similarity is a robust and reliable

technique for ﬁngerprint matching. The reason is that

the ﬁnal similarity degree could be computed by giv-

ing the same contribution to each of the local simi-

larities and by so doing, the distorted regions is taken

into account as one value (local similarity) and it is

not affecting the similarity of other regions. Hence,

in our method, ﬁrst the Normalized Cross Correla-

tion (NCC) of each two corresponding regions is com-

puted as local similarities. The NCC of 2-dimensional

images f and t is calculated as (aka Pearson’s r corre-

lation) (Yoo and Han, 2009):

NCC =

∑

x,y

( f (x, y) −

f )(t(x, y) −

, (3)

where

f and

t are the mean and σ

and σ

are the

standard deviation of the images f and t respectively

and n is the number of pixels of the images.

Common regions between registered and query

ﬁngerprint are not always detected completely accu-

rately due to the following two reasons. First: as men-

tioned in section 2.2, extracting common regions is

based on the position of the common reference point.

However, the reference points are not always pre-

cisely located. Therefore, the detected common re-

gions based on the location of these points are also

not always precisely located. Second: even if the ref-

erence points are located precisely, it is still very chal-

lenging to precisely locate the corresponding regions

due to the intra-class variation and non-linear distor-

tion. Therefore, the corresponding region on regis-

tered ﬁngerprint needs to be chosen greater than the

one in query image to compensate for the small errors

in computing the exact location of the corresponding

regions.

After the local similarities are computed, a partic-

ular value (as global score) needs to be obtained from

the local similarities to indicate their overall degree

of similarity (Cappelli et al., 2010). In our method, to

obtain a degree of similarity between the two ﬁnger-

prints (global score/similarity), the local similarities

are averaged. It should be mentioned that computing

the similarity of ﬁngerprints in such a way reasonably

handles the intra-class variation and inter-class sim-

ilarity, however to get the best out of this method it

still could be improved. One promising technique to

add to the current method is measuring the quality of

small regions and compute the local similarities only

based on the good quality regions. This is part of our

future wok which is explained more in section 4.

3 EXPERIMENTAL RESULT

An experiment is performed on DB1 of the public

dataset FVC 2002 (Fingerprint Veriﬁcation Compe-

tition) which contains 800 ﬁngerprints from 100 dif-

ferent ﬁngers (8 impressions per ﬁnger). As discussed

in (Maio et al., 2002), for the data set FVC2002 DB1,

the participants that volunteered to provide their ﬁn-

gerprints, were asked to intentionally change the ori-

entation of their ﬁnger on the scanner when scan-

ning different impressions (to make the different im-

pressions vary rotationally). In addition, no effort

was made to control the image quality and the sen-

sor plates were not systematically cleaned and high

quality images were removed from the dataset. There-

fore, due to rotation and displacement of the ﬁnger

when scanning, there is often only a partial overlap

between different impressions of the same ﬁnger and

hence, the images in the data set include low qual-

ity and partial ﬁngerprints as well. As discussed in

previous sections, no matter how partial the ﬁnger-

prints are, they can be aligned, their common regions

are extracted (as long as a common reference point is

available), and their local and global similarities are

computed. The proposed method is designed in such

a way to fulﬁl the requirements of partial ﬁngerprint

matching as well as complete ﬁngerprint matching.

Regarding the time cost of the proposed method,

the matching process of two ﬁngerprints takes about

1.5 minutes on a computer with 3.1 GHz CPU and

8 GB RAM. This time has a direct relationship with

how partial a ﬁngerprint is. The smaller the avail-

able valid regions are, the less time is required for

matching process. Considering the size of the dataset,

and the time cost of the proposed method, the com-

parisons were conducted on Monash University High

Performance Computing Cluster.

Table 1 indicates the result of the proposed

method on the FVC2002 data set (in terms of the met-

PartialFingerprintIdentificationThroughCorrelation-basedApproach

281

Table 2: Comparison of the proposed method with previous works in terms of EER(%) value on dataset FVC2002 DB1. The

methods are roughly categorised into the three major groups of ﬁngerprint approaches.

Category Method EER (%)

(Kovacs-Vajna, 2000) 4.3

(Tico and Kuosmanen, 2003) 4.0

Minutiae (Chen et al., 2005) 4.6

(Liu et al., 2005) 4.3

(Gao et al., 2011) 3.5

(Sha et al., 2003) 6.23

Non-Minutaie (Yang et al., 2007) 3.64

(Lumini and Nanni, 2006) 4.2

(Qader et al., 2007) 7.13

Hybrid (Benhammadi et al., 2007) 4.2

Single-Region Conventional Method 7.1

Multiple-Region with

region size: 50 × 50 pixels Proposed Method 2.32

Table 1: The result of the proposed method in terms of EER

(%) value on data set FVC 2002 DB1 by using different

region size. The last column shows the threshold used to

compute the EER.

Proposed Correlation-Based Method EER (%)

Region Size = 100 × 100 4.37

Region Size = 90 × 90 3.27

Region Size = 80 × 80 2.92

Region Size = 70 × 70 2.58

Region Size = 60 × 60 2.35

Region Size = 50 × 50 2.32

Region Size = 40 × 40 2.40

Region Size = 30 × 30 2.48

Region Size = 20 × 20 2.79

ric Equal Error Rate, EER) where the ﬁngerprints are

decomposed to different region sizes in order to ex-

tract their common regions (section 2.2) and compute

their similarity degree (section 2.3). As shown in this

table, the smaller the region size is, the more accu-

rate the system performance will be. It is empirically

observed that the region size 50 × 50 is the optimum

region size for this data set which is required to ex-

tract the available features in a ﬁngerprint.

Table 2 illustrates the comparison of our method

with previous works in terms of EER value. Our

method produces the lowest EER of 2.32%. The main

advantage of our method compared to the others is

using all the available dimensional attributes of the

ﬁngerprint. That includes all the three level of fea-

tures mentioned in section 1. In addition, many meth-

ods are proposed to extract the level-3 features of the

ﬁngerprint, but extracting the level-3 features such as

pores from low resolution ﬁngerprints is very chal-

lenging. On the other hand, our proposed method is

able to take into account all the possible distinguish-

ing information in the ﬁngerprint, regardless of the

image quality (not very dependent on few particular

features).

To demonstrate the effectiveness of the proposed

multiple-region based method, its result is com-

pared with the single-region correlation (conventional

correlation-based method). It was observed that aver-

aging method improved the EER from 7.1% to 2.32

% with respect to the single-region correlation-based.

This improvement is achieved due to the robustness

of the proposed method in reasonably handling the

non-linear distortion and lowering the effect of the

distorted regions in the ﬁngerprint images (refer to

section 2.3 for details).

Cappelli et al. (Cappelli et al., 2010) stated that lo-

cal minutiae matching techniques can be categorised

into two family of nearest neighbour-based and ﬁxed

radius-based. Methods in nearest neighbour-based

family (i.e. Gao et al.’s approach (Gao et al., 2011))

the k closest minutiae to a central minutiae are deﬁned

as the neighbours of the central one. These methods

lead to a ﬁxed-length descriptor that can be matched

efﬁciently. Gao et al.’s method uses the nearest neigh-

bour structure information to match the points which

carries on global matching at the end. In addition,

their method is invariant to rotation and translation

which saves the effort needed to align the ﬁnger-

prints.These are the main advantages of Gao et al.’s

method which lead to the lowest EER in the table.

On the other hand, further to the issues which Gao et

al.’s method suffer from as a minutiae-based method

(refer to section 1), their method is not able to con-

sider the effect of non-linear distortion of ﬁngerprint

images. Also nearest neighbour-based methods are

not very tolerant to missing and spurious minutiae as

the objective in these methods is to ﬁnd the k nearest

minutiae points (Cappelli et al., 2010).

SECRYPT2014-InternationalConferenceonSecurityandCryptography

282

The best EER in non-minutiae category belongs

to Yang et. al’s (Yang et al., 2007) method. Yang et

al.’s method is based on extracting invariant moments

of the ﬁngerprint. Invariant moments were ﬁrst intro-

duced by Hu (Ming-Kuei, 1962). Hu proved that his

seven moments are invariant to RTS (rotation, trans-

lation, and scaling). These moments are widely used

in pattern recognition. Yang et al. applied these mo-

ments in ﬁngerprint matching. Although their method

is invariant to RTS and is efﬁcient in terms of compu-

tation, there are some limitations in their work. First

problem is that they only make use of a small region

of the ﬁngerprint (around reference points) while the

rest of the information remains unused. Second prob-

lem is that they used 75% of the dataset as training

set, while all the dataset (including the training set) is

used to evaluate their method (as test set). This sig-

niﬁcantly affects the performance of the system and

lead to a lower EER compared to evaluating the sys-

tem only on the test set.

4 CONCLUSION AND FUTURE

WORK

In this paper, we proposed a new method to mea-

sure the similarity of the ﬁngerprints based on corre-

lation coefﬁcient. The method is composed of three

main steps: alignment, common region extraction,

and computing the ﬁnal degree of similarity. Regard-

ing to the alignment, pros and cons of the two strate-

gies discussed which lead to combining them together

to end up with an accurate and efﬁcient method. The

common region extraction was obtained by dividing

the images into smaller regions, and projecting them

on each other with respect to their common reference

points. The most important step that had a great ef-

fect on the EER, is measuring the degree of similarity

between two ﬁngerprints. Based on the correlation

coefﬁcient, a new methodology to improve the accu-

racy for reliable ﬁngerprint recognition proposed with

especial interest in partial ﬁngerprints. To this end,

computing the similarity degree was decomposed in

two sub-steps. First, the two images were divided

into smaller regions, and the correlation of the cor-

responding regions were computed (as local similar-

ities). Thereafter, the mean value of the local simi-

larities is calculated as the ﬁnal degree of similarity.

It was observed that computing local similarities and

assigning their average as a ﬁnal degree of similarity

result in a higher recognition accuracy compared to

its conventional single region calculation. As a con-

sequence, the EER is enhanced by almost 3 times as

compared to a single region correlation. This proves

the effectiveness of including an appropriate averag-

ing method in the recognition algorithm. Regarding

other available studies, our result gives a 33.7% im-

provement over the previous works.

Regarding our future work, as mentioned in sec-

tion 2.3, measuring the quality of the small regions

and processing only the good quality ones is a promis-

ing step to add to the current method. By so doing,

inter and intra cases are more discriminated. Two in-

tra ﬁngerprints are supposed to have a high correla-

tion in every region and vice versa for inter ﬁnger-

prints. However, one of the main reasons that intra

ﬁngerprints result in low similarity is that some parts

of the ﬁngerprint are distorted. Therefore, identifying

the low quality regions and ignoring the correlation of

those regions will help to increase the similarity of in-

tra cases. On the other hand, this strategy will not sig-

niﬁcantly affect the similarity degree of inter-cases.

The low similarity in inter cases is the result of the

difference between the ridges and valleys structure of

the two ﬁngerprints and not only the quality. In other

words, the similarity on inter-cases will increase but

not as much as it does for intra-cases.

ACKNOWLEDGEMENT

The authors would like to thank Li Wang (Wang et al.,

2011) and Sharat Chikkerur (Chikkerur et al., 2007)

for providing us with the source code. This research

was supported in part by the Monash e-Research Cen-

tre and eSolutions-Research Support Services through

the use of the Monash Campus HPC Cluster.

REFERENCES

Benhammadi, F., Amirouche, M. N., Hentous, H.,

Bey Beghdad, K., and Aissani, M. (2007). Finger-

print matching from minutiae texture maps. Pattern

Recognition, 40(1):189–197.

Cappelli, R., Ferrara, M., and Maltoni, D. (2010). Minu-

tia cylinder-code: A new representation and matching

technique for ﬁngerprint recognition. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

32(12):2128–2141.

Cappelli, R., Maio, D., Maltoni, D., Wayman, J. L., and

Jain, A. K. (2006). Performance evaluation of ﬁnger-

print veriﬁcation systems. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 28(1):3–18.

Chen, Y., Dass, S. C., and Jain, A. (2005). Fingerprint

Quality Indices for Predicting Authentication Perfor-

mance, pages 160–170. Lecture Notes in Computer

Science. Springer.

PartialFingerprintIdentificationThroughCorrelation-basedApproach

283

Chikkerur, S., Cartwright, A. N., and Govindaraju, V.

(2007). Fingerprint enhancement using stft analysis.

Pattern Recognition, 40(1):198–211.

Donida Labati, R. and Scotti, F. (2011). Fingerprint. In van

Tilborg, H. and Jajodia, S., editors, Encyclopedia of

Cryptography and Security, pages 460–465. Springer

US.

Douglas A., L. (2010). The discrete fourier transform, part

6: Cross-correlation. Journal of Object Technology,

9(2):17–22.

Gao, Z., You, X., Zhou, L., and Zeng, W. (2011). A

novel matching technique for ﬁngerprint recognition

by graphical structures. In International Confer-

ence on Wavelet Analysis and Pattern Recognition

(ICWAPR), pages 77–82.

Jain, A. K., Yi, C., and Demirkus, M. (2007). Pores

and ridges: High-resolution ﬁngerprint matching us-

ing level 3 features. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 29(1):15–27.

Karna, D. K., Agarwal, S., and Nikam, S. (2008). Normal-

ized cross-correlation based ﬁngerprint matching. In

Fifth International Conference on Computer Graph-

ics, Imaging and Visualisation, CGIV, pages 229–232.

IEEE.

Khalil, M. S., Muhammad, D., Khan, M. K., and AL-

Nuzaili, Q. (2009). Fingerprint veriﬁcation using ﬁn-

gerprint texture. In IEEE International Symposium

on Signal Processing and Information Technology (IS-

SPIT), pages 591–594.

Kovacs-Vajna, Z. M. (2000). A ﬁngerprint veriﬁcation sys-

tem based on triangular matching and dynamic time

warping. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22(11):1266–1276.

Labati, R. D., Genovese, A., Piuri, V., and Scotti, F. (2014).

Touchless ﬁngerprint biometrics: a survey on 2d and

3d technologies. Journal of Internet Technology,

15(3):325–332. 1607-9264.

Lindoso, A., Entrena, L., Liu-Jimenez, J., and Millan, E. S.

(2007). Increasing security with correlation-based ﬁn-

gerprint matching. In 41st Annual IEEE International

Carnahan Conference on Security Technology, pages

37–43.

Liu, N., Yin, Y., and Zhang, H. (2005). A ﬁngerprint match-

ing algorithm based on delaunay triangulation net. In

The Fifth International Conference on Computer and

Information Technology, CIT, pages 591–595. IEEE.

Lumini, A. and Nanni, L. (2006). Two-class ﬁngerprint

matcher. Pattern Recognition, 39(4):714–716.

Maio, D., Maltoni, D., Cappelli, R., Wayman, J., and Jain,

A. (2002). Fvc2002: Second ﬁngerprint veriﬁcation

competition. In 16th International Conference on Pat-

tern Recognition, volume 3, pages 811–814.

Maltoni, D., Maio, D., Jain, A., and Prabhakar, S. (2009).

Handbook of Fingerprint Recognition. Springer, New

York, 2nd edition.

Ming-Kuei, H. (1962). Visual pattern recognition by mo-

ment invariants. IRE Transactions on Information

Theory, 8(2):179–187.

Nandakumar, K. and Jain, A. K. (2004). Local correlation-

based ﬁngerprint matching. In Indian Conference on

Computer Vision, Graphics and Image Processing,

pages 503–508.

Pankanti, S., Prabhakar, S., and Jain, A. K. (2002). On

the individuality of ﬁngerprints. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

24(8):1010–1025.

Parziale, G. (2008). Touchless ﬁngerprinting technology.

In Ratha, N. and Govindaraju, V., editors, Advances

in Biometrics, pages 25–48. Springer London.

Qader, H. A., Ramli, A. R., and Al-Haddad, S. (2007). Fin-

gerprint recognition using zernike moments. The In-

ternational Arab Journal of Information Technology,

4(4):372–376.

Ross, A., Jain, A., and Reisman, J. (2002). A hybrid ﬁn-

gerprint matcher. In 16th International Conference on

Pattern Recognition, volume 3, pages 795–798 vol.3.

Sha, L., Zhao, F., and Tang, X. (2003). Improved ﬁnger-

code for ﬁlterbank-based ﬁngerprint matching. In In-

ternational Conference on Image Processing, ICIP,

volume 2, pages II–895. IEEE.

Soweon, Y., Jianjiang, F., and Jain, A. K. (2012). Altered

ﬁngerprints: Analysis and detection. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

34(3):451–464.

Tico, M. and Kuosmanen, P. (2003). Fingerprint matching

using an orientation-based minutia descriptor. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 25(8):1009–1014.

Vaidehi, V., Naresh, B. N. T., Ponsamuel, M. A., Praveen,

K. S., Velmurugan, S., Balamurali, and Chandra, G.

(2010). Fingerprint identiﬁcation using cross correla-

tion of ﬁeld orientation. In Second International Con-

ference on Advanced Computing, ICoAC, pages 66–

69.

Wang, L., Bhattacharjee, N., and Srinivasan, B. (2011).

A novel technique for singular point detection based

on poincar

e index. In 9th International Conference

on Advances in Mobile Computing and Multimedia,

pages 12–18. ACM.

Yager, N. and Amin, A. (2004). Fingerprint veriﬁcation

based on minutiae features: a review. Pattern Analysis

and Applications, 7(1):94–113.

Yang, J., Shin, J., and Park, D. (2007). Fingerprint Match-

ing Using Invariant Moment Features, volume 4456

of Lecture Notes in Computer Science, pages 1029–

1038. Springer Berlin / Heidelberg.

Yoo, J.-C. and Han, T. H. (2009). Fast normalized cross-

correlation. Circuits, Systems and Signal Processing,

28(6):819–843.

Yoon, S., Zhao, Q., and Jain, A. K. (2012). On matching

altered ﬁngerprints. In 5th IAPR International Con-

ference on Biometrics, ICB, pages 222–229. IEEE.

Zhao, Q., Zhang, D., Zhang, L., and Luo, N. (2010). High

resolution partial ﬁngerprint alignment using pore-

valley descriptors. Pattern Recognition, 43(3):1050–

1061.

SECRYPT2014-InternationalConferenceonSecurityandCryptography

284