
Multiple Camera Human Detection and Tracking
Inside a Robotic Cell
An Approach based on Image Warping, Computer Vision,
K-d Trees and Particle Filtering
Matteo Ragaglia, Luca Bascetta and Paolo Rocco
Dipartimento di Elettronica, Informazione e Bioingegneria,
Politecnico di Milano, Piazza Leonardo da Vinci - 32, 20133, Milan, Italy
Keywords:
Human Detection and Tracking, Robotic Cell Supervision, Computer Vision, Image Warping, Back-
ground/Foreground Segmentation, K-d Tree, Particle Filtering.
Abstract:
In an industiral scenario the capability to detect and track human workers entering a robotic cell represents
a fundamental requirement to enable safe and efficient human-robot cooperation. This paper proposes a new
approach to the problem of Human Detection and Tracking based on low-cost commercial RGB surveil-
lance cameras, image warping techniques, computer vision algorithms, efficient data structures such as k-
dimensional trees and particle filtering. Results of several validation experiments are presented.
1 INTRODUCTION
Nowadays a structured and fruitful Human-Robot In-
teraction (HRI) represents the key factor that will
facilitate industrial robots to be massively used in
SMEs. Obviously, in order to allow an efficient HRI,
physical separation of robot and human workspaces
must beovercomeand safety fences must be removed.
This lack of artificially imposed safety must be com-
pensated for by endowing robot control systems with
more advancedsafety functionalities, like for instance
Human Detection and Tracking (HDT).
The problem of HDT consists in detecting the
presence of one or more human beings inside a spe-
cific environment and track their motion (in terms of
position and, if possible, velocity) on the basis of a
series of consecutive “descriptions” of the supervised
scene provided by one or more sensors. As a mat-
ter of fact, knowing if a human worker has entered a
robotic cell and being able to follow his/her motion
would allow the control system to choose the most
suitable control strategy in order to avoid collisions
(by keeping the robot as distant as possible from the
human) or to allow safe HRI (by enforcing a compli-
ant behaviour of the manipulator).
In this context the most typical choice is to use
surveillance RGB cameras (especially fish-eye cam-
eras), since they are both convenient and easily de-
ployable, but depth sensors or mixed RGB-D sensors
(like for instance Microsoft Kinect
r
) can be used as
well.
1.1 State of the Art
Although HDT can be used in several contexts,
we will address only its use in industrial robotics.
Techniques to perform HDT in an industrial en-
vironment using respectively a single camera or
multiple cameras are described in (Rogez et al.,
2014) and (Elshafie and Bone, 2008), while high-
visibility industrial clothing detection strategies based
on RGB and IR cameras have been proposed in (Mos-
berger and Andreasson, 2013) and (Mosberger et al.,
2013). Approaches based on pressure-sensitive sen-
sors mounted on the floor have been proposed as well,
like for instance (Najmaei et al., 2011). Finally exam-
ples of HDT relying on RGB-D sensor can be found
in (Munaro et al., 2012) and (Munaro et al., 2013).
Sometimes the problem of HDT has been tack-
led simultaneously with the problem of predicting
online the motion and/or the trajectory followed by
a human (also known as Human Intention Estima-
tion). In (Kuli´c and Croft, 2007) techniques combin-
ing vision and psychological signal measurement for
human motion estimation during HRI are presented,
while (Asaula et al., 2010) describe a system for pre-
Ragaglia M., Bascetta L. and Rocco P..
Multiple Camera Human Detection and Tracking Inside a Robotic Cell - An Approach based on Image Warping, Computer Vision, K-d Trees and Particle
Filtering.
DOI: 10.5220/0005045703740381
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 374-381
ISBN: 978-989-758-040-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

dicting the probability of an accident in a HRI indus-
trial scenario based on a dynamic stochastic model
of the human motion. Finally, (Bascetta et al., 2011)
present a strategy, based on HDT, to estimate the des-
tination of a human walking inside a robotic cell.
1.2 Main Contributions and Outline
In this paper we propose a solution to HDT organised
in a pipeline of different steps. Starting from a scene
monitored by multiple RGB surveillance cameras, the
different RGB images are acquired and warped to-
gether to create a unique combined image. Back-
ground/Foreground Segmentation (BG/FG Segmen-
tation) is applied to the combined image to detect hu-
man workers. K-dimensional trees data structures (k-
d trees) are then used to efficiently update in time the
information regarding humans’ silhouettes detected
via BG/FG Segmentation. Finally multiple Particle
Filters perform the tracking functionality.
With respect to the previously mentioned state of
the art, the main contributions of this work can be
summarized as follows:
• Image Fusion: multiple images simultaneously
acquired from different surveillance cameras are
warped together to obtain a unique combined im-
age describing the whole supervised environment;
• Abstraction from Physical Sensors: Image Fu-
sion completely decouples the HDT processing
pipeline from physical sensors. Though multi-
ple physical cameras are used, the HDT pipeline
“sees” only one logical sensor from which the
combined image is acquired;
• K-d Trees: the use of k-d trees provides an effi-
cient and elegant solution to the problem of up-
dating in time the information regarding detected
human workers;
The remainder of this work is organized as fol-
lows. Section 2 describes the image warping tech-
niques used for image fusion, while the BG/FG Seg-
mentation algorithm is presented in Section 3. The
usage of k-dimensional tree data structure is covered
in Section 4 and the adopted particle filtering strategy
is described in Section 5. Finally Section 6 shows the
results obtained from several validation experiments.
2 MULTIPLE CAMERAS IMAGE
FUSION
The fusion of images acquired from R different cam-
eras relies on calibration of every vision sensor. For
−5
0
5
0
1
2
3
4
0
1
2
3
u
1
v
1
y
w
x
w
z
w
u
2
v
2
y
2
x
2
z
2
y
1
x
1
z
1
E
1
E
2
I
1
I
2
Figure 1: Example of a setup including two calibrated cam-
eras and corresponding image planes.
every available surveillance camera both the intrinsic
and the extrinsic calibration matrices, respectively I
r
and E
r
, are identified. While I
r
maps the r-th camera
Cartesian frame to the r-th camera pixel coordinate
frame, E
r
maps 3D points expressed in the world-base
Cartesian frame to the r-th camera Cartesian frame, as
sketched in Figure 1. Moreover, also the radial and
tangential distortion coefficients d
r
are identified:
d
r
= {k
1r
, k
2r
, p
1r
, p
2r
, k
3r
} (1)
In order to obtain a unique image describing the
whole supervised environment, images acquired from
several surveillance cameras must be compensated for
distortion effects (using d
r
) and then they must be
warped together. Image warping consist in mapping
every pixel P
o
in the original image to a different pixel
P
w
through a warping matrix W:
P
w
= [u
w
,v
w
]
T
= W P
o
= W [u
o
,v
o
]
T
(2)
A reference camera is selected so that the coor-
dinate transform between the world frame and the
combined image pixel coordinate frame (and vicev-
ersa) can be described by the extrinsic and intrin-
sic calibration matrices of the reference camera. At
this point images must be warped together in such
a way that pixels describing corresponding points on
the floor plane can be exactly overlapped. To obtain
this result the homography matrix H
r
of the r-th (non-
reference) camera image plane with respect to the ref-
erence camera image plane must be identified, with
both image planes corresponding to the scene floor.
Since H
r
is a 3x3 matrix defined up to a scale fac-
tor, the problem of identifying its elements can be
solved by considering four corresponding points be-
tween the reference camera image and the r-th cam-
era image. In order to find the homography matri-
ces that map the r-th camera image plane to the refer-
ence camera image plane while preserving the scene
floor, four different points P
W
i
belonging to the scene
floor (z
W
i
= 0) are chosen and mapped to both the ref-
erence camera and the r-th camera pixel coordinate

frame (p
ref
i
and p
r
i
respectively):
∀i ∈ [1,4] P
W
i
=
x
W
i
,y
W
i
,0,1
T
(3)
P
ref
i
= E
ref
P
W
i
=
h
x
ref
i
,y
ref
i
,z
ref
i
,1
i
T
(4)
P
r
i
= E
r
P
W
i
= [x
r
i
,y
r
i
,z
r
i
,1]
T
(5)
p
ref
i
= I
ref
h
x
ref
i
/z
ref
i
,y
ref
i
/z
ref
i
,1
i
T
(6)
p
r
i
= I
r
[x
r
i
/z
r
i
,y
r
i
/z
r
i
,1]
T
(7)
Finally, to determine the r-th homography matrix
H
r
so that:
p
ref
i
= H
r
p
r
i
i ∈ [1,4] (8)
the procedure described in (Hartley and Zisserman,
2004) is followed. Since surveillance cameras are
fixed, the identification of homograpy matrices H
r
can
be performed entirely offline so that the warping stage
of the HDT pipeline simply warps every acquired im-
age using the corresponding homography and over-
laps the warped images to obtain the combined image,
as shown in Figure 2.
3 HUMAN DETECTION VIA
BG/FG SEGMENTATION
Having warped together all the images acquired by
the different RGB surveillance cameras, it is possi-
ble to perform BG/FG Segmentation on the combined
image in order to detect human beings entering the
robotic cell or walking inside it.
3.1 BG/FG Segmentation Algorithm
The BG/FG Segmentation algorithm adopted in this
work is part of the OpenCV library (Bradski, 2000)
and it is described in (Zivkovic, 2004) and (Zivkovic
and Van Der Heijden, 2006). It consists in an efficient
adaptive algorithm that performs background subtrac-
tion at pixel level and that relies on Gaussian mixture
probability density. It also offers the possibility to
trigger online background update. As shown in Fig-
ure 3, the algorithm’s output consists in two different
images:
• Foreground Mask: binary image whose pixels
are white (black) if the corresponding pixel of
the input image belongs to the foreground (back-
ground);
• Foreground Image: RGB colour image contain-
ing only the foreground pixels. It is obtained by
simply applying the binary mask to the input im-
age.
Moreover the algorithm provides a shadow de-
tection functionality (KaewTraKulPong and Bowden,
2002) that allows to perform object detection while
discarding shadows of segmented objects.
3.2 BG/FG Segmentation
Post-processing
After BG/FG Segmentation, the Foreground Mask is
further processed performing “image opening”, i.e.
applying in sequence an erosion and a dilation ker-
nel (Bradski and Kaehler, 2008). The main advantage
brought by applying image opening to the Foreground
Mask consists in removing image noise (especially
isolated pixels erroneously classified as foreground)
while preserving large foreground areas.
At this point the contours of the connected compo-
nents in the Foreground Mask image are extracted and
a last “plausibility check” is introduced. As a mat-
ter of fact it is reasonable to assume that foreground
areas must be large enough to represent a human be-
ing walking inside the scene. Consequently if a fore-
ground area’s surface (measured in square pixels) is
smaller than an experimentally determined threshold
value, the object is considered a false positive and it
is discarded. Otherwise it is actually classified as a
detected human worker.
4 USING K-d Trees TO UPDATE
DETECTED HUMANS
The main problem related to the output of BG/FG
Segmentation stage is to determine for every fore-
ground area detected at time step i, the corresponding
area inside the foreground image computed at time
step i − 1. As a matter of fact a continuous update
of the contours of the silhouette describing the same
human being across a series of consecutive time in-
stants is fundamental to feed the different particle fil-
ters with coherent information (see Section 5). To
solve this issue the informationregarding detected hu-
mans is structured in k-d trees, but first the following
“plausibility hypotheses” are considered:
• humans cannot suddenly appear inside the robotic
cell or either disappear from it;
• humans can enter/exit the cell only through one or
more access areas (i.e. gates, doors, ecc.);
• it is likely that the position of the same human be-
ing will undergo limited variations from one time
step to the following one.

(a) (b) (c)
Figure 2: Example of multiple camera image fusion. Left: image acquired from camera #01. Middle: image acquired from
camera #02. Right: combined image resulting from image fusion.
(a) (b) (c)
Figure 3: Example of Single Camera BG/FG Segmentation. Left: input image. Middle: foreground mask. Right: foreground
image.
Thanks to these hypotheses the problem of erroneous
robot detection can be easily overcome: even if a
moving industrial robot is detected by BG/FG Seg-
mentation, it won’t be considered as a human being.
While (Bascetta et al., 2011) tackled this problem
by masking out the entire robot’s workspace inside
the Foreground Image, the approach here presented
does not require this further image-processing step
and avoids large parts of the acquired image to be ig-
nored, thus resulting simpler, more efficient and more
effective.
4.1 K-d Trees
A k-d tree (or k-dimensional tree) is a space-
partitioning data structure that allows to organize
points belonging to a k-dimensional space (Moore,
1991) in a binary tree. Considering a variant of k-d
trees, where actual points can be stored only in the
leaf nodes, every non-leaf node represents a splitting
hyperplane that divides the k-d space into two half-
spaces. Points to the left of this hyperplane are repre-
sented by the left subtree of that node and points right
of the hyperplane are represented by the right subtree.
An example of a 2-dimensional tree is shown in Fig-
ure 4.
4.2 Detected Humans’ Update via
Nearest Neighbour Search
Using k-d trees the problem of updating online the
Figure 4: Example of k-d tree where non-leaf nodes repre-
sent splitting hyperplanes and leaf nodes consist in actual
2-dimensional points.
information regarding detected humans can be ele-
gantly formalized as the identification of couples of
nearest neighbours between two different 2-d trees:
one (named
FG previous
) containing the Center-of-
Gravity (CoG) of the human silhouettes detected on
the combined image at the previous time step and an-
other one (named
FG now
) containing the CoG of the
foreground areas segmented at the current time step.
The following pseudo-code explains how this nearest
neighbour search can be performed:
for(f_now in FG_Now)
f_prev := nearest(FG_Previous, f_now)
if f_now == nearest(FG_Now, f_prev)
add (f_prev, f_now) to results
end if
end for
Not only this solution is very elegant, but it is also

very efficient. If we suppose that both sets contain n
elements, the time complexity of building the corre-
sponding 2-d trees and searching for couples of near-
est neighbours is O(n logn), while the time complex-
ity of performing distance checks between every pos-
sible pair of elements would be O(n
2
).
After identifying the couples of nearest neigh-
bours between the two 2-d trees, two last checks are
performed: every foreground area detected near an
entrance zone, but not associated to a previously de-
tected human, is considered as a new human entering
the cell, and every detected human no longer associ-
ated to a foreground area is considered as a person
that left the cell.
5 HUMAN TRACKING VIA
PARTICLE FILTERING
The tracking strategy here adopted is inspired by the
one proposed in (Bascetta et al., 2011). After BG/FG
Segmentation and foreground areas update, human
workers are tracked by a series of particle filters that
rely on a simplified human walking motion model.
The choice of both the motion model and the particle
filtering strategy results from the following assump-
tions:
• the scene consists of a flat ground plane on which
humans walk around;
• a human worker does not walk sideways;
• human workers and industrial robots are the
unique moving objects in the camera field of view,
but, since robots do not enter the scene from the
entrance zones, their detection is automatically
avoided.
5.1 Human Motion Model
A simple and effectiveway of tracking a human being
motion consists in considering his/her volumetric oc-
cupancy. By circumscribing a rectangular box around
a walking person, we are able to describe his/her mo-
tion in terms of translation on the floor and rotation
around the vertical axis crossing the base in its centre
(see Figure 5(a)).
Having fixed on the ground plane a world-base
Cartesian frame, the pose of a human can be com-
pletely described as p = (x, y, θ), where x and y are
the box base coordinate with respect to the world base
frame X-axis and Y-axis respectively and θ is the an-
gle formed between the tangent to the walking path
and the world base frame X-axis.
Finally, according to the assumption that both
the linear velocity v (i.e. the nonholonomic veloc-
ity along the direction of motion) and the angular ve-
locity ω are piece-wise constant, the adopted human
walking dynamic model can be rendered as a slightly
modified version of the unicycle model presented in
(Arechavaleta et al., 2008):
˙x = v cos(θ)
˙y = v sin(θ)
˙
θ = ω
˙v = σ
˙
ω = η
(9)
where σ and η are two independent and uncorre-
lated Gaussian white noises acting respectively on the
linear velocity v and on the angular velocity ω.
5.2 Particle Filtering Strategy
In our scenario deterministic evaluation of the human
motion state is not possible mainly because of signif-
icant measurement noise. Moreover, analytical calcu-
lation of the motion model output in terms of multiple
rectangular boxes (each one projected according to a
single camera point of view) is not feasible.
Consequently, our tracking strategy consists in as-
signing to every detected human a probability distri-
bution over the possible states in the form of a set
weighted particles, propagated in time according to
the motion model presented in Section 5.1. In this
way, for every moving worker, multiple virtual rep-
resentations are generated and his/her motion state is
estimated by selecting the particle whose representa-
tion best matches the measured foreground. At any
time instant i the motion state of a single walking hu-
man being is composed by a set of N particles:
Q
i
=
n
q
( j)
i
| j = 1, . . . ,N
o
(10)
where every particle represents a possible motion
state configuration:
q
( j)
i
=
x
( j)
i
, y
( j)
i
, θ
( j)
i
, v
( j)
i
, ω
( j)
i
(11)
The initial distribution can be considered known
a priori and it corresponds to a scene without mov-
ing workers. Right after instantiation, every filter is
considered “inactive” and its particle set is initialised
via uniform random sampling inside a subspace of the
model state space defined around the entrance areas.
As soon as a new human is detected (see Section 3),
an “inactive” filter is assigned the corresponding fore-
ground area and thus, it becomes “active”.
While receiving continuously updated informa-
tion regarding the foreground area it is tracking (see

(a) (b) (c)
Figure 5: Left: human worker detected silhouette (grey), pose and circumscribed box according to the explained motion
model. Middle: graphic output of a particle motion model state considering a single camera. Right: pixel determining the
particle’s value considering a single camera.
Section 4), the particle filter keeps propagating par-
ticles. Naming f the transfer function corresponding
to the discrete motion model, the particle set propaga-
tion from time step i to time step i+ 1 can be simply
defined as:
Q
i+1
=
n
q
( j)
i+1
= f
q
( j)
i
| j = 1, . . . ,N
o
(12)
The probability that each particle corresponds to the
actual state of the walking human is computed on the
basis of two binary images: the first contains the fore-
ground area describing the human appearance (see
Figure 5(c)), the latter represents the appearance of
the particle itself. The box vertices are computed on
the basis of the particle and projected in every camera
perspective. A binary image is created where non-
zero pixels belong to the superposition of the box pro-
jections (see Figure 5(b)). The probability measure is
finally obtained by counting the number of non-zero
pixels contained in the logic AND of the two binary
images, as depicted in Figure 5(c). After evaluation,
particles probabilities are normalised using their sum
¯
α
i
=
∑
N
j=1
α
( j)
i
as a normalizing factor:
α
( j)
i
:= α
( j)
i
/
¯
α
i
, ∀ j ∈ [1,...,N] (13)
To update the estimate of the human state, a best par-
ticle is extracted from the filter’s particle set. Particles
are sorted in descending order with respect to proba-
bility values and the best particle is computed as the
weighted average of the best n particles (i.e. the first
n particles within the sorted set).
The re-sampling stage realizes a balance between
exploitation and exploration. Particles being the near-
est with respect to the actual state of the walking hu-
man are mixed to new particles obtained via uniform
random sampling inside a subspace of the model state
space defined around the best particle previously ex-
tracted.
Finally, when the tracked human being exits the
supervised environment, the filter goes back to the
“inactive” state and waits until it is assigned another
human to track. The design and implementationof the
filtering stage has been realized so that the number M
Figure 6: The experimental setup comprising the two AXIS
fish-eye surveillance cameras, the PC running the HDT ap-
plication and the Ethernet connection between the different
components. The entrance area is highlighted in yellow and
the two walking paths and the corresponding destination ar-
eas are highlighted respectively in black and grey.
of particle filters running in parallel, the dimension N
of each filter particle set, the number n of particles
to average during best particle extraction and the per-
centage of maintained particles can be configured by
the user prior to the actual execution.
6 EXPERIMENTAL RESULTS
Experimental validation of the proposed HDT ap-
proach has been performed in our laboratory. The ex-
perimental setup depicted in Figure 6 includes three
industrial robots (an ABB IRB140, an ABB FRIDA
prototype robot and a COMAU Smart-Six) and two
AXIS 212 PTZ RGB Network cameras connected via
Ethernet to the PC hosting both the ROS network and
the HDT application. Walking paths and destination
areas have been drawn on the floor in order to provide
ground-truth for the experiments described in the fol-
lowing.
The particle filters’ parametrization adopted dur-
ing the experiments was the following:
• 3 particle filters running in parallel;
• 250 particles composing each particle set;
• best particle extraction via weighted average of
the 1% best particles;
−2 −1.5 −1 −0.5 0 0.5 1 1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
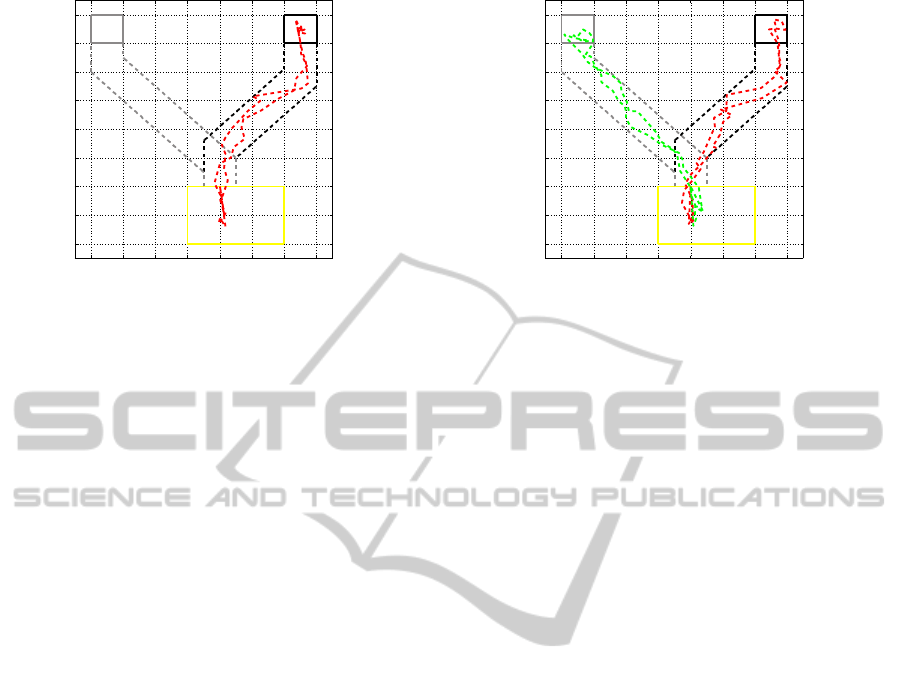
Figure 7: Graph showing that the human position estimate
computed by the HDT System (dashed red) is always in-
cluded inside the path drawn on the ground (dashed black).
• 20% best particles maintained during re-
sampling.
6.1 Experiment #1: Single Person
Detection and Tracking
In the first experiment a human worker enters the
robotic cell and reaches the destination area #1 (the
one coloured in black in Figure 6) following the path
defined by the black dotted lines drawn on the floor.
Considering the drawn black path as ground-truth,
Figure 7 demonstrates the effectiveness of our ap-
proach to HDT by showing that the best particle two-
dimensional position (i.e the human worker trajectory
estimated by the particle filter) is always included in
the area delimited by the black dotted lines.
6.2 Experiment #2: Multiple Person
Detection and Tracking
During the second experiment two human workers en-
ter the robotic cell. The first directs himself towards
destination area #1, following the path drawn in black,
while the latter reaches destination area #2, following
the path defined by grey dotted lines. Figure 8 shows
once again that the trajectories followed by the two
human workers estimated by the particle filters are al-
ways included in the area delimited by the drawn dot-
ted lines.
7 CONCLUSIONS
The paper discusses an approach to Human Detec-
tion and Tracking in a robotic cell. The proposed
solution is characterized by fusion of images coming
from multiple fish-eye RGB surveillance cameras into
a unique image that is fed to a BG/FG Segmentation
−2 −1.5 −1 −0.5 0 0.5 1 1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
Figure 8: Graph showing that the human worker position
estimates computed by the HDT System (dashed red and
dashed green) are always included inside the corresponding
paths drawn on the ground (respectively dashed black and
dashed grey).
algorithm. K-d trees are used to store and update in-
formation regarding detected humans in time. Finally
a series of particle filters, based on a human motion
model, are used to track detected humans. Software
engineering aspects are discussed and experimental
results are presented.
The HDT approach presented in this paper lends
itself to several future developments:
• integration of different kind of sensors (like for in-
stance range finders or RGB-D sensors) that will
possibly allow to exploit more sophisticated kine-
matic models of the human motion;
• integration of fine-grained geometric models of
the manipulators installed inside the cell to com-
pletely mask their motion and definitively avoid
their detection via BG/FG Segmentation;
• development of a suitable interface to directly
send the information computed by HDT to a stan-
dard robot controller.
REFERENCES
Arechavaleta, G., Laumond, J.-P., Hicheur, H., and Berthoz,
A. (2008). An optimality principle governing human
walking. Robotics, IEEE Transactions on, 24(1):5–
14.
Asaula, R., Fontanelli, D., and Palopoli, L. (2010). Safety
provisions for human/robot interactions using stochas-
tic discrete abstractions. In Intelligent Robots and
Systems (IROS), 2010 IEEE/RSJ International Con-
ference on, pages 2175–2180.
Bascetta, L., Ferretti, G., Rocco, P., Ardo, H., Bruyninckx,
H., Demeester, E., and Di Lello, E. (2011). Towards
safe human-robot interaction in robotic cells: An ap-
proach based on visual tracking and intention estima-
tion. In Intelligent Robots and Systems (IROS), 2011

IEEE/RSJ International Conference on, pages 2971–
2978.
Bradski, G. (2000). The OpenCV Library. Dr. Dobb’s Jour-
nal of Software Tools.
Bradski, G. and Kaehler, A. (2008). Learning OpenCV:
Computer Vision with the OpenCV Library. O’Reilly
Media.
Elshafie, M. and Bone, G. (2008). Markerless human track-
ing for industrial environments. In Electrical and
Computer Engineering, 2008. CCECE 2008. Cana-
dian Conference on, pages 001139–001144.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, ISBN: 0521540518, second edition.
KaewTraKulPong, P. and Bowden, R. (2002). An im-
proved adaptive background mixture model for real-
time tracking with shadow detection. In Remagnino,
P., Jones, G., Paragios, N., and Regazzoni, C., edi-
tors, Video-Based Surveillance Systems, pages 135–
144. Springer US.
Kuli´c, D. and Croft, E. (2007). Pre-collision safety strate-
gies for human-robot interaction. Auton. Robots,
22(2):149–164.
Moore, A. (1991). A tutorial on kd-trees. Ex-
tract from PhD Thesis. Available from
http:
//www.ri.cmu.edu/pub_files/pub1/moore_
andrew_1991_1/moore_andrew_1991_1.pdf
.
Mosberger, R. and Andreasson, H. (2013). An inexpen-
sive monocular vision system for tracking humans in
industrial environments. In Robotics and Automa-
tion (ICRA), 2013 IEEE International Conference on,
pages 5850–5857.
Mosberger, R., Andreasson, H., and Lilienthal, A. (2013).
Multi-human tracking using high-visibility clothing
for industrial safety. In Intelligent Robots and Systems
(IROS), 2013 IEEE/RSJ International Conference on,
pages 638–644.
Munaro, M., Basso, F., and Menegatti, E. (2012). Tracking
people within groups with rgb-d data. In Intelligent
Robots and Systems (IROS), 2012 IEEE/RSJ Interna-
tional Conference on, pages 2101–2107.
Munaro, M., Lewis, C., Chambers, D., Hvass, P., and
Menegatti, E. (2013). Rgb-d human detection and
tracking for industrial environments. In 13th Interna-
tional Conference on Intelligent Autonomous Systems
(IAS-13). accepted.
Najmaei, N., Kermani, M., and Al-Lawati, M. (2011).
A new sensory system for modeling and track-
ing humans within industrial work cells. Instru-
mentation and Measurement, IEEE Transactions on,
60(4):1227–1236.
Rogez, G., Orrite, C., Guerrero, J., and Torr, P. H.
(2014). Exploiting projective geometry for view-
invariant monocular human motion analysis in man-
made environments. Computer Vision and Image Un-
derstanding, 120(0):126 – 140.
Zivkovic, Z. (2004). Improved adaptive gaussian mixture
model for background subtraction. In Pattern Recog-
nition, 2004. ICPR 2004. Proceedings of the 17th In-
ternational Conference on, volume 2, pages 28–31
Vol.2.
Zivkovic, Z. and Van Der Heijden, F. (2006). Efficient
adaptive density estimation per image pixel for the
task of background subtraction. Pattern Recogn. Lett.,
27(7):773–780.
