
The Effective Radius and Resistance to Slippage
Pavel Dzitac
1
, Abdul Md Mazid
2
, Guy Littlefair
1
and Ashwin Polishetty
1
1
School of Engineering, Deakin University, Geelong, Australia
2
School of Engineering and Technology, Central Queensland University, Rockhampton, Australia
Keywords: Gripper Design, Slippage Control, Manipulation Reliability.
Abstract: This work reveals that parallel gripper flat-jaw configuration affects grasping effectiveness. An important
finding is the fact that object grasp reliability is influenced significantly by gripper’s ability to develop high
resistance to object rotation in the gripper. The concept of effective torque radius, which increases resistance
to object rotation in the gripper, is presented here and can be extrapolated to other grasping devices and
grasping strategies to improve their reliability and make them more effective. Grippers with full-jaw contact
surface and those with discrete contact areas have been investigated using simple experimental setups.
Essential mathematical models needed for analytical investigation, based on simple mechanics for full-jaw
contact surfaces and discrete-jaw contact surfaces, are presented. These may be useful for gripper jaw
design purposes.
1 INTRODUCTION
Robotic parallel grippers, used in many real-life
applications have to grasp and manipulate a variety
of small and large objects safely.
An important requirement in safe object grasping
and manipulation is reliability, which can be
assessed via some quality measures (Chinellato et
al., 2004; Morales et al., 2004). There are many
possible views as to what constitutes “reliable”
object grasping and manipulation (Chinellato et al.,
2004; Morales et al., 2004; Flanagan et al., 2004;
Diankov et al., 2009; Ciocarlie et al., 2010).
There are also many factors that influence object
manipulation reliability (Dzitac and Mazid, 2013);
the configuration of gripper jaws is one of them. As
a result of correct gripper jaw configuration it is also
possible to reduce the required grasp forces and
therefore the energy necessary to grasp and
manipulate an object.
This paper uses a paralle gripper to show how a
flat gripper jaw design and its object grasping
strategy can be modified and to increase resistance
to object slippage by increasing griper’s resistance to
object rotation in the gripper. These concepts are
applicable to most robotic grasping devices.
2 ANALISYS
It is known from automotive disk braking
technology used in modern vehicles that the
effective torque radius
of the brake pads, together
with the coefficient of friction µ between the brake
pads and brake disk, and the normal force F applied
to the brake pads determine the braking torque
capacity T of the braking system (Budynas and
Nisbett, 2006).
μ
(1)
The effective torque radius
of a brake pad is
given by
1
2
(2)
Where,
is the outside radius of the brake pad and
is the inside radius of the brake pad relative to the
axis of rotation of the brake disk (Budynas and
Nisbett, 2006).
Equation 1 implies that a parallel gripper with
longer jaws has a higher torque capacity than a
parallel gripper with short jaws due to a larger
effective torque radius
.
For a flat parallel gripper that is grasping a flat
object, the effective torque radius
can be
estimated as
396
Dzitac P., Mazid A., Littlefair G. and Polishetty A..
The Effective Radius and Resistance to Slippage.
DOI: 10.5220/0005048103960401
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 396-401
ISBN: 978-989-758-040-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
1
2
2
0
4
(3)
Where, L is the gripper jaw length.
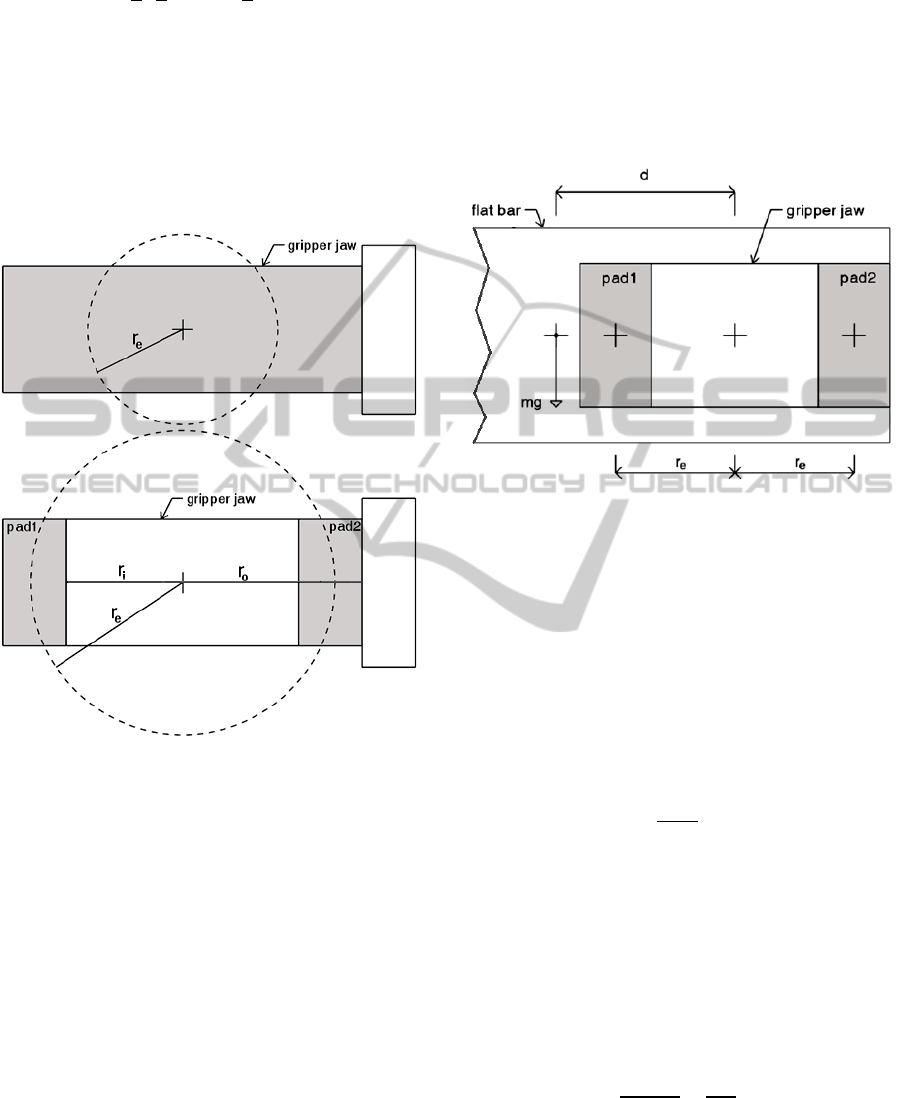
The flat jaws of a parallel gripper have been
modified to contain discrete grasp surfaces referred
to as “pads” in this paper, and used to test their
influence on the effective torque radius as shown in
Figure 1. The pads are formed by machining a recess
at the centre of the gripper jaw contact surface such
that only the pads are in contact with the object.
Figure 1: Comparison of effective torque radius
for a
gripper with full jaw contact surface and a gripper with
discrete pad contact areas.
Notice that for the same gripper jaw length, the
gripper with discrete pad contact areas has a larger
effective torque radius
than the gripper with full
jaw contact surface. In this jaw design the effective
torque radius can be increased by increasing the
distance from the centre of the jaw to the centre of
the pad. Equation 1 can be used to estimate the
torque radius
of the jaw with pads shown
schematically in Figure 1 (bottom sketch).
The following analysis attempts to show that the
choice of grasp point locations influences not only
the object stability during object manipulation but
also the grasp force required.
For simplicity the parallel gripper with pads is
used to explain this concept. The sketch in Figure 2
shows the parallel gripper with pads holding a flat
bar in horizontal orientation. The force, mg, at the
centre of the flat bar develops a moment
at the
centre of the gripper that is given by
(4)
Where, m is the mass of the flat bar, g is the
gravitational acceleration and d is the distance from
the centre of gravity of the flat bar to the centre of
the gripper jaw.
Figure 2: Gripper jaws fitted with pads holding a flat bar.
Each of the gripper jaws must develop equal and
opposing moments in order to keep the flat bar from
rotating in the gripper jaws, plus additional reaction
forces necessary at each pad to support a share of the
flat bar weight.
The required minimum opposing moment at the
gripper
is given by
2
(5)
Where,
is the force couple necessary to counteract
the moment
, and is given by
2
(6)
Note that the gripper has two opposing jaws that
develop friction reaction forces on two independent
flat bar surfaces and therefore each gripper jaw has
to develop only sufficient reaction forces to support
half of the weight of the flat bar.
For clarity, the analysis is done on one jaw only
and therefore only half of the actual applied force to
the gripper is used in the analysis. As a result each
pad has to develop a reaction force
given by
0.5
2
4
(7)
Figure 3 shows the free body diagram of the gripper
in Figure 2. The forces acting on one gripper jaw are
the moment M
, the weight of the flat bar
supported by one jaw (mg/2), and the reaction forces
TheEffectiveRadiusandResistancetoSlippage
397

(force couple F
c
and the reaction force F
mg
at each
pad supporting the weight of the flat bar).
Figure 3: Free body diagram of gripper with pads.
The net reaction forces,
at gripper “pad1”
and
at gripper “pad2” respectively, are given by
2
4
(8)
2
4
(9)
It can be seen from Equations 8 and 9 that the
required reaction force at “pad1” is greater than that
at “pad2” by mg/2.
Considering this fact, it is expected that slippage
and therefore loss of grasp control is most likely to
occur at “pad1” first, even though the same grasp
force is applied to both gripper pads. The expected
behaviour has been tested by gradually decreasing
the grasp force on the flat bar until slippage is
noticed. It has been confirmed that for the grasp
configuration shown in Figure 2, slippage starts at
“pad1” first.
It can therefore be concluded that holding a flat
bar with the gripper in horizontal orientation is not
an optimum solution. However, most common
object grasping and manipulation in industry, using
parallel grippers, is done this way.
The minimum static gripper force F
s
that needs
to be applied to the gripper in Figure 2 to prevent
slippage at “pad1” is given by
μ
(10)
Where, µ
s
is the static coefficient of friction between
the gripper pads and the flat bar.
A different gripper configuration is presented in
Figure 4. In this configuration the gripper jaws are
still the same as in the previous design, but in this
case the jaws are in vertical orientation relative to
the flat bar.
Figure 4: Gripper with vertical jaws.
Figure 5 shows the free body diagram of the
gripper with vertical jaws from Figure 4. The forces
acting on one jaw of the gripper are the moment
, the weight of the flat bar supported by one
jaw (mg/2), and the reaction forces (force couple F
c
and the reaction force F
mg
at each pad supporting the
weight of the flat bar).
Figure 5: Free body diagram of gripper with vertical jaws.
In this configuration the force mg/2 acts equally
through both gripper pads. The force couple also
acts through the gripper pads as before, resulting in
equal forces being applied to both. The resultant
reaction vectors
and
at the two gripper pads
are shown in Figure 6 and are given by
(11)
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
398

/
(12)
Figure 6: Resultant vectors F
r1
and F
r2.
In this gripper configuration the forces on the
object are smaller and equal at both pads. This
means that the gripper has to apply a smaller overall
grasp force to hold the object successfully, which in
turn means that a fragile object can be held safer in
this gripper configuration. Consequently this gripper
requires less energy and has a longer useful life.
To help illustrate the concept of effective torque
radius only static analysis has been used in this
paper. However, for a moving gripper, dynamic
forces must be considered. Although not discussed
here in detail, the dynamic force components acting
on the gripper are given below with respect to
gripper coordinates x, y, z (Figure 4).
The F
x
component acts along the x axis and
tends to pull the object out of the robot gripper;
The F
y
component acts along the y axis to
“wedge” the gripper open;
The F
z
component acts along the z axis and
produces object rotation tendency at the centre
of the gripper.
(13)
Where, α is the “altitude” angle from the XY plane
and β is the “azimuth” angle from the XZ plane, at
which the gripper acceleration vector a acts (XYZ
are world coordinates).
sin
cos
cos
cos
(14)
Where, ϕ is the angle of the gripper when gripper is
rotated around X world coordinate, θ is the angle
when gripper is rotated around the Y world
coordinate, and w is the horizontal width of the
gripper in Figure 4.
cos
sin
cos
2
cos
sin
4
(15)
Note that F
x
and F
z
combine into a larger net
resultant force F
R
acting in the xz plane, and is given
by
(16)
For reliable object manipulation the gripper must
develop a reaction force equal to or greater than the
largest force that pulls the object out of the gripper
or acts to “wedge” the gripper open.
The experiments and observations in this project
indicate that higher resistance to object rotation in
the gripper contributes to object manipulation
reliability.
However the benefits of improved gripper
mechanical ability can only be maximised when
used in conjunction with adequate manipulator
intelligence, which is necessary to make better grasp
decisions and manipulate the object in such a way as
to avoid gripper weaknesses, while making the most
of its strengths.
3 EXPERIMENTATION AND
RESULTS
To test the above described concept, a flat disk made
of Acetal has been grasped using a spring-loaded
parallel gripper, equipped with flat jaws made also
of Acetal. Two pairs of flat jaws of different sizes
are illustrated in Figure 7. The experimental setup is
illustrated in Figures 8 and 9. The experimentation
carried out in this section is not aimed at high
accuracy results but rather to demonstrate the
difference in the effective torque of short flat jaws
compared to long flat jaws.
Figure 7: Short and long flat jaws made of Acetal.
TheEffectiveRadiusandResistancetoSlippage
399

The experiment with short flat jaws, as shown in
Figure 8, has been carried out as follows:
The 50mm long jaws were mounted on the
gripper plates (either side of the 86mm disk)
and clamped using a centre screw, spring,
washer and force adjustment nut.
The spring compression required to produce a
force of approximately 70N has been
determined by compressing the spring on
calibrated digital scales and measuring the
compressed spring length that produced 70N.
The spring compression has then been
replicated on the gripper setup by adjusting the
nut until approximately the same spring
compression has been achieved.
The disc has been rotated by applying a
tangential force to the disc using a force gauge
and a string attached to the disk such as to
maintain the axis of rotation of the disk at the
centre of the jaws.
The force required to cause the disk to slip has
been recorded five times and an average has
been calculated and recorded in Table 1.
Figure 8: Spring-loaded gripper with 50mm flat jaws.
The same experimental procedure has been
followed for the experiment in Figure 9, except that
in this case the long jaws were used instead of the
short ones.
It has been noticed that for the same clamping
force, a slightly larger force is required to cause disk
slippage when it is held in the gripper fitted with
long jaws than when it is held in the gripper fitted
with short jaws.
Figure 9: Spring-loaded gripper with 80mm jaws (flat side
is gripping the disc).
The experimental results are summarised in Table 1.
Both, the short and long jaws used for
experimentation had approximately the same total
contact surface area.
Table 1: Effective torque radius experiment – short and
long gripper jaws without pads.
Jaw
length
(mm)
Effective
radius
(mm)
Force
applic.
radius
(mm)
Clamp
force
(N)
Average slip
force (N)
50 25 43 70 7.1
80 40 43 70 10.3
The results in Table 1 agree with the concept of
effective torque radius (Budynas and Nisbett, 2006),
which is influenced more by how the contact area is
distributed rather that the size of the contact surface
area.
In both cases the inside radius r
i
is assumed to be
equal to 0mm and therefore the effective torque
radius is assumed to depend only on the outside
radius r
o
of the jaw, which in turn is assumed to be
equivalent to half of the jaw length.
It is also assumed that the applied grasp force is
evenly distributed at each of the two gripper jaws.
To test the gripper pad principle the long jaws were
machined such as to obtain two discrete pads on
each jaw as shown in Figure 10.
Figure 10: Long jaws with pads.
The same experimental procedure has also been
carried out for the long jaws with pads as that
described for Figure 9, except the jaw pads were
now gripping the disk as shown in Figure 11.
Figure 11: Spring-loaded gripper jaws with the pads
gripping the disc.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
400

Five samples of pull forces necessary to cause disk
slippage in gripper jaws with pads were averaged
and recorded in Table 2.
The additional pull force required to cause disk
slippage is significantly larger, which confirms that
jaws with discrete peripheral pads result in a larger
effective torque radius r
e
than flat jaws without
peripheral pads.
Table 2: Effective torque radius experiment – long flat
gripper jaws with pads.
Jaw
length
(mm)
Effective
radius
(mm)
Force
applic.
radius
(mm)
Clamp
force
(N)
Average slip
force (N)
80 30 43 70 16.9
Just like in the previous experiments, the
experimentation carried out here is not aimed at high
accuracy results but rather to highlight the difference
in the effective torque radius of jaws with pads
compared to jaws without pads.
4 CONCLUSION AND FUTURE
WORK
While performing object grasping and manipulation
experiments it was noticed that object manipulation
reliability was influenced significantly by the ability
of a parallel gripper to develop optimum reaction
forces at all grasp points. It was found that this
ability was dependent on the ability to resist object
rotation in the gripper, which in turn was dependent
on the gripper design and the locations of grasp
points on the grasped object.
Equal load sharing by all grasp points resulted in
higher resistance to slippage. When one grasp point
was holding a higher share of the load it was more
likely to slip during manipulation.
A modified gripper jaw design and grasping
strategy that together offered a higher resistance to
object rotation in the gripper and minimised the
required grasp forces was also proposed.
It is believed that the concept of effective torque
radius presented here can be extrapolated to other
gripper types and grasping strategies to improve
their reliability and effectiveness.
The concepts in this paper are applicable to most
object grasping devices that create contact points
with the object, including multi-finger humanoid
hands.
Future work can be done to develop designs and
grasping strategies for multi-finger robotic grasping
devices that would increase their resistance to object
rotation and therefore minimise the effect of
torsional forces at the object-gripper interface that
contribute to object slippage.
REFERENCES
Chinellato, E., Morales, A., Fisher, R.B., del Pobil, A.P.,
2004. Visual quality measures for characterizing
planar robot grasps. In IEEE Trans. Systems, Man and
Cybernetics - Part C: Applications and Reviews, pp.
30–41.
Morales, A., Chinellato, E., Fagg, A.H., del Pobil, A.,
2004. Using experience for assessing grasp reliability.
In International Journal of Humanoid Robotics, vol. 1,
no. 4, pp. 671–691.
Flanagan, J.R., King, S., Wolpert, D.M., Johansson, R.S.,
2001, Sensorimotor prediction and memory in object
manipulation. In Canadian Journal of Experimental
Psychology, no. 55, vol. 2, pp. 87 - 95.
Diankov, R., Kanade, T., Kuffner, J., 2009. Integrating
grasp planning and visual feedback for reliable
manipulation. In IEEE/RAS International Conference
on Humanoid Robots (Humanoids), pp. 646–652.
Ciocarlie, M., Hsiao, K., Jones, E. G., Chitta, S., Rusu, R.
B., Sucan, I. A., 2010, Towards reliable grasping and
manipulation in household environments. In
International Symposium on Experimental Robotics,
New Delhi, India, pp. 241-252.
Dzitac, P., Mazid, A. M., 2013. Factors that influence
reliable object manipulation. In Proceedings of the
IEEE Industrial Electronics and Applications
International Conference (ICIEA), Melbourne,
Australia, pp. 1468-1473.
Budynas R. G., Nisbett, J.K., 2006. Shigley's Mechanical
Engineering Design (8th Ed.), McGraw-Hill, pp. 826-
829.
TheEffectiveRadiusandResistancetoSlippage
401
