Automated Segmentation of Folk Songs

Using Artificial Neural Networks

Andreas Neocleous

1,2

, Nicolai Petkov

and Christos N. Schizas

Department of Computer Science, University of Cyprus, 1 University Avenue, 2109 Nicosia, Cyprus

Johann Bernoulli Institute for Mathematics and Computer Science, University of Groningen, Groningen, The Netherlands

Keywords: Audio Thumbnailing, Singal Processing, Computational Intelligence.

Abstract: Two different systems are introduced, that perform automated audio annotation and segmentation of Cypriot

folk songs into meaningful musical information. The first system consists of three artificial neural networks

(ANNs) using timbre low-level features. The output of the three networks is classifying an unknown song as

“monophonic” or “polyphonic”. The second system employs one ANN using the same feature set. This

system takes as input a polyphonic song and it identifies the boundaries of the instrumental and vocal parts.

For the classification of the “monophonic – polyphonic”, a precision of 0.88 and a recall of 0.78 has been

achieved. For the classification of the “vocal – instrumental” a precision of 0.85 and recall of 0.83 has been

achieved. From the obtained results we concluded that the timbre low-level features were able to capture the

characteristics of the audio signals. Also, that the specific ANN structures were suitable for the specific

classification problem and outperformed classical statistical methods.

1 INTRODUCTION

The automatic annotation of a musical piece is an

important subject in the field of computational

musicology. The annotation of a musical piece

indicates interesting and important musical events.

Such events include the start and the end positions of

a note, the start and the end positions of a part in

which a singing voice is present, the repetitions of a

melody and others. This procedure is often called

audio thumb-nailing.

The main melody of a song is usually located

where a singing voice is present. The knowledge of

the position of a song that contains the main melody

can give insights in the structure of the song and it is

a starting point for further analysis and study. It is

also desirable to detect the part in a song where only

instruments are performing and no vocal singing is

present. This can be considered a classification task

of two classes. One class is the “vocal” where a

singing voice is performing and the other is the

“instrumental” where only instruments are

performing. Several methods that tend to solve

similar classification problems have been proposed

in the past by Lu et al (Lu, Zhang, Li, 2003),

Scheirer and Slaney (Scheirer and Slaney, 1997),

Fuhrmann et al (Fuhrmann, Herrera and Serra, 2009)

and Vembu and Baumann (Vembu and Baumann,

2005). Panagiotakis and Tziritas (Panagiotakis and

Tziritas 2004) propose a speech/music discriminator

based on the Root Mean Square (RMS) and the zero

crossing rates (ZCR). For the classification they

employ a set of rules such as void interval

frequencies between consecutive frames,

information gathered by the product between RMS

and ZCR, the probability of no zero crossings etc.

Another common approach is the extraction of

features from a training set that was previously

annotated with the desired classes and the

application of standard machine learning techniques.

In the work of Pfeiffer et al, (Pfeiffer, Fischer and

Effelsberg, 1996) perceptual features such as

loudness or pitch were taken into account in their

experiments. They claim that these features play a

semantic role for the performance of their

classifications and the audio content analysis.

Experiments with additional features rather than

using only the RMS and the ZCR were also

introduced by Scheirer et al and Slaney (Scheirer

and Slaney, 1997).

The latest publication and the most relevant to our

work, is found in literature by Bonjyotsna and

Bhuyan (Bonjyotsna and Bhuyan, 2014). They

144

Neocleous A., Petkov N. and N. Schizas C..

Automated Segmentation of Folk Songs Using Artiﬁcial Neural Networks.

DOI: 10.5220/0005049101440151

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 144-151

ISBN: 978-989-758-054-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

suggest as main feature the Mel-Frequency Cepstral

Coefficients (MFCC) for the classification of

vocal/instrumental parts applied in the

MUSCONTENT database. Three machine learning

techniques were used for the classification: Gaussian

Mixture Model (GMM), Artificial Neural Network

(ANN) with Feed Forward Backpropagation

algorithm and Learning Vector Quantization (LVQ).

From their results, they claim that LVQ yields the

higher accuracy in the classification. More precisely,

they report 77% classification accuracy for the

ANNs, 77.6% for the LVQ and 60.24% for the

GMM. In our work, we included additional low-

level features and we achieved higher accuracy by

modeling our data with ANN.

In this paper, we introduce a two-stage approach

for (a) the classification of an unknown song into

“monophonic” or “polyphonic” and (b) the

segmentation of a polyphonic song into positions of

interest. Such positions include the boundaries of a

part in a song that only instruments are performing

and no vocal singing is present. We used low-level

timbre features and we built trained artificial neural

networks that are able to discriminate and predict

with high accuracy the unknown songs as

“monophonic” or “polyphonic” and polyphonic

music as “vocal” or “instrumental”.

The main contribution of our work is the use of

ANNs and their application in audio thumb-nailing.

This use has numerous advantages in wide range of

applications (Benediktsson, J., et. al., 1990). The

ability of the adaptation of complex nonlinear

relationships between variables arises from the

imitation of the biological function of the human

brain. Disadvantages include the greater time of

training, and the empirical nature of model

development. The authors have demonstrated how

the disadvantages can be minimized in a wide area

of applications including medicine (Neocleous C.C.,

et. al. 2011).

While the interest of the MIR community on the

audio thumb-nailing focused in popular music, little

work has been done for folk music. Main differences

between popular music and folk music include the

western/non-western instrumentation as well as

fundamental rules in music theory. For instance, the

use of traditional instruments in folk music, create a

significantly different sound in comparison to the

popular music. One common feature of the folk

music is the monophonic performances. These can

be either using a musical instrument or only with

singing voice. Our contribution with a classification

system of a song into “monophonic” or

“polyphonic” is reported in this paper.

We compare our results with two other methods,

named Support Vector Machines and the statistical

Bayesian Classification.

2 METHODS

2.1 Overview

The database we used contains audio signals of 98

Cypriot folk songs. Each audio signal has been

extracted from original cd’s and it has been encoded

with a sampling frequency of 44100 Hz and 16 bit

amplitude. The sampling frequency of 44100 Hz and

the amplitude of 16 bit is the quality that is typically

used in the audio cd’s.

From this database, we isolated 24 songs for

creating a training set while the remaining 74 songs

were used for validation of our system. In the

training set, 17 monophonic songs and 7 polyphonic

songs were chosen. The monophonic songs were 6

vocal songs sung by male performers, 6 vocal songs

sung by female performers and 5 songs performed

with the traditional Cypriot instrument called

“pithkiavli”.

The main idea of our method is illustrated in

Figure 1. The first system takes as input an unknown

song and predicts if it is monophonic or polyphonic.

The second system takes a polyphonic song and

predicts the boundaries of parts of the song that only

instruments are performing (instrumental parts) and

parts in which a singing voice is present (vocal

parts).

Each audio signal was segmented into a sequence

of overlapping audio frames of length 2048 samples

(46 ms) overlapping by 512 samples (12 ms). For

each of these audio frames we extracted the

following audio features: Zero Crossing Rate,

Spectral Centroid, MFCC (13 coefficients). For the

first system the mean and the standard deviation

values of each feature are calculated and are used to

build three feed-forward ANNs. Each of them has 20

neurons in the hidden layer and was trained for 200

epochs. The ANNs were built using monophonic

songs for the first class and polyphonic songs for the

second class. The difference between the three

ANNs is that the instrument that is performing in the

monophonic songs is different for each network.

This system classifies an unknown song into the

class “monophonic” or “polyphonic”. Both systems

1 and 2 require audio frame segmentation and

feature extraction.

For the second system, the entire feature vectors

were used to build one ANN that predicts a value in

AutomatedSegmentationofFolkSongsUsingArtificialNeuralNetworks

145

Figure 1: (a) System 1 takes as an input an unknown song

and classifies the song as “monophonic” or “polyphonic”.

(b) System 2 takes as an input a polyphonic song and

segments it into “vocal” and “instrumental” parts.

the range between 0 and 1 for every audio frame.

The output is then quantified with a threshold to the

binary values 0 or 1. The value 0 corresponds to a

frame from a purely instrumental part. The output is

1 if vocal singing is present in the frame. We use

this system to annotate the instrumental and the

vocal parts in a song.

2.2 Neural Network

Many different ANN structures had been proposed

and used by researchers in different fields. The most

common and widely used for classification,

generalization, and prediction is the commonly

known fully connected multilayer feed forward

structure (FCMLFF). Mathematically this is

represented by equation 1 as:























][

][][][

wyfy

(1)

where,

][L

is the output value of each neuron

layer L that has a total of

neurons.

Typically, this function has a squashing

function form such as the logistic or the

hyperbolic tangent.

,1

is the set of weights associating neurons in

layer L-1 to neurons in layer L.

Once the ANN is decided, an effective training

and tuning procedure needs to be implemented, so

that the network will achieve a useful capability for

doing the desired task, such as classification,

generalization, recognition etc. Many training

procedures had been proposed and are available for

implementation. The most widely used for feed

forward networks is the backpropagation algorithm

(Werbos, 1974). In this work, we implemented fully

connected feed-forward neural networks with

backpropagation learning.

2.3 Feature Selection

Twenty-four songs were selected to form a training

set to be used in the artificial neural network

classifier. The training set was chosen in such a way

that all the musical instruments that were of our

interest for classifying them were present. The

positions of the vocal parts and the instrumental

parts were manually annotated to the training data

and a set of low-level timbre features were extracted

for each class respectively. Specifically, the features

extracted were the Zero Crossing Rate, Spectral

Centroid, Spectral Spread and 13 coefficients of

MFCC, thus creating a feature set of 16 features in

total. We applied a statistical analysis to the features

and from the results we assume that this set of

features is considered to be suitable for solving the

particular classification problem.

2.3.1 Zero Crossing Rate

The feature Zero Crossing Rate (Benjamin 1986) is

a measure on how many times does the waveform

crosses the value of zero within a frame:













)](sgn[)1(sgn[

)1(2

nxnx

ZCR

(2)

Where:

)(nX

: is the discrete audio signal, n=1…N

sgn[.]: is a sign function.

The ZCR is a powerful feature for identifying

noisy signals. It is also used as a main feature for

fundamental frequency detection algorithms (Roads

1996).

2.3.2 Spectral Centroid

The feature Spectral Centroid it is the geometric

center of the distribution of the spectrum and is a

measure of the spectral tendency of a random

variable x. It is a useful feature for classification

problems such as instrument identification or the

separation of audio signals into speech/music. It is

defined as:



 dxxxf )(



(3)

Where:

x: is a random variable

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

146

f(x): is the probability distribution of the random

variable x characterized by that distribution.

2.3.3 Spectral Spread

The feature Spectral Spread it is defined in eq. 4 and

it is essentially the standard deviation of the

spectrum. It describes how much energy is

distributed by the frequencies across the spectrum.

dxxfx )()(





(4)

2.3.4 Mel Frequency Cepstral Coefficients

(Mfcc)

The feature MFCC (Mermelstein 1976) describes

the timbre characteristics of an audio file within a

number of coefficients. Usually the number of the

coefficients taken into account is 13. The

computation of the MFCCs is as follow: first the

spectrum of a framed windowed excerpt audio signal

is computed using the Fast Fourier Transformation

(FFT). The result from the FFT is then mapped into

13 Mel bands using triangular overlapping windows.

The cosine transformation is applied to the logarithm

of each one of those Mel bands. The results of each

transformation for every band are considered to be

the MFCC coefficients. The mapping of the

spectrum from the linear scale to the Mel scale is

done in order to approximate the functionality of the

human auditory system where, in one of its

processes it separates the perceived sound into non-

linear frequency bands. The most popular formula

for converting the frequencies from hertz to Mel is

described below:















700

1log2595

mel

(5)

Where:

f: is the frequency in Hertz.

The mel scale has been proposed by Stevens et al

in 1937 (Stevens, Volkman and Newman, 1937) and

the name comes from the word melody. It is pointed

that the MFCC features are widely used in speech

processing and are considered to be a powerful

feature for describing timbre characteristics. They

carry most of the spectral information within 13

coefficients, in contrast with the row spectrum that

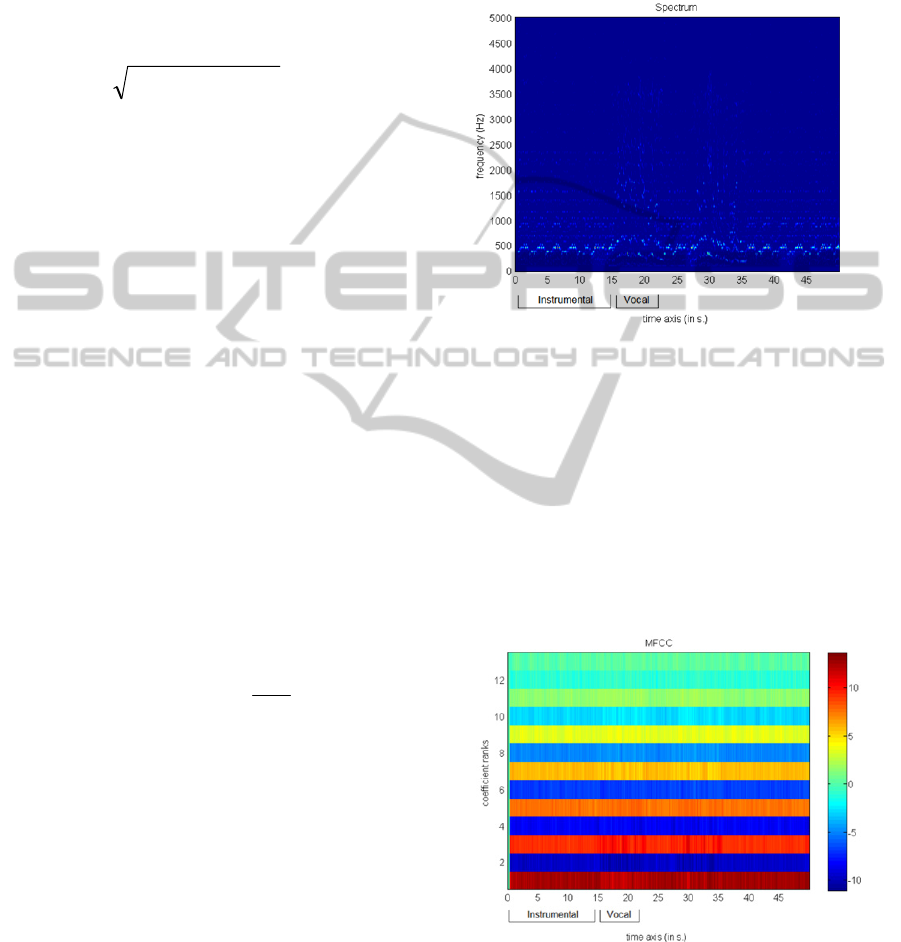
has at least 5000 frequency values. In Figure 2 we

present an example of the spectrogram of a

polyphonic song for an excerpt of 50 seconds. In this

case, there are three positions where only

instruments are performing, and two positions where

the singing voice is also performing together with

the instruments. The first parts of the instrumental

and the singing voice are annotated in the same

Figure, on the lower plot. It is rather obvious that the

distribution of the energy across the spectrum for the

two classes “vocal” and “instrumental” is different.

Figure 2: Spectrogram of a polyphonic song. The first 15

seconds in this figure are being performed with

instruments. The position from the 15

to 20

second is

performed with singing voice together with instruments. It

is shown that the distribution of the energy across

frequencies between the two positions “instrumental” and

“vocal” significantly differ.

Figure 3 shows the 13 coefficients of the MFCC

features for the same excerpt of the same song. It is

also clear that the MFCC in the instrumental part

have higher values with respect to the part of a

singing voice.

Figure 3: The 13 coefficients of MFFCs versus time. The

“instrumental” and the “vocal” parts are annotated

manually in the lower plot.

2.4 Statistical Analysis

In an attempt to visualize the data and to understand

AutomatedSegmentationofFolkSongsUsingArtificialNeuralNetworks

147

better the contribution of each feature to the

performance of the system, we applied statistical

methods and we report our results in this section. In

this analysis we are concerned to explore how

significant is the difference between the values of a

given feature for the two classes “instrumental” and

“vocal”. Our null hypothesis is that the median of

the data in class “instrumental” is equal with the

median of the data in class “vocal”.

Several methods exist for testing a statistical

hypothesis, such as z-test, t-test, Chi-squared test,

Wilcoxon signed-rank test and others. The t-test is

the most widely used method for testing significant

differences between two populations whose size is

less than 30 (Mankiewicz, R., 2004). It assumes that

the distribution of the two populations being

compared is normal. In our case, not all features we

used are following a normal distribution. More

precisely, the features Zero Crossing Rate, Spectral

Centroid and Spectral Spread did not follow a

normal distribution for any of the two classes. These

features were tested with the Wilcoxon signed-rank

test (Siegel, 1956). The 13 coefficients of the MFFC

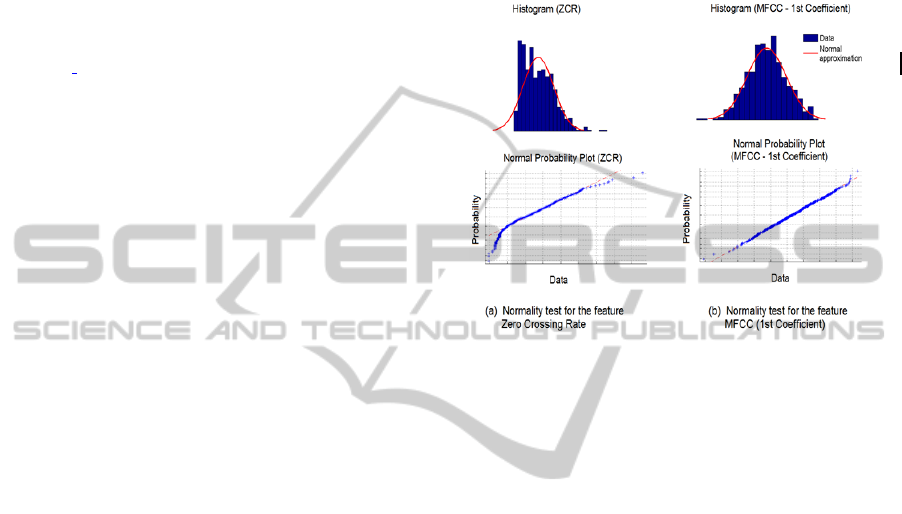
were following a normal distribution. The normality

of each distribution was tested with a graphical

method and with the Kolmogorov-Smirnov test

(Stephens, 1974). For the graphical method we used

a normal probability plot. In order to get such plot,

first the histogram of the data is approximated with a

normal distribution.

In the normal probability plot, the probability

distribution follows a normal distribution and it is

plotted against the unknown distribution of the data.

If the data follow a normal distribution, the function

of the normal probability plot will be a straight line.

If the normal probability plot does not fit to a

straight line, it is an indication that the distribution

of the data does not follow a normal distribution. In

Figure 4 we present an example of this method for

the features (a) Zero Crossing Rate and (b) MFCC of

the first coefficient.

In Figure 4a the upper plot shows with blue color

the distribution of the feature ZCR and with red

color the normal approximation. From this plot it is

obvious that the normal distribution cannot model

the distribution of the data. This is also observable

from the normal probability plot in the lower plot. In

Figure 4b we present an example where the

distribution of the data of the feature MFCC can be

modeled with a normal distribution.

The Wilcoxon signed-rank test is a non-

parametric method for testing the significance of the

difference between two populations. This method

does not assume that the distribution of the

populations is normal. We used this method for

testing the features that did not have normal

distribution. For the 13 MFFC coefficients we used

the t-test. Both the t-test and the Wilcoxon signed-

rank test rejected the null hypothesis that the two

populations are not different for all the features we

used.

Figure 4: Normality test for the features (a) ZCR and (b)

MFCC. In the upper plot, the histogram of every feature is

plotted together with the approximation with a normal

distribution. Lower plot shows the normal probability

plots.

2.5 Classification into “Monophonic”

or “Polyphonic”

For the classification into the two classes

“monophonic” or “polyphonic” we built three ANN

using the mean and the standard deviation of each

feature. In total, 32 features were used to train the

ANNs. The first ANN is called “male vocal –

polyphonic” and is trained with 720 seconds of

monophonic male singing performances which form

the first class and 115 seconds of polyphonic music

which form the second class. The second ANN is

called “female vocal – polyphonic” and is trained

with 720 seconds of monophonic female singing

performances (1st class) and the same 115 seconds

of polyphonic music (2nd class). The third ANN is

called “pithkiavli – polyphonic” and is trained with

600 seconds of monophonic performances by the

instrument “pithkiavli” (1st class) and 115 seconds

of polyphonic music (2nd class). The output target

for the polyphonic music was set to 1 and the output

target for the class “female vocal”, “male vocal” and

“pithkiavli” was set to 0.

The classification is done with the following

procedure: an unknown song is represented

numerically by a vector of 32 that is fed to the three

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

148

ANN “male vocal - polyphonic”, “female vocal -

polyphonic” and “pithkiavli - polyphonic”. We

quantize the outputs of the models to 0 or 1 by using

a threshold of 0.5. We classified a song as

“monophonic” if the binary output of at least two

models is 0; otherwise the song is classified as

“polyphonic”.

2.6 Classification into “Vocal” or

“Instrumental”

The fourth ANN was built using all feature vectors

that were extracted for all audio frames. The output

target was added to the database after a manual

segmentation of the training set into the “vocal” and

“instrumental” positions. For every audio frame of a

song the ANN gives a prediction value in the range

0 or 1. One example of the output of the ANN is

shown in Figure 5 with continuous black line. The

vocal parts and the instrumental parts are annotated

manually. Even though in this example it is shown

that most of the output values correspond to the

correct class (if we set a threshold), some of the

frames are misclassified.

In order to solve the misclassification problem, we

introduced a set of rules and we used dynamic

programming for correcting the possible

misclassifications. In a first step we divide the frame

sequence in groups of 100 frames each and we

compute their vector mean as shown with red dots in

Figure 5. These values are then converted into

binary vales by using an appropriate threshold. The

threshold is calculated as the mean of the mean

values and is shown with green line in the same

figure. In this example the threshold is 0.6. The

mean values that fall above the threshold are

classified as “instrumental” while the values that fall

below the threshold are classified as “vocal”.

Further processing was needed in order to correct

additional misclassifications. One example of a

misclassified sample is encircled in figure 5. In this

example, the encircled output value exceeds the

threshold and the system wrongly classifies that

position as instrumental. For solving such

misclassification problems, we introduced the

following rule:

Each sample of the quantized vector is tested with

the classes that belong to the frames around it. To

consider a classification of a sample as true, the

class of the previous frame has to be the same with

the class of the following two frames. Regardless on

what the classification of the testing frame is, after

we apply this rule, the classification may change.

In order to illustrate an example, in Figure 5 we

present a frame that was wrongly classified as

instrumental while the annotation of this frame is to

be vocal. This frame is encircled with yellow colour

and in this example it is the testing frame. The

previous frame and the two frames after the testing

frame belong to the class “vocal” while the testing

frame belong to the class “instrumental”. After we

apply the rule described above, the class of the

testing frame turns from “instrumental” to “vocal”.

Figure 5: Black continuous line shows the output of the

ANN for a chunk of 30 seconds of a polyphonic song. Red

dots show the mean values for groups of 100 frames each.

Blue continuous line shows the binary quantization of the

mean values with respect to the threshold. Yellow circle

shows an example of a misclassified value.

3 EVALUATION AND RESULTS

The validation set contained 74 songs of a total

duration of 230 minutes. 46 songs were monophonic

and the remaining 28 were polyphonic. For the

classification of the “monophonic – polyphonic”, we

call a “false positive” prediction when a song is

annotated as “monophonic” and the prediction of the

system is “polyphonic”. We present our results in

terms of precision and recall. ANNs achieved a

precision of 0.88 and recall of 0.78. SVMs gave

precision of 0.85 and recall of 0.81 and Bayesian

Statistics precision of 0.71 and recall of 0.69.

The precision is defined as:

PTP

precision





(6)

The recall is defined as:

recall





(7)

AutomatedSegmentationofFolkSongsUsingArtificialNeuralNetworks

149

For the classification of the “vocal – instrumental”

we call a false positive if a part of the signal was

annotated as “vocal” but the prediction of the system

was “instrumental”. Figure 6 shows an example on

how we define the terms false positive, false

negative and true positive for the specific

classification problem. The audio signal is plotted

with black continuous line. The red vertical lines

indicate the limits in the audio signal where only

instruments are performing, while the green vertical

lines indicate an example of the limits where a

prediction was done from our system. We call false

positive the duration of the signal that the ground

truth is annotated as “vocal” and the prediction was

“instrumental”. ANNs achieved a precision of 0.85

and recall of 0.83. SVMs gave precision of 0.86 and

recall of 0.82 and Bayesian Statistics precision of

0.76 and recall of 0.72.

Figure 6: The interpretation of the terms “false positive”,

“True positive” and “False negative”.

Where:

TP: True positive

FP: False positive

FN: False negative

4 CONCLUSIONS

We described a method for automatic annotation of

Cypriot folk music into “polyphonic” or

“monophonic” music. In the validation procedure,

the audio signal is segmented into audio frames of

46 ms. A set of low level features are being

extracted from each such audio frame and given to

the input layer of the neural network. In the output

layer, a value between 0 and 1 is extracted. This

value is used for the classification using a threshold.

For polyphonic music we presented an automatic

annotation into instrumental or singing parts. The

system identifies these positions by classifying each

audio frame into instrumental or vocal. This is done

automatically, while there is no need for any

external assistance or guidance.

From our experiments we observed that timbre

low-level features are suitable to capture the

characteristics of each class. The advantage of our

system is the use of ANNs and standard timbre low-

level features. We consider ANNs a very powerful

technique for classification problems. They have the

ability to imitate the biological function of the

human brain. Thus, they are able to efficiently

identify patterns and correlations in the feature

space. Our method does not need any perceptual

features and it uses the row values of the features

without any pre-processing such as feature

normalization. The selected features are state of the

art for audio analysis and classification.

The ANNs and the SVMs had similar results. In

comparison with the statistical Bayesian

classification the ANNs and the SVMs performed

better. We present a precision of 0.78 and recall of

0.88 for the first system and a precision of 0.85 and

recall of 0.83 for the second system. The results are

not yet finalised but represent the basis on our future

research will be based. Improvements of the results

reported in this paper could be achieved by

introducing additional features such as mid-level

features. Principal component analysis could also be

applied to the feature set for dimensionality

reduction. These problems are currently under study

and the results will be reported in the near future.

ACKNOWLEDGEMENTS

This work is supported by the research grant

Ανθρωπιστικες/Ανθρω/0311(ΒΕ)/19 funder by the

Cyprus Research Promotion Foundation.

REFERENCES

Bonjyotsna A., Bhuyan M., 2014. Performance

Comparison of Neural Networks and GMM for

Vocal/Nonvocal segmentation for Singer

Identification. International Journal of Engineering

and Technology (IJET), Vol. 6, No 2.

Benediktsson J., Swain P, and Ersoy, O., 1990. Neural

Network Approaches Versus Statistical Methods in

Classification of Multisource Remote Sensing Data.

IEEE Transactions on Geoscience and Remote

Sensing, Vol. 28, No 4.

Benjamin, K., 1986. Spectral analysis and discrimination

by zero-crossings. In Proceedings of the IEEE, pp.

1477–1493.

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

150

Fuhrmann, F, Herrera, P, Serra, X., 2009. Detecting Solo

Phrases in Music using Spectral and Pitch-related

Descriptors. Journal of New Music Research, 2009,

pp. 343–356.

Lu, L, Zhang, H, J, Li, S, Z., 2003. Content-based audio

classification and segmentation by using support

vector machines. In Multimedia Systems.

Mankiewicz, R., 2004. The Story of Mathematics.

Princeton University Press, p. 158.

Mermelstein, P., 1976. Distance measures for speech

recognition, psychological and instrumental. Pattern

Recognition and Artificial Intelligence, pp. 374–388.

Muller, M, Grosche, P, Wiering, F., 2009. Robust

segmentation and annotation of folk song recordings.

International Society for Music Information Retrieval

(ISMIR), pp. 735–740.

Neocleous C.C., Nikolaides K.H., Neokleous K.C.,

Schizas C.N. 2011, Artificial neural networks to

investigate the significance of PAPP-A and b-hCG for

the prediction of chromosomal abnormalities. IJCNN -

International Joint Conference on Neural Networks,

San Jose, USA.

Panagiotakis, C, Tziritas, G., 2004. A Speech/Music

Discriminator Based on RMS and Zero-Crossings. In

IEEE Transactions on Multimedia.

Pfeiffer, S, Fischer, S, Effelsberg, W., 1996. Automatic

Audio Content Analysis. In Proceedings of the fourth

ACM international conference on Multimedia, pp. 21-

30.

Roads, C., 1996. The Computer Music Tutorial. MIT

Press.

Scheirer, E, Slaney, M., 1997. Construction and evaluation

of a robust multi feature speech/music discriminator.

In IEEE International Conference On Acoustics,

Speech, And Signal Processing, pp. 1331–1334.

Siegel, S., 1956. Non-parametric statistics for the

behavioral sciences. New York: McGraw-Hill, pp. 75–

83.

Stephens, M, A., 1974. EDF Statistics for Goodness of Fit

and Some Comparisons. Journal of the American

Statistical Association (American Statistical

Association), pp. 730–737.

Stevens, S, S, Volkman J, Newman, E, B., 1937. A scale

for the measurement of the psychological magnitude

pitch. Journal of the Acoustical Society of America,

pp. 185–190.

Vembu, S, Baumann, S., 2005. Separation of vocals from

polyphonic audio recordings. International Society for

Music Information Retrieval (ISMIR), pp. 337–334.

Werbos P., 1974. Beyond Regression: New Tools for

Prediction and Analysis in the Behavioural Sciences.

Ph.D. dissertation Applied Mathematics, Harvard

University.

AutomatedSegmentationofFolkSongsUsingArtificialNeuralNetworks

151