
Multi-agent Cooperative Algorithms of Global Optimization
Maxim Sidorov
1
, Eugene Semenkin
2
and Wolfgang Minker
1
1
Institute of Communication Engineering, Ulm University, Ulm, Germany
2
Institute of System Analysis, Siberian State Aerospace University, Krasnoyarsk, Russia
Keywords:
Genetic Algorithm, Evolution Strategy, Particle Swarm Optimization, Island and Co-evolution Cooperation
Models.
Abstract:
In this paper we present multi-agent cooperative algorithms of global optimization based on a genetic algo-
rithm, an evolution strategy and particle swarm optimization. Island and co-evolution approaches have been
selected as a main scheme of cooperation. The proposed techniques have been implemented and evaluated on
a set of 22 multivariate functions. We assert that the proposed techniques could achieve much higher results in
terms of reliability and speed criteria than the performance of corresponding conventional algorithms (without
cooperative schemes) with average parameters on 18 functions from the 22 selected for the evaluation proce-
dure. Such advantages are much more observable with increasing dimensionality of functions. Furthermore,
the performance of the suggested algorithms was even higher than the performance of conventional algorithms
with the best parameters for 5 functions.
1 INTRODUCTION
Evolutionary and behavioural algorithms such as a
genetic algorithm (GA), an evolution strategy (ES)
and particle swarm optimization (PSO) have recently
been successfully applied to a wide variety of prob-
lems including machine learning, multi-modal func-
tion optimization, the evolution of complex structures
such as artificial neural networks or even computer
programs. However, one of the most significant weak-
nesses of these algorithms is the necessity of setting
parameters. Moreover, it could be difficult to opti-
mize a high-dimensional, multivariate functions us-
ing the mentioned algorithms due to a large number
of local extremums, a complex function’s surface, etc.
One of the possible solutions to these problems could
be a combination of the algorithms. Whereas many
researchers have already worked on the combination
of different instances of the same algorithm but with
different parameters, we have proposed here to use a
multi-agent cooperative schemes in order to improve
the quality of complex function optimization. GA, ES
and PSO have been included as the main components
of the cooperative schemes.
The proposed methods have been implemented
and evaluated on a set of 22 multivariate functions
for unconstrained global optimization. We have com-
pared these results with the results of conventional
algorithm (without cooperative schemes) applications
on the same set of functions using the same number of
resources. The performance of the proposed methods
has also been evaluated on a set of higher-dimensional
functions (up to 25 variables).
The rest of the paper is organized as follows: Sig-
nificant related work is presented in Section 2. Sec-
tion 3 describes the suggested algorithms with their
results of numerical evaluations in Section 4. The
conclusion and future work are described in Section 5.
2 SIGNIFICANT RELATED
WORK
A genetic algorithm and an evolution strategy, orig-
inally conceived by Holland (Holland, 1975) and
Schwefel, and Rechenberg (Beyer and Schwefel,
2002) respectively, represent an abstract model of
Darwinian evolution and biological genetics with fur-
ther applications in optimization and machine learn-
ing domains. The algorithms evolve competing solu-
tions of the particular optimization task called indi-
viduals. A group of individuals forms a population.
A selective pressure within populations is organized
through the value of the fitness function which is the
main criterion of each individual. Basic evolutionary
operators such as selection, recombination and mu-
259
Sidorov M., Semenkin E. and Minker W..
Multi-agent Cooperative Algorithms of Global Optimization.
DOI: 10.5220/0005049402590265
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 259-265
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

tation are iteratively applied to the population of in-
dividuals encouraging them to approach an optimum
point. GA and ES can be distinguished by the type
of individual encoding. GA is a pseudo-boolean opti-
mization technique whereas ES works with real num-
bers directly.
Being a behavioral algorithm, a particle swarm
optimization technique (Kennedy et al., 1995) sim-
ulates the behaviour of animal swarms in their natu-
ral habitats. The algorithm optimizes a function by
having a number of solutions or particles and mov-
ing these particles within the search-space according
to the mathematical formulas. Each particle is char-
acterised by position and velocity values. The move-
ment of a particular solution within the search-space
is influenced by its local best known position and the
global best known position in the search-space, which
was achieved by other particles.
We provide a discussion about the possible ways
of cooperation amid these algorithms in the next sec-
tion.
3 SUGGESTED ALGORITHMS
State-of-the-art cooperation methods of optimization
algorithms include an island and a co-evolution ap-
proaches. The description of these models can be
found in the following subsections.
3.1 Island Model
A multi-agent scheme called the island model repre-
sents a number of algorithms which solve the partic-
ular optimization function independently exchanging
some information about found solutions. Each opti-
mization algorithm in this ontology called an island
has its own resources and parameters.
A parallel implementation of genetic algorithms
with different parameters (Whitley et al., 1997) has
shown not just an ability to preserve genetic diver-
sity, since each island can potentially follow a dif-
ferent search trajectory, but also could be applied to
separable problems.
Our idea is to include in the island model not
just different instances of the same algorithms, but
also different algorithms such as GA, ES and PSO. A
transfer of individuals between pseudo-boolean GA
and real ES and PSO could be easily implemented
by the encoding of corresponding individuals from bi-
nary to real representation and vice versa.
Cooperation could be implemented in many ways,
hence we propose to exchange the best solutions,
which were achieved by different algorithms, each n
population. In this case, algorithms solve the same
problem for the first n populations independently,
then all achieved solutions are placed into the same
pool and ranged by corresponding fitness values. Fur-
ther, N best solutions are set as a current population
for all algorithms, where N stands for the number of
individuals in the corresponding population. It should
be noted that in this case after every n population
the algorithms will have the same set of individuals
in their populations. The algorithms solve the opti-
mization problem independently for the next n popu-
lations, until the exchange phase is reached. This pro-
cedure iterates until the termination condition is true.
In our case, the termination condition is the maximum
number of available populations.
The multi-agent island model is expected to pre-
serve a higher level of genetic diversity. What is more,
the benefits of the particular algorithms could be ad-
vantageous in different stages of optimization. For in-
stance, thr ES algorithm, having better features for the
global optimization procedure, outperforms the GA
and PSO algorithms on the initial stages of the opti-
mization procedure. Due to the exchange of the best
individuals, GA and PSO have the opportunity to op-
erate with better solutions much faster. In the progress
of application, the local features of GA and PSO yield
more accurate results of optimization.
The pseudo-code in Figure 1 illustrates this ap-
proach.
n: A number of populations before exchange of
solutions;
gen = 0;
for each species s do
Pop
s
(gen) = randomly initialized
population;
evaluate fitness of each individual in
Pop
s
(gen);
end
while termination condition = f alse do
gen = gen + 1;
for each species s do
select Pop
s
(gen) from Pop
s
(gen −1)
based on fitness;
apply genetic or behavioral operators to
Pop
s
(gen);
evaluate fitness of each individual in
Pop
s
(gen);
end
if gen % n = 0 then
exchange of the best solutions ;
end
end
Figure 1: An island model of cooperation.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
260

3.2 Co-evolution Model
The idea of the co-evolution model of cooperation
(Potter and De Jong, 1994) is quite similar to the is-
land model, but in this case not just the best solutions
are exchanged, but also resources are redistributed. It
is intuitively clear that the better an algorithm can
solve an optimization problem, the more resources
could be used by the algorithm. Analogically, the
worse an algorithm copes with the optimization prob-
lem, the fewer resources could be utilized by the algo-
rithm. Nevertheless, a bad solution could also bring
some useful information to the common task, which is
why each algorithm, even the worst one, could have
an opportunity to solve the problem. Practically, it
could be implemented by adding one more parameter
to the co-evolution algorithm called social card. This
parameter represents the minimum amount of avail-
able resources for each algorithm, i.e. the number of
target function calculations.
Another aspect of the algorithm is the number of
resources to redistribute. This procedure can be or-
ganized in many ways, however, we propose to redis-
tribute k individuals from less efficient algorithms (in
terms of already found solutions) to the most efficient
one. Such an operation could be applied unless the
number of individuals in the non-optimal algorithms
is equal to the social card parameter.
The an algorithm of the co-evolution model is
quite similar to the island model (see. Figure 1). The
main difference is an additional block called resource
redistribution in the if construction.
4 EVALUATION
There is a number of standard functions (Adorio and
Diliman, 2005) which have different features and are
difficult to optimize. The community uses such func-
tions to examine the optimization ability of developed
algorithms.
The suggested algorithms as well as the baseline
implementation of GA, ES and PSO have been tested
on 22 multivariate functions for unconstrained global
optimization. The selected functions are listed in Ta-
ble 2, where F and D stand for the function id and its
dimensionality correspondingly. It should be noted
that the corresponding formulas can be found here
(Adorio and Diliman, 2005).
Several functions have a fixed number of parame-
ters, whereas some of them could have different di-
mensionality. Such functions have also been opti-
mized on a variety of dimensionality (see Table 2)
by cooperative methods and conventional algorithms
with empirically set parameters.
Some functions can be characterized in the follow-
ing way.
Many Local Minima: The Ackly function is char-
acterized by a nearly flat outer region, and a large
hole at the centre. The function poses a risk for
optimization algorithms to be trapped in one of its
many local minima. The Griewank function has many
widespread local minima, which are regularly dis-
tributed. The Rastrigin function has several local min-
ima. It is highly multi-modal, but the locations of the
minima are regularly distributed.
Bowl-shaped: The Bohachevsky functions are
slightly different but all of them have the same similar
bowl shape. The Sphere function has 2 local minima
in addition to the global one. It is continuous, con-
vex and unimodal. The Sum Squares function, also
referred to as the Axis Parallel Hyper-Ellipsoid func-
tion, has no local minimum except the global one.
Valley-shaped: The Rosenbrock function is re-
ferred to as the Valley or Banana function, and is a
popular test problem for gradient-based optimization
algorithms. The function is unimodal, and the global
minimum lies in a narrow, parabolic valley. However,
even though this valley is easy to find, convergence to
the minimum is difficult.
In fact, the efficiency of an optimization algorithm
highly depends on its parameters, therefore the pa-
rameters of standard algorithms have been optimized
with the brute force approach using the grid tech-
nique. The optimized parameters and their potential
values can be found in Table 2.
Table 1: Selected multivariate functions of global uncon-
strained optimization, where 5-25 stands for 5, 10, 15, 20,
25 variables.
F. Title D. F. Title D.
0 Ackley 2,5-25 11 Levy 2,5-25
1 Beale 2 12 Matyas 2
2 Bohachevsky
1
2 13 Rastrigin 2,5-25
3 Bohachevsky
2
2 14 Rosenbrock 2,5-25
4 Bohachevsky
3
2 15 Schwefel 2,5-25
5 Booth 2 16 Shekel
5
4
6 Colville 4 17 Shekel
7
4
7 Easom 2 18 Shekel
10
4
8 Goldstein-Price 2 19 Sphere 2,5-25
9 Griewank 2,5-25 20 Sum Squeres 2,5-25
10 Hartman
3
3 21 Zakharov 2,5-25
Here, the gray parameter indicates whether the
gray coding (Wright et al., 1990) should be applied to
encode individuals from real to binary representation.
The elitism parameter shows whether the best individ-
Multi-agentCooperativeAlgorithmsofGlobalOptimization
261

Table 2: Parameters optimization set up, having parameter’s
abbreviations in parenthesis (see Table 4)
Parameter Values
GA
Gray (G.) false, true
Elitism (E.) false, true
Selection (S.) proportional, rank, tournament
Recombination (R.) one-, two-points, uniform
Mutation (M.) weak, normal, strong
Tournament [3, 6, ..., 12]
ES
Recombination (R.) dominant, intermediate
Selection (P.) (µ, λ), (µ + λ)
Parents pool (N.) [10, 11, ..., 49]
PSO
c
1
[1.5, 1.6, ..., 1.9]
c
2
[1.5, 1.6, ..., 1.9]
k [0.1, 0.3, ..., 0.9]
w [0.8, 0.9, ..., 1.1]
ual should be placed into the next generation directly.
The description of the standard schemes of GA and its
operators such as selection, recombination and muta-
tion could be found for example here (Semenkin and
Semenkina, 2012).
The evolution strategy algorithm has been im-
plemented in conformity with (Beyer and Schwefel,
2002), where a description of the corresponding pa-
rameters can also be found. It should be noted that in
the cited paper only the best individuals are included
into the next population. Nonetheless, an application
of the GA’s selection strategies (tournament, rank and
proportional) might significantly improve the perfor-
mance of ES.
The parameter k in the algorithm of PSO corre-
sponds to the maximum velocity (m) and could be rep-
resented as follows:
m = k
(r − l)
2
, (1)
where r and l are the left and right borders of the
search-space correspondingly. The rest of the param-
eters are the same as in (Beyer and Schwefel, 2002).
The efficiency of the optimization algorithms can
be measured in terms of reliability and speed. The
reliability is a major criterion and it indicates the per-
centage of algorithm runs when the global optimum
has been found. The speed shows an average number
of target function calculations until the global opti-
mum is achieved. If two algorithms have the same
value for reliability, then the better algorithm has a
lower value for the speed criterion.
In order to generate more statistically significant
results, the complete optimization process was run
100 times for each function and all possible param-
eter combinations (See Table 2). For each run, the
reliability and the speed have been calculated as the
main criteria of the optimization procedure.
The results of the optimization procedure for stan-
dard functions can be found in Table 4. The order of
representation of the parameters is the same as they
are listed in Table 2. In other words, the best per-
formance of the 0 function optimization is 100 and
3592.2 (reliability and speed correspondingly) and
has been calculated as the reliability and as the aver-
age value of speed criteria on 100 runs. It means, that
the global optimum has been successfully found in
each run of GA and it takes on average 3592.2 target
function calculations. The GA instance resulting in
this performance had the following parameters: gray
coding (1), elitism (1), tournament selection, having
the size of tournament in parentheses (12), uniform
recombination (2) and weak (0) mutation (see Ta-
ble 4).
Further, in order to test the suggested cooperative
methods, the same experiments were conducted with
island and co-evolution models. One instance of each
conventional algorithm with the same parameters was
included into the cooperative models. The parameters
of the selected algorithms were set empirically in the
following way. The genetic algorithm without gray
coding, tournament selection with the size of tourna-
ment equal to 12 and elitism, uniform recombination
and normal mutation was the first part of coopera-
tive algorithms, both island and co-evolution models.
The evolution strategy component was included into
multi-agent algorithms with the dominant recombina-
tion, (µ+ λ) selection strategy and the number of par-
ents equal to 30. Finally, the particle swarm optimiza-
tion with c
1
= c
2
= 1.5, k = 0.1 and w = 0.8 formed
the last component of the models.
Further, to investigate the performance of algo-
rithms on functions of higher dimensionality, an op-
timization procedure has also been conducted on a
subset of functions with various numbers of variables.
Cooperative models have been compared against con-
ventional algorithms with the same parameters as they
have in cooperative schemes. The results of the di-
mensional study are in Table 3.
In order to perform a fair comparison, an equal
number of resources has been allocated for all algo-
rithms. Each conventional algorithm had 300 individ-
uals and 300 populations for each run. Correspond-
ingly, each conventional algorithm, as a part of multi-
agent algorithms, had 173 individuals and 173 popu-
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
262
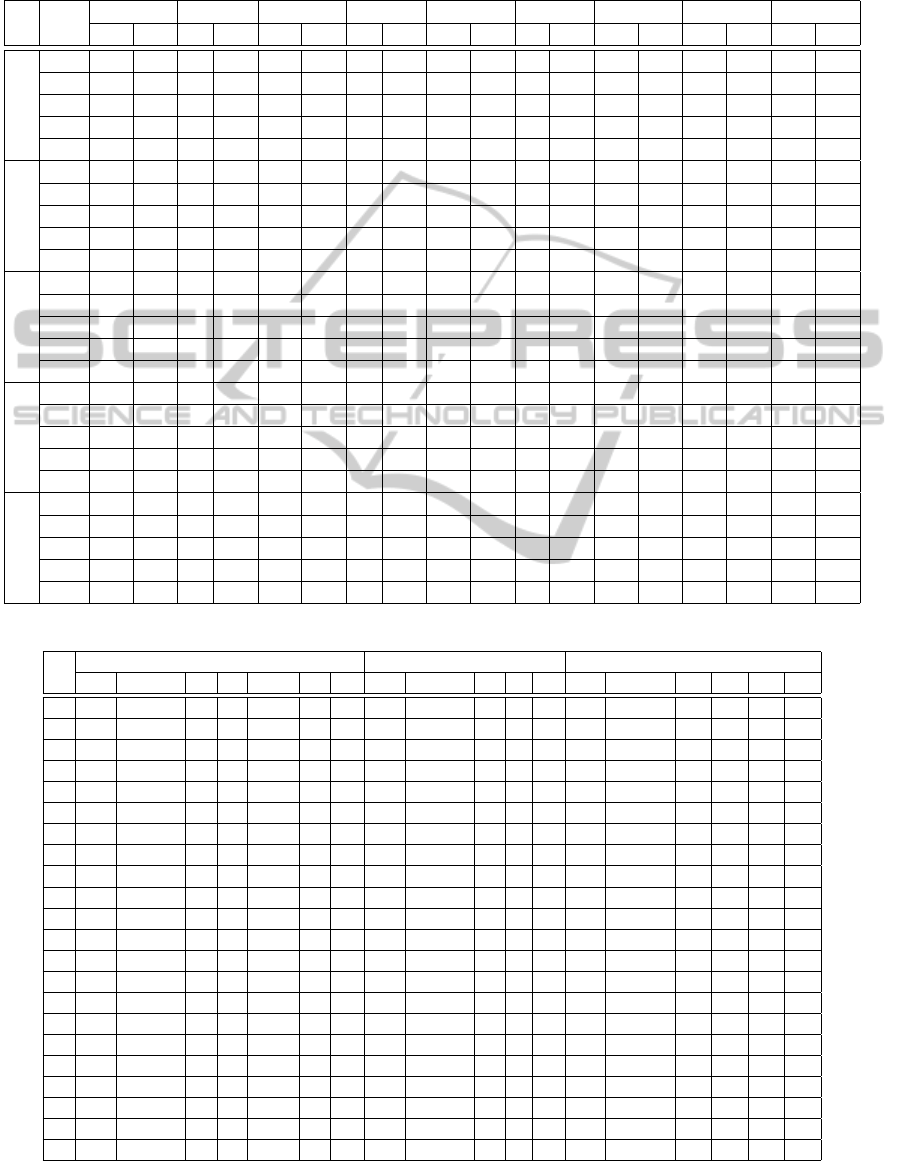
Table 3: The results of standard functions optimization. Dimensionality study. D stands for dimensionality of corresponding
optimization function (ids are the same as in Table 2). Alg denotes used algorithm, R and S are reliability and speed corre-
spondingly. IS and CO are island and coevolution models. The parameters of conventional algorithms are the same as for
corresponding algorithms in cooperative models.
D. Alg.
0 9 12 14 15 16 20 21 22
R. S. R. S. R. S. R. S. R. S. R. S. R. S. R. S. R. S.
5
GA 100 10k 2 12k 1 83k 47 22k 0 - 0 - 100 9k 100 9k 0 -
ES 96 32k 3 52k 97 41k 93 39k 0 - 0 - 95 35k 98 37k 7 74k
PSO 100 29k 0 - 100 26k 2 25k 90 26k 4 40k 100 23k 100 25k 100 25k
IS 100 19k 4 49k 100 22k 98 37k 100 32k 0 - 100 16k 100 18k 100 25k
CO 100 18k 7 51k 100 28k 98 25k 98 41k 0 - 100 15k 100 18k 100 34k
10
GA 95 24k 4 27k 0 - 1 76k 0 - 0 - 100 17k 100 18k 0 -
ES 1 84k 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 -
PSO 70 39k 0 - 67 37k 0 - 0 - 0 - 100 32k 100 35k 100 38k
IS 98 45k 7 56k 80 46k 5 73k 34 75k 0 - 100 35k 100 38k 100 58k
CO 100 22k 46 20k 90 47k 93 31k 22 70k 0 - 100 22k 100 23k 100 68k
15
GA 79 39k 12 40k 0 - 0 - 0 - 0 - 100 25k 100 27k 0 -
ES 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 -
PSO 17 55k 0 - 19 61k 0 - 0 - 0 - 100 44k 68 59k 10 72k
IS 55 70k 15 82k 37 62k 0 - 1 87k 0 - 100 54k 100 58k 48 85k
CO 98 20k 0 - 62 47k 60 29k 1 80k 0 - 100 21k 100 24k 21 55k
20
GA 35 48k 33 53k 0 - 0 - 0 - 0 - 100 32k 100 35k 0 -
ES 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 -
PSO 0 - 0 - 0 - 0 - 0 - 0 - 13 65k 0 - 0 -
IS 11 86k 0 - 9 76k 0 - 0 - 0 - 100 74k 88 80k 0 -
CO 100 17k 0 - 71 55k 64 19k 0 - 0 - 100 19k 100 25k 23 46k
25
GA 20 54k 32 66k 0 - 0 - 0 - 0 - 100 41k 100 44k 0 -
ES 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 -
PSO 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 - 0 -
IS 0 - 0 - 0 - 0 - 0 - 0 - 21 84k 1 87k 0 -
CO 93 14k 0 - 67 50k 77 13k 0 - 0 - 100 16k 100 25k 15 58k
Table 4: The results of standard functions optimization. Algorithms with the best parameters.
F.
GA ES PSO
R. Speed G. E. S. R. M. R. Speed R. P. N. R. Speed c
1
c
2
k w
0 100 3592.2 1 1 2(12) 2 0 100 8199.6 0 1 40 100 20316.5 1.6 1.5 0.1 0.8
1 100 30157.5 1 1 2(9) 0 2 100 33351.0 0 1 20 100 15438.3 1.6 1.7 0.1 0.8
2 100 4141.4 1 0 2(12) 2 1 100 9058.2 0 1 43 100 23582.0 1.8 1.9 0.1 0.8
3 100 4392.3 1 0 2(12) 2 1 100 9354.0 0 1 29 100 23719.0 1.5 1.5 0.1 0.8
4 100 6645.2 0 1 2(6) 2 1 100 26011.7 0 1 24 100 23817.3 1.8 1.9 0.1 0.8
5 100 13615.4 0 1 2(3) 1 1 100 13104.5 0 1 31 100 17375.7 1.7 1.8 0.1 0.8
6 0 – – – – – – 2 61111.5 1 0 19 98 61629.3 1.9 1.8 0.3 0.9
7 55 17182.2 0 1 2(3) 0 1 100 10843.7 0 1 35 100 23834.5 1.7 1.8 0.1 0.8
8 100 2726.3 0 1 2(12) 2 0 100 8096.1 0 1 39 100 12859.3 1.6 1.5 0.1 0.8
9 47 25330.3 0 1 2(3) 1 1 66 15623.0 0 1 47 99 64855.3 1.8 1.9 0.1 0.9
10 100 10767.1 0 1 2(3) 1 1 99 11568.0 0 1 45 100 13568.9 1.9 1.7 0.1 0.8
11 100 5836.9 1 1 2(6) 1 1 100 8068.9 0 1 49 100 17208.6 1.6 1.6 0.1 0.8
12 100 4769.8 0 0 2(12) 2 1 100 9909.5 1 0 12 100 17215.7 1.5 1.7 0.1 0.8
13 100 3444.2 0 0 2(12) 1 0 100 7460.9 0 1 43 100 17076.0 1.9 1.5 0.3 0.8
14 63 51422.7 1 1 2(9) 2 2 28 49928.4 1 1 10 100 13650.3 1.7 1.6 0.1 0.8
15 97 15329.8 0 1 2(3) 1 1 0 – – – – 100 61257.8 1.9 1.7 0.1 0.9
16 44 31323.5 0 1 2(3) 1 1 52 44438.8 1 0 24 97 57668.7 1.5 1.7 0.9 0.9
17 4 45275.3 1 0 2(12) 1 2 14 36148.0 1 0 20 39 60237.4 1.9 1.5 0.1 0.9
18 5 39652.4 0 1 2(12) 0 2 15 51545.7 1 0 21 31 61949.1 1.5 1.6 0.1 0.9
19 100 3101.3 0 1 2(12) 2 0 100 3004.3 1 0 10 100 15340.5 1.9 1.5 0.1 0.8
20 100 3235.4 0 1 2(12) 2 0 100 3452.2 1 0 11 100 17110.1 1.5 1.8 0.1 0.8
21 100 4211.6 1 0 2(12) 2 1 100 8105.5 0 1 12 100 16281.0 1.5 1.7 0.1 0.8
Multi-agentCooperativeAlgorithmsofGlobalOptimization
263

Table 5: The results of standard functions optimization. An average performance for conventional algorithms.
F.
GA ES PSO Island Coevolution
R. Speed R. Speed R. Speed R. Speed R. Speed
0 72.0 18558.4 79.0 18103.0 81.0 42351.9 100 6456.1 100 6523.9
1 26.9 22783.0 63.2 43053.2 64.0 41154.9 100 9592.6 100 14951.9
2 72.6 21044.0 64.2 20929.5 96.9 42335.9 100 7572.1 100 7656.8
3 73.7 21912.7 53.6 22422.2 95.5 42394.1 100 8094.7 100 8006.6
4 71.4 25862.3 45.7 38552.0 95.1 43462.2 100 9761.2 100 10027.6
5 36.1 21412.1 73.0 37551.4 63.6 45246.5 100 9086.3 100 13091.9
6 0 – 1.2 62800.9 86.3 46880.1 98 37265.5 94 45488.2
7 20.8 25351.8 45.2 27302.1 93.0 43277.8 100 10702.1 100 13214.0
8 74.0 16703.9 51.3 26549.8 66.4 43285.9 100 5168.4 100 5271.4
9 18.1 24554.9 51.5 18461.4 83.3 53898.2 55 20340.5 98 18713.1
10 60.0 20373.1 62.6 30991.5 62.2 42326.4 100 8749.6 100 11741.8
11 63.6 19523.5 82.1 19203.0 72.3 41004.8 100 7433.5 100 9111.5
12 69.9 24079.2 72.8 35017.1 60.9 46934.5 100 8516.9 100 9669.0
13 73.3 19220.3 77.8 15167.9 60.5 46311.8 100 6723.1 100 7067.9
14 25.2 35730.3 9.8 58048.6 58.0 41030.6 100 10957.5 100 17412.6
15 31.7 24409.4 0 – 70.3 41654.1 2 7732.0 4 41071.3
16 8.2 37708.9 29.7 40202.4 59.0 39023.1 43 17044.9 45 27400.6
17 1.8 38786.0 5.2 46081.2 14.9 49103.9 1 15317.0 7 34713.9
18 1.8 38037.3 5.3 43624.9 11.5 48939.7 0 – 9 34137.0
19 74.5 17396.3 93.4 11258.3 60.0 46413.5 100 5592.1 100 5566.1
20 74.0 18870.0 91.5 13846.2 63.4 45355.8 100 6501.3 100 6161.1
21 76.3 18628.7 76.6 23629.0 60.6 46370.7 100 7019.2 100 8634.4
lations. For the evolution strategy µ = 45 and λ = 300
in the conventional case and µ = 26, λ = 173 as a part
of cooperative algorithms. By doing that we achieved
around an equal number of target function calcula-
tions for each algorithm.
The number of populations before the exchange
of the best solutions was set as 5% of the whole num-
ber of initially available individuals in the population
(n = 5%, see Figure 1). The number of individuals
to migrate to the best algorithm was equal to 10% of
the whole population. Finally, social card = 15% of
initially available individuals.
The results of the evaluation can be found in Ta-
ble 5, which contains the results of the cooperative
algorithm applications and the performance of aver-
age individual algorithms. The idea that lies behind
this comparison is that the end-user, who may not
have any experience in evolutionary and behavioural
algorithms, could set random parameters and conse-
quently could expect an average performance of the
optimization procedure. As an alternative way it is
possible to use the proposed methods, and in this case
the end-user does not need to set any parameters but
use the default ones.
5 CONCLUSIONS
Regarding the results of standard algorithm (without
cooperation) applications one may conclude that GA
is the best algorithm. The best parameters were a wide
variety of all possible settings, except for selection
type, since the tournament selection was an optimal
choice for all optimization functions. However, for
some optimization functions GA was outperformed
by ES and PSO (see Table 4).
An evaluation of suggested methods has revealed
the fact that the cooperative algorithms (mainly the is-
land model) have achieved significantly higher results
than the performance of conventional algorithms with
average parameters. It is true for 18 functions (see the
bold values in Table 5).
Furthermore, the performance of the suggested al-
gorithms was even higher than the performance of
conventional algorithms with the best parameters in
the case of 5 functions (see the highlighted cells in
Table 5). Further optimization of suggested algorithm
parameters could improve this result.
Optimization experiments on the set of functions
with various numbers of variables have revealed the
beneficial characteristics of the co-evolution model.
In most of the cases this algorithm has achieved much
better results, especially on the functions of higher di-
mensionality (see Table 3).
It could be concluded that by using the suggested
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
264

methods we do not need to set any parameters of the
algorithm, and we still could achieve a result that
is much better than the performance of correspond-
ing algorithms with average parameters almost for all
functions.
It should be noted that the accuracy parameter
for all considered algorithms was set as 0.0001. By
increasing this parameter, much higher performance
criteria could be achieved.
One of the possible further directions of the inves-
tigation might be the usage of more than one instance
of the individual algorithms in cooperative schemes.
The co-evolution approach can also be improved by
changing the strategy of resource redistribution. The
implementation of the self-adaptive genetic operators
for GA and ES (Sidorov et al., 2014) could signif-
icantly simplify the process of parameters setting.
Such algorithms could also be included in coopera-
tive schemes.
REFERENCES
Adorio, E. P. and Diliman, U. (2005). Mvf-multivariate test
functions library in c for unconstrained global opti-
mization.
Beyer, H.-G. and Schwefel, H.-P. (2002). Evolution
strategies–a comprehensive introduction. Natural
computing, 1(1):3–52.
Holland, J. H. (1975). Adaptation in natural and artificial
systems: An introductory analysis with applications to
biology, control, and artificial intelligence. U Michi-
gan Press.
Kennedy, J., Eberhart, R., et al. (1995). Particle swarm op-
timization. In Proceedings of IEEE international con-
ference on neural networks, volume 4, pages 1942–
1948. Perth, Australia.
Potter, M. A. and De Jong, K. A. (1994). A cooperative
coevolutionary approach to function optimization. In
Parallel Problem Solving from NaturePPSN III, pages
249–257. Springer.
Semenkin, E. and Semenkina, M. (2012). Spacecrafts’
control systems effective variants choice with self-
configuring genetic algorithm. In ICINCO (1), pages
84–93.
Sidorov, M., Brester, K., Minker, W., and Semenkin, E.
(2014). Speech-based emotion recognition: Feature
selection by self-adaptive multi-criteria genetic algo-
rithm. In International Conference on Language Re-
sources and Evaluation (LREC).
Whitley, D., Rana, S., and Heckendorn, R. B. (1997). Is-
land model genetic algorithms and linearly separable
problems. In Evolutionary computing, pages 109–
125. Springer.
Wright, A. H. et al. (1990). Genetic algorithms for real
parameter qptimization. In FOGA, pages 205–218.
Citeseer.
Multi-agentCooperativeAlgorithmsofGlobalOptimization
265
