A Novel Pseudo Random Number Generator Based on L’Ecuyer’s
Scheme
Francesco Buccafurri and Gianluca Lax
DIIES Dept., University of Reggio Calabria, Reggio Calabria, Italy
Keywords:
Pseudo Random Number Generator, L’Ecuyer’s Scheme, Cryptographic Applications.
Abstract:
In this paper, we propose a new lightweight L’Ecuyer-based pseudo random number generator (PRNG). We
show that our scheme, despite the very simple functions on which it relies on, is strongly secure in the sense
that our number sequences pass the state-of-the-art randomness tests and, importantly, an accurate and deep
security analysis shows that it is resistant to a number of attacks.
1 INTRODUCTION
A pseudo random number generator (PRNG, for
short) based on L’Ecuyer’s scheme (L’Ecuyer, 1994)
is able to deterministically generate, starting only
from an initial secret seed, a sequence of numbers
which is indistinguishable from a true random se-
quence and such that there is no way for the attacker
to predict the future output by knowing past subse-
quences of outputs. The scheme is composed of (1) a
constant transition function that maps any inner state
s
i
to the successive state s
i+1
only on the basis of s
i
(with no other input) and (2) an output function g such
that the i-th element of the pseudo-random sequence
is computed as u
i
= g(s
i
). PRNGs have a lot of appli-
cations, such as the generation of the keystream of a
stream cipher, the generation of keys of block ciphers,
the implementation of protocols of strong authentica-
tion and so on.
Typically, PRNGs use cryptographic functions
such as ciphers or one-way functions (Blum et al.,
1986; Li and Zhang, 2005; Cox et al., 2011). Ob-
viously, this introduces a certain degree of compu-
tational complexity. As a matter of fact, in many
situations, it would be desirable to reduce as much
as possible the overall computational effort of the
device, anyway keeping high the security level of
adopted algorithms. This is for example the case
of cryptography-based applications in wireless sensor
networks (Tang et al., 2004; Alcaraz and Lopez, 2010;
Wang, 2011) or in wireless devices (mobile phones,
WLANs, etc.), where the efficiency of algorithms is
required both for real-time strict limitations and for
minimizing power consumption. Observe that there
exist a number of PRNGs, like those presented in
(Meli`a-Segu´ı et al., 2013; Dolev et al., 2011; Huang
et al., 2010), specifically designed for EPC Gen2 stan-
dard (EPCglobal, 2004); however, their use is limited
to this scope (where, for example, random numbers
are 16-bit wide).
In this paper, starting from an initial idea pre-
sented in the e-commerce setting (Buccafurri and
Lax, 2011), by improving it and testing its security,
we propose a lightweight PRNG based on L’Ecuyer’s
scheme which relies on very simple functions easily
implementable in hardware for the transition function
and a slight modification of CRC (Hill, 1979) for the
output function. Thus, our PRNG does not make use
of cryptographic functions in favor of computational
efficiency.
We show that number sequences generated by our
scheme pass the most known state-of-the-art random-
ness tests (National Institute of Standards and Tech-
nology, 2014); moreover, a preliminary security anal-
ysis does not disclose any weakness w.r.t all the at-
tacks we can hypothesize. In other words, we ar-
gue that our schema is compliant with the security
requirements of the German Federal Office for Infor-
mation Security (Bundesamt f¨ur Sicherheit in der In-
formationstechnik, 2014).
This position paper represents a first checkpoint of
our research aimed at (1) presenting the new PRNG,
(2) highlighting that it is is very cheap from a compu-
tational point of viewfor the reasons illustrated above,
and (3) giving a first solid argumentation about its se-
curity (proof of full randomness and partial analysis
on resistance to cryptanalysis attacks). The next step
is to deepen the study of the PRNG security against
321
Buccafurri F. and Lax G..
A Novel Pseudo Random Number Generator Based on L’Ecuyer’s Scheme.
DOI: 10.5220/0005050303210328
In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 321-328
ISBN: 978-989-758-045-1
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

cryptanalysis attacks and to compare our PRNG with
existing PRNGs on the aspect of efficiency.
The structure of the paper is the following. In the
next section, we define the notation used in the pa-
per. In Section 3, we provide the detailed definition
of the elements composing our scheme. We analyze
the security of our scheme both theoretically and ex-
perimentally in Section 4. In Section 5, we deal with
the computational costs of our PRNG. Finally, in Sec-
tion 6, we draw our conclusions.
2 NOTATION
In order to define our scheme, we need the following
notations.
• We denote by x
k
= (x
1
,.. ., x
k
) a k-bit string,
where x
j
, with 1 ≤ j ≤ k, represents the j-th bit
numbered from left to right.
• We denote by ex
k
= (x
k
,.. ., x
1
) the reverse string
of x
k
.
• Given a positive integer p, x
k
+ p denotes the k-bit
string representing the number obtained by sum-
ming (in 2
k
-modulo arithmetic) x
k
thought as a bi-
nary number and p. For example, given p = 1 and
x
3
= 111, x
3
+ 1 = 000, since (111+ 001)(mod
1000) = 000.
• Given a k-bit string x
k
, we denote by [x
k
]
i, j
with
1 ≤ i ≤ j ≤ k the sub-string of x
k
obtained by
keeping the j − i + 1 bits starting from the i-
th left-most bit. For example, given x
k
= 1000,
[x
k
]
1,2
= 10.
• Given a k-bit string x
k
, we denote by [x
k
]
i
with
1 ≤ i ≤ k the i-th left-most bit, i.e., [x
k
]
i,i
.
• We denote by x
i
x
j
the (i+ j)-bit string obtained
by appending x
j
to x
i
.
• Given a k-bit string x, we denote by
−→
x the k-bit
string obtained from x by circularly right shifting
it as many times as the number of 1s occurring in
it. For example, given x = 1100, then
−→
x = 0011.
• Finally, we denote by 1
k
(0
k
, resp.) the k-bit string
composed of all 1s (0s, resp.).
3 PRNG SCHEME
In this section, we define our PRNG that adopt a
1023-bit states and generates 128-bit numbers. Our
PRNG is based on the L’Ecuyer definition (L’Ecuyer,
1994). Thus, it consists of a tuple hS,T,O ,g,s
0
i
where S is the finite state set, T : S → S the tran-
sition function, O the output space, g : S → O the
output function, and s
0
∈ S the (initial) seed of the
generator. Starting from the initial state s
0
and using
the transition function, the PRNG produces a chain
of states s
0
,s
1
,s
2
,.. . such that s
i
= T(s
i−1
) for each
i ≥ 1. From each state of this chain, say s
c
, it is pos-
sible to compute x
c
= O(s
c
) which is the c-th random
number generated starting from the initial seed s
0
.
States of our PRNG consists in 1023-bit strings,
so that |S| = 2
1023
. The transition function T is para-
metric with respect to a positive odd integer m and is
defined as follows.
Definition 3.1. Given a k-bit string s
k
, with k = 1023,
we define T(s
k
) =
e
s
k
+ m.
In words, T(s
k
) is obtained by reversing the string
s
k
and, then, by summing m (modulo 2
k
).
Obviously, the first requirement for a good
L’Ecuyer PRNG is that the period of the function T is
as large as possible, hopefully 2
k
(the upper bound).
Theorem 4.1 in Section 4.4 proves that the function T
of our PRNG has maximum period (i.e., 2
k
).
The output function is used to produce a random
number x from the current state s, with the require-
ment that the knowledge of x does not give an at-
tacker the possibility of guessing s. To do this, a one-
way function, such as a cryptographic hash function,
can be adopted (as it often happens in state-of-the-art
PRNG). With the purpose of saving computational ef-
fort, we observethat we can be satisfied also by a non-
cryptographic hash function whose inversion is com-
putational feasible, but the number of average collid-
ing states generating the same output is so big that it
is infeasible to guess the actual state (corresponding
to the observed output). This principle can be prof-
itable applied in our case if the knowledge of a col-
liding state does not give the attacker any advantage,
and the weakness of the hash function does not allow
the attacker to apply cryptanalysis-based attacks.
Following the above approach, we implement the
output function as a modified version of CRC (Cyclic
Redundancy Check) (Hill, 1979), which is a non-
cryptographic hash function widely used in error-
detection context.
Classical CRC is computed to produce a n-bit
string, named checksum, starting from an arbitrary
length string, called frame, such that also a slight
change of the frame produces a different checksum.
The checksum is computed as the rest of the binary
division with no carry bit (it is identical to XOR),
of the frame, by a predefined generator polynomial,
a (n + 1)-bit string representing the coefficients of a
polynomial with degree n. CRC is thus parametric
w.r.t. the generator polynomial and for this reason
SECRYPT2014-InternationalConferenceonSecurityandCryptography
322

there are many kinds of CRCs. For example, the most
frequently used are CRC32 or CRC64, which gener-
ate a checksum of length 32 and 64 bits, respectively.
Obviously, the higher the checksum length, the better
the effectiveness of CRC in error-detecting is. In our
PRNG, we use a 128-bit CRC.
Observe that, given a k-bit frame s
k
and its w-
bit (with k > w) checksum c
w
computed by CRC,
there exist 2
k−w
(colliding) k-bit strings s
k
i
such that
CRC(s
k
i
) = c
w
. Moreover, its implementation easi-
ness and efficiency make CRC very appealing to be
used in this context.
Besides these nice features, CRC is not immune
from malicious attacks exploiting its linearity w.r.t.
XOR. As a consequence, we have modified CRC de-
sign keeping the nice computational features of CRC
but eliminating its weakness. The new CRC is ob-
tained by applying r cyclic right shifts to the state be-
fore the standard CRC computation, where r is equal
to the number of 1s occurring in the state itself.
We have seen that CRC is parametric w.r.t. the
length of the generator-polynomial and the values of
its coefficients. Consequently, the efficacy of CRC
strictly depends also on the latter parameter.
Now we are ready to define our output function g
(recall that we denote by
−→
s
k
c
the k-bit string obtained
from s
k
c
by circularly right shifting it as many times as
the number of 1s occurring in it).
Definition 3.2. Given a k-bit string s
k
c
, with k = 1023,
then g(s
k
c
) =CRC128(
−→
s
k
c
).
Concerning the implementation of CRC adopted
in our output function, we use the 128-bit CRC hav-
ing coefficients set according to the ECMA standard
(ECMA, 1992) (thus choosing a concrete application
setting among others).
4 SECURITY ANALYSIS
In this section, we analyze the robustness of the pro-
posed number generation scheme both by statistical
analysis of randomness and by considering a number
of possible strategies followed by an attacker to guess
future output.
4.1 Randomness of the Generation
Scheme
To check whether the output of our PRNG seems to be
random, we used the National Institute of Standards
and Technology statistical test suite, named NIST
800-22 (Rukhin et al., 2001), which consists of 16
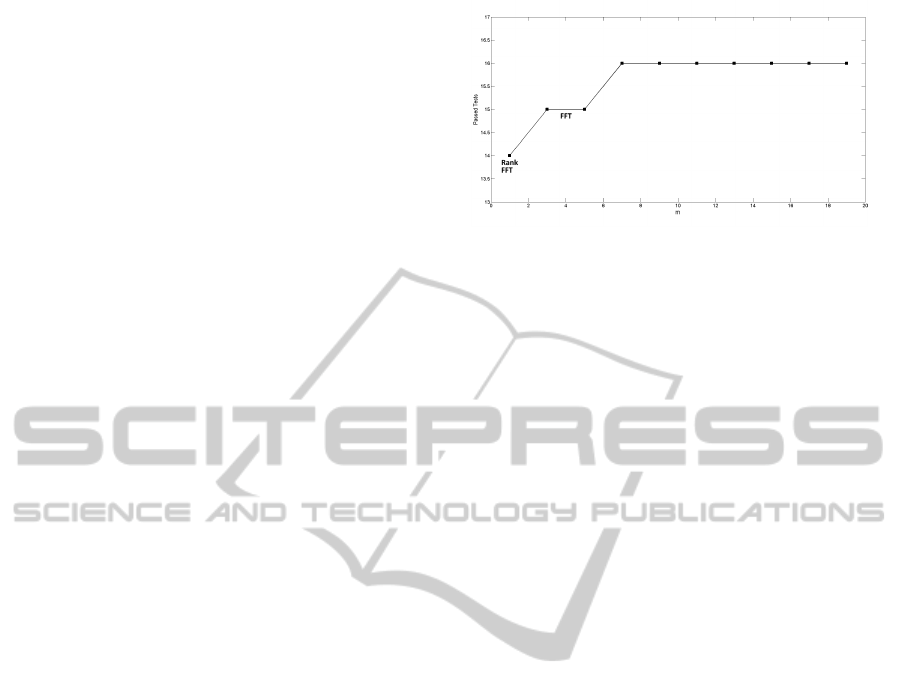
Figure 1: Passed tests for different values of m.
tests focusing on a variety of different types of non-
randomness that could exist in a sequence.
The results of our experimental campaign allow
us to state that, according to the German Federal
Office for Information Security (BSI) (Bundesamt
f¨ur Sicherheit in der Informationstechnik, 2014), our
PRNG is at least in class K2. Schemes in K2 generate
random numbers having similar statistical properties
to random numbers which have been generated by an
ideal random number generator (Schindler, 1999).
In order to test our PRNG, we have generated 100
sequences of 10
6
bits as required by the suite (Rukhin
et al., 2001) and then we have performed all the sta-
tistical tests. Each test is based on a calculated test
statistic value, which is a function of the data. The
test statistic is used to calculate a P-value representing
the probability that a perfect random number genera-
tor would have produced a sequence less random than
the sequence that was tested. If a P-value for a test
is equal to 1, then the sequence appears to have per-
fect randomness. A P-value equal to zero indicates
that the sequence appears to be completely non ran-
dom. Typically, a significance level α is fixed for the
test. As suggested by the suite, in our experiments, we
fixed α = 0.01, thus expecting one sequence in 100
sequences to be rejected by the test if the sequence
was random.
In the first experiment, we test the randomness of
the numbers produced by our PRNG varying the pa-
rameter m of the transition function, which, we recall,
represents the number of increments of the state to be
performed. In Figure 1, we report the overall number
of tests passed by our PRNG for different values of m.
Moreover, whenever this number is less than 16, we
report also which tests failed.
From the analysis of this figure, we observe that
even low values of m produce numbers with good
randomness properties, only for m ≥ 7, our PRNG is
able to pass all the tests. In particular for m = 1, both
Rank and FFT tests fail, while for m = 3 and m = 5
only FFT test is not passed. Recall that the purpose of
the rank test is to check for linear dependence among
fixed length substrings of the original sequence, while
ANovelPseudoRandomNumberGeneratorBasedonL'Ecuyer'sScheme
323

FFT test is able to detect periodic features (i.e., repet-
itive patterns that are near each other) in the tested
sequence that would indicate a deviation from the as-
sumption of randomness.
Now, we focus on the analysis of our PRNG when
m = 7. We report in Table 1 the results obtained with
the NIST test battery (Rukhin et al., 2001). When
a test produces more than one P-value, we averaged
them and marked the test by the symbol
⋄
. The min-
imum pass rate for each statistical test is about 0.96.
From the analysis of these results, we can conclude
that the output produced by our PRNG set m = 7
seems to be random.
We have performed another experiment aimed at
showing that the randomness of our PRNG derives by
the combination of the transition function T and the
output function g. In particular, we havesubstituted in
the scheme the function T with a simple counter func-
tion. Indeed, it is well known that full randomnesscan
be obtained by applying a cryptographic hash func-
tion like SHA-1 to just a counter. But recall that our
output function is a non-cryptographic hash function,
so we cannot expect the same result. Indeed, the ob-
tained sequences are very far from being random, as
shown by the randomness tests whose results are re-
ported in Table 2. In this table, we mark by the sym-
bol * the six failed tests.
In the next sections, we provide a first analysis
of the security of our PRNG under the cryptanalysis
point of view. Such an analysis is necessary to argue
that our schema is in class K3 and K4 according to
the German Federal Office for Information Security.
4.2 CRC-Linearity-based Attack
It is well known that CRC is not immune from mali-
cious attacks exploiting its linearity w.r.t. XOR. In
particular, it holds that CRC(a XOR b) =CRC(a)
XOR CRC(b), that is, the checksum of the XOR of
two numbers is equal to the XOR of the checksums
of the two numbers. In the case of our output func-
tion, which is based on CRC, this property could be in
principle exploited by an attacker to obtain the output
of the i-th state of an user (i.e., x
i
=CRC(s
k
i
)) start-
ing from the knowledge of (1) the output of the j-
th state of the user and (2) the XOR between s
k
i
and
s
k
j
. Moreover, observe that the transition function op-
erates a reverse of the string at each step just to in-
troduce a suitable “noise”, moving away its behavior
from the pure XOR (that would allow the attack de-
scribed above). The simple increment
1
(the simplest
1
In favor of security, we set the step size of the transition
function m = 1, which is obviously the most advantageous
case for the adversary.
transition function that one could imagine) behaves
exactly as a XOR every time the sum does not pro-
duce carry (i.e., every two steps). Unfortunately, it
is easy to verify that the introduction of the reverse
operation, even though beneficial, is not enough. In-
deed, every two steps, the “noise” introduced by the
reverse operation is quasi-cancelled. We use the pre-
fix quasi because the transition function includes also
the increment at each step.
To understand how this could be exploited for an
attack, we observe that when a state s
k
i
has both the
left-most and the right-most bit 0 (i.e., every four
steps), the attacker knows that s
k
i
XOR s
k
i+2
= 10
k−2
1
(recall that, according to our preliminary notations,
10
k−2
1 denotes a k-bit string of the form 1· ··1, with
k− 2 0s). Thus, the CRC of s
k
i+2
is easily predictable
by exploiting the above property. This behavior can
be generalized also for other bit configurations. It
is easy to see that if s
k
i
is of the form 00···01, then
we expect that the XOR with the state generated two
steps ahead is of the form 10
k−3
11. Again, if s
k
i
is of
the form 10·· ·00, then we expect that the XOR with
s
k
i+2
is of the form 110
k−3
1. Finally, if s
k
i
is of the
form 10· ··01, then we expect that the XOR with s
k
i+2
is of the form 110
k−4
11. This is a symptom of the
alternating destructive effect of the reverse operation
and, further, of the general invariance of the internal
part of the state, when the transition function is ap-
plied. Observe that this negative effect is maximum
whenever the state is palindromic, because the effect
of the reverse is null also on a single step.
The next theorem gives us the probabilistic sup-
port that a quasi-random generation of the initial seed
prevents this drawback for the entire life time of the
PRNG in a real-life application.
Theorem 4.1. Let t and k be two positive integers
such that t < 2
k−4
2
. Let s
k
be a k-bit state of the form
10c
j
d
k−4−2 j
e
j
00, where c
j
and e
j
are j-bit strings,
d
k−4−2 j
is a (k− 4− 2j)-bit string containing at least
one 0 and j = ⌈log
2
t⌉ + 1. It holds that the sequence
S
t
= hs
k
0
,.. ., s
k
t
i such that s
k
0
= T(s
k
) and s
k
r
= T(s
k
r−1
)
for 1 ≤ r ≤ t does not contain any state of the form
10f
k−4
01, where f
k−4
is a (k− 4)-bit string.
Proof. The proof is omitted for space reasons.
The theorem states that (i) fixing both the first and
the last two bits of the initial seed (to 10 and 00, re-
spectively), and (ii) ensuring that the seed contains
an internal centered range whose bounds are distant
⌈log
2
t⌉ + 1 from the bottom (and the top) of the seed
itself such that at least one 0 occurs in this interval,
then it results that for at least t/m applications of the
transition function (considering now any value for m),
SECRYPT2014-InternationalConferenceonSecurityandCryptography
324

Table 1: Results obtained with the NIST battery.
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 P-VALUE PROPORTION STATISTICAL TEST
9 6 6 19 7 11 7 8 15 12 0.055361 0.99 Frequency
13 11 6 9 8 15 14 13 5 6 0.202268 0.98 BlockFrequency
11 7 12 2 10 13 15 7 8 15 0.090936 1.00 CumulativeSums
12 11 8 11 7 10 10 11 9 11 0.987896 0.99 CumulativeSums
4 11 12 7 14 8 10 11 11 12 0.574903 0.99 Runs
9 7 11 9 13 9 9 12 11 10 0.971699 0.99 LongestRun
8 11 11 8 10 12 9 11 10 10 0.996335 0.98 Rank
15 11 7 15 8 7 9 6 8 14 0.275709 1.00 FFT
9 9 7 13 10 6 15 12 8 11 0.637119 0.99 NonOverlappingTemplate
⋄
15 7 12 11 8 12 9 7 10 9 0.759756 0.97 OverlappingTemplate
9 12 9 12 10 11 8 13 10 6 0.911413 1.00 Universal
5 16 11 12 13 7 9 9 7 11 0.383827 0.98 ApproximateEntropy
5 6 5 7 4 5 8 9 10 5 0.706149 0.98 RandomExcursions
⋄
4 4 3 6 7 12 4 10 5 9 0.122325 0.98 RandomExcursionsVariant
⋄
9 9 7 10 13 10 9 13 7 13 0.851383 0.97 Serial
9 11 7 7 9 20 8 10 10 9 0.181557 0.98 Serial
11 5 7 15 11 9 8 12 11 11 0.616305 1.00 LinearComplexity
Table 2: Results obtained when T is replaced by the counter function.
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 P-VALUE PROPORTION STATISTICAL TEST
6 8 4 12 7 10 12 11 13 17 0.153763 1.00 Frequency
6 14 19 10 6 7 6 7 11 14 0.035174 0.99 BlockFrequency
3 11 7 6 8 9 11 14 11 20 0.019188 1.00 CumulativeSums
2 10 5 6 12 7 11 6 15 26 0.000004 1.00 CumulativeSums
39 8 7 9 5 9 7 5 6 5 0 0.83 * Runs
11 13 8 9 10 7 11 13 11 7 0.883171 1.00 LongestRun
100 0 0 0 0 0 0 0 0 0 0 0.00 * Rank
100 0 0 0 0 0 0 0 0 0 0 0.00 * FFT
16 10 9 10 8 8 12 9 11 7 0.739918 0.97 NonOverlappingTemplate
⋄
13 16 8 12 14 5 10 12 5 5 0.096578 1.00 OverlappingTemplate
13 10 10 14 5 6 5 12 16 9 0.153763 0.98 Universal
34 4 3 2 6 6 4 3 5 33 0 0.79 * ApproximateEntropy
10 4 5 7 8 8 4 6 5 3 0.602458 0.95 * RandomExcursions
⋄
8 8 5 12 3 4 1 7 3 9 0.048716 0.98 RandomExcursionsVariant
⋄
50 6 3 4 5 2 3 6 7 14 0 0.67 * Serial
34 12 3 4 3 4 5 3 11 21 0 0.82 * Serial
6 12 10 7 9 18 10 15 7 6 0.108791 1.00 LinearComplexity
we do not generate bad seeds (i.e., seeds of the form
10· ··01). For example, given m = 7, in order to have
the above property for the first 2
64
output numbers,
we have to consider t = 7· 2
64
≈ 2
67
, and we have to
set the initial seed to 10s
65
1
s
k−134
s
65
2
00, where s
65
1
, s
65
2
and s
k−134
are randomly generated, with the only con-
straint that s
k−134
contains at least one 0. It is easy to
verify that the probability that a randomly generated
string s
k−134
does not satisfies the above requirement
is
1
2
k−134
. Thus, the blind random generation could be
also accepted, because, in our case in which k = 1023,
this probability is
1
2
889
.
4.3 Palindrome-based Attack
As described in Section 3, our generation scheme
needs an initial seed s
k
. The natural way to set the
initial seed is clearly its random generation. Nothing
seems to dissuade from this simple and effective ap-
proach.
However, note that the reverse done by the transi-
tion function is vanished whenever the string is palin-
dromic. This forces us to understand if a random
generation of a seed can (probabilistically) result in
such a bad situation. The next theorem shows that
the probability of this event is actually negligible for
sufficiently large k.
Theorem 4.2. The probability that a randomly gen-
erated k-bit string, with k mod 2 6= 0, is palindromic
is 2
−
k−1
2
.
Proof. First we prove the following claim. Claim 1.
ANovelPseudoRandomNumberGeneratorBasedonL'Ecuyer'sScheme
325

The number of palindromic k-bit strings such that k
is odd is 2
k+1
2
. We prove Claim 1 by induction on k
(odd). Basis (k = 1). Trivial. Induction (k > 1 and
k mod 2 6= 0). We assume that the claim holds for
a k > 1 such that k mod 2 6= 0. We have to prove
that it holds for k + 2 too. The palindromic strings
of length k + 2 are of the form: either 0p
k
0 or 1p
k
1,
where p
k
denotes a palindromic k-bit string. As a con-
sequence the number of palindromic strings of length
k + 2 is twice the number of palindromic strings of
length k. The statement is thus proved. The theorem
statement follows immediately from Claim 1, since
the probability of occurrence of a palindromic string
is
2
k+1
2
2
k
.
On the basis of the above theorem, we can eas-
ily realize that for treatable values of k, the resulting
probability is negligible. For example, if k = 1023,
then the probability of having a palindromic initial
seed is 2
−511
.
4.4 Output-Observation-Based Brute
Force Attacks
In this section, we examine the attack carried out by
observing the output generated by the PRNG. As we
have shown that cryptographic attacks cannot be car-
ried out, in this section we consider brute force at-
tacks.
The first attack we examine is the naive one: The
adversary observes the output looking for some peri-
odic repetition of generated numbers. To show that
this attack is unfeasible it suffices to prove that the
periodicity of the function T(s
k
) =
e
s
k
+ m is as large
as possible, hopefully 2
k
(i.e., the upper bound). This
means that, starting from a k-bit string s
k
, it is possi-
ble to generate 2
k
− 1 different new states before re-
obtaining s
k
. This is guaranteed by the next theorem.
Theorem 4.3. Given a k-bit string s
k
0
with k mod 2 6=
0, let S
k
be the sequence hs
k
0
,.. ., s
k
2
k
−1
i such that s
k
i
=
T(s
k
i−1
) for 1 ≤ i ≤ 2
k
− 1.
Then it holds that s
k
i
6= s
k
j
, for any i, j such that
0 ≤ i < j ≤ 2
k
− 1.
Proof. We proceed by induction on the length k of the
strings.
Basis (k = 1). Trivial: the sequence R
1
is h0,1i.
Induction (k > 1 and k mod 2 6= 0). We assume that
the theorem holds for a k > 1 such that k mod 2 6= 0.
We have to prove that it holds for k + 2 too. We start
the proof by considering r
k+2
0
as the (k + 2)-bit string
obtained by 0r
k
0
0. We proceed by computing the next
values of r
k+2
0
. By reversing r
k+2
0
and by adding 1, we
have r
k+2
1
= T(r
k+2
0
) = (0er
k
0
0) + 1 = 0er
k
0
1. Similarly,
we obtain r
k+2
2
= (0er
k
0
1) + 1 = (1r
k
0
0) + 1 = 1r
k
0
1.
Now, after the inversion of r
k+2
2
we obtain the string
1er
k
0
1, and after the increasing, the last bit of the string
becomes 0, with a carry bit to er
k
0
. Thus, r
k+2
3
=
1(er
k
0
+1)0 = 1r
k
1
0, since r
k
1
= T(r
k
0
) = (er
k
0
+1). Again,
we obtain that r
k+2
4
= (0er
k
1
1)+ 1 = 0(er
k
1
+1)0 = 0r
k
2
0,
since r
k
2
= T(r
k
1
) = er
k
1
+ 1. We can easily generalize
the above reasoning to the first 2
k+1
elements of R
k+2
.
In particular, for each r
k+2
i
with 0 ≤ i < 2
k+1
, we have
that:
1. if i mod 4 = 0, then r
k+2
i
= 0r
k
j
0
2. if i mod 4 = 1, then r
k+2
i
= 0er
k
j
1
3. if i mod 4 = 2, then r
k+2
i
= 1r
k
j
1
4. if i mod 4 = 3, then r
k+2
i
= 1r
k
j+1
0
where j = (i/4)∗2 and / denotes the integer division.
Now we have to characterize the remaining values
of R
k+2
. The last value generated by the rules aboveis
r
k+2
2
k+1
−1
= 1r
k
(2
k+1
−1)/4∗2+1
0 = 1r
k
2
k
−1
0. By inductive
hypothesis,r
k
2
k
−1
= 1
k
(i.e., it is the k-string composed
by all 1s). Thus, r
k+2
2
k+1
−1
= 1
k+1
0, that is, it is com-
posed by all 1s but the last right-most bit. After the
inversion we obtain er
k+2
2
k+1
−1
= 01
k+1
and after adding
1, it results that r
k+2
2
k+1
= 10
k+1
= 1r
k
0
0, since r
k
0
= 0
k
.
Then we compute r
k+2
2
k+1
+1
= 1er
k
0
0+ 1 = (0er
k
0
1) + 1 =
0(er
k
0
+1)0 = 0r
k
1
0. Again, r
k+2
2
k+1
+2
= (0er
k
1
0)+1 = 0er
k
1
1
and r
k+2
2
k+1
+3
= 1r
k
1
1. Thus, the general rules character-
izing the last 2
k+1
values of R
k+2
are the following.
For each r
k+2
i
such that 2
k+1
≤ i < 2
k+2
, we have that:
1. if i mod 4 = 0, then r
k+2
i
= 1r
k
j
0
2. if i mod 4 = 1, then r
k+2
i
= 0r
k
j+1
0
3. if i mod 4 = 2, then r
k+2
i
= 0er
k
j+1
1
4. if i mod 4 = 3, then r
k+2
i
= 1r
k
j+1
1
where j = (i−2
k+1
)/4∗ 2. Observe that the last value
is thus r
k+2
2
k+2
−1
= 1r
k
2
k
−1
1. By inductive hypothesis,
r
k
2
k
−1
= 1
k
. As a consequence, we have proved item
(2) of the theorem. Let us prove now item (1). By
construction, all 2
k+2
elements of R
k
differ each other
at least either on the left-most bit, or on the right-most
bit or on the sub-string r
k
i
. This proves the item (1) of
the claim.
Theorem 4.1 follows immediately from Claim 1. In-
deed, we know that r
k
0
∈ S
k
since S
k
contains all 2
k
k-bit strings. Let i be such that s
k
i
= r
k
0
. To prove
the statement we will show that each element of R
k
is
equal to an element of S
k
and in particular that r
k
a
= s
k
b
where b = (a+ i) mod 2
k
. We will demonstrate this
equality for (1) 0 ≤ a < 2
k
− i, (2) a = 2
k
− i and
SECRYPT2014-InternationalConferenceonSecurityandCryptography
326

(3) 2
k
− i < a < 2
k
. (1) By construction, r
k
a
= s
k
a+i
for 0 ≤ a < 2
k
− i. As a consequence, r
k
2
k
−i−1
=
s
k
2
k
−1
= 1
k
. (2) Since T(r
k
2
k
−i−1
) = T(1
k
) = 0
k
we
have that r
k
2
k
−i
= s
k
0
. (3) By construction, r
k
a
= s
k
a+i
for 0 ≤ j < 2
k
− i.
Now we prove that also the definition of g pre-
serves the property of the transition function of gen-
erating 2
k
different states. Thus, we have to guarantee
that two different states do not collide into the same
value after the shifting. The next theorem ensures
this.
Theorem 4.4. Given a sequence (of k-bit strings)
S
k
= hs
k
0
,.. .,s
k
2
k
−1
i such that s
k
i
= T(s
k
i−1
) for 1 ≤ i ≤
2
k
− 1, let
−→
S
k
= h
−→
s
k
0
,.. .,
−−→
s
k
2
k
−1
i.
Then it holds that
−→
s
k
i
6=
−→
s
k
j
, for each i and j such
that 0 ≤ i < j ≤ 2
k
− 1.
Proof. We proceed by contradiction. Suppose that
−→
s
k
i
=
−→
s
k
j
with i 6= j. Let u be the number of 1s in
−→
s
k
i
(and, consequently, also in
−→
s
k
j
). Now, shifting both
numbers by u left circular shifts, we obtain s
k
i
and s
k
j
,
respectively, with s
k
i
= s
k
j
by construction. Since this
contradicts Theorem 4.1, it results that
−→
s
k
i
6=
−→
s
k
j
.
Now consider more sophisticated attacks based on
the observation of the output. The most simple case is
when the attacker knows just one output number, say
PRN
i
. At this point the attacker has to find the orig-
inal state s
i
such that g(s
i
) =CRC128(
−→
s
i
) = PRN
i
.
Since the number of colliding states w.r.t. CRC128 is
2
1023
/2
128
= 2
895
, guessing one of these states is in-
feasible. Let check now what happens if the adversary
randomly selects one of the above states. If the value
s
i
chosen by the attacker (among the 2
895
states) dif-
fers from the actual s
i
(i.e., the current state), then the
probability that g(T(
s
i
)) = g(T(s
i
)) is
1
2
128
. Observe
that the above probability coincides with the probabil-
ity of guessing a valid output number with no back-
ground knowledge.
Now consider the case the attacker knows a se-
quenceC of c consecutive output numbers. By a brute
force attack, the attacker should test (
2
128
2
)
c
states to
find a state
s such that it produces such a sequence C.
Observe that, since our generation scheme produces
a mapping between a set of 2
1023
strings and a set of
2
128
numbers, by relying on oracles able to guess the
used state among the 2
128
ones, the adversary would
be able to guess the future output if the length of the
observed string is at least 8, since 1023/128− 1 ≈ 8.
However, the probability of having such oracles is
Algorithm 1: The Transition Function.
Input: m ≥ 1 odd
Input: s
k
1: for a = 1 to m do
2: b = 0
3: while [s
k
]
k−b
= 1 do
4: [s
k
]
k−b
= 0, b = b+ 1
5: end while
6: [s
k
]
k−b
= 1
7: end for
8: for a = 1 to ⌊k/2⌋ do
9: swap [s
k
]
a
and [s
k
]
k−a+1
10: end for
11: return s
∑
8
i=1
2
−128
= 2
−1024
, which represents obviously an
impossible event.
5 COMPLEXITY ISSUES
In this section, we show that our PRNG is efficient in
both the transition and the output function.
Concerning the transition function, we show by
Algorithm 1 how to compute s
k
+ p starting from s
k
.
An improved version of this algorithm will be pre-
sented after. The first one (Lines 1-7) produces p in-
crements by 1 of the state. Each increment is achieved
as follows. If the right-most bit is 0, then it is set to 1
and the single increment ends. Otherwise, it is set to 0
and the procedure is iterated to the left-most adjacent
bit. The second block (Lines 8-10) performs the state
reversing.
Concerning the second block, we observe that it
can be omitted provided that a slight modification in
the first block is implemented. Indeed, instead of re-
versing the state at each step, we can apply the incre-
ments alternatively on the left side (for the first, third,
fifth, and so on, generated PRNs) and on the right side
(for the second, fourth, and so on generated PRNs).
The next theorem shows that the implementation
of the transition function is very efficient.
Theorem 5.1. The amortized cost of the transition
function algorithm is constant in the number of bits of
the state.
Proof. The algorithm requires to set to 1 either the
right-most bit, when the last bit of the state is 0 (the
probability that this case occurs is 1/2), or the second
last bit when the state ends by 01 (this has probabil-
ity 1/4), or the third last one if the string ends by 011
(the probability is 1/8), and so on. The same occurs
when increments are done on the left side. As a con-
sequence, the amortized complexity of m increments
is
∑
m
a=1
a·
1
2
a
≤ 2.
ANovelPseudoRandomNumberGeneratorBasedonL'Ecuyer'sScheme
327

Concerning the output function, we observe that
CRC is widely used thanks to its efficiency. Indeed,
CRC efficiency is reached in hardware by a modified
shift register (Dubrova and Mansouri, 2012) and in
software by processing the state in units larger than
one single bit. Depending on the architecture on
which CRC is carried out, the unit can be composed of
4, 8, 16, 32, 64 or 128 bits. The algorithm is speed up
by means of a pre-computed lookup table depending
only on the coefficients of the CRC generator polyno-
mial.
6 CONCLUSION AND FUTURE
WORK
In this paper, we have presented a new lightweight
pseudo random number generator and we have shown
both its randomness and security. The PRNG is
based on very simple operations performed on 1023-
bit states, which correspond to increment a state by
a suitable odd value m and then to reverse the so ob-
tained bit string. Finally, an extended version of CRC
is applied, allowing us to produce at each step a 128-
bit output number. In this position paper, we have
provided a first deep security analysis of our scheme,
by showing that it is truly random and resistant to
a number of possible attacks. As a future work we
plan to deepen the study of the PRNG security against
cryptanalysis attacks and to compare our PRNG with
existing PRNGs on the aspect of efficiency, also by
means of a hardware implementation. Indeed, we
guess that our PRNG is very competitive under this
point of view, as it is based on very simple operations.
ACKNOWLEDGEMENTS
This work has been partially supported by the
TENACE PRIN Project (n. 20103P34XC) funded
by the Italian Ministry of Education, University and
Research and by the Program “Programma Operativo
Nazionale Ricerca e Competitivit`a” 2007-2013, Dis-
tretto Tecnologico CyberSecurity funded by the Ital-
ian Ministry of Education, University and Research.
REFERENCES
Alcaraz, C. and Lopez, J. (2010). A security analysis
for wireless sensor mesh networks in highly criti-
cal systems. Systems, Man, and Cybernetics, Part
C: Applications and Reviews, IEEE Transactions on,
40(4):419–428.
Blum, L., Blum, M., and Shub, M. (1986). A simple un-
predictable pseudo-random number generator. SIAM
Journal on computing, 15(2):364–383.
Buccafurri, F. and Lax, G. (2011). Implementing dispos-
able credit card numbers by mobile phones. Electronic
Commerce Research, 11(3):271–296.
Bundesamt f¨ur Sicherheit in der Informationstechnik
(2014). http://www.bsi.de/english/index.htm.
Cox, G., Dike, C., and Johnston, D. (2011). Intels Digi-
tal Random Number Generator (DRNG). Technical
report, Intel.
Dolev, S., Gilboa, N., Kopeetsky, M., Persiano, G., and
Spirakis, P. G. (2011). Information security for sen-
sors by overwhelming random sequences and permu-
tations. Ad Hoc Networks.
Dubrova, E. and Mansouri, S. S. (2012). A bdd-based ap-
proach to constructing lfsrs for parallel crc encoding.
In Multiple-Valued Logic (ISMVL), 2012 42nd IEEE
International Symposium on, pages 128–133. IEEE.
ECMA (1992). ECMA-182: Data Interchange on 12,7 mm
48-Track Magnetic Tape Cartridges — DLT1 Format.
EPCglobal, E. (2004). Radio-frequency identity protocols
class-1 generation-2 uhf rfid protocol for communica-
tions at 860 mhz–960 mhz version 1.0. 9. K. Chiew et
al./On False Authenticationsfor C1G2 Passive RFID
Tags, 65.
Hill, J. R. (1979). A table driven approach to cyclic redun-
dancy check calculations. SIGCOMM Comput. Com-
mun. Rev., 9(2):40–60.
Huang, Y.-J., Yuan, C.-C., Chen, M.-K., Lin, W.-C., and
Teng, H.-C. (2010). Hardware implementation of rfid
mutual authentication protocol. Industrial Electron-
ics, IEEE Transactions on, 57(5):1573–1582.
L’Ecuyer, P. (1994). Uniform random number generation.
Annals of Operations Research, 53(1):77–120.
Li, Y. and Zhang, X. (2005). Securing credit card trans-
actions with one-time payment scheme. Electronic
Commerce Research and Applications, 4:413–426.
Elsevier Science Publishers B. V.
Meli`a-Segu´ı, J., Garcia-Alfaro, J., and Herrera-
Joancomart´ı, J. (2013). J3gen: A prng for low-cost
passive rfid. Sensors, 13(3):3816–3830.
National Institute of Standards and Technology (2014).
Federal Information Processing Standards Publica-
tion, Washington.
Rukhin, A., Soto, J., Nechvatal, J., Smid, M., and Barker,
E. (2001). A statistical test suite for random and pseu-
dorandom number generators for cryptographic appli-
cations. Technical report, DTIC Document.
Schindler, W. (1999). Functionality classes and evaluation
methodology for deterministic random number gener-
ators. Federal Office for Information Security (BSI).
Tang, B.-y., ZENG, N., ZHENG, L.-x., and CHEN, H.-
h. (2004). Design and implementation of web-
based remote supervisory system in the embedded
system. Journal-Xiamen University Natural Science,
43(5):632–635.
Wang, Y. (2011). sSCADA: securing SCADAinfrastructure
communications. International Journal of Communi-
cation Networks and Distributed Systems, 6(1):59–78.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
328