Nonlinear Models of BPSK Costas Loop
E. V. Kudryashova
1
, O. A. Kuznetsova
1
, N. V. Kuznetsov
1,2
, G. A. Leonov
1
, S. M. Seledzhi
1
,
M. V. Yuldashev
1,2
and R. V. Yuldashev
1,2
1
Faculty of Mathematics and Mechanics, Saint-Petersburg State University,
Universitetsky pr. 28, Saint-Petersburg, 198504, Russia
2
Dept. of Mathematical Information Technology, University of Jyv
¨
askyl
¨
a, P.O. Box 35 (Agora), FIN-40014, Finland
Keywords:
Costas Loop, BPSK, PLL, Phase-locked Loop, Simulation, Nonlinear Analysis.
Abstract:
Rigorous nonlinear analysis of the physical model of Costas loop is very difficult task, so for analysis, simpli-
fied mathematical models and numerical simulation are widely used. In the work it is shown that the use of
simplified mathematical models, and the application of non rigorous methods of analysis may lead to wrong
conclusions concerning the operability of Costas loop.
1 INTRODUCTION
The Costas loop is a classical phase-locked loop
(PLL) based circuit for carrier recovery (Costas,
1956; Costas, 1962). Nowadays various modifica-
tions of Costas loop circuit are used in many com-
munication devices, e.g. Global Positioning Systems
(GPS) (Kaplan and Hegarty, 2006). In the paper the
classical analog Costas loop (Costas, 1956; Gardner,
1966; Lindsey, 1972; Best, 2007), used for BPSK de-
modulation, is considered (similar analysis can also
be done for QPSK Costas loop).
Costas loop is essentially a nonlinear control sys-
tem and its physical model is described by a nonlinear
non-autonomous discontinuous system of differential
equations (mathematical model in the signal space).
This system is a slow-fast system since there is con-
sidered simultaneously both very fast time scale of
signals and slow time scale of phase difference be-
tween the signals.
Thus in practice, for the analysis of Costas loop it
is widely used various simplified mathematical mod-
els and their numerical simulation (Costas, 1956;
Gardner, 1966; Lindsey, 1972; Best, 2007; Best et al.,
2014b).
In the work it is shown that 1) the use of simplified
mathematical models, and 2) the application of non
rigorous methods of analysis (e.g., a simulation) may
lead to wrong conclusions concerning the operability
of physical model of Costas loop.
To demonstrate this, below Costas loop operation
will be considered in details.
2 BPSK COSTAS LOOP
OPERATION
Consider Costas loop operation (see Fig. 1) after tran-
sient processes.
=
1
2
g(t)≡const
LPF1
LPF2
Loop filter
VCO
sin(ωt-θ
Δ
)
m(t)sin(ωt)
90
o
data
carrier
(m(t)cos(θ
Δ
)-m(t)cos(2ωt-θ
Δ
))
1
2
(m(t)sin(θ
Δ
)+m(t)sin(2ωt-θ
Δ
))
input
φ(t)≡φ(θ
Δ
)
Figure 1: Costas loop is in lock (the case of nonequal fre-
quencies of input carrier and free running VCO output):
there is a constant phase difference θ
∆
after synchroniza-
tion.
The input signal is BPSK signal, which is a prod-
uct of the transferred data m(t) = ±1 and the har-
monic carrier sin(ωt) with a high frequency ω. Since
the Costas loop is considered to be in the locked state,
VCO (Voltage-Controlled Oscillator) signal is syn-
chronized with the carrier.
Assumption 1. The terms, whose frequency is about
twice the carrier frequency, do not affect the synchro-
nization of the loop.
By Assumption 1 the outputs of low-pass filters
LPF1 and LPF2 can be approximated in the follow-
ing way. After the multiplication of VCO signal and
the input signal by multiplier block (⊗) on the upper
branch one has
704
Kudryasoha E., Kuznetsova O., Kuznetsov N., Leonov G., Seledzhi S., Yuldashev M. and Yuldashev R..
Nonlinear Models of BPSK Costas Loop.
DOI: 10.5220/0005050707040710
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 704-710
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

=
1
2
g(t)
g
1
(t)
g
2
(t)
LPF1
LPF2
Loop filter
VCO
sin(θ
2
(t))
90
o
data
carrier
φ
1
(t)= m(t)(cos(θ
Δ
(t))-cos(θ
1
(t)+θ
2
(t)))
input
φ(t)≈ sin(2θ
Δ
(t))
1
8
m(t)sin(θ
1
(t))
1
2
φ
2
(t)= m(t)(sin(θ
Δ
(t))+sin(θ
1
(t)+θ
2
(t)))
Figure 2: Costas loop is out of lock: there is time-varying phase difference θ
∆
(t) = θ
1
(t) − θ
2
(t).
ϕ
1
(t) =
1
2
m(t) cos(0) − m(t)cos(2ωt)
=
=
1
2
m(t) − m(t)cos(2ωt)
≈
1
2
m(t),
(1)
i.e the upper loop works as demodulator. On the lower
branch the output signal of VCO, shifted by 90
◦
, is
multiplied by the input signal:
ϕ
2
(t) = m(t) sin(ωt)cos(ωt) =
=
1
2
m(t) sin(0) + m(t)sin(2ωt)
=
=
1
2
m(t) sin(2ωt) ≈ 0.
(2)
Since after a transient processes there is no phase
difference, the control signal at the input of VCO,
which is used for VCO frequency adjustment to the
frequency of input carrier signal, has to be constant:
g(t) = const. (3)
Consider Costas loop before synchronization (see
Fig. 2) in the case when the phase of the input carrier
θ
1
(t) and the phase of VCO θ
2
(t) are different:
θ
∆
(t) = θ
1
(t) − θ
2
(t) 6= 0. (4)
In this case the signals ϕ
1,2
(t) on the upper and lower
branches can be approximated as
ϕ
1
(t) =
1
2
m(t)
cos(θ
1
(t) − θ
2
(t)) − cos(θ
1
(t) + θ
2
(t))
≈
1
2
m(t)cos(θ
∆
(t)),
ϕ
2
(t) =
1
2
m(t)
sin(θ
1
(t) − θ
2
(t)) + sin(θ
1
(t) + θ
2
(t))
≈
1
2
m(t)sin(θ
∆
(t)).
(5)
Assumption 2. The data signal m(t) does not affect
the synchronization of the loop.
Thus after multiplication of the outputs of LPF1
and LPF2 the transmitted data m(t) is neglected in the
signal ϕ(t), i.e. one has m(t)
2
= (±1)
2
= 1.
Approximations (6) depend on the phase differ-
ence of signals, i.e. two multiplier blocks (⊗) on the
upper and lower branches operate as phase detectors.
Caveat to Assumptions. Low-pass filters can not
operate perfectly, especially, during the moments of
changing m(t), therefore the data pulse shapes are no
longer ideal rectangular pulses after filtration due to
distortion, created by the low-pass filters. This can
lead to incorrect conclusions on the performance of
the loop. One of such known examples is so-called
false-lock: while for m(t) ≡ const the loop acquires
lock and proper synchronization of the carrier and
VCO frequencies, for time-varying m(t) 6= const the
loop can acquire lock without proper synchronization
of the frequencies (false lock) (Olson, 1975; Simon,
1978; Hedin et al., 1978). To avoid such undesirable
situation one may try to choose loop parameters in
such a way that the synchronization time is less than
the time between changes in the data signal m(t) or to
modify the loop design (see, e.g., (Olson, 1975)).
Finally, by Assumption 2, one can use the follow-
ing approximation for the input of loop filter
ϕ(t) ≈ ϕ(θ
∆
(t)) =
1
8
sin(2θ
∆
(t)). (6)
Such an approximation, which depends on the phase
difference of signals, is called a phase detector char-
acteristic of Costas loop.
The relation between the input ϕ(t) and the output
g(t) of linear loop filter (Thede, 2005) has the form
dx
dt
= Ax + bϕ(t), g(t) = c
∗
x + hϕ(t),
(7)
where A is a constant matrix, the vector x(t) is a fil-
ter state, b,c are constant vectors, h is constant, and
x(0) is initial state of filter. The control signal g(t)
is used to adjust VCO frequency to the frequency of
input carrier signal
˙
θ
2
(t) = ω
2
(t) = ω
free
2
+ Lg(t). (8)
Here ω
f ree
2
is free-running frequency of VCO and L is
VCO gain.
If the frequency of input carrier is a constant:
˙
θ
1
(t) = ω
1
(t) ≡ ω
1
, (9)
then equations (7)-(9) give the following mathemati-
cal model of Costas loop:
NonlinearModelsofBPSKCostasLoop
705

˙x = Ax + bϕ(θ
∆
),
˙
θ
∆
= ω
∆
− L(c
∗
x) − Lhϕ(θ
∆
),
(10)
where θ
∆
(t) = θ
1
(t)−θ
2
(t) and ϕ(θ
∆
) corresponds to
expression (7). Note that the initial frequencies differ-
ence (at t = 0) has the form
˙
θ
∆
(0) = ω
∆
+ Lc
∗
x(0) + Lhϕ(θ
∆
(0)). (11)
Here to consider one-dimensional stability ranges de-
fined only by |ω
∆
| (see, e.g., capture and hold ranges)
it is necessary to assume that h = 0 and x(0) = 0.
For high-order filter, two different initial states ˜x(0)
and
˜
˜x(0) may lead to identical values of α
0
(0, ˜x(0)) =
α
0
(0,
˜
˜x(0)) but different functions α
0
(t, ˜x(0)) and
α
0
(t,
˜
˜x(0)) (to avoid this effect it is possible to require
the observability of system (8)).
G(t)
Loop filter
VCO
PD
θ
2
(t)
input
θ
1
(t) φ(θ
Δ
(t))
Figure 3: Classical (simplified) mathematical model of
BPSK Costas loop in the signal’s phase space.
System (11) considered in the classical works
(Costas, 1962; Lindsey, 1972) and corresponds to the
block-diagram shown in Fig. 3, where ϕ(θ
∆
) is phase
detector (PD) characteristic of Costas loop for sinu-
soidal signals.
Since mathematical model of Costas loop (11) is
nonlinear, in practice, for its analysis numerical sim-
ulation and linearization are widely used (Gardner,
2005; Lindsey, 1972; Best, 2007). Note that the lin-
earization without justification and the analysis of lin-
earized models of nonlinear control systems may re-
sult in incorrect conclusions
1
. Also the application
of standard numerical analysis of PLL-based circuits
cannot guarantee to find undesired multiple steady-
state solutions: see, e.g., examples of hidden oscilla-
tions
2
.
1
See, e.g., counterexamples to the filter hypothesis,
hidden oscillations in counterexamples to Aizerman’s and
Kalman’s conjectures on the absolute stability of nonlinear
control systems (Bragin et al., 2011), and the Perron effects
of the largest Lyapunov exponent sign reversal for a non-
linear system and its linearization (Kuznetsov and Leonov,
2005; Leonov and Kuznetsov, 2007).
2
An attractor is called a hidden attractor if its basin
of attraction does not intersect with small neighborhoods
of equilibria, otherwise it is called a self-excited attractor.
For example, hidden attractors are attractors in the systems
with no-equilibria or with the only stable equilibrium (a
special case of multistability and coexistence of attractors);
they arise in the study of well-known fundamental problems
such as 16th Hilbert problem, Aizerman & Kalman conjec-
In the next section a rigorous mathematical ap-
proach to derivation of nonlinear mathematical model
of Costas loop will be discussed.
3 RIGOROUS MATHEMATICAL
APPROACH TO DERIVATION
OF NONLINEAR
MATHEMATICAL MODEL OF
COSTAS LOOP
The relation between the inputs ϕ
1,2
(t) and the out-
puts g
1,2
(t) of linear low-pass filters is as follows
(Thede, 2005)
dx
1,2
dt
= A
1,2
x
1,2
+ b
1,2
ϕ
1,2
(t), g
1,2
(t) = c
∗
1,2
x
1,2
.
(12)
Here A
1,2
are constant matrices, the vectors x
1,2
(t) are
filter states, b
1,2
,c
1,2
are constant vectors, and the vec-
tors x
1,2
(0) are initial states of filters. For the loop
filter one can consider more general equation (8).
Taking into account (13), (8), and (9), one obtains
the mathematical model in the signal space describing
the physical model of BPSK Costas loop:
˙x
1
= A
1
x
1
+ b
1
m(t) sin(θ
1
(t))sin(θ
2
),
˙x
2
= A
2
x
2
+ b
2
m(t) sin(θ
1
(t))cos(θ
2
),
˙x = Ax + b(c
∗
1
x
1
)(c
∗
2
x
2
),
˙
θ
2
= ω
f ree
2
+ L(c
∗
x) + Lh(c
∗
1
x
1
)(c
∗
2
x
2
).
(13)
Here θ
2
(0) is the initial phase shift of VCO, and the
vectors x
1,2
(0),x(0) are initial states of filters. Thus
the initial VCO frequency (at t = 0) has the form
ω
2
(0) = ω
f ree
2
+ Lc
∗
x(0) + Lhc
∗
1
x
1
(0)c
∗
2
x
2
(0). (14)
The mathematical model in the signal space (14)
is nonlinear nonautonomous discontinuous differen-
tial system, so in general case its analytical study
is a difficult task even for the continuous case when
m(t) ≡ const. Besides it is a slow-fast system, so its
numerical study is rather complicated for the high-
frequency signals. The problem is that it is necessary
to consider simultaneously both very fast time scale of
the signals sin(θ
1,2
(t)) and slow time scale of phase
difference between the signals θ
∆
(t), therefore one
very small simulation time-step must be taken over a
tures and in applied research of Chua circuits, drilling sys-
tem, phase-locked loop based circuits, aircraft control sys-
tems and others (Kuznetsov et al., 2010; Bragin et al., 2011;
Leonov et al., 2012; Kuznetsov et al., 2013; Andrievsky
et al., 2013; Leonov and Kuznetsov, 2013; Leonov et al.,
2014).
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
706

very long total simulation period (Goyal et al., 2006;
Abramovitch, 2008a; Abramovitch, 2008b).
To overcome these problems, in place of using As-
sumption 1 one can apply averaging methods (Krylov
and Bogolyubov, 1947; Mitropolsky and Bogolubov,
1961; Samoilenko and Petryshyn, 2004; Sanders
et al., 2007) and consider a simplified mathematical
model in the signal’s phase space. However, this re-
quires the consideration of constant data signal (As-
sumption 2) and constant frequency of input carrier
(10):
θ
1
(t) = ω
1
t + θ
1
(0).
In this case (14) is equivalent to
˙x
1
= A
1
x
1
+ b
1
sin(ω
1
t + θ
1
(0))sin(ω
1
t + θ
1
(0) + θ
∆
),
˙x
2
= A
2
x
2
+ b
2
sin(ω
1
t + θ
1
(0))cos(ω
1
t + θ
1
(0) + θ
∆
),
˙x = Ax + b(c
∗
1
x
1
)(c
∗
2
x
2
),
˙
θ
∆
= ω
∆
− L(c
∗
x) − Lh(c
∗
1
x
1
)(c
∗
2
x
2
),
(15)
Assuming that input carrier is a high-frequency
signal (i.e. ω
1
is large), one can consider small pa-
rameter ε =
1
ω
1
and apply classical averring theory for
the equations of low-pass filters. Thus one can obtain
a mathematical model of BPSK Costas loop in the sig-
nal’s phase space (see Fig. 4):
˙x
1
= A
1
x
1
+
b
1
2
cos(θ
∆
),
˙x
2
= A
2
x
2
+
b
2
2
sin(θ
∆
),
˙x = Ax + b(c
∗
1
x
1
)(c
∗
2
x
2
),
˙
θ
∆
= ω
∆
− L(c
∗
x) − Lh(c
∗
1
x
1
)(c
∗
2
x
2
).
(16)
1
2
g(t)
G
1
(t)
G
2
(t)
LPF1
LPF2
Loop filter
VCO
PD
PD
θ
2
(t)
90
o
φ
1
(θ
Δ
(t))= cos(θ
Δ
(t))
input
φ(t)≈ sin(2θ
Δ
(t))
1
8
θ
1
(t)
1
2
φ
2
(θ
Δ
(t))= sin(θ
Δ
(t))
Figure 4: Mathematical model of BPSK Costas loop in the
signal’s phase space
Remark that here the initial frequencies difference
(at t = 0)
˙
θ
∆
(0) = ω
∆
− Lc
∗
x(0) − Lhc
∗
1
x
1
(0)c
∗
2
x
2
(0) (17)
is the same for system (17) and system (16) and it
does not coincide with expression (18) for classical
system (11). Here to consider one-dimensional sta-
bility ranges defined only by |ω
∆
| (see, e.g., capture
and hold ranges) it is necessary to assume that h = 0
and x(0) = x
1
(0) = x
2
(0) = 0.
In the general case one has to consider multi-
dimensional stability domain (ω
∆
,x(0), x
1
(0),x
2
(0)).
4 COUNTEREXAMPLES TO THE
ASSUMPTIONS
Note once more that various simplifications and the
analysis of linearized models of control systems may
result in incorrect conclusions
3
. At the same time the
attempts to justify analytically the reliability of con-
clusions, based on engineering approaches, and rigor-
ous study of nonlinear models are quite rare (see, e.g.,
(Abramovitch, 1990; Chang et al., 1993; Stensby,
1997; Shirahama et al., 1998; Watada et al., 1998;
Hinz et al., 2000; Wu, 2002; Piqueira and Mon-
teiro, 2003; Suarez and Quere, 2003; Margaris, 2004;
Vendelin et al., 2005; Banerjee and Sarkar, 2006;
Kudrewicz and Wasowicz, 2007; Wang et al., 2008;
Bueno et al., 2010; Wiegand et al., 2010; Stensby,
2011; Suarez et al., 2012; Sarkar et al., 2014; Chicone
and Heitzman, 2013; Yoshimura et al., 2013; Best
et al., 2014a)). One of the reasons is that “nonlin-
ear analysis techniques are well beyond the scope of
most undergraduate courses in communication the-
ory” (Tranter et al., 2010).
Further examples demonstrate that the use of As-
sumptions 1-2 requires further study and rigorous jus-
tification. The following examples demonstrate that
for the same parameters the behaviors of considered
models
• physical model (with data signal and low-pass fil-
ters) or its mathematical model in the signal space
(Figs. 2,5 and system (14))
• simplified mathematical model in the signal space
(without data signal and with low-pass filters))
(Figs. 2,5 with m(t) = const and system (16));
• simplified mathematical model the signal’s phase
space (with low-pass filters and without data sig-
nal) (Fig. 4 and system (17));
• classical mathematical model the signal’s phase
space (without low-pass filters and data signal)
(Fig. 3 and system (11))
may be very different from each other.
Simulation Parameters. Low pass filters transfer
functions H
l p f
(s) =
1
s/ω
3
+1
, ω
3
= 1.2566 ∗ 10
6
and
corresponding equations (8) parameters are A
1,2
=
−ω
3
, b
1,2
= 1, c
1,2
= 1; Loop filter transfer function
H
l f
(s) =
τ
2
s+1
τ
1
s
, τ
2
= 3.9789 ∗ 10
−6
, τ
1
= 2 ∗ 10
−5
,
3
see also counterexamples to the filter hypothesis, Aiz-
erman’s and Kalman’s conjectures on the absolute stability
of nonlinear control systems (Kuznetsov et al., 2011; Bra-
gin et al., 2011; Leonov and Kuznetsov, 2013), and the Per-
ron effects of the largest Lyapunov exponent sign inversions
(Kuznetsov and Leonov, 2005; Leonov and Kuznetsov,
2007), etc.
NonlinearModelsofBPSKCostasLoop
707
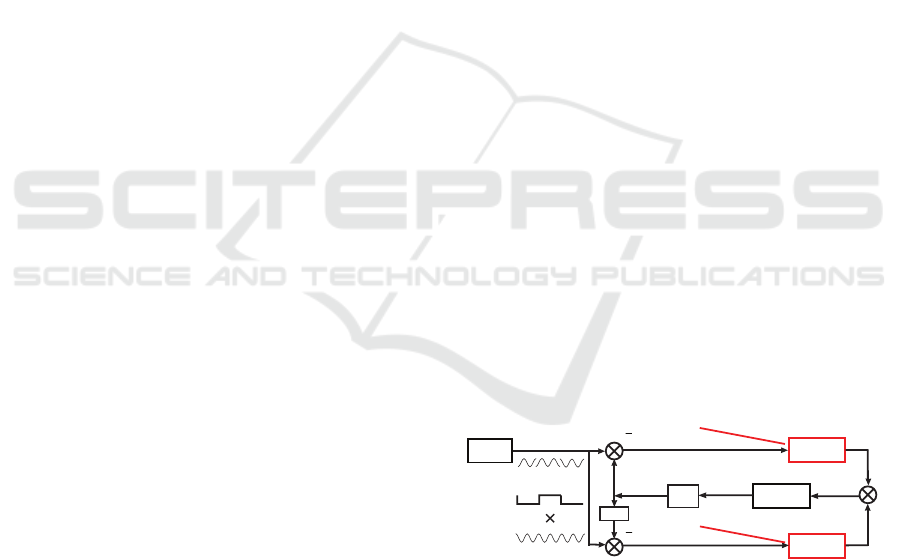
1
2
H
lpf
(s)
H
lpf
(s)
H
lf
(s)
sin(θ (t))
m(t)sin(θ (t))
90
o
g
1
(t)
g
2
(t)
input
x(0)
x
1
(0)
x
2
(0)
θ
2
(0)
1
s
sin
+
ω
free
(m(t)cos(θ
Δ
(t))-m(t)sin(θ
1
(t)+θ
2
(t)))
φ(t)≈ sin(2θ
Δ
(t))
1
2
(m(t)sin(θ
Δ
(t))+m(t)sin(θ
1
(t)+θ
2
(t)))
1
8
L
g(t)
θ
2
(t)
Figure 5: Block-diagram of Costas loop mathematical model in the signal space described by transfer functions and initial
conditions.
0
-0.9
-0.6
-0.3
0
0.02 0.04
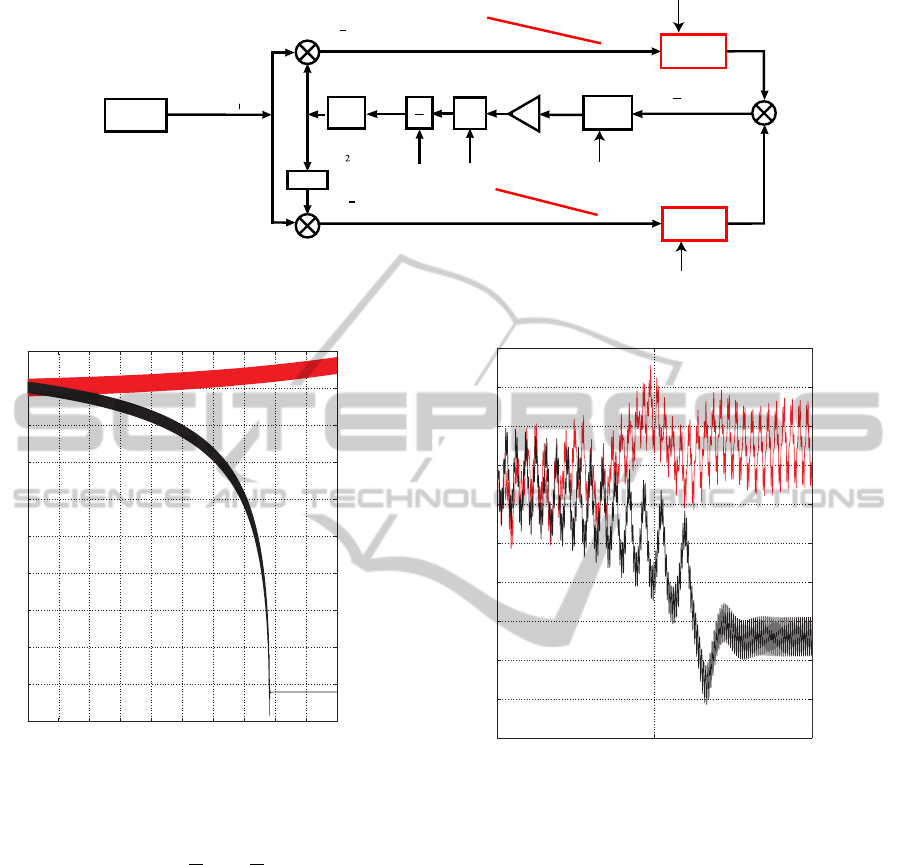
Figure 6: Loop filter output g(t) for averaged model (17)
(black) and physical model (red) in Fig. 2.
and corresponding differential equations (8) parame-
ters are A = 1, b = 0, c =
1
τ
1
, h =
τ
2
τ
1
; carrier frequency
is ω
1
= 2∗ π ∗ 400000 and initial carrier phase is zero:
θ
1
(0) = 0.
Example 1. In Fig. 6 is shown that Assumption 1 may
not be valid: while simplified mathematical model in
the signal’s phase space (17) (see Fig. 4) acquires
lock (black), physical model (14) (see Fig. 5) is out
of lock (red).
Here VCO free-running frequency: ω
f ree
2
=
3.5500 ∗ 10
6
; initial states of filters are all zero
α
0
(t) = x(0) = x
1
(0) = x
2
0 = 0.
Example 2. In Fig. 7 is shown that Assumption 2 may
not be valid: while simplified mathematical model in
the signal space (16) (see physical model in Fig. 5
with constant data signal m(t) ≡ 1) acquire lock
(black), physical model with periodic data signal (14)
0
-0.6
-0.4
-0.2
0
0.2
1 x10
-4
Figure 7: Loop filter output g(t) for physical model (black)
with periodic data signal, physical model (red) with con-
stant data signal m(t) ≡ 1.
(see Fig. 5) is out of lock (red).
Here VCO free-running frequency ω
f ree
2
=
3.0753 ∗ 10
6
, initial states of filters are all zero
α
0
(t) = x(0) = x
1
(0) = x
2
(0) = 0, data signal is pe-
riodic m(t) = sign sin(100000 ∗ 2 ∗ πt).
Example 3. In Fig. 8 is shown that low-pass filters
may affect stability of models in the signal’s phase
space: while simplified mathematical model the sig-
nals phase space (17) (see Fig. 4) is out of lock (red),
classical mathematical model the signals phase space
(11) (see Fig. 3), where low-pass filters are not taken
into account, acquires lock (black). Therefore the
consideration of classical (simplified) model in sig-
nal’s phase space (Fig. 3 and system (11)) may lead
to wrong conclusion.
Here VCO free-running frequency ω
f ree
2
=
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
708
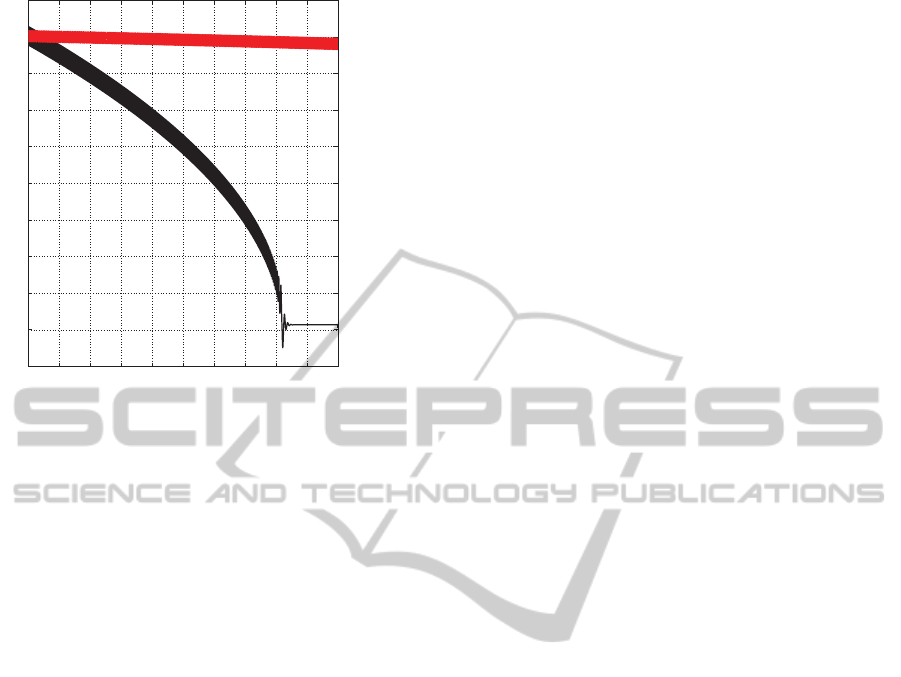
0
-0.9
-0.7
-0.5
-0.3
-0.1
0.1
1 2 3 4 x10
-3
Figure 8: Loop filter output g(t) for signal’s phase space
model (black curve) without low-pass filters, signal’s phase
space model (red curve) with low-pass filters.
3.5133 ∗ 10
6
, initial states of filters are zero: α
0
(t) =
x(0) = x
1
(0) = x
2
(0), no data is being transmitted
m(t) = 1.
5 CONCLUSION
In the work it is shown that 1) the consideration
of simplified mathematical models, constructed intu-
itively by engineers, and 2) the application of non rig-
orous methods of analysis can lead to wrong conclu-
sions concerning the operability of Costas loop.
ACKNOWLEDGEMENTS
This work was supported by Saint-Petersburg State
University (project 6.39.416.2014).
REFERENCES
Abramovitch, D. (1990). Lyapunov redesign of analog
phase-lock loops. Communications, IEEE Transac-
tions on, 38(12):2197–2202.
Abramovitch, D. (2008a). Efficient and flexible simula-
tion of phase locked loops, part I: simulator design.
In American Control Conference, pages 4672–4677,
Seattle, WA.
Abramovitch, D. (2008b). Efficient and flexible simulation
of phase locked loops, part II: post processing and a
design example. In American Control Conference,
pages 4678–4683, Seattle, WA.
Andrievsky, B. R., Kuznetsov, N. V., Leonov, G. A., and
Pogromsky, A. Y. (2013). Hidden oscillations in air-
craft flight control system with input saturation. IFAC
Proceedings Volumes (IFAC-PapersOnline), 5(1):75–
79.
Banerjee, T. and Sarkar, B. (2006). A new dynamic gain
control technique for speed enhancement of digital
phase locked loops (DPLLs). Signal Processing.,
86:1426–1434.
Best, R. E. (2007). Phase-Lock Loops: Design, Simulation
and Application. McGraw-Hill.
Best, R. E., Kuznetsov, N. V., Leonov, G. A., Yuldashev,
M. V., and Yuldashev, R. V. (2014a). Discontinuity
and Complexity in Nonlinear Physical Systems, vol-
ume 6, chapter Nonlinear analysis of phase-locked
loop based circuits. Springer.
Best, R. E., Kuznetsov, N. V., Leonov, G. A., Yuldashev,
M. V., and Yuldashev, R. V. (2014b). Simulation of
analog Costas loop circuits. International Journal of
Automation and Computing. accepted.
Bragin, V. O., Vagaitsev, V. I., Kuznetsov, N. V., and
Leonov, G. A. (2011). Algorithms for finding hid-
den oscillations in nonlinear systems. The Aizerman
and Kalman conjectures and Chua’s circuits. Jour-
nal of Computer and Systems Sciences International,
50(4):511–543.
Bueno, A., Ferreira, A., and Piqueira, J. (2010). Modeling
and filtering double-frequency jitter in one-way mas-
terslave chain networks. IEEE transactions on circuits
and systemsI, 57(12):3104–3111.
Chang, F.-J., Twu, S.-H., and Chang, S. (1993). Global
bifurcation and chaos from automatic gain control
loops. Circuits and Systems I: Fundamental Theory
and Applications, IEEE Transactions on, 40(6):403–
412.
Chicone, C. and Heitzman, M. (2013). Phase-locked
loops, demodulation, and averaging approximation
time-scale extensions. SIAM J. Applied Dynamical
Systems, 12(2):674–721.
Costas, J. (1956). Synchoronous communications. In Proc.
IRE, volume 44, pages 1713–1718.
Costas, J. P. (1962). Receiver for communication system.
US Patent 3,047,659.
Gardner, F. (1966). Phase–lock techniques. John Wiley,
New York.
Gardner, F. (2005). Phaselock Techniques. Wiley.
Goyal, P., Lai, X., and Roychowdhury, J. (2006). A fast
methodology for first-time-correct design of PLLs us-
ing nonlinear phase-domain VCO macromodels. In
Proceedings of the 2006 Asia and South Pacific De-
sign Automation Conference, pages 291–296.
Hedin, G., Holmes, J., Lindsey, W., and Woo, K. (1978).
Theory of false lock in costas loops. Communications,
IEEE Transactions on, 26(1):1–12.
Hinz, M., Konenkamp, I., and Horneber, E.-H. (2000).
Behavioral modeling and simulation of phase-locked
loops for RF front ends. In Proc. 43rd BEE Midwest
Symp. on Circuits and Systems, pages 194–197. IEEE.
Kaplan, E. and Hegarty, C. (2006). Understanding GPS:
Principles and Applications. Artech House.
NonlinearModelsofBPSKCostasLoop
709

Krylov, N. and Bogolyubov, N. (1947). Introduction to non-
linear mechanics. Princeton Univ. Press, Princeton.
Kudrewicz, J. and Wasowicz, S. (2007). Equations of
Phase-Locked Loops: Dynamics on the Circle, Torus
and Cylinder, volume 59. World Scientific.
Kuznetsov, N., Kuznetsova, O., Leonov, G., and Vagait-
sev, V. (2013). Informatics in Control, Automation
and Robotics, Lecture Notes in Electrical Engineer-
ing, Volume 174, Part 4, chapter Analytical-numerical
localization of hidden attractor in electrical Chua’s cir-
cuit, pages 149–158. Springer.
Kuznetsov, N. V. and Leonov, G. A. (2005). On stabil-
ity by the first approximation for discrete systems.
In 2005 International Conference on Physics and
Control, PhysCon 2005, volume Proceedings Volume
2005, pages 596–599. IEEE.
Kuznetsov, N. V., Leonov, G. A., and Seledzhi, S. M.
(2011). Hidden oscillations in nonlinear con-
trol systems. IFAC Proceedings Volumes (IFAC-
PapersOnline), 18(1):2506–2510.
Kuznetsov, N. V., Leonov, G. A., and Vagaitsev, V. I. (2010).
Analytical-numerical method for attractor localization
of generalized Chua’s system. IFAC Proceedings Vol-
umes (IFAC-PapersOnline), 4(1):29–33.
Leonov, G. A. and Kuznetsov, N. V. (2007). Time-varying
linearization and the Perron effects. International
Journal of Bifurcation and Chaos, 17(4):1079–1107.
Leonov, G. A. and Kuznetsov, N. V. (2013). Hidden attrac-
tors in dynamical systems. From hidden oscillations
in Hilbert-Kolmogorov, Aizerman, and Kalman prob-
lems to hidden chaotic attractors in Chua circuits. In-
ternational Journal of Bifurcation and Chaos, 23(1).
art. no. 1330002.
Leonov, G. A., Kuznetsov, N. V., Kiseleva, M. A.,
Solovyeva, E. P., and Zaretskiy, A. M. (2014). Hidden
oscillations in mathematical model of drilling system
actuated by induction motor with a wound rotor. Non-
linear Dynamics, 77(1-2):277–288.
Leonov, G. A., Kuznetsov, N. V., and Vagaitsev, V. I. (2012).
Hidden attractor in smooth Chua systems. Physica D:
Nonlinear Phenomena, 241(18):1482–1486.
Lindsey, W. (1972). Synchronization systems in communi-
cation and control. Prentice-Hall, New Jersey.
Margaris, W. (2004). Theory of the Non-Linear Analog
Phase Locked Loop. Springer Verlag, New Jersey.
Mitropolsky, Y. and Bogolubov, N. (1961). Asymptotic
Methods in the Theory of Non-Linear Oscillations.
Gordon and Breach, New York.
Olson, M. (1975). False-lock detection in costas demodula-
tors. Aerospace and Electronic Systems, IEEE Trans-
actions on, AES-11(2):180–182.
Piqueira, J. R. C. and Monteiro, L. H. A. (2003). Con-
sidering second-harmonic terms in the operation of
the phase detector for second-order phase-locked
loop. IEEE Transactions On Circuits And Systems–
I, 50(6):805–809.
Samoilenko, A. and Petryshyn, R. (2004). Multifrequency
Oscillations of Nonlinear Systems. Mathematics and
Its Applications. Springer.
Sanders, J. A., Verhulst, F., and Murdock, J. (2007). Av-
eraging Methods in Nonlinear Dynamical Systems.
Springer.
Sarkar, B. C., Sarkar, S. S. D., and Banerjee, T. (2014).
Nonlinear dynamics of a class of symmetric lock
range DPLLs with an additional derivative control.
Signal Processing, 94:631 – 641.
Shirahama, H., Fukushima, K., Yoshida, N., and Taniguchi,
K. (1998). Intermittent chaos in a mutually coupled
pll’s system. Circuits and Systems I: Fundamen-
tal Theory and Applications, IEEE Transactions on,
45(10):1114–1117.
Simon, M. K. (1978). The false lock performance of costas
loops with hard-limited in-phase channel. Communi-
cations, IEEE Transactions on, 26(1):23–34.
Stensby, J. (1997). Phase-Locked Loops: Theory and Ap-
plications. Phase-locked Loops: Theory and Applica-
tions. Taylor & Francis.
Stensby, J. (2011). An exact formula for the half-plane pull-
in range of a PLL. Journal of the Franklin Institute,
348(4):671–684.
Suarez, A., Fernandez, E., Ramirez, F., and Sancho, S.
(2012). Stability and bifurcation analysis of self-
oscillating quasi-periodic regimes. IEEE Transactions
on microwave theory and techniques, 60(3):528–541.
Suarez, A. and Quere, R. (2003). Stability Analysis of Non-
linear Microwave Circuits. Artech House.
Thede, L. (2005). Practical analog and digital filter design.
Artech House.
Tranter, W., Bose, T., and Thamvichai, R. (2010). Ba-
sic Simulation Models of Phase Tracking Devices Us-
ing MATLAB. Synthesis lectures on communications.
Morgan & Claypool.
Vendelin, G., Pavio, A., and Rohde, U. (2005). Microwave
Circuit Design Using Linear and Nonlinear Tech-
niques. Wiley.
Wang, T.-C., Chiou, T.-Y., and Lall, S. (2008). Nonlinear
phase-locked loop design using semidefinite program-
ming. In 16th Mediterranean Conference on Control
and Automation, pages 1640–1645. IEEE.
Watada, K., Endo, T., and Seishi, H. (1998). Shilnikov
orbits in an autonomous third-order chaotic phase-
locked loop. IEEE transactions on circuits and
systems–I, 45(9):979–983.
Wiegand, C., Hedayat, C., and Hilleringmann, U. (2010).
Non-linear behaviour of charge-pump phase-locked
loops. Advances in Radio Science, 8:161–166.
Wu, N. (2002). Analog phaselock loop design using Popov
critereon. In Proceedings of the 2002 American Con-
trol Conference, volume 1, pages 16–18. IEEE.
Yoshimura, T., Iwade, S., Makino, H., and Matsuda, Y.
(2013). Analysis of pull-in range limit by charge
pump mismatch in a linear phase-locked loop. Cir-
cuits and Systems I: Regular Papers, IEEE Transac-
tions on, 60(4):896–907.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
710
